Badania

operacyjne

(#6)

dr inż. Marek Rabiński

Wyższa Szkoła Działalności Gospodarczej

2

Badania operacyjne (część 6)



Teoria gier



Pojęcia podstawowe



Historia teorii gier



Modele gier



Równowaga Nasha



Prezentacja różnych gier

3

Pojęcia podstawowe



Działanie (ang: course of action) – zmiana, transformacja stanu
systemu lub aktywność systemu podporządkowana osiągnięciu
celu, dążenie do osiągnięcia konkretnego rezultatu. Skutkiem
działania są wywołane przez nie zmiany stanów systemu.
Działanie może być świadome lub nieświadome, konstruktywne
lub destrukcyjne. Możliwość przewidzenia skutków działania
pozwala wybrać takie alternatywy działań, które spełnią zadane
kryteria, np. minimalizują jakiś wskaźnik jakości lub zwiększają
skuteczność w sensie prakseologicznym.
W miarę pojawiania się w działaniu coraz większej liczby
elementów nowatorskich, niepowtarzalnych – staje się ono coraz
bardziej twórczym i w niektórych dziedzinach nazywane bywa
twórczością. Poczynając od rzemiosła artystycznego, poprzez
projektowanie, komponowanie – działanie coraz bardziej twórcze.

4

Pojęcia podstawowe



Decyzja (ang: decision) – nielosowy wybór konkretnego wariantu

działania lub podzbioru ich alternatyw, świadome rozstrzygnięcie

w sytuacji wyboru między różnymi możliwościami działania.

Podjęta decyzja w istotny sposób wpływa na dalsze zachowanie

systemu – zmienia lub transformuje jego przyszłe stany. Wyboru

wariantu dokonuje się na podstawie kryterium decyzyjnego wśród

znanych i możliwych do osiągnięcia celów lub sposobów działania.
Przykład alternatywnych sposobów podzielenia pomarańczy – na

ćwiartki, cząstki równolegle do osi lub prostopadle (plasterki).

Wybór najwłaściwszego zależy od postawionego przed działaniem

celu.
Przykład: decyzje związane z kierowaniem statkiem polegają na

dokonywaniu wyborów spośród repertuaru możliwych położeń

steru (kąta jego wychylenia i momentu zmiany kursu) oraz

następujących stanów silnika – cała naprzód, powoli naprzód,

maszyny stop, powoli wstecz, cała wstecz.

5

Pojęcia podstawowe



Decydent (ang: decision maker) – osoba lub instytucja
podejmująca decyzję.



Kryterium decyzyjne (ang: criterion) – zdefiniowany przez
decydenta wskaźnik, pozwalający ocenić rozważane warianty pod
względem spełniania określonych celów.



Strategia (ang: strategy) – zasada nakazująca w sytuacji
podejmowania decyzji podjęcie określonego działania ze zbioru
dostępnych działań alternatywnych, przyporządkowująca
wystąpieniu konkretnej sytuacji podjęcie określonych działań.
Wybór strategii zależy od zasobu informacji posiadanych w chwili
podejmowania decyzji. Np. strategia marketingu – sposób
prowadzenia działań na rynku, mający na celu zachęcenie do
nabywania towaru.
Określenie ‘strategia' pierwotnie było związane ze sztuką
dowodzenia.

6

Pojęcia podstawowe



Walka, konflikt (ang: conflict) – świadome działania co najmniej
dwóch różnych podmiotów, dążących do niezgodnych ze sobą
celów, usiłujących przeszkadzać sobie nawzajem w realizacji
swoich celów. Pojęcie walki uogólnia wszelkie przypadki działań
przeszkadzających (utrudniających) innym w ich dążeniach, jest
też uniezależnione od specyficznych cech walki zbrojnej jako takiej.
Obejmuje nie tylko przypadki działań militarnych ale także
rywalizację gatunków, wszelkiego rodzaju współzawodnictwo,
konkurencję handlową, debaty parlamentarne, spory prawne,
dyskusje, starania o rękę lub względy wybranki, grę w szachy,
zawody sportowe. Działania walki mogą obejmować fizyczne
zniszczenie drugiej jednostki, fizyczne lub psychiczne
obezwładnienie, podporządkowanie sobie, pozbawienie narzędzi
działania, dostępu do określonych miejsc w przestrzeni lub
zasobów (między innymi informacji), możliwości wykonywania
skutecznych działań przez stronę przeciwną.

7

Pojęcia podstawowe



Teoria gier (ang: game theory) – matematyczna metoda
analizy zachowań racjonalnych przez niezależnego decydenta,
w sytuacjach gdy najlepsza strategia uczestnika zależy od
przewidywań posunięć przeciwnika. Badania zachowań
racjonalnych w sytuacjach gdy wybór decydenta wpływa na
innych a wybory dokonywane przez innych wpływają na niego.

8

Historia teorii gier



I–VI wiek – wykształcenie się formy Talmudu babilońskiego ze zbiorem

utrwalonych tradycją rozwiązań prawa karnego, cywilnego oraz norm

życia społecznego. Jednym z omawianych zagadnień był następujący

problem kontraktu małżeńskiego. Mężczyzna ma trzy żony, których

kontrakty małżeńskie gwarantują w przypadku jego śmierci

odpowiednio 100, 200 i 300 jednostek pieniężnych. Jeśli mąż umiera

pozostawiając majątek w wysokości 100 jednostek – Talmud poleca

równy podział majątku między wdowy, jeśli wynosi on 300 – podział

proporcjonalny 50, 100 i 150. Natomiast w przypadku 200 – podział 50,

75 i 75. W 1985 roku odkryto, że sugerowane proporcje wynikają z

rozwiązania zagadnienia zgodne z teorią gier kooperacyjnych.



1713 – James Waldegrave podaje rozwiązanie mieszanej strategii

minimaksu dla dwuosobowej gry w karty.



1838 – Augustin Cournot opisuje w jednym z rozdziałów swojej książki

przypadek konkurencji producentów duopolu, wykorzystując koncepcję

nazwaną później równowagą Nasha.



1881 – Francis Ysidro Edgeworth przedstawia esej na temat krzywej

rozwiązania zagadnienia handlu między poszczególnymi osobami.

9

Historia teorii gier



1925 – polski matematyk Hugo Dionizy Steinhaus publikuje po

niemiecku pierwsze prace z teorii gier.



1928 – John von Neumann przeprowadza dowód zagadnienia minimax w

artykule „Zur Theorie der Gesellschaftsspiele”. Zgodnie z nim każda

dwuosobowa gra o sumie zerowej ze skończoną liczbą czystych strategii

dla każdego gracza jest zdeterminowana, to znaczy po dopuszczeniu

strategii mieszanych cała różnorodność gry ma dokładnie jeden wektor

indywidualnie racjonalnych wypłat.



1944 – wydanie książki „Teoria gier i zachowań ekonomicznych” (Theory

of Games and Economic Behavior) przez Johna von Neumanna i Oskara

Morgensterna. Książka zostaje uznana za punkt zwrotny rozwoju teorii

gier.



1950 – Melvin Dresher i Merrill Flood z Rand Corporation przedstawiają

modelową sytuację znaną w teorii gier jako ‘dylemat więźnia’.



1981 – R. J. Aumann wprowadza koncepcję gier powtarzalnych,

rozgrywanych przez automat.



1982 – publikacja „Evolution and the Theory of Games” Johna Maynarda

Smitha.

10

Hugo Dionizy Steinhaus (1887–
1972)



Polski matematyk ze Szkoły Lwowsko–
Warszawskiej.
Znany z niezwykle ciętych określeń i
specyficznego humoru.

11

John von Neumann (1903–
1957)



Amerykański matematyk
pochodzenia węgierskiego,
uznawany za ojca informatyki i
techniki komputerowej.
Współautor „Theory of Games and
Economic Behavior” (1944).

12

Oskar Morgenstern (1902–
1976)



Amerykański matematyk pochodzenia
austriackiego (urodzony w Zgorzelcu).
Współautor „Theory of Games and
Economic Behavior” (1944).

13

John Forbes Nash, jr. (1928–)



Matematyk amerykański, twórca
podstaw teorii gier
ekonomicznych.
Od 1958 roku popadł w
schizofrenię maniakalną. Zaczął z
niej wychodzić dopiero w latach
1990-tych. Na jego biografii oparto
film „Piękny umysł”.
1994 rok – laureat nagrody Nobla
w dziedzinie ekonomii.

14

Zasada minimaks



Metoda rozwiązywania zagadnień decyzyjnych polegająca na
minimalizowaniu maksymalnych możliwych strat. Zainicjowana
została dla gier dwuosobowych o sumie zero, obejmując
przypadki gdy obaj gracze podejmują na przemian decyzje lub
jednocześnie. Obecnie teoria obejmuje również zagadnienia z
niepełną informacją.

15

Modele gier



Normalna postać gry w formie ustalonej listy graczy, zbioru
strategii każdego gracza i macierzy wygranych. O decyzji
przeciwnika gracz jest informowany po podjęciu przez siebie
swojej decyzji.



Ekstensywna (rozwinięta) forma zapisu gry, w formie drzewa
decyzyjnego – spójnego grafu z wyróżnionym wierzchołkiem
początku.



Diagramy przepływu do przedstawienia skomplikowanych gier
wieloosobowych.

16

Racjonalność i strategia
dominująca



Racjonalność wymaga wybierania strategii dominującej, bez
względu na to, czy pozostali są racjonalni.



Racjonalność i strategie dominujące wyznaczają równowagę
Nasha.



Nie jest wymagana wiedza o poczynaniach przeciwnika ani
prawidłowe przekonania co do oceny sytuacji.

17

Równowaga Nasha



Równowaga Nasha jest profilem strategii dla każdego z graczy, w
której każda jest najlepszą odpowiedzią na jakąkolwiek inną
strategię rozgrywania gry przez przeciwnika (nie istnieje
jakakolwiek inna strategia, której wykorzystanie mogłoby
doprowadzić do wyższych wypłat, w każdej sytuacji
zastosowania przez przeciwnika jakiejkolwiek innej strategii).



Jest zbiorem takich strategii (po jednej dla każdego gracza), że
żaden z graczy nie jest w stanie osiągnąć zysku na jednostronnej
zmianie swojej strategii dopóki pozostali pozostają przy
strategiach równowagi. Dla szerokiego zakresu gier równowaga
zawsze istnieje.



Koncepcja równowagi Nasha jest zbiorem strategii, które są
najlepszymi odpowiedziami na strategie przeciwników –
uwzględnia więc ich działania (w odróżnieniu od strategii
dominującej).

18

Równowaga Nasha



Gry o sumie niezerowej są związane z konfliktem interesów graczy.



Niekooperacyjne gry polegają na braku współpracy graczy.



Każda gra macierzowa ma rozwiązanie w strategiach mieszanych.



Równowaga punktu siodłowego gry dwuosobowej o sumie stałej –
optymalne strategie prowadzące do punktu siodłowego są dla
każdego z graczy optymalne. Odejście od tej optymalnej strategii
może tylko pogorszyć wynik gracza.



Wyznaczanie strategii mieszanych następuje na drodze
rozwiązania odpowiednio sformułowanego zagadnienia
programowania liniowego.



Podstawa równowagi Nasha żartobliwie bywa określana jako –
„myślę, że przeciwnik zrobi ruch X, ponieważ myśli, że zrobię Y,
więc powinienem zrobić ruch Z.”

19

Równowaga Nasha

Pierwszy gracz
A

B

C

Drugi
gracz

D

3, 1

2, 3

10, 2

E

4, 5

3, 0

6, 4

F

2, 2

5, 4

12, 3

G

6, 6

4, 5

9, 7

20

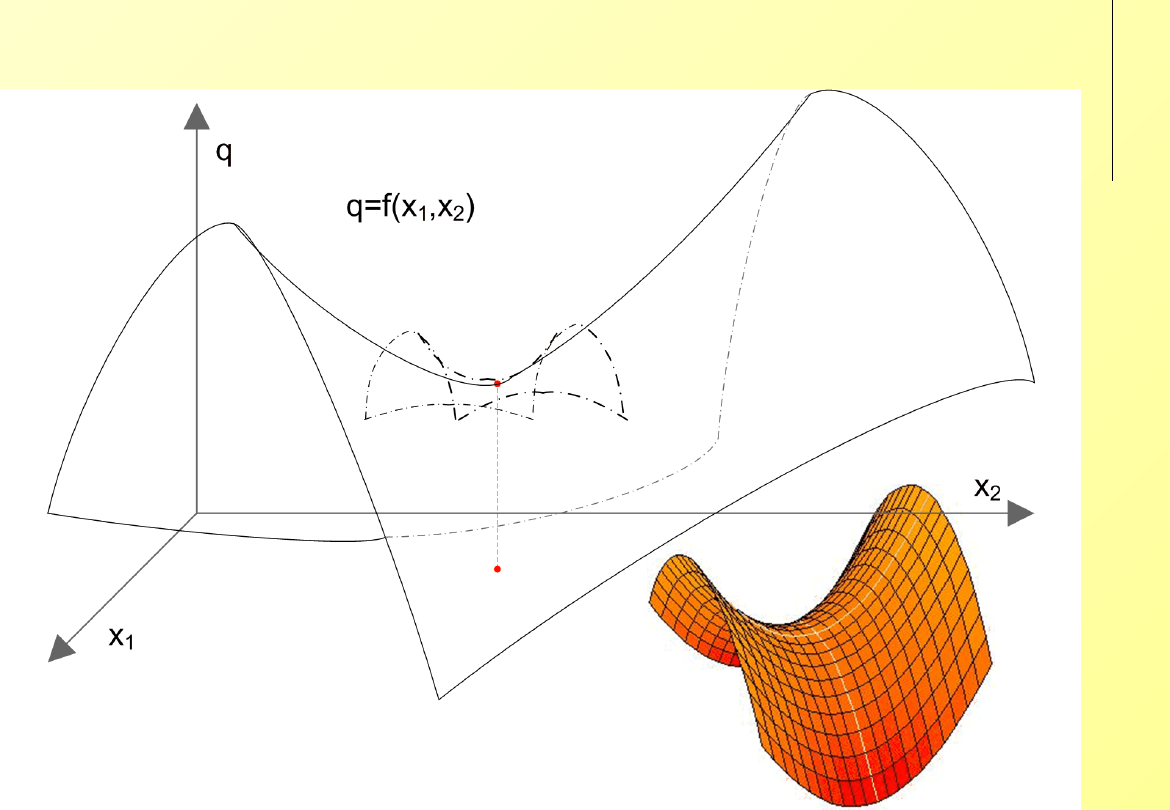
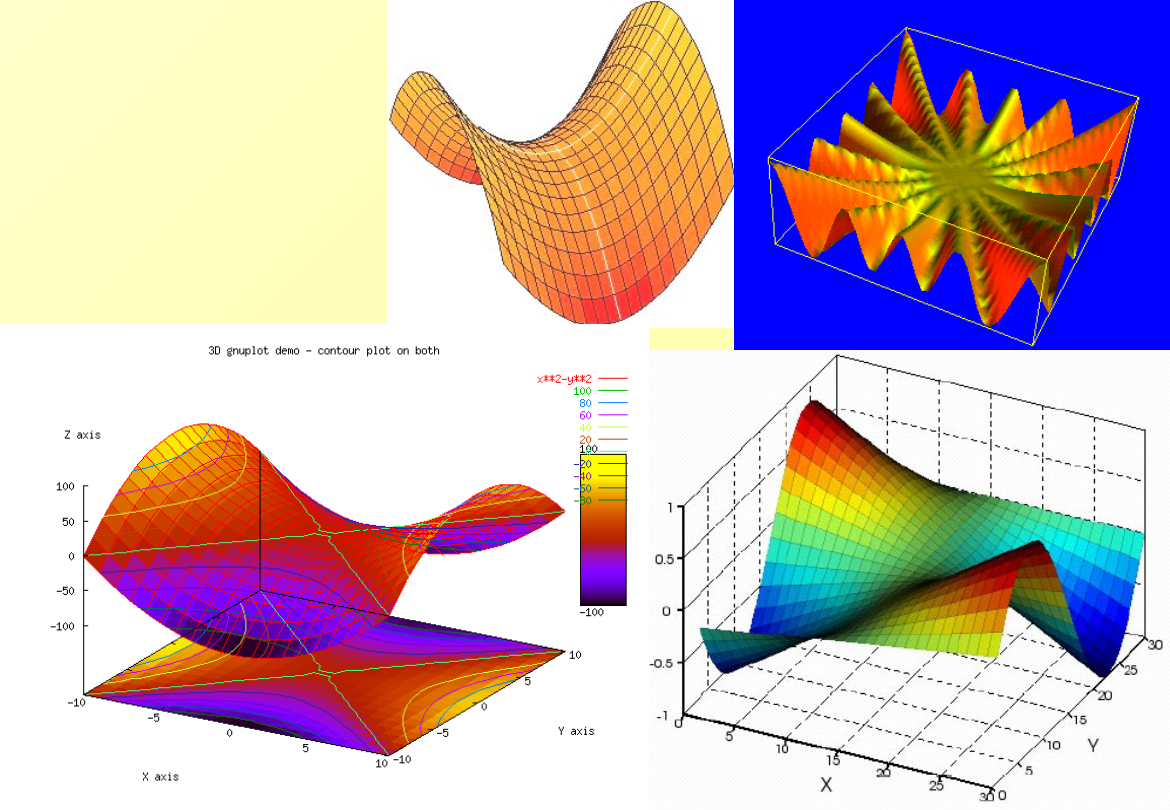
Paraboloida hiperboliczna

21

Paraboloida hiperboliczna



Punkt siodłowy

22

Gry
symetryczne/asymetryczne



Gry symetryczne (wypłaty dla konkretnego gracza zależą od
zastosowanych przez drugą stronę strategii, a nie od tego
przez kogo są rozgrywane)



‘Dylemat więźnia’



‘Cykor’



‘Walka płci’



‘Polowanie na jelenia’



Gry asymetryczne (strategie dla graczy są różne lub pomimo
identycznych strategii wypłaty powodują asymetrię), o
asymetryczności może przesądzać rodzaj sytuacji generowanej
przez zasady gry i/lub kolejność podejmowania decyzji



Gra w ultimatum



Gra w dyktatora

23

Gry z naturą



Przeciwnik (natura) nie stosuje złośliwych strategii
wymierzonych w grającego. W naturze np. deszcz pada z
pewnym prawdopodobieństwem a nie dlatego by zniweczyć
wysiłek zasiania plonów przez rolnika (przeciwnika natury w tej
grze).

24

Gry o sumie
zerowej/niezerowej



Gry o sumie zerowej (wypłata jednego gracza jest stratą
drugiego/drugich)



Poker



Gra w ultimatum



Pasujące monety



Go



Szachy



Gry o sumie niezerowej



Dylemat więźnia

25

Gry jednoczesne/sekwencyjne



Gry jednoczesne (obaj gracze wykonują swój ruch jednocześnie
lub wykonujący ruch jako drugi nie uwzględnia posunięcia
poprzedniego gracza)



Gry sekwencyjne/dynamiczne (gracz posiada pewną wiedzę,
choć nie zawsze pełną, o poprzednim posunięciu przeciwnika)



Gra w ultimatum (pełna wiedza)



‘Stonoga’ (pełna wiedza)

26

Dylemat więźnia



Żadna kolumna ani wiersz nie dominują nad pozostałymi –
rozwiązanie może istnieć tylko w strategiach mieszanych.
Temptation(pokusa)
>Reward(nagroda)>Punishment(kara)>Sucker(frajer),
T>R>P>=S lub T>=R>P>S

‘Dylemat więźnia’

Pierwszy więzień
współpraca odmowa

Drugi
więzień

współpraca R, R

-2, -2

T, S
0, -10

odmowa

S, T
-10, 0

P, P
-0.5, -0.5

27

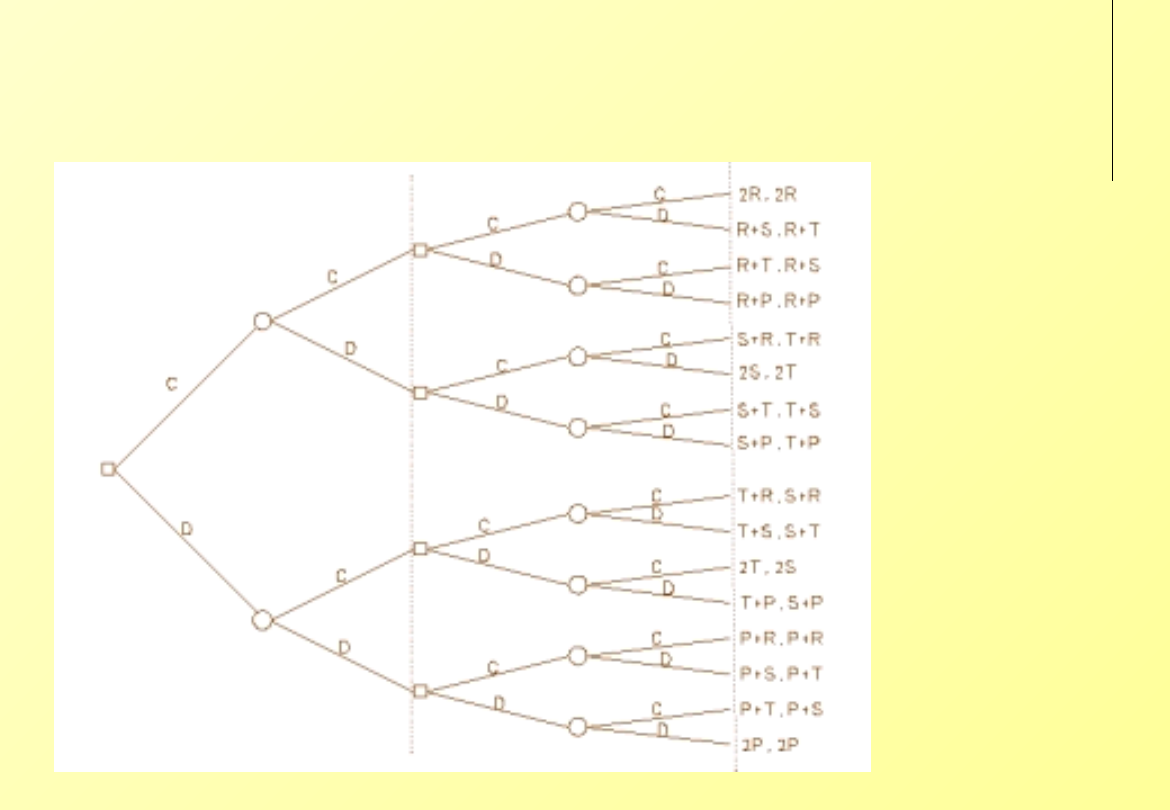
Dylemat więźnia
(sekwencyjny)



T+S<2R

28

Warianty ‘dylematu więźnia’



Wyścig zbrojeń – zimna wojna w latach 1950–1980



Wymiana typu ‘kot w worku’ (obie strony wymieniają się
nieprzezroczystymi torbami; zakładając, że w jednej są
pieniądze a w drugiej towar)



Podkładanie sobie agentów szpiegowskich przez hackerów
komputerowych



Dylemat rowerzystów z peletonu



Beczka z wódką przynoszoną przez gości na wesele

29

Rywalizacja koncernów
tytoniowych



Gracze: firmy Reynolds i Philip Morris



Strategie: reklamować papierosy, nie reklamować



Wygrane: dochody firm (w milionach dolarów)



Każda z firm zarabiała 50 mln USD



Reklama każdej firmy kosztowała 20 mln USD



Reklama pozwalała przechwycić 30 mln USD od konkurenta

Reynolds
reklamowa
ć

bez reklam

Philip
Morris

reklamowa
ć

30, 30

20, 60

bez reklam 60, 20

50, 50

30

Rywalizacja koncernów
tytoniowych



W 1964 roku naczelny lekarz USA wydał oficjalne ostrzeżenie o ryzyku

palenia, pojawiło się realne zagrożenie prawną odpowiedzialnością

firm.



1970 rok – porozumienie firm o wprowadzeniu napisów ostrzegawczych

na pudełkach i ograniczeniu reklam telewizyjnych. Tym samym

pozostało jedynie rozwiązanie o wygranych (50, 50) – znacznie

korzystniejsze dla firm niż ‘dylemat więźnia’ w warunkach rywalizacji.



Po wprowadzeniu w 1970 roku zakazu reklamy wydatki firm na

ogłoszenia spadły o 63 mln USD a ich zyski wzrosły o 91 mln USD.



Rezultat: wprowadzenie napisów ostrzegających o szkodliwości palenia

i zakaz reklamy papierosów doprowadziły do znacznego wzrostu

zysków koncernów tytoniowych.



Analogiczna sytuacja: w 1637 roku japońscy władcy uzgodnili zakaz

używania w walkach między sobą europejskiej broni palnej (obowiązywał

ponad 200 lat).

31

Reklama – ‘dylemat więźnia’



Rywalizacja dwóch sieci telekomunikacyjnych Telstra i Optus



Silna reklama obu firm prowadzi do uzyskania dochodów rzędu 70 mln
USD (Telstra) i 50 mln USD (Optus).



Silna reklama jednaj z firm przy średniej reklamie drugiej prowadzi do
podziału dochodów 140 mln USD (silniej reklamowany) do 25 mln
USD.



Średni poziom reklamy obu prowadzi do dochodów 120 mln USD
(Telstra) / 90 mln USD (Optus).

Telstra
Silna
reklama

Średni poziom
reklamy

Optus Silna reklama

70, 50

140, 25

Średni poziom
reklamy

25, 140

120, 90

32

Warianty ‘dylematu więźnia’



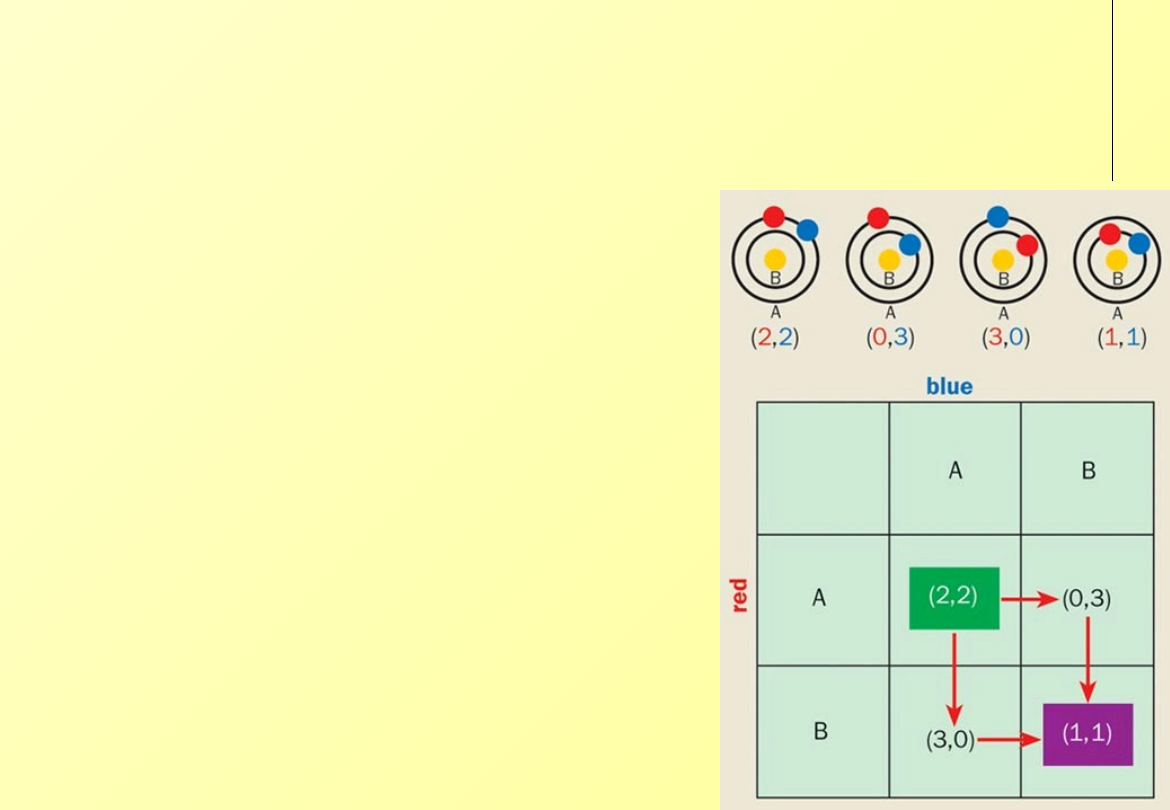
Dwa elektrony starają się osiągnąć
stan minimalizujący ich energię. Każdy
elektron stara się zająć miejsce jak
najbliżej jądra, ale jednocześnie nie
chce doświadczać elektrostatycznego
odpychania od jednoimiennie
naładowanego drugiego elektronu.
Kompromisowym rozwiązaniem
okazuje się wspólne zajęcie orbity
dalszej od jądra atomu, na której
przyciąganie od jądra jest mniejsze ale
także mniejsze jest odpychanie od
drugiego elektronu.

33

Propozycja Warrena Buffetta

(2000 r.)



Ekscentryczny miliarder przedstawia następującą propozycję:



Jeśli ustawa zostanie odrzucona – partia, której większa liczba

posłów głosowała za jej przyjęciem otrzyma miliard dolarów.



Jest jeden demokrata i jeden republikanin zainteresowani

przejściem ustawy.



Zyski partii z wyniku głosowania:

Demokraci

nie

tak

Republikani
e

nie

0, 0

- , +

tak

+, -

-, -

34

‘Dylemat uczestników kolacji’



Ang: diners dilemma – wieloosobowa gra typu ‘dylematu więźnia’



Grupa osób idzie do restauracji, obowiązuje zasada podziału

rachunku na równe części. Każda z osób może wybrać tanie danie,

oszczędzając (na korzyść innych) na wysokości rachunku lub wybrać

drogie danie, za które zapłacą inni oszczędni.



g oznacza przyjemność ze zjedzenia drogiego dania, b radość z

zamówienia taniego, h jest kosztem drogiego dania, l kosztem

taniego, n liczbą gości. Zachodzi nierówność h>g>b>l. Każdy z

uczestników stara się zamówić drogie danie na kosz innych
g – (1/n)*h > b – (1/n)*l



Strategie pozostałych graczy wynikają z ceny x dań pozostałych

graczy. Koszt zamówienia taniego dania wynosi (1/n)*x + (1/n)*l a

drogiego odpowiednio (1/n)*x + (1/n)*h. Zadowolenie z drogiego

dania wynosi g – (1/n)*x – (1/n)*h a z taniego b – (1/n)*x – (1/n)*l.

Wybór drogiego dania jest oczywisty. Jeśli wszyscy zamówią drogie

danie każdy zapłaci h i uzyska zadowolenie g – h > 0. Gdyby wszyscy

wybrali najtańsze byłoby to b – l > 0. Sytuacja wyboru jest

analogiczna do dylematu więźnia.



Analogiczna sytuacja – wspólny licznik gazu w dużym budynku.

35

‘Wspólne pastwisko’



Każdy z m wypasających owce na wspólnym pastwisku stara
się zwiększyć zysk zwiększając swoje stado. Powoduje to
zmniejszanie ilości paszy.



Jeśli s jest średnią liczebnością stada nie powodującą
degradacji pastwiska a N całkowitą liczbą owiec to N=ms.
Wartość zysku z pojedynczej sztuki w takiej sytuacji jest 1,
strata z dodania nowej sztuki wynosi b, x jest liczbą dodanych
sztuk, spadek zysku każdej sztuki z nadmiernej ilości owiec
wynosi 1-bx, całkowita wartość stada wynosi (N+x)(1-bx). Jeśli
b>1/N dochodzi do załamania dochodów wywołanego
nadmierną eksploatacją pastwiska.



Gra rozgrywa się między konkretnym pastuchem a resztą
wypasających swoje stada.

36

‘Wspólne pastwisko’



W rezultacie takiego postawienia zagadnienia każdy dodaje
kolejne owce do swojego stada, powodując katastrofalny
spadek dochodów na skutek nadmiernego wyeksploatowania
pastwiska (wspólnych zasobów).



Model nastawienia każdej jednostki w komunizmie (nakraść
wspólnego dobra by nie dać się przegonić pozostałym w ilości
łupów).

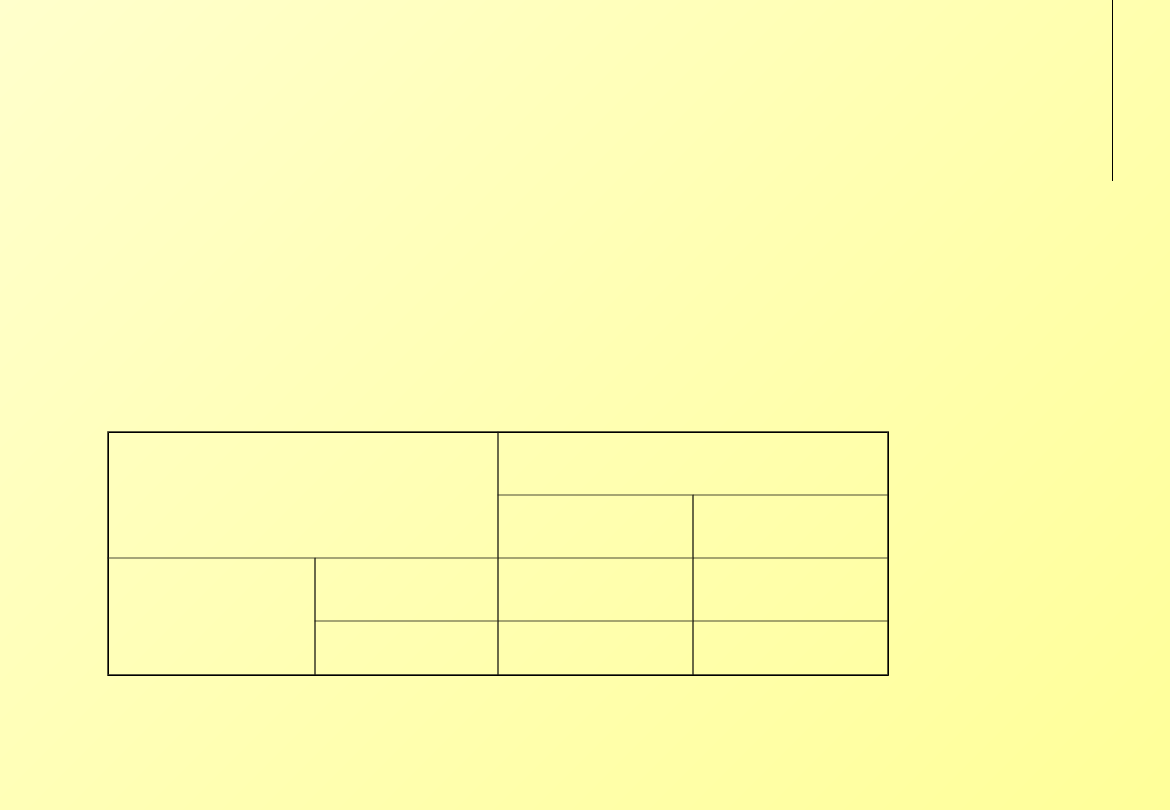
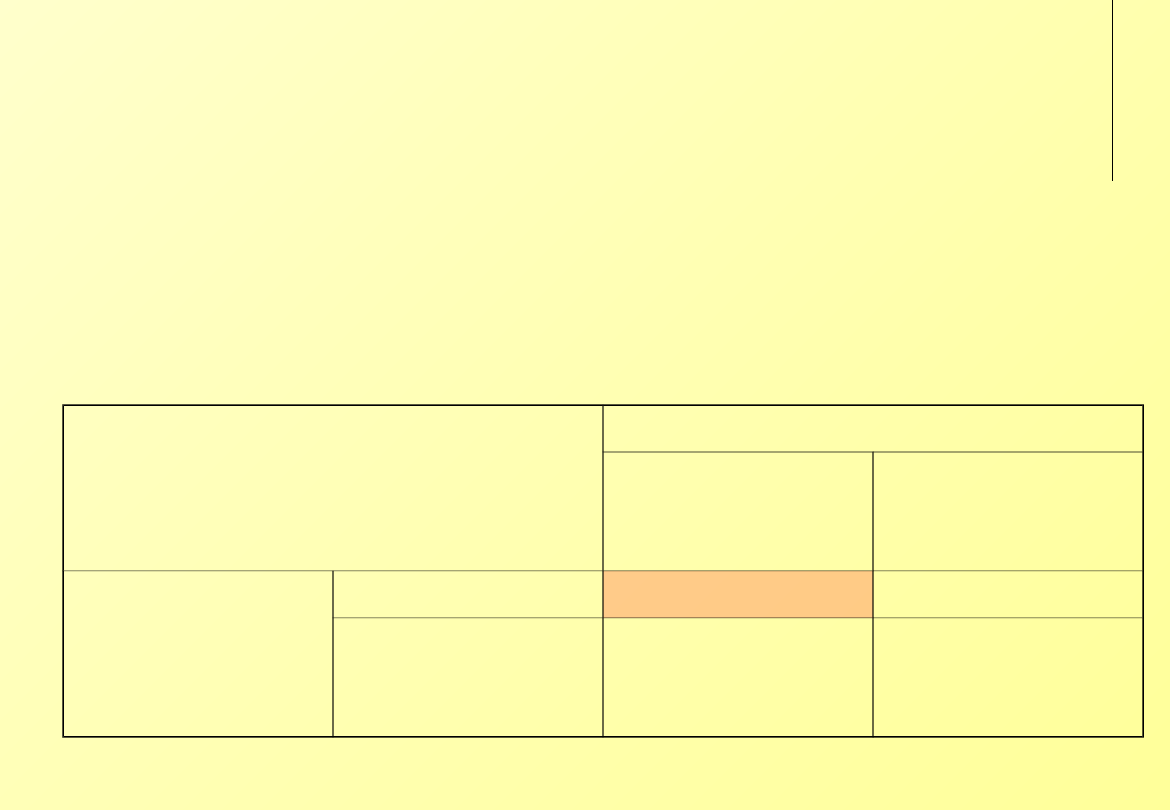
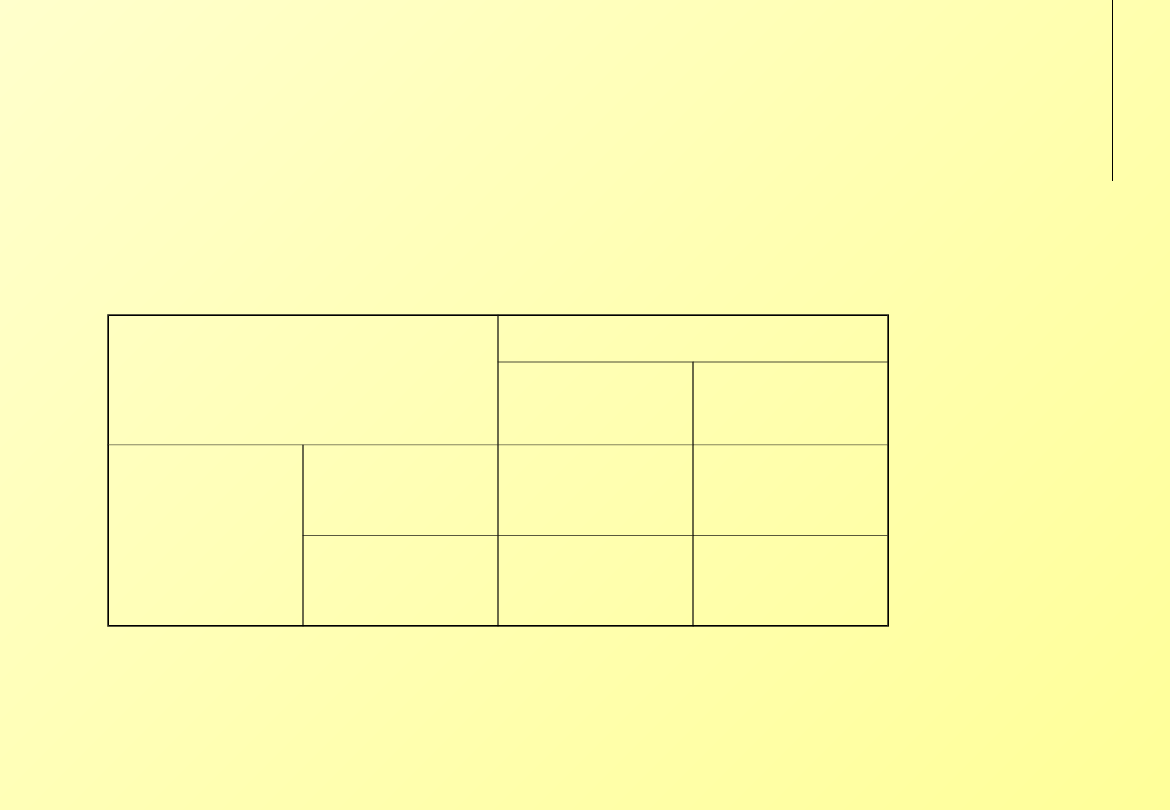
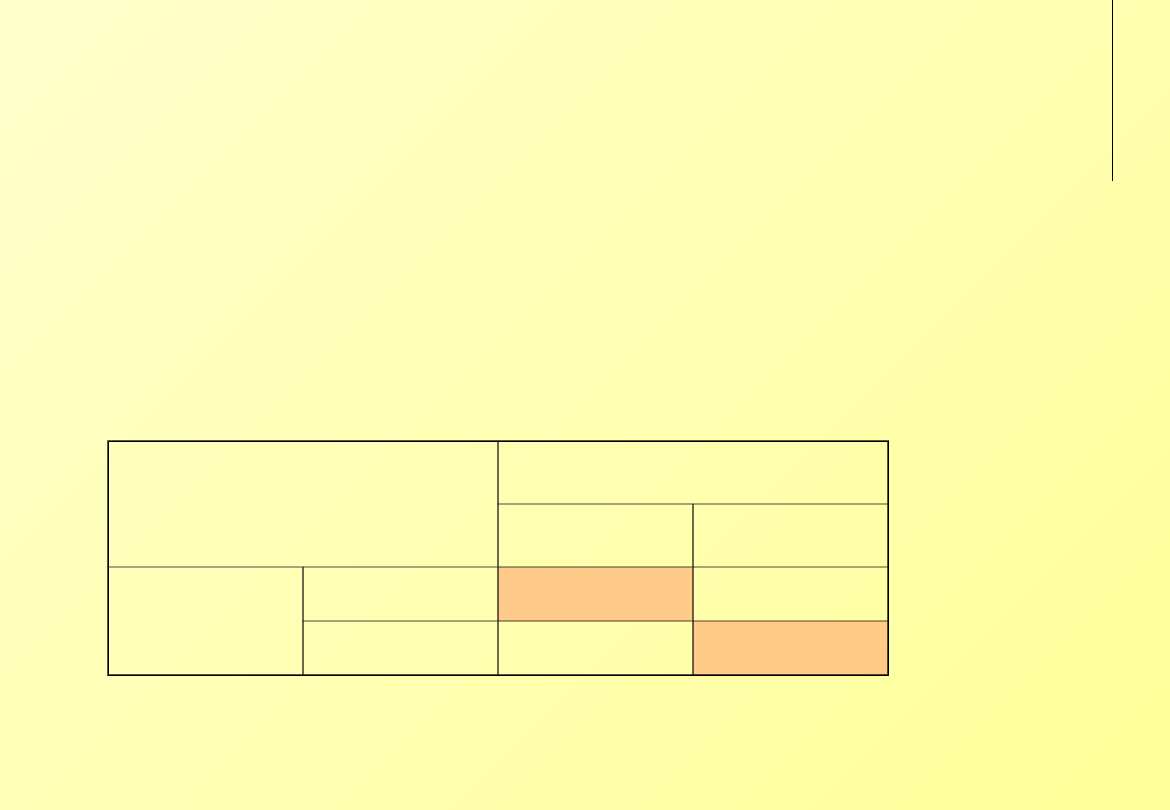
Macierz wygranych
pojedynczego właściciela
stada

Reszta właścicieli stad
dodaje owcę

utrzymuje
liczebność stad

Pojedynczy
właściciel
stada

dodanie owcy

(s+1)(1-bm)

(s+1)(1-b)

utrzymanie
liczebności
stada

s[1-b(m-1)]

s

37

Zależności macierzy wypłat



‘Dylemat więźnia’ – T>R>P>S



‘Cykor’ – T>R>S>P



‘Gra w bohatera’ – S>T>R>P



‘Gra w lidera’ (w tym ‘walka płci’) – T>S>R>P



‘Polowanie na jelenia’ – R>T>P>S



Temptation (pokusa)



Reward (nagroda)



Punishment (kara)



Sucker (frajer)

38

‘Cykor’ (jastrząb i gołąb)



Dylemat więźnia – T>R>P>S



‘Cykor’ – T>R>S>P (obopólna konfrontacja jest gorsza niż

utrata twarzy – uznanie za tchórza)

‘Cykor’

Pierwszy gracz
unik

konfrontacj
a

Drugi
gracz

unik

R, R
0, 0

S, T
-1, 1

konfrontacj
a

T, S
1, -1

P, P
-20, -20

39

‘Cykor’ (jastrząb i gołąb)



Ang: chicken, nuclear chicken, hawk-dove.



T>R>S>P (obopólna konfrontacja jest znacznie gorsza niż
utrata twarzy – uznanie za tchórza)



Zalety uniku są tak oczywiste, że w praktyce by uniknąć
liczenia przez przeciwnika na wykonanie uniku należy blefować
postawę gotowego na wszystko szaleńca. Tylko taka postawa
może zmusić drugą stronę do poważnego wzięcia pod uwagę
konieczności wykonania uniku.



W praktyce odpowiednią strategią jest blefowanie postawy
nieprzewidywalnego ryzykanta.

40

Kryzys kubański



Stan zagrożenia konfliktem między ZSRR a USA (dwoma
supermocarstwami dysponującymi ogromnymi arsenałami broni
jądrowej i środkami jej przenoszenia), który mógł się przekształcić
w wojnę globalną (III wojnę światową). Był wywołany
rozmieszczeniem na Kubie przez ZSRR rakiet średniego zasięgu i
dostawami kolejnych na statkach morskich.



Prawdopodobieństwo wybuchu wojny jądrowej w dniach 15–28
października 1962 roku osiągało według J.F.Kennedy’ego poziom
1/3 – 1/2.



Kryzys zakończył się zawróceniem przez sekretarza generalnego
KC KPZR Nikitę Chruszczowa statków w zamian za gwarancje
nieagresji na Kubę i wycofanie amerykańskich rakiet z terytorium
Turcji.



Ogromną rolę w podejmowaniu decyzji odegrał sekretarz obrony
Robert McNamara – prekursor wprowadzania badań operacyjnych.

41

Kryzys kubański



Możliwości działań USA



Blokada morska, zapobiegająca instalacji nowych wyrzutni,

połączona z silnymi naciskami na ZSRR by zdemontować istniejące

rakiety



Chirurgiczne uderzenia lotnictwa na zainstalowane wyrzutnie

radzieckich rakiet z głowicami jądrowymi, połączone ewentualnie z

inwazją na Kubę.



Możliwości działań ZSRR



Wycofanie rakiet z Kuby



Utrzymanie wyrzutni pocisków jądrowych.

Kryzys kubański

ZSRR (Nikita Chruszczow)

wycofanie

utrzymanie

USA
(John
Kennedy)

blokada

Kompromis
3, 3

Wygrana ZSRR
2, 4

uderzenie
lotnictwa

Wygrana USA
4, 2

Wojna jądrowa
1, 1

42

‘Walka płci’



Oboje preferują wspólne spędzenie czasu pomimo skrajnie
różnych gustów.



Dwie równowagi czystych strategii Nasha – razem do opery lub

razem na mecz, przypadkowy wybór wariantu przez rzut

monetą.



Dwa punkty równowagi dla strategii mieszanych gdy każda ze

stron uczęszcza na ulubione przez przedstawienie z

prawdopodobieństwem 2/3.

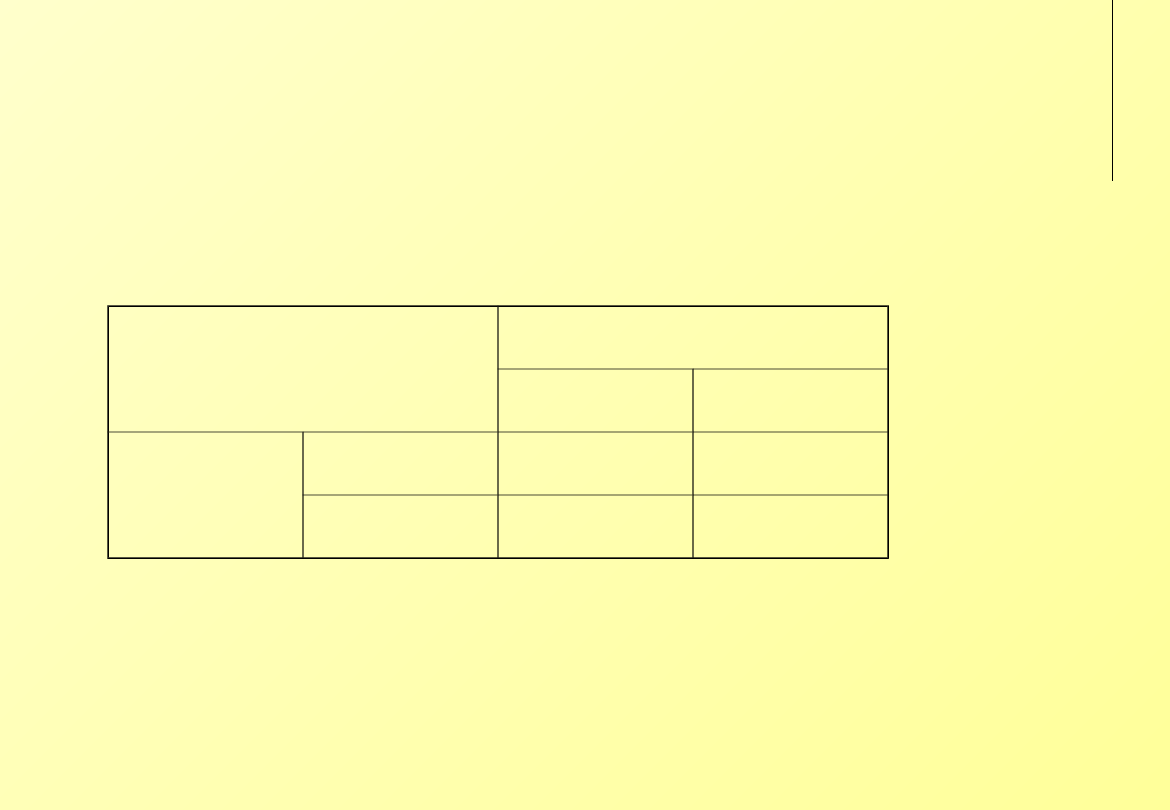
‘Walka płci’

Ona

opera

mecz

On

opera

2, 1

-1, -1

mecz

-1, -1

1, 2

43

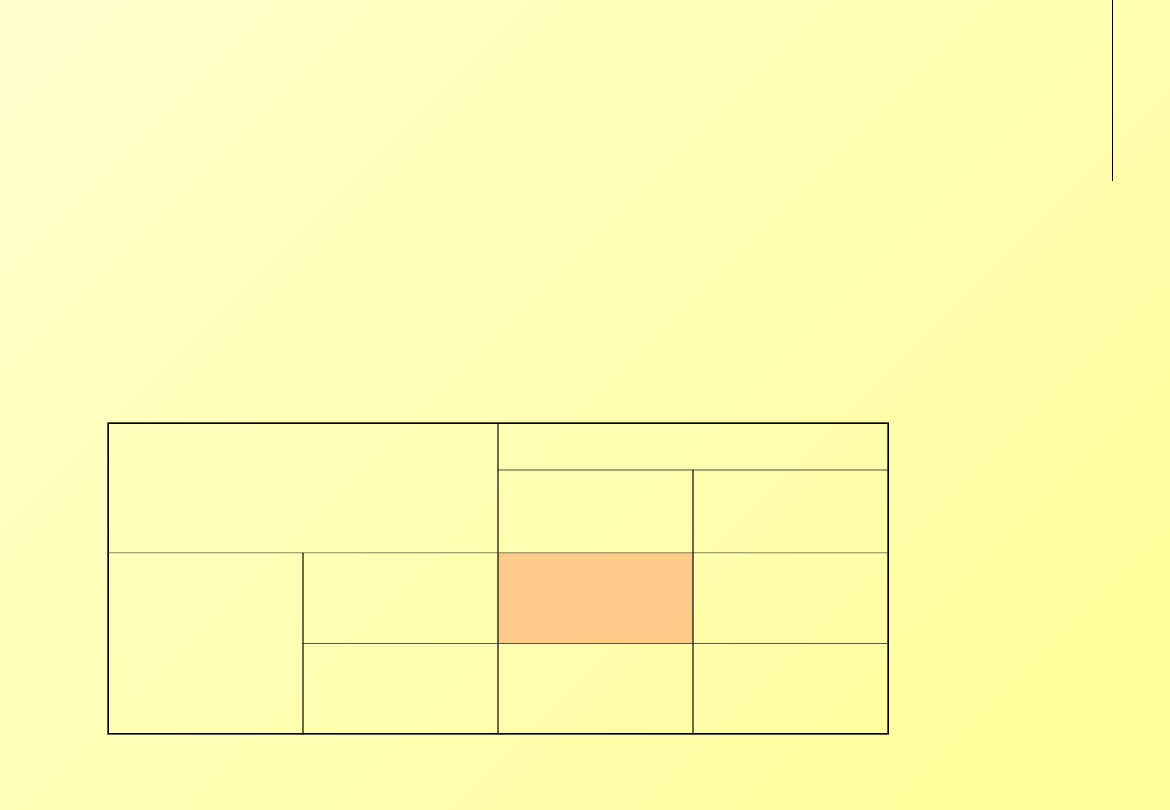
‘Walka płci’ (wariant #2)



Istnieje nierównowaga preferencji obu stron.

‘Walka płci #2’

Ona

opera

mecz

On

opera

2, 1

0, 0

mecz

-1, -1

1, 2

44

Polowanie na jelenia



Indywidualnie każdy myśliwy może sam upolować zająca, ale

jest on mniej wart niż udział we wspólnym polowaniu na

jelenia.



Gra jest analogiem współpracy jednostek w ramach

społeczeństwa.



R>T>=P>S. (P, P) pozostaje równowagą Nasha, ale nie jest

związane z dominującym ryzykiem.



Wprowadzenie kary za brak współpracy w ‘dylemacie więźnia’

może przekształcić tę grę w ‘polowanie na jelenia’.

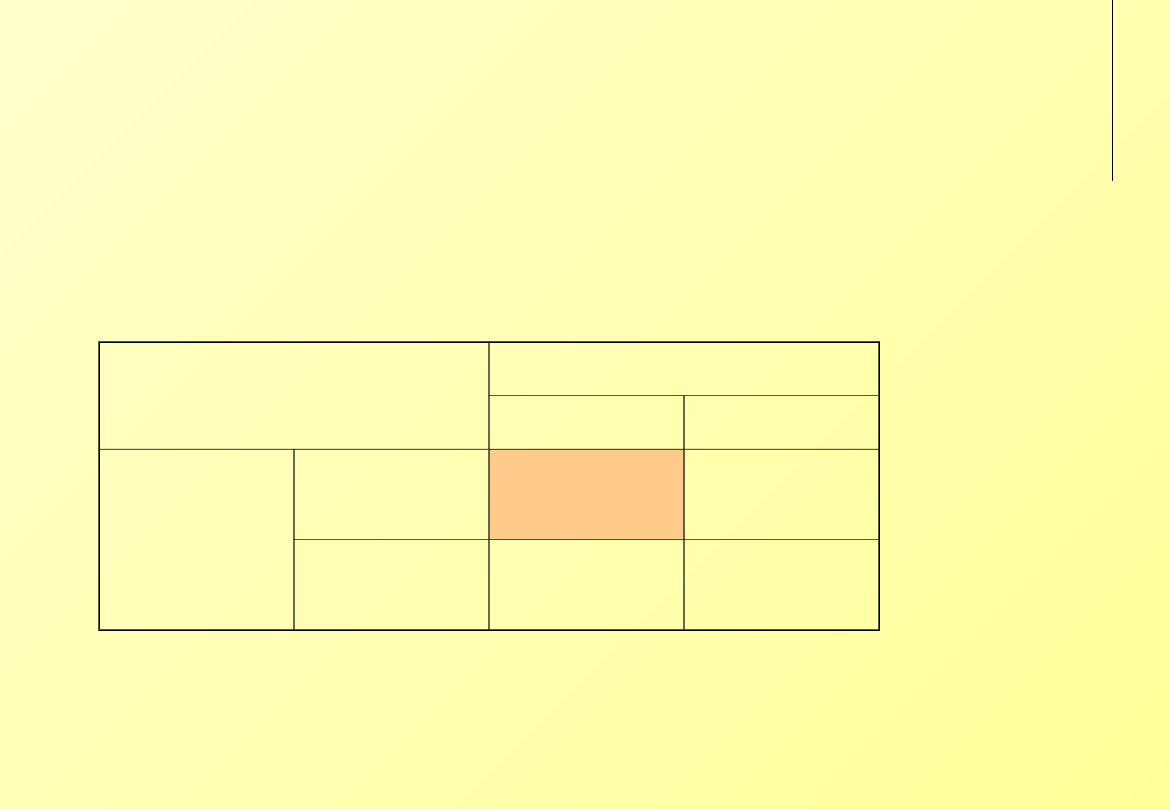
‘Polowanie na
jelenia’

Pierwszy myśliwy
jeleń

zając

Drugi
myśliwy

jeleń

R, R
4, 4

S, T
0, 3

zając

T, S
3, 0

P, P
3, 3

45

Gra w ubezpieczenie



Dylemat więźnia – T>R>P>S



Cykor – T>R>S>P (obopólna odmowa jest gorsza niż utrata

twarzy)



Ubezpieczenie – R>T>S>P (nagroda za współpracę jest wyższa

od nagrody za odmowę)
‘Ubezpieczenie’

Pierwszy

współpraca odmowa

Drugi

współpraca R, R

10, 10

S, T
5, 1

odmowa

T, S
1, 5

P, P
3, 3

46

Przyjaciel czy wróg



Ang: FoE, Friend or Enemy



W konkursie wygrywają trzy pary zawodników, w miarę
eliminowania każdej pary rozgrywają grę typu ‘dylematu
więźnia’, przy przyjęciu postawy przyjacielskiej w zależności od
wyboru drugiej osoby mogą zdobyć całą nagrodę (jeśli drugi
uznał go za wroga), lub podzielić się nagrodą po połowie (obaj
przyjęli postawę przyjaciół), jeśli jednak obaj traktują się jak
wrogowie – żaden nie dostaje nic.



W podtekście propozycja: „Jeśli uznam cię za wroga to wygrywasz
wszystko, jeśli obaj sobie zaufamy to dzielimy się nagrodą. Jeśli
uznasz mnie za wroga to zawsze przegrasz, bo albo ja biorę
wszystko, albo żaden z nas nie bierze nic. Dlatego tylko
współpraca ze mną może ci cokolwiek dać.”



Macierz wygranych jest przypadkiem pośrednim między
‘dylematem więźnia’ a grą w ‘cykora’ gdy P=S.

47

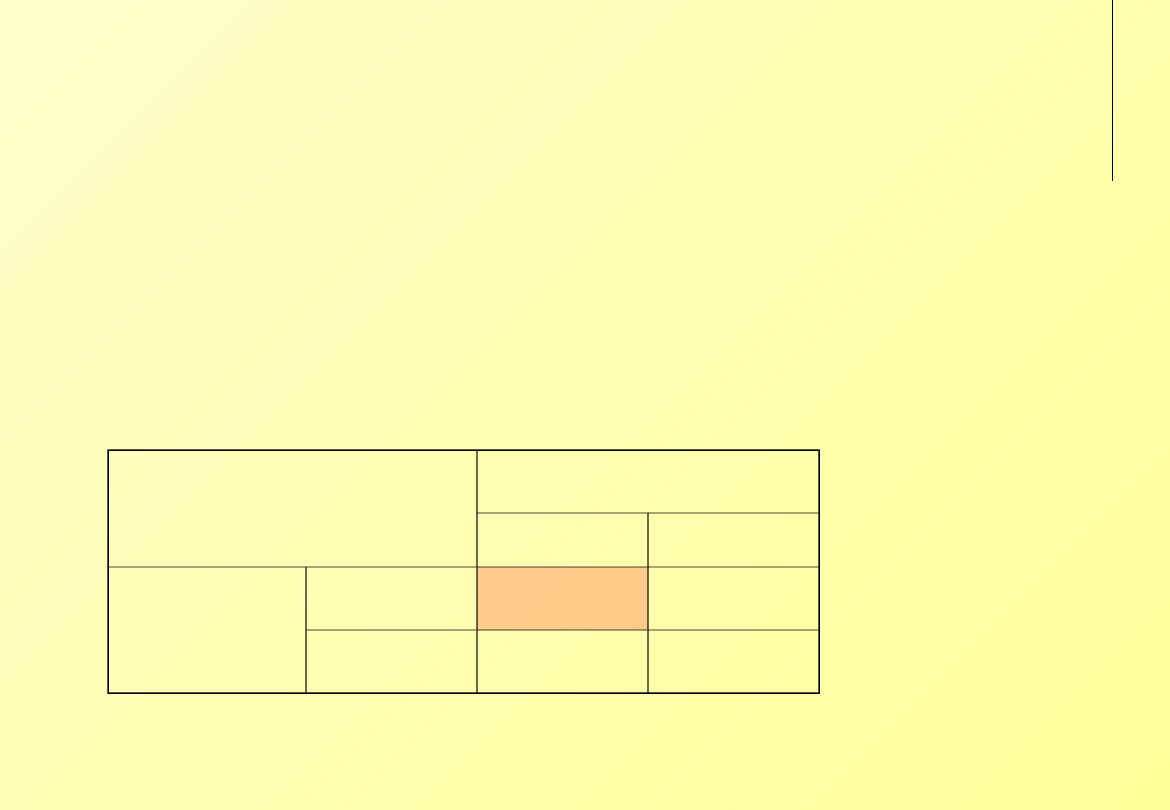
Przyjaciel czy wróg



‘Dylemat więźnia’ – T>R>P>S



‘Cykor’ – T>R>S>P



‘Przyjaciel czy wróg’ – P=S

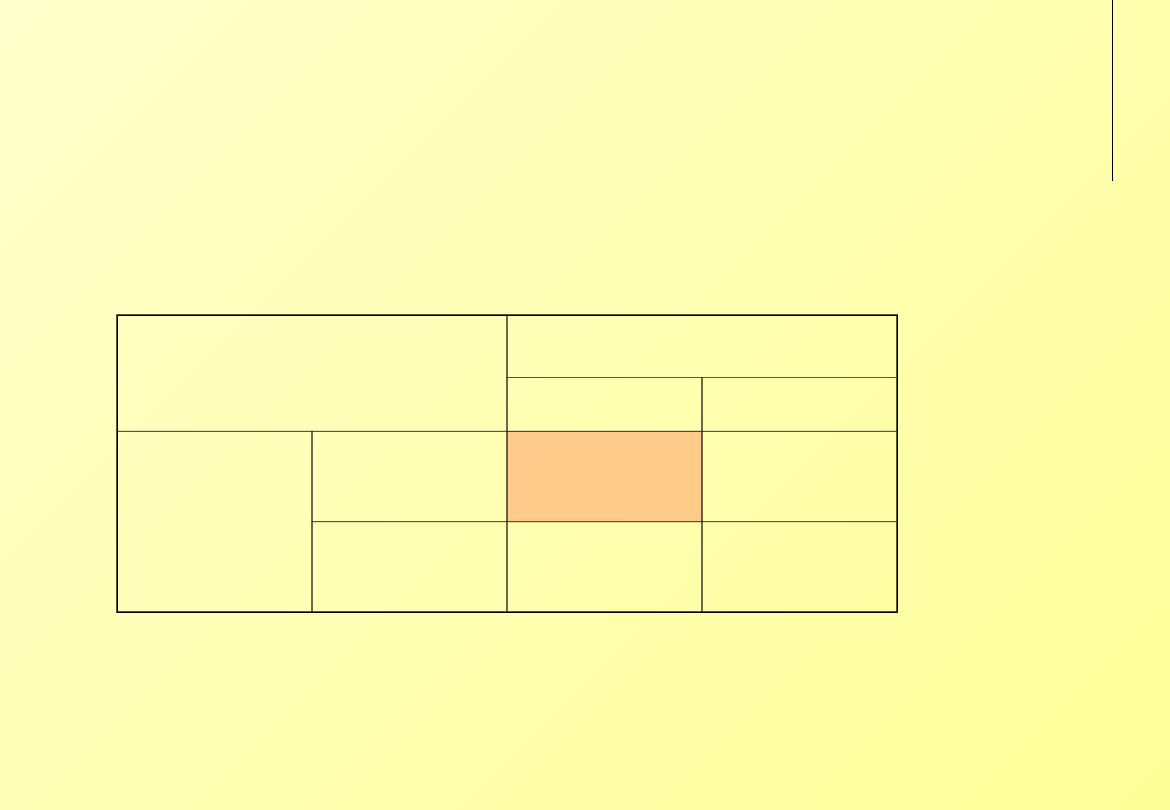
‘Przyjaciel czy wróg’

Pierwszy

współpraca odmowa

Drugi

współpraca R, R

1, 1

S, T
0, 2

odmowa

T, S
2, 0

P, P
0, 0

48

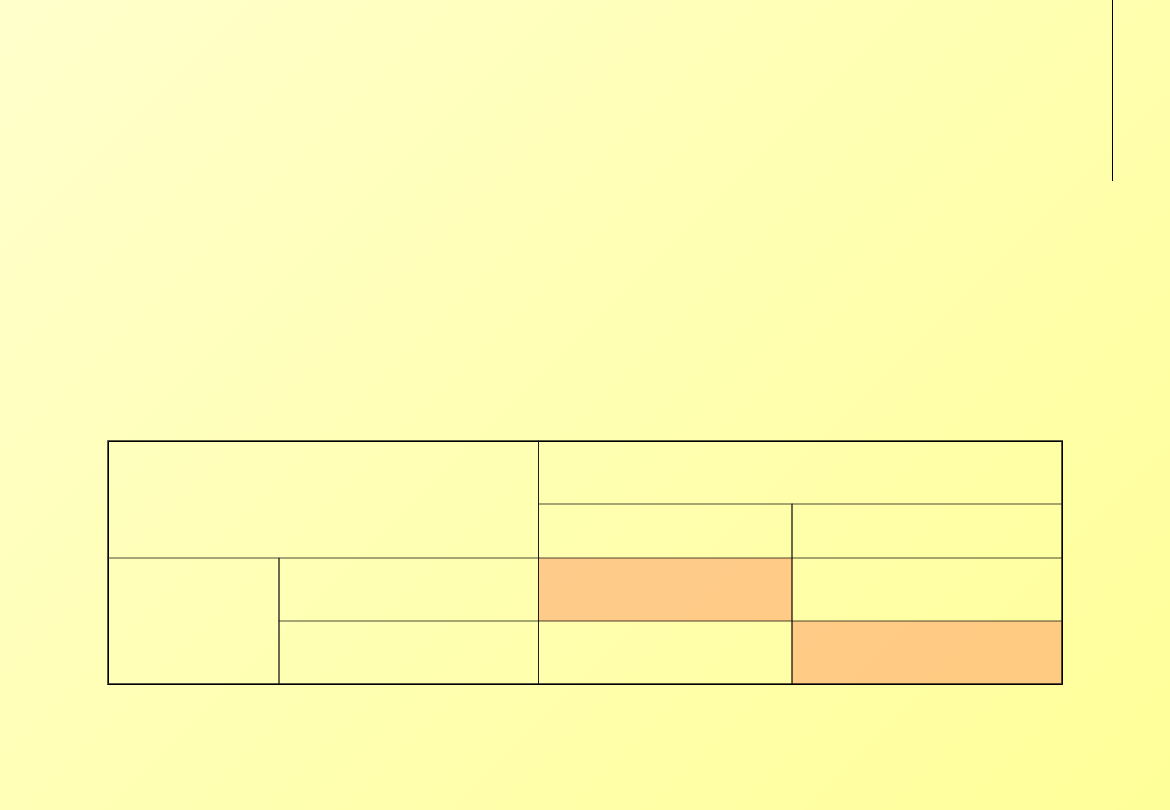
Gra we współpracę



Wspólne interesy ale niezależna warianty rozwiązań.



Dwa rozwiązania równowagi Nasha powodują konieczność
współpracy.



Bez środków porozumiewania się między graczami uzyskanie
rozwiązania jest praktycznie niemożliwe.

‘Współpraca’

Pierwszy gracz

wariant A wariant B

Drugi gracz wariant A 1, 1

0, 0

wariant B 0, 0

1, 1

49

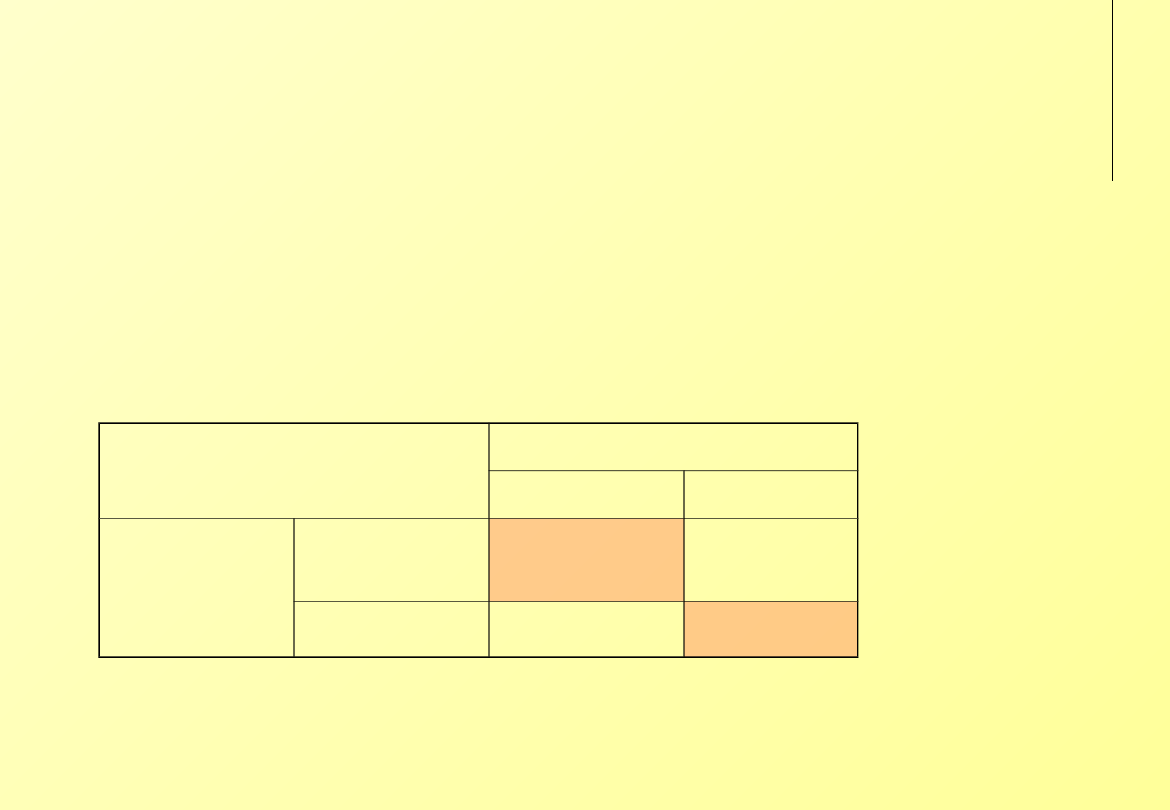
Gra we współpracę



Nowy produkt wprowadzany na rynek przez dwie firmy może
być wytwarzany dwiema technologiami. Jeśli firmy uzgodnią
wybór rozwiązania, które stanie się powszechnym standardem,
uzyskają duże zyski. Jeśli tego nie zrobią – ich zyski będą
minimalne.



Przykłady: VHS / Betamax Sony; standardy telewizji wysokiej
rozdzielczości.

‘Współpraca’

Firma A

technologia #1 technologia #2

Firma B

technologia #1 100, 100

0, 0

technologia #2 0, 0

100, 100

50

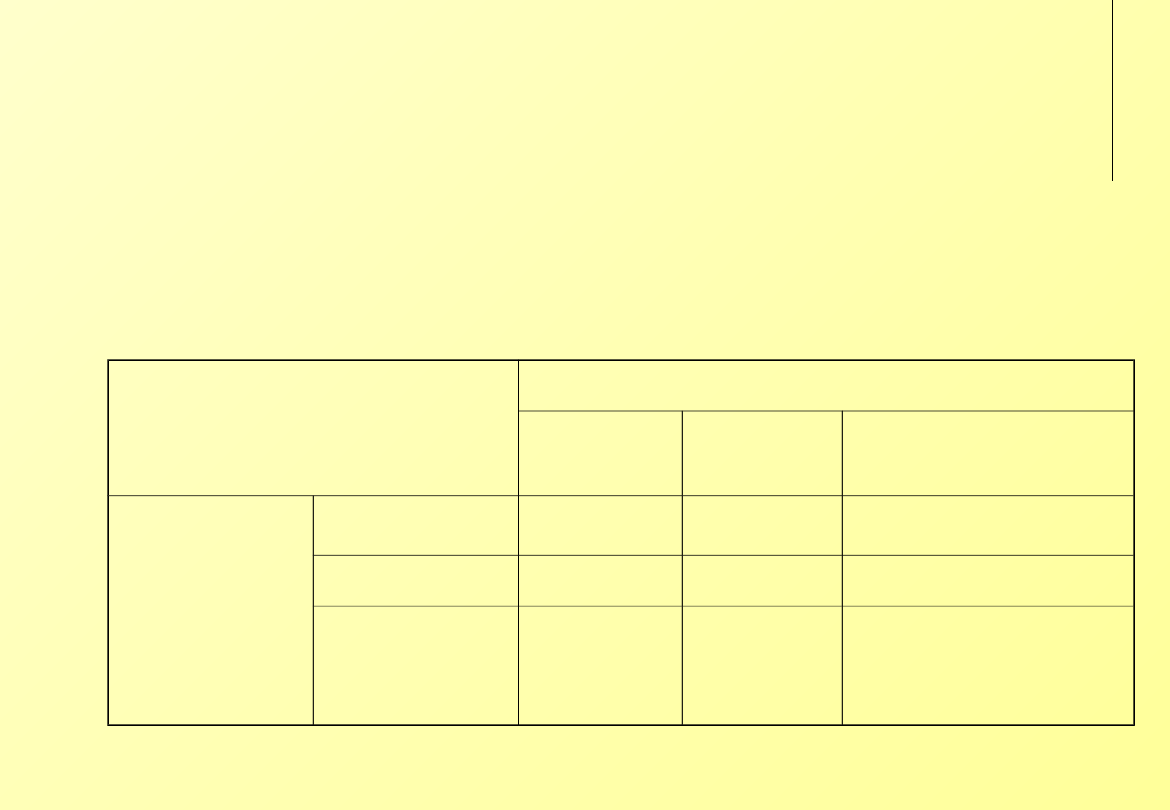
Gra we współpracę



Inny wariant gry – ustalenie kierunku ruchu samochodów
(prawostronny lub lewostronny). Przy nieuzgodnionym wyborze
następuje kolizja (koszt: –100). Dwiema czystymi strategiami
równowagi są (prawa, prawa) i (lewa, lewa).



Istnieje paradoksalna mieszana strategia równowagi – kierunek
ruchu jest zmieniany na średnio połowę czasu jazdy.

‘Współpraca’

Kierowca A
prawa

lewa

Kierowca B prawa

0, 0

-100,
-100

lewa

-100, -100

0, 0

51

Ścigający i ścigany



Żadna kolumna ani wiersz nie dominują nad pozostałymi –
rozwiązanie może istnieć tylko w strategiach mieszanych.



Uciekinier może zginąć na skałach lub od ukąszenia
grzechotnika nawet gdy w tych miejscach nie ma ścigającego
go policjanta.

Ścigający policjant (zastawia pułapkę)
Most

Skały

Pustynia
(grzechotniki)

Ścigany
uciekinier
(wybiera
drogę

ucieczki)

Most

0, 1

1, 0

1, 0

Skały

0.9, 0.1

0, 1

0.9, 0.1

Pustynia
(grzechotni
ki)

0.8, 0.2

0.8, 0.2

0, 1

52

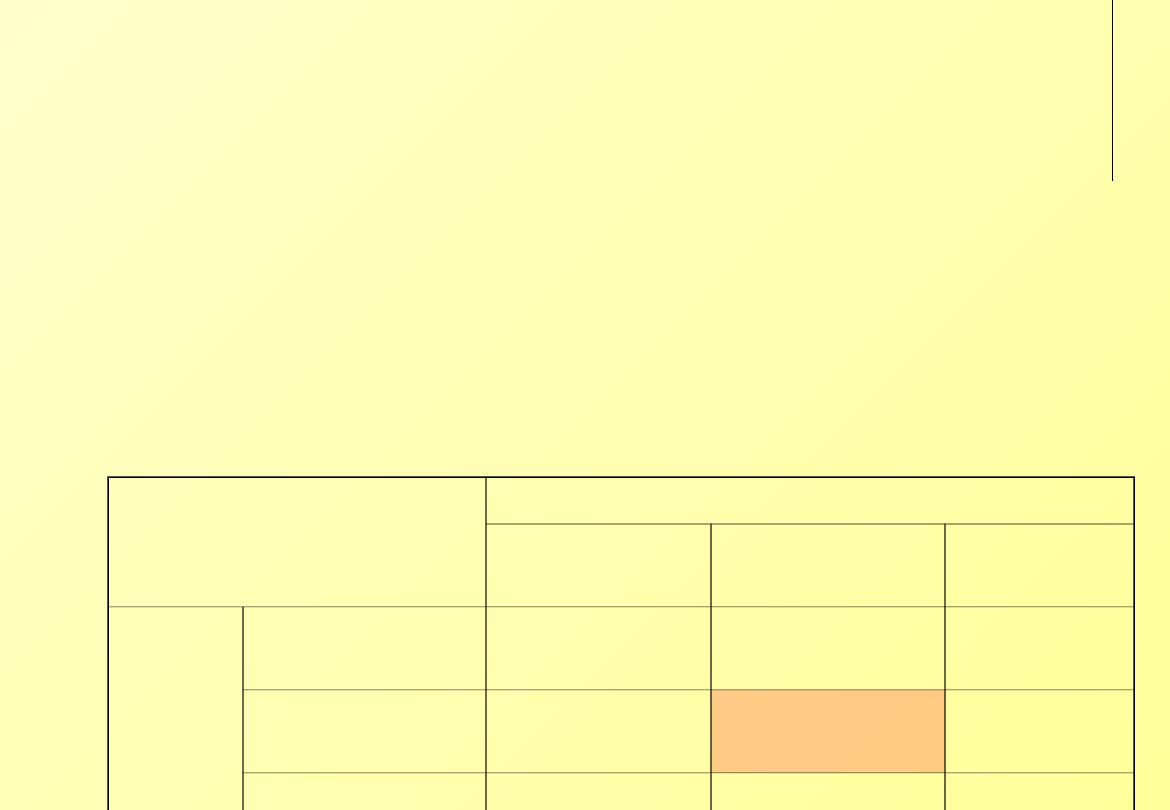
Ustalenie poziomu produkcji



Każda z dwóch firm ma trzy strategie



nie zwiększać produkcji



niewielki wzrost produkcji



silna ekspansja.



Większa produkcja > większa sprzedaż > niższe ceny > niższe
dochody.

Firma A
obecny
poziom

niewielki
wzrost

silny
wzrost

Firma B obecny

poziom

18, 18

15, 20

9, 18

niewielki
wzrost

20, 15

16, 16

8, 12

silny wzrost

18, 9

12, 8

0, 0

53

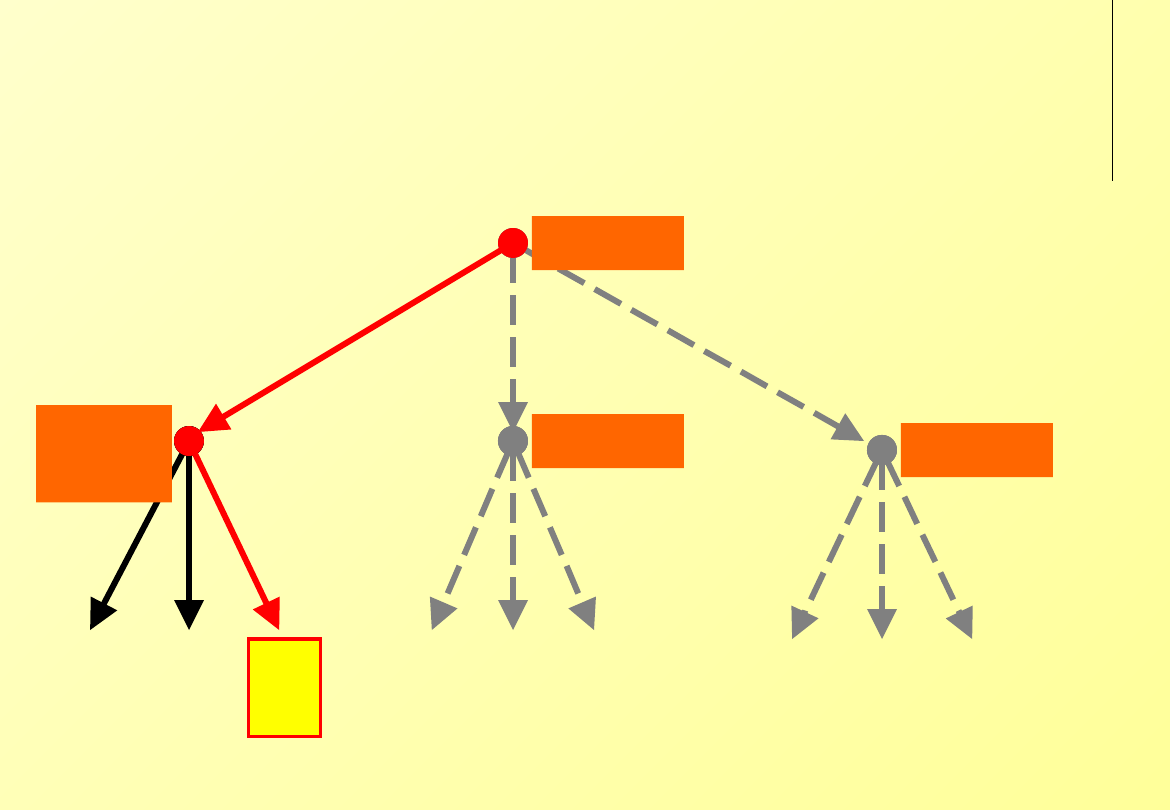
Ustalenie poziomu produkcji



Przewaga wykonującego pierwszy ruch w grze sekwencyjnej

firma A

firma
B

firma B

firma B

obecny poziom produkcji

niewielki wzrost

silny wzrost

obecny poziom

obecny poziom

obecny poziom

silny wzrost

silny
wzrost

18
18

15
20

9
18

20
15

16
16

8
12

18
9

12
8

0
0

54

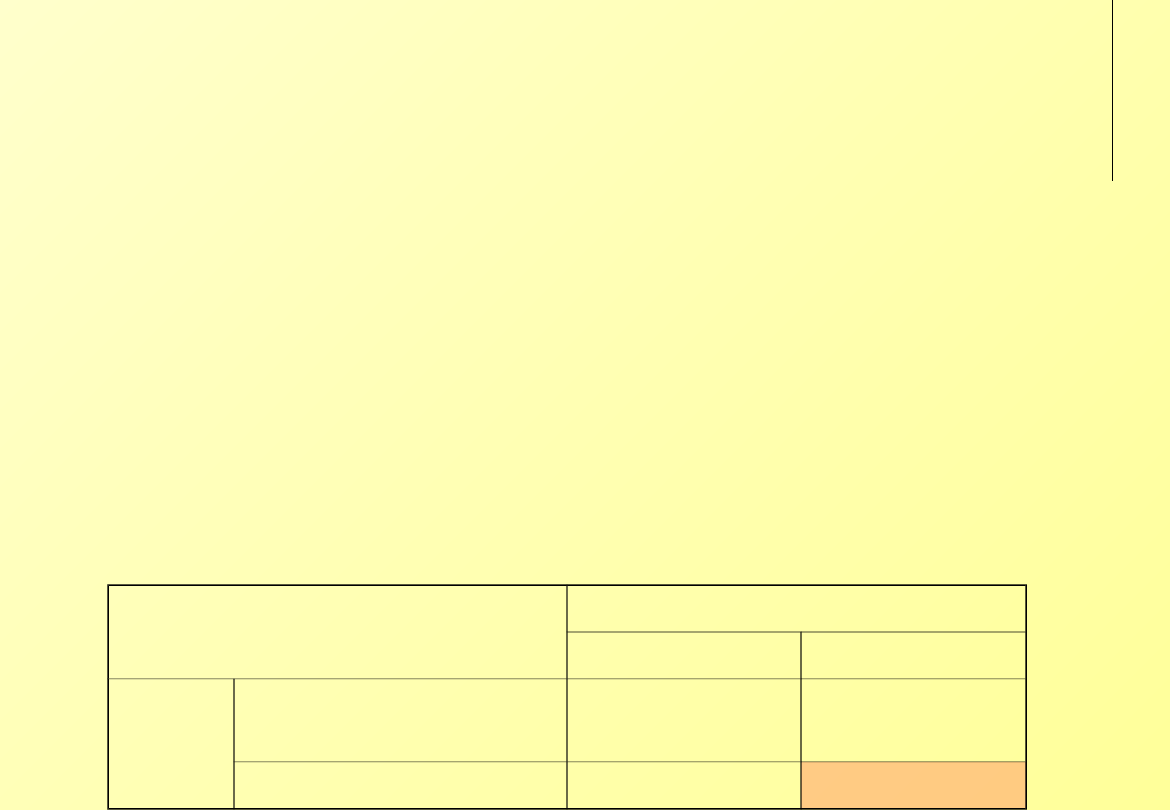
Budżet rządowy / polityka
finansowa



Gracze:



rząd – polityka fiskalna (podatki, akcyzy, wydatki

budżetowe)



Rada Polityki Pieniężnej – polityka monetarna (bilans

interesów)



Działania:



rząd – budżet zbilansowany lub deficyt budżetowy



Rada – wysokie lub niskie oprocentowanie kapitału.



Strategie:



strategia Rady zależy od wyboru wariantu wybieranego

przez rząd



rząd dąży do wysokich wydatków i deficytu budżetowego



wariant zbilansowanego budżetu i niskiego oprocentowania

jest najlepszy ale praktycznie niemożliwy do zrealizowania.

Rada
niskie %

wysokie %

Rząd

zbilansowany
budżet

3, 4

1, 3

deficyt

4, 1

2, 2

55

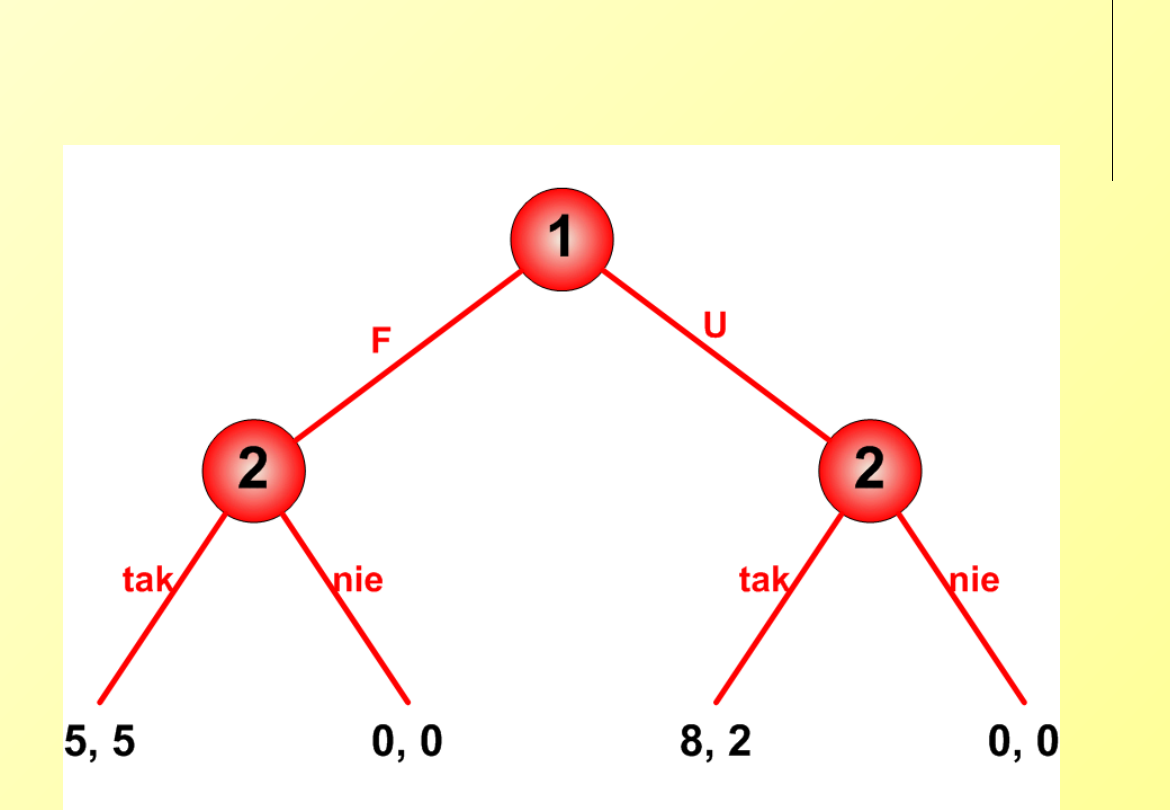
Ultimatum (gra
asymetryczna)



Pierwszy gracz proponuje drugiemu udział p w wygranej (zyskach z
rynku, podziale tortu, łupu) w przedziale [0,1]. Jeśli druga strona
przystaje na propozycję – dokonują podziału w przyjętej do wiadomości
proporcji. Jeśli drugi odrzuci propozycję, żaden nie bierze nic (pierwszy
nie może bowiem bez udziału drugiego niczego zyskać). Drugi gracz
dokonuje wyboru pewnej funkcji profilu strategii (p, f), gdzie p jest
składaną propozycją a f funkcją odpowiedzi, przybierającą wartość f(p)
= ‘tak’ lub ‘nie’.



Pierwszy gracz chce zwiększyć swój udział w wygranej wykorzystując
sytuację, że drugi gracz nie jest zainteresowany odrzuceniem nawet
nieproporcjonalnie niskich propozycji by nie dostać niczego.

A

B

pA

pA

0,0

56

Ultimatum (gra
asymetryczna)



Czynnik socjologiczny. W praktyce propozycje podziału 50:50
między A:B są uznawane za sprawiedliwe, najczęściej
proponowane mieszczą się w przedziale od 70:30 do 50:50,
podczas gdy mniejsze od 20% są w połowie przypadków
odrzucane. Wykazano, że Mongołowie dążą do proponowania
równego podziału – nawet wiedząc, że nieproporcjonalny podział
jest też z reguły akceptowany przez drugą stronę. Oznacza to, że
reputacja kontrahenta w tym społeczeństwie jest równie ważna
co zysk ekonomiczny. Z drugiej strony wysokość wygranej też
odgrywa swoją rolę – mało kto odrzuci niesprawiedliwy podział
90:10 z 10 milionów dolarów. Jednak oferty 70:30 ze 100 dolarów
są równie często odrzucane w Indonezji (średni dochód 670 USD)
co w USA.

57

Ultimatum (gra
asymetryczna)

58

Gra w dyktatora (gra
asymetryczna)



Pierwszy gracz proponuje drugiemu udział p w wygranej (zyskach
z rynku, podziale tortu, łupu) w przedziale [0,1]. W odróżnieniu od
‘ultimatum’ drugi gracz nie ma możliwości odrzucenia propozycji.
Doświadczalnie wyznaczone udziały proponowane w tej grze są
rzędu 20%, 1/3 ‘dyktatorów’ nie daje niczego, 1/5 daje połowę.



Pełna anonimowość zmniejsza o połowę proponowany udział,
zmniejszenie anonimowości zwiększa udział (przedstawienie się
obdarowywanego, listy potwierdzające otrzymanie darowizny).

A

B

pA

59

‘Pasujące monety’



Ang: matching pennies



Każdy z graczy kładzie swoją monetę orłem lub reszką do góry.

Jeśli monety pasują do siebie – pierwszy gracz wygrywa i

przejmuje monetę drugiego, jeśli nie – wygrywa drugi.



Gra nie posiada strategii punktu równowagi Nasha, ponieważ

taka strategia (wybór orła lub reszki) nie istnieje. Jedyną

strategią równowagi Nasha jest strategia mieszana – każdy

gracz dokonuje wyboru strony monety z równym

prawdopodobieństwem. Jeśli kieruje się jakimiś innymi

zasadami i możliwe jest przewidzenie jego wyboru –

przegrywa.

‘Pasujące monety’

Pierwszy gracz

orzeł

reszka

Drugi
gracz

orzeł

1, -1

-1, 1

reszka

-1, 1

1, -1

60

‘Kamień, papier, nożyczki’



Gracze jednocześnie pokazują dłonie zwinięte w pięść

(kamień), płaskie (papier) lub z rozwartymi palcami (nożyczki).

Wygrane określają zasady logiki nieprzechodniej:



Papier zakrywa kamień



Kamień tępi nożyczki



Nożyczki tną papier.



W grze nie istnieje jakakolwiek strategia prowadząca do

wygranej. Jedynym optymalnym wyborem jest całkowicie

przypadkowy. Jeśli jednak którykolwiek z graczy stosuje

nieprzypadkową strategię dającą się przewidzieć – przegrywa.

‘Kamień, papier,
nożyczki’

Pierwszy gracz
kamień

papier

nożyczki

Drugi gracz kamień

0, 0

-1, 1

1, -1

papier

1, -1

0, 0

-1, 1

nożyczki

-1, 1

1, -1

0, 0

61

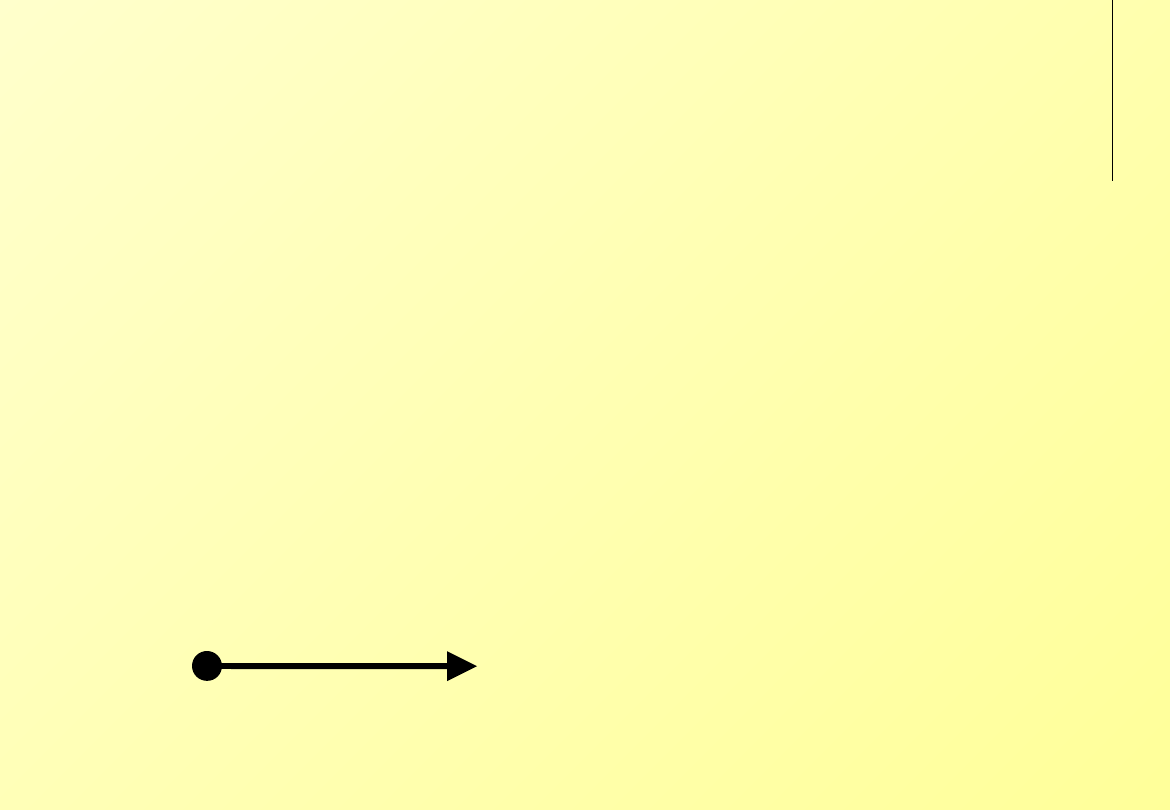
Gra w ‘stonogę’
(sekwencyjna)



Gra sekwencyjna o 100 etapach. Każdy z graczy ma na zmianę
możliwość zatrzymania gry i zagarnięcia znacząco w danej
chwili większej części wolno rosnącej puli nagrody, lub
zaryzykować chwilową małą przegraną w stosunku do
przeciwnika. Po przekazaniu kolejki drugiej stronie i zagarnięciu
przez nią wygranej jest ona nieco mniejsza. Jedynym punktem
równowagi Nasha jest dla pierwszego gracza przejęcie puli w
początkowym stadium gry, jednak w praktyce gracze rzadko
wybierają to rozwiązanie.

62

Bar ‘El Farol’



Nazwa gry pochodzi od nazwy baru w Santa Fe w stanie Nowy Meksyk.

W lokalu tym w czwartkowe wieczory grano muzykę irlandzką.

Zagadnienie zdefiniował irlandzki ekonomista W.Brian Arthur w 1994 r.



Wszyscy zainteresowani chcą pójść do baru, który jest jednak zbyt

mały by pomieścić wszystkich chętnych a przebywanie w nadmiernie

zatłoczonym lokalu psuje wszystkim zabawę.



Jeśli 60% mieszkańców pójdzie do baru – będą z tego bardziej

zadowoleni, niż gdyby pozostali w domu.



Jeśli do baru pójdzie ponad 60% – wszyscy będą bardziej

niezadowoleni, niż gdyby zostali w domu.



Korzystanie przez wszystkich z tej samej strategii prowadzi do sytuacji

absurdalnej – bar albo stoi pusty, albo jest ponad miarę zatłoczony.



W jednym z wariantów gry dopuszczalną jest wzajemna wymiana

informacji o swych zamierzeniach. Nie jest jednak wymagane mówienie

innym prawdy. Stąd w praktyce można przyjąć strategię

dezinformowania pozostałych by nie przyszli do baru i nie przeszkadzali

nam w zabawie.

63

Odgadywanie 2/3 średniej



Dowolna liczba graczy podaje liczby od 0 do 100.



Wygrywa osoba, której liczba będzie najbliższą 2/3 średniej ze
wszystkich ocen.



Jedyną czystą strategią Nasha jest wartość 0. Podanie dowolnej
liczby większej niż 66 jest strategią zdominowaną przez
pozostałych, nie jest bowiem możliwym określenie 2/3 średniej.
Analogicznie rozumując oszacowanie powyżej 40 bo żaden gracz
nie powinien zaryzykować ponad 2/3 z 66, co wynosi ponad 40.
Kontynuacja tego toku myślenia prowadzi do wyeliminowania
wszystkich liczb powyżej 0.



Biorący udział w grze muszą jednak uwzględniać, że wśród
pozostałych graczy wielu będzie zbyt mało inteligentnych by
przeprowadzić takie rozumowanie. Eksperymentalne rozegranie
gry w Danii przy ponad 19 tysiącach graczy i nagrodzie 5 tysięcy
koron dało średnią ocen 21.6.

64

‘Turyści i tubylcy’



Konkurencja dwóch barów, które mogą ustalić cenę na

poziomie 2, 4 lub 5 jednostek monetarnych.



6000 turystów wybiera bar przypadkowo



4000 miejscowych wybiera tańszy bar.



Dochody barów (w tysiącach jednostek monetarnych)

‘Turyści i tubylcy’

Bar A
cena: 2

cena: 4

cena: 5

Bar B

cena: 2

10, 10

14, 12

14, 15

cena: 4

12, 14

20, 20

28, 15

cena: 5

15, 14

15, 28

25, 25

65

Negocjacje



Sprzedawca używanych samochodów twierdzi, że najniższą

możliwą ceną jest 20 000 (naprawdę jest to 17 000)



Kupujący twierdzi, że może zapłacić najwyżej 18 000 (aktualna

cena to 21 000)



Każda ze stron ma dwie możliwości: zaakceptować, odrzucić.



Dwie równowagi czystych strategii: (tak, nie) i (nie, tak);

równowaga strategii mieszanej przy prawdopodobieństwie

decyzji każdej ze stron 50% – szansa zgody wynosi 25%.



Zyski stron w tysiącach:

‘Negocjacje’

Sprzedawca

akceptacja odrzucenie

Kupujący

akceptacja 2, 2

1, 3

odrzucenie 3, 1

0, 0

66

‘Leniwy mąż’



Oboje małżonków pracuje, nie stać ich jednak na sprzątaczkę.



Żona jest skłonna wykonać prace domowe jeśli mąż jej

pomaga, odmawia ich wykonania jeśli mąż odmawia pomocy.



Dominującą strategią męża jest unikanie sprzątania.



Oboje bardziej cenią wspólne sprzątanie niż mieszkanie w

brudzie.



Wynik: mąż musi się pogodzić z nieunikaniem prac domowych.

‘Leniwy mąż’

Mąż

sprzątanie

lenistwo

Żona

sprzątanie

-1, 1

3, -1

odmowa

-1, 0

-2, -2

67

Wymuszanie wyboru menu



Dziecko decyduje czy jeść szpinak, nie lubi go ale bardzo lubi

desery.



Rodzice decydują o podaniu deseru, chcą by dziecko było

zadowolone, bardzo chcą też by jadło szpinak.



Przy jednoczesnym podejmowaniu decyzji obie strony mają

dominujące strategie: bez szpinaku i deser. Jeśli dziecko

pierwsze podejmuje decyzję w grze sekwencyjnej – równowagą

podgry jest rozwiązanie bez szpinaku i z deserem.

Dziecko

deser

bez deseru

Rodzice

szpinak

0, 1

-2, 1

bez szpinaku

2, -1

-1, 0

68

Wymuszanie wyboru menu



Dla rodziców rozwiązaniem jest stawianie ultimatum po
przekształceniu gry w grę sekwencyjną: „nie dostaniesz deseru
dopóki nie zjesz szpinaku”.



Rodzice mogą przechylić szanse rozwiązania na swą korzyść
przez wprowadzenie zasady odpowiedzi. ‘Groźbą’ jest reguła
odpowiedzi, która karze przeciwników w grze jeśli nie
podejmują współpracy, w sposób obracający się przeciw
intencjom danej strony. ‘Obietnicą’ jest reguła odpowiedzi
nagradzająca innych gdy podejmują współpracę, w sposób
niezgodny z własnymi intencjami.

69

Rozbieżności z sytuacjami
realnymi



Istotność sposobu podania informacji o wygranych.



Grupie ludzi przedstawiono możliwość dokonania wyboru strategii

zapobiegającej rozprzestrzenianiu zarazy w grupie 600 osób:



Strategia A ocali życie 200 ludziom, strategia B daje szansę 1/3

ocalenia wszystkich i 2/3 ocalenia nikogo. (Uwaga: obie strategie mają

te same wartości średnie). 72% ludzi wybrało strategię A.



Przy stwierdzeniu, że strategia A doprowadzi do śmierci 400 osób –

zaledwie 22% decydentów dokonało jej wyboru. Tymczasem jeśli

poprzednio stwierdzono, że z 600 osób ma ocaleć 200 – oznaczało to,

że 400 umrze. Czyli dokładnie to samo w obu przypadkach, tylko

inaczej podane.



Wniosek: unikanie ryzyka przez podejmujących decyzje nawet gdy

daje ono większe szanse wygranej niż zapewniony każdemu poziom

pewności. W sytuacji perspektywy pewnej straty – postępowanie staje

się odwrotne.

70

Kierunki rozwoju teorii gier



Gry sekwencyjne (np. drapieżnik i ofiara), w których kolejność
podejmowania decyzji lub naprzemienne wykonywanie ruchów
staje się istotnym czynnikiem.



Gry sekwencyjne rozgrywane przez automaty (agentów) jako
strategie reagowania na sytuacje w swoim otoczeniu.



Gry z niepełną informacją o działaniach przeciwnika, gry z
dezinformacją.



Ewolucja jako gra, gry ewolucyjne.



Gry w gry (hipergry), w których elementami macierzy wypłat
są rezultaty optymalnego rozegrania podgier. (wybory Jimmy
Carter/Ronald Regan jako hipergra z ZSRR o zaufanie)



Gry, w których każda ze stron gra w inną grę (inaczej
interpretuje sytuację).

71