KLASYFIKACJA MODELI
EKONOMETRYCZNYCH -
WERYFIKACJA
JEDNORÓWNANIOWEGO
MODELU
EKONOMETRYCZNEGO

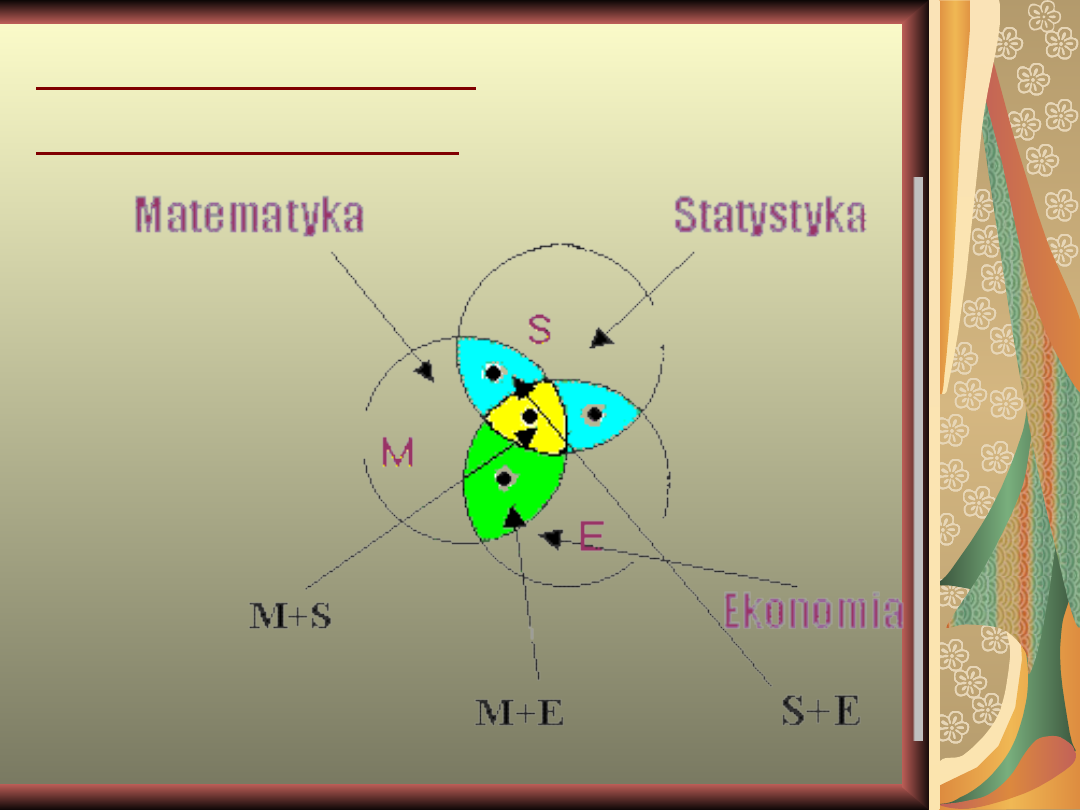
POCHODZENIE
EKONOMETRII

MODEL
EKONOMETRYCZNY

Modelem ekonometrycznym nazywamy

formalny opis stochastycznej zależności

wyróżnionej wielkości, zjawiska lub przebiegu

procesu ekonomicznego od czynników, które je

kształtują, wyrażony w formie pojedynczego

równania bądź układu równań. Strukturę każdego

równania określają: zmienna objaśniana,

zmienne objaśniające (nielosowe lub losowe)

mające ustaloną treść ekonomiczną, parametry

strukturalne ,zmienna losowa (tradycyjnie

nazywana składnikiem losowym) o nieznanej

treści oraz określony typ związku funkcyjnego

między zmienną objaśnianą a zmiennymi

objaśniającymi i składnikiem losowym.

KLASYFIKACJA ZMIENNYCH
WYSTĘPUJĄCYCH W MODELU
EKONOMETRYCZNYM

A - zmienne endogeniczne: bieżące i
opóźnione (wyjaśniane przez model),
B - zmienne egzogeniczne: bieżące i
opóźnione (nie wyjaśniane przez
model).
C - zmienne objaśniane
D - zmienne objaśniające.

KLASYFIKACJA MODELI
EKONOMETRYCZNYCH

- modele jednorównaniowe
-modele wielorównaniowe,
- modele nieliniowe
- modele nieliniowe
 - modele proste,   
- modele rekurencyjne,   
- modele o równaniach

współzależnych

RODZAJE WERYFIKACJI

weryfikację merytoryczną,

która ma na celu stwierdzenie
merytorycznej poprawności
modelu,

weryfikację statystyczną,

która ma celu stwierdzenie czy
model spełnia postulaty
sformułowane w teorii
ekonometrii i statystyki.

Współczynnik determinacji R

2

wskazuje, jaka część ogólnej
zaobserwowanej
Zmienności zmiennej objaśnianej
została wyjaśniona przez model
ekonometryczny.
Współczynnik indeterminacji φ

2

mierzy natomiast tę część
zaobserwowanej zmienności
zmiennej objaśnianej, która nie
została przez model wyjaśniona.

Współczynnik determinacji R

2

wskazuje, jaka część ogólnej
zaobserwowanej
Zmienności zmiennej objaśnianej
została wyjaśniona przez model
ekonometryczny.
Współczynnik indeterminacji φ

2

mierzy natomiast tę część
zaobserwowanej zmienności
zmiennej objaśnianej, która nie
została przez model wyjaśniona.

Współczynnik indeterminacji
określony jest wzorem

Φ

2

= Σ (y – ŷ)

2

/ Σ (y - ỹ)

2

Wspólczynnik determinacji
oznaczany jest natomiast jako

R

2

= 1 – φ

2

o ile φ

2

jest mniejsze lub równe

1.

Współczynnik indeterminacji
określony jest wzorem

Φ

2

= Σ (y – ŷ)

2

/ Σ (y - ỹ)

2

Wspólczynnik determinacji
oznaczany jest natomiast jako

R

2

= 1 – φ

2

o ile φ

2

jest mniejsze lub równe

1.

Istotność zmiennych
objaśniających

Zmienna objaśniająca jest
„istotna”, gdy w zauważalny
(wyraźny) sposób wpływa na
zmienną objaśnianą.
W wypadku modelu liniowego Y =
a0 + a1X1 + ... + anXn zmienna
jest istotna, gdy parametr przy niej
stojący jest istotnie różny od zera.

Zmienna objaśniająca jest
„istotna”, gdy w zauważalny
(wyraźny) sposób wpływa na
zmienną objaśnianą.
W wypadku modelu liniowego Y =
a0 + a1X1 + ... + anXn zmienna
jest istotna, gdy parametr przy niej
stojący jest istotnie różny od zera.

1Obliczamy tzw., empiryczną statystykę
Studenta, t

k ,

dotyczącą badanej zmiennej

objaśniającej.

2Ustalamy krytyczną wartość statystyki
Studenta, t

KR

.

3Porównujemy moduł empirycznej statystyki
Studenta z wartością krytyczną:

oZmienną objaśniającą uznaje się za
istotną, jeśli związana z nią
statystyka empiryczna jest co do
modułu większa od wartości
krytycznej, tzn. , jeśli

| t

k

|

> t

KR

,

oJeśli natomiast jest odwrotnie, tzn. |
t

k

| ≤ t

KR

to badaną zmienną

objaśniającą uznajemy za nieistotną.

1Obliczamy tzw., empiryczną statystykę
Studenta, t

k ,

dotyczącą badanej zmiennej

objaśniającej.

2Ustalamy krytyczną wartość statystyki
Studenta, t

KR

.

3Porównujemy moduł empirycznej statystyki
Studenta z wartością krytyczną:

oZmienną objaśniającą uznaje się za
istotną, jeśli związana z nią
statystyka empiryczna jest co do
modułu większa od wartości
krytycznej, tzn. , jeśli

| t

k

|

> t

KR

,

oJeśli natomiast jest odwrotnie, tzn. |
t

k

| ≤ t

KR

to badaną zmienną

objaśniającą uznajemy za nieistotną.