Klasyfikacja modeli ekonometrycznych

KRÓTKA DEFINICJA SŁOWA EKONOMETRIA I MODELI EKONOMETRYCZNYCH

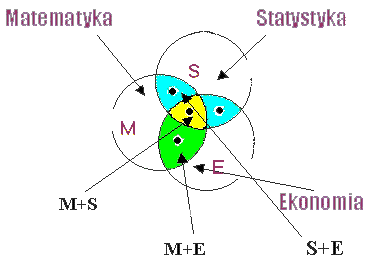
Przedmiotem Ekonometrii jest statystyczne badanie ilościowych prawidłowości ekonomicznych. Ekonomista chcąc wpływać na kształtowanie się zjawisk gospodarczych, przewidywać je i kontrolować zmuszony jest badać poznawać te zjawiska. W odkrywaniu i formułowaniu ilościowych praw ekonomicznych zasadniczą rolę odgrywa badanie statystycznych prawidłowości w kształtowaniu się procesu gospodarczego. Ekonometria wywodzi się z połączenia trzech podstawowych nauk; matematyki, statystyki i ekonomii. Z połączenia Matematyki i statystyki powstała Statystyka Matematyczna, a z połączenia Statystyki i Ekonomi - Statystyka ekonomiczna. Wspólne zainteresowania Matematyki i Ekonomi utworzyły Ekonomię matematyczną, wspólne zainteresowania zaś Ekonomii, Matematyki i Statystyki są podstawą rozwoju nauki zwanej Ekonometrią.

MODEL EKONOMETRYCZNY

   Podstawowym obiektem rozpatrywanym w ekonometrii jest model ekonometryczny. Modelem ekonometrycznym nazywamy formalny opis stochastycznej zależności wyróżnionej wielkości, zjawiska lub przebiegu procesu ekonomicznego     ( zjawisk, procesów) od czynników, które je kształtują, wyrażony w formie pojedynczego równania bądź układu równań. Strukturę każdego równania określają: zmienna objaśniana, zmienne objaśniające (nielosowe lub losowe) mające ustaloną treść ekonomiczną, parametry strukturalne ,zmienna losowa (tradycyjnie nazywana składnikiem losowym) o nieznanej treści oraz określony typ związku funkcyjnego między zmienną objaśnianą a zmiennymi objaśniającymi i składnikiem losowym.

Przykład:1.1

Dany jest model ekonometryczny     

w którym Y oznacza produkcję cukru w Polsce (tys.t), X-powierzchnię uprawy buraka cukrowego (tys. ha). Zmienną Y nazywamy zmienną objaśnianą, zmienną X -objaśniającą,     
   
   są nieznanymi parametrami strukturalnymi modelu. Składnik losowy   
         wyraża tzw. błąd w równaniu, czyli wpływ na Y czynników nie uwzględnionych w modelu w sposób bezpośredni, takich jak: warunki klimatyczne, zawartość cukru w burakach cukrowych, przygotowanie cukrowni do kampanii cukrowniczej itp. Zależność produkcji cukru od powierzchni uprawy buraka cukrowego jest liniowa.

KLASYFIKACJA ZMIENNYCH WYSTĘPUJĄCYCH W MODELU EKONOMETRYCZNYM

Rozważamy dwa rozłączne podzbiory zmiennych występujących w modelach ekonometrycznych:

A - zmienne endogeniczne: bieżące i opóźnione (wyjaśniane przez model),

B - zmienne egzogeniczne: bieżące i opóźnione (nie wyjaśniane przez model).

Ze względu na rolę pełnioną przez poszczególne zmienne w modelu możemy jeszcze wprowadzić podział na:

C - zmienne objaśniane

D - zmienne objaśniające.

W ogólnym przypadku zbiory C i D nie są zbiorami rozłącznymi, ponieważ zmienna objaśniana może być jednocześnie ( w tym samym modelu) zmienną objaśniającą. Z taką sytuacją można zetknąć się w modelach wielorównaniowych.

KLASYFIKACJA MODELI EKONOMETRYCZNYCH

Modele ekonometryczne klasyfikujemy ze względu na pięć kryteriów.

KRYTERIUM 1. Liczba równań w modelu.

Podział: - modele jednorównaniowe (patrz przykład 1.1),

             -modele wielorównaniowe, w których każde równanie objaśnia jedną zmienną.

Przykład 1.2   Dany jest model ekonometryczny 

 w którym: 

PKB - produkt krajowy brutto,  

I - inwestycje, 

 Z - zatrudnienie,                                    

  - parametry modelu,  

  - składniki losowe, 

t - numer roku.

Wcześniej zdefiniowane, odpowiednie podzbiory zmiennych modelu ekonometrycznego są następujące:

A={PKB,I}    ,     B={Z}   ,     C= 
          , D=

Zmienne  
        nazywamy zmiennymi opóźnionymi.

KRYTERIUM 2. Postać analityczna zależności funkcyjnych modelu.

Podział: 

- modele liniowe (przykłady 1.1 i 1.2), w których wszystkie zależności modelu są liniowe,   

- modele nieliniowe, w których chociaż jedna zależność modelu jest nieliniowa.

Przykład 1.3  Dany jest jednorównaniowy, nieliniowy model ekonometryczny

 

w którym:     

 
- produkt krajowy brutto w roku t,  

- majątek produkcyjny w roku t,   

- zatrudnienie w gospodarce w roku t,   

- parametry,   

- czynnik losowy. 

Zmienną losową    w przykładach 1.1 i 1.2 włączoną do modelu przez dodawanie  nazywamy addytywnym składnikiem losowym, a zmienną losową w przykładzie 1.3 włączoną do modelu przez mnożenie nazywamy multiplikatywnym składnikiem losowym.

KRYTERIUM 3. Rola czynnika czasu w równaniach modelu.

Podział: 

- modele statyczne (przykłady 1.1 i 1.3), nie uwzględniają czynnika czasu, wśród zmiennych objaśniających nie występują zmienne opóźnione ani zmienna losowa,    

 - modele dynamiczne, w których uwzględnia ie czynnik czasu (przykład 1.2). Najlepiej znanym przypadkiem modelu dynamicznego jest model autoregresyjny,  w którym wśród zmiennych objaśniających występują jedynie opóźnione w czasie zmienne objaśniane.

KRYTERIUM 4. Ogólno poznawcze cechy modelu.

Podział: 

- modele przyczynowo opisowe wyrażające związki przyczynowo skutkowe między zmiennymi objaśniającymi i objaśnianymi,  

- modele symptomatyczne, w których rolę zmiennych objaśniających pełnią zmienne skorelowane z odpowiednimi zmiennymi objasnianymi a nie wyrażające źródeł zmienności zmiennych objaśnianych.

Ostatnie kryterium podziału modeli ekonometrycznych dotyczy modeli wielorównaniowych.

KRYTERIUM 5. Charakter powiązań między nieopóźnionymi zmiennymi endogenicznymi w modelu wielorównaniowym.

Podział:

 - modele proste,   

- modele rekurencyjne,   

- modele o równaniach współzależnych.

WERYFIKACJA MODELU EKONOMETRYCZNEGO JEDNORÓWNANIOWEGO

Proces weryfikacji modelu ekonometrycznego składa się z wielu kroków. Rodzaj obliczanych mierników statystycznych, oraz przeprowadzonych testów zależą od konkretnego modelu, od rodzaju danych statystycznych, na podstawie których szacowano parametry tego modelu, od liczby obserwacji. Nie powodzenie w badaniu jakiejkolwiek pożądanej cechy modelu powinno spowodować powrót do wcześniejszych etapów modelowania ekonometrycznego ( zmiana postaci analitycznej modelu, zmiana zestawu zmiennych egzogenicznych, zmiana metody szacunku parametrów) i rozpoczęcie procedury weryfikacji od początku.

Ogół działań w zakresie weryfikacji modelu można podzielić na :

weryfikację merytoryczną, która ma na celu stwierdzenie merytorycznej poprawności modelu,

weryfikację statystyczną, która ma celu stwierdzenie czy model spełnia postulaty sformułowane w teorii ekonometrii i statystyki.

Podczas weryfikacji merytorycznej badamy, np.:

czy sensowne są znaki parametrów modelu,

czy skala parametrów jest do przyjęcia,

czy model można sensownie ekstrapolować,

czy z modelu dla zmiennej Y wynikają sensowne modele dla zmiennych związanych z badaną zmienną.

Dopasowanie modelu. Współczynnik determinacji

Zgodność ( zbieżność) między zaobserwowanymi wartościami zmiennej objaśnianej a odpowiadającymi im wartościami modelowymi może być mierzona za pomocą współczynnika determinacji, zaś rozbieżność - za pomocą współczynnika indeterminacji ( rozbieżności).

Jest oczywiście tym lepiej, im współczynnik determinacji jest większy ( a współczynnik indeterminacji - mniejszy). Możemy, na przykład przyjąć, że dobry model to taki, w którym współczynnik determinacji jest większy od 0,9, ( czyli d 90% ),
a współczynnik indeterminacji - mniejszy od 0,1, ( czyli 10% ).

Współczynnik determinacji R² można obliczyć dla każdego modelu ekonometrycznego, bez względu na jego postać
i zastosowaną metodę estymacji parametrów. Trzeba jednak pamiętać, że odpowiednią interpretację można nadać współczynnikowi determinacji tylko wtedy, gdy zależność pomiędzy zmienną objaśnianą a zmiennymi objaśniającymi jest liniowa, parametry modelu oszacowano metodą najmniejszych kwadratów oraz model ekonometryczny zawiera wyraz wolny.

Standardowo przyjmuje się, że:

miarą ogólnej zaobserwowanej zmienności zmiennej Y jest suma kwadratów odchyleń wartości tej zmiennej od jej średniej, czyli tzw. ogólna suma kwadratów:

Σ (y - ỹ)²
miarą obserwowanej zmienności Y, nie wyjaśnionej przez model jest suma kwadratów odchyleń zmiennej Y od modelu, czyli suma kwadratów reszt:

Σ (y - ŷ)²

Współczynnik indeterminacji przyjmuje wartości nieujemne, a współczynnik determinacji i ile jest mniejszy lub równy 1 - wartości z przedziału < 0,1>.

Istotność zmiennych objaśniających

Konieczność badania istotności zmiennych objaśniających bierze się z oczywistego spostrzeżenia, że materiał statystyczny użyty do wyznaczenia parametrów modelu jest na ogół niewielkim fragmentem zbioru wszystkich możliwych wyników obserwacji zmiennej objaśnianej i zmiennych objaśniających.

W zbiorze możliwych wyników obserwacji zależność zmiennej Y od zmiennej X może w ogóle nie mieć miejsca, a to, że dla danego materiału statystycznego uzyskaliśmy parametr niezerowy, mogło być tylko przypadkowe.

Wszystkie zmienne objaśniające modelu ekonometrycznego muszą być istotne.

Badanie istotności może odbywać się w różny sposób. Standardowy sposób polega na wykorzystaniu założeń stochastycznych o sposobie powstawania wyników obserwacji zmiennej objaśnianej.

W przypadku modeli liniowych, spośród wielu układów założeń stochastycznych, najczęściej przyjmuje się założenia tzw. klasycznej normalnej regresji liniowej.
Przy tych założeniach, i gdy model wyznaczono klasyczną metodą najmniejszych kwadratów, badanie istotności zmiennej objaśniającej przebiega następująco:

Wartość krytyczną t_KR odczytujemy z tablic jako wartość rozkładu t - Studenta przy przyjętym poziomie istotności α (α - zazwyczaj 5%) oraz dotyczącej badanego modelu liczbie stopni swobody Q:

Q = T - K,

(gdzie T jest liczbą wyników obserwacji, zaś K jest liczbą szacowanych parametrów).

Aby obliczyć empiryczne statystyki t-Studenta, postępujemy następująco:

1. Najpierw liczymy oszacowanie odchylenia standardowego składników losowych, S:

2. Następnie liczymy tzw. szacunkowe błędy średnie

gdzie c_k - jest k- tym przekątniowym elementem macierzy odwrotnej ( X^TX )^-1.

3. Na koniec, liczymy empiryczną statystykę Studenta na podstawie wzoru:

, ( k=1,...,K ), gdyż

„empiryczna statystyka Studenta = parametr modelu / szacunkowy błąd średni”.

Interpretacja szacunkowego błędu średniego

Założenia stochastyczne regresji liniowej m.in. orzekają, że:

istnieje prawdziwy model Ω = α₁X₁ + ... + α_kX_k zmiennej Y,
z „prawdziwymi” parametrami α₁,...,α_k. Jest to tzw. model hipotetyczny zmiennej Y.

• Wartość y zmiennej Y w danej obserwacji jest jedną z wielu możliwych realizacji zmiennej Y, jakie mogły się w tej obserwacji ujawnić.

Możliwość innych wartości zmiennej Y wynika z działania tzw. składnika losowego, reprezentującego, na przykład, wpływ okoliczności losowych.W tej sytuacji użyty do wyznaczenia parametrów modelu materiał statystyczny jest z jednym z wielu materiałów statystycznych, a parametry a₁, ..., a_k modelu ekonometrycznego są jedną z wielu możliwych ocen parametrów α₁, ...,α_k modelu hipotetycznego. W szczególności parametr a_k jest jedną z wielu możliwych ocen parametru hipotetycznego α_k.

Szacunkowy błąd średni d_k jest oceną rozbieżności możliwych ocen parametru α_k wokół tego parametru.

Jest oczywiście tym lepiej im szacunkowy błąd średni jest mniejszy. Oznacza to bowiem, że możliwe oceny parametru α_k mniej się odchylają od tego parametru. A ponieważ jedną z tych możliwych ocen jest nasza ocena a_k dlatego sądzimy, że im szacunkowy błąd średni d_k jest mniejszy, tym przypuszczalna precyzja estymacji α_k przez a_k jest większa, a im jest on większy, tym przypuszczalna precyzja estymacji α_k przez a_k jest mniejsza.

Interpretacja oszacowania odchylenia standardowego składników losowych

Oszacowanie odchylenia standardowego składników losowych S jest oceną rozbieżności możliwych wartości zmiennej objaśnianej wokół modelu hipotetycznego.

Współczynnik zmienności losowej - Ve.

Współczynnik zmienności losowej jest definiowany następująco:

Współczynnik ten informuje, jaki procent średniej arytmetycznej zmiennej objaśnianej modelu stanowi odchylenie standardowe reszt. Mniejsze wartości tego współczynnika wskazują na lepsze dopasowanie modelu do danych empirycznych.

Jeżeli dla założonej z góry krytycznej wartości współczynnika zmienności losowej V* (np.V* = 10%) zachodzi nierówność:

V_e ≤ V*

To model uznaje się za dostatecznie dobrze dopasowany do danych empirycznych. Przy przeciwnym kierunku nierówności dopasowanie uznaje się za zbyt słabe. Współczynnik zmienności losowej ma zastosowanie także przy przeprowadzaniu porównania stopnia zgodności z danymi modeli opisujących kształtowanie się różnych zmiennych objaśnianych.

Współczynnik determinacji R² wskazuje, jaka część ogólnej zaobserwowanej

Zmienności zmiennej objaśnianej została wyjaśniona przez model ekonometryczny.

Współczynnik indeterminacji φ² mierzy natomiast tę część zaobserwowanej zmienności zmiennej objaśnianej, która nie została przez model wyjaśniona.

Współczynnik indeterminacji określony jest wzorem

Φ² = Σ (y - ŷ)²/ Σ (y - ỹ)²

Wspólczynnik determinacji oznaczany jest natomiast jako

R² = 1 - φ²

o ile φ² jest mniejsze lub równe 1.

Zmienna objaśniająca jest „istotna”, gdy w zauważalny (wyraźny) sposób wpływa na zmienną objaśnianą.

W wypadku modelu liniowego Y = a₀ + a₁X₁ + ... + a_nX_n zmienna jest istotna, gdy parametr przy niej stojący jest istotnie różny od zera.

1. Obliczamy tzw., empiryczną statystykę Studenta, t_{k ,} dotyczącą badanej zmiennej objaśniającej.

2. Ustalamy krytyczną wartość statystyki Studenta, t_KR.

3. Porównujemy moduł empirycznej statystyki Studenta z wartością krytyczną:

• Zmienną objaśniającą uznaje się za istotną, jeśli związana z nią statystyka empiryczna jest co do modułu większa od wartości krytycznej, tzn. , jeśli

| t_k | > t_KR,

• Jeśli natomiast jest odwrotnie, tzn. | t_k | ≤ t_KR to badaną zmienną objaśniającą uznajemy za nieistotną.

---