2014-10-15

1

Budowa i szacowanie modeli
ekonometrycznych

Witold Jurek

Etapy budowy modelu
ekonometrycznego



Określenie zjawiska, które ma być opisane za pomocą
modelu ekonometrycznego



Dobór zmiennej objaśnianej i zmiennych objaśniających



Dobór typu zależności pomiędzy zmiennymi



Zebranie danych statystycznych (wartości zmiennych)



Oszacowanie modelu



Weryfikacja oszacowanego modelu ekonometrycznego
(merytoryczna i statystyczna)

W.J. - Budowa i szacowanie modeli
ekonometrycznych

2

Idea metody
najmniejszych kwadratów



Hipoteza teoretyczna



Dane statystyczne (wartości zmiennych)

W.J. - Budowa i szacowanie modeli
ekonometrycznych

3

2014-10-15

2

Idea metody
najmniejszych kwadratów



Hipoteza empiryczna (model oszacowany)

𝑦

𝑡

= 𝑏

1

𝑥

𝑡1

+ 𝑏

2

𝑥

𝑡2

+ ⋯ + 𝑏

𝐾

𝑥

𝑡𝐾

(𝑡 = 1,2, … 𝑇)



Kryterium dopasowania (minimalizacja sumy
kwadratów odchyleń):

W.J. - Budowa i szacowanie modeli
ekonometrycznych

4

Idea metody
najmniejszych kwadratów

Warunek konieczny istnienia ekstremum:

…

W.J. - Budowa i szacowanie modeli
ekonometrycznych

5

















0

)

)(

...

(

2

)

(

2

2

2

1

1

2

t

tK

K

t

t

t

x

x

b

x

b

x

b

y

b

SKO





Idea metody
najmniejszych kwadratów



Układ równań normalnych

𝑏

1

𝑥

𝑡1

𝑥

𝑡1

+ 𝑏

2

𝑥

𝑡1

𝑥

𝑡2

+ ⋯ + 𝑏

𝐾

𝑥

𝑡1

𝑥

𝑡𝐾

= 𝑥

𝑡1

𝑦

𝑡

𝑏

1

𝑥

𝑡2

𝑥

𝑡1

+ 𝑏

2

𝑥

𝑡2

𝑥

𝑡2

+ ⋯ + 𝑏

𝐾

𝑥

𝑡2

𝑥

𝑡𝐾

= 𝑥

𝑡2

𝑦

𝑡

…

𝑏

1

𝑥

𝑡𝐾

𝑥

𝑡1

+ 𝑏

2

𝑥

𝑡𝐾

𝑥

𝑡2

+ ⋯ + 𝑏

𝐾

𝑥

𝑡𝐾

𝑥

𝑡𝐾

= 𝑥

𝑡𝐾

𝑦

𝑡

W.J. - Budowa i szacowanie modeli
ekonometrycznych

6

2014-10-15

3

Idea metody
najmniejszych kwadratów



Układ równań normalnych w zapisie macierzowym:



Rozwiązanie układu równań normalnych



Przypadek szczególny
– model z jedną zmienną objaśniającą:

– oceny (oszacowania) parametrów:

W.J. - Budowa i szacowanie modeli
ekonometrycznych

7

y

X

X

X

b

T

T

1

)

(





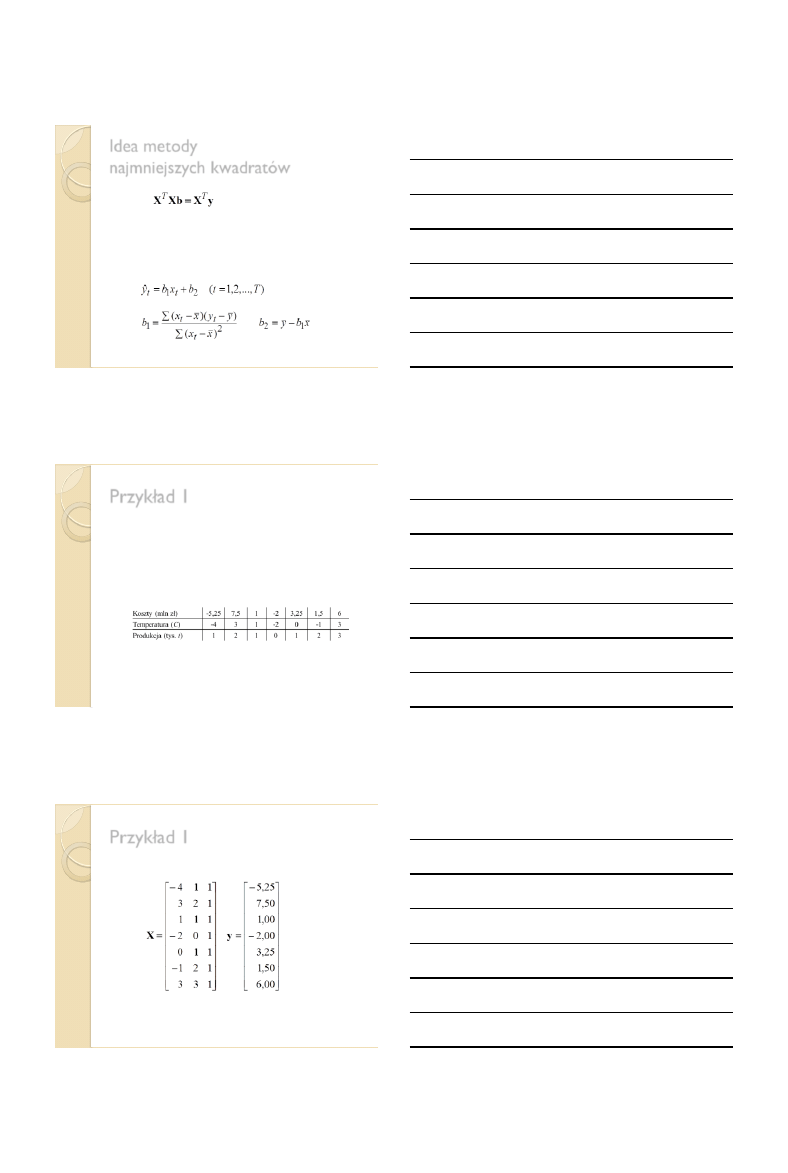
Przykład 1

Na całkowite koszty produkcji przedsiębiorstw przemysłu
owocowo-warzywnego, obok wielkości produkcji wpływają m.
in. warunki przechowywania surowców zależne od temperatury.
Wylosowano 7 przedsiębiorstw i stwierdzono, że koszty
całkowite, wielkość produkcji i temperatura przechowywania
surowców w okresie produkcji pewnego wyrobu kształtowały
się następująco:

(Liczby w tabeli są wyrażone w postaci odchyleń od wartości przeciętnych
zaobserwowanych w tym samym okresie roku poprzedniego).

W.J. - Budowa i szacowanie modeli
ekonometrycznych

8

Przykład 1



Dane statystyczne:

W.J. - Budowa i szacowanie modeli
ekonometrycznych

9

2014-10-15

4

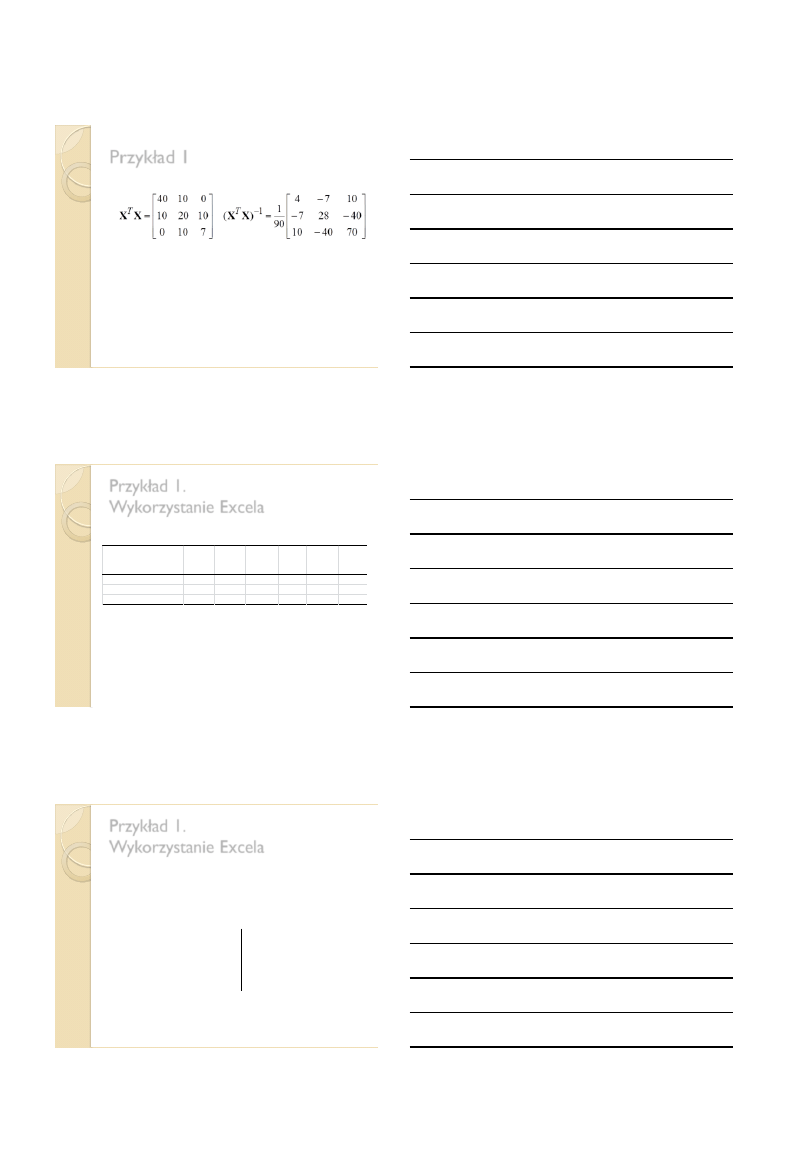
Przykład 1

Obliczenia

Oszacowany model ekonometryczny:

𝑦

𝑡

= 1,5𝑋

𝑡1

+ 0,5𝑋

𝑡2

+ 1,0

W.J. - Budowa i szacowanie modeli
ekonometrycznych

10

𝐗

𝑻

𝐲 =

65
35

12

𝐛 =

1,5

0,5
1,0

Przykład 1.
Wykorzystanie Excela

W.J. - Budowa i szacowanie modeli
ekonometrycznych

11

Współcz

ynniki

Błąd

standard

owy

t Stat

Wartość-

p

Dolne

95%

Górne

95%

Przecięcie

1,0

1,43735

0,69573 0,52491 -2,99072 4,99072

Zmienna X 1

1,5

0,34359

4,36564 0,01201 0,54604 2,45396

Zmienna X 2

0,5

0,90906

0,55002 0,61157 -2,02395 3,02395

Przykład 1.
Wykorzystanie Excela



Funkcja: reglinp(znane_y; znane_x; [stała]; [statystyka])



Wprowadzanie funkcji: Ctrl+Shift Enter



Wyniki obliczeń:

W.J. - Budowa i szacowanie modeli
ekonometrycznych

12

0,5

1,5

1

Oceny parametrów

0,90906 0,34359 1,43735

Średnie błędy

0,90923

1,6298 #N/D!

R2

s

#N/D!

20,0336

4 #N/D!

F

T-K

#N/D!

106,429

10,625 #N/D!

RSK

SKO #N/D!

2014-10-15

5

Wartości teoretyczne. Reszty



Wartości teoretyczne zmiennej objaśnianej:

𝒚 = 𝐗𝐛



Reszty:

𝐞 = 𝐲 − 𝐲

Własności reszt (model dowolny):



Układ równań normalnych:



Z układu równań wynika, że:

𝐗

𝑇

𝐲 = 𝐗

𝑇

y



Reszty spełniają warunek:

𝐗

𝑇

e =

𝟎

(𝐾,1)

albo warunek:

𝐞

𝑇

𝐗 = 𝟎

(1,𝐾)



Z definicji wartości teoretycznych wynika, że

𝐞

𝑻

𝒚 = 𝐞

𝑻

𝐗𝐛 = 𝟎

W.J. - Budowa i szacowanie modeli
ekonometrycznych

13

Własności oszacowań otrzymanych
metodą najmniejszych kwadratów



Własności reszt z modelu z wyrazem wolnym
(w macierzy wartości zmiennych objaśniających X jest
kolumna jedynek):

◦

Suma reszt jest równa zeru:

◦

Suma wartości empirycznych = suma wartości teoretycznych
zmiennej objaśnianej:

W.J. - Budowa i szacowanie modeli
ekonometrycznych

14

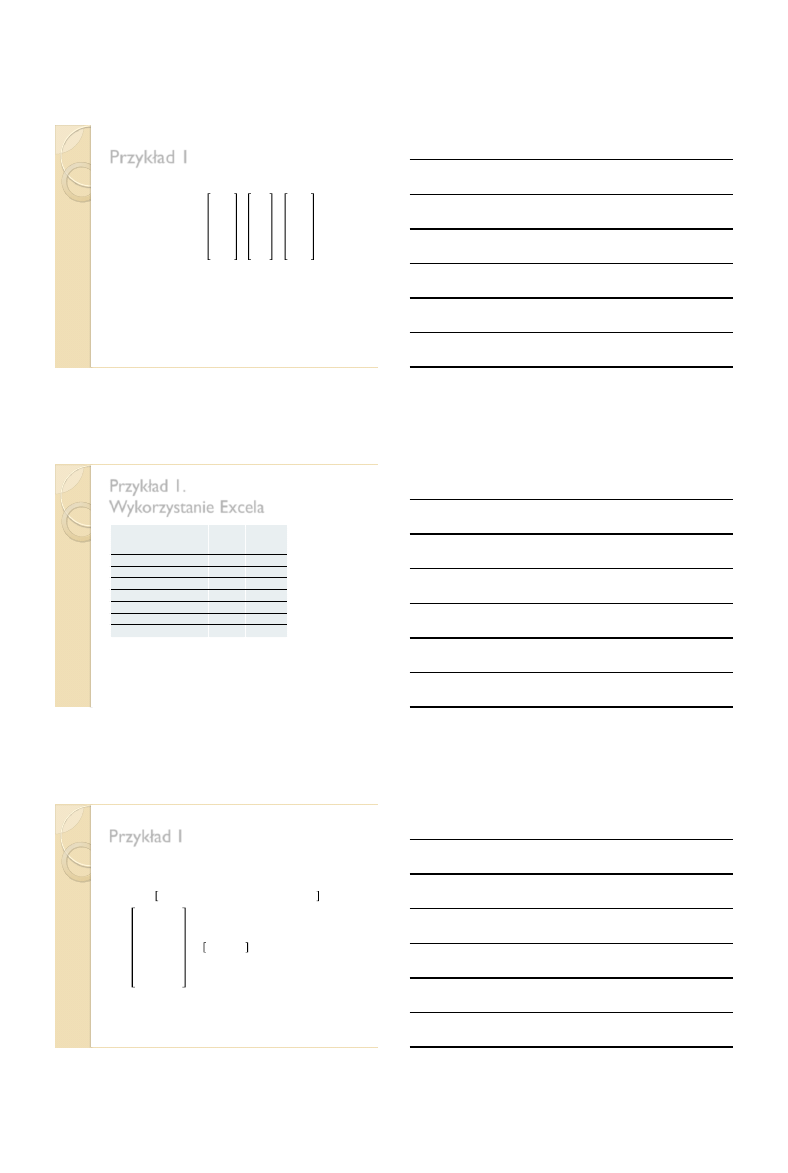
Wartości teoretyczne zmiennej objaśnianej





























































































































7

5

,

0

5

,

1

2

3

5

,

6

5

,

4

1

5

,

0

5

,

1

1

3

3

1

2

1

1

1

0

1

0

2

1

1

1

1

2

3

1

1

4

ˆ

Xb

y

W.J. - Budowa i szacowanie modeli
ekonometrycznych

15

2014-10-15

6

Przykład 1



Wektor reszt:

𝐞 = 𝐲 − 𝐲 =

−5,25

7,5

1

−2

3,25

1,5

6

−

−4,5

6,5

3

−2

1,5
0,5

7

=

−0,75

1

−2

0

1,75

1

−1



Szacowany model zawiera wyraz wolny. Można
zauważyć, że

◦

Suma reszt wynosi zero

◦

Suma wartości teoretycznych (12) jest równa sumie wartości
empirycznych (12) zmiennej objaśnianej

W.J. - Budowa i szacowanie modeli
ekonometrycznych

16

Przykład 1.
Wykorzystanie Excela

W.J. - Budowa i szacowanie modeli
ekonometrycznych

17

Obserwacja

Przewidy

wane Y

Składniki

resztowe

1

-4,5

-0,75

2

6,5

1,00

3

3,0

-2,00

4

-2,0

0,00

5

1,5

1,75

6

0,5

1,00

7

7,0

-1,00

Przykład 1



Reszty ortogonalne do kolumn macierzy X

𝐞

𝑇

X=

−0,75 1 −2 0 1,75 1 −1 X

X

−4 1 1

3

2 1

1

1 1

−2 0 1

0

1 1

−1 2 1

3

3 1

= 0 0 0

W.J. - Budowa i szacowanie modeli
ekonometrycznych

18

2014-10-15

7

Przykład 1



Reszty ortogonalne do wektora wartości teoretycznych
zmiennej objaśnianej

𝐲

𝐞

𝑇

𝐲 = −0,75 1 −2 0 1,75 1 −1 X

X

−4,5

6,5

3

−2

1,5

0,5

7

= 0

W.J. - Budowa i szacowanie modeli
ekonometrycznych

19

Sumy kwadratów
w modelu z wyrazem wolnym



Ogólna suma kwadratów:



Regresyjna suma kwadratów:



Suma kwadratów odchyleń:



Jeśli model zawiera wyraz wolny, to
OSK = RSK + SKO

W.J. - Budowa i szacowanie modeli
ekonometrycznych

20

Przykład 1
Sumy kwadratów



Obliczenia pomocnicze:



Sumy kwadratów:

OSK = 137,625 – 20, 5714 = 117,0536
RSK = 127,000 – 20,5714 = 106,4286
SKO = 137,625 – 127,000 = 10,625

(Można sprawdzić, że OSK = RSK + SKO)

W.J. - Budowa i szacowanie modeli
ekonometrycznych

21

2014-10-15

8

Ocena dopasowania oszacowanego
modelu do danych rzeczywistych



Współczynnik zbieżności:



Współczynnik determinacji:



Jeżeli szacowany model zawiera wyraz wolny, to

W.J. - Budowa i szacowanie modeli
ekonometrycznych

22

Ocena dopasowania oszacowanego
modelu do danych rzeczywistych



Współczynnik determinacji skorygowany
(ze względu na liczbę stopni swobody)

W.J. - Budowa i szacowanie modeli
ekonometrycznych

23

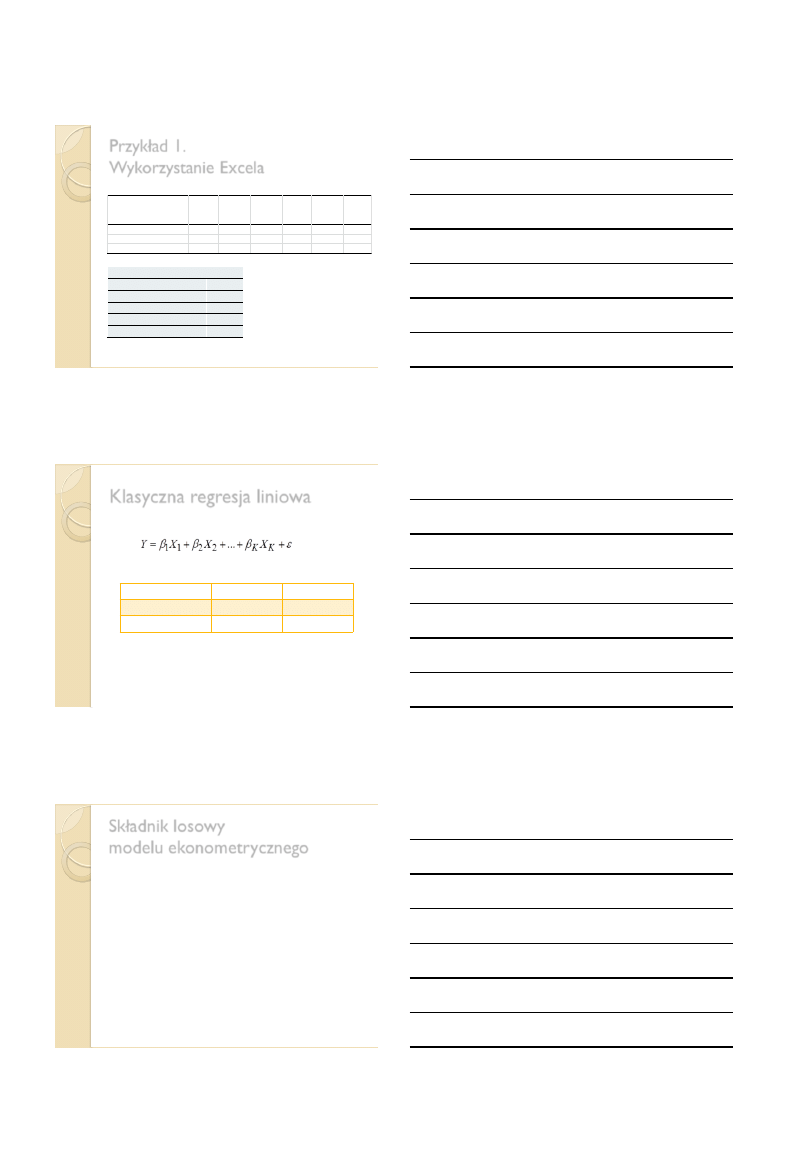
Przykład 1. Ocena dopasowania
oszacowanego modelu



Współczynnik zbieżności i determinacji:



Skorygowany współczynnik determinacji:

W.J. - Budowa i szacowanie modeli
ekonometrycznych

24

2014-10-15

9

Przykład 1.
Wykorzystanie Excela

W.J. - Budowa i szacowanie modeli
ekonometrycznych

25

Współcz

ynniki

Błąd

standard

owy

t Stat

Wartość-

p

Dolne

95%

Górne

95%

Przecięcie

1,0

1,43735

0,69573 0,52491 -2,99072 4,99072

Zmienna X 1

1,5

0,34359

4,36564 0,01201 0,54604 2,45396

Zmienna X 2

0,5

0,90906

0,55002 0,61157 -2,02395 3,02395

Statystyki regresji

Wielokrotność R

0,95354

R kwadrat

0,90923

Dopasowany R kwadrat

0,86384

Błąd standardowy

1,62980

Obserwacje

7

Klasyczna regresja liniowa



Hipoteza ekonometryczna – model



Charakterystyka wielkości występujących w modelu

W.J. - Budowa i szacowanie modeli
ekonometrycznych

26

Wielkości

Losowe

Nielosowe

Obserwowalne

Y

X

Nieobserwowalne

ε

β

Składnik losowy
modelu ekonometrycznego



Składnik losowy - zmienna losowa opisująca
(sumarycznie) wszystkie zakłócenia w obserwacji
opisywanego zjawiska i błędy poczynione w konstrukcji
modelu:

◦

zakłócenia czysto losowe

◦

błędy pomiaru zmiennych

◦

brakujące i „nietypowe” dane statystyczne

◦

nieuwzględnienie istotnej zmiennej objaśniającej

◦

uwzględnienie nieistotnej zmiennej objaśniającej

◦

przybliżenia funkcyjne

◦

zły typ funkcji wiążącej zmienne

◦

itd.

W.J. - Budowa i szacowanie modeli
ekonometrycznych

27

2014-10-15

10

Założenia dotyczące składnika
losowego



Hipoteza ekonometryczna zapisana dla danych
statystycznych (t = 1, 2, …, T) będących w dyspozycji

𝑦

𝑡

= 𝛽

1

𝑥

𝑡1

+ 𝛽

2

𝑥

𝑡2

+ ⋯ + 𝛽

𝐾

𝑥

𝑡𝐾

+ 𝜀

𝑡



Jest tyle składników losowych ile danych statystycznych



Każdy składnik losowy może powodować odchylenia
dodatnie i ujemne, ale średnia ze wszystkich

możliwych odchyleń wynosi zero



Rozproszenie składników losowych jest takie samo



Składniki losowe mają rozkład normalny



Składniki losowe dla różnych danych statystycznych są

niepowiązane ze sobą

W.J. - Budowa i szacowanie modeli
ekonometrycznych

28

Rozkład normalny



Funkcja gęstości

𝑓 𝑥 =

1

𝜎 2𝜋

𝑒

−

(𝑥−𝜇)

2

2𝜎

2



Dystrybuanta

𝐹 𝑥 = 𝑓 𝑡 𝑑𝑡

𝑥

−∞



Momenty

E(

𝑥) = μ

𝐷

2

𝑥 = 𝜎

2



Rozkład standaryzowany: E(

𝑥) = 0 , 𝐷

2

𝑥 = 1

29

W.J. - Budowa i szacowanie modeli
ekonometrycznych

Rozkład normalny



Funkcja gęstości (rozkład standaryzowany)

30

W.J. - Budowa i szacowanie modeli
ekonometrycznych

0

0,1

0,2

0,3

0,4

0,5

-4

-3

-2

-1

0

1

2

3

4

2014-10-15

11

Rozkład normalny



Dystrybuanta (rozkład standaryzowany)

31

W.J. - Budowa i szacowanie modeli
ekonometrycznych

0

0,2

0,4

0,6

0,8

1

1,2

-4

-3

-2

-1

0

1

2

3

4

Założenia dotyczące składnika
losowego



Zerowa wartość oczekiwana (średnia):
𝐸 𝜀

𝑡

= 0 dla t = 1, 2, …, T



Jednakowa wariancja (jednakowe rozproszenie):
𝐷

2

𝜀

𝑡

= 𝜎

2

dla t = 1, 2, …, T



Zerowa kowariancja (brak powiązania):

𝑐𝑜𝑣 𝜀

𝑡

, 𝜀

𝑠

= 0 dla 𝑡 ≠ 𝑠

W.J. - Budowa i szacowanie modeli
ekonometrycznych

32

Macierz wariancji i kowariancji
wektora estymatorów



Oszacowanie wariancji składników losowych:

𝑠

2

=

𝑆𝐾𝑂

𝑇 − 𝐾

=

𝑒

𝑡

2

𝑇 − 𝐾

=

(𝑦

𝑡

− 𝑦

𝑡

)

2

𝑇 − 𝐾



Przykładowe oszacowanie wariancji składników
losowych



Odchylenie standardowe składników losowych
s = 1,6298

W.J. - Budowa i szacowanie modeli
ekonometrycznych

33

2014-10-15

12

Macierz wariancji i kowariancji
wektora estymatorów



Skoro zmienna objaśniana Y jest zmienną losową, to
estymator,

𝐁 = (𝐗

𝑇

𝐗)

−1

𝐗

𝑇

𝐘, jest zmienną losową



Jest to zmienna losowa K – wymiarowa, o macierzy
wariancji i kowariancji

𝐒

𝐁

= 𝑠

2

(𝐗

𝑇

𝐗)

−1



Przykładowe oszacowanie

W.J. - Budowa i szacowanie modeli
ekonometrycznych

34







































70

40

10

40

28

7

10

7

4

90

1

65625

,

2

)

(

1

2

X

X

S

B

T

s































06597

,

2

18056

,

1

29514

,

0

18056

,

1

82639

,

0

20660

,

0

29514

,

0

20660

,

0

11806

,

0

Średnie błędy szacunku parametrów



Średnie błędy szacunku parametrów
(odchylenia standardowe estymatorów)

W.J. - Budowa i szacowanie modeli
ekonometrycznych

35

90906

,

0

82639

,

0

2





s

43735

,

1

06597

,

2

0





s

Przykład 1.
Wykorzystanie Excela

W.J. - Budowa i szacowanie modeli
ekonometrycznych

36

Współcz

ynniki

Błąd

standard

owy

t Stat

Wartość-

p

Dolne

95%

Górne

95%

Przecięcie

1,0

1,43735

0,69573 0,52491 -2,99072 4,99072

Zmienna X 1

1,5

0,34359

4,36564 0,01201 0,54604 2,45396

Zmienna X 2

0,5

0,90906

0,55002 0,61157 -2,02395 3,02395

Statystyki regresji

Wielokrotność R

0,95354

R kwadrat

0,90923

Dopasowany R kwadrat

0,86384

Błąd standardowy

1,62980

Obserwacje

7

2014-10-15

13

Wnioskowanie o istotności
parametrów modelu



Hipotezy:



Wartość statystyki testowej (statystyki o rozkładzie t
Studenta):

W.J. - Budowa i szacowanie modeli
ekonometrycznych

37

k

k

k

k

s

b

t







Wnioskowanie o istotności
parametrów modelu



Wartość krytyczna statystyki t Studenta: t(α, T-K):

◦

α – poziom istotności

◦

T – K – liczba stopni swobody (liczba danych – liczba
szacowanych parametrów)



Jeżeli , to nie ma podstaw do
odrzucenia hipotezy zerowej



Jeżeli , to hipotezę zerową należy
odrzucić na rzecz hipotezy alternatywnej

W.J. - Budowa i szacowanie modeli
ekonometrycznych

38

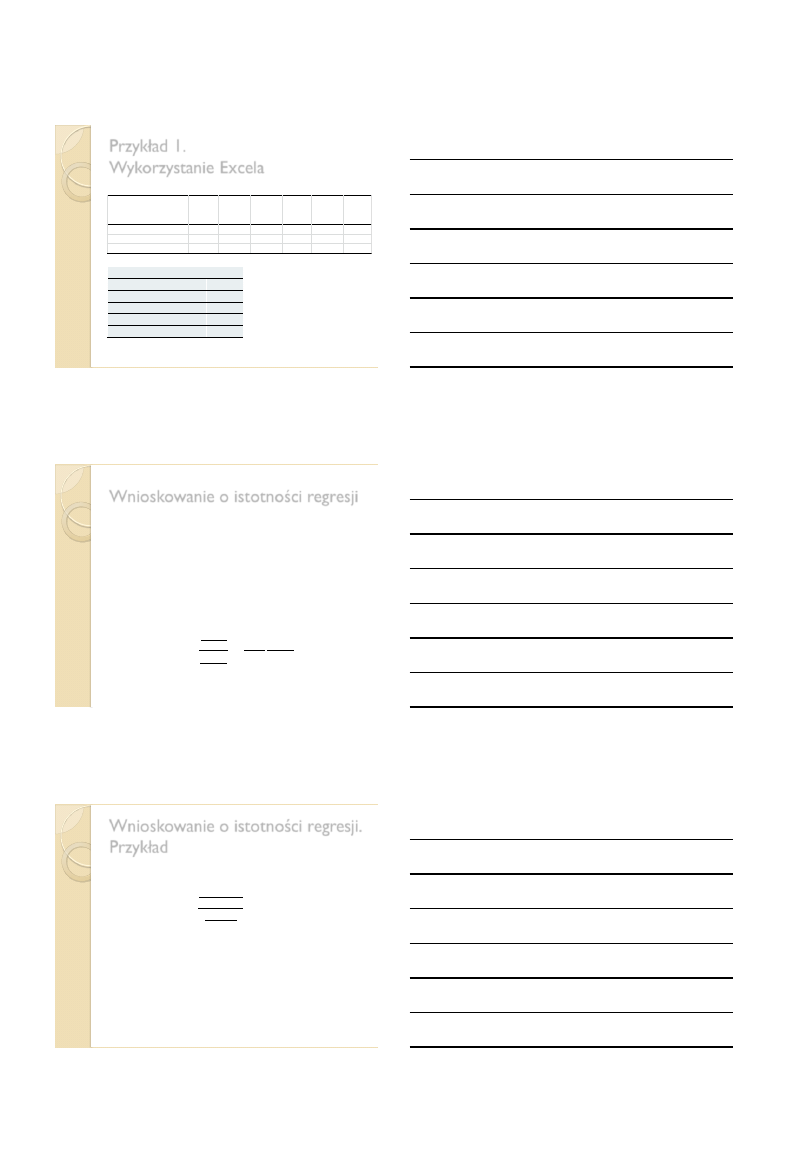
Funkcja gęstości rozkładu t Studenta

Wartości krytyczne dla α = 0,05; T - K = 4

W.J. - Budowa i szacowanie modeli
ekonometrycznych

39

0

0,1

0,2

0,3

0,4

-4

-3

-2

-1

0

1

2

3

4

2,776

-2,776

0,95

0,025

0,025

2014-10-15

14

Przykład 1.
Istotność parametrów modelu



Wartości empiryczne statystyki t Studenta, przy
założeniu o prawdziwości

𝐻

0

𝑡

1

=

1,5

0,34359

= 4,36564

𝑡

2

=

0,5

0,90906

= 0,69573

𝑡

0

=

1,0

1,43735

= 0,55002

Wartość krytyczna t(α, T – K) = t(0,05; 4) = 2,776

W.J. - Budowa i szacowanie modeli
ekonometrycznych

40

Przedział ufności dla parametru
szacowanego modelu



Przedział ufności dla parametru:

𝑏

𝑘

− 𝑠

𝑘

𝑡 𝛼, 𝑇 − 𝐾 < 𝛽

𝑘

< 𝑏

𝑘

+ 𝑠

𝑘

𝑡 𝛼, 𝑇 − 𝐾



W przykładzie 1 przedziały ufności zostaną wyznaczone



przy poziomie ufności 1 – α = 0,95



przy liczbie stopni swobody równej T – K = 7 – 3 = 4



Wartość statystyki t Studenta

𝑡 0,05; 4 = 2,776

W.J. - Budowa i szacowanie modeli
ekonometrycznych

41

Przedziały ufności dla parametrów
szacowanego modelu

0,54604 < 𝛽

1

< 2,45396

−2,02395 < 𝛽

2

< 3,02395

−2,99072 < 𝛽

0

< 4,99072

W.J. - Budowa i szacowanie modeli
ekonometrycznych

42

776

,

2

9091

,

0

5

,

0

776

,

2

9091

,

0

5

,

0

2















2014-10-15

15

Przykład 1.
Wykorzystanie Excela

W.J. - Budowa i szacowanie modeli
ekonometrycznych

43

Współcz

ynniki

Błąd

standard

owy

t Stat

Wartość-

p

Dolne

95%

Górne

95%

Przecięcie

1,0

1,43735

0,69573 0,52491 -2,99072 4,99072

Zmienna X 1

1,5

0,34359

4,36564 0,01201 0,54604 2,45396

Zmienna X 2

0,5

0,90906

0,55002 0,61157 -2,02395 3,02395

Statystyki regresji

Wielokrotność R

0,95354

R kwadrat

0,90923

Dopasowany R kwadrat

0,86384

Błąd standardowy

1,62980

Obserwacje

7

Wnioskowanie o istotności regresji



Wnioskowanie odnosi się modelu z wyrazem wolnym



Wnioskowanie dotyczy wszystkich parametrów
będących składowymi wektora

𝛃

𝑏𝑒𝑧 𝑤𝑤

(jest to wektor

𝛃 bez wyrazu wolnego)



Hipotezy:

𝐻

0

: 𝛃

𝑏𝑒𝑧 𝑤𝑤

= 𝟎

𝐻

1

: 𝛃

𝑏𝑒𝑧 𝑤𝑤

≠ 𝟎



Statystyka:

𝐹 =

𝑅𝑆𝐾

𝐾 − 1

𝑆𝐾𝑂

𝑇 − 𝐾

=

𝑅𝑆𝐾
𝑆𝐾𝑂

𝑇 − 𝐾
𝐾 − 1

W.J. - Budowa i szacowanie modeli
ekonometrycznych

44

Wnioskowanie o istotności regresji.
Przykład



Wartość statystyki testowej

𝐹 =

106,4286

2

10,625

4

= 20,0336



Wartość krytyczna: F(0,05; 2; 4) = 6,944

W.J. - Budowa i szacowanie modeli
ekonometrycznych

45

2014-10-15

16

Przykład 1.
Wykorzystanie Excela

Analiza wariancji

W.J. - Budowa i szacowanie modeli
ekonometrycznych

46

df

SS

MS

F

Istotność

F

Regresja

2

106,4286

53,2143 20,0336

0,0082

Resztkowy

4

10,6250

2,6563

Razem

6

117,0536

Model z jedną zmienną objaśniającą.
Linia charakterystyczna



Notowania PKO bp względem WIG
(okres: 29 czerwca 2012 – 30 sierpnia 2012;
stopy zwrotu składane ciągle; 42 dane)

W.J. - Budowa i szacowanie modeli
ekonometrycznych

47

Model z jedną zmienną objaśniającą.
Linia charakterystyczna

W.J. - Budowa i szacowanie modeli
ekonometrycznych

48

df

SS

MS

F

Istotność F

Regresja

1

0,00465

0,00465 51,12197

0,00000

Resztkowy

40

0,00364

0,00009

Razem

41

0,00829

Statystyki regresji

Wielokrotność R

0,74902

R kwadrat

0,56103

Dopasowany R kwadrat

0,55005

Błąd standardowy

0,00954

Obserwacje

42

2014-10-15

17

Założenia, przy jakich stawiane są
prognozy



Założenia przyjmowane przy szacowaniu

◦

Zależność

𝑦

𝑡

= 𝛽

1

𝑥

𝑡1

+ 𝛽

2

𝑥

𝑡2

+ ⋯ + 𝛽

𝐾

𝑥

𝑡𝐾

+ 𝜀

𝑡

dla t =1,…,T

◦

Dana macierz X wartości zmiennych objaśniających

◦

Składniki losowe

𝜀

𝑡



mają zerową średnią, wariancję równą

𝜎

2

, są ze sobą niepowiązane



mają rozkład normalny N(0, σ)



Założenia przyjmowane przy prognozowaniu

◦

Zależność

𝑦

𝑁

= 𝛽

1

𝑥

𝑁1

+ 𝛽

2

𝑥

𝑁2

+ ⋯ + 𝛽

𝐾

𝑥

𝑁𝐾

+ 𝜀

𝑁

dla N > T

◦

Dany jest wektor

𝐱

𝑁

wartości zmiennych objaśniających

◦

Składnik losowy

𝜀

𝑁



ma zerową średnią, wariancję równą

𝜎

2

, jest niepowiązany z

𝜀

𝑡



ma rozkład normalny N(0, σ)

W.J. - Budowa i szacowanie modeli
ekonometrycznych

49

Prognozowanie na podstawie
modelu ekonometrycznego

W.J. - Budowa i szacowanie modeli
ekonometrycznych

50



Wektor wartości zmiennych objaśniających



Prognoza



Wariancja błędu prognozowania (pojedynczej wartości)



Przedział ufności dla przyszłej wartości zmiennej
objaśnianej

𝑦

𝑁

− 𝑠

𝑁

𝑡 𝛼, 𝑇 − 𝐾 < 𝑦

𝑁

< 𝑦

𝑁

+ 𝑠

𝑁

𝑡 𝛼, 𝑇 − 𝐾

𝑠

𝑁

2

= 𝑠

2

(1 + 𝐱

𝑁

(𝐗

𝑇

𝐗)

−1

𝐱

𝑁

𝑇

)

Prognozowanie na podstawie modelu
ekonometrycznego. Przykład 1



Jakich kosztów może się spodziewać przykładowe
przedsiębiorstwo przetwórstwa owocowo – warzywnego
w przyszłym roku, jeżeli – według planów – produkcja
będzie o 6 tys. t wyższa od produkcji tegorocznej a
temperatura przechowywania surowców o 4

o

C wyższa

od temperatury, w jakiej przechowywano surowiec w
bieżącym roku?



Wektor wartości zmiennych objaśniających

W.J. - Budowa i szacowanie modeli
ekonometrycznych

51

2014-10-15

18

Prognozowanie na podstawie modelu
ekonometrycznego. Przykład 1



Prognoza



Wariancja błędu prognozowania

W.J. - Budowa i szacowanie modeli
ekonometrycznych

52

64

,

14

)

90

406

1

(

65625

,

2

2







N

s

Prognozowanie na podstawie modelu
ekonometrycznego. Przykład 1



Średni błąd prognozowania



Przedział ufności dla przyszłej wartości zmiennej
objaśnianej

W.J. - Budowa i szacowanie modeli
ekonometrycznych

53

6

,

20

6

,

0







N

y