mgr Grzegorz Stolarczyk

1

Ekonometria 1

BLOK 4

Weryfikacja liniowych modeli ekonometrycznych

Weryfikacja modelu liniowego szacowanego klasyczn

ą

metod

ą

najmniejszych kwadratów polega

na zbadaniu:

•

merytorycznej oceny sensowno

ś

ci ocen parametrów strukturalnych modelu,

•

dopasowania modelu do danych empirycznych,

•

istotno

ś

ci parametrów strukturalnych modelu,

•

własno

ś

ci składnika losowego

Przykład 1.

Na podstawie danych dotycz

ą

cych wydajno

ś

ci pracy prosz

ę

zweryfikowa

ć

model liniowy

26

9

,

0

8

,

4

3

2

^

+

⋅

−

⋅

=

x

x

y

Y

X

2

X

3

14

0,4

15

17

0,6

13

14,5

0,4

15

20

0,7

11

21,6

1

10

23

1,2

10

24,5

1

7

28

1,5

6

26,4

1,5

8

29

1,7

5

Rozwi

ą

zanie:

1. Badanie merytorycznej oceny sensowno

ś

ci ocen parametrów strukturalnych modelu

Sprawdzamy czy współczynnik korelacji pomi

ę

dzy zmiennymi Y, X

2

i X

3

i znak ocen parametrów s

ą

jednakowe.

R

yx2

= 0,972, R

yx3

= -0,985

Znaki parametrów:

a

1

= 4,8, a

2

= -0,9

Znaki si

ę

zgadzaj

ą

, wi

ę

c uzyskane szacunki parametrów modelu wskazuj

ą

kierunek zale

ż

no

ś

ci

mi

ę

dzy zmienn

ą

obja

ś

nian

ą

a zmiennymi obja

ś

niaj

ą

cymi x

2

i x

3

zgodny z zale

ż

no

ś

ci

ą

wynikaj

ą

c

ą

z danych empirycznych. Przechodzimy do nast

ę

pnego etapu weryfikacji.

mgr Grzegorz Stolarczyk

2

Ekonometria 1

2. Badanie dopasowania modelu do danych empirycznych

Ocena dopasowania modelu do danych empirycznych ma na celu sprawdzenie, czy model ten

w wystarczaj

ą

co wysokim stopniu wyja

ś

nia kształtowanie si

ę

zmiennej obja

ś

nianej.

Obliczamy współczynnik zgodno

ś

ci ze wzoru:

∑

∑

=

=

−

=

n

i

n

i

Y

Y

e

1

2

1

2

2

)

(

ϕ

∑

=

n

i

e

1

2

= 1,24

Y

2

)

(

Y

Y

−

14

60,84

17

23,04

14,5

53,29

20

3,24

21,6

0,04

23

1,44

24,5

7,29

28

38,44

26,4

21,16

29

51,84

ś

rednia

21,8

suma

260,62

=

2

ϕ

004758

,

0

2

,

260

24

,

1

=

Liczymy współczynnik determinacji:

2

2

1

ϕ

−

=

R

=

2

R

1 - 0,004758 = 0,995242

Trzeci

ą

miar

ą

dopasowania jest współczynnik zmienno

ś

ci losowej, który wyra

ż

a si

ę

wzorem:

%

100

⋅

=

Y

Se

We

gdzie:

Se

2

Se

=

- odchylenie standardowe składnika losowego

mgr Grzegorz Stolarczyk

3

Ekonometria 1

W naszym przykładzie wynosi on:

=

We

%

93

,

1

%

100

8

,

21

421

,

0

=

⋅

Z oblicze

ń

wynika,

ż

e model jest bardzo dobrze dopasowany do danych empirycznych. Jak wynika

ze współczynnika determinacji ponad 99% zmienno

ś

ci zmiennej obja

ś

nianej została wyja

ś

niona

przez model.

Przykład 2.

Prosz

ę

na podstawie danych zbada

ć

dopasowanie modelu do danych empirycznych za pomoc

ą

współczynnika zgodno

ś

ci i determinacji:

Model ma posta

ć

:

1

^

48

,

0

87

,

111

X

y

⋅

−

=

Rozwi

ą

zanie:

Liczymy miary dopasowania modelu:

=

2

ϕ

0,90

=

2

R

0,10

Jak wida

ć

z oblicze

ń

model wyja

ś

nia zaledwie 10% zmienno

ś

ci zmiennej obja

ś

nianej i jest

ź

le

dopasowany do danych empirycznych.

Powinni

ś

my zatem zmieni

ć

posta

ć

analityczn

ą

modelu i poszuka

ć

modelu nieliniowego,

który by najlepiej opisywał badane zjawisko lub znale

źć

inne zmienne obja

ś

niaj

ą

ce liniowo powi

ą

zane

ze zmienn

ą

obja

ś

nian

ą

.

Y

X

1

99

1

107

2

115

2

113

3

116

4

117

5

109

7

107

9

101

14

mgr Grzegorz Stolarczyk

4

Ekonometria 1

Przykład 3.

Prosz

ę

na podstawie danych zbada

ć

dopasowanie modelu do danych empirycznych:

Y

X

1

X

2

10

6

8

10

6

8

16

10

12

16

10

12

12

8

8

14

10

8

20

12

14

20

12

16

20

12

16

22

14

18

Rozwi

ą

zanie:

Szacujemy parametry i otrzymujemy nast

ę

puj

ą

c

ą

posta

ć

modelu:

252

,

0

447

,

0

039

,

1

2

1

^

+

⋅

+

⋅

=

x

x

y

Obliczamy miary dopasowania modelu:

=

2

ϕ

0,011

=

2

R

0,989

=

We

3%

Model jest bardzo dobrze dopasowany do danych rzeczywistych. Wyja

ś

nia prawie 99% zmienno

ś

ci

zmiennej obja

ś

nianej.

3. Badanie istotno

ś

ci parametrów strukturalnych modelu

Przykład 1.

Sprawdzamy na podstawie modelu opisuj

ą

cego wydajno

ść

pracy czy parametry modelu istotnie

ró

ż

ni

ą

si

ę

od zera, a tym samym czy zmienne obja

ś

niaj

ą

ce w sposób istotny wpływaj

ą

na zmienn

ą

obja

ś

nian

ą

.

Sprawdzamy istotno

ść

ze wzoru:

)

(

j

j

a

S

a

I

=

gdzie:

j

a -

warto

ść

szacunku j-tego parametru

)

(

j

a

S

- standardowy bł

ą

d szacunku j-tego parametru

mgr Grzegorz Stolarczyk

5

Ekonometria 1

Sprawdzamy istotno

ść

parametrów: a

1

i a

2

I

1

=

04

,

6

794

,

0

8

,

4

=

I

2

=

55

,

8

105

,

0

9

,

0

=

−

Warto

ść

krytyczna I* dla poziomu istotno

ś

ci

∝

= 0,05 i n-m stopni swobody wynosi I* = 2,365.

Obliczone I

1

i I

2

s

ą

wi

ę

ksze od warto

ś

ci krytycznej, wi

ę

c parametry istotnie ró

ż

ni

ą

si

ę

od zera,

a tym samym zmienne obja

ś

niaj

ą

ce X

2

i X

3

w sposób istotny wpływaj

ą

na zmienn

ą

obja

ś

nian

ą

.

Przykład 2.

Prosz

ę

zbada

ć

istotno

ść

parametrów a

1

i a

2

modelu wiedz

ą

c,

ż

e:

657

,

1

044

,

0

193

,

0

2

1

^

+

⋅

+

⋅

=

x

x

y

Y

X

1

X

2

1,8

2,2

2

2,1

2,5

5

2,3

3

7

2,8

3,4

5

2,8

4

8

3,4

4,6

9

3,2

5,3

10

3,6

6,1

10

3,5

6,9

9

3,7

7,9

12

3,8

9

14

4,2

9,5

15

4,8

12,3

22

Rozwi

ą

zanie:

Wyznaczamy standardowe bł

ę

dy szacunku parametrów:

S(a

1

) = 0,094

S(a

2

) = 0,056

Sprawdzamy istotno

ść

parametrów:

I

1

= 2,056

I

2

= 0,786

Warto

ść

krytyczna I* dla poziomu istotno

ś

ci

∝

= 0,05 i n-m stopni swobody wynosi I* = 2,228.

Obliczone I

1

i I

2

s

ą

mniejsze od warto

ś

ci krytycznej, wi

ę

c parametry nieistotnie ró

ż

ni

ą

si

ę

od zera,

a tym samym zmienne obja

ś

niaj

ą

ce X

1

i X

2

nie wpływaj

ą

w sposób istotny na zmienn

ą

obja

ś

nian

ą

.

mgr Grzegorz Stolarczyk

6

Ekonometria 1

Nale

ż

y zmodyfikowa

ć

zestaw zmiennych obja

ś

niaj

ą

cych i dobra

ć

takie, które b

ę

d

ą

silnie wpływa

ć

na zmienn

ą

obja

ś

nian

ą

.

4. Badanie własno

ś

ci składnika losowego

Przykład 1.

Procedur

ę

badania własno

ś

ci składnika losowego przeprowadzamy na podstawie wektora reszt.

Badanie przeprowadzamy na warto

ś

ciach wektora reszt z zadania dotycz

ą

cego wydajno

ś

ci pracy.

a. Badanie symetryczno

ś

ci

Weryfikacja hipotezy o symetryczno

ś

ci rozkładu odchyle

ń

losowych modelu ma na celu ocen

ę

trafno

ś

ci wyboru postaci analitycznej modelu.

Do sprawdzania symetryczno

ś

ci stosujemy test symetrii. Sprawdzamy ile w wektorze reszt

znajduje si

ę

reszt dodatnich:

e

-0,42

-0,18

0,08

0,54

-0,2

0,24

-0,00000000000034

0,2

0,4

-0,66

Mamy 5 reszt dodatnich. Wg tablic do testu symetrii dla n=10 liczba reszt dodatnich powinna

mie

ś

ci

ć

si

ę

w przedziale <2,8>. Mie

ś

ci si

ę

, wi

ę

c wektor reszt jest symetryczny.

Przykład 2.

Prosz

ę

zbada

ć

symetryczno

ść

wektora reszt.

e

0,40

-1,16

0,02
0,04

0,10

0,01

0,09

0,50

mgr Grzegorz Stolarczyk

7

Ekonometria 1

Mamy 7 reszt dodatnich. Wg tablic do testu symetrii dla n=8 liczba reszt dodatnich powinna mie

ś

ci

ć

si

ę

w przedziale <2,6>. Nie mie

ś

ci si

ę

, wi

ę

c wektor reszt nie jest symetryczny. Mo

ż

e to by

ć

spowodowane niewła

ś

ciwym doborem postaci analitycznej modelu.

b. Losowo

ść

Weryfikacja hipotezy o losowo

ś

ci rozkładu odchyle

ń

losowych modelu ma na celu, tak jak

w przypadku symetryczno

ś

ci, ocen

ę

trafno

ś

ci wyboru postaci analitycznej modelu.

Do sprawdzania losowo

ś

ci wykorzystujemy test serii. Seria jest to ci

ą

g kolejnych reszt o tym

samym znaku.

Przykład 1:

e

-0,42

-0,18

1 seria

0,08

0,54

2 seria

-0,2

3 seria

0,24

4 seria

-0,00000000000034

5 seria

0,2

0,4

6 seria

-0,66

7 seria

Sprawdzamy czy liczba serii mie

ś

ci si

ę

w przedziale odczytanym z tablic do testu serii dla poziomu

istotno

ś

ci

∝

= 0,05.

Dolna granica przedziału odczytana z tablic to 3, a górna granica to 8 serii. Liczba serii w zadaniu

to 7, wi

ę

c wektor reszt ma charakter losowy.

mgr Grzegorz Stolarczyk

8

Ekonometria 1

Przykład 2.

Prosz

ę

zbada

ć

losowo

ść

wektora reszt.

Y

^

Y

3086,07 2901,313
3336,04 3177,106
3407,02 3452,898
3644,65 3646,897
3888,45 3987,356
4160,02 4239,379
4456,29 4637,861
4712,43 4930,781
5135,22 5254,113
5283,35 5519,422
5558,01 5842,754
6008,58 6329,672
6644,31 6799,464
7363,37 7187,463
8131,80 7510,795
8863,20 7912,079
9464,98 8323,848
9937,15 9389,962

10236,50

10169,8

10001,96 10319,06

9403,26 10251,59
8273,76 7984,427
7820,10 8234,373
8289,19 8854,465
8752,10 9000,925

Liczymy warto

ś

ci wektora reszt i sprawdzamy liczb

ę

serii:

e

184,76
158,94

-45,88

-2,25

-98,91
-79,36

-181,57
-218,35
-118,89
-236,07
-284,74
-321,09
-155,15

175,90
621,00
951,12

1141,13

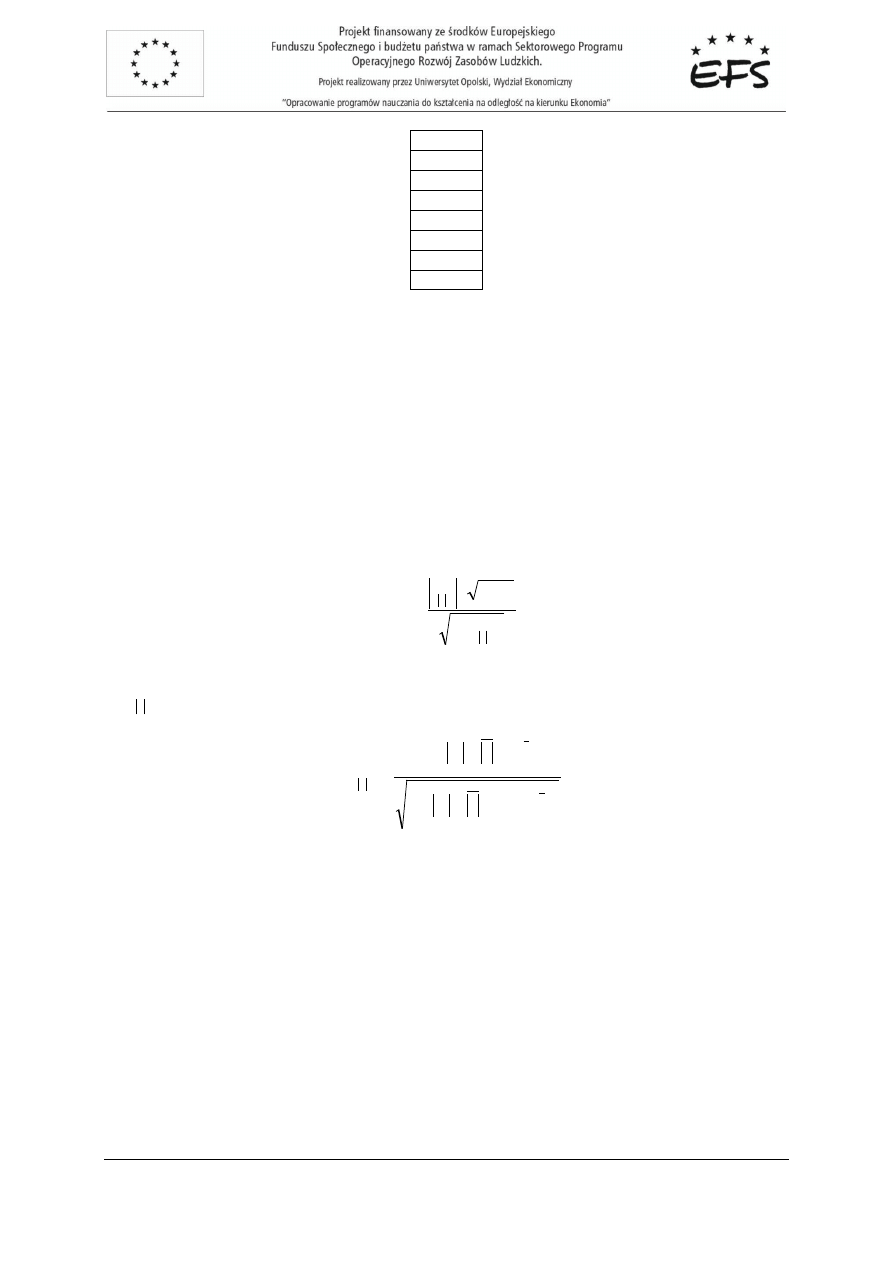
mgr Grzegorz Stolarczyk

9

Ekonometria 1

547,19

66,70

-317,11
-848,33

289,33

-414,27
-565,28
-248,83

Dolna granica przedziału odczytana z tablic testu serii to 8, a górna granica to 16 serii. Liczba serii

w zadaniu to 6, wi

ę

c wektor reszt nie ma charakteru losowego. Nale

ż

y zmieni

ć

posta

ć

analityczn

ą

modelu.

c. Stacjonarno

ść

Badanie stacjonarno

ś

ci odchyle

ń

losowych ma na celu sprawdzenie stało

ś

ci ich wariancji.

Badanie stacjonarno

ś

ci odnosi si

ę

modeli dynamicznych i polega na sprawdzeniu czy moduł wektora

reszt jest liniowo zale

ż

ny od czasu.

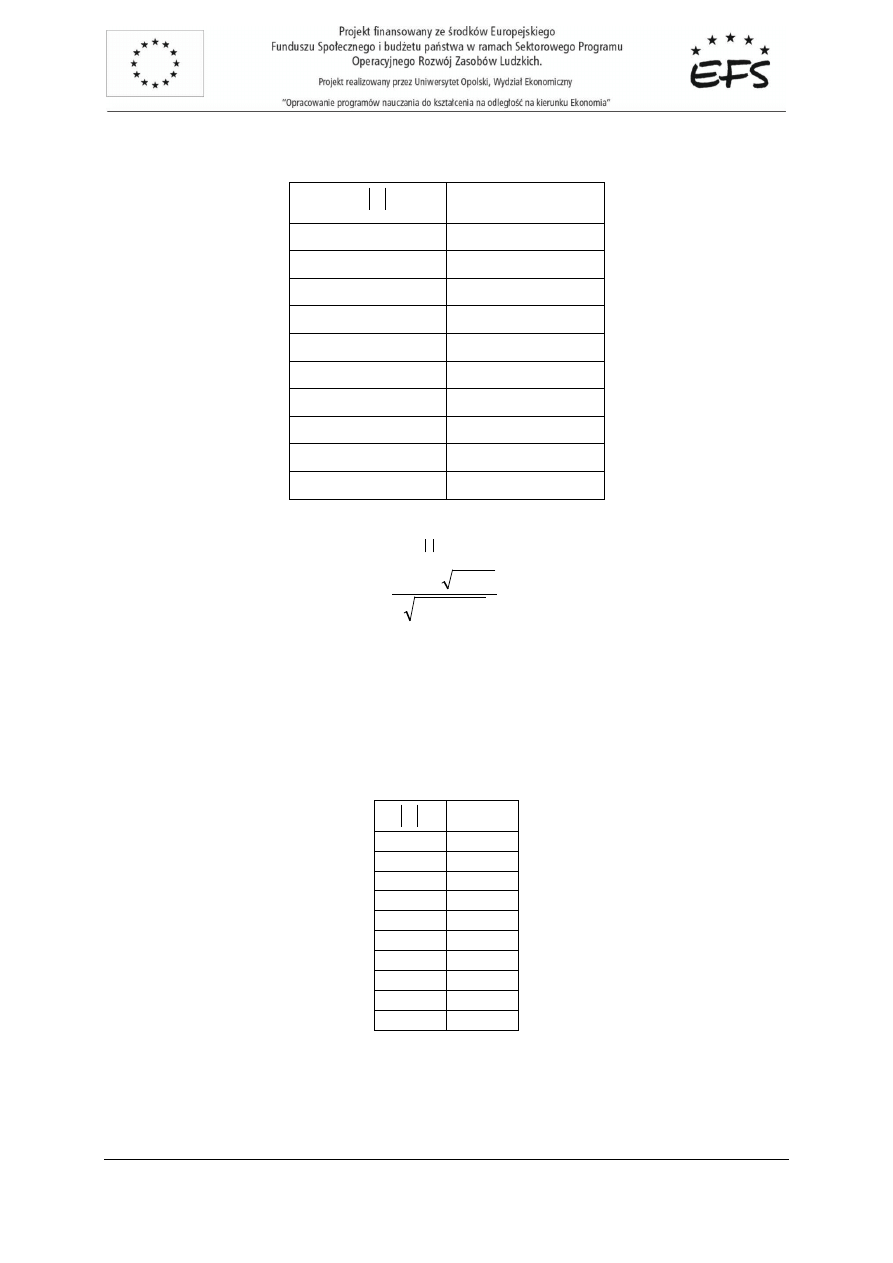
Sprawdzamy statystyk

ę

na stacjonarno

ść

wg wzoru:

2

,

,

1

2

t

e

t

e

r

n

r

f

−

−

⋅

=

gdzie:

t

e

r

,

-

współczynnik korelacji pomi

ę

dzy modułem wektora reszt i czasem:

(

)

( )

(

)

( )

∑

∑

∑

=

=

=

−

−

−

−

=

n

t

n

t

t

n

t

t

t

e

t

t

e

e

t

t

e

e

r

1

1

2

2

1

,

Przypominamy,

ż

e jest to statystyka pozwalaj

ą

ca bada

ć

istotno

ść

dowolnego współczynnika

korelacji liniowej.

mgr Grzegorz Stolarczyk

10

Ekonometria 1

Przykład 1.

Obliczamy współczynnik korelacji na podstawie obserwacji (dane z zadania z wydajno

ś

ci

ą

pracy):

t

e

t

0,42

1

0,18

2

0,08

3

0,54

4

0,2

5

0,24

6

0,00000000000034

7

0,2

8

0,4

9

0,66

10

t

e

r

,

=

0,241

=

f

2

241

,

0

1

2

10

241

,

0

−

−

⋅

= 0,701

Z tablic rozkładu Studenta odczytujemy dla poziomu istotno

ś

ci

∝

= 0,05 i n-2 stopni swobody

warto

ść

krytyczn

ą

f

*=

2,306. Jest ona wi

ę

ksza od obliczonej warto

ś

ci

f

, wi

ę

c wektor reszt jest

stacjonarny, czyli niezale

ż

ny od czasu. Wariancja odchyle

ń

losowych jest tym samym stała w czasie.

Przykład 2.

Prosz

ę

sprawdzi

ć

stacjonarno

ść

wektora reszt

t

e

t

0,01

1

0,1

2

0,25

3

0,3

4

0,5

5

0,9

6

0,55

7

0,6

8

0,7

9

0,86

10

mgr Grzegorz Stolarczyk

11

Ekonometria 1

Rozwi

ą

zanie:

Liczymy współczynnik korelacji

t

e

r

,

:

t

e

r

,

= 0,886

Warto

ść

statystyki:

=

f

5,411

Z tablic rozkładu Studenta odczytujemy dla poziomu istotno

ś

ci

∝

= 0,05 i n-2 stopni swobody

warto

ść

krytyczn

ą

f

*=

2,306. Jest ona mniejsza od obliczonej warto

ś

ci

f

, wi

ę

c wektor reszt nie jest

stacjonarny, czyli jest zale

ż

ny od czasu. Aby spróbowa

ć

wyeliminowa

ć

zjawisko stacjonarno

ś

ci mo

ż

na

zastosowa

ć

inn

ą

metod

ę

estymacji parametrów modelu.

d. Autokorelacja

Jednym z warunków stosowalno

ś

ci KMNK jest zało

ż

enie o niezale

ż

no

ś

ci składników losowych.

Zjawisko takie ( istotna zale

ż

no

ść

składników losowych z ró

ż

nych momentów czasu) nazywamy

zjawiskiem autokorelacji

Badanie autokorelacji, tak jak w przypadku stacjonarno

ś

ci, odnosi si

ę

do modeli dynamicznych.

Jest to zjawisko niepo

żą

dane.

Do badania autokorelacji stosujemy test Durbina – Watsona.

Obliczamy statystyk

ę

:

(

)

∑

∑

=

=

−

−

=

n

t

t

n

t

t

t

e

e

e

f

1

2

2

2

1

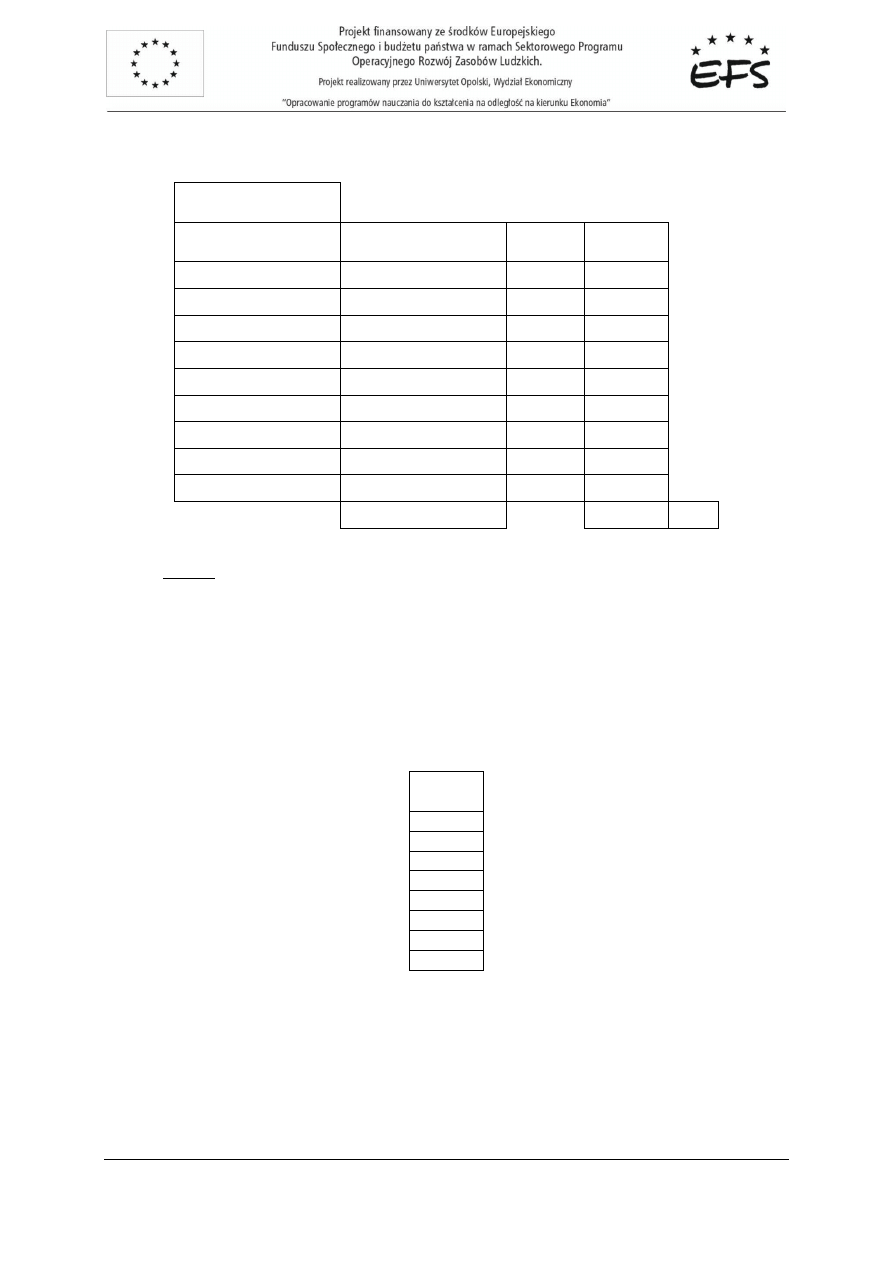
mgr Grzegorz Stolarczyk

12

Ekonometria 1

Przykład 1.

t

e

-0,42

1

−

t

e

(

)

1

−

−

t

t

e

e

(

)

2

1

−

−

t

t

e

e

-0,18

-0,42

0,24

0,0576

0,08

-0,18

0,26

0,0676

0,54

0,08

0,46

0,2116

-0,2

0,54

-0,74

0,5476

0,24

-0,2

0,44

0,1936

-0,00000000000034

0,24

-0,24

0,0576

0,2

-0,00000000000034

0,2

0,04

0,4

0,2

0,2

0,04

-0,66

0,4

-1,06

1,1236

-0,66

2,3392 suma

=

f

886

,

1

24

,

1

3392

,

2

=

Sprawdzamy warto

ś

ci krytyczne dla rozkładu statystyki Durbina – Watsona. Odczytany przedział z

tablic dla poziomu istotno

ś

ci

∝

= 0,05, n=10 i liczby zmiennych obja

ś

niaj

ą

cych k=2 to <0,697, 1,641>.

Warto

ść

statystyki f jest wi

ę

ksza od górnej granicy przedziału, wi

ę

c autokorelacja nie wyst

ę

puje.

Przykład 2.

Prosz

ę

na podstawie danych zbada

ć

czy wyst

ę

puje autokorelacja wektora reszt.

t

e

3,362
3,660
0,661

-2,520
-3,383
-3,041
-0,864

2,126

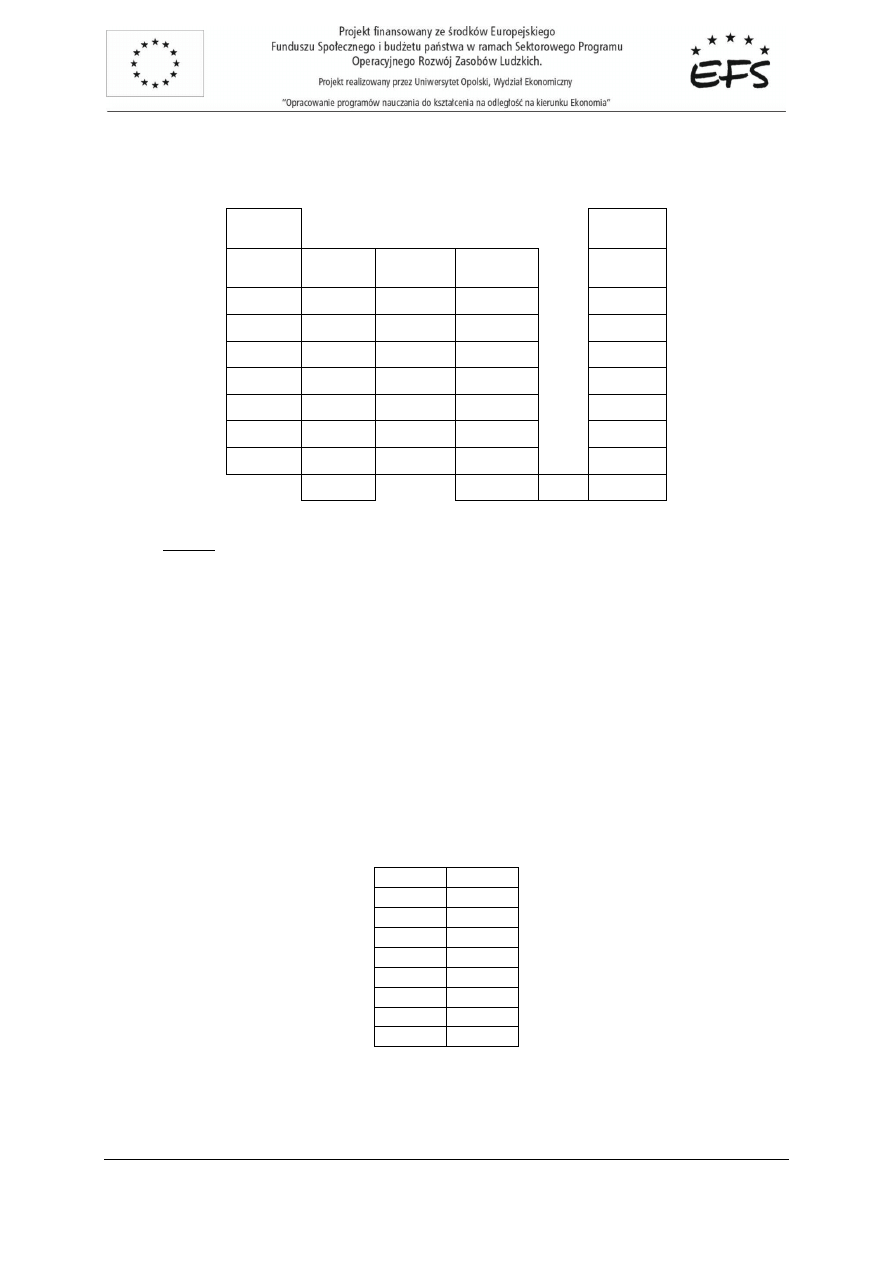
mgr Grzegorz Stolarczyk

13

Ekonometria 1

Rozwi

ą

zanie:

Stosujemy test Durbina – Watsona.

Obliczamy statystyk

ę

do testu Durbina – Watsona:

t

e

t

e

2

3,362

1

−

t

e

(

)

1

−

−

t

t

e

e

(

)

2

1

−

−

t

t

e

e

11,302

3,660

3,362

0,298

0,089

13,392

0,661

3,660

-2,999

8,993

0,437

-2,520

0,661

-3,180

10,114

6,349

-3,383

-2,520

-0,863

0,745

11,444

-3,041

-3,383

0,341

0,117

9,250

-0,864

-3,041

2,177

4,740

0,747

2,126

-0,864

2,990

8,943

4,520

2,126

33,740 suma

57,440

=

f

587

,

0

440

,

57

740

,

33

=

Sprawdzamy warto

ś

ci krytyczne dla rozkładu statystyki Durbina – Watsona. Odczytany przedział

z tablic dla poziomu istotno

ś

ci

∝

= 0,05, n=8 i liczby zmiennych obja

ś

niaj

ą

cych k=1 to <0,763, 1,332>.

Warto

ść

statystyki f jest mniejsza od dolnej granicy przedziału, wi

ę

c autokorelacja wyst

ę

puje. Mo

ż

e

to by

ć

spowodowane np. nieprawidłowym doborem postaci analitycznej modelu lub złym wyborem

zmiennych obja

ś

niaj

ą

cych. W przypadku wyst

ą

pienia autokorelacji mo

ż

na równie

ż

zastosowa

ć

inn

ą

metod

ę

szacowania parametrów modelu.

Przykład 3.

Na podstawie danych prosz

ę

sprawdzi

ć

autokorelacj

ę

składnika losowego

830

,

1

005

,

1

3

^

−

⋅

=

x

y

Y

x

3

100

100

106,3

103,7

108,7

111,9

114,4

119,7

119,3

123,3

123,2

126,1

133,4

131,8

142,6

140,8

mgr Grzegorz Stolarczyk

14

Ekonometria 1

Rozwi

ą

zanie:

Wyznaczamy warto

ś

ci teoretyczne zmiennej obja

ś

nianej i wektora reszt.

^

Y

e

98,717

1,283

102,438

3,862

110,683

-1,983

118,525

-4,125

122,145

-2,845

124,960

-1,760

130,691

2,709

139,741

2,859

Obliczamy statystyk

ę

do testu Durbina – Watsona:

t

e

t

e

2

1,283

1

−

t

e

(

)

1

−

−

t

t

e

e

(

)

2

1

−

−

t

t

e

e

1,645

3,862

1,283

2,580

6,655

14,918

-1,983

3,862

-5,845

34,162

3,930

-4,125 -1,983

-2,143

4,591

17,017

-2,845 -4,125

1,280

1,639

8,093

-1,760 -2,845

1,085

1,177

3,098

2,709 -1,760

4,469

19,970

7,337

2,859

2,709

0,151

0,023

8,176

2,859

68,217

suma

64,215

=

f

062

,

1

215

,

64

217

,

68

=

Sprawdzamy warto

ś

ci krytyczne dla rozkładu statystyki Durbina – Watsona. Odczytany przedział

z tablic dla poziomu istotno

ś

ci

∝

= 0,05, n=8 i liczby zmiennych obja

ś

niaj

ą

cych k=1 to <0,763, 1,332>.

Warto

ść

statystyki f mie

ś

ci si

ę

w przedziale, wi

ę

c test Durbina – Watsona nie rozstrzyga o tym,

czy autokorelacja wyst

ę

puje. Musimy w takim przypadku zastosowa

ć

test na istotno

ść

współczynnika

korelacji zgodnie ze wzorem:

2

,

,

1

1

1

2

−

−

−

−

⋅

=

t

t

t

t

e

e

e

e

r

n

r

f

gdzie:

1

,

−

t

t

e

e

r

- współczynnik korelacji pomi

ę

dzy wektorem reszt i wektorem reszt przesuni

ę

tym o jedn

ą

jednostk

ę

czasu

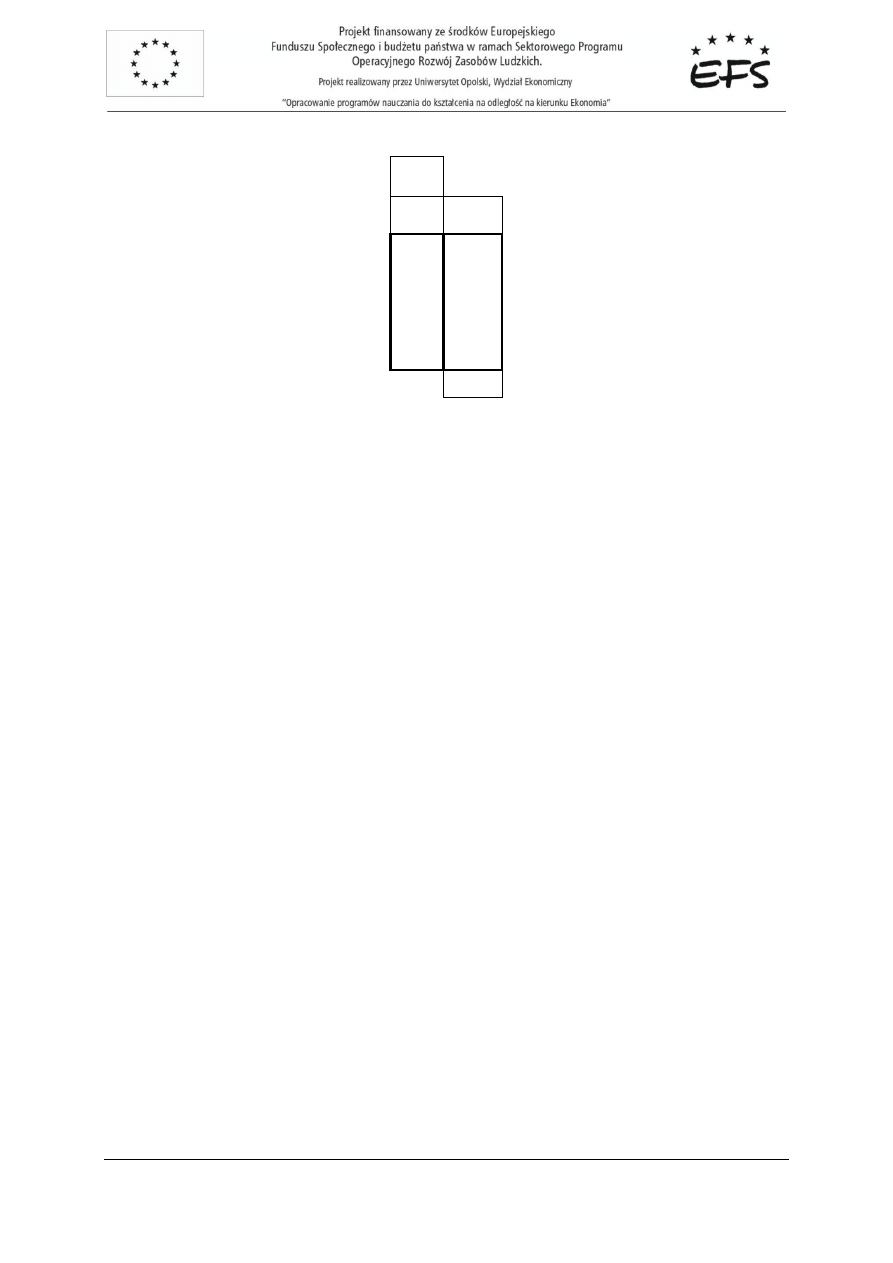
mgr Grzegorz Stolarczyk

15

Ekonometria 1

Obliczamy:

t

e

1,283

1

−

t

e

3,862

1,283

-1,983

3,862

-4,125 -1,983
-2,845 -4,125
-1,760 -2,845

2,709 -1,760
2,859

2,709

2,859

Współczynnik korelacji obliczony z cz

ęś

ci wspólnej tych dwóch wielko

ś

ci wynosi:

1

,

−

t

t

e

e

r

=

0,422

St

ą

d:

=

f

1,140

Z tablic rozkładu Studenta odczytujemy dla poziomu istotno

ś

ci

∝

= 0,05 i n-2 stopni swobody

warto

ść

krytyczn

ą

f *=

2,447. Jest ona wi

ę

ksza od obliczonej warto

ś

ci

f

, wi

ę

c współczynnik

korelacji jest nieistotny, co powoduje,

ż

e autokorelacja nie wyst

ę

puje.

e. Rozkład normalny

Badanie normalno

ś

ci rozkładu odchyle

ń

losowych sprowadza si

ę

do porównania warto

ś

ci

empirycznych dystrybuanty wektora reszt z dystrybuant

ą

rozkładu normalnego.

Badanie rozkładu normalnego jest szczególnie wa

ż

ne w przypadku modeli przeznaczonych

do prognozowania. Do badania rozkładu wykorzystujemy test zgodno

ś

ci Hellwiga.

mgr Grzegorz Stolarczyk

16

Ekonometria 1

Przykład 1.

e

e'=

j

S

e

e' uporz

ą

dkowany F(e')

Cele

Cele puste

-0,42

-1,132

-1,778 0,038

[0 0,1)

-0,18

-0,485

-1,132 0,129 [0,1 0,2)

0,08

0,216

-0,539 0,295 [0,2 0,3)

0,54

1,455

-0,485 0,314 [0,3 0,4)

-0,2

-0,539

0,000 0,500 [0,4 0,5) pusta

0,24

0,647

0,216 0,585 [0,5 0,6)

-0,00000000000034

0,000

0,539 0,705 [0,6 0,7) pusta

0,2

0,539

0,647 0,741 [0,7 0,8)

0,4

1,078

1,078 0,859 [0,8 0,9)

-0,66

-1,778

1,455 0,927 [0,9 1,0]

Odchylenie
Standardowe - S

j

0,371

F(e') – warto

ść

dystrybuanty rozkładu normalnego liczona za pomoc

ą

funkcji dost

ę

pnej w Excelu

„Rozkład. Normalny. S.”

Liczba cel pustych wynosi K=2. Przedział z tablic testu Hellwiga wynosi <1,5>. Liczba cel pustych

K=2 mie

ś

ci si

ę

w przedziale, wi

ę

c wektor reszt ma rozkład normalny.

Przykład 2.

Prosz

ę

zbada

ć

normalno

ść

rozkładu wektora reszt:

e

0,1
0,1

0,15

1,4
0,5

3

0,7
0,9
1,4

-8,25

mgr Grzegorz Stolarczyk

17

Ekonometria 1

Rozwi

ą

zanie:

e

e'=

j

S

e

e' uporz

ą

dkowany

F(e')

Cele

Cele puste

0,1

0,033

-2,724

0,003

[0

0,1)

0,1

0,033

0,033

0,513

[0,1

0,2) pusta

0,15

0,050

0,033

0,513

[0,2

0,3) pusta

1,4

0,462

0,050

0,520

[0,3

0,4) pusta

0,5

0,165

0,165

0,566

[0,4

0,5) pusta

3

0,990

0,231

0,591

[0,5

0,6)

0,7

0,231

0,297

0,617

[0,6

0,7)

0,9

0,297

0,462

0,678

[0,7

0,8) pusta

1,4

0,462

0,462

0,678

[0,8

0,9)

-8,25

-2,724

0,990

0,839

[0,9

1,0] pusta

Odchylenie
Standardowe - S

j

3,029

Liczba cel pustych wynosi K=6. Przedział z tablic testu Hellwiga wynosi <1,5>. Liczba cel pustych

K=2 nie mie

ś

ci si

ę

w przedziale, wi

ę

c wektor reszt nie ma rozkładu normalnego. Nie dyskwalifikuje

to modelu, jednak w przypadku tworzenia na jego podstawie prognoz mog

ą

wyst

ą

pi

ć

ich zbyt du

ż

e

bł

ę

dy i mo

ż

liwo

ść

nie uzyskania prognozy dopuszczalnej.

Zadanie 1.

Prosz

ę

zweryfikowa

ć

model liniowy:

82

,

2310

97

,

408

77

,

23

3

1

^

−

⋅

+

⋅

=

x

x

y

Y

X

1

X

3

3086,07

104

6,7

3336,04

107

7,2

3407,02

110

7,7

3644,65

113

8

3888,45

117

8,6

4160,02

119

9,1

4456,29

122

9,9

4712,43

124

10,5

5135,22

129

11

5283,35

135

11,3

5558,01

140

11,8

6008,58

145

12,7

6644,31

151

13,5

7363,37

157

14,1

8131,80

162

14,6

8863,20

172

15

9464,98

179

15,6

9937,15

186

17,8

10236,50

193

19,3

10001,96

201

19,2

9403,26

193

19,5

8273,76

163

15,7

mgr Grzegorz Stolarczyk

18

Ekonometria 1

7820,10

189

14,8

8289,19

191

16,2

8752,10

192

16,5

S(a

1

)

12,26

S(a

2

)

100,74

S(a

0

)

670,35

Zadanie 2.

Prosz

ę

na podstawie danych zbada

ć

stacjonarno

ść

wektora reszt.

055

,

83

136

,

0

2

^

+

⋅

=

x

y

e

3,362
3,660
0,661

-2,520
-3,383
-3,041
-0,864

2,126

Zadanie 3.

Prosz

ę

na podstawie danych zbada

ć

dopasowanie modelu do danych empirycznych

oraz symetryczno

ść

i losowo

ść

składnika losowego.

Y

X

1

X

2

10

6

8

10

6

8

16

10

12

16

10

12

12

8

8

14

10

8

20

12

14

20

12

16

20

12

16

22

14

18

252

,

0

447

,

0

039

,

1

2

1

^

+

⋅

+

⋅

=

x

x

y

mgr Grzegorz Stolarczyk

19

Ekonometria 1

Zadanie 4.

Dane s

ą

warto

ś

ci wektora reszt:

e

2,4
3,5
0,4

-1,5
-2,3

0,1

-0,1
-2,4
-1,5

1,3
2,3
0,5

-3

1,6
2,2

-0,5

-3

Prosz

ę

sprawdzi

ć

czy wektor reszt ma rozkład normalny.

Zadanie 5.

Do opisu PKB w Polsce w latach 1990 – 2003 zaproponowano wst

ę

pnie nast

ę

puj

ą

ce zmienne

obja

ś

niaj

ą

ce:

X1 – ko

ń

cowa produkcja rolnicza

X2 – zbiory zbó

ż

w mln ton

X3 – produkcja

ż

ywca w tys. ton

X4 – skup produktów rolnych

X5 – produkcja sprzedana przedsi

ę

biorstw

X6 – wielko

ść

inwestycje

X7 – warto

ść

ś

rodków trwałych

PKB

Ko

ń

cowa produkcja

rolnicza

Zbiory zbó

ż

w

mln t

Pr.

ż

ywca w

tys. ton

Skup

pr. rol.

Pr.

sprzedana

przedsieb.

Wielko

ść

inwestycji

Warto

ść

ś

r.

Trwałych

100

100

24,1

3325

100

100

100

100

93

98,4

23,7

3348

82,8

92

97,2

100,9

95,4

87,9

17,1

3211

74,9

94,6

95,4

102,1

99

94,9

19,9

2954

71,9

100,7

96,1

103,8

104,1

84,7

18,5

2694

65,4

112,8

116

106,7

111,4

98,5

21,8

2959

74,9

123,7

133,3

107

118,1

97,6

21,4

3105

78,1

134

160,1

113,5

126,1

99,4

20,8

3021

83,6

149,4

182,2

117,6

mgr Grzegorz Stolarczyk

20

Ekonometria 1

132,2

104,6

22,3

3242

91,5

154,7

202,6

121,4

137,6

100,4

21,2

3296

96,5

160,3

193,1

125,8

143,1

97,2

18,3

3119

99,1

171

170,1

130

144,5

105,6

21,5

3119

100,4

172

163

133,1

146,5

105,7

21

3339

110,3

173,9

150

136,4

152,1

108,3

17,9

3640

117,9

188

159,5

139,1

Prosz

ę

dobra

ć

zmienne obja

ś

niaj

ą

ce do modelu, oszacowa

ć

parametry i przeprowadzi

ć

weryfikacj

ę

modelu.