mgr Grzegorz Stolarczyk

1

Ekonometria 1

BLOK 3

Szacowanie parametrów modeli liniowych i nieliniowych klasyczn

ą

metod

ą

najmniejszych

kwadratów

Szacowanie parametrów modeli liniowych

Przykład 1.

Prosz

ę

na podstawie danych oszacowa

ć

parametry ekonometrycznego modelu liniowego

opisuj

ą

cego wydatki na

ż

ywno

ść

gospodarstwa domowego w zł na 1 osob

ę

(Y) w zale

ż

no

ś

ci

od dochodów na 1 osob

ę

(X

1

).

Y

X

1

100

750

125

790

130

820

140

860

152

890

160

900

180

925

190

960

210

980

220

1000

Rozwi

ą

zanie:

Szacujemy parametry modelu o postaci:

ε

β

α

+

+

=

1

x

y

Oceny a i b parametrów

α

i

β

wyznaczamy ze wzorów:

(

)( )

( )

∑

∑

=

=

−

−

−

=

n

i

i

n

i

i

i

x

x

x

x

y

y

a

1

2

1

1

x

a

y

b

−

=

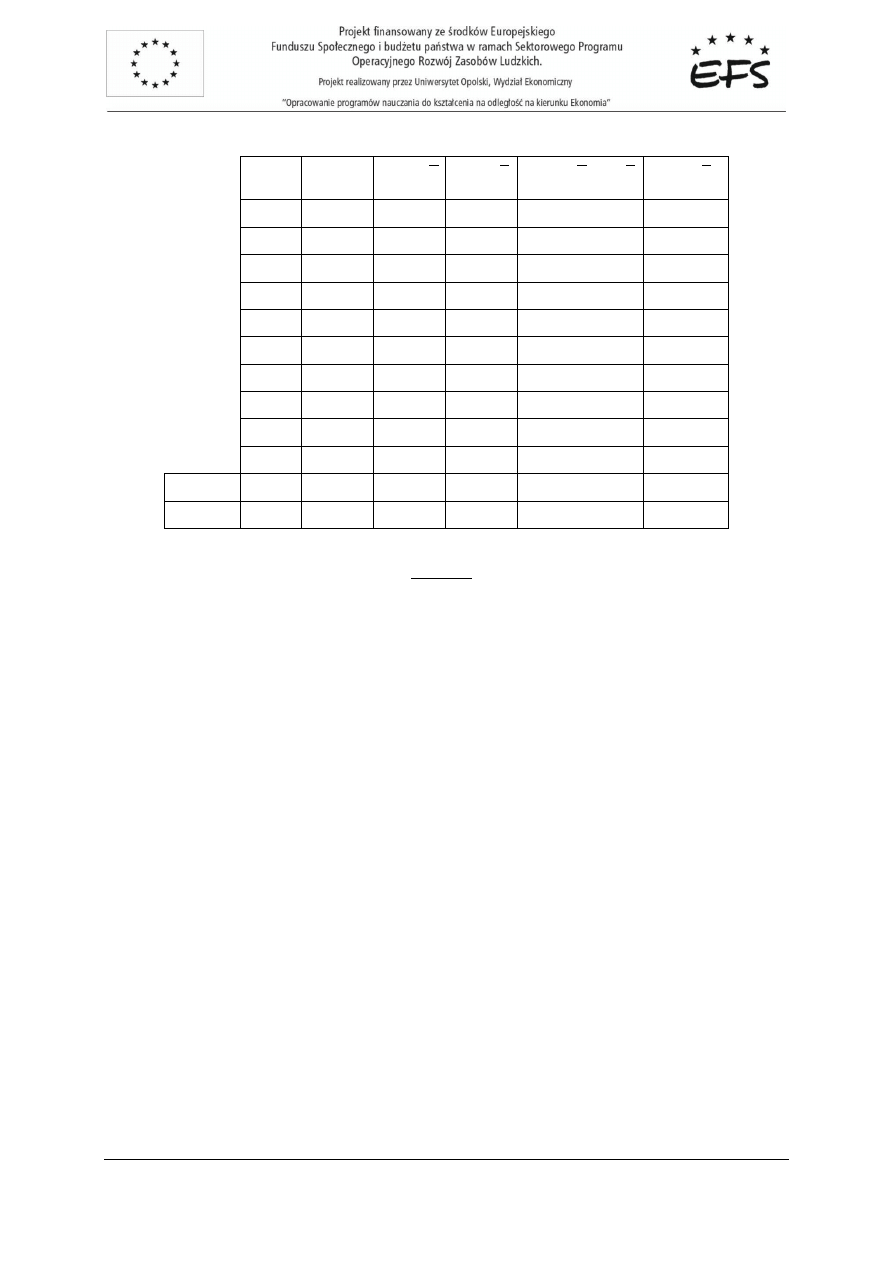
mgr Grzegorz Stolarczyk

2

Ekonometria 1

Tabela 1. Obliczenia pomocnicze

i

y

i

x

y

y

i

−

x

x

i

−

(

)( )

x

x

y

y

i

i

−

−

( )

2

x

x

i

−

100

750

-60,7

-137,5

8346,25

18906,25

125

790

-35,7

-97,5

3480,75

9506,25

130

820

-30,7

-67,5

2072,25

4556,25

140

860

-20,7

-27,5

569,25

756,25

152

890

-8,7

2,5

-21,75

6,25

160

900

-0,7

12,5

-8,75

156,25

180

925

19,3

37,5

723,75

1406,25

190

960

29,3

72,5

2124,25

5256,25

210

980

49,3

92,5

4560,25

8556,25

220

1000

59,3

112,5

6671,25

12656,25

ś

rednia

160,7

887,5

-----

------

---------------

----------

suma

------

-------

-----

------

28517,5

61762,5

462

,

0

5

,

61762

5

,

28517

≈

=

a

1

,

249

5

,

887

462

,

0

7

,

160

−

≈

⋅

−

=

b

Oszacowany model:

1

,

249

462

,

0

1

^

−

⋅

=

x

y

Interpretacja modelu:

Wzrost dochodu w gospodarstwie domowym o 1 zł na osob

ę

powoduje wzrost wydatków

na

ż

ywno

ść

o 0,462 zł na 1 osob

ę

.

Te same oceny parametrów wyznaczymy ze wzoru:

Y

X

X

X

a

T

T

1

)

(

−

=

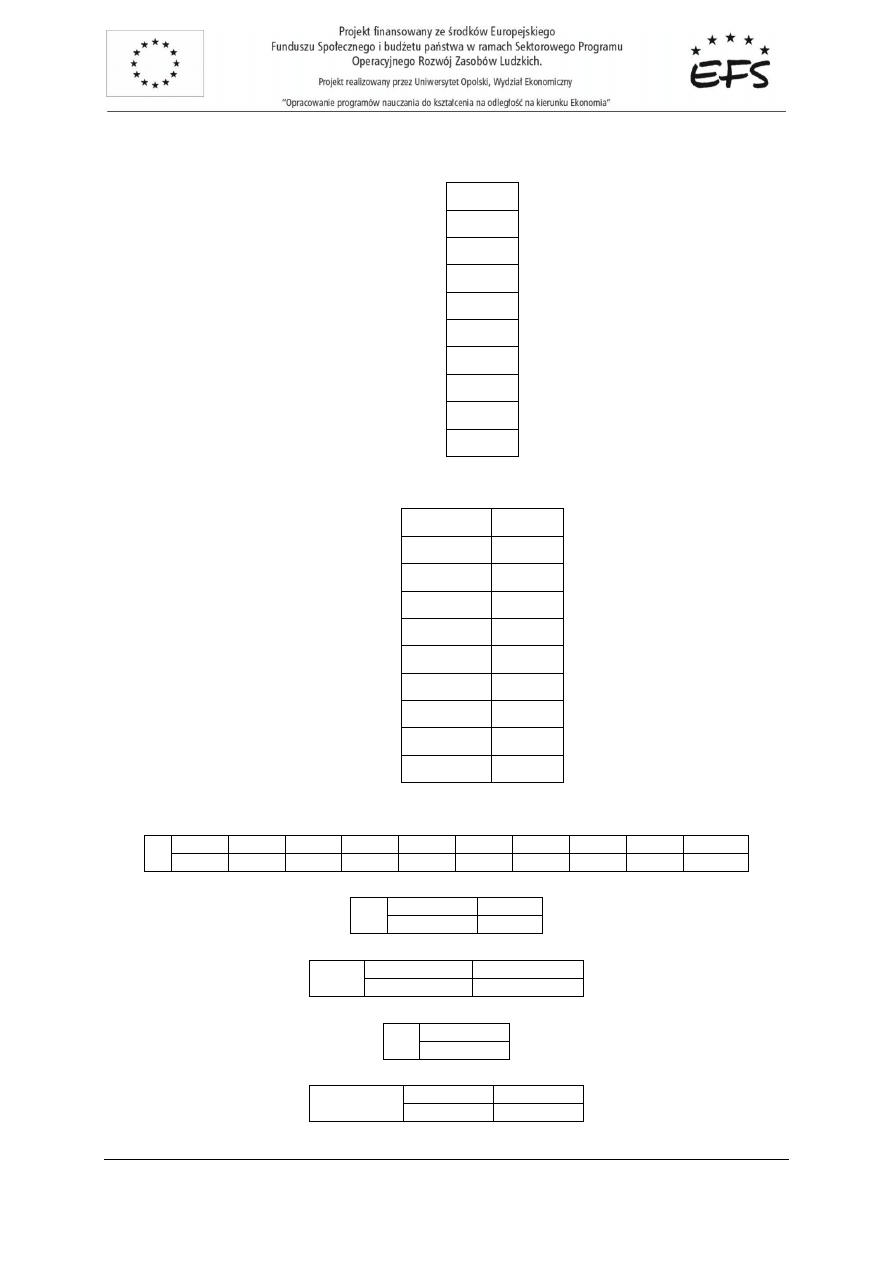
mgr Grzegorz Stolarczyk

3

Ekonometria 1

Wektor Y obserwacji zmiennej obja

ś

nianej oraz macierz X obserwacji zmiennych obja

ś

niaj

ą

cych

wygl

ą

daj

ą

nast

ę

puj

ą

co:

100

125

130

Y=

140

152

160

180

190

210

220

750

1

790

1

820

1

860

1

X=

890

1

900

1

925

1

960

1

980

1

1000

1

Obliczenia:

750

790

820

860

890

900

925

960

980

1000

X

T

1

1

1

1

1

1

1

1

1

1

7938325

8875

X

T

X

8875

10

0,0000162

-0,0143696

(X

T

X)

-1

-0,0143696

12,8529852

1454730

X

T

Y

1607

a

0,462

(X

T

X)

-1

X

T

Y=

b

-249,1

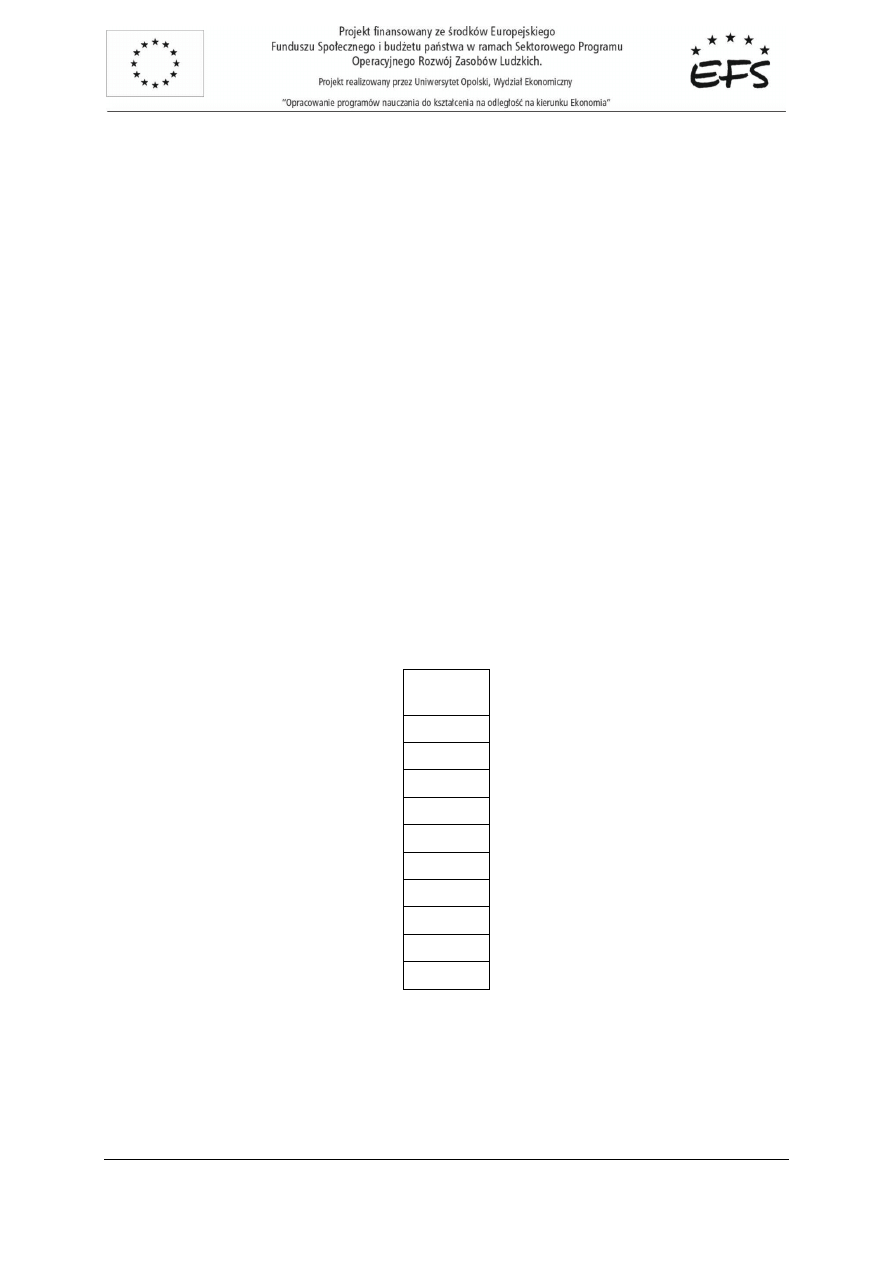
mgr Grzegorz Stolarczyk

4

Ekonometria 1

Jak wida

ć

warto

ś

ci ocen parametrów szacowane za pomoc

ą

dwóch wzorów s

ą

takie same.

Kolejnym krokiem jest wyliczenie z modelu warto

ś

ci teoretycznych zmiennej obja

ś

nianej

y

:

1

,

249

750

462

,

0

^

1

−

⋅

=

y

1

,

249

790

462

,

0

^

2

−

⋅

=

y

1

,

249

820

462

,

0

^

3

−

⋅

=

y

1

,

249

860

462

,

0

^

4

−

⋅

=

y

1

,

249

890

462

,

0

^

5

−

⋅

=

y

1

,

249

900

462

,

0

^

6

−

⋅

=

y

1

,

249

925

462

,

0

^

7

−

⋅

=

y

1

,

249

960

462

,

0

^

8

−

⋅

=

y

1

,

249

980

462

,

0

^

9

−

⋅

=

y

1

,

249

1000

462

,

0

^

10

−

⋅

=

y

^

y

97,21235

115,6815

129,5333

148,0025

161,8543

166,4716

178,0148

194,1753

203,4099

212,6444

mgr Grzegorz Stolarczyk

5

Ekonometria 1

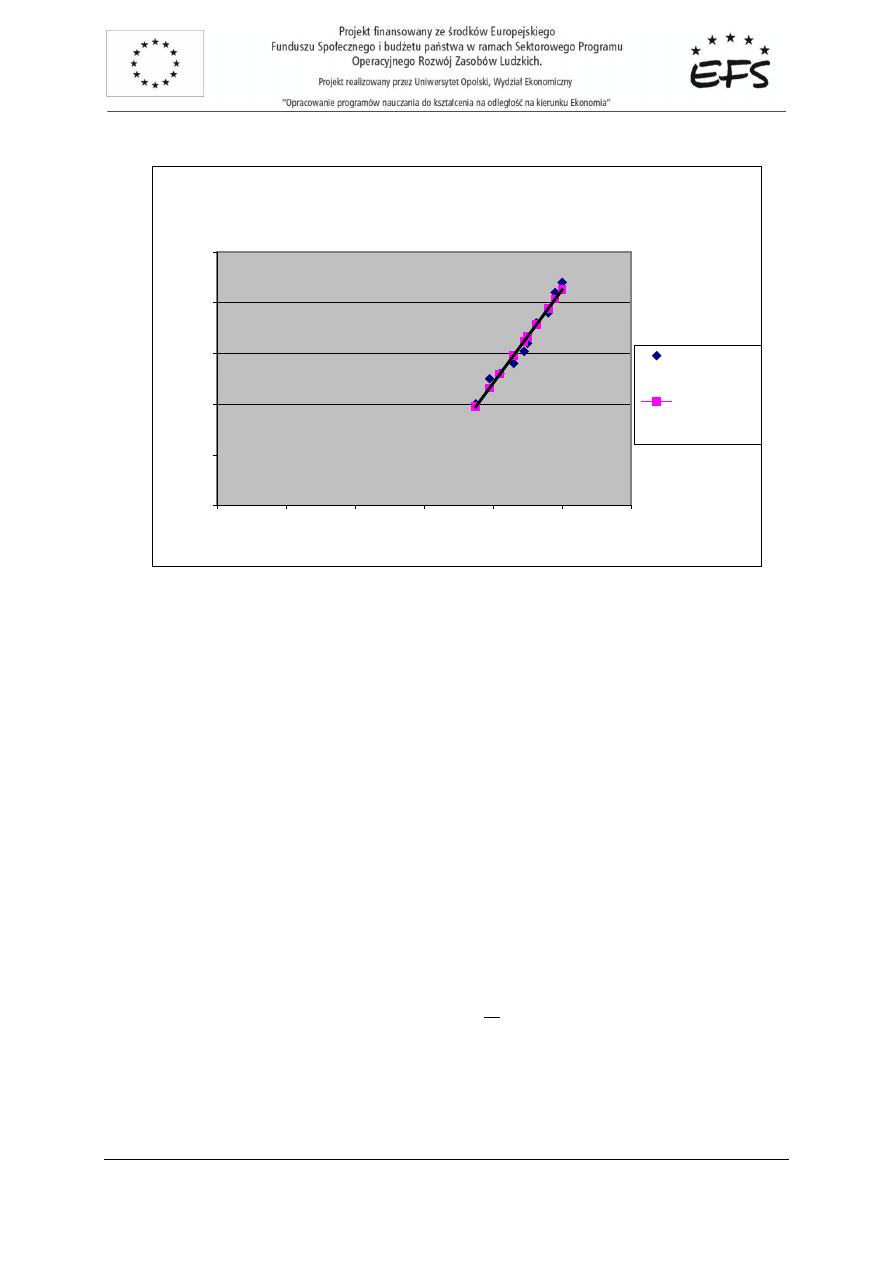
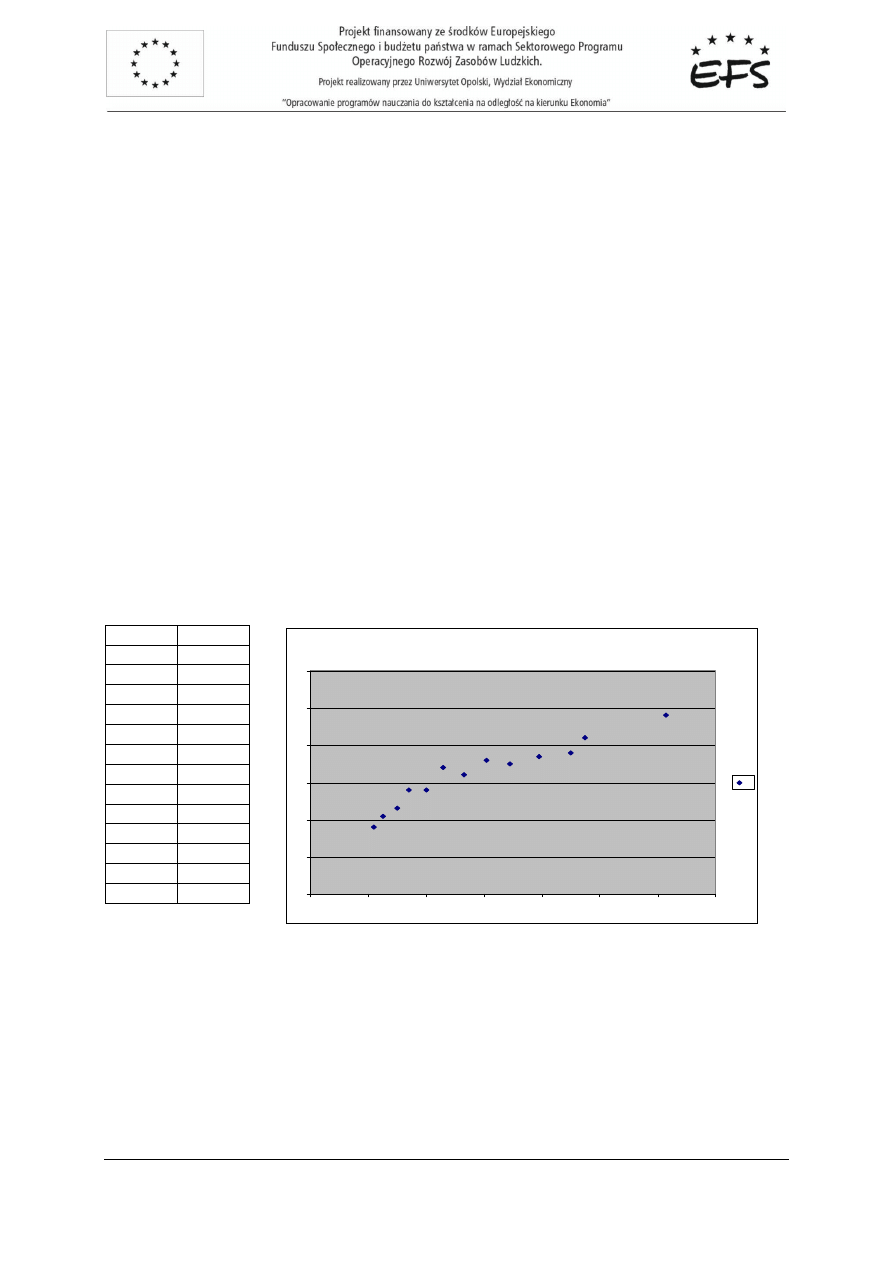
Na podstawie danych empirycznych oraz warto

ś

ci teoretycznych zmiennej

y

sporz

ą

dzamy wykres:

Punkty empiryczne i prosta wyznaczona metod

ą

najmniejszych kwadratów

0

50

100

150

200

250

0

200

400

600

800

1000

1200

Dochód

W

y

d

a

tk

i

Punkty
empiryczne

Warto

ś

ci

teoretyczne

Liniowy

Szacowanie parametrów modeli nieliniowych

Jednorównaniowe modele nieliniowe dzielimy na:

1. sprowadzalne do postaci liniowej:

a) modele liniowe wzgl

ę

dem parametrów, lecz nieliniowe wzgl

ę

dem zmiennej obja

ś

niaj

ą

cej

b) modele nieliniowe wzgl

ę

dem parametrów oraz nieliniowe wzgl

ę

dem zmiennej

obja

ś

niaj

ą

cej.

2. niesprowadzalne do postaci liniowej

Przykłady modeli liniowych wzgl

ę

dem parametrów, lecz nieliniowych wzgl

ę

dem zmiennej

obja

ś

niaj

ą

cej:

a) model logarytmiczny

x

y

ln

1

0

α

α

+

=

b) model wielomianowy

2

1

2

1

1

0

x

x

y

α

α

α

+

+

=

c) model hiperboliczny

1

1

0

1

x

y

α

α

+

=

mgr Grzegorz Stolarczyk

6

Ekonometria 1

Przykłady modeli nieliniowych wzgl

ę

dem parametrów oraz nieliniowych wzgl

ę

dem zmiennej

obja

ś

niaj

ą

cej:

a) model pot

ę

gowy

1

1

0

α

α

x

y

⋅

=

b) model wykładniczy

x

a

e

y

1

0

α

=

Wybór postaci analitycznej modeli nieliniowych ustala si

ę

w oparciu o wiedz

ę

dotycz

ą

c

ą

kształtowania si

ę

badanych zjawisk oraz analiz

ę

rozrzutu punktów empirycznych na wykresie

Sposoby linearyzacji (sprowadzenia do postaci liniowej) modeli nieliniowych

1. Poprzez

podstawienie

–

w

przypadku

modelu

logarytmicznego

wielomianowego,

hiperbolicznego,

2. Poprzez logarytmowanie stronami – w przypadku modelu pot

ę

gowego, wykładniczego.

Estymacja parametrów modeli liniowych wzgl

ę

dem parametrów, lecz nieliniowych wzgl

ę

dem

zmiennej obja

ś

niaj

ą

cej.

Przykład 1:

Zbuduj model zale

ż

no

ś

ci wydatków na

ż

ywno

ść

w tys. zł (Y) od dochodu na osob

ę

w tys. zł.(X).

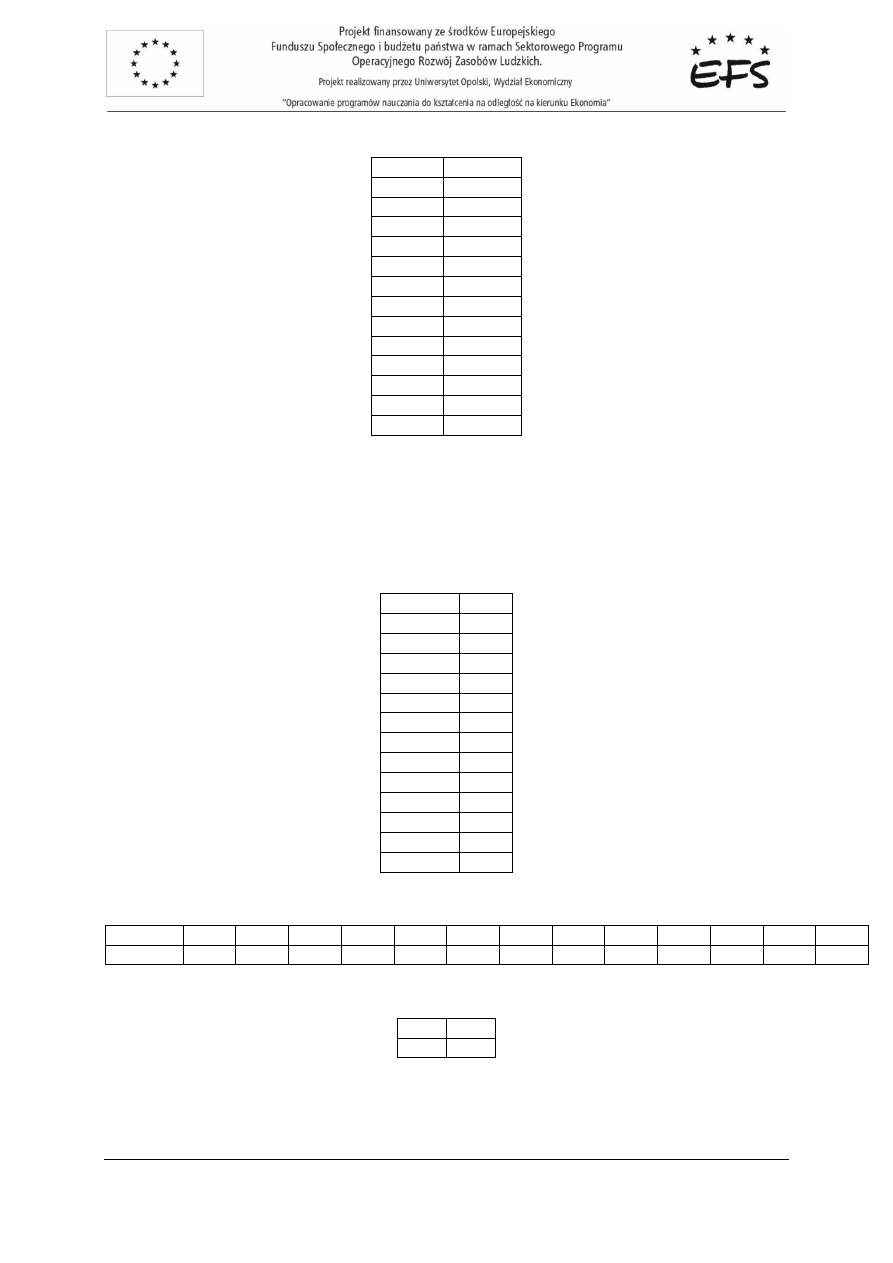
Macierz obserwacji zmiennych oraz wykres rozrzutu punktów empirycznych:

Wykres rozrzutu punktów em pirycznych

0

1

2

3

4

5

6

0

2

4

6

8

10

12

14

Y

Rozwi

ą

zanie:

Analiza rozrzutu punktów empirycznych na wykresie wskazuje na mo

ż

liw

ą

posta

ć

modelu

logarytmicznego

x

y

ln

1

0

α

α

+

=

poprzez podstawianie budujemy posta

ć

zlinearyzowan

ą

:

z

y

1

0

α

α

+

=

gdzie: z=lnx,

Y

X

1,8

2,2

2,1

2,5

2,3

3

2,8

3,4

2,8

4

3,4

4,6

3,2

5,3

3,6

6,1

3,5

6,9

3,7

7,9

3,8

9

4,2

9,5

4,8

12,3

mgr Grzegorz Stolarczyk

7

Ekonometria 1

Macierz obserwacji zmiennych dla modelu zlinearyzowanego:

y

z=ln(x)

1,8

0,8

2,1

0,9

2,3

1,1

2,8

1,2

2,8

1,4

3,4

1,5

3,2

1,7

3,6

1,8

3,5

1,9

3,7

2,1

3,8

2,2

4,2

2,3

4,8

2,5

Nast

ę

pnie korzystaj

ą

c z KMNK definiowanej nast

ę

puj

ą

co:

a

i

= (Z

T

Z)

-1

Z

T

y

szacujemy parametry a

0

, a

1

,

Macierz:

Z

Z=ln(x)

z

0

0,8

1,0

0,9

1,0

1,1

1,0

1,2

1,0

1,4

1,0

1,5

1,0

1,7

1,0

1,8

1,0

1,9

1,0

2,1

1,0

2,2

1,0

2,3

1,0

2,5

1,0

Z

T

z=ln(x)

0,8

0,9

1,1

1,2

1,4

1,5

1,7

1,8

1,9

2,1

2,2

2,3

2,5

z

0

1,0

1,0

1,0

1,0

1,0

1,0

1,0

1,0

1,0

1,0

1,0

1,0

1,0

Z

T

Z

39

21

21

13

mgr Grzegorz Stolarczyk

8

Ekonometria 1

(Z

T

Z)

-1

0,3

-0,5

-0,5

0,8

(Z

T

Z)

-1

Z

T

y=a

i

A zatem oszacowano model zlinearyzowany postaci:

yˆ

=1,5z+0,7

Na podstawie postaci pierwotnej wyznaczono warto

ś

ci teoretyczne zmiennej obja

ś

nianej Y:

1,9
2,1
2,4
2,6
2,8

3

3,3
3,5
3,7
3,9
4,1
4,2
4,6

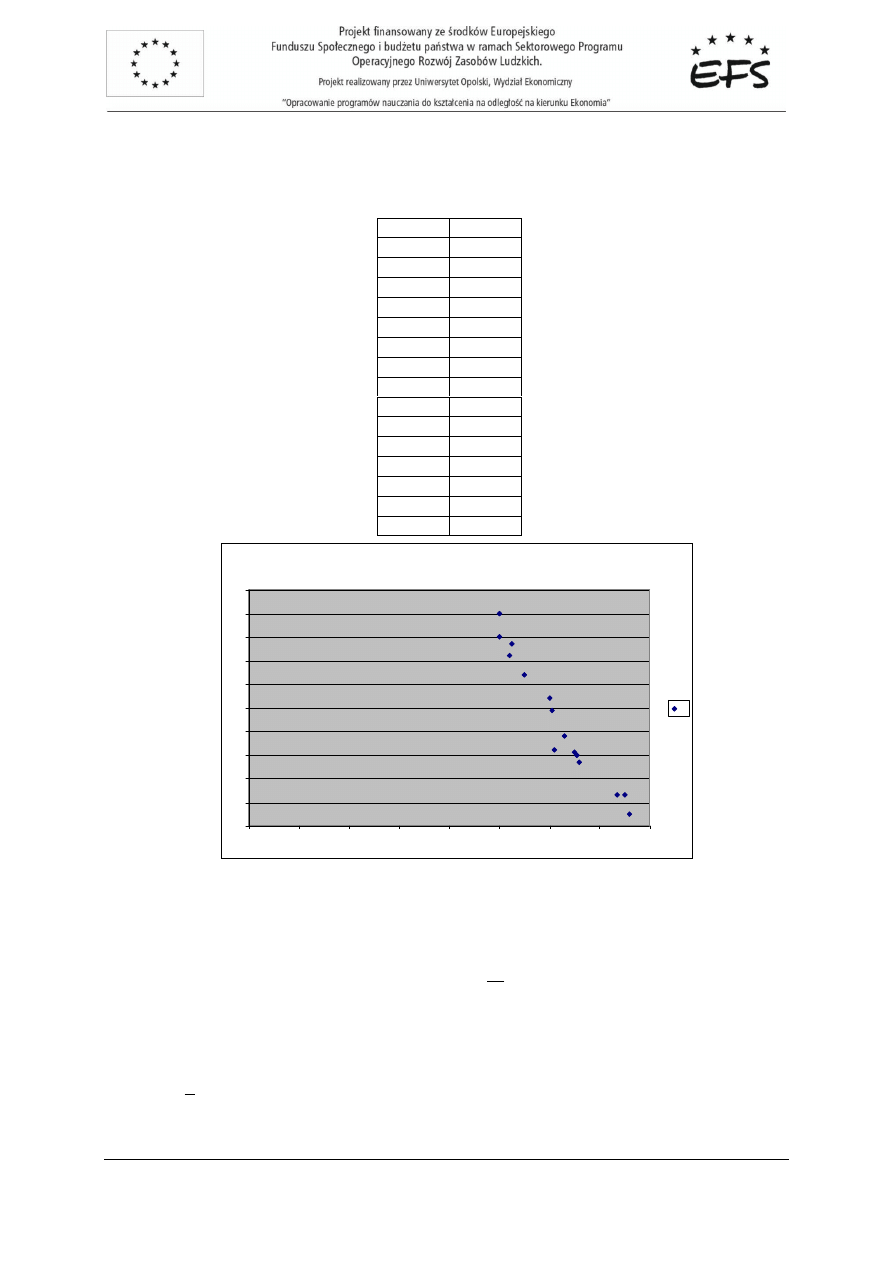
które naniesiono na wykres w postaci linii trendu (kolor ró

ż

owy):

0

1

2

3

4

5

6

0

2

4

6

8

10

12

14

Y

Yteor.

1,5

=a

1

0,7

=a

0

mgr Grzegorz Stolarczyk

9

Ekonometria 1

Przykład 2:

Zbuduj model zale

ż

no

ś

ci jednostkowych stałych kosztów produkcji w tys. zł, ceny stałe (Y)

od wielko

ś

ci produkcji w tys. sztuk (X). Macierz obserwacji zmiennych oraz wykres rozrzutu punktów

empirycznych:

Wykres rozrzutu punktów empirycznych

57

58

59

60

61

62

63

64

65

66

67

0

20

40

60

80

100

120

140

160

Y

Rozwi

ą

zanie:

Analiza rozrzutu punktów empirycznych na wykresie wskazuje na mo

ż

liw

ą

posta

ć

modelu

hiperbolicznego:

1

1

0

1

x

y

α

α

+

=

poprzez podstawianie budujemy posta

ć

zlinearyzowan

ą

:

z

y

1

0

α

α

+

=

gdzie:

x

z

1

=

,

Y

X

66

100

64,2

104

61,9

121

60,8

126

59,7

132

58,3

150

57,5

152

58,3

147

60,1

130

60

131

60,2

122

63,4

110

65

100

64,7

105

62,4

120

mgr Grzegorz Stolarczyk

10

Ekonometria 1

Macierz obserwacji zmiennych dla modelu zlinearyzowanego:

y

z

=

x

1

66

0,010

64,2

0,010

61,9

0,008

60,8

0,008

59,7

0,008

58,3

0,007

57,5

0,007

58,3

0,007

60,1

0,008

60

0,008

60,2

0,008

63,4

0,009

65

0,010

Nast

ę

pnie korzystaj

ą

c z KMNK szacujemy parametry

α

0

,

α

1

.

Oszacowano model zlinearyzowany o postaci:

yˆ

=2269z+43

Posta

ć

pierwotna:

yˆ

=2269

x

1

+43;

Na podstawie postaci pierwotnej wyznaczono warto

ś

ci teoretyczne zmiennej obja

ś

nianej y:

65,4
64,6
61,5
60,8
59,9
57,9
57,7
58,2
60,2
60,1
61,4
63,4
65,4

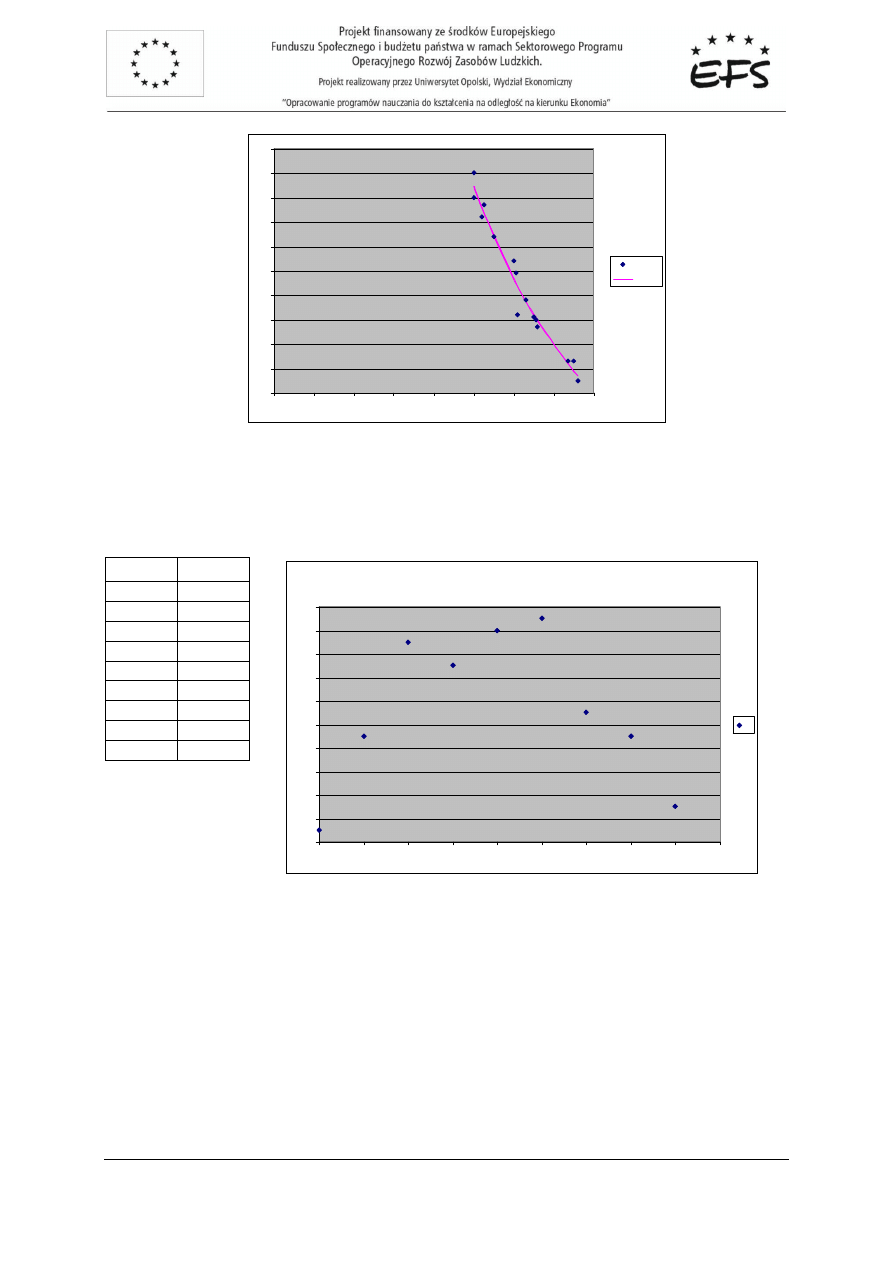
które naniesiono na wykres w postaci linii trendu (kolor ró

ż

owy):

mgr Grzegorz Stolarczyk

11

Ekonometria 1

57

58

59

60

61

62

63

64

65

66

67

0

20

40

60

80

100

120

140

160

Y

Yteor.

Przykład 3:

Zbuduj model zale

ż

no

ś

ci wydajno

ś

ci pracy robotników (Y) od ich wieku (X). Macierz obserwacji

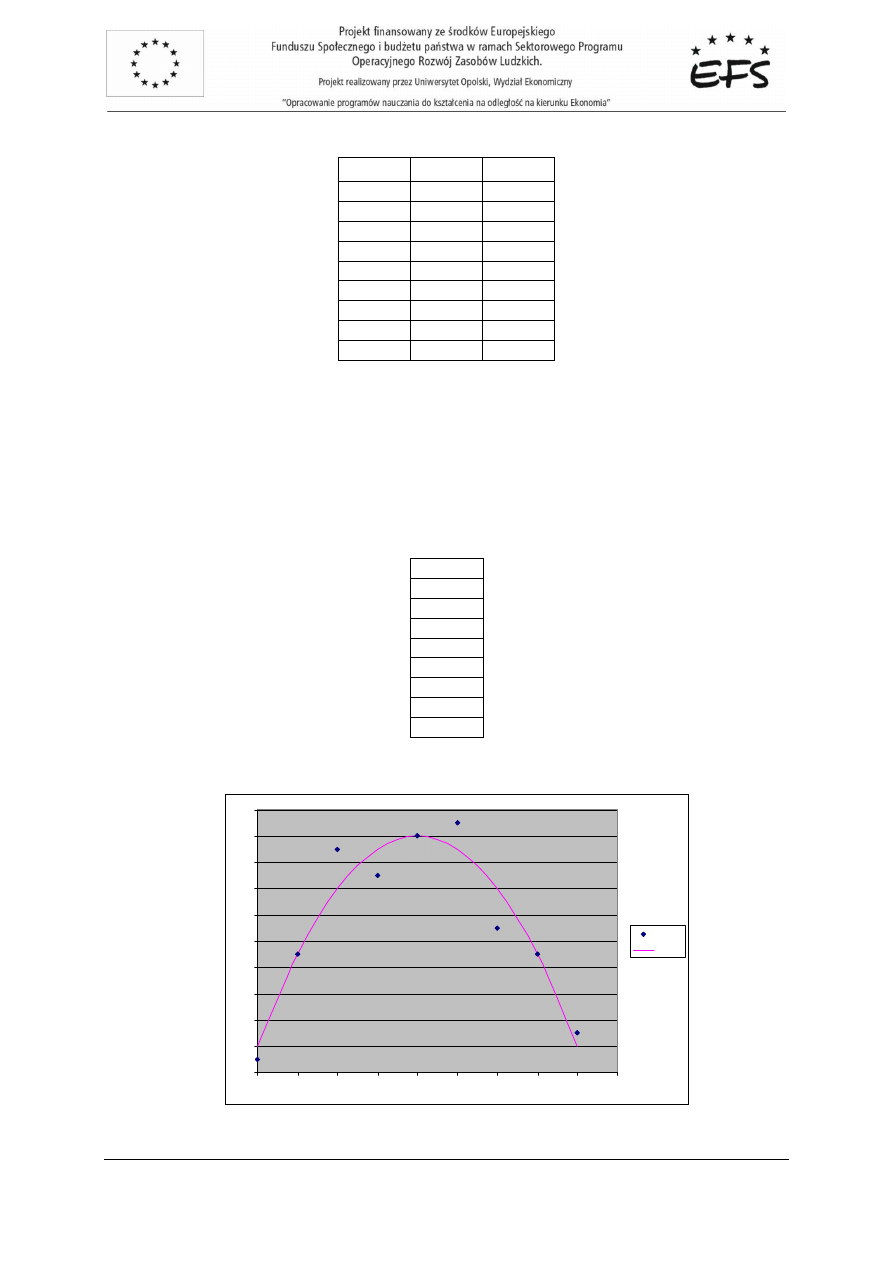
zmiennych oraz wykres rozrzutu punktów empirycznych:

Wykres rozrzutu punktów empirycznych

98

100

102

104

106

108

110

112

114

116

118

0

1

2

3

4

5

6

7

8

9

Y

Rozwi

ą

zanie:

Analiza rozrzutu punktów empirycznych na wykresie wskazuje na mo

ż

liw

ą

posta

ć

modelu

wielomianowego stopnia drugiego:

2

2

1

0

x

x

y

α

α

α

+

+

=

poprzez podstawianie budujemy posta

ć

zlinearyzowan

ą

:

z

x

y

2

1

0

α

α

α

+

+

=

gdzie: z=x

2

Y

X

99

0

107

1

115

2

113

3

116

4

117

5

109

6

107

7

101

8

mgr Grzegorz Stolarczyk

12

Ekonometria 1

Macierz obserwacji zmiennych dla modelu zlinearyzowanego:

y

x

z=x

2

99

0

0

107

1

1

115

2

4

113

3

9

116

4

16

117

5

25

109

6

36

107

7

49

101

8

64

Nast

ę

pnie korzystaj

ą

c z KMNK szacujemy parametry

α

0

,

α

1

,

α

2.

Oszacowano model zlinearyzowany o postaci:

yˆ

=-z+8x+100

Posta

ć

pierwotna:

yˆ

=-x

2

+8x+100;

Na podstawie postaci pierwotnej wyznaczono warto

ś

ci teoretyczne zmiennej obja

ś

nianej Y:

100
107
112
115
116
115
112
107
100

które naniesiono na wykres w postaci linii trendu (kolor ró

ż

owy):

98

100

102

104

106

108

110

112

114

116

118

0

1

2

3

4

5

6

7

8

9

Y

Yteor.

mgr Grzegorz Stolarczyk

13

Ekonometria 1

Estymacja parametrów modeli nieliniowych wzgl

ę

dem parametrów oraz nieliniowych wzgl

ę

dem

zmiennej obja

ś

niaj

ą

cej.

Przykład 4:

Zbuduj model zale

ż

no

ś

ci pomi

ę

dzy wydatkami na luksusowe samochody (Y), a dochodami (X).

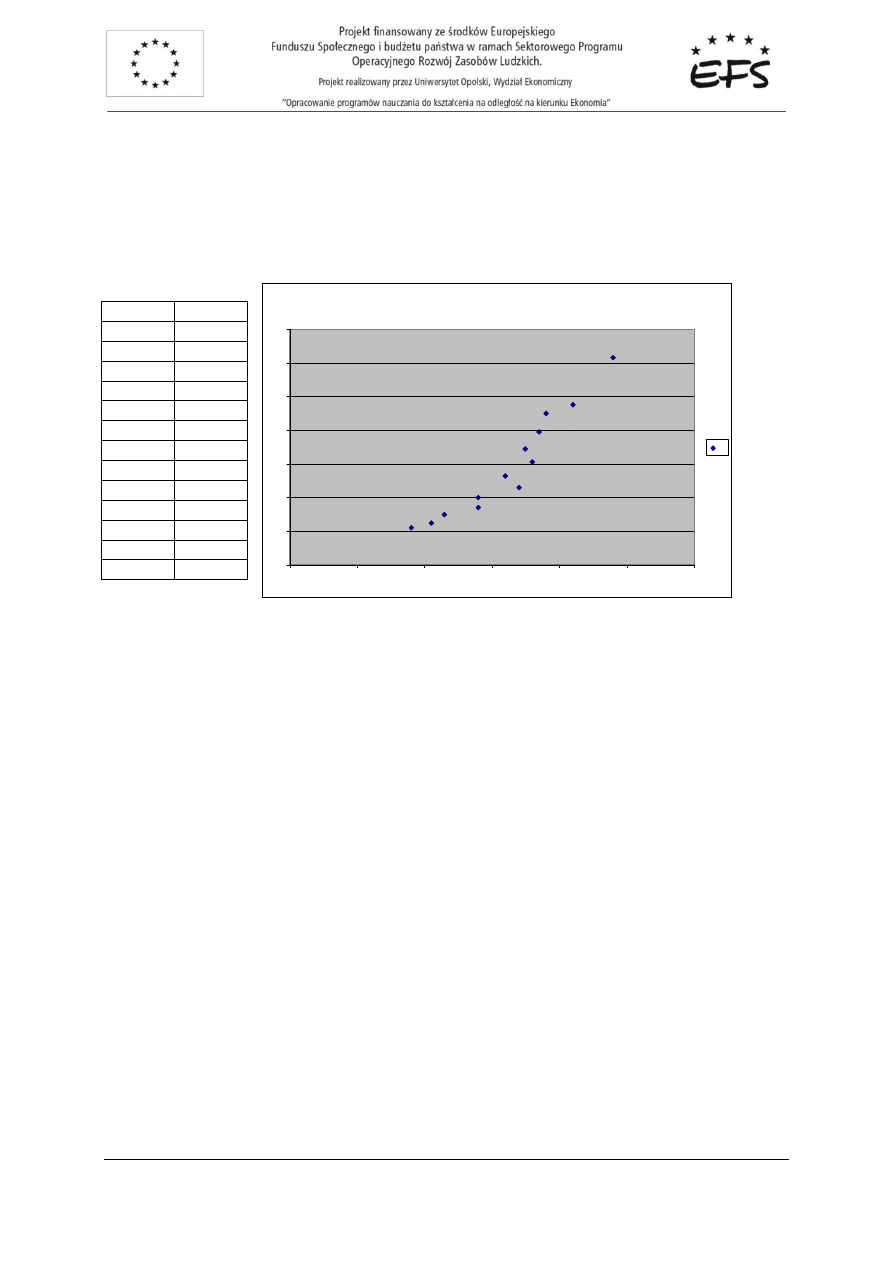
Macierz obserwacji zmiennych oraz wykres rozrzutu punktów empirycznych:

Wykres rozrzutu punktów empirycznych

0

2

4

6

8

10

12

14

0

1

2

3

4

5

6

Y

Rozwi

ą

zanie:

Analiza rozrzutu punktów empirycznych na wykresie wskazuje na mo

ż

liw

ą

posta

ć

modelu

pot

ę

gowego

1

0

α

α

x

y

⋅

=

logarytmujemy obustronnie:

ln(y)=ln(

α

0

)+

α

1

⋅

⋅

ln(x)

poprzez podstawianie budujemy posta

ć

zlinearyzowan

ą

:

v=

β

0

+

α

1

⋅

z

gdzie :

v=lny,

z=lnx,

β

0

=ln

α

0

,

Y

X

2,2

1,8

2,5

2,1

3

2,3

3,4

2,8

4

2,8

4,6

3,4

5,3

3,2

6,1

3,6

6,9

3,5

7,9

3,7

9

3,8

9,5

4,2

12,3

4,8

mgr Grzegorz Stolarczyk

14

Ekonometria 1

Macierz obserwacji zmiennych dla modelu zlinearyzowanego:

v=ln(y)

z=ln(x)

0,8

0,6

0,9

0,7

1,1

0,8

1,2

1,0

1,4

1,0

1,5

1,2

1,7

1,2

1,8

1,3

1,9

1,3

2,1

1,3

2,2

1,3

2,3

1,4

2,5

1,6

Nast

ę

pnie korzystaj

ą

c z KMNK szacujemy parametry

β

0

,

α

1.

Oszacowano model zlinearyzowany o postaci:

yˆ

=1,9z+(-0,5)

α

0

=e

β

0

⇒α

0

=0,6269

Posta

ć

pierwotna:

yˆ

=0,6x

1,9

Na podstawie postaci pierwotnej wyznaczono warto

ś

ci teoretyczne zmiennej obja

ś

nianej Y:

1,9
2,5
2,9
4,2
4,2
6,1
5,4
6,8
6,4
7,1
7,5
9,0

11,5

mgr Grzegorz Stolarczyk

15

Ekonometria 1

które naniesiono na wykres w postaci linii trendu (kolor ró

ż

owy):

0

2

4

6

8

10

12

14

0

1

2

3

4

5

6

Y

yteor.

Przykład 5:

Zbuduj model zale

ż

no

ś

ci pomi

ę

dzy jednostkowymi kosztami produkcji (Y) a wielko

ś

ci

ą

produkcji

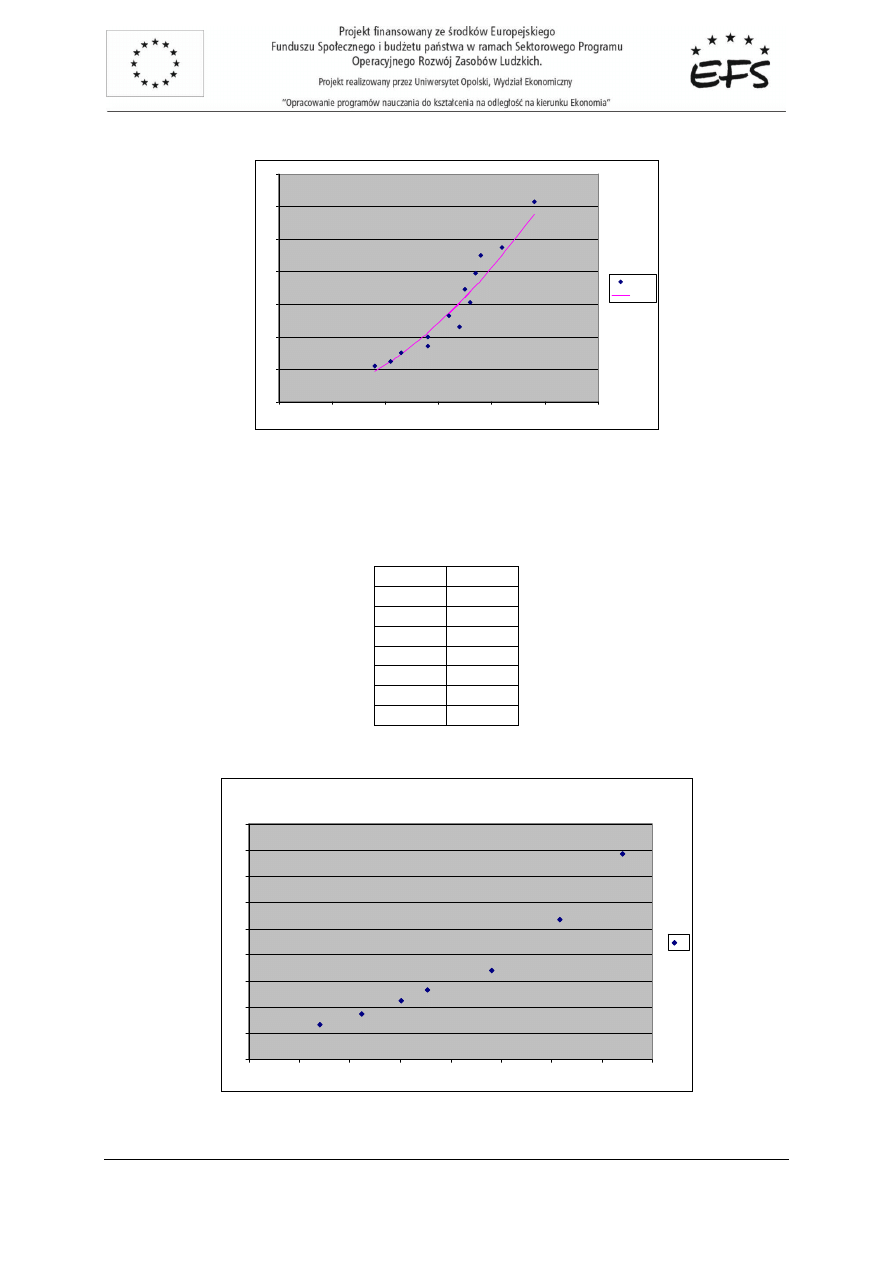
(X). Macierz obserwacji zmiennych oraz wykres rozrzutu punktów empirycznych:

Wykres rozrzutu punktów empirycznych

0

5

10

15

20

25

30

35

40

45

0

10

20

30

40

50

60

70

80

Y

Y

X

6,7

14,2

8,7

22,4

11,2

30,2

13,3

35,5

17

48,2

26,7

61,8

39,3

74,2

mgr Grzegorz Stolarczyk

16

Ekonometria 1

Rozwi

ą

zanie:

Analiza rozrzutu punktów empirycznych na wykresie wskazuje na mo

ż

liw

ą

posta

ć

modelu

wykładniczego:

x

e

y

1

0

α

α

=

logarytmujemy obustronnie:

ln(y)=ln(

α

0

)+

α

1

x

poprzez podstawianie budujemy posta

ć

zlinearyzowan

ą

:

v=

β

0

+

α

1

⋅

z

gdzie:

v=lny,

z=x,

β

0

=ln

α

0

,

Macierz obserwacji zmiennych dla modelu zlinearyzowanego:

v=ln(y)

x

1,9

14,2

2,2

22,4

2,4

30,2

2,6

35,5

2,8

48,2

3,3

61,8

3,7

74,2

Nast

ę

pnie korzystaj

ą

c z KMNK szacujemy parametry

β

0

,

α

1.

Oszacowano model zlinearyzowany o postaci:

vˆ

=0,03

⋅

Z+1,52

α

0

=e

β

0

⇒α

0

=4,5616

Posta

ć

pierwotna:

yˆ

=0,03

⋅

e

4,6X

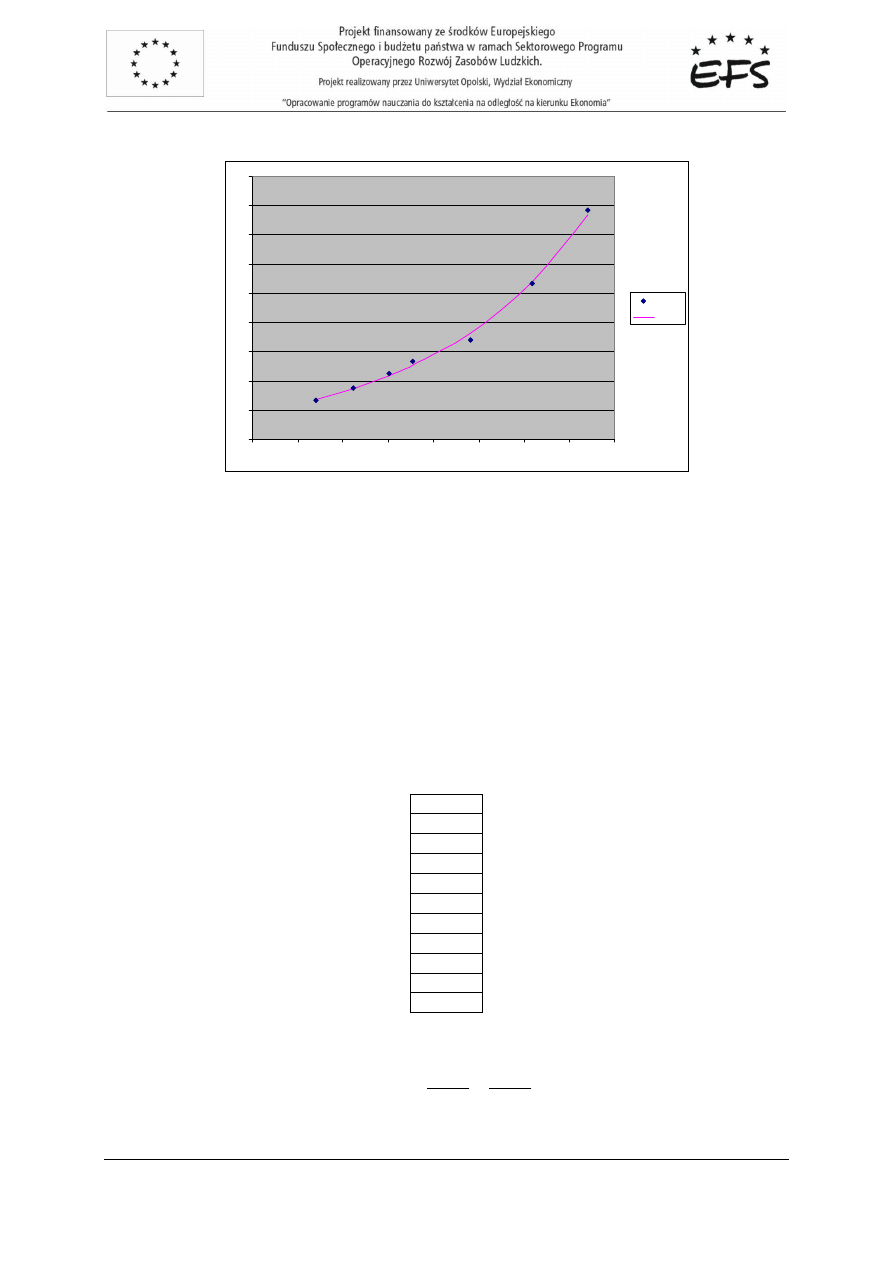
Na podstawie postaci pierwotnej wyznaczono warto

ś

ci teoretyczne zmiennej obja

ś

nianej Y:

6,9
8,7

10,9
12,7
18,2
26,9
38,5

mgr Grzegorz Stolarczyk

17

Ekonometria 1

które naniesiono na wykres w postaci linii trendu (kolor ró

ż

owy):

0

5

10

15

20

25

30

35

40

45

0

10

20

30

40

50

60

70

80

Y

Yteor.

Estymacja parametrów struktury stochastycznej

Przykład 1

Prosz

ę

na podstawie danych z danych z przykładu 1 z etapu szacowania parametrów modeli

linowych dokona

ć

estymacji parametrów struktury stochastycznej.

Rozwi

ą

zanie:

Do estymacji parametrów struktury stochastycznej niezb

ę

dne jest wyznaczenie reszt modelu e jako

ró

ż

nicy pomi

ę

dzy Y rzeczywistym a Y teoretycznym wyznaczonym z modelu:

e

2,79
9,32
0,47

-8,00
-9,85
-6,47

1,99

-4,18

6,59
7,36

Nast

ę

pnie wyznaczamy ocen

ę

wariancji składnika losowego ze wzoru:

m

n

e

e

m

n

e

Se

T

n

i

−

=

−

=

∑

=

1

2

2

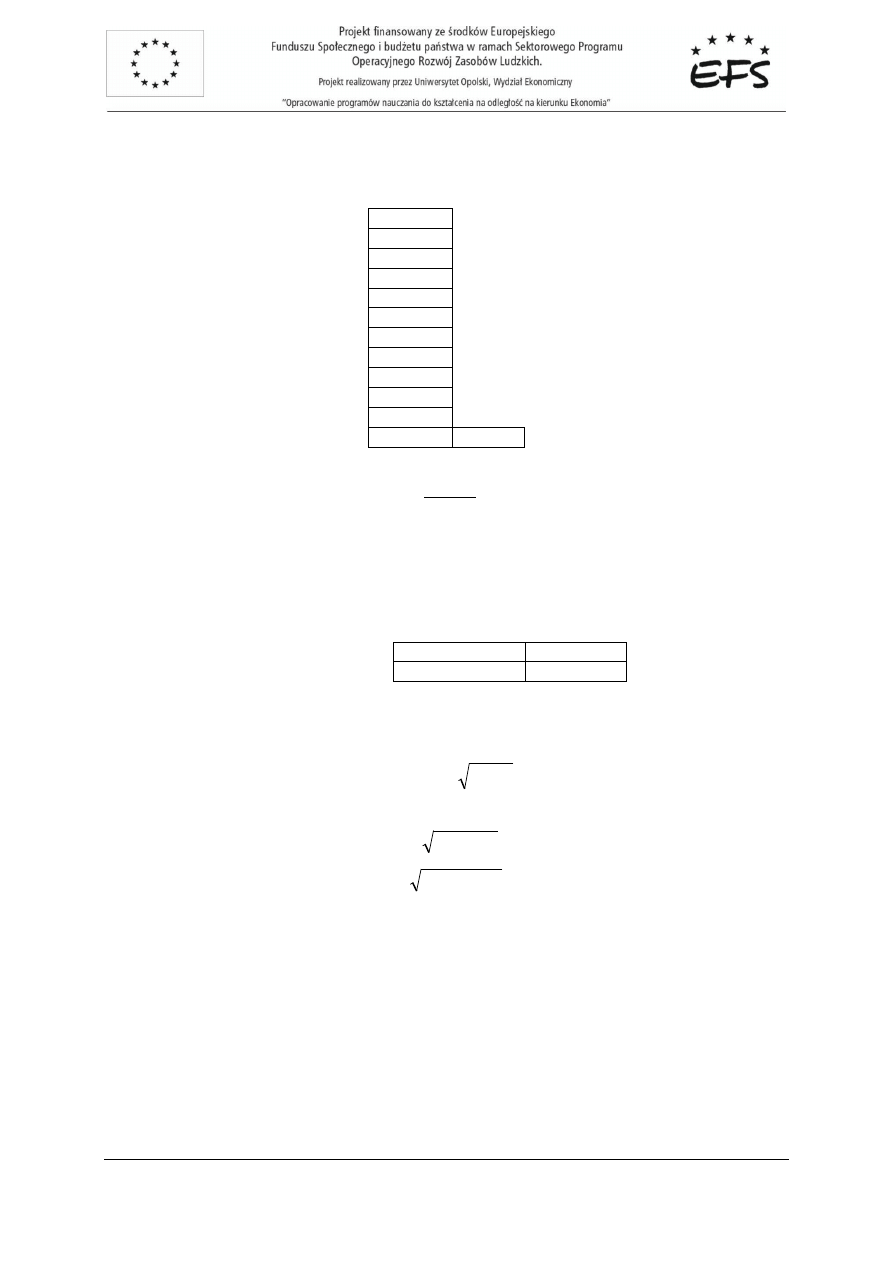
mgr Grzegorz Stolarczyk

18

Ekonometria 1

gdzie:

n – liczba obserwacji

m – liczba parametrów w modelu

e

2

7,77

86,83

0,22

64,04

97,11

41,88

3,94

17,43

43,43

54,10

416,76

suma

10

,

52

2

10

76

,

416

2

=

−

=

Se

Macierz wariancji i kowariancji ocen parametrów szacujemy na podstawie wzoru:

1

2

2

)

(

)

(

−

⋅

=

X

X

Se

a

D

T

0,0008

-0,7486

)

(

2

a

D

=

-0,7486

669,5771

W tej macierzy na głównej przek

ą

tnej wyznaczone s

ą

oceny wariancji szacunku parametrów V(a

j

).

Obliczone wielko

ś

ci

)

(

)

(

j

j

a

V

a

S

=

s

ą

to standardowe bł

ę

dy szacunku parametrów i wynosz

ą

kolejno:

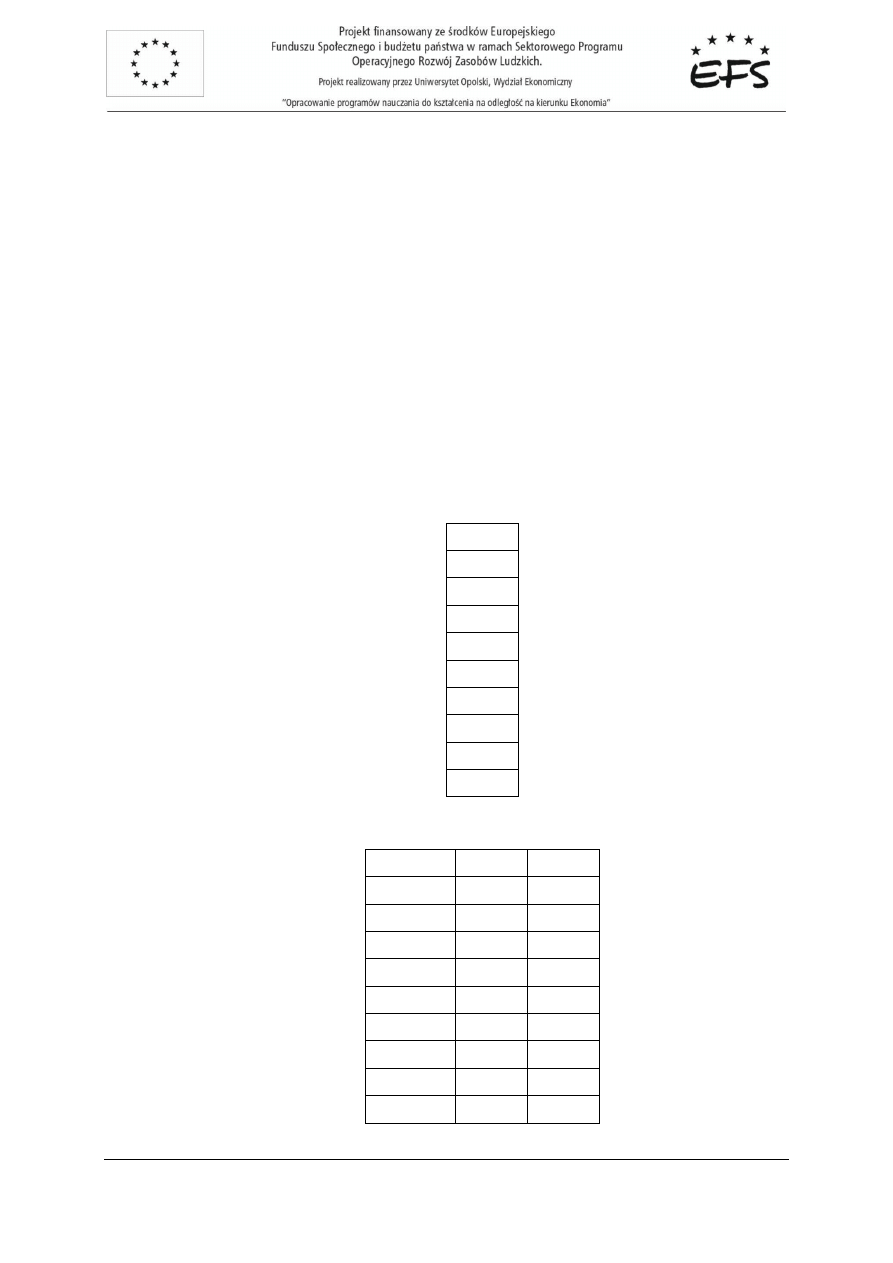
S(a) =

=

0008

,

0

0,029

S(b) =

=

5771

,

669

25,876

Jak wyszło z oblicze

ń

warto

ść

oceny a ró

ż

ni si

ę

o 0,029 od rzeczywistej warto

ś

ci parametru,

a ocena b o 25,876.

mgr Grzegorz Stolarczyk

19

Ekonometria 1

Przykład 2.

Prosz

ę

oszacowa

ć

parametry modelu liniowego opisuj

ą

cego zespołow

ą

wydajno

ść

pracy

na podstawie danych z przykładu 1 przedstawionego w etapie doboru zmiennych obja

ś

niaj

ą

cych

do modelu.

Rozwi

ą

zanie:

Do modelu weszły zmienne obja

ś

niaj

ą

ce X

2

i X

3

dobrane z wykorzystaniem metody wska

ź

ników

pojemno

ś

ci informacji.

Model ma posta

ć

:

0

3

2

2

1

^

α

α

α

+

+

=

x

x

y

Parametry b

ę

dziemy szacowa

ć

wg wzoru:

Y

X

X

X

a

T

T

1

)

(

−

=

Wektor Y obserwacji zmiennej obja

ś

nianej oraz macierz X obserwacji zmiennych obja

ś

niaj

ą

cych

wygl

ą

daj

ą

nast

ę

puj

ą

co:

14

17

14,5

Y=

20

21,6

23

24,5

28

26,4

29

0,4

15

1

0,6

13

1

0,4

15

1

0,7

11

1

X=

1

10

1

1,2

10

1

1

7

1

1,5

6

1

1,5

8

1

1,7

5

1

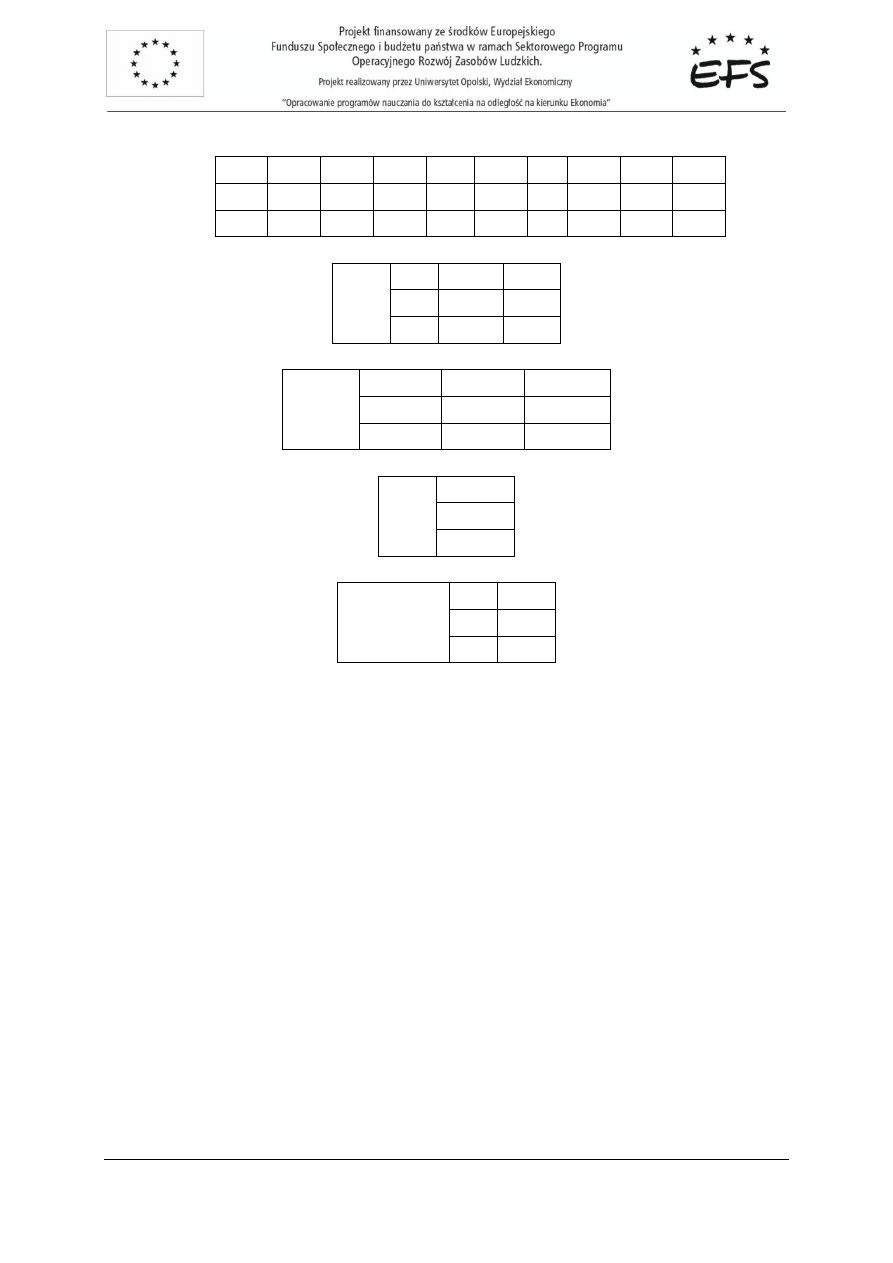
mgr Grzegorz Stolarczyk

20

Ekonometria 1

Obliczenia:

0,4

0,6

0,4

0,7

1

1,2

1

1,5

1,5

1,7

X

T

15

13

15

11

10

10

7

6

8

5

1

1

1

1

1

1

1

1

1

1

12

86

10

86

1114

100

X

T

X

10

100

10

3,5625

0,4375

-7,9375

0,4375

0,0625

-1,0625

(X

T

X)

-1

-7,9375

-1,0625

18,6625

240,2

2010,2

X

T

Y

218

a1

4,8

a2

-0,9

(X

T

X)

-1

X

T

Y=

a0

26

Zatem oszacowany model ma posta

ć

:

26

9

,

0

8

,

4

3

2

^

+

⋅

−

⋅

=

x

x

y

W naszym przykładzie mo

ż

na interpretowa

ć

parametry nast

ę

puj

ą

co:

Wzrost technicznego uzbrojenia pracy (x2) o 1 tys. zł na 1 zatrudnionego spowoduje wzrost

zespołowej wydajno

ś

ci pracy o 4,8 tys. zł na 1 zatrudnionego, przy zało

ż

eniu,

ż

e pozostałe zmienne

nie ulegn

ą

zmianie. Je

ż

eli wzro

ś

nie zatrudnienie (x3) o tysi

ą

c osób, to wydajno

ść

pracy powinna si

ę

zmniejszy

ć

o 900 zł na 1 zatrudnionego, przy zało

ż

eniu,

ż

e pozostałe zmienne nie ulegn

ą

zmianie.

Wyliczamy z modelu warto

ś

ci teoretyczne zmiennej obja

ś

nianej

y

:

26

15

9

,

0

4

,

0

8

,

4

^

1

+

⋅

−

⋅

=

y

26

13

9

,

0

6

,

0

8

,

4

^

1

+

⋅

−

⋅

=

y

26

15

9

,

0

4

,

0

8

,

4

^

1

+

⋅

−

⋅

=

y

26

11

9

,

0

7

,

0

8

,

4

^

1

+

⋅

−

⋅

=

y

26

10

9

,

0

1

8

,

4

^

1

+

⋅

−

⋅

=

y

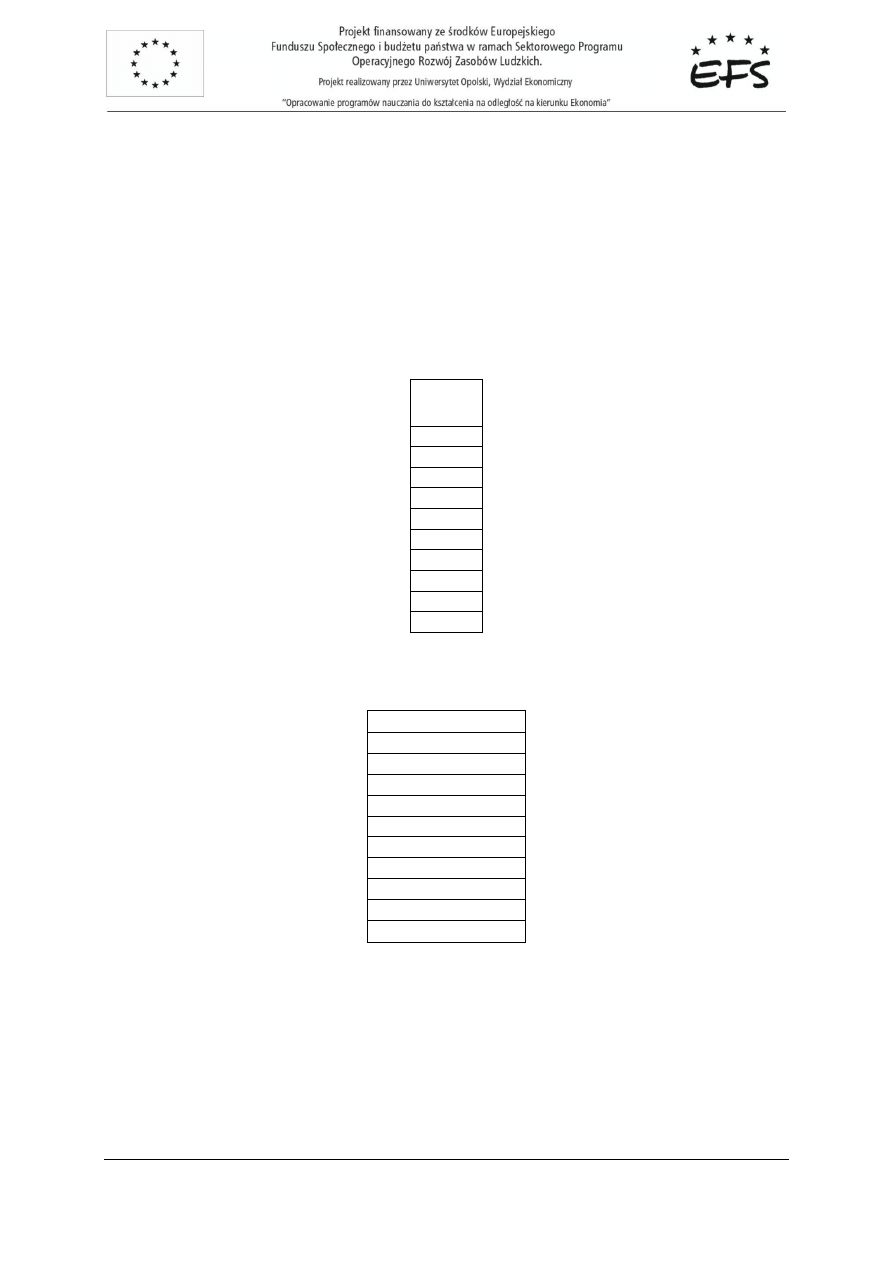
mgr Grzegorz Stolarczyk

21

Ekonometria 1

26

10

9

,

0

2

,

1

8

,

4

^

1

+

⋅

−

⋅

=

y

26

7

9

,

0

1

8

,

4

^

1

+

⋅

−

⋅

=

y

26

6

9

,

0

5

,

1

8

,

4

^

1

+

⋅

−

⋅

=

y

26

8

9

,

0

5

,

1

8

,

4

^

1

+

⋅

−

⋅

=

y

26

5

9

,

0

7

,

1

8

,

4

^

1

+

⋅

−

⋅

=

y

^

y

14,42
17,18
14,42
19,46

21,8

22,76

24,5
27,8

26

29,66

Dokonujemy estymacji parametrów struktury stochastycznej.

Szacujemy reszty modelu i wariancj

ę

składnika losowego:

e

-0,42

-0,18

0,08

0,54

-0,2

0,24

-0,00000000000034

0,2
0,4

-0,66

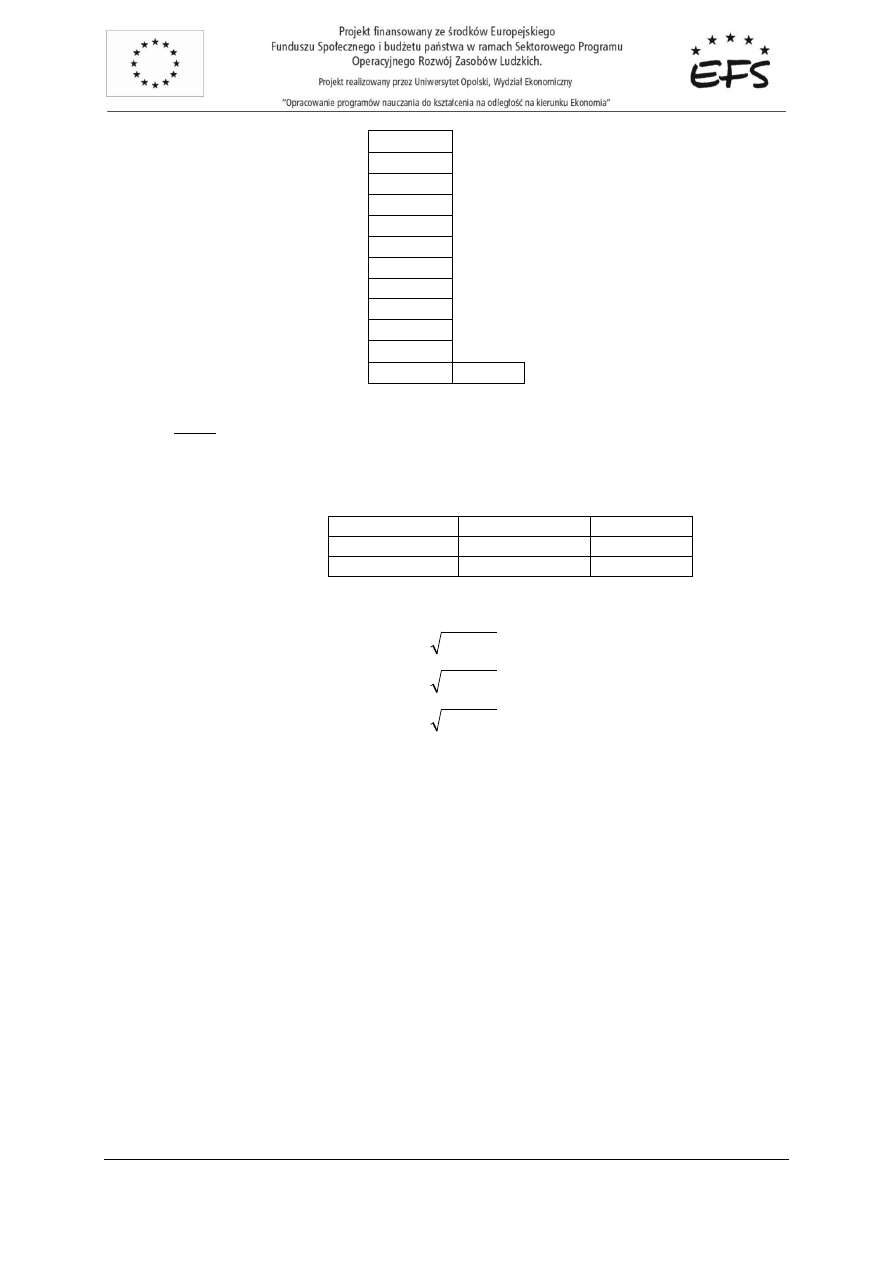
mgr Grzegorz Stolarczyk

22

Ekonometria 1

e

2

0,1764

0,0324

0,0064

0,2916

0,04

0,0576

1,16E-25

0,04

0,16

0,4356

1,24

suma

177

,

0

3

10

24

,

1

2

=

−

=

Se

Macierz wariancji i kowariancji ocen parametrów:

0,631

0,077

-1,406

0,077

0,011

-0,188

)

(

2

a

D

=

-1,406

-0,188

3,306

Standardowe bł

ę

dy szacunku parametrów wynosz

ą

:

S(a

1

) =

=

631

,

0

0,794

S(a

2

) =

=

011

,

0

0,105

S(a

0

) =

=

306

,

3

1,818

Warto

ść

oceny a

1

ró

ż

ni si

ę

o 0,794 od rzeczywistej warto

ś

ci parametru, warto

ść

oceny a

2

o 0,105,

a warto

ść

oceny a

0

o 1,818.

Zadanie 1.

Wyznaczy

ć

standardowe bł

ę

dy szacunku parametrów modelu

3

2

2

1

0

^

x

x

y

α

α

α

+

+

=

na podstawie

danych:

589

,

0

2

=

Se

(X

T

X)

-1

=





















3

2

4

2

1

5

4

5

4

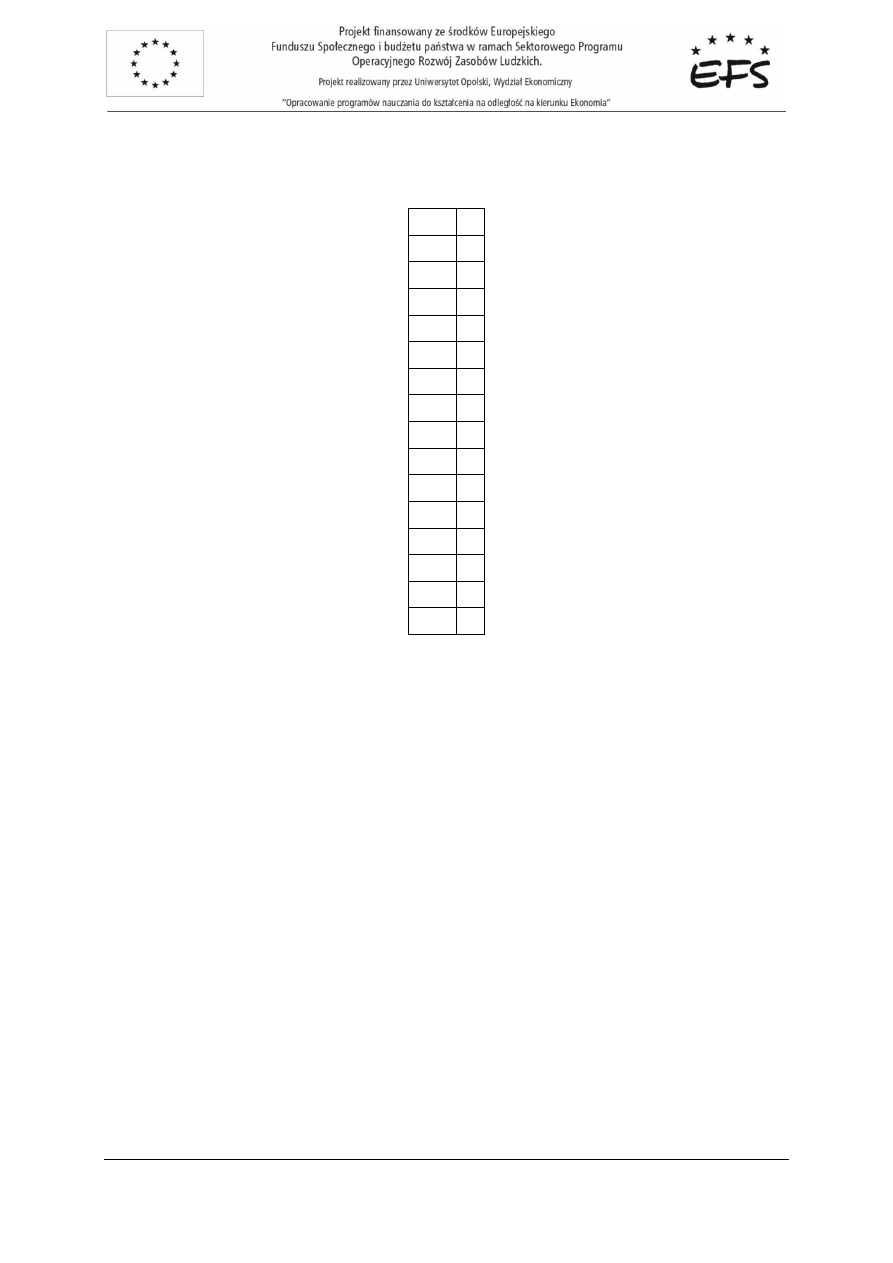
mgr Grzegorz Stolarczyk

23

Ekonometria 1

Zadanie 2.

W tabeli przedstawiono miesi

ę

czne dane z pewnego przedsi

ę

biorstwa dotycz

ą

ce wielko

ś

ci

przychodów ze sprzeda

ż

y w tys. zł. z okresu stycze

ń

2005r – marzec 2006r.

Y

T

34,7

1

37

2

58

3

62

4

67,8

5

75,3

6

79,9

7

85,6

8

90,4

9

99

10

105,6 11

111

12

119,3 13

127,8 14

135

15

Prosz

ę

oszacowa

ć

parametry modelu liniowego opisuj

ą

cego kształtowanie si

ę

wielko

ś

ci sprzeda

ż

y

w czasie t i wyznaczy

ć

warto

ś

ci wektora reszt.

Zadanie 3.

Oszacowa

ć

parametry modelu liniowego

3

2

2

1

0

^

x

x

y

α

α

α

+

+

=

na podstawie danych:





















=

160

2068

1704

Y

X

T





















−

−

=

71

,

1

04

,

0

21

,

0

?

04

,

0

05

,

0

?

?

08

,

0

)

(

2

a

D

266

,

0

2

=

Se

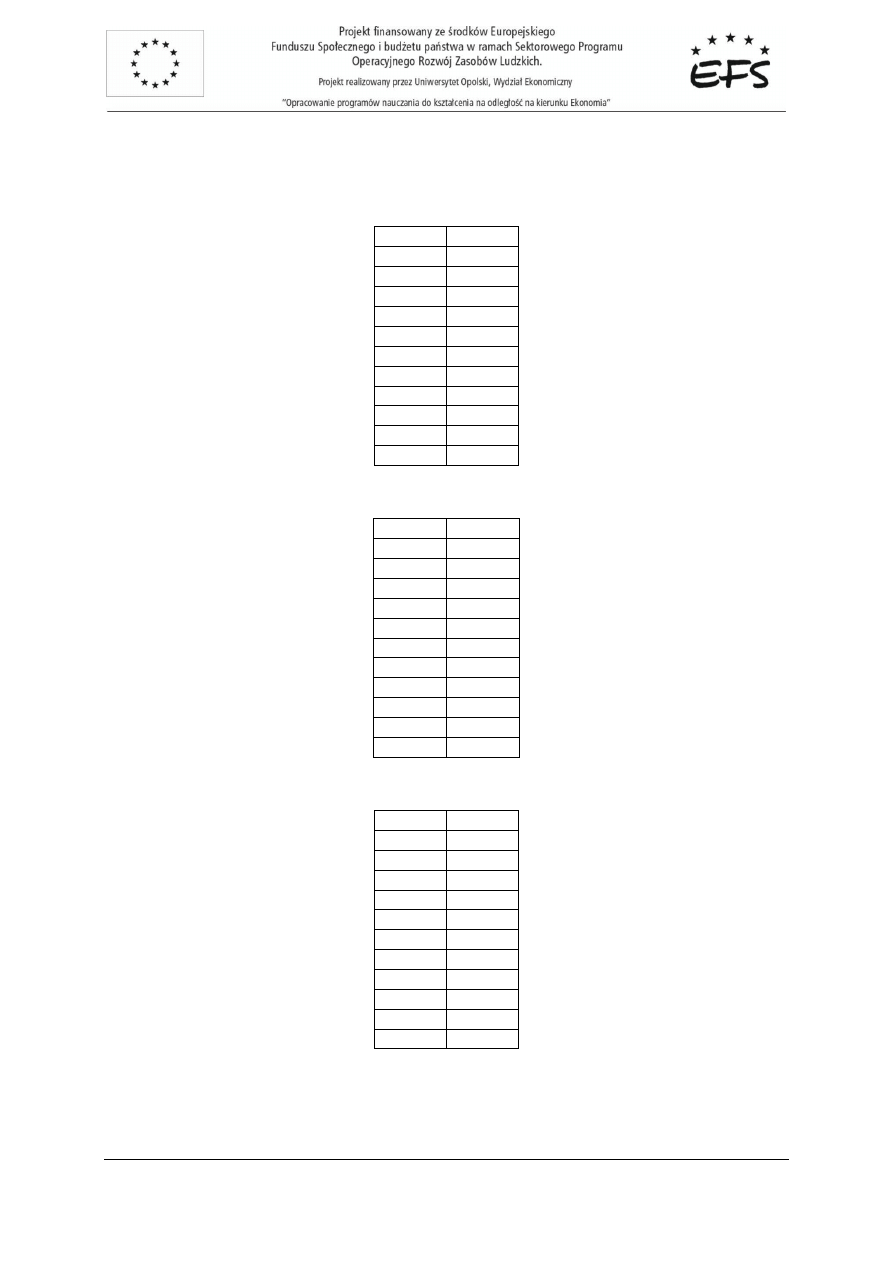
mgr Grzegorz Stolarczyk

24

Ekonometria 1

Zadanie 4.

Na podstawie danych empirycznych okre

ś

l posta

ć

analityczn

ą

modelu nieliniowego i oszacuj

parametry modelu:

a) Zale

ż

no

ść

pomi

ę

dzy wydatkami na markowe ubrania (Y) a dochodami (X)

Y

X

24

46

25

48

25

49

26

52

27

52

27

54

28

57

29

59

31

59

33

60

35

61

b) Zale

ż

no

ść

pomi

ę

dzy jednostkowymi kosztami produkcji (Y) a wielko

ś

ci

ą

produkcji (X)

Y

X

2,19

2,62

6,97

10

10

11

8,18

12

10,5

14

11,75

16

12,75

19

15

21

18

21,93

22,8

24

36,93

26,64

c) Zale

ż

no

ść

pomi

ę

dzy warto

ś

ci

ą

maj

ą

tku trwałego (Y), a warto

ś

ci

ą

pracy (X) w przedsi

ę

biorstwie

Y

X

3,4

35

3,4

33

3,5

31

3,7

29

3,8

28

3,8

27

3,9

27

4

26

4,3

25

4,5

25

4,8

24

mgr Grzegorz Stolarczyk

25

Ekonometria 1

d) Zale

ż

no

ść

pomi

ę

dzy wydajno

ś

ci

ą

pracy (Y), a sta

ż

em pracy (X)

Y

X

2

2,6

7

10

10

11

8

12

10,5

14

11,75

16

12,75

19

15

21

18

22

23

24

37

26,5

e) Zu

ż

ycie paliwa w silnikach spalinowych (Y) w zale

ż

no

ś

ci od wysoko

ś

ci obrotów silnika (X)

Y

X

7,6

1,7

5

2,4

3,9

2,8

4

3,2

5

3,4

5

3,4

6

3,6

7

4,2

9

4,8

11

5,3

15,6

5,7