Klasyczna metoda najmniejszych kwadratów (etap IV - estymacja).
Załóżmy, że przyjęta hipoteza modelową możemy przedstawić w postaci liniowego równania regresji:
![]()
Przyjmując notację macierzową mamy, że Y to wektor obserwacji dokonanych na zmiennej objaśnianej.
Xk - wektory obserwacji dokonanych na zmiennych objaśniających. Zwykle zapisuje się wartości z poszczególnych wektorów jako kolumny w łącznej macierzy X. Tym samym X to macierz obserwacji dokonanych na zmiennych objaśniających,
βi = to parametr strukturalny stojący przy i - tej zmiennej objaśniającej,
U - to wektor składnika losowego.
Poszczególne parametry strukturalne modelu zapisać można również w formie wektora parametrów strukturalnych β wprowadzając więc następujące oznaczenia:
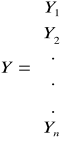
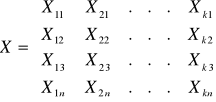
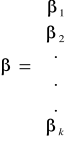
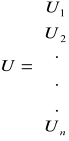
możemy zapisać model ekonometryczny w postaci macierzy jako:
![]()
Jeżeli w modelu ma być obecny wyraz wolny - jedną ze zmiennych (np. Xk) przyjmujemy jako równą jedności dla każdej obserwacji, co przy pomocy następującej macierzy X:
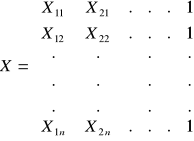
Jeżeli dokonamy estymacji powyższego modelu to w jej wyniku otrzymamy wektor ocen parametrów strukturalnych modelu (b):
![]()
Istota metody najmniejszych kwadratów polega na takim oszacowaniu wartości parametrów strukturalnych w modelu, przy których suma kwadratów odchyleń obserwacji od hiperpłaszczyzny wyznaczonym powyższym równaniem będzie minimalna.
![]()
![]()
y
MNK
x
Minimalizacja sumy kwadratów odchyleń dokonujemy poprzez zróżniczkowanie równania tych odchyleń wyrażonego macierzami X, Y i b i przyrównanie otrzymanego wyniku do zera. Otrzymywany w ten sposób wektor estymatorów parametrów strukturalnych modelu w MNK przedstawia się następująco:![]()
b - wektor ocen parametrów strukturalnych modelu.
Warto pamiętać, że MNK jest metodą uniwersalną. Aby estymatory MNK posiadały wymagane własności muszą być spełnione następujące założenia:
zmienne objaśniające tworzą nielosową macierz obserwacji X i macierz ta jest rzędu k
postać modelu jest liniowa względem parametrów (może być nieliniowa względem zmiennych)
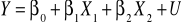
![]()
liczba obserwacji n jest większa od liczby szacowanych parametrów,
kolumny macierzy X muszą być liniowo niezależne tzn. w macierzy X nie może występować współliniowość,
składnik losowy U posiada następujące własności:
nadzieję matematyczną =0,
![]()
, t = 0,1,...,n
stałą i skończoną wariancję,
![]()
zerowe kowariancje (miara siły związku),
![]()
, s ≠ t; s, t = 0, 1,...,n
rozkład normalny
![]()
0 - średnia, δ - odchylenie standardowe
Jeżeli chociaż jeden z warunku od 2 do 4 nie jest spełniony, wówczas estymatory MNK nie istnieją. Jeżeli spełnione są wszystkie założenia od 1 do 5 wówczas i estymatory MNK posiadają pewne cenne własności tj.:
nieobciążalność,
zgodność,
efektywność.
Twierdzenie dotyczące własności estymatorów uzyskanych MNK nosi nazwę twierdzenia Gaussa - Markowa:
Twierdzenie 1:
Jeżeli spełnione są założenia od 1 do 5 to wektor b estymatorów parametrów β uzyskanych MNK jest zgodny, nieobciążony i najefektywniejszy w klasie estymatorów liniowych.
Twierdzenie 2:
Jeżeli spełnione są założenia od 2 do 5 a macierz X jest losowa, ale niezależna od U, to wektor b jest zgodny i nieobciążony.
Twierdzenie 3:
Jeżeli spełnione są założenia twierdzeń 1 i 2 to nieobciążony estymator S2 wariancji składnika losowego δ2 wyraża się wzorem:
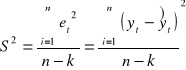
, gdzie:
n - to liczba obserwacji,
k - liczba szacowanych parametrów.
Wariancja estymatorów parametrów strukturalnych liczona jest wg wzoru:
![]()
dii - elementy leżące na głównej przekątnej macierzy (XTX)-1
Z uwagi na to, że nieznana jest prawdziwa wartość δ2 zastępujemy ją estymatorem S2.
Weryfikacja założeń klasycznej MNK
I etap - Badanie dokładności dopasowania modelu do danych empirycznych.
Miarę stopnia dopasowania modelu jest współczynnik zbieżności określany wzorem:
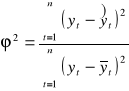
Współczynnik zbieżności (indeterminacji)
Miara ta mówi o udziale wariancji reszt w ogólnej wariancji zmiennej objaśnianej. Informuje ile % zmienności zmiennej objaśnianej Y nie zostało wyjaśnione przez model.
Współczynnik zbieżności φ2 jest bliższa 0 tym model lepiej opisuje badane zjawisko.
Zamiast współczynnika zbieżności można używać współczynnika determinacji:
![]()
Informuje on o udziale wariancji wytłumaczonej przez model w ogólnej wariancji zmiennej objaśnianej. Jest również miarą unormowaną na przedziale <0,1>. Im jego wartość bliższa jedności tym lepiej model opisuje kształtowanie się zmiennej objaśnianej.
![]()
czyli R jest współczynnikiem korelacji wielorakiej ![]()
.
II etap - Badanie dokładności szacunku
Miarami dokładności szacunku są parametry struktury stochastycznej składnika losowego, tj.:
jego odchylenie standardowe,
współczynnik zmienności losowej.
Zgodnie z twierdzeniem Gaussa - Markowa estymatorem wariancji składnika losowego (wariancji resztowej) w MNK jest:
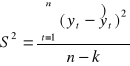
S2 = (Se2)
![]()
to odchylenie standardowe składnika losowego, inaczej odchylenie resztowe (S).
Odchylenie to informuje jakie przeciętnie wahania mogą wykonywać wartości realizacji zmiennej Y w stosunku do modelu.
Współczynnik zmienności losowej dany jest wzorem:
![]()
Współczynnik ten informuje o udziale odchylenia resztowego w przeciętnej wartości zmiennej endogenicznej. Weryfikacja tego współczynnika polega na obraniu krytyczniej wartości Vs* najczęściej niewiększej niż 15%.
III etap - Badanie statystycznej istotności ocen parametrów strukturalnych.
Aby stwierdzić, które z obecnych w modelu zmiennych objaśniających mają istotny wpływ na kształtowanie się zmiennej objaśnianej, należy po estymacji parametrów dokonać weryfikacji hipotezy o ich istotności tzn. zbadać , czy otrzymane wartości statystyczne istotnie różnią się od zera.
Test istotności, który służy do weryfikacji powyższej hipotezy jest następujący:
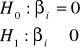
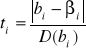
βi = 0
ti - ma rozkład t - Studenta o (n - k) stopniach swobody.
Jeżeli nie dysponujemy dodatkowymi informacjami o wartościach βi, przyjmujemy, że równe są 0.
D(bi) - standardowe błędy szacunków parametrów bi czyli pierwiastki kwadratowe elementów głównej przekątnej macierzy wariancji i kowariancji estymatorów parametrów strukturalnych.
![]()
D2(β) - macierz wariancji kowariancji parametrów strukturalnych.
Ponieważ w praktyce wartość δ2 nie jest znana, macierz powyższą przybliża się następującym wzorem:
![]()
Obliczone wartości statystyki t porównujemy z wartościami krytycznymi z tablic rozkładu t - studenta dla założonego poziomu istotności α (czyli prawdopodobieństwa popełnienie błędu polegającego na odrzuceniu hipotezy prawdziwej) dla danej liczby spodni swobody (n - k).
Jeżeli ![]()
to H0 zostaje odrzucone co oznacza, że ocena parametrów jest istotnie różne od 0. Jeżeli ![]()
to nie ma podstaw do odrzucenia H0 co oznacza nieistotność parametru i.
IV etap - Weryfikacja wybranych hipotez dotyczących składnika losowego.
Do podstawowych hipotez, które należy zweryfikować na tym etapie należą:
hipotezy dotyczące normalności rozkładu,
braku autokorelacji reszt,
jednorodności wariancji.
IVa Badanie autokorelacji składnika losowego.
Do badania hipotezy o nieskorelowaniu składników losowych wykorzystywany jest test Durbina-Watsona. Zakłada się w nim, że składniki losowe maja rozkład normalny. Hipoteza zerowa przyjmuje postać:
H0: ζ = 0
H1: ζ ≠ 0
Gdzie przez ζ oznaczamy współczynnik autokorelacji rzędu pierwszego. Statystyka testowa przybiera następującą postać:
![]()
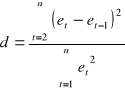
r, t - reszty modelu
Statystyka ta jest unormowana w przedziale od 0 do 4. Jej nadzieja matematyczna jest równa 2. Statystyka d ma rozkład Durbina-Watsona. Który jest stablicowany, a jej wartości krytyczne odczytujemy w zależności od liczebności próby n oraz ilości stopni swobody n - k.
n - liczebność,
k - liczba szacowanych parametrów w modelu.
Przy danym poziomie istotności α z tablic rozkładu Durbina-Watsona odczytujemy dwie wartości krytyczne, wartość dolną dL i wartość górną du.
Możemy spotkać się z następującymi sytuacjami:
dL du
0 3˚ 2 4˚ 4
H1 H0 (brak autokorelacji)
Jeżeli d znajduje się w przedziale od 0 do dL to odrzucamy H0 na korzyść na korzyść H1. alternatywny składnik losowy jest autoskorelowany.
3˚ - nie można podjąć decyzji co do stawianych hipotez na podstawie testu Durbina-Watsona.
4˚ - w przypadku gdy statystyka d przyjmuje wartość z przedziału od 2 do 4 obliczamy statystykę pomocniczą wg wzoru:
d' = 4 - d
i przeprowadzamy wnioskowanie na podstawie statystyki d'.
y
x
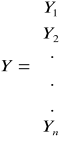
Wyszukiwarka
Podobne podstrony:
3 ćwiczenia szacowanie parametrów modeli liniowych klasyczną metodą najmniejszych kwadratów
6 własności estymatora parametrów klasycznego modelu liniowego uzyskanego metodą najmniejszych kwadr
Identyfikacja Procesów Technologicznych, Identyfikacja parametrycznarekurencyjną metodą najmniejszyc
metoda najmniejszych kwadratów wzory
Założenia klasycznej metody najmniejszych kwadratów, Wykłady rachunkowość bankowość
Nieliniowa metoda najmniejszych kwadratów, Ekonometria
METODA NAJMNIEJSZYCH KWADRA, Inne
SPRAWKO Metoda Najmniejszych Kwadratów- SVD, Automatyka i robotyka air pwr, VI SEMESTR, Metody numer
Metoda najmniejszych kwadratów
16 opracowanie rzutowanie metoda najmniejszych kwadratow
Podstawy Metrologii metoda najmniejszych kwadratów
Metoda najmniejszych kwadratów
Aproksymacja metodą najmniejszych kwadratów
metoda najmniejszych kwadratów
Odchylenie standartowe i metoda najmniejszych kwadratów
więcej podobnych podstron