Algorytmy Grafowe
Algorytmy Grafowe
Spis treści
1 Algorytm Forda-
Bellmana
2 Algorytm Dijkstry
3 Algorytm Floyda
Algorytmy Grafowe
1 Algorytm Forda-Bellmana
2 Algorytm Dijkstry
3 Algorytm Floyda
Grafy – podstawowe
definicje
Graf: G = (V, E)
Zbiór wierzchołków grafu:
V = {1, 2, …, n}
Zbiór krawędzi grafu:
E { {i, j} : i ≠ j i i, jV}
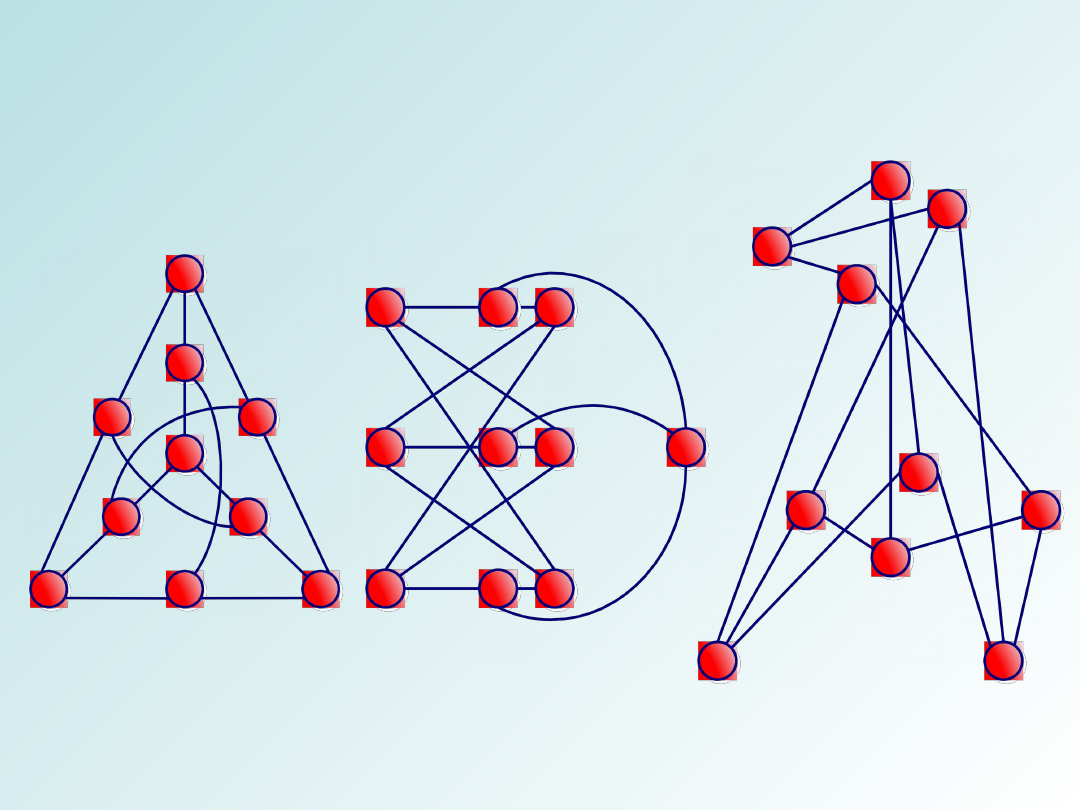
Rysunek grafu:
- wierzchołek i przedstawia symbol
- krawędź {i, j} przedstawia odcinek łączący dwa
wierzchołki
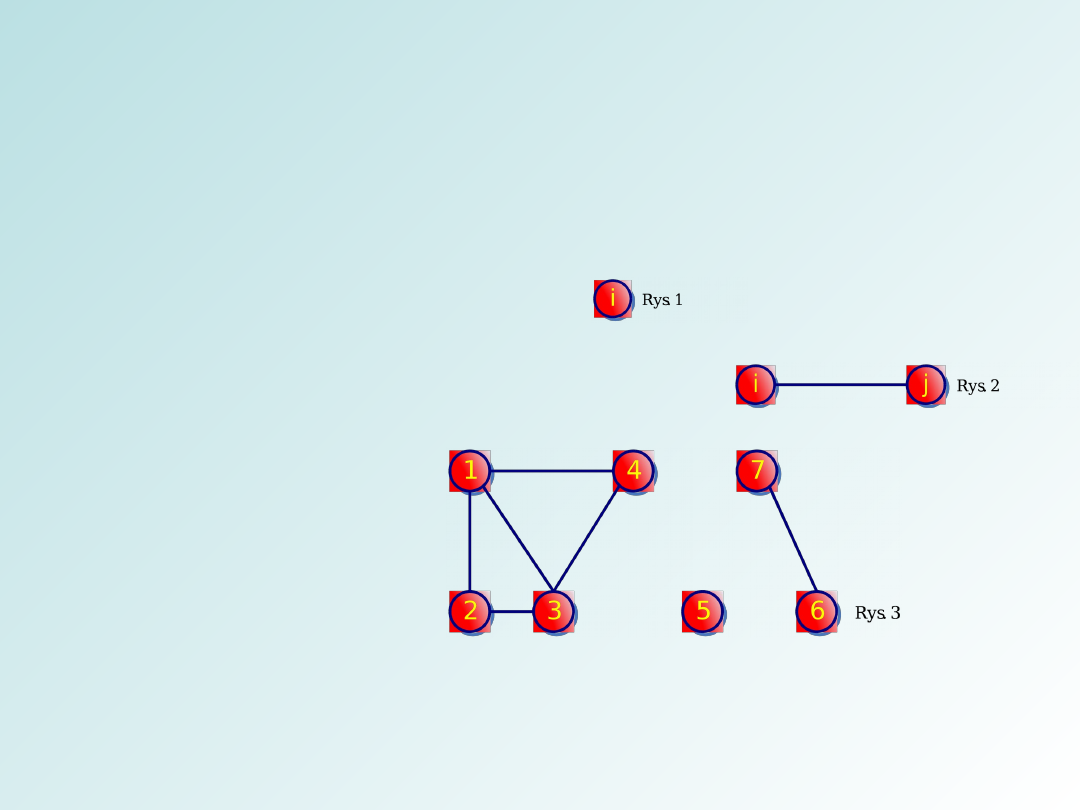
Przykład grafu i jego rysunek:
G = (V, E)
V = {1, 2, 3, 4, 5, 6, 7 }
E = { {1, 2 }, {1, 3 }, {1, 4 }, {2, 3 }, {3, 4 }, {6, 7 } }
Graf prosty i graf ogólny
Grafem prostym, nazywamy graf G = (V, E) – (gdzie V jest
niepustym
skończonym
zbiorem
elementów
zwanych
wierzchołkami lub węzłami, a E jest skończonym zbiorem
nieuporządkowanych par różnych (w parach) elementów zbioru V
zwanym krawędziami). W każdym grafie prostym istnieje co
najwyżej jedna krawędź łącząca daną parę wierzchołków.
Jednakże wiele wyników dotyczących grafów prostych można
rozszerzyć tak, by dotyczyły obiektów ogólniejszych, w których
dwa wierzchołki mogą być połączone więcej niż jedna krawędzią.
Ponadto możemy pozbyć się ograniczenia mówiącego, że
krawędź łączy dwa różne wierzchołki i dopuścić pętle.
Graf prosty i graf ogólny
Powyższy obiekt, w którym mogą występować krawędzie
wielokrotne i pętle, nazywamy grafem ogólnym, lub po prostu
grafem. Zatem każdy graf prosty jest grafem ogólnym, ale nie
każdy graf ogólny jest grafem prostym. Zatem graf G składa się
z niepustego zbioru skończonego V (G), którego elementy
nazywamy wierzchołkami, i skończonej rodziny E (G) par nie
uporządkowanych (niekoniecznie różnych) elementów zbioru V
(G) nazywanych krawędziami.
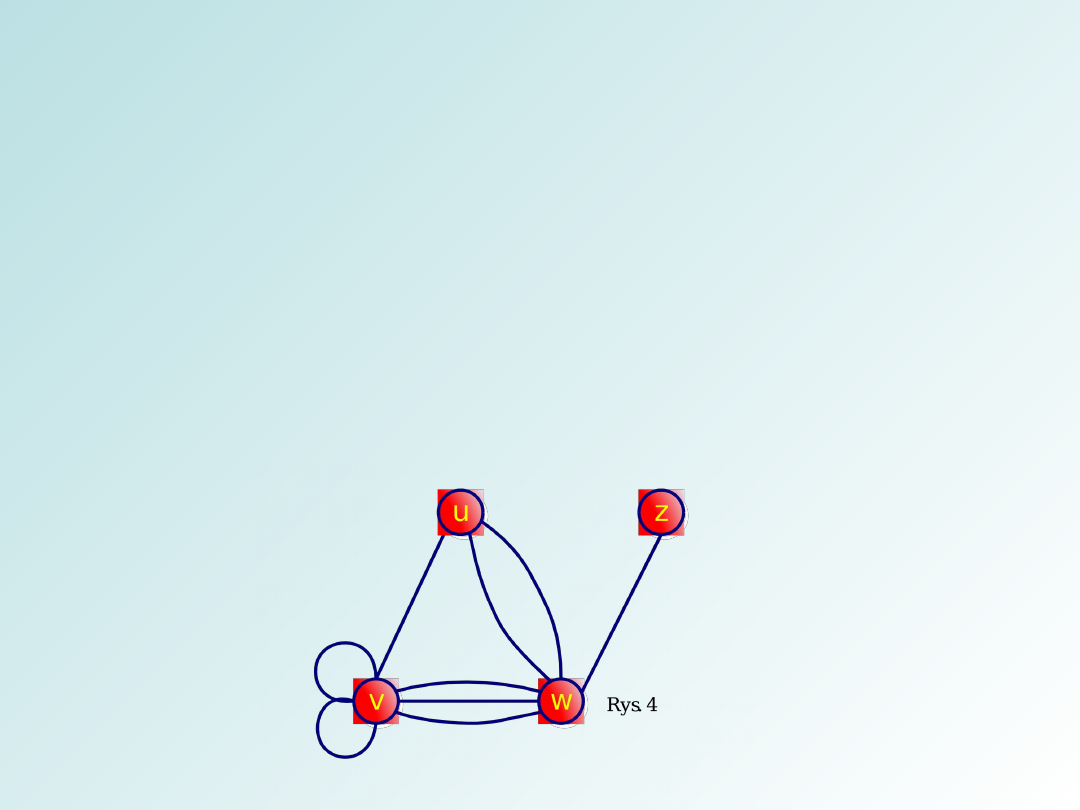
Zatem na rysunku 4 zbiorem wierzchołków V (G) jest zbiór {u,
v, w, z}, a rodzina E (G) składa się z krawędzi uv, vv
(występującej dwukrotnie), vw (występującej trzykrotnie), uw
(występującej dwukrotnie) i wz.
Użycie słowa „rodzina” oznacza, że dopuszczamy istnienie
krawędzi wielokrotnych, zbioru z powtórzeniami, czyli
zbiorowości elementów z których niektóre mogą występować
wielokrotnie.
Elementy grafów
Trasą w grafie G łączącą wierzchołki x i y nazywamy ciąg x,
e1, u, e2, v…, w, ek-1, y, gdzie e1 = {x,u}, e2 = {u,v}, …,
ek-1 = {w,y} i k ≥ 1, inaczej mówiąc trasa jest to „linia” po
której przedostajemy się z jednego wierzchołka do innego,
składająca się z ciągu kolejno przechodzonych krawędzi.
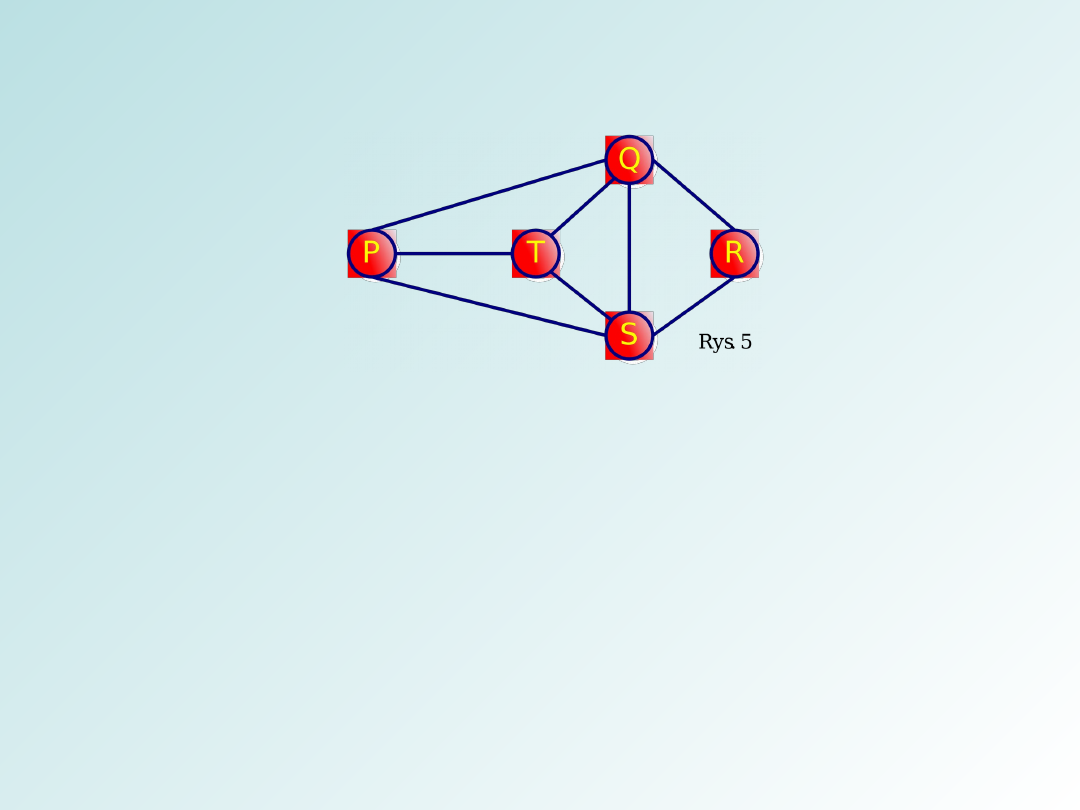
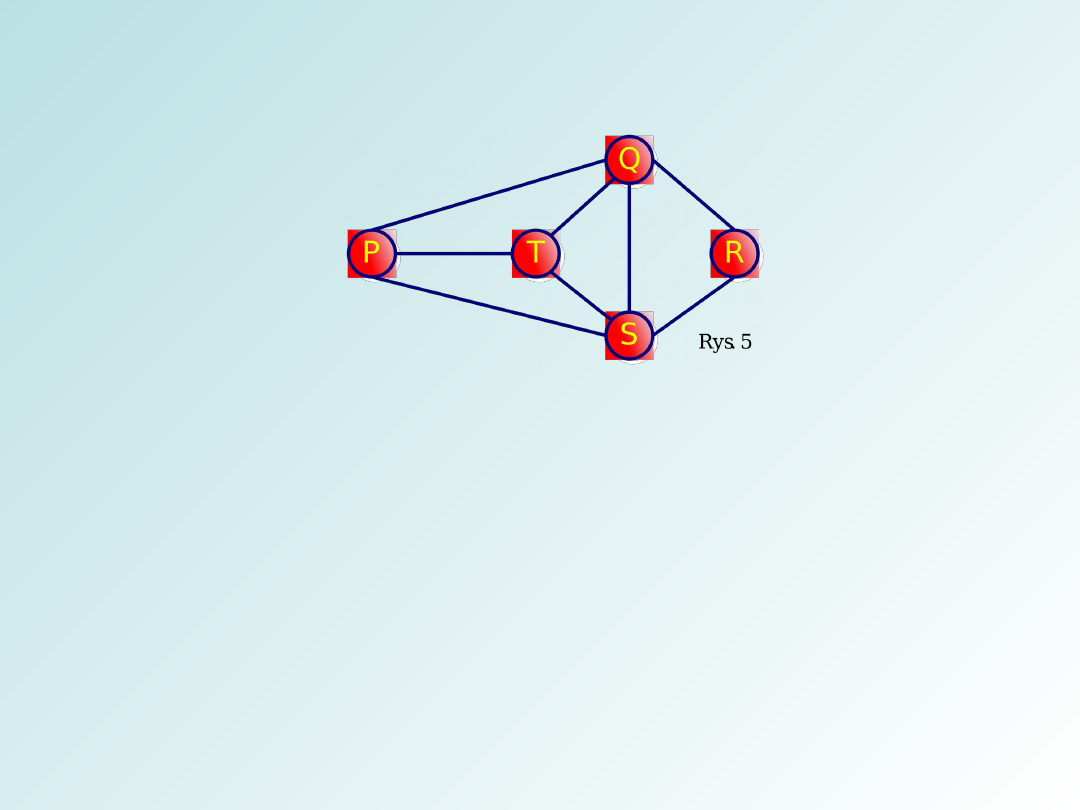
Na przykład ciąg P
Q
R w grafie przedstawionym na
rysunku 5 jest trasą o długości 2, a ciąg P
S
Q
T
S
R jest trasą długości 5.
Elementy grafów
Drogą w grafie G= (V, E) nazywamy ciąg
wierzchołków vi
V, gdzie i = 1, …n, taki, że dla
dowolnego k = 1, …n-1, (vk, vk+1)
E, czyli taki ciąg
jego wierzchołków, że każde dwa kolejne wierzchołki
w tym ciągu są połączone trasą, gdzie wszystkie
krawędzie i wierzchołki są różne. Inaczej mówiąc
drogą nazywamy taką trasę, w której żaden
wierzchołek nie występuje więcej niż jeden raz.
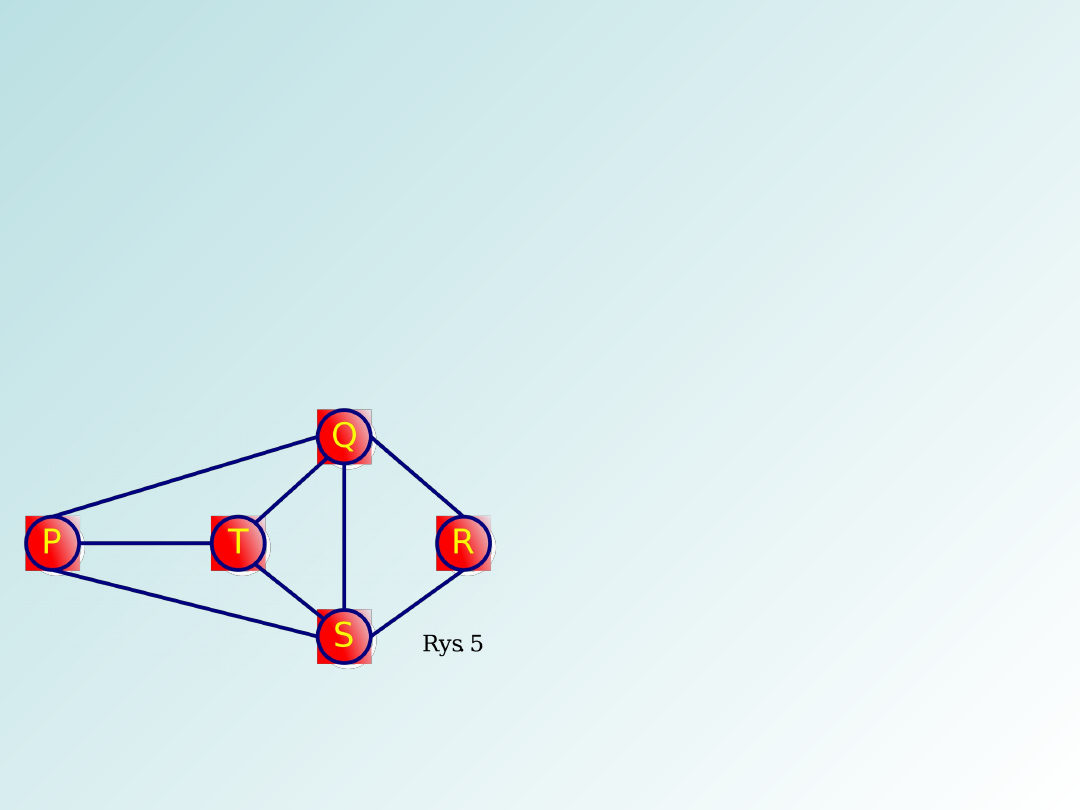
Na przykład P
T
S
R jest drogą.
Elementy grafów
Drogą w grafie G= (V, E) nazywamy ciąg wierzchołków vi
V,
gdzie i = 1, …n, taki, że dla dowolnego k = 1, …n-1, (vk,
vk+1)
E, czyli taki ciąg jego wierzchołków, że każde dwa
kolejne wierzchołki w tym ciągu są połączone trasą, gdzie
wszystkie krawędzie i wierzchołki są różne. Inaczej mówiąc
drogą nazywamy taką trasę, w której żaden wierzchołek nie
występuje więcej niż jeden raz.
Na przykład P
T
S
R jest drogą.
Drogę v = (v1,…, vn) w grafie
G = (V, E) nazywamy
skończoną, jeśli istnieje n
N, dla którego nie ma
określonego wierzchołka vn+1, długość tą oznacza
się
v = n -1.
Drogę (lub ścieżkę) v = (v1,…, vn) w grafie G = (V,E)
nazywamy zamkniętą, jeśli v1 = vn.
Elementy grafów
Ścieżka i cykl
Ścieżką nazywamy trasę, w której wszystkie krawędzie
są różne, ponadto jeśli wierzchołki są różne to taka
ścieżkę nazywamy drogą. Natomiast cyklem nazywamy
ścieżkę zamkniętą zawierającą co najmniej jedną
krawędź, można zauważyć że każda pętla lub para
krawędzi wielokrotnych tworzą cykl.
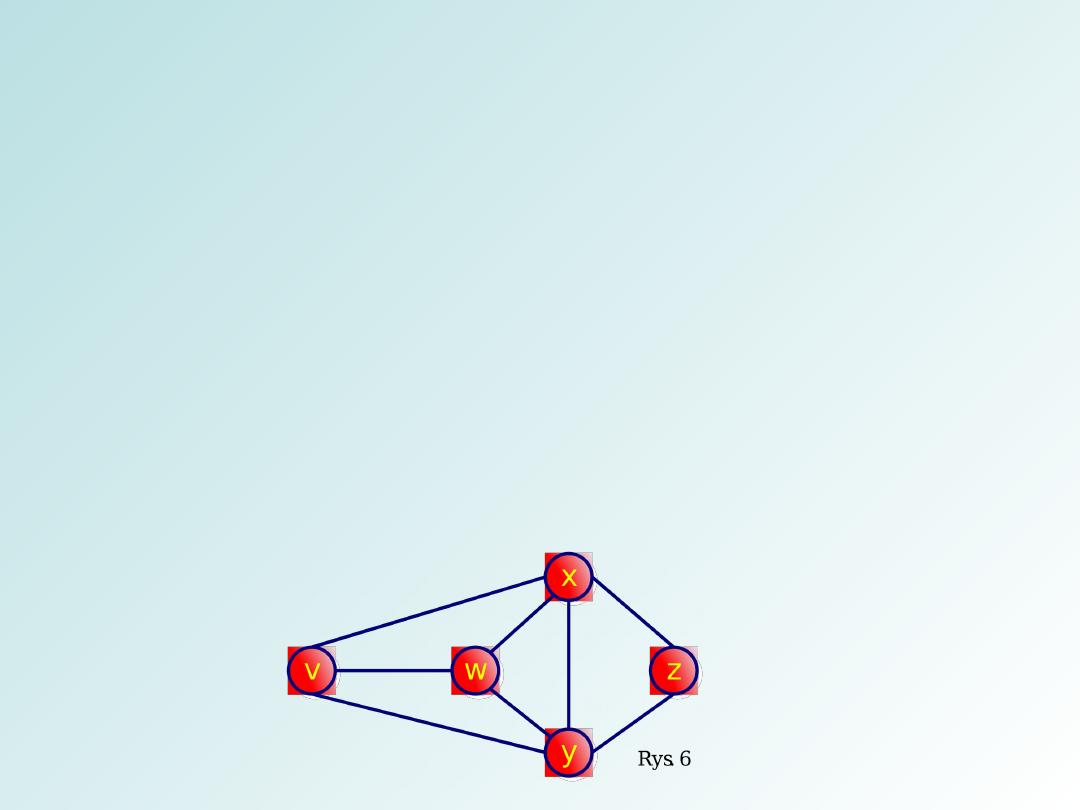
Na przykład: trasa v
w
x
y
z
z
x jest
ścieżką
trasa v
w
x
y
z
x
v jest ścieżką
zamkniętą
a trasa v
w
x
v jest cyklem
Elementy grafów
Stopnie wierzchołków na przykładzie grafu
skierowanego.
Dla grafu G = (V, E) i jego łuku a = (i, j)
E mówimy że
wierzchołki i, j są incydentne z łukiem a tzn. że łuk a prowadzi
z wierzchołka i do j. Wierzchołki incydentne z danym łukiem
nazywamy odpowiednio jego początkiem (i) i końcem (j).
V
+
(i) – zbiór końców łuków wychodzących z wierzchołka i :
V
+
(i) = { j
V : (i, j)
E }
V
-
(i) – zbiór początków łuków wchodzących do wierzchołka i :
V
-
(i) = { j
V : (i, j)
E }
d
+
(i) = | V
+
(i) | – stopień wyjściowy wierzchołka i
d
-
(i) = | V
-
(i) | – stopień wejściowy wierzchołka i
d(i) = d
+
(i) + d
-
(i) – stopień wierzchołka i
Elementy grafów
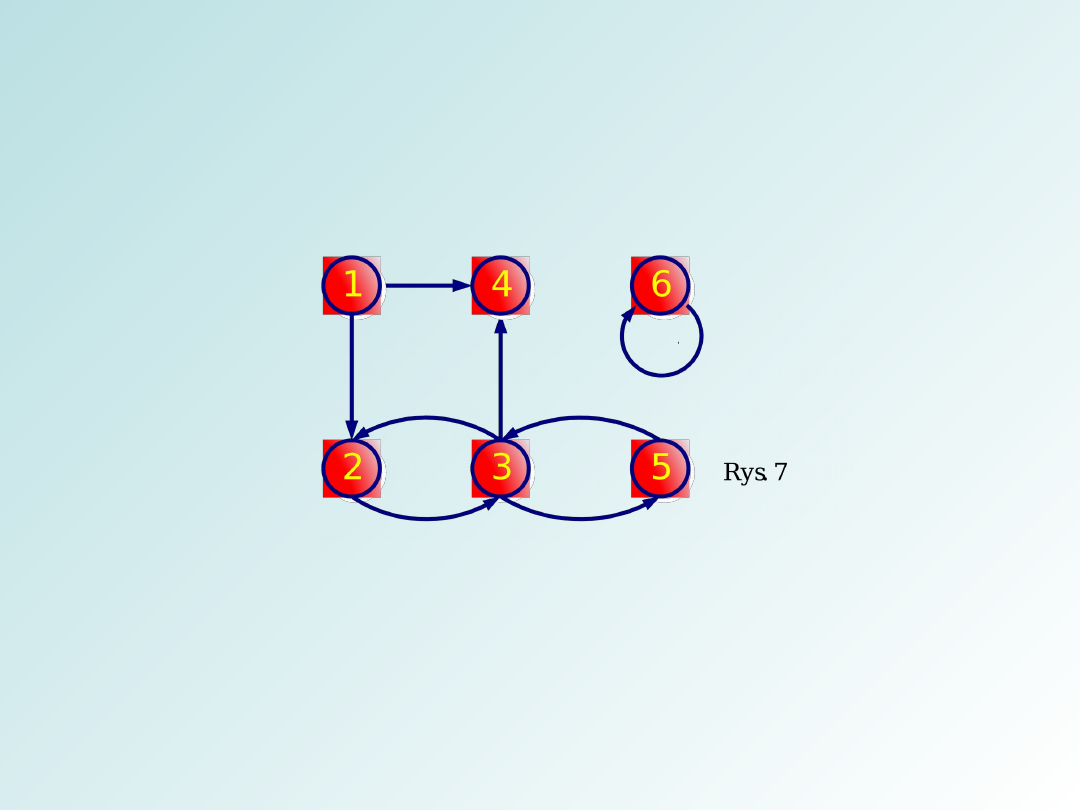
Przykład wyznaczania stopni wierzchołków w grafie
V
+
(3) = {2, 4, 5} d
+
(3) = 3; V
-
(3) = {2, 5} d
-
(3) = 2;
d(3) = 5
V
+
(6) = {6} d
+
(6) = 1; V
-
(6) = {6} d
-
(6) = 1; d(6) = 2
Rodzaje grafów
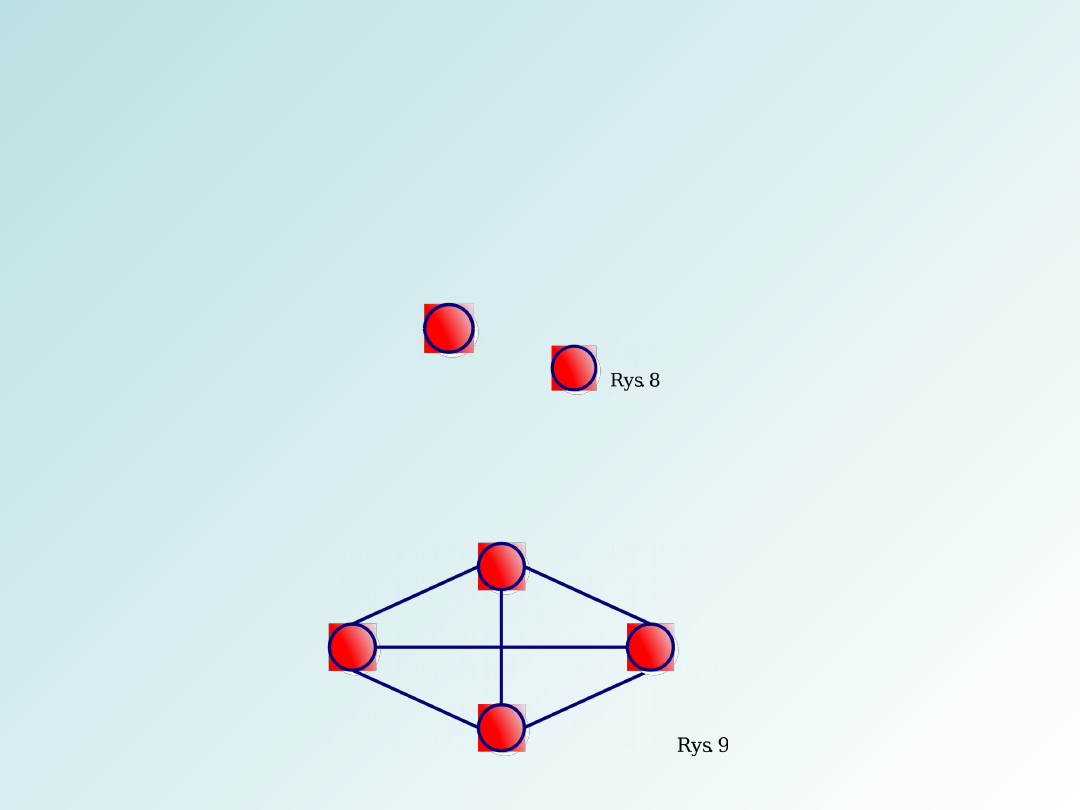
Wśród grafów rozróżniamy następujące rodzaje:
Graf pusty – graf, którego zbiór krawędzi jest zbiorem
pustym tzn. składa się tylko z wierzchołków, oznaczany
Nn gdzie n to liczba wierzchołków
Graf pełny – graf prosty w którym dowolne dwa
wierzchołki są sąsiednie, oznaczany Kn gdzie n to liczba
wierzchołków a liczba krawędzi to n ( n - 1 ) / 2
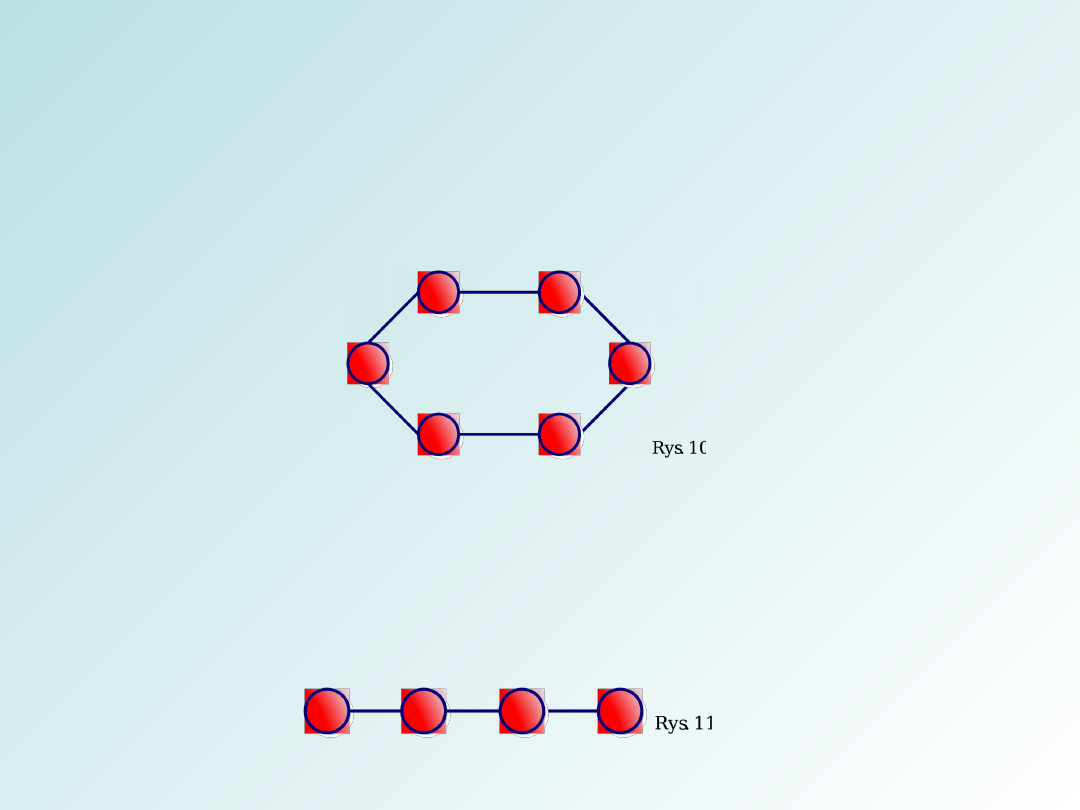
Rodzaje grafów
Graf cykliczny – Graf spójny, regularny stopnia
drugiego oznaczany jako Cn gdzie n to liczba
wierzchołków.
Graf liniowy – Graf otrzymany z grafu cyklicznego
poprzez usunięcie jednej krawędzi jest oznaczany przez
Pn gdzie n to liczba wierzchołków.
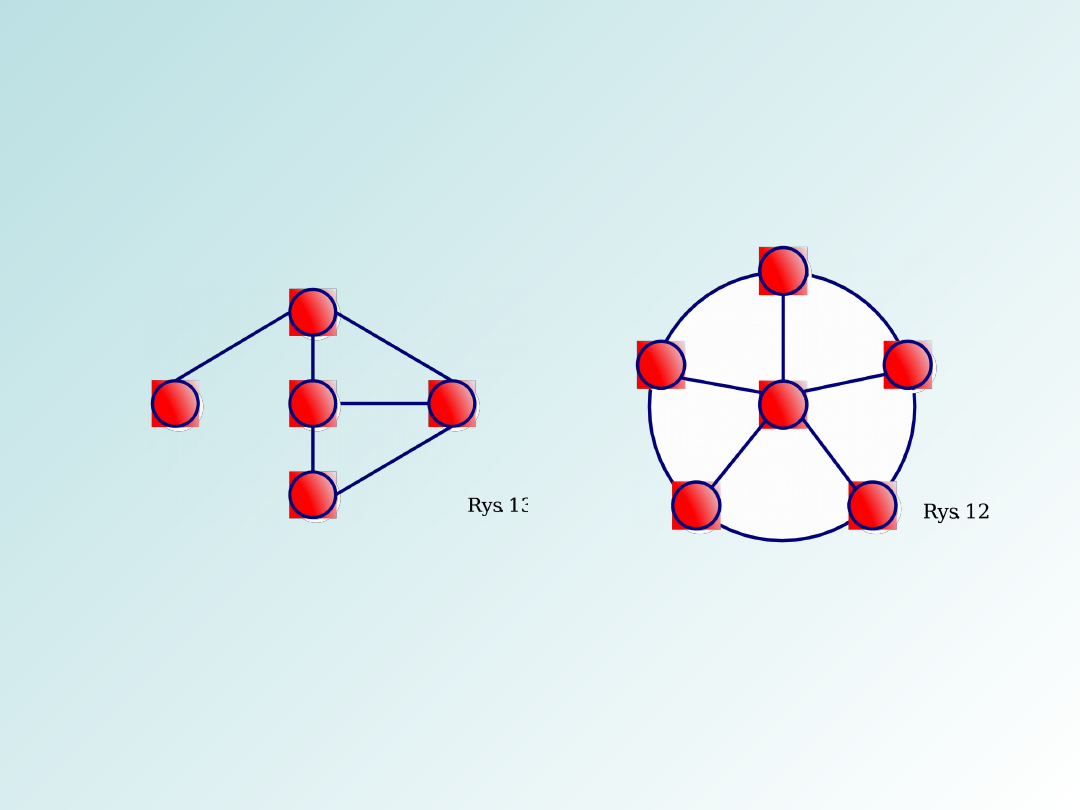
Rodzaje grafów
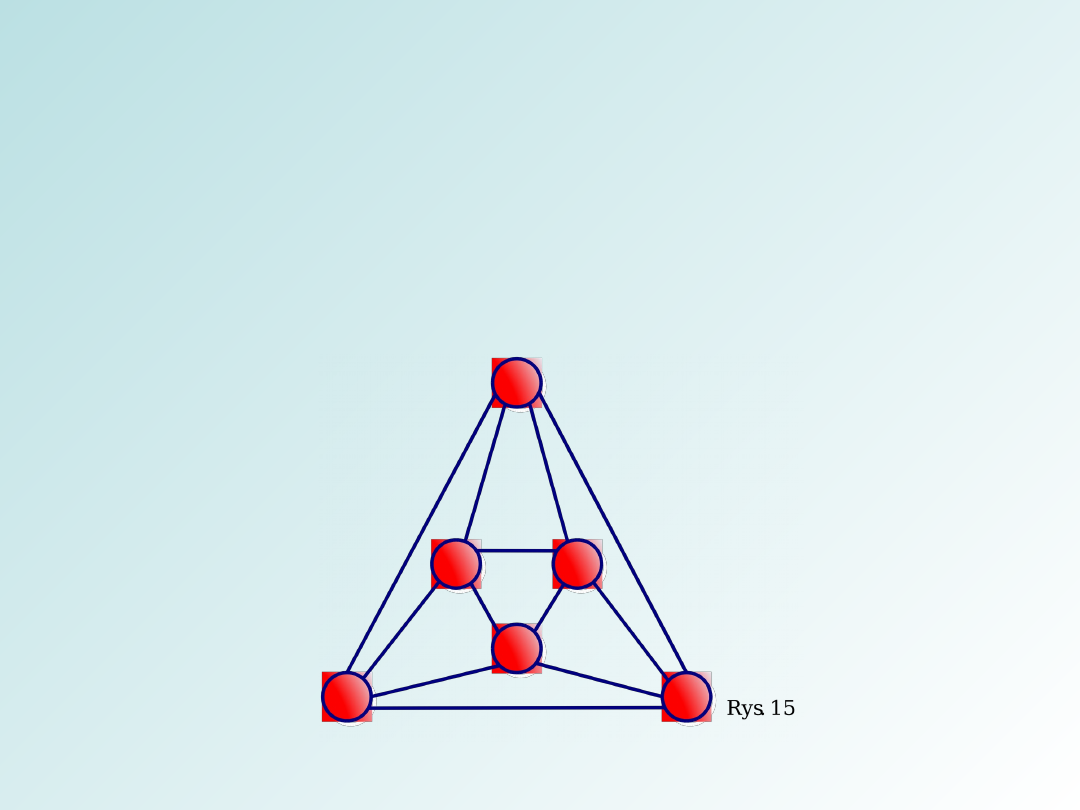
Graf koło – Graf powstały z grafu cyklicznego poprzez
połączenie każdego wierzchołka z nowym, dodanym
wierzchołkiem oznaczany Wn gdzie n to liczba
wierzchołków – rys 12.
Graf planarny – to graf, który można przedstawić na
płaszczyźnie tak, by żadne dwie krawędzie się nie
przecinały – rys 13.
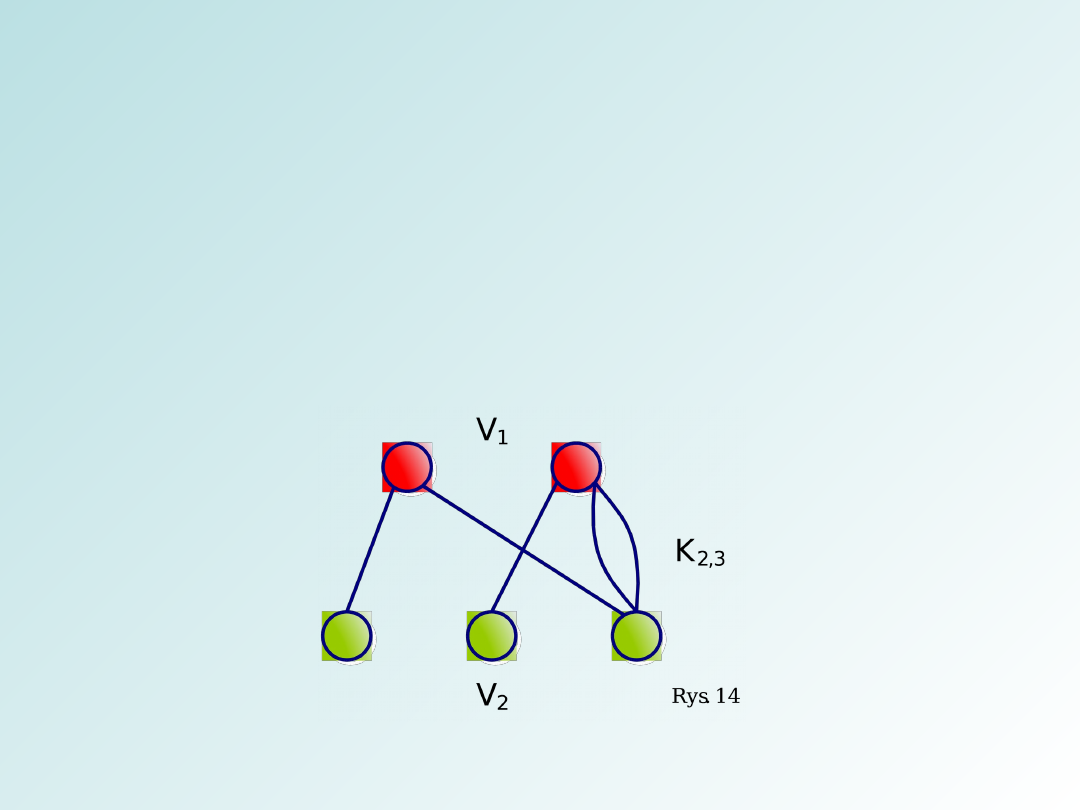
Rodzaje grafów
Graf dwudzielny – Graf jest dwudzielny jeżeli zbiór
wierzchołków grafu G można podzielić na dwa rozłączne
zbiory V
1
i V
2
w taki sposób, że każda krawędź grafu G
łączy dowolny wierzchołek ze zbioru V
1
z dowolnym
wierzchołkiem ze zbioru V
2
i jest oznaczany K
r
, s gdzie r
to ilość wierzchołków zbioru V
1
, a s to ilość
wierzchołków zbioru V
2
.
Rodzaje grafów
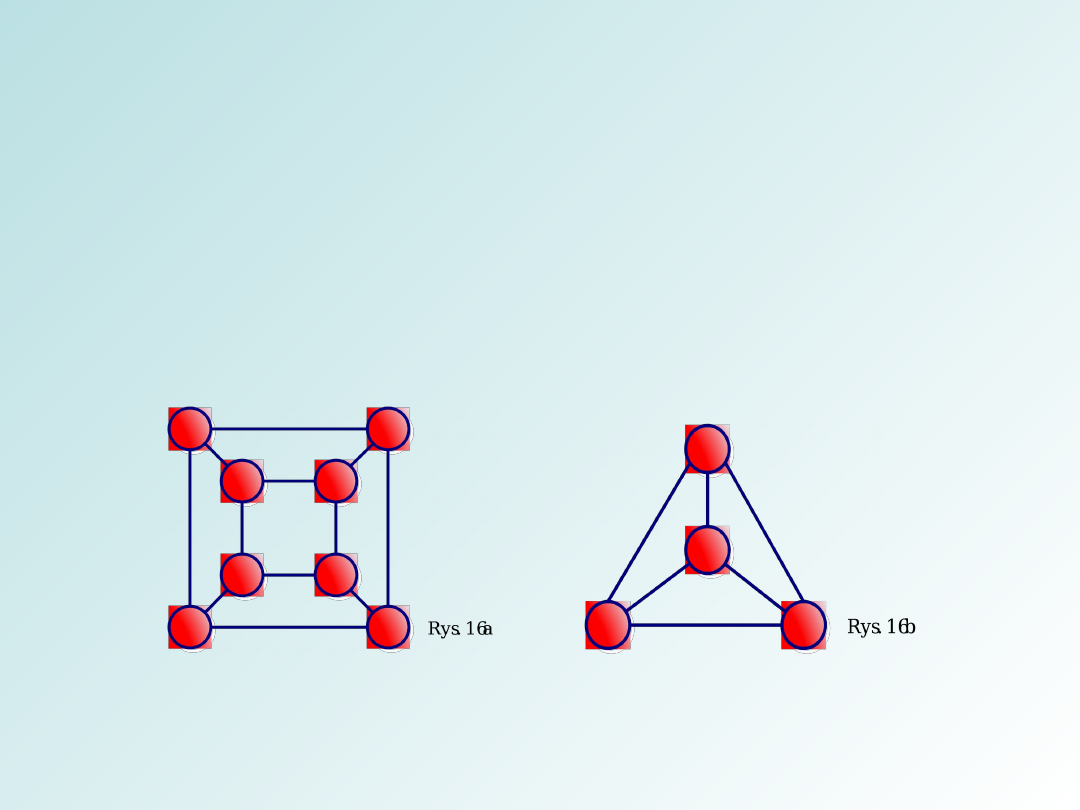
Graf regularny – każdy wierzchołek grafu ma taki sam
stopień. Jeżeli każdy wierzchołek jest stopnia r, to graf
jest regularny stopnia r i oznacza się go Kn gdzie n to
liczba wierzchołków. Szczególne znaczenie mają grafy
kubiczne, tzn. grafy regularne stopnia 3.
Rodzaje grafów
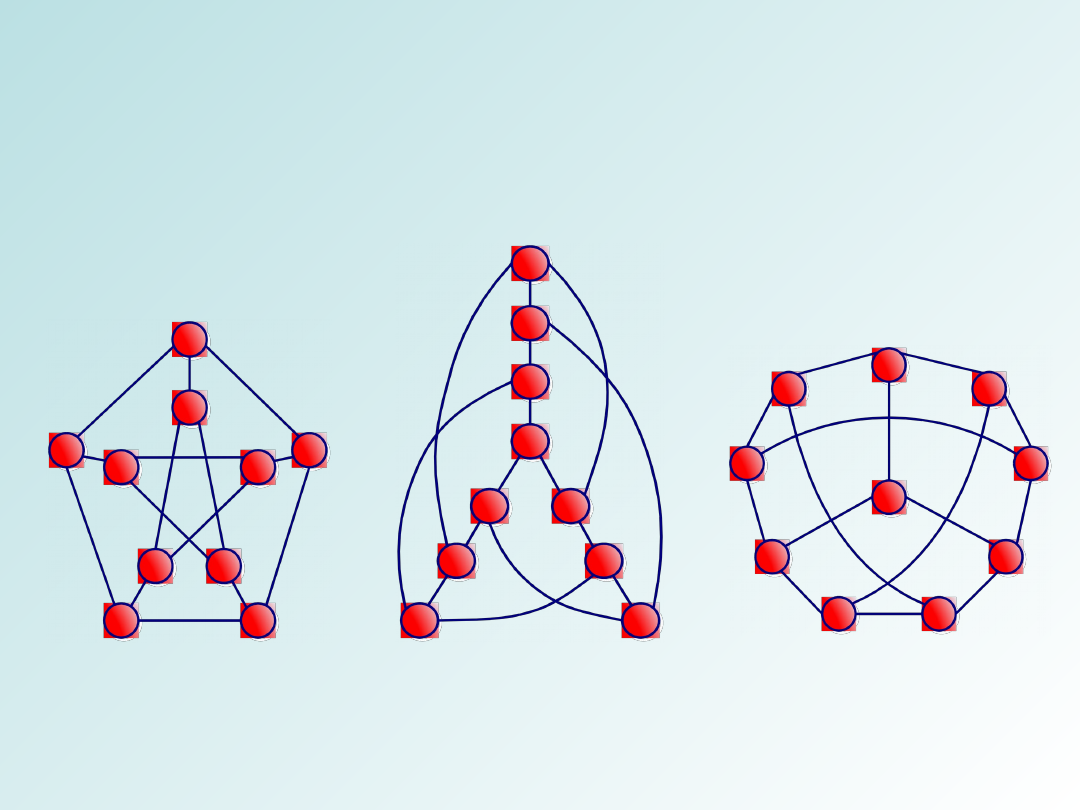
Graf kubiczny (w tym graf Petersena) – Graf r-
regularny jest grafem, dla którego stopień każdego
wierzchołka jest równy r. Graf 3-regularny nazywamy
grafem kubicznym, w którym wszystkie wierzchołki
mają stopień równy 3, tzn. że z każdego wierzchołka
wychodzi tyle samo krawędzi tj. 3.
Rodzaje grafów
Spis treści
Sześć postaci grafu Petersena
Rodzaje grafów
Spis treści
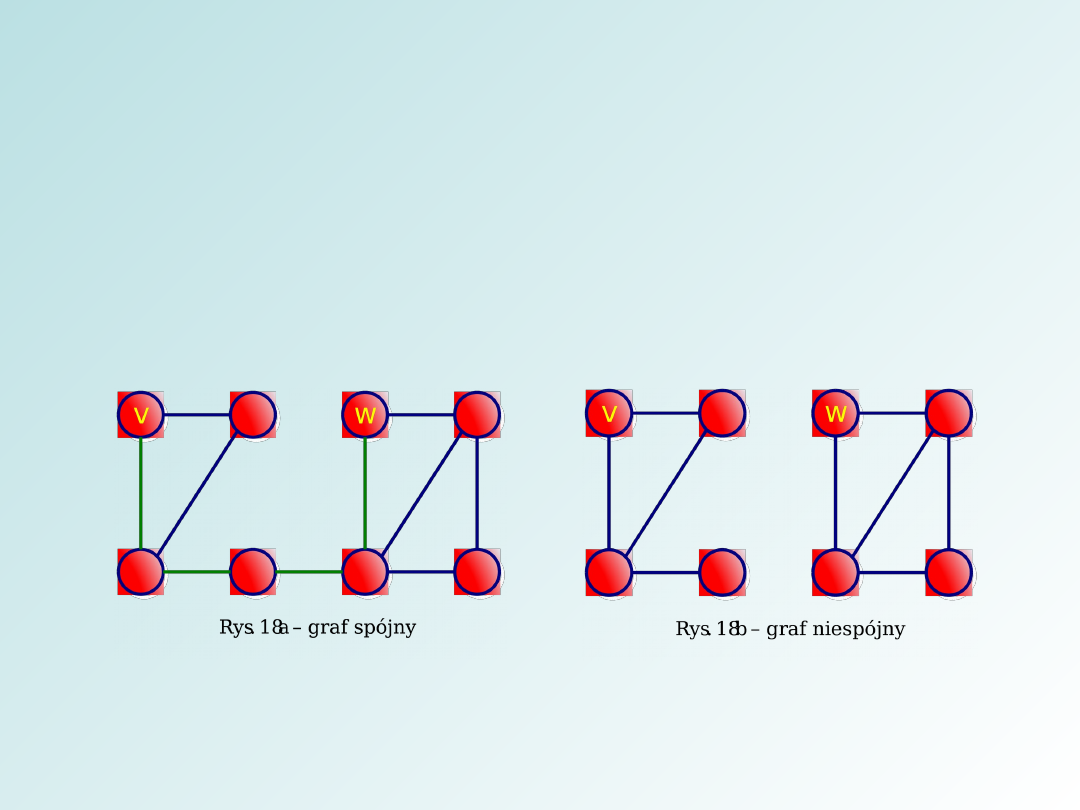
Graf spójny i graf niespójny – graf jest spójny wtedy i
tylko wtedy, gdy każda para wierzchołków jest
połączona drogą, w przeciwnym razie nazywamy go
grafem nie spójnym. Poniżej umieszczono przykład dla
pary wierzchołków v, w.
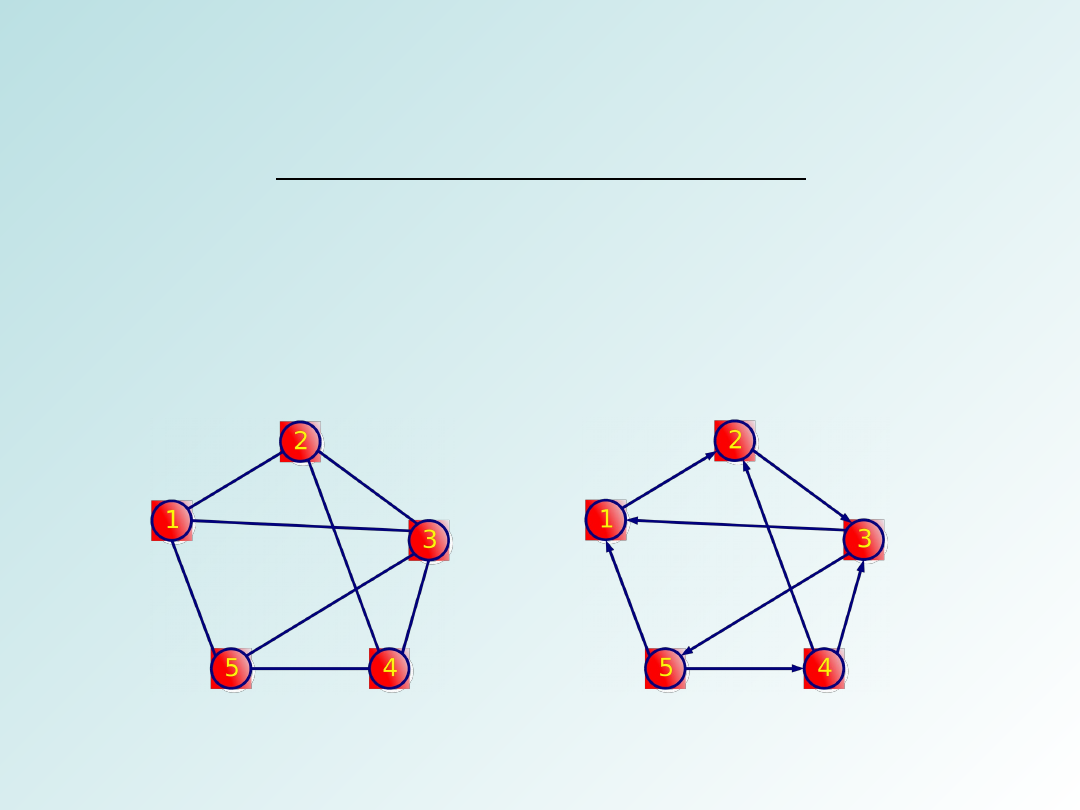
Grafy i ich reprezentacje
Graf skierowany i nieskierowany
W informatyce grafem nazywamy strukturę G=(V, E) składającą
się z węzłów (wierzchołków, oznaczanych przez V) wzajemnie
połączonych za pomocą krawędzi (oznaczanych przez E).
Grafy dzielimy na grafy skierowane i nieskierowane:
Graf nieskierowany Graf skierowany
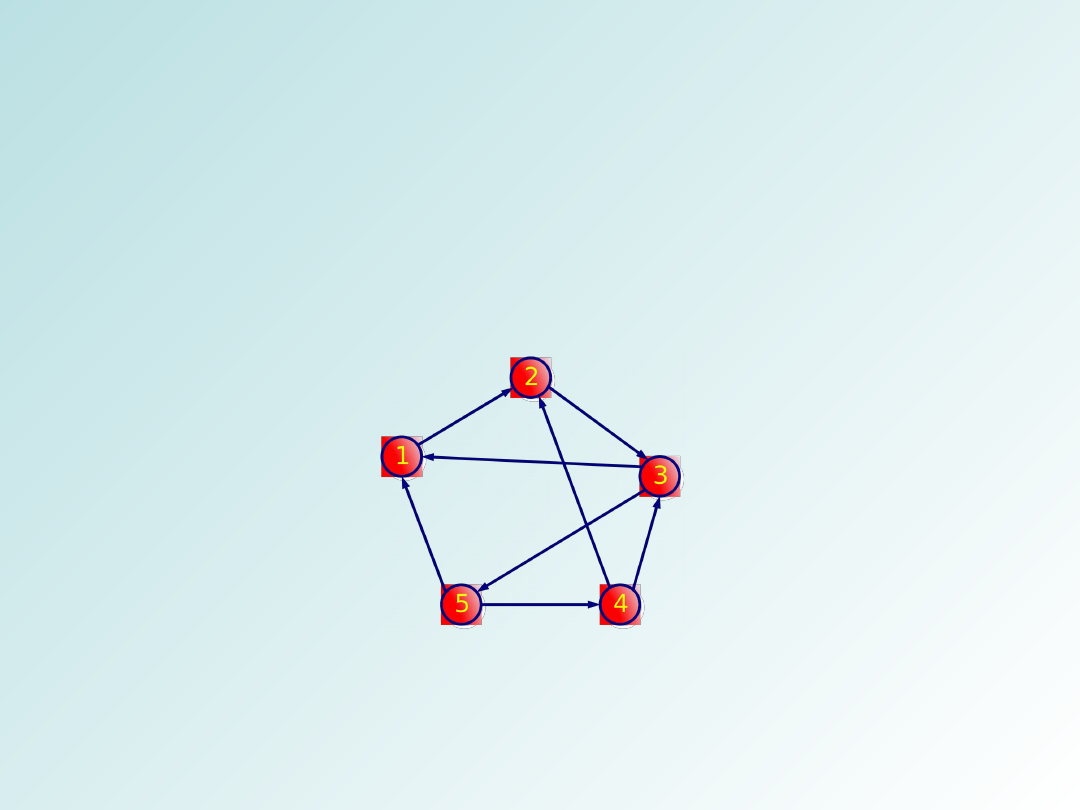
Grafy i ich reprezentacje
Graf skierowany (lub diagraf) G jest opisaną parą (V, E),
gdzie V jest zbiorem skończonym, a E jest relacją binarną
w V. Zbiór V jest nazywany zbiorem wierzchołków G, a
jego elementy są nazywane wierzchołkami. Zbiór E jest
nazywany zbiorem krawędzi G, a jego elementy
nazywamy krawędziami.
Graf skierowany
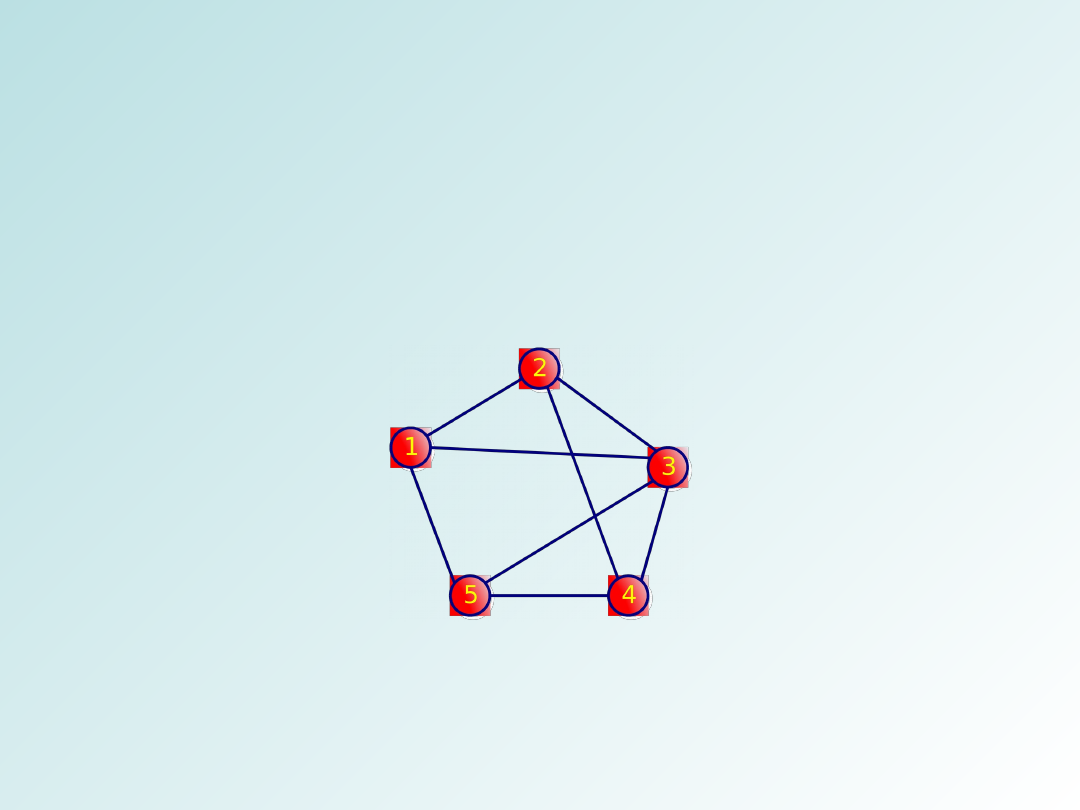
Grafy i ich reprezentacje
W grafie nieskierowanym G=(V, E), zbiór krawędzi E to
zbiór nieuporządkowanych par wierzchołków. Oznacza to,
iż krawędź E jest zbiorem {u, v}, gdzie, u, v
V i u
v.
W grafie nieskierowanym nie mogą występować pętle,
więc każda krawędź zawiera dokładnie dwa różne
wierzchołki.
Graf nieskierowany
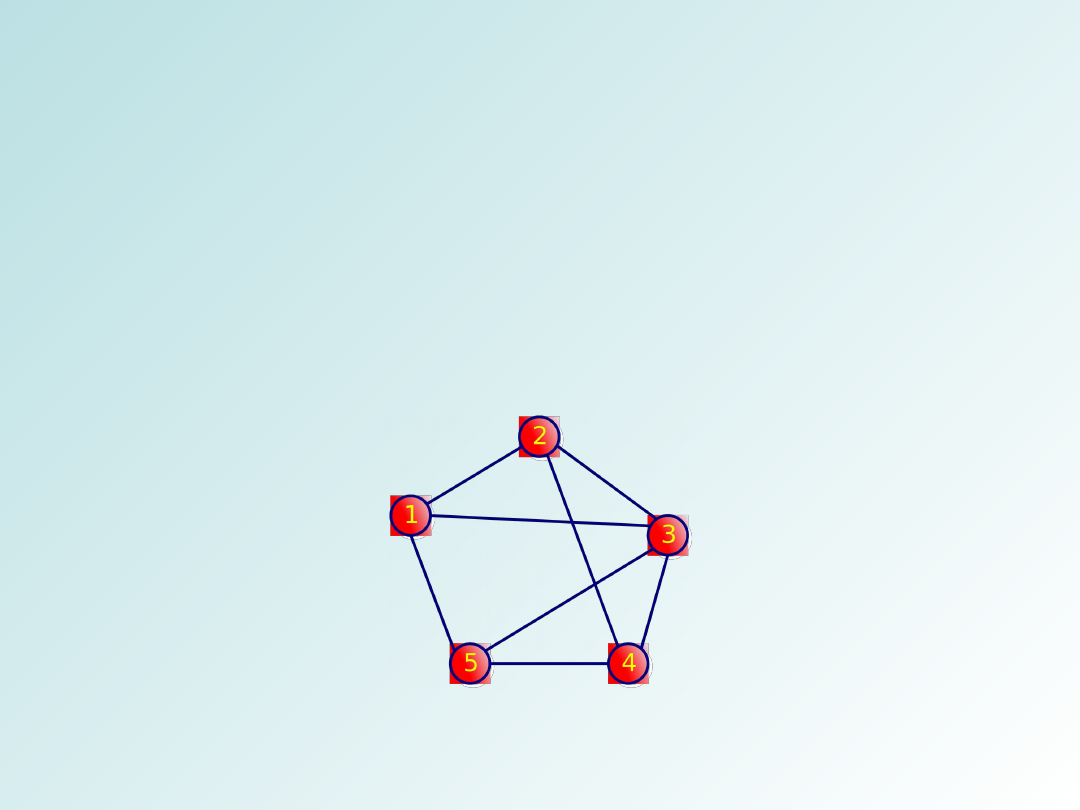
Grafy i ich reprezentacje
Jeśli krawędź łączy dwa wierzchołki to jest z nimi
incydentna. Pętla własna to krawędź łączące wierzchołek z
samym sobą. Stopień wierzchołka w grafie nieskierowanym
to liczba incydentnych z nim krawędzi.
Istnieje kilka algorytmów do przechowania grafu w pamięci.
Graf nieskierowany
Grafy i ich reprezentacje
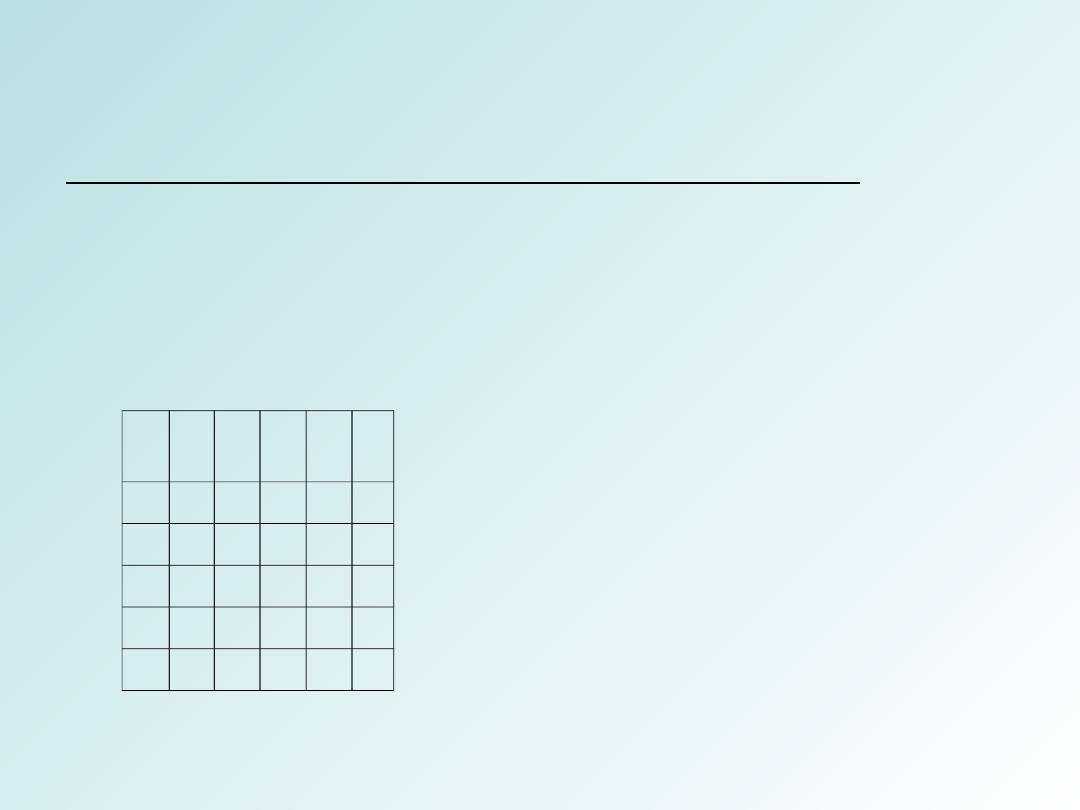
Poniżej została omówiona macierz sąsiedztwa
Budujemy tablicę o rozmiarach V*V, gdzie V-liczba
wierzchołków. Następnie wypełniamy ją zerami- jeśli
dwa wierzchołki nie są połączone krawędzią i
jedynkami- jeśli dwa wierzchołki są połączone. Oto
macierz sąsiedztwa dla grafu z rysunku 1:
1
2
3
4
5
1
0
1
1
0
1
2
1
0
1
1
1
3
1
1
0
1
0
4
0
1
1
0
1
5
1
1
0
1
0
Złożoność pamięciowa O(V2)
Widać, że macierz jest
symetryczna.
Stosując
tablicę dynamiczną można
więc zmniejszyć rozmiar
macierzy
do
połowy
zapisując ją jako macierz
dolno-
(lub
górno)
-trójkątną.
Grafy i ich reprezentacje
Lista incydencji
Należy utworzyć listę dla każdego wierzchołka v, w której
przechowujemy zbiór wierzchołków połączonych krawędzią
z v. Lista dla grafu z rysunku 1 wygląda następująco:
• 1: 2, 3, 5
• 2: 1, 3, 4
• 3: 1, 2, 4
• 4: 2, 3, 5
• 5: 4, 1, 5
Złożoność pamięciowa O(V+E)
Grafy i ich reprezentacje
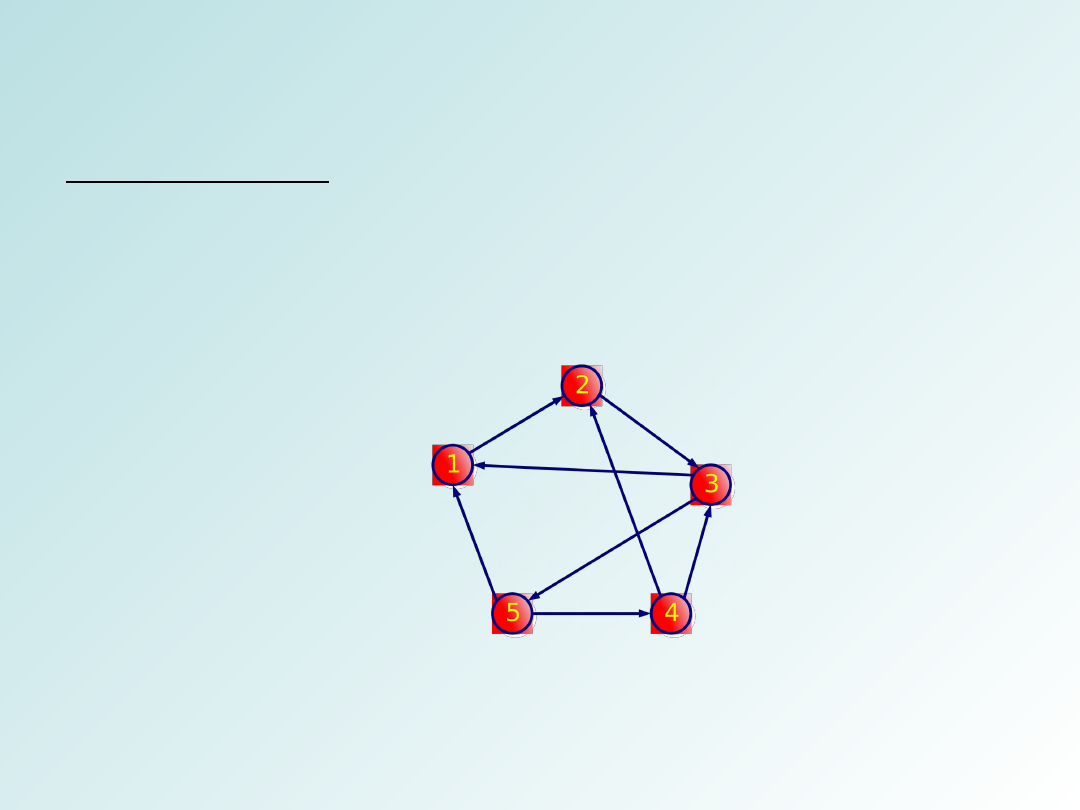
Lista krawędzi
Lista krawędzi jest to lista, na której przechowujemy
wszystkie krawędzie występujące w grafie.
Przykład dla grafu skierowanego
Złożoność pamięciowa O(E)
•1 - 2
•2 - 4
•2 - 5
•3 - 1
•3 - 2
•4 - 3
•5 - 1
•5 - 4
Zapisując przy pomocy
tej reprezentacji
graf, w którym
występują krawędzie
skierowane i
nieskierowane należy
w przypadku krawędzi
nieskierowanej z u do v
zapisać krawędź dwukrotnie: u
- v oraz v - u.
Grafy i ich reprezentacje
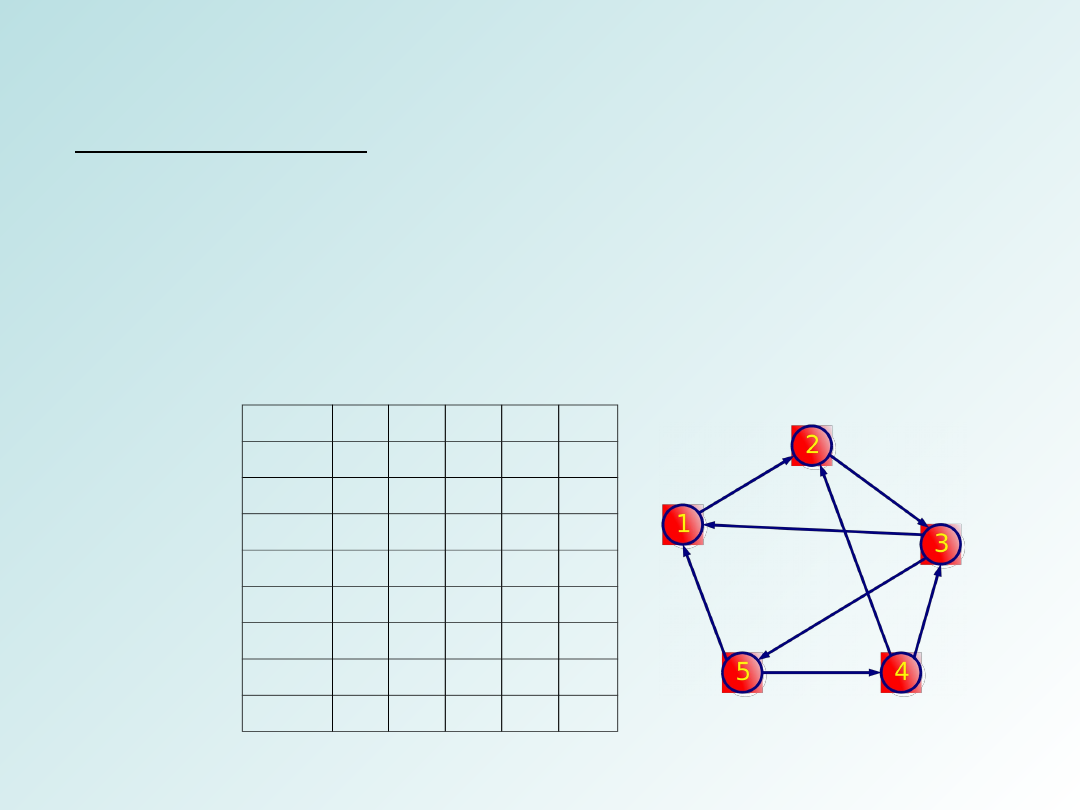
Macierz incydencji
Macierz incydencji to tablica o rozmiarach V*E. Składa się ona z E
kolumn i V wierszy, jeśli krawędź wychodzi z danego wierzchołka
to piszemy w odpowiedniej kolumnie (-1), jeśli do niego wchodzi
piszemy (+1), jeśli wierzchołek nie należy do krawędzi piszemy 0,
jeśli jest to pętla własna
piszemy 2.
Złożoność pamięciowa O(E*V)
1
2
3
4
5
1 - 2
-1
1
0
0
0
1 - 3
1
0
-1
0
0
1 - 5
1
0
0
0
-1
2 - 4
0
-1
0
1
0
2 - 5
0
-1
0
0
1
2 - 3
0
1
-1
0
0
3 - 4
0
0
1
-1
0
5 - 4
0
0
0
1
-1
Grafy i ich reprezentacje
Macierz grafu jest to trochę bardziej skomplikowana
reprezentacja grafu niż poprzednie.
Należy utworzyć tablicę o rozmiarach (V+2)2. Wiersze i kolumny
numerujemy od 0 do V+1. Najpierw zajmiemy się częścią macierzy
ograniczoną przez indeksy od 1 do V. Załóżmy, że w wierszach
mamy i-te wierzchołki a w kolumnach j-te wierzchołki. Liczby,
które mogą znaleźć się na skrzyżowaniu wierzchołka i oraz j
można podzielić na 3 grupy:
od 1 do V - istnieje krawędź skierowana: i <- j
od V+1 do 2*V - istnieje krawędź skierowana: i -> j
od (-V) do (-1) - brak incydentnych krawędzi
Sedno macierzy grafu polega jednak na tym, że odczytana wartość
nie tylko informuje nas, czy istnieje krawędź łącząca wierzchołki i
oraz j, ale zawiera też adres następnego wierzchołka, który jest w
takiej samej relacji z wierzchołkiem i co wierzchołek j.
Algorytm Forda-
Bellmana
Algorytm
Bellmana-Forda
wyznacza
najmniejszą
odległości od ustalonego wierzchołka s do wszystkich
pozostałych w skierowanym grafie bez cykli o ujemnej
długości.
Algorytm Forda-Bellmana w każdym kroku oblicza
górne oszacowanie D(v
i
) odległości od wierzchołka s do
wszystkich pozostałych wierzchołków v
i
. W pierwszym kroku
przyjmujemy D(v
i
)=A(s,v
i
). Gdy stwierdzimy, że D(v)>D(u)
+A(u,v), to każdorazowo polepszamy aktualne oszacowanie i
podstawiamy D(v):=D(u)+A(u,v). Algorytm kończy się, gdy
żadnego oszacowania nie można już poprawić, macierz D(v
i
)
zawiera najkrótsze odległości od wierzchołka s do wszystkich
pozostałych.
Algorytm Forda-
Bellmana
Pseudokod wygląda następująco: (n- liczba wierzchołków)
begin;
for v:=[1..n] do D(v):=A(s,v); - przyjmujemy, że najkrótszą drogą z u do v
jest
krawędź (u,v)
for k:=1 to (n-2) do - w (n-2) krokach można zbadać każdą drogę o (n-1)
krawędziach i wybrać najkrótszą
begin
for v:=[1..n]-{s} do - odległość od s do s wynosi 0 i już się na pewno nie
zmieni
for u:=[1..n] do
D(v):=min{D(v), D(u)+A(u,v)}; - wybierz krótszą drogę
end;
Algorytm można ulepszyć sprawdzając w każdej iteracji, czy coś się
zmieniło od poprzedniej i jeśli nie, to można zakończyć obliczenia.
Algorytm Forda-
Bellmana
1
2
3
4
5
6
1
0
2
4
∞
∞
∞
2
∞
0
∞
∞
4
∞
3
∞
∞
0
-2
3
∞
4
1
∞
∞
0
∞
2
5
∞
∞
∞
∞
0
∞
6
∞
2
∞
∞
1
0
Spis treści
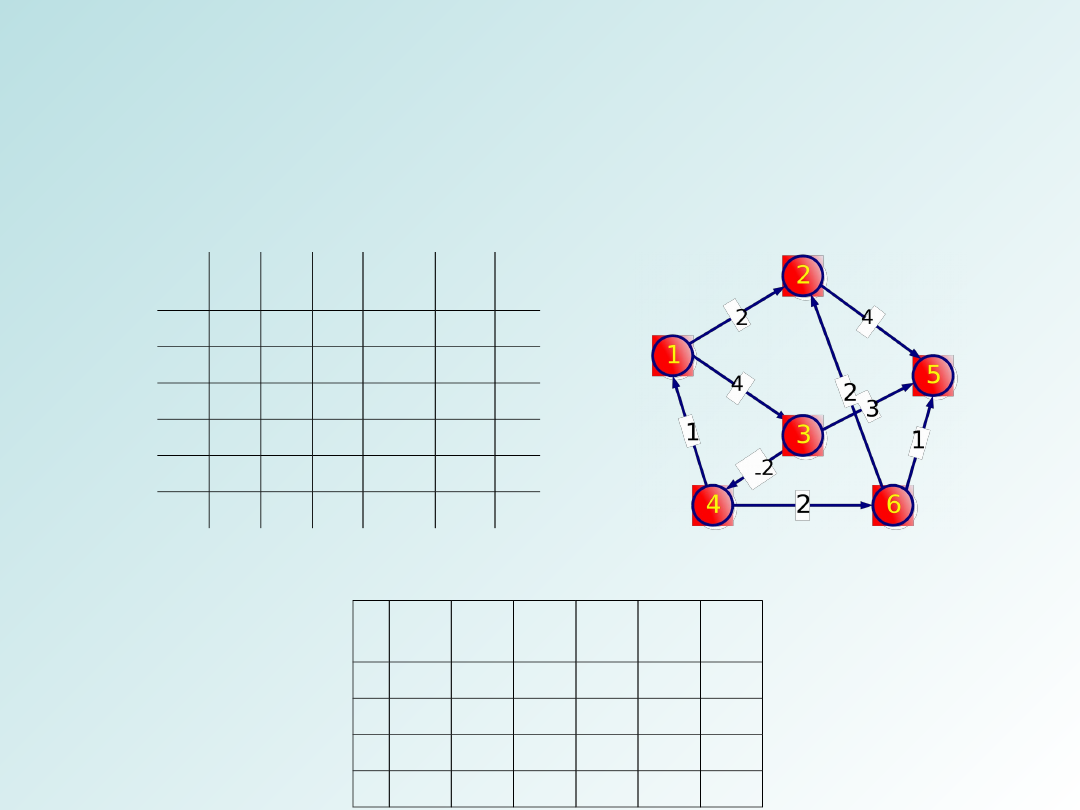
Dla pełnej jasności poniżej zamieszczono prosty przykład:
Oto graf i jego reprezentacja w postaci macierzy wag krawędzi.
Przyjmujemy s=1:
Przebieg obliczeń:
K
D(
1)
D(
2)
D(
3)
D(
4)
D(
5)
D(
6)
0
0
2
4
∞
∞
∞
1
0
2
4
2a
6b
4c
2
0
2
4
2
5d
4
3
0
2
4
2
5
4
Algorytm Forda-
Bellmana
Spis treści
Objaśnienia:
W pierwszym kroku (k=0) D(vi)=A(1,vi). Przepisujemy pierwszy wiersz macierzy
wag krawędzi.
a) Pierwsze skrócenie drogi:
w poprzednim kroku D(4)= ∞, gdyż nie istnieje krawędź od 1 do 4. Teraz jednak
możemy przejść przez wierzchołek 3 (odległość od 1 do 3 wynosi 4) a następnie
do 4 (waga krawędzi [3,4]=-2), długość drogi od 1 do 4 wynosi więc 4-2=2.
b) Podobnie jest tu, do wierzchołka 5 możemy dojść przez 2, 3, lub 6. Wybieramy
oczywiście drogę o mniejszej długości:
D(2)+A(2,5)=2+4=6 (ta wartość jest najmniejsza)
D(3)+A(3,5)=4+3=7
D(6)+A(6,5)= ∞+1 (ta wartość jest największa)
Wybieramy opcję z wierzchołkiem nr. 2.
c) Do wierzchołka 6 możemy dojść przez 4 (do którego dochodzimy przez 3)
droga jest więc następująca: 1, 3, 4, 6 a jej długość wynosi D(4)+A(4,6)=2+2=4
d) Jak wynika z punktu b), do wierzchołka 5 możemy dojść także poprzez
wierzchołek 6.
W poprzednim kroku poznaliśmy odległość do wierzchołka 6 i nie wynosi ona już
nieskończoność. Sprawdźmy więc, jaka byłaby długość drogi do wierzchołka 5
poprzez 6: D(6)+A(6,5)=4+1=5. Jest to wartość mniejsza niż aktualna (6), więc
znaleźliśmy krótszą drogę.
W kroku k=3 nic się nie zmieniło od kroku k=2. Kończymy obliczenia i mamy
wektor najkrótszych dróg od wierzchołka s=1 do wszystkich pozostałych.
Złożoność obliczeniowa: O(n3).
Algorytm Dijkstry
Spis treści
Algorytm Dijkstry służy do wyznaczania najmniejszej
odległości od ustalonego wierzchołka s do wszystkich
pozostałych w skierowanym grafie, jednakże graf wejściowy
nie może zawierać krawędzi o ujemnych wagach.
W
algorytmie
tym
pamiętany
jest
zbiór
Q
wierzchołków, dla których nie obliczono jeszcze najkrótszych
ścieżek, oraz wektor D[i] odległości od wierzchołka s do i.
Początkowo zbiór Q zawiera wszystkie wierzchołki a wektor
D jest pierwszym wierszem macierzy wag krawędzi A.
Algorytm Dijkstry
Spis treści
Algorytm przebiega następująco:
•Dopóki zbiór Q nie jest pusty wykonuj:
•Pobierz ze zbioru Q wierzchołek v o najmniejszej wartości D[v] i usuń
go ze zbioru.
•Dla każdego następnika i, wierzchołka v dokonaj relaksacji ścieżki, tzn.
sprawdź, czy D[i]>D[v]+A[v,i], tzn. czy aktualne oszacowanie odległości
do wierzchołka i jest większe od oszacowania odległości do wierzchołka
v plus waga krawędzi (v,i). Jeżeli tak jest, to zaktualizuj oszacowanie D[i]
przypisując mu prawą stronę nierówności (czyli mniejszą wartość).
Jak widać z powyższego pseudokodu, algorytm wybiera z kolejki Q
"najlżejszy" wierzchołek, tzn. jest oparty na strategii zachłannej.
Wprawdzie metoda zachłanna nie zawsze daje wynik optymalny, jednak
algorytm Dijkstry jest algorytmem dokładnym.
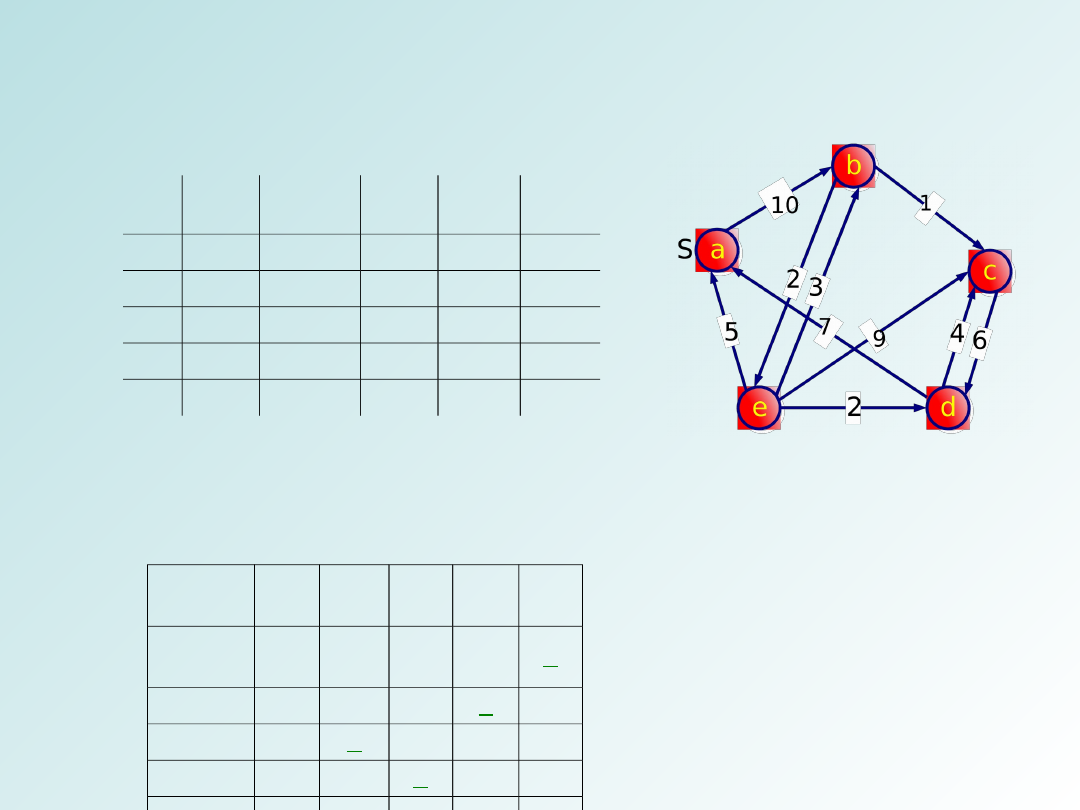
Algorytm Dijkstry
a
b
c
d
e
a
0
10
∞
∞
5
b
∞
0
1
∞
2
c
∞
∞
0
4
∞
d
7
∞
6
0
∞
e
∞
3
9
2
0
Spis treści
Oto przykładowy graf oraz jego macierz wag krawędzi (nieskończoność oznacza brak krawędzi):
Obliczenia przebiegają następująco: (Dla S=a)
najlżejszy wierzchołek jest podkreślony, wierzchołki, dla których
wyznaczono już najkrótsze ścieżki są zaznaczone kolorem jaśniejszym
Złożoność obliczeniowa: O(n2).
Q
D(a
)
D(b
)
D(c
)
D(d
)
D(e
)
{b,c,d,
e}
0
10
∞
∞
5
{b,c,d}
0
8
14
7
5
{b,c}
0
8
13
7
5
{c}
0
8
9
7
5
{}
0
8
9
7
5
Algorytm Floyda
Spis treści
Algorytm ten służy do wyznaczania najmniejszej odległości
pomiędzy wszystkimi parami wierzchołków w skierowanym grafie bez
cykli o ujemnej długości.
Warunek nieujemności cyklu jest spowodowany faktem, że w grafie o
ujemnych cyklach najmniejsza odległość między niektórymi wierzchołkami
jest nieokreślona, ponieważ zależy od liczby przejść w cyklu.
Algorytmu tego można również użyć do obliczenia domknięcia
przechodniego relacji binarnej przedstawionej w postaci grafu
skierowanego G. Wówczas domknięcie przechodnie definiuje się jako:
En={(x,y): istnieje w G droga o niezerowej długości od x do y}
(przy tej definicji każda krawędź ma wagę 1)
Algorytm Floyda opiera się na następującym spostrzeżeniu. Niech d
ij(k)
oznacza długość najkrótszej spośród najkrótszej v
i
do v
j
o wierzchołkach
pośrednich w zbiorze {v
1
,...,v
k
}
Algorytm Floyda
Spis treści
Pseudokod wygląda następująco: (n- liczba
wierzchołków)
begin;
for i:=1 to n do
for j:=1 to n do d(i,j)=A(i,j);
for i:=1 to n do d(i,i)=0;
for k:=1 to n do
for i:=1 to n do
for j:=1 to n do
d(i,j)=min( d(i,j), d(i,k)+d(k,j) );
end;
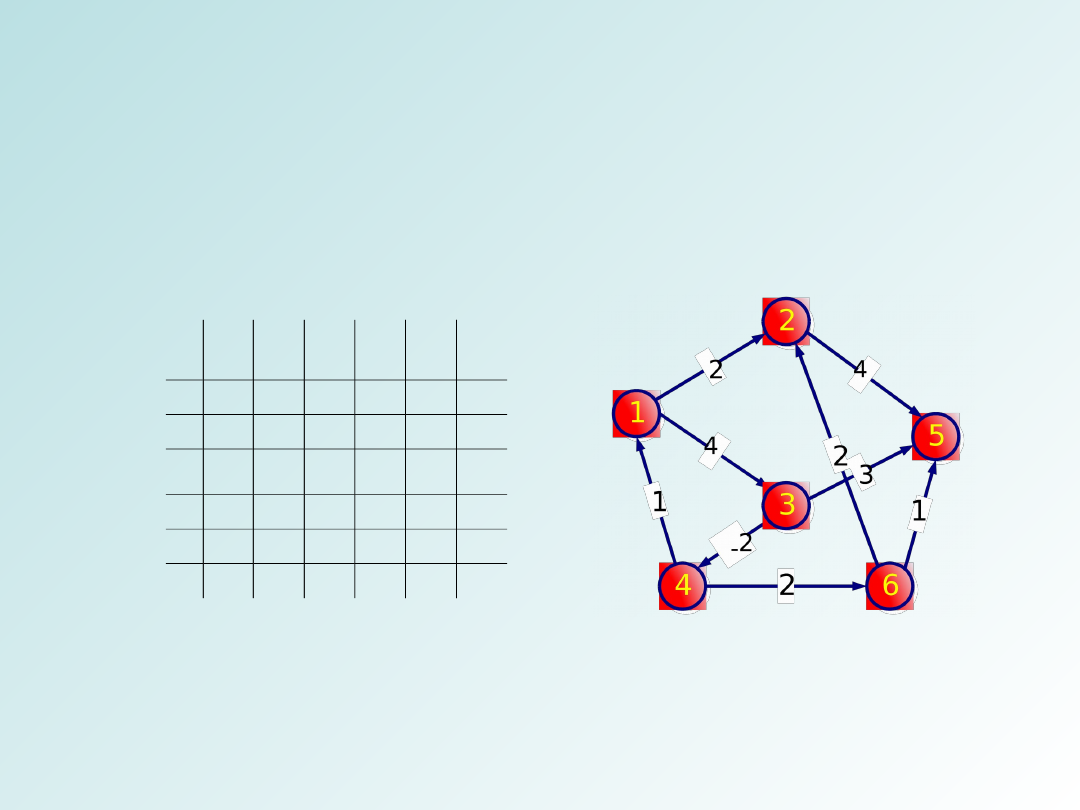
Algorytm Floyda
Spis treści
Dla przykładu graf i jego reprezentacja w postaci
macierzy wag krawędzi:
1
2
3
4
5
6
1
0
2
4
∞
∞
∞
2
∞
0
∞
∞
4
∞
3
∞
∞
0
-2
3
∞
4
1
∞
∞
0
∞
2
5
∞
∞
∞
∞
0
∞
6
∞
2
∞
∞
1
0
