8. Naturalna stopa

bezrobocia i krzywa

Philipsa

Ramowy plan prezentacji



1. Funkcja łącznej podaży jako

zależność

między

inflacją,

oczekiwaną inflacją i bezrobociem.



2.

Różne

warianty

krzywej

Philipsa.



3. Zależność między inflacją a

bezrobociem w różnych krajach i
okresach.

Początki



1958r. – A. W. Philips przedstawia wykres pokazujący
kształtowanie się stopy inflacji względem bezrobocia
w Wlk. Brytanii dla lat 1861-1957 ujemna
zależność między inflacją a bezrobociem.



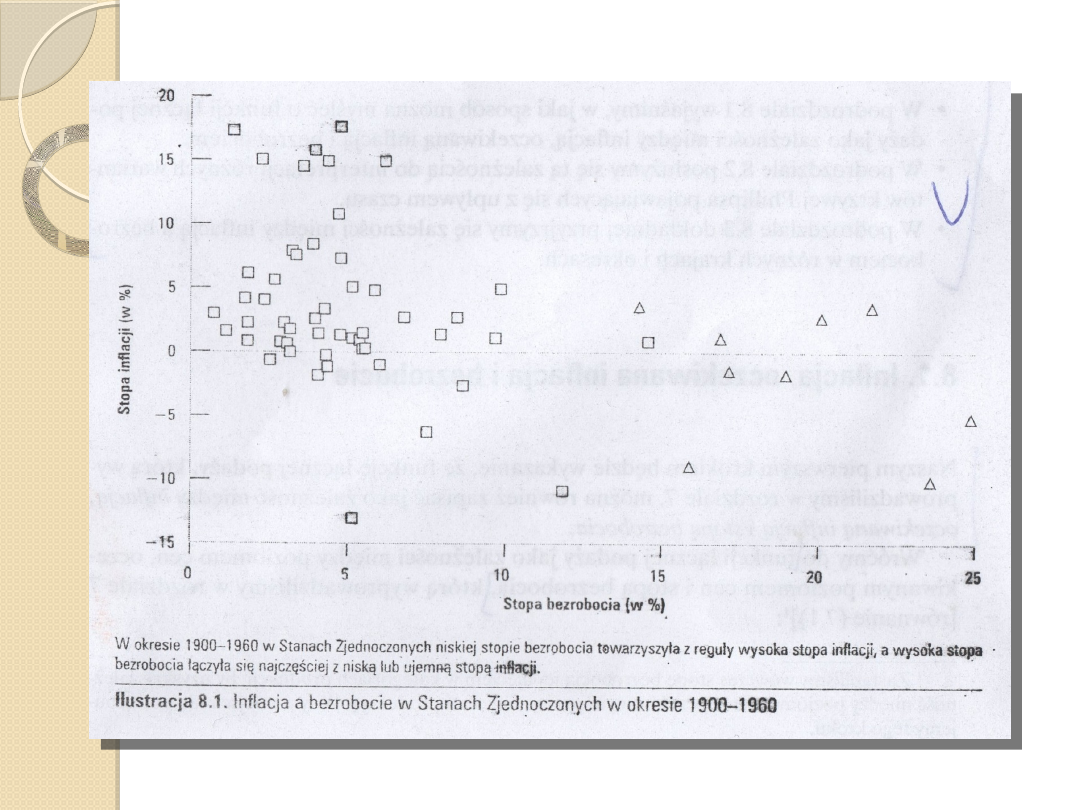
1960r. – Paul Samuelson i Robert Solow odtwarzają
doświadczenie Philipsa dla Stanów Zjednoczonych,
dla lat 1900-1960 potwierdzenie ujemnej
zależności między inflacją a bezrobociem (z
wyłączeniem lat 30. ).

Zależność ta zostaje przez nich nazwana krzywą
Philipsa.

Inflacja, oczekiwana inflacja i bezrobocie



1. Funkcja łącznej podaży

P = P

c

(1 + µ)F(u, z)

P – poziom cen
P

c

– oczekiwany poziom cen

µ - marża
u – stopa bezrobocia
z – inne czynniki wpływające na ustalanie płac

F(u, z) = 1 – αu + z
α – siła wpływu bezrobocia na płacę

Inflacja, oczekiwana inflacja i bezrobocie



1. Funkcja łącznej podaży

P = P

c

(1 + µ)F(u, z)

P – poziom cen
P

c

– oczekiwany poziom cen

µ - marża
u – stopa bezrobocia
z – inne czynniki wpływające na ustalanie płac

F(u, z) = 1 – αu + z

α – siła wpływu bezrobocia na płacę

P = P

c

(1 + µ)(1 – αu + z) π = π

e

+ (µ + z)

- αu

π = π

e

+ (µ + z) - αu

•

Wzrost oczekiwanej inflacji π

e

prowadzi

do wzrostu rzeczywistej inflacji.

•

Przy danej oczekiwanej inflacji π

e

wzrost marży µ lub wzrost czynników
oddziałujących na ustalanie płac z
prowadzi do wzrostu inflacji π.

•

Przy danej oczekiwanej inflacji π

e

wzrost stopy bezrobocia u prowadzi do
spadku inflacji π.

Krzywa Philipsa – wczesne
wersje



Założenie: π

e

= 0

π

t

= (µ + z) – αu

t

Interpretacja: przy danym oczekiwanym
poziomie cen z poprzedniego roku,
niższe bezrobocie prowadzi do wyższej
płacy

nominalnej.

Wyższa

płaca

nominalna

prowadzi

do

wyższego

poziomu cen, czyli do wyższej inflacji.

Spirala płacowo – cenowa



Niskie bezrobocie wyższa płaca nominalna.



Wzrost płacy nominalnej poziom cen rośnie.



Wyższy poziom cen większe żądania pracowników
dot. Płacy nominalnej przy kolejnym ustalaniu płac.



Wyższa płaca nominalna ponowne podniesienie
poziomu cen przez firmy.



Przy kolejnym ustalaniu płac pracownicy znowu będą
domagali się podniesienia płacy nominalnej itd.



Wniosek: Wyścig między cenami i płacami prowadzi do
ciągłej inflacji płac i cen.

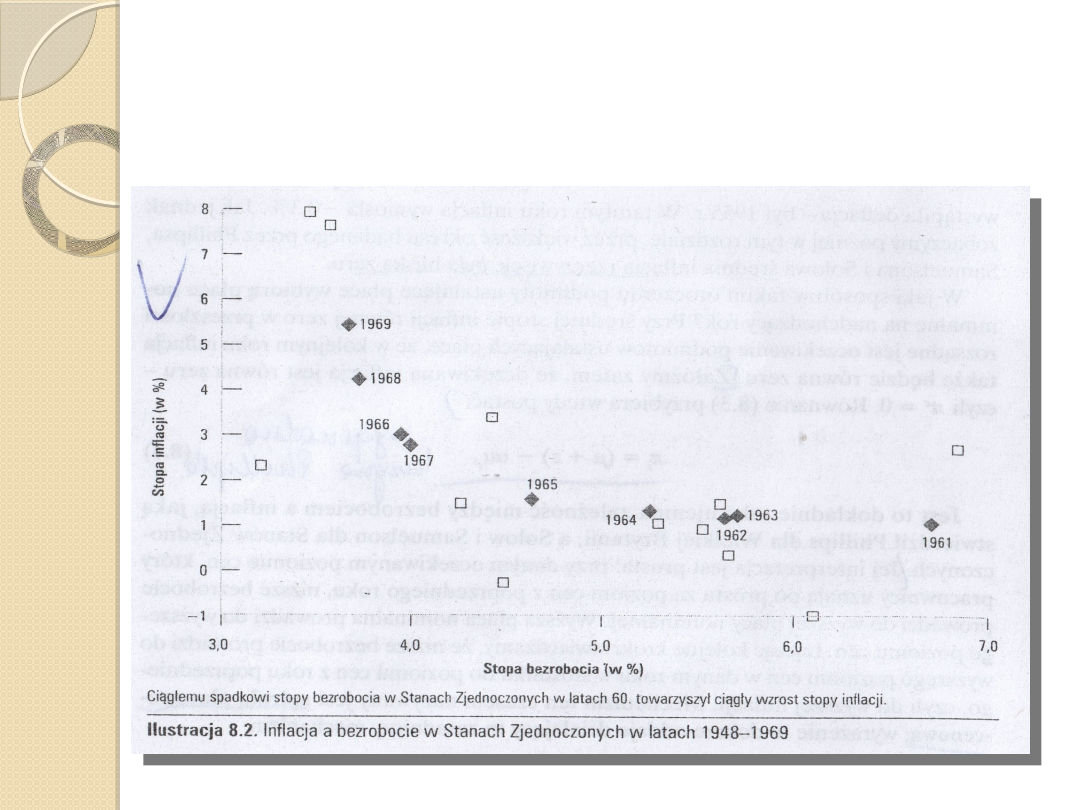
Krzywa Philipsa – późniejsze
warianty

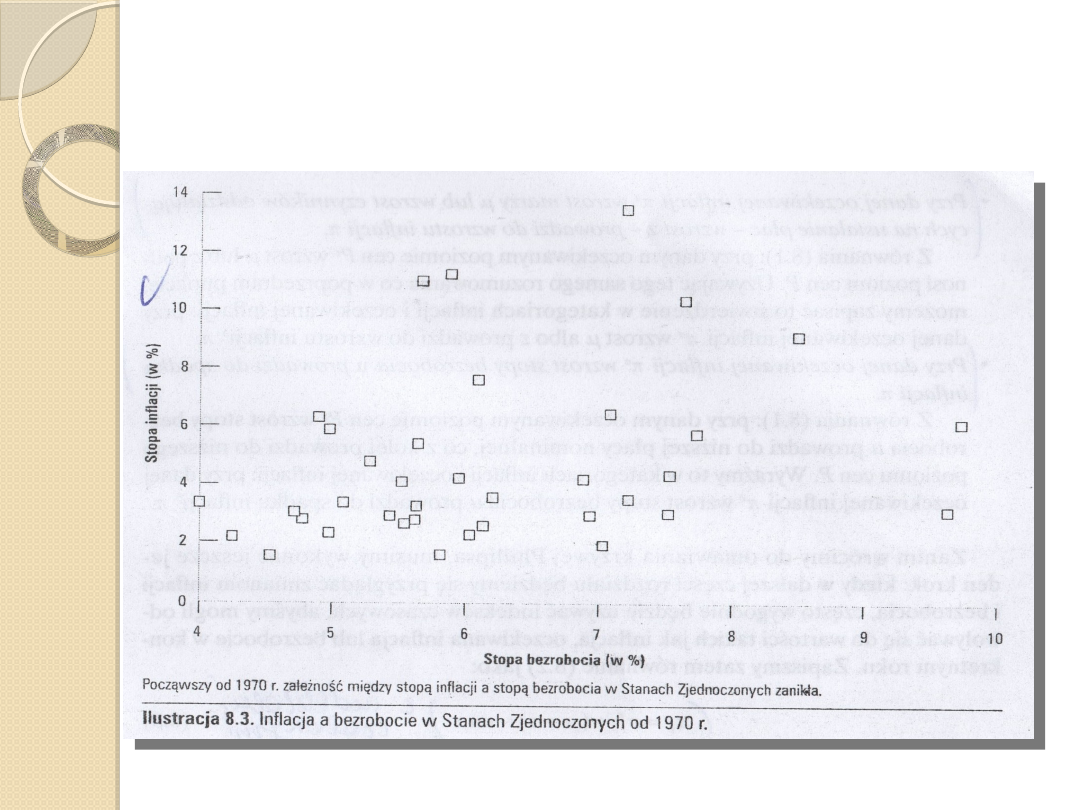
Załamanie trendu w
latach 70.

Przyczyny:



Dwukrotny, ostry wzrost cen ropy naftowej w latach 70.

Wzrost pozapłacowych kosztów produkcji
podnoszenie cen przez firmy (wzrost
marży µ) w stosunku do wypłacanych wynagrodzeń
wzrost inflacji.

•

Zmiana w kształtowaniu się stopy inflacji.

Trwałość inflacji skłaniała pracowników i firmy do rewizji
sposobu formułowania swoich oczekiwań zmiana
relacji między bezrobociem a inflacją.

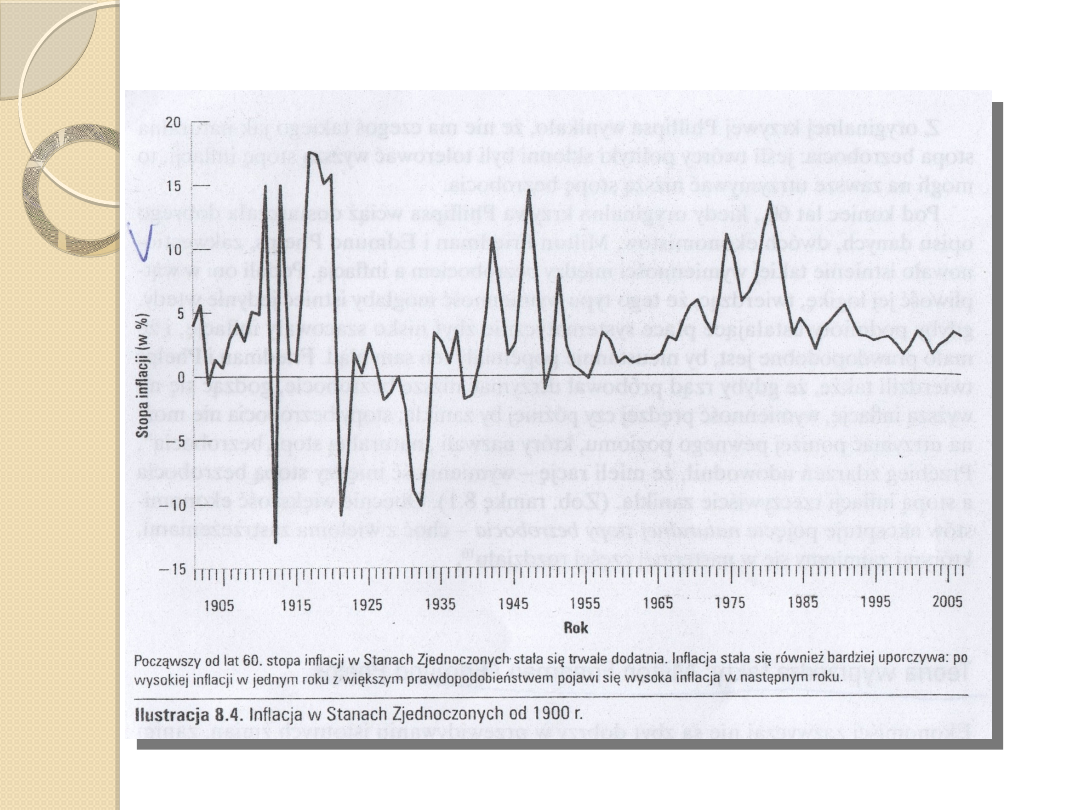
Załamanie trendu (c.d.)

π

t

e

= θ π

t-1

θ – ujmuje wpływ ubiegłorocznej inflacji π

t-1

na tegoroczną oczekiwaną stopę inflacji π

t

e

Wniosek: Im wyższa wartość θ, tym bardziej
ubiegłoroczna inflacja skłania pracowników i
firmy do korekty swoich oczekiwań odnośnie
do tegorocznej inflacji.

Wydarzenia z lat 70. można interpretować jako
wzrost wartości θ w czasie.



Dopóki inflacja była niska pracownicy i firmy postępowali
rozsądnie, ignorując inflację z przeszłości.

W okresie, który analizowali Samuelson i Solow, wartość θ
była bliska zeru, a oczekiwania były dane przez π

te

.



Kiedy inflacja stawała się bardziej trwała, pracownicy i
firmy zaczęli zmieniać sposób formułowania oczekiwań.

Wartość parametru θ zaczęła wzrastać, aż do osiągnięcia
wartości θ = 1.

Wpływ θ na zależność między inflacją a
bezrobociem.



π

t

= π

t

e

+ (µ + z) – αu

t

π

t

= θ π

t-1

+ (µ + z) – αu

t

π

t

e

= θ π

t-1

Wpływ θ na zależność między inflacją a
bezrobociem.



π

t

= π

t

e

+ (µ + z) – αu

t

π

t

= θ π

t-1

+ (µ + z) – αu

t

π

t

e

= θ π

t-1



Kiedy θ równa się 0, otrzymujemy oryginalną krzywą
Philipsa, zależność między stopą inflacji a stopą
bezrobocia:

π

t

= (µ + z) – αu

t

Wpływ θ na zależność między inflacją a
bezrobociem.



π

t

= π

t

e

+ (µ + z) – αu

t

π

t

= θ π

t-1

+ (µ + z) – αu

t

π

t

e

= θ π

t-1



Kiedy θ równa się 0, otrzymujemy oryginalną krzywą
Philipsa, zależność między stopą inflacji a stopą
bezrobocia:

π

t

= (µ + z) – αu

t



Kiedy θ jest dodatni, stopa inflacji zależy nie tylko od
stopy bezrobocia, ale także od stopy inflacji z
poprzedniego roku:

π

t

= θ π

t-1

+ (µ + z) – αu

t

Wpływ θ na zależność między inflacją a
bezrobociem.



π

t

= π

t

e

+ (µ + z) – αu

t

π

t

= θ π

t-1

+ (µ + z) – αu

t

π

t

e

= θ π

t-1



Kiedy θ równa się 0, otrzymujemy oryginalną krzywą
Philipsa, zależność między stopą inflacji a stopą
bezrobocia:

π

t

= (µ + z) – αu

t



Kiedy θ jest dodatni, stopa inflacji zależy nie tylko od
stopy bezrobocia, ale także od stopy inflacji z
poprzedniego roku:

π

t

= θ π

t-1

+ (µ + z) – αu

t



Kiedy θ równa się 1, zależność – po przeniesieniu
ubiegłorocznej stopy inflacji na lewą stronę – przyjmuje
postać:

π

t

– π

t-1

= (µ + z) – αu

t

π

t

– π

t-1

= (µ + z) – αu

t



Kiedy zatem θ = 1, stopa bezrobocia wpływa
nie na stopę inflacji, lecz na zmianę stopy
inflacji: wysokie bezrobocie prowadzi do
obniżenia inflacji w czasie; niskie bezrobocie
prowadzi do wzrostu inflacji w czasie.



Analiza ta wyjaśnia to, co stało się w latach 70.
w Stanach Zjednoczonych.

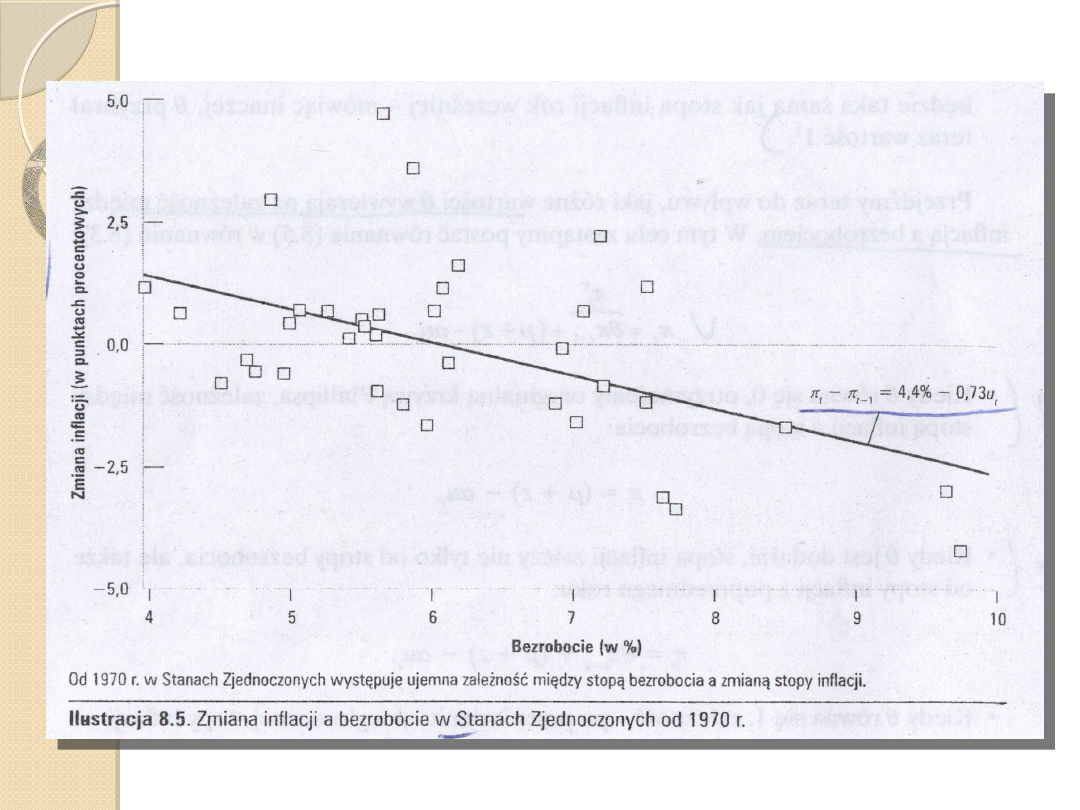
1)

π

t

– π

t-1

= (µ + z) – αu

t

2)

π

t

– π

t-1

= 4,4 % - 0,73u

t

Przy niskim bezrobociu zmiana inflacji jest
dodatnia. Przy wysokim bezrobociu zmiana
inflacji jest ujemna.

Taką postać krzywa Philipsa – zależność między
bezrobociem a inflacją – przyjmuje obecnie.

Równanie 1) – lub jego empiryczny odpowiednik,
równanie 2) – nazywamy zmodyfikowaną krzywą
Philipsa, jednak w dalszej części prezentacji
będziemy ja nazywać po prostu krzywą Philipsa.

Teoria wyprzedza fakty: Milton Friedman i
Edmund Phelps



Pod koniec lat 60. dwóch tych dwóch ekonomistów, zaczęło
dowodzić, że wymienialność między inflacją a bezrobocie to
czysta iluzja.



Friedman

uważał,

że

zawsze

istnieje

przejściowa

wymienialność między inflacją a bezrobociem; nie ma
natomiast trwałej wymienialności. Przejściowa wymienialność
wynika nie z inflacji jako takiej, lecz z rosnącej stopy inflacji.



Co więcej, Friedman oszacował na podstawie dowodów
historycznych, że początkowy efekt wyższej i
nieprzewidzianej stopy inflacji trwa od dwóch do pięciu lat,
a następnie trend ulega odwróceniu.



Kilka lat później oryginalna krzywa Philipsa zaczęła zanikać,
dokładnie w taki sam sposób jak przewidział Friedman.

Związek między krzywą Philipsa a naturalną stopą
bezrobocia.

Naturalna stopa bezrobocia to taka stopa bezrobocia, przy
której rzeczywisty poziom cen równy jest oczekiwanemu.

π

t

= π

te

+ (µ + z) – αu

t

0 = (µ + z) – αu

n

π

t

= π

te

u

n

– naturalna stopa bezrobocia

0 = (µ + z) – αu

n

Im wyższa marża µ, lub im wyższa wartość czynników
oddziałujących na ustalanie płac z, tym wyższa jest
naturalna stopa bezrobocia.

π

t

= π

te

+ (µ + z) – αu

t

π

t

- π

te

= – α

(

u

t

-

)

π

t

- π

te

= – α(u

t

-

u

n

)

Jeżeli – jak to jest obecnie w Stanach Zjednoczonych –
dobrym przybliżeniem oczekiwanej inflacji (π

te

) jest

inflacja z roku poprzedniego roku π

t-1

to równanie

przyjmuje ostatecznie postać:

π

t

– π

t-1

= – α(u

t

- u

n

)



 

π

t

– π

t-1

= – α(u

t

- u

n

)



Zależność opisana równaniem ważna jest z dwóch
powodów:

◦

Pokazuje, że zmiana inflacji zależy od różnicy między
rzeczywistą a naturalną stopą bezrobocia.

◦

Kiedy rzeczywista stopa bezrobocia jest wyższa od naturalnej,
stopa inflacji spada:

u

t

> u

n

π

t

< π

t-1

◦

Kiedy rzeczywista stopa bezrobocia jest niższa od naturalnej, stopa
inflacji rośnie:

u

t

< u

n

π

t

> π

t-1

◦

Pokazuję, że naturalną stopą bezrobocia jest stopa
bezrobocia konieczna do utrzymania stałej stopy inflacji
(stopa bezrobocia nieprzyśpieszająca inflacji – NAIRU).

Co wyjaśnia bezrobocie w Europie?



Hojny system ubezpieczeń na wypadek
bezrobocia.



Wysoki stopień ochrony zatrudnienia.



Zbyt wysoki stosunek płacy minimalnej
do średniego wynagrodzenia w wielu
krajach.



Niekorzystne

zasady

negocjacji

zbiorowych/zbyt silna pozycja związków
zawodowych.

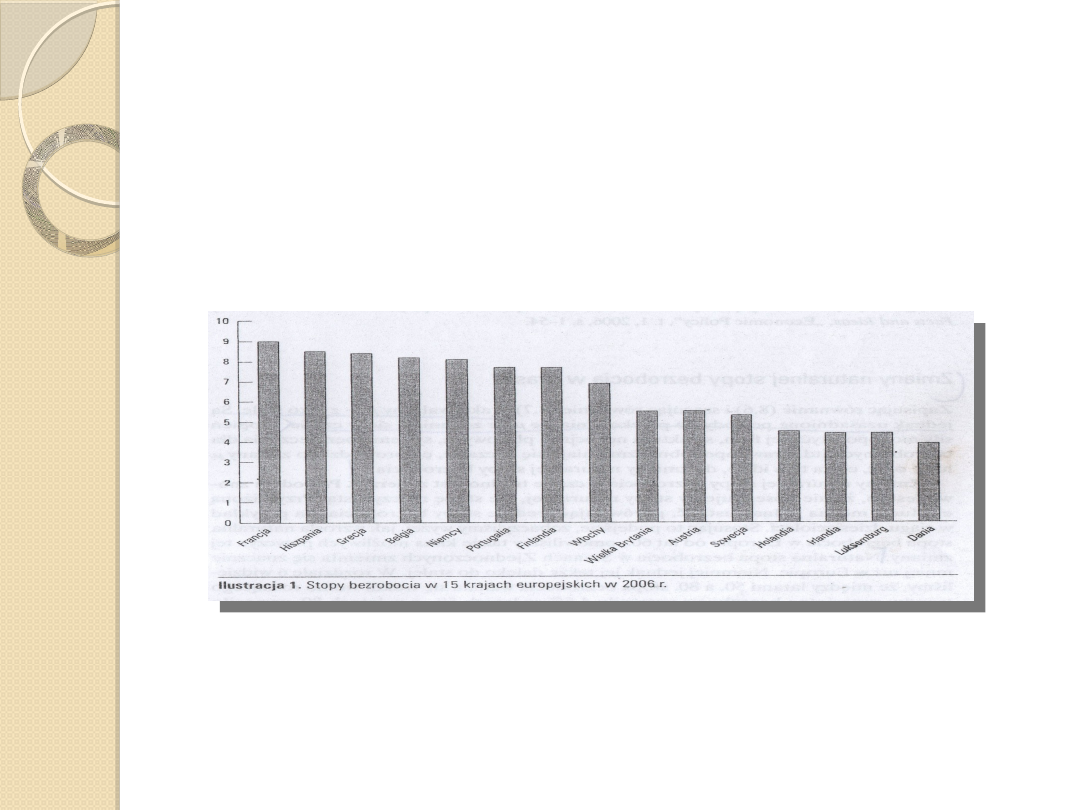
Rozpatrując problem wysokiego
bezrobocia w Europie należy pamiętać:



Fakt 1: Bezrobocie w Europie nie zawsze było wysokie. W latach
60. bezrobocie w czterech największych gospodarkach
kontynentu było niższe niż w Stanach Zjednoczonych, mimo
silniejszej ochrony socjalnej.



Fakt 2: Wiele krajów europejskich ma naprawdę niskie
bezrobocie.



Wniosek: hojna opieka socjalna może być spójna z niskim
bezrobocie, ale tylko wtedy, gdy jest zapewniana w sposób
efektywny, np. zasiłki dla bezrobotnych mogą być hojne, jeśli
bezrobotni są jednocześnie zmuszani do podjęcia pracy, kiedy
jest ona dostępna.

Wysoka inflacja i krzywa Philipsa

Zależność między inflacją a bezrobociem zmienia się wraz z
poziomem i trwałością inflacji. Kiedy stopa inflacji staje
się wysoka, inflacja staje się bardziej zmienna.

W rezultacie pracownicy i firmy niechętnie zawierają
umowy, w których płaca nominalna ustalana jest na dłuższy
czas: jeśli inflacja okaże się wyższa od oczekiwanej, płace
realne

gwałtownie

spadną,

a pracownicy odczują

pogorszenie poziomu życia. Jeśli inflacja okaże się niższa od
oczekiwanej, to płace realne wzrosną, a firmy mogą mieć
problemy z opłaceniem swoich pracowników i w rezultacie
zbankrutować.

Z tego powodu coraz powszechniej stosowana jest
indeksacja (waloryzacja) płac – automatycznie podnosi
płace równolegle z inflacją.

Waloryzacja płac

Załóżmy: λ - część waloryzowana wszystkich umów
1- λ - część niewaloryzowana wszystkich
umów

π

t

=

[

λ π

t

+ (1- λ) π

te

]

– α(u

t

- u

n

)

Wyrażenie w nawiasie kwadratowym odzwierciedla
fakt, że część λ umów jest waloryzowana, a więc
reaguje na rzeczywistą inflację π

t

, zaś część (1-

λ) reaguje na oczekiwaną inflację π

te

.



Kiedy λ = 0, wszystkie płace są ustalane na podstawie
inflacji oczekiwanej – która równa jest inflacji z
poprzedniego roku π

t-1

:

π

t

– π

t-1

= – α(u

t

- u

n

)



Kiedy λ jest dodatnia, część λ płac ustalana jest na
podstawie inflacji rzeczywistej, a nie oczekiwanej:

π

t

– π

t-1

= – – α(u

t

- u

n

)

Indeksacja płac wzmacnia wpływ bezrobocia na inflację.

Jeśli dąży do 1 – czyli kiedy większość umów płacowych
przewiduje indeksację płac – małe zmiany bezrobocia mogą
prowadzić do bardzo dużych zmian inflacji.



 

Deflacja i krzywa Philipsa

Co dzieje się z krzywą Philipsa kiedy występuje deflacja?

Przy danej wysokiej stopie bezrobocia stopa inflacji jest
zaskakująco wysoka. Mówiąc inaczej, przy bardzo wysokiej stopie
bezrobocia oczekiwalibyśmy wysokiej stopy deflacji. W
rzeczywistości deflacja była niewielka, a począwszy od okresu
1934-1937 inflacja osiągnęła wartość dodatnią.



Możliwe przyczyny zjawiska:

◦

Wielkiemu Kryzysowi towarzyszył nie tylko
wzrost rzeczywistej stopy bezrobocia, ale
także stopy naturalnej.

◦

Kiedy gospodarka zaczyna doświadczać
deflacji,

zależność

opisująca

krzywą

Philipsa

przestaje

istnieć.

Jedna

z

możliwych

przyczyn

to

niechęć

pracowników do zaakceptowania obniżki
płac nominalnych.

Dziękujemy za uwagę.



Natalia Gula



Natalia Dobczyńska



Ilona Domańska



Paweł Kamiński