Matematyka

Matematyka

(„nauka, lekcja,

poznanie”)– nauka dostarczająca
narzędzi do otrzymywania ścisłych
wniosków z przyjętych założeń,
zatem dotycząca prawidłowości
rozumowania. Ponieważ ścisłe
założenia mogą dotyczyć
najróżniejszych dziedzin myśli
ludzkiej, a muszą być czynione w
naukach ścisłych, technice a nawet
w naukach humanistycznych, zakres
matematyki jest szeroki i stale się
powiększa.

Najwięksi matematycy

Największymi matematykami są
między innymi:
- Pitagoras
- Tales z Minetu
- Euklides

Pitagoras

Pitagoras

(ur. ok. 572

p.n.e. na Samos lub w Sydonie,
zm. ok. 497 p.n.e. w
Metaponcie) – grecki
matematyk, filozof, mistyk
kojarzony ze słynnym
twierdzeniem matematycznym
nazwanym jego imieniem. Z
relacji anonimowego autora
wiadomo, że Pitagoras żył 104
lata, ale większość opisów
wzmiankuje jedynie około 80
lat.

Dokonania Pitagorasa :

-Sformułował ,,twierdzenie
Pitagorasa’’
-dowód, że suma kątów trójkąta
równa jest

dwóm kątom prostym,

-wprowadzenie średniej
arytmetycznej
-konstrukcje wielościanów
foremnych

i odkrycie dwunastościanu

foremnego

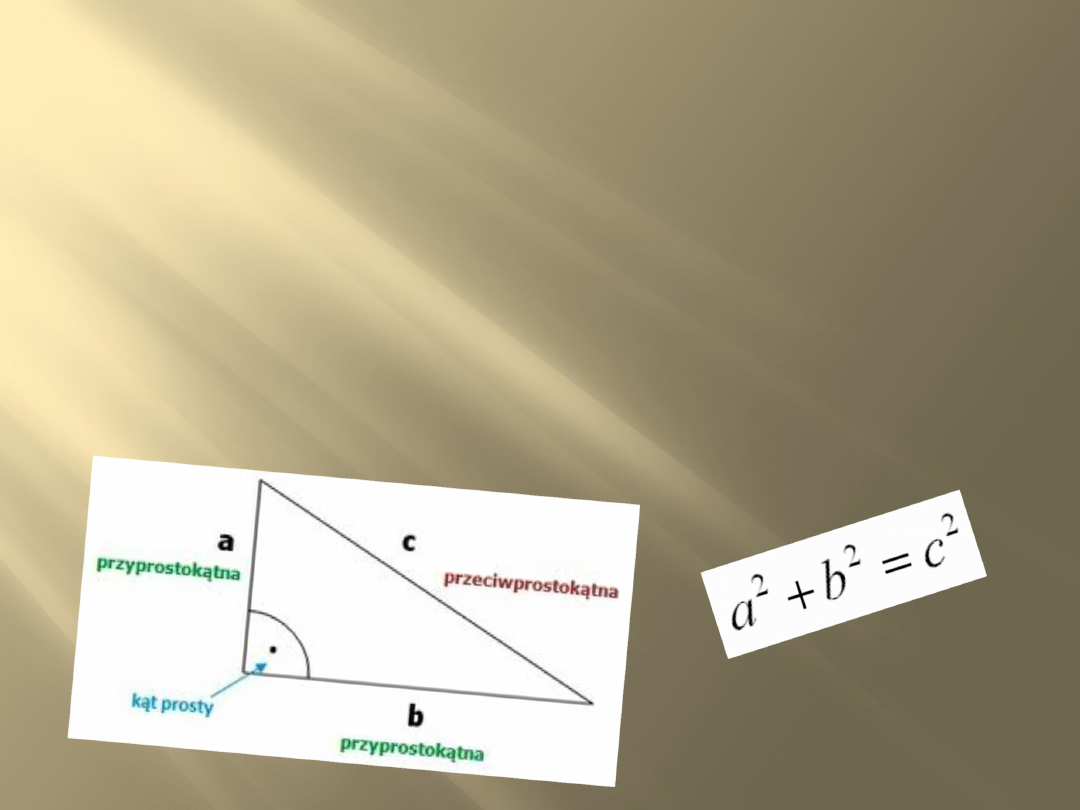
Twierdzenie Pitagorasa

Twierdzenie pitagorasa mówi:
W dowolnym trójkącie prostokątnym
suma kwadratów długości
przyprostokątnych jest równa
kwadratowi długości
przeciwprostokątnej tego trójkąta

Średnia

arytmetyczna



Średnia arytmetyczna n liczb, to
suma tych liczb podzielona przez
ilość n liczb.

Wielościany Foremne

Wielościan foremny (bryła
platońska) – wielościan
spełniający następujące trzy
warunki:

-ściany są przystającymi wielokątami
foremnymi
-w każdym wierzchołku zbiega się
jednakowa liczba ścian
-jest bryłą wypukłą

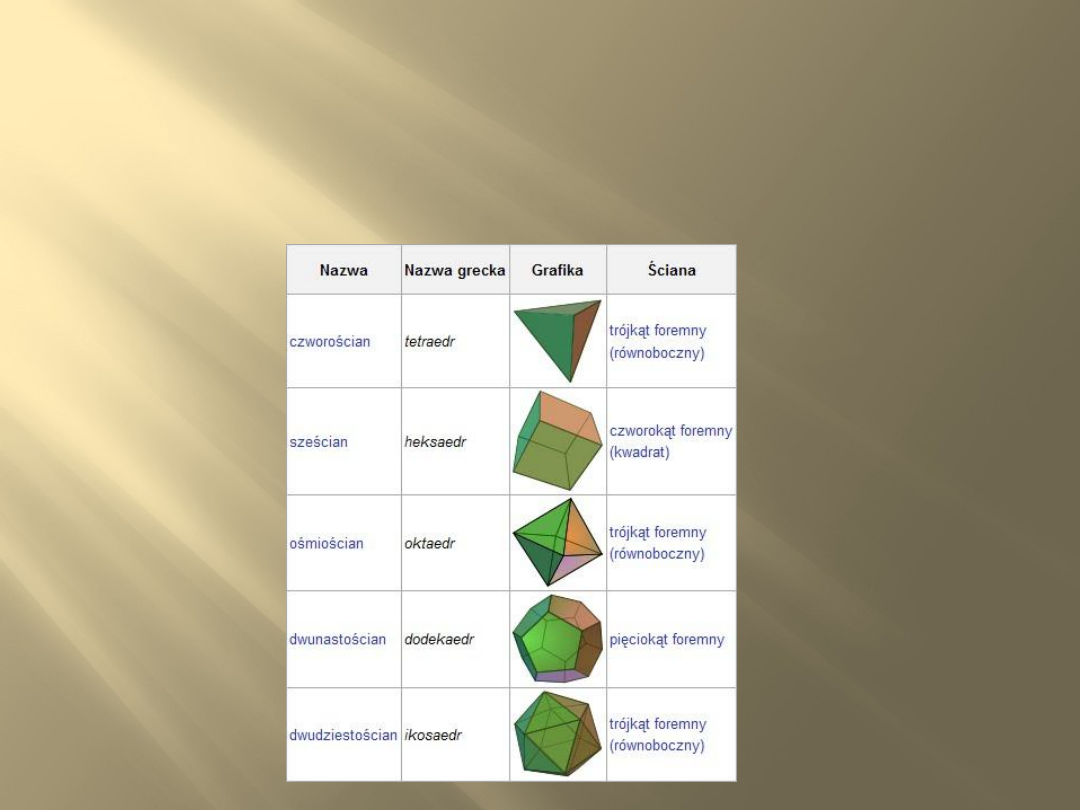
Przykłady

wielościanów

foremnych

Tales z Miletu

Tales z Miletu – filozof (uczony)
grecki okresu przedsokratejskiego.
Powszechnie uznawany za pierwszego
filozofa cywilizacji zachodniej
oraz za inicjatora badań nad przyrodą
jako nauki. Talesa postrzega się jako
pierwszego filozofa głównie dlatego, że
zainicjował wyjaśnianie rzeczywistości
przez odwoływanie się do natury i
rozumu bardziej niż do mitologii i
tradycji – Grecy widzieli w nim jednak
raczej mędrca, niż filozofa.

Odkrycia Talesa

-Twierdzenie Talesa
-kąt wpisany w półkole jest kątem
prostym
-dwa kąty przy podstawie trójkąta
równoramiennego są równe,
-jeżeli dwie linie proste przecinają
się, przeciwległe kąty są równe,
-trójkąt jest określony, jeżeli dana
jest jego podstawa i kąty przy
podstawie.

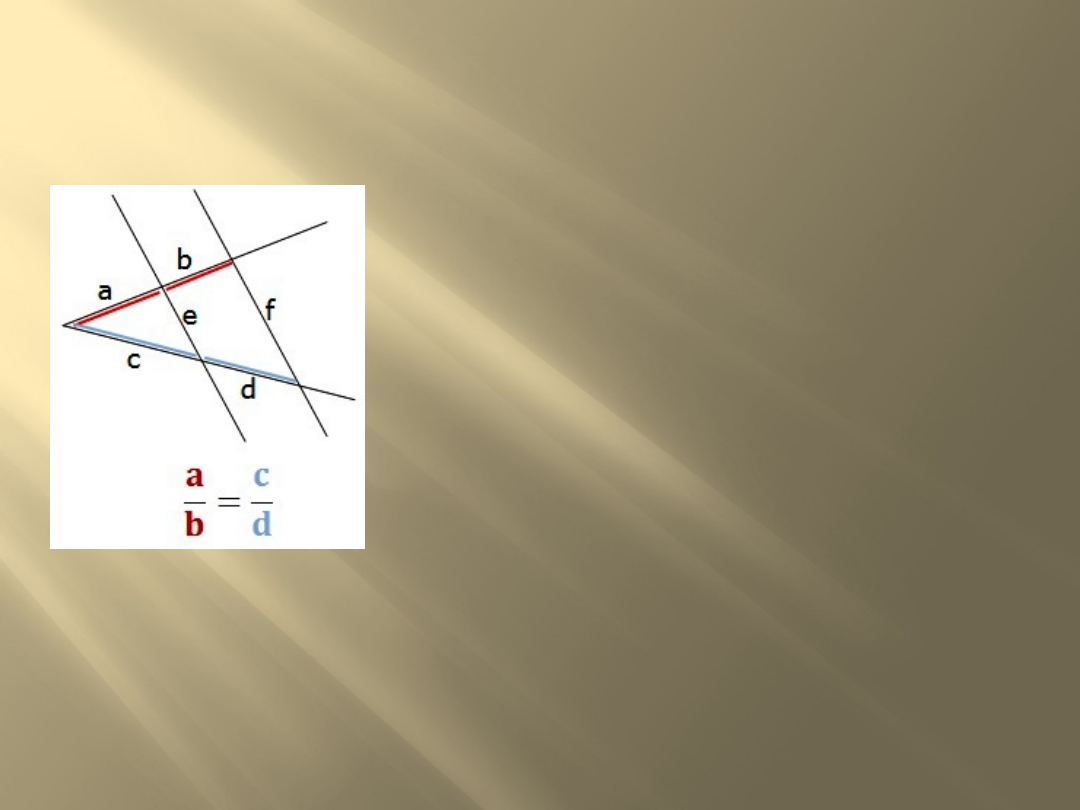
Twierdzenie Talesa

Jeżeli ramiona kąta
przecięte
są prostymi
równoległymi,
to odcinki wyznaczone
przez
te proste na jednym
ramieniu kąta, są
proporcjonalne
do odpowiednich
odcinków wyznaczonych
przez te proste
na drugim ramieniu kąta.

K

ą

t wpisany w

półkole jest k

ą

tem

prostym

Jeśli A, B i C są punktami na
okręgu gdzie odcinek AC jest
średnica, to kąt ABC jest prosty.

Je

ż

eli dwie linie

proste przecinaj

ą

si

ę

, przeciwleg

ł

e

k

ą

ty s

ą

równe

Euklides

Euklides z Aleksandrii ( ur.
ok. 365 r. p.n.e., zm. ok.
300 r. p.n.e.) – matematyk
grecki pochodzący z Aten,
przez większość życia
działający w Aleksandrii.

Odkrycia Euklidesa

-Algorytm Euklidesa
-Geometria Euklidesowa
-Przestrzeń euklidesowa

Algorytm Euklidesa

Algorytm Euklidesa to algorytm
znajdowania największego wspólnego
dzielnika (NWD) dwóch różnych liczb
naturalnych dodatnich.

Nie wymaga rozkładania liczb na

czynniki pierwsze

.

Geometria Euklidesowa



Sformułowany w podstawach przez
Euklidesa zbiór pojęć i twierdzeń
geometrycznych dla płaskiej
przestrzeni opartych na systemie
pięciu aksjomatów.

Najwi

ę

ksi

Polscy

Matematycy

- Jan Śniadecki
- Stefan Banach
-Włodzimierz Stożek
- Adam Adymandy Kochański
-Karol Borsuk
-Zygmunt Janiszewski
-Andrzej Turowicz

Jan Śniadecki

Jan Śniadecki

-żył w latach

1756-1830,

-polski astronom

, matematyk, geograf i

filozof,

- jeden

z najwybitniejszych uczonych okresu

oświecenia,
- kształcił się w Akademii Krakowskiej, a
także w Getyndze i Paryżu,
-opublikował Geografię, czyli opisanie
matematyczne i fizyczne Ziemi,
-twórca polskiej terminologii matematycznej
i astronomicznej,
-pionier rachunku prawdopodobieństwa w
Polsce.

Stefan Banach

Stefan Banach

- żył w latach

1892-1945,

- polski

matematyk,

- od dzieciństwa

wykazywał nieprzeciętne

zdolności

matematyczne i lingwistyczne,

- studiował

na Wydziale Inżynierii Lądowej

Politechniki Lwowskiej,
- był kilkakrotnie laureatem nagród
naukowych,
- w 1939 zostaje wybrany na prezesa
Polskiego Towarzystwa Matematycznego.

Włodzimierz Stożek

Włodzimierz Stożek

- żył w latach 1883-1941

,

- polski matematyk

, jeden z

przedstawicieli

lwowskiej

szkoły

matematycznej,
- studiował na Uniwersytecie
Jagiellońskim,
- zamordowany przez Niemców,
- zajmował się m.in. teorią
potencjału logarytmicznego i
newtonowskiego,
- podczas I wojny światowej służył w
armii

Adam

Adymandy

Kocha

ń

ski

Adam

Adymandy

Kocha

ń

ski

-żył w latach

1631-1700,

- kształcił się na

Uniwersytecie Wileńskim,

na którym później

wykładał matematykę,

- był

nadwornym matematykiem

i

bibliotekarzem

króla Jana III Sobieskiego

oraz nauczycielem

królewicza Jakuba,

-

podał konstrukcję prostowania okręgu,

która polega na skonstruowaniu odcinka
równego długości okręgu z dużą
dokładnością.

Karol Borsuk

Karol Borsuk

- żył w latach

1905-1982

- był wybitnym

specjalistą w zakresie topologii,

-

opublikował

ponad 170 prac badawczych

oraz monografie

i podręczniki m.in. Geometria

analityczna

wielowymiarowa, Podstawy

geometrii,

- wprowadził

metodę badania topologicznych

własności przestrzeni za pomocą własności ich
przekształceń w sfery,
- jako pierwszy podał przykład w teorii
punktów stałych.

Zyg

munt

Janiszewski

Zyg

munt Janiszewski

-żył w latach 1888-1920,
- wykładał na Uniwersytecie

Lwowskim teorię funkcji

analitycznych i "rachunek

funkcyjny”,

- jako jeden z pierwszych

wstąpił do Legionów, pełniąc

- z własnej woli

- służbę szeregowca

w

artylerii,

- środki, jakimi

rozporządzał, rozdzielał w całości

na kształcenie młodych talentów, a majątek
odziedziczony po rodzicach zapisał na cele oświatowe,
- wspólnie z Mazurkiewiczem i Sierpińskim był
założycielem czasopisma "Fundamenta Mathematicae”.

Andrzej

Turowicz

Andrzej

Turowicz

-żył w latach 1904-1989
- otrzymał w Uniwersy

tecie Jagiellońskim

stopień doktora filozofii

na podstawie rozprawy

O funkcjonałach multiplikatywnych

ciągłych.

- wstąpił do

klasztoru benedyktynów w Tyńcu;

w

latach 1946-1950

odbył studia teologiczne.

- opublikował

kilkadziesiąt prac dotyczących

równań różniczkowych, analizy funkcjonalnej,
algebry, teorii sterowania i teorii automatycznej.

Koniec

Prezentacj

ę

Przygotował