Polityka ochrony prywatności O Wikibooks Informacje prawne Dla deweloperów Komunikat na temat ciasteczek Wersja dla urządzeń mobilnych
Matematyka dla liceum/Liczby i ich zbiory/Działania na zbiorach
Tę stronę ostatnio edytowano 9 mar 2018, 21:56.
licencji Creative Commons: uznanie autorstwa, na tych samych warunkach
, z możliwością obowiązywania dodatkowych ograniczeń. Zobacz szczegółowe informacje o
.
>
> Działania na zbiorach
»
Spis treści
[
ukryj
]
1
Suma zbiorów
2
Iloczyn zbiorów
3
Różnica zbiorów
4
Dopełnienie zbioru
5
Własności działań na zbiorach i prawa De Morgana
Suma zbiorów
[
]
DEFINICJA
Sumą zbiorów A i B nazywamy zbiór tych elementów, które należą do zbioru A lub do zbioru B, matematycznie zapisujemy ją tak:
.
Sumę zbiorów A i B ilustruje poniższy diagram Venna:
Przykład.
Jeżeli
i
, to
. Pomimo tego, że 1 występuje w obydwu zbiorach, w sumie tych zbiorów występuje tylko jeden raz.
Iloczyn zbiorów
[
]
DEFINICJA
Iloczynem/Częścią wspólną zbioru A i B nazywamy zbiór tych elementów, które należą jednocześnie do zbioru A i do zbioru B, formalnie zapisujemy ją tak:
. Iloczyn zbiorów nazywany jest także częścią wspólną zbiorów lub przekrojem zbiorów.
Przykład.
Jeśli
i
, to
. Liczba 1 jest jedynym wspólnym elementem tych zbiorów.
Różnica zbiorów
[
]
DEFINICJA
Różnicą zbiorów A i B nazywamy zbiór tych elementów, które należą do zbioru A, a które nie należą do zbioru B, możemy ją zapisać tak:
. Różnica zbiorów A i B zapisywana jest też
.
Jeśli
i
, to
. Jedynym wspólnym elementem obydwu zbiorów jest liczba 1, więc otrzymany zbiór będzie bardzo podobny do zbioru A, lecz nie posiadający liczby 1.
Dopełnienie zbioru
[
]
DEFINICJA
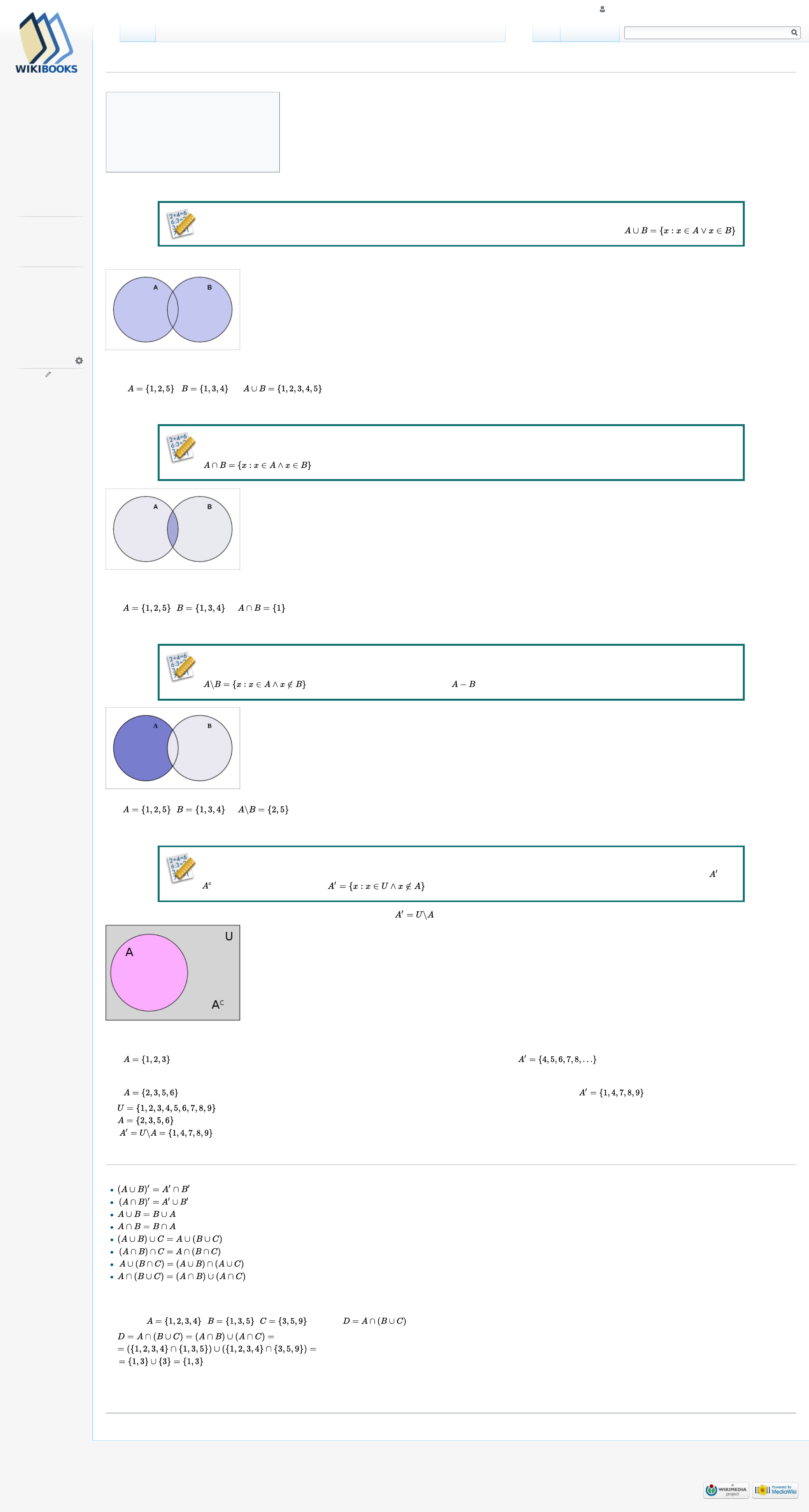
Dopełnieniem zbioru A z przestrzeni U nazywamy zbiór tych elementów przestrzeni U, które nie należą do zbioru A. Dopełnienie zbioru A oznaczamy jako
lub
. Dopełnienie możemy zapisać tak:
.
Z definicji dopełniania wynika także, że jest to po prostu różnica przestrzeni U i zbioru A:
. Zbiór U zwany jest zbiorem uniwersum. Czasami zamiast U używa się innego oznaczenia przestrzeni np. X.
Przykład.
Jeśli
, a przestrzenią U jest zbiór wszystkich liczb całkowitych dodatnich, to dopełnieniem zbioru A będzie zbiór
.
Przykład.
Jeśli
, a przestrzenią U jest zbiór wszystkich liczb całkowitych dodatnich jednocyfrowych, to dopełnieniem zbioru A będzie zbiór
, ponieważ:
Własności działań na zbiorach i prawa De Morgana
[
]
Prawa przedstawione wyżej mają pewne własności, które zaraz przedstawimy. Dla dowolnych zbiorów A, B, C zachodzą prawa:
-- I prawo De Morgana
-- II prawo De Morgana
-- przemienność dodawania zbiorów
-- przemienność mnożenia zbiorów
-- łączność dodawania zbiorów
-- łączność mnożenia zbiorów
-- rozdzielność dodawania zbiorów względem mnożenia
-- rozdzielność mnożenia zbiorów względem dodawania
Przykład.
Mamy zbiór
,
,
. Obliczyć
:
(W rozwiązaniu celowo wykorzystano własności działań na zbiorach. Gdyby ich nie użyto rozwiązanie byłoby odrobinę krótsze.)
«
Zbiór liczb rzeczywistych i jego podzbiory
»
Przeszukaj Wikibooks
Strona główna
Wikijunior
Księgozbiór
Książka kucharska
Pomoc
Portal użytkowników
Ostatnie zmiany
Losowa strona
Ogłoszenia
Kontakt
Drukuj lub eksportuj
Utwórz książkę
Pobierz jako PDF
Wersja do druku
Narzędzia
Szukaj w podręczniku
Linkujące
Zmiany w linkowanych
Prześlij plik
Strony specjalne
Link do tej wersji
Informacje o tej stronie
Cytowanie tego artykułu
Języki
Nie jesteś zalogowany