Zbiory i działania na

zbiorach

Co to jest zbiór ?

Zbiorem określamy zazwyczaj jakąś grupę,

kolekcję pewnych obiektów.

Pojęcie zbioru jest pojęciem pierwotnym, tzn. takim,

którego się nie definiuje. Zbiór jest określony, jeżeli
wiemy, jakie są jego elementy lub jaką mają własność
wszystkie jego elementy.

Zbiory oznaczamy dużymi literami alfabetu, np. A, B, X,
zaś elementy zbiorów – literami małymi a,b, x, y.
Zapis „a  X” oznacza, że a jest elementem zbioru X.

Zbiór, który nie ma żadnych elementów

nazywamy zbiorem pustym.

Zbiór skończony to zbiór, którego

wszystkie elementy możemy
wymienić i jest ich skończona liczba.

Zbiór nieskończony ma nieskończenie

wiele elementów.

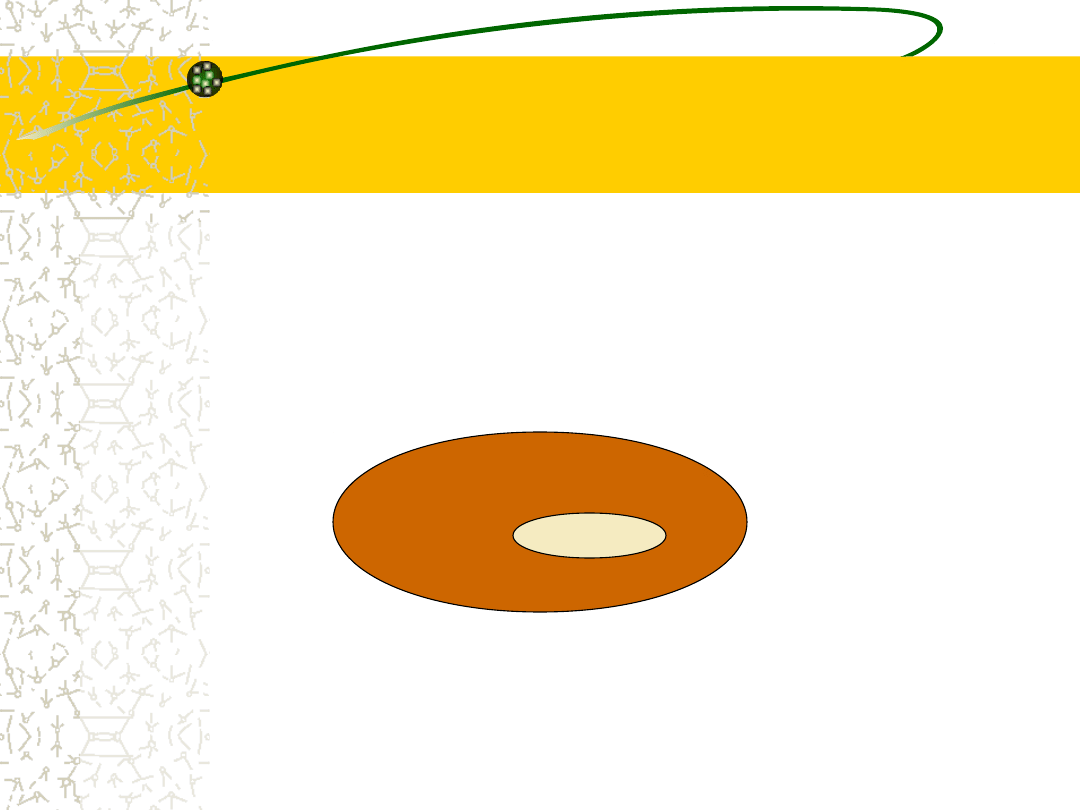
Podzbiór

Jeżeli każdy element zbioru A należy

do zbioru B, to zbiór A jest
podzbiorem zbioru B.

A  B

B

A

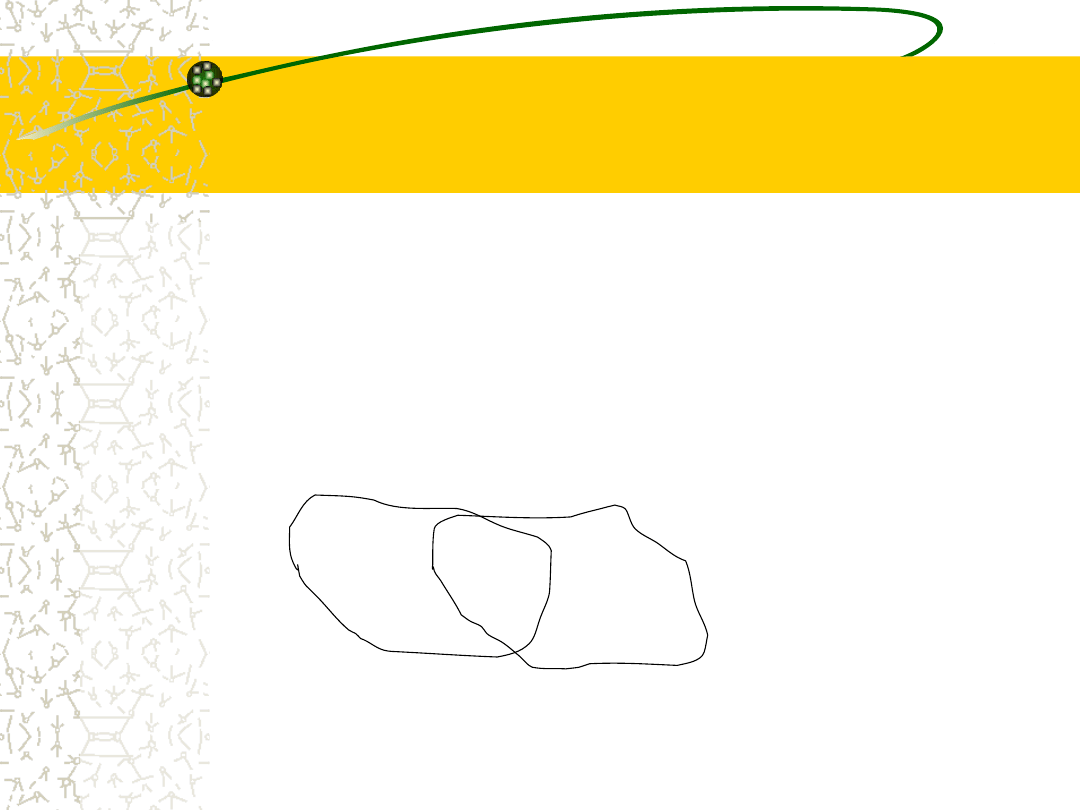
Suma dwóch zbiorów

Sumą dwóch zbiorów A i B nazywamy

zbiór utworzony ze wszystkich
elementów należących do zbioru A lub
do zbioru B.

Ozn. A B

A

B

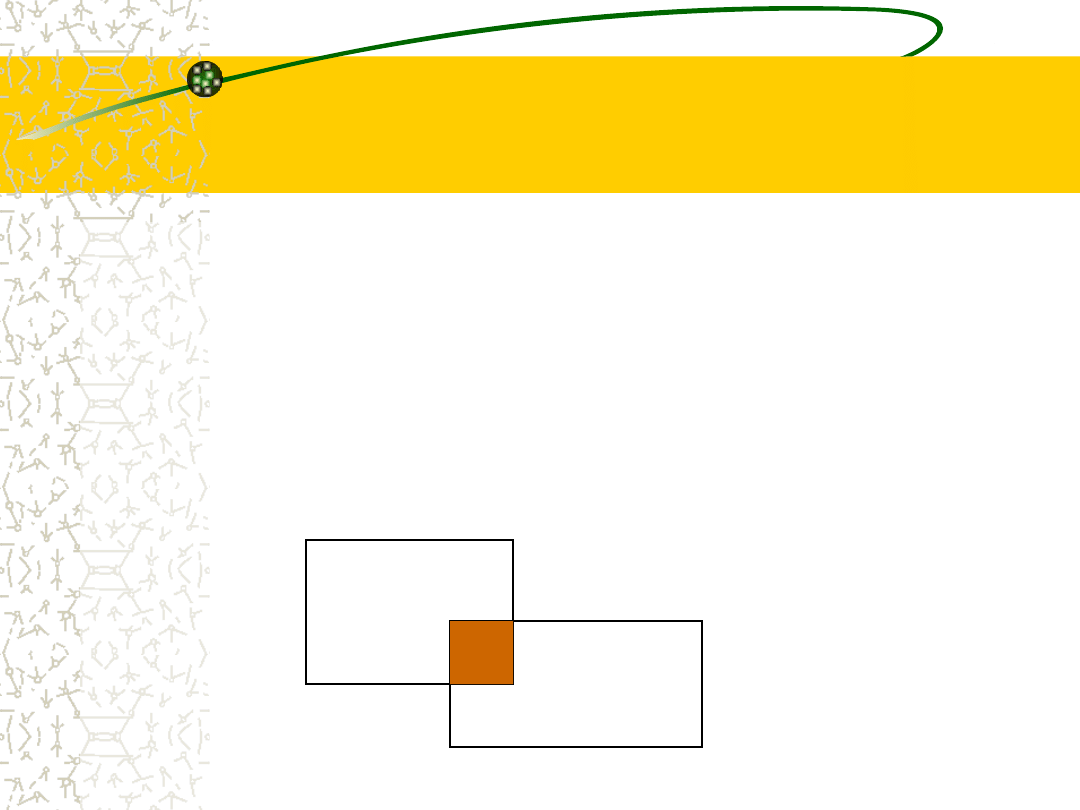
Iloczyn

Iloczynem (częścią wspólną) zbiorów

nazywamy zbiór, którego wszystkie
elementy jednocześnie należą do
obu zbiorów.

Ozn. AB

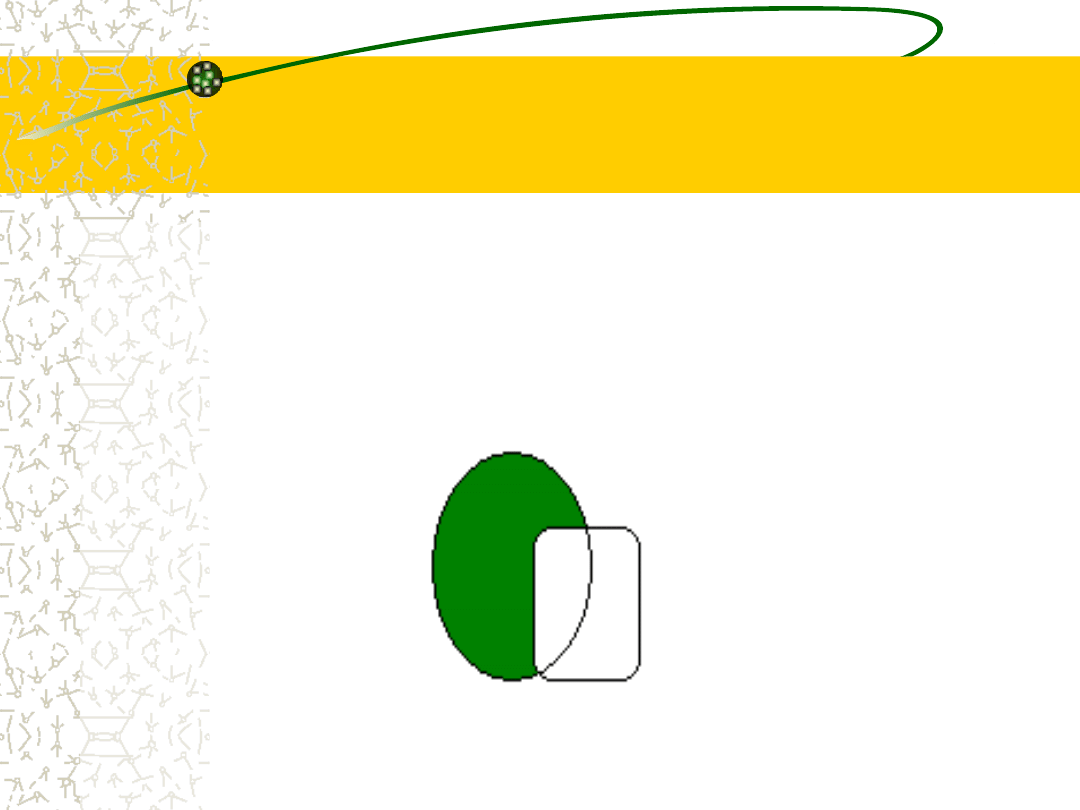
Różnica

Różnicą zbiorów A i B nazywamy zbiór

utworzony z tych elementów zbioru A,
które nie należą do zbioru B.

ozn. A\B

A
B