Modelowanie równań

strukturalnych

Wykład 13

• Modelowanie strukturalne służy do analizy

struktury oraz siły liniowych zależności pomiędzy
badanymi zjawiskami.

• Punktem wyjścia dla modelowania strukturalnego

powinna być zawsze teoria, dotycząca badanego
zjawiska. To właśnie teoria stanowi podstawę do
określenia zmiennych uwzględnianych w modelu
i ich wzajemnych zależności.

• Modelowanie strukturalne umożliwia analizę

zależności przyczynowo-skutkowych – tak jak
regresja, ale również zależności korelacyjnych.

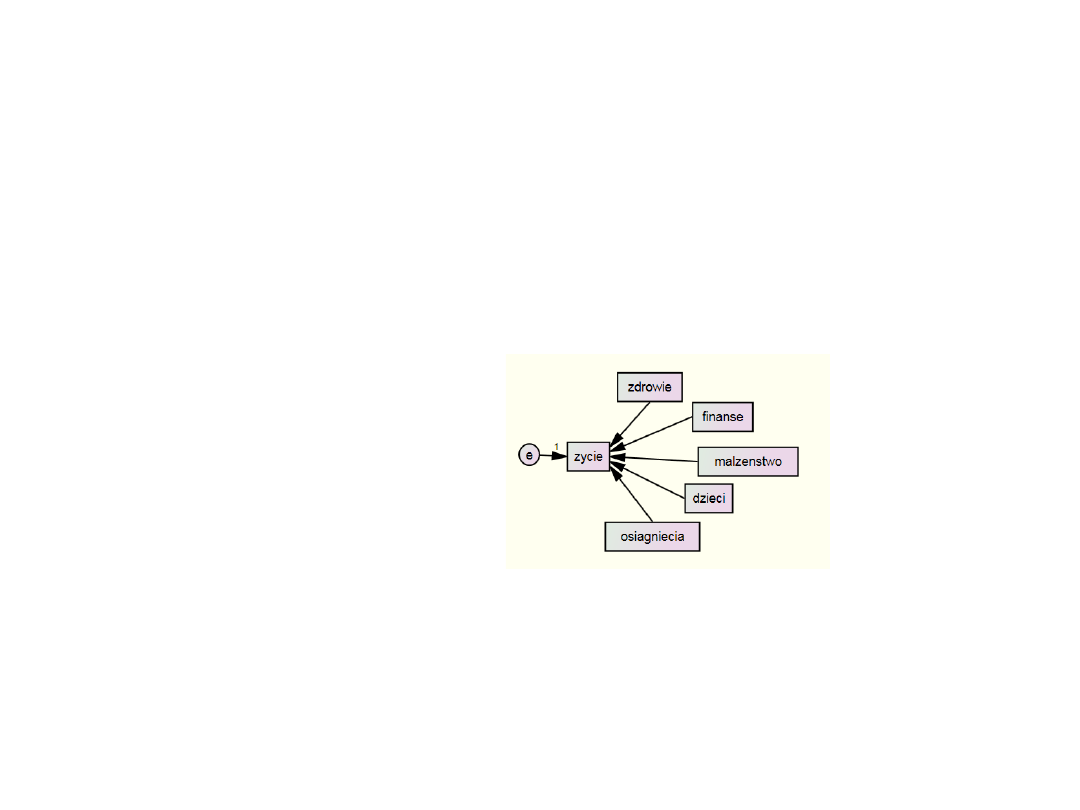
Model

Model to zestaw równań regresji oraz
korelacji pomiędzy zmiennymi. Może być
prezentowany w postaci wzorów, albo za
pomocą schematu graficznego.

życie =

1

zdrowie + 

2

finanse +



3

małżeństwo + 

4

dzieci + 

5

osiągnięcia + e.

Zmienne w modelowaniu

strukturalnym

• Zmienne występujące w modelach strukturalnych można

podzielić na obserwowalne i nieobserwowalne. Zmienne
obserwowalne to te, które znajdują się w zbiorze danych.
Wśród zmiennych nieobserwowalnych można wyróżnić
składniki losowe (reszty), opisujące tę część zmienności
modelowanych zjawisk, której nie wyjaśniają inne zmienne
modelu. Pozostałe zmienne nieobserwowalne to zmienne
opisujące badane zjawiska, które ze względu na swą naturę
wymagają bardziej złożonego pomiaru. Większość
zmiennych stosowanych w naukach społecznych ma taki
właśnie charakter.

• W modelach graficznych zmienne obserwowalne

umieszczane są w prostokątach a nieobserwowalne w
kółkach

Relacje w modelowaniu

strukturalnym

•

Korelacje i kowariancje

•

Kowariancja to miara powiązania zmiennych ale
nie pokazująca siły powiązania, obliczona dla
danych niestandaryzowanych

•

Korelacja to miara powiązania zmiennych
pokazująca zarówno kierunek jak i siłę
powiązania, gdyż jest obliczona dla danych
standaryzowanych

•

Korelacje w modelach graficznych przedstawiane
są w postaci strzałek jednokierunkowych a
kowariancje w postaci strzałek dwukierunkowych

Kroki modelowania

• Specyfikacja modelu – zapisanie modelu za pomocą równań

albo modelu graficznego

• Oszacowanie parametrów modelu (korelacji, kowariancji),

tak, by były jak najbardziej zbliżone do rzeczywistych
właściwości danych

• Określenie stopnia dopasowania modelu oszacowanego i

rzeczywistych korelacji – test chi kwadrat – zależy nam na
tym, y model oszacowany był jak najbardziej zbliżony do
rzeczywistego a więc zależy nam na tym, by te dwa modele
się nie różniły istotnie statystycznie

• Jeśli model jest dobrze dopasowany do danych to

interpretujemy uzyskane współczynniki (parametry) modelu

• Określenie stopnia dopasowania modelu

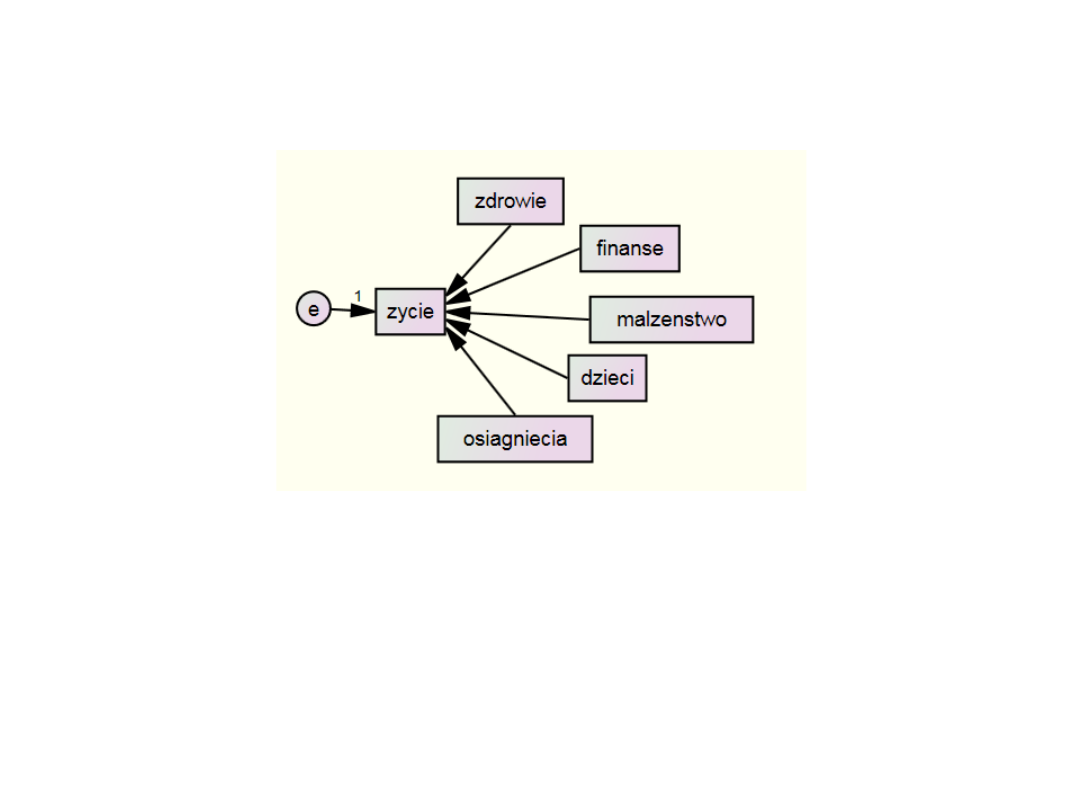
Regresja wielokrotna

Zmienną objaśnianą jest ocena całego życia, a pozostałe zmienne są
zmiennymi objaśniającymi. Strzałki odpowiadają współczynnikom
ścieżkowym – tutaj współczynnikom regresji β. Zmienna
nieobserwowalna, oznaczona elipsą i oznaczona literą e to składnik
losowy, czyli reszta regresji.
W modelu regresji przy składniku losowym ε nigdy nie stoi żaden
parametr – to tak, jakby stała przy nim liczba 1. Wobec tego w
modelu strukturalnym nad strzałką łączącą zmienne e i życie jest
liczba 1.

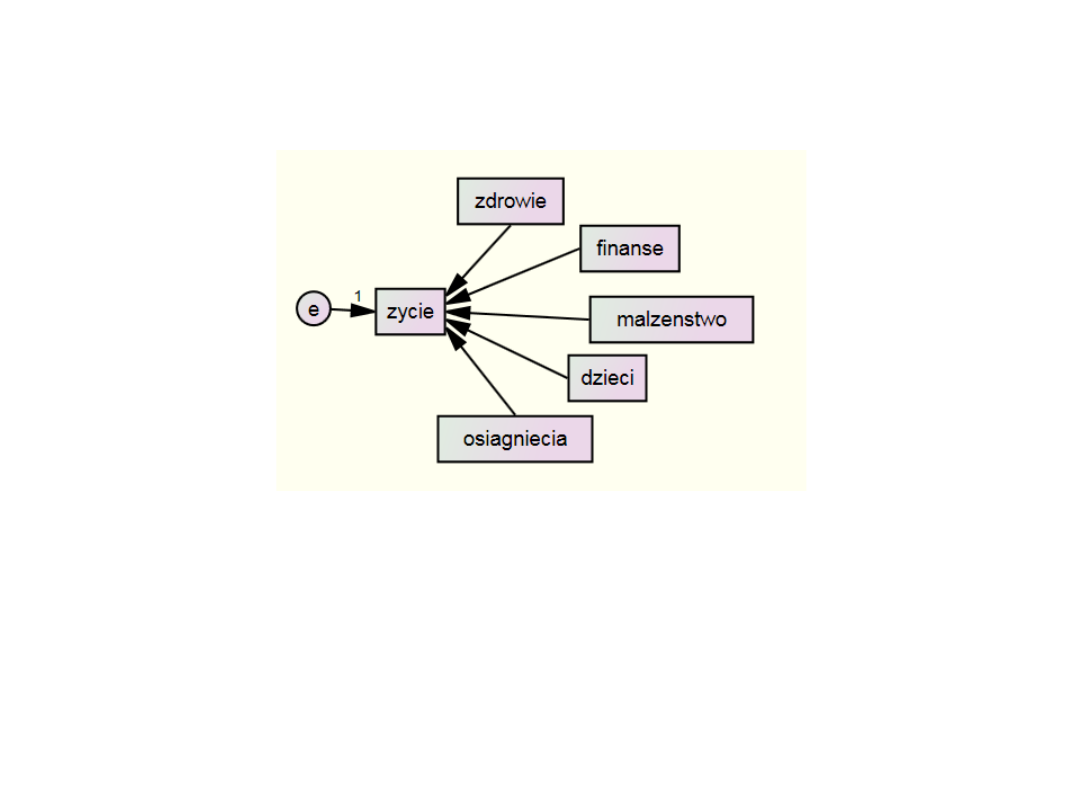
Regresja wielokrotna – nieskorelowane

predyktory

Bardzo ważne w modelowaniu jest także to, że jakieś zmienne nie są
połączone strzałkami. Jeśli zmienne nie są powiązane to zakładamy,
że korelacja między nimi jest równa 0. Tutaj zakładamy, że
predyktory oceny własnego życia są ze sobą nieskorelowane, bo nie
łączą ich żadne strzałki

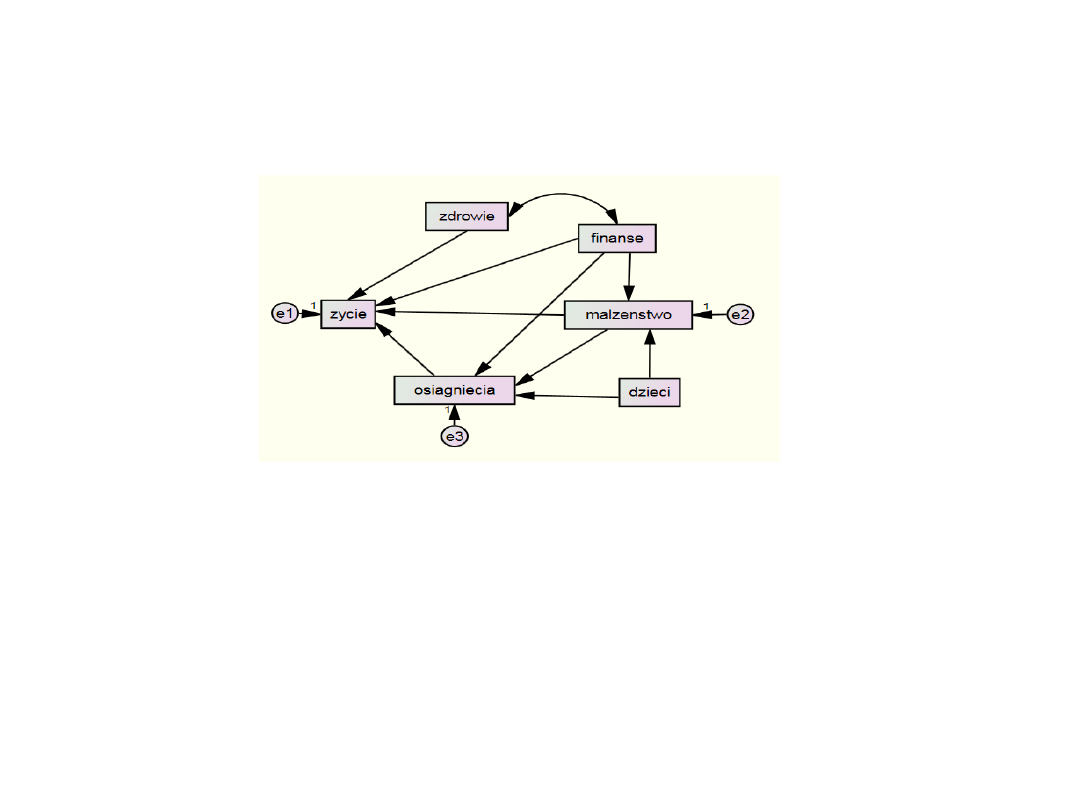
Regresja wielokrotna – skorelowane

predyktory

Ponieważ predyktory mogą być skorelowane możemy testować
alternatywny model zakładający powiązania miedzy predyktorami.
zadowolenie z życia jest objaśniane przez zadowolenie z osiągnięć,
małżeństwa, finansów i stanu własnego zdrowia, natomiast nie jest
objaśniane bezpośrednio przez zadowolenie z dzieci. Zadowolenie z
dzieci, podobnie jak zadowolenie z finansów wpływa jednak na
zadowolenie z własnych osiągnięć i małżeństwa. Zadowolenie z
finansów jest ponadto skorelowane z zadowoleniem ze stanu
własnego zdrowia.

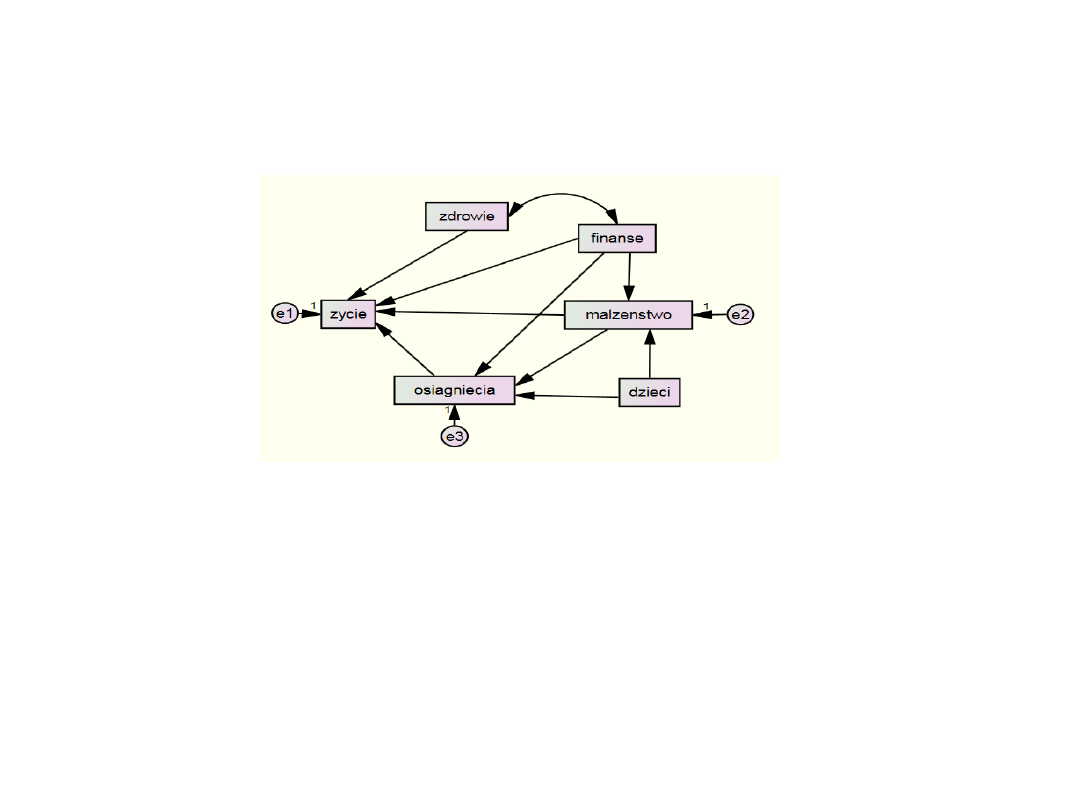
Regresja wielokrotna – skorelowane

predyktory

Podmodele:

• Predyktory zadowolenia z małżeństwa

• Predyktory osiągnięć

• Predyktory satysfakcji z życia
Każda zmienna objaśniana musi mieć swój składnik błędu
Szacowane są trzy równania regresji – rodzaj układu równań

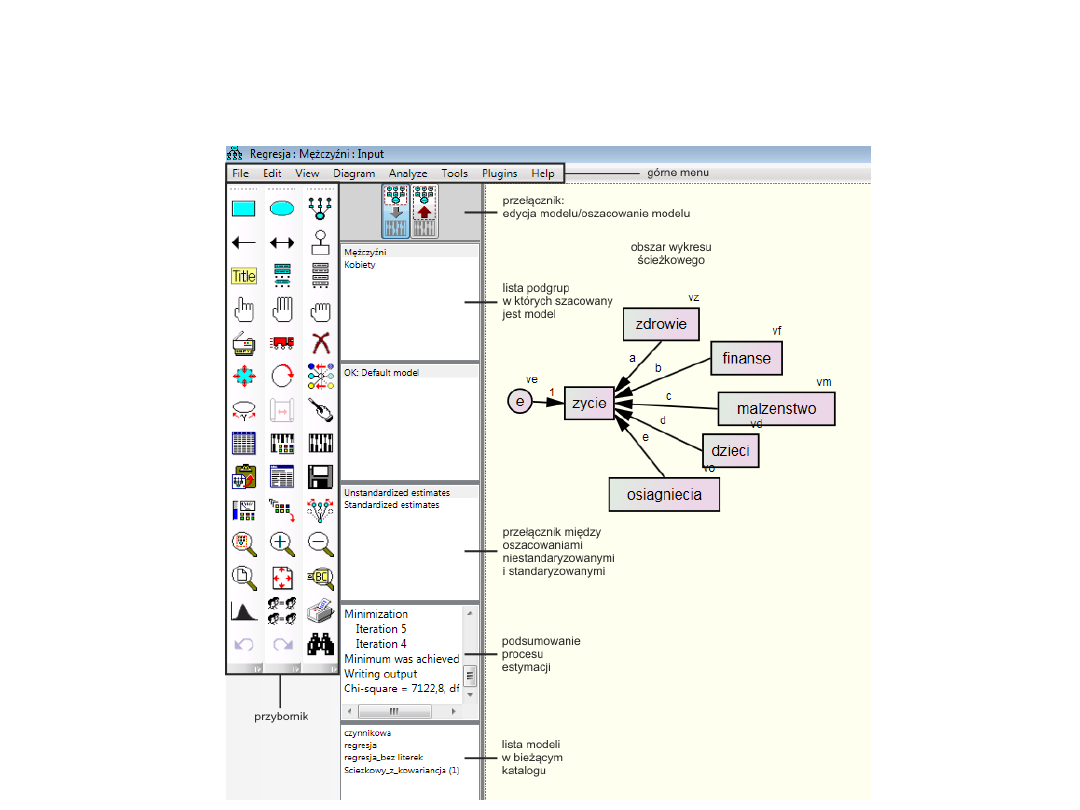
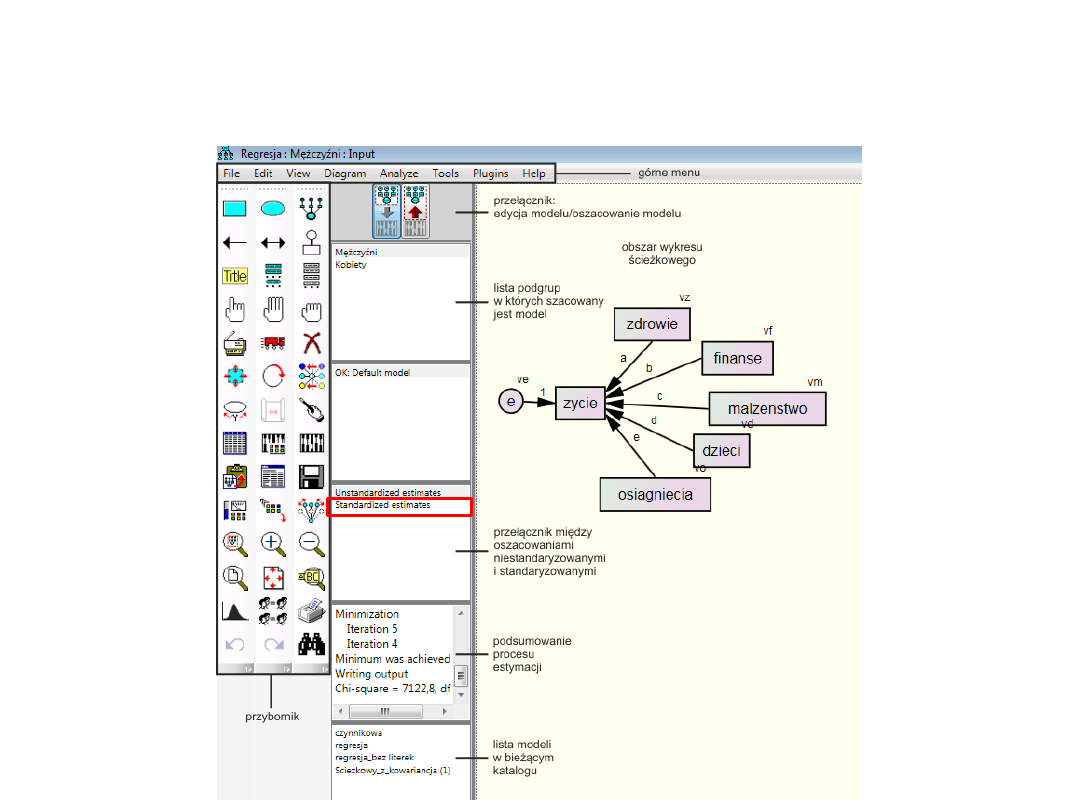
Modelowania w programie

AMOS

Przybornik

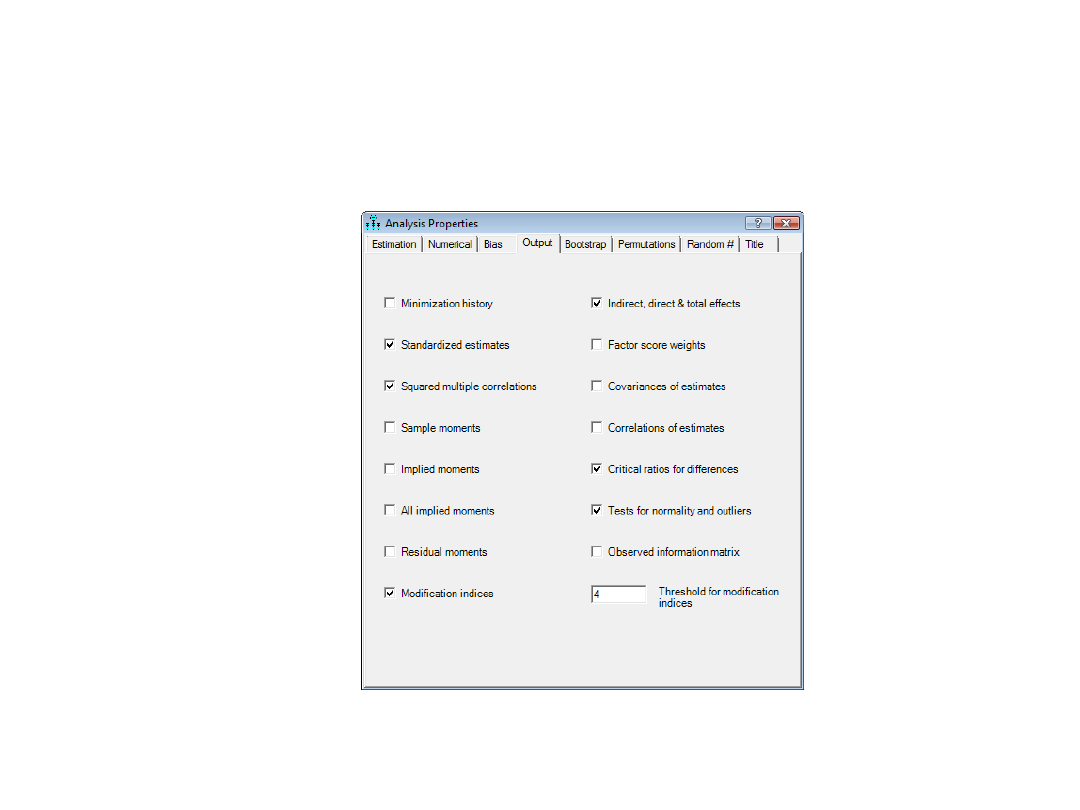
Definicja elementów

wydruku

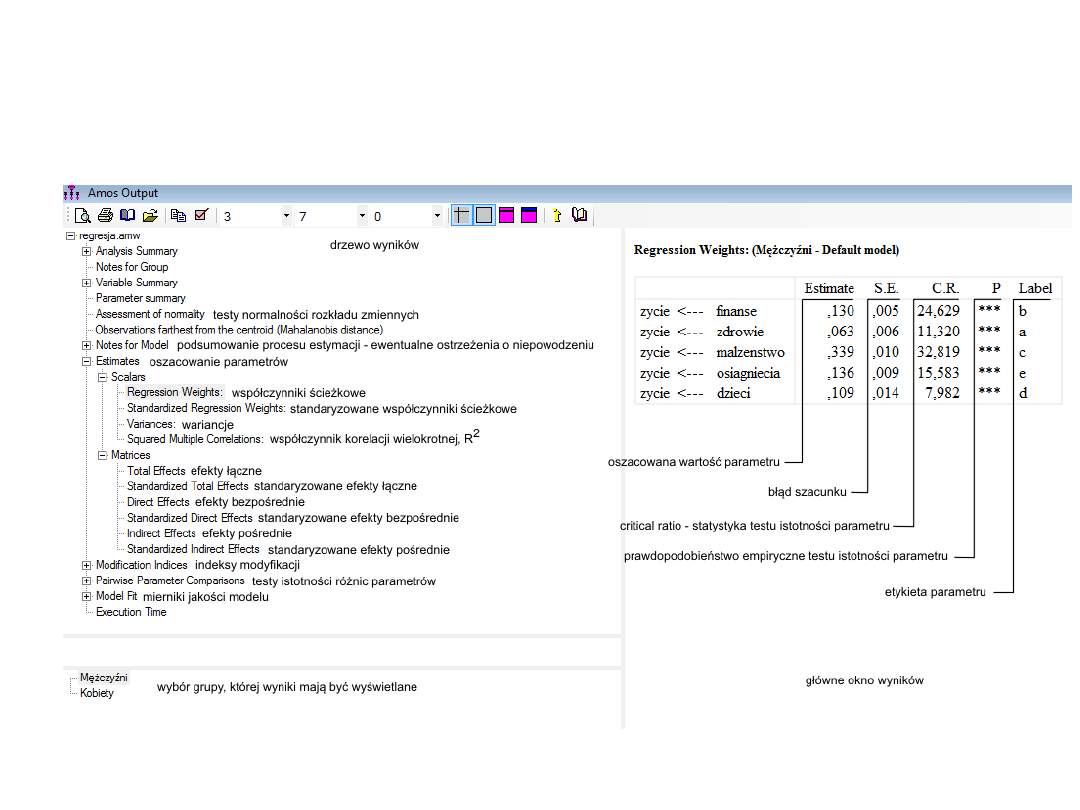
Składowe wydruku – wagi

regresji

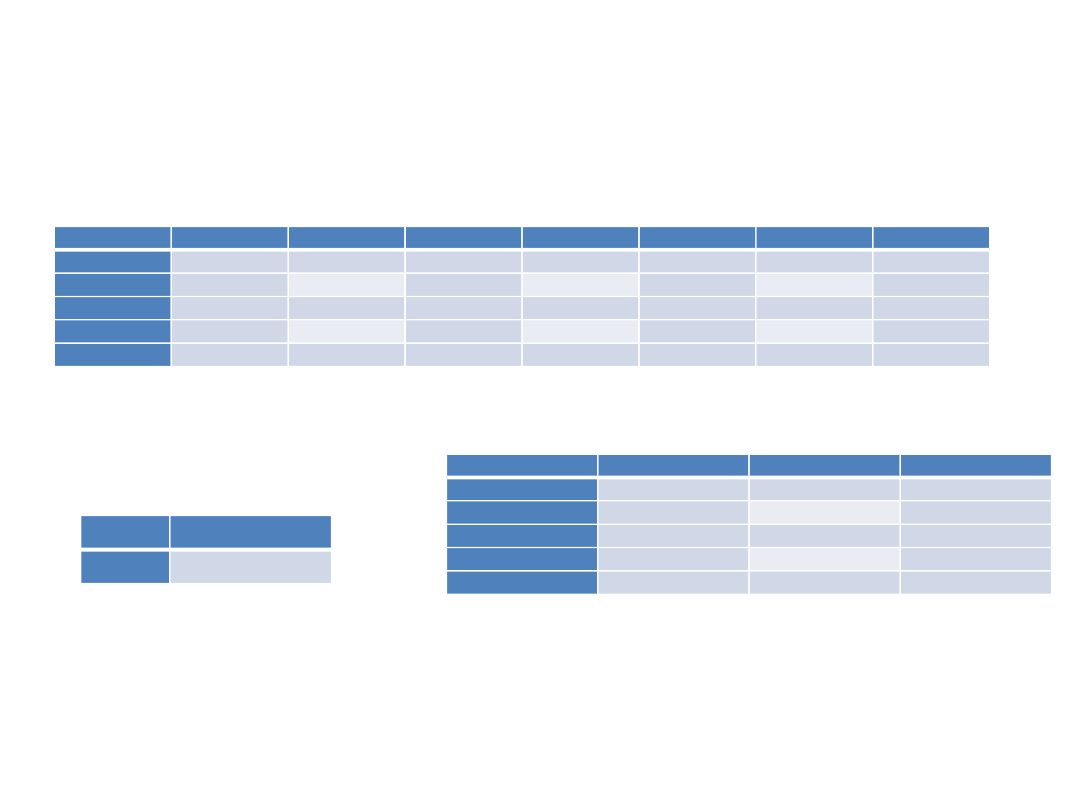
Parametry modelu

 

 

 

Estimate

S.E.

C.R.

P Label

zycie

<---

finanse

,128

,005

24,203

***  

zycie

<---

zdrowie

,058

,005

10,869

***  

zycie

<---

malzenstwo

,313

,007

46,749

***  

zycie

<---

osiagniecia

,143

,006

22,740

***  

zycie

<---

dzieci

,011

,008

1,323

,186  

 

 

 

Estimate

zycie

<---

finanse

,184

zycie

<---

zdrowie

,083

zycie

<---

malzenstwo

,356

zycie

<---

osiagniecia

,173

zycie

<---

dzieci

,010

Standardized Regression Weights: współczynniki beta

Regression Weights: współczynniki b (Estimate) i ich poziomy istotności (P),
S.E. – błąd standardowy,

 

Estimate

zycie

,197

Squared Multiple Correlations: R kwadrat

Współczynniki na modelu

ścieżkowym

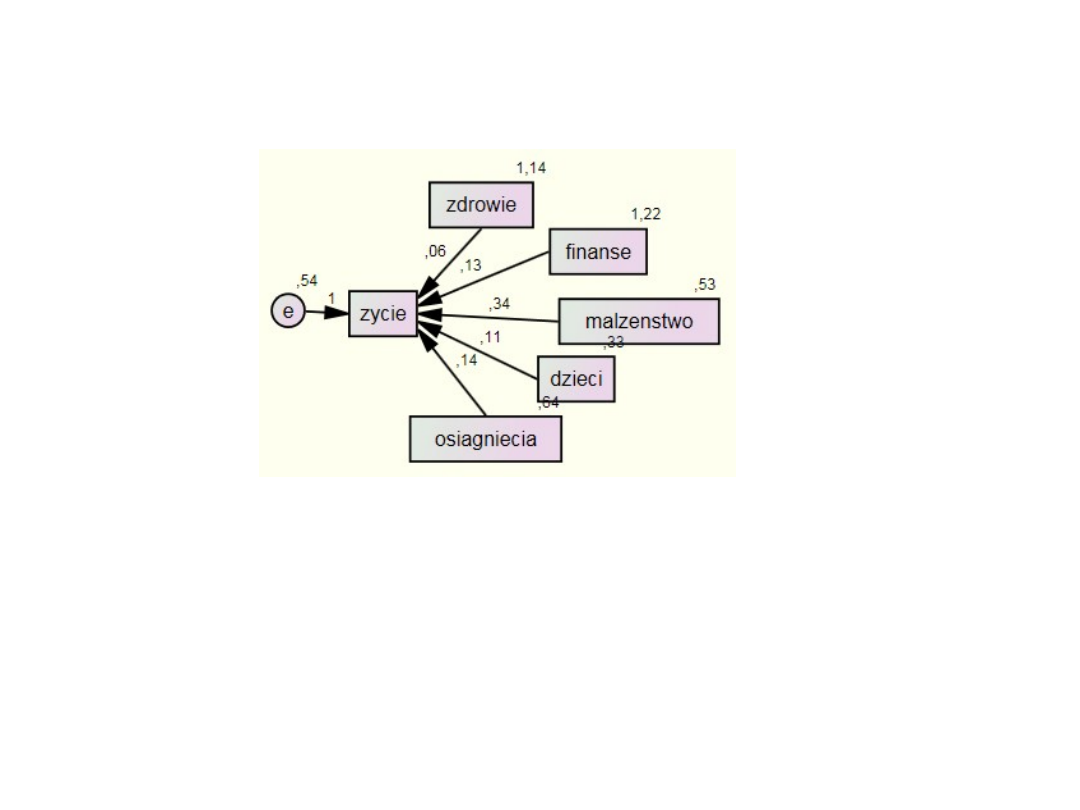
Parametry graficznie

• Na podstawie wartości współczynników standaryzowanych można

powiedzieć, że najważniejszą determinantą oceny całego życia jest
zadowolenie z małżeństwa. Prawie o połowę mniejsze znaczenie ma
zadowolenie z własnych osiągnięć i stanu finansów własnej rodziny, a
jeszcze mniej ważne jest zadowolenie ze stanu własnego zdrowia.
Zadowolenie ze wszystkich tych aspektów życia oddziałuje pozytywnie na
ocenę całego życia. Wpływ zadowolenia z dzieci na ocenę całego życia jest
nieistotny. Model wyjaśnia 20% zmienności satysfakcji z własnego życia.

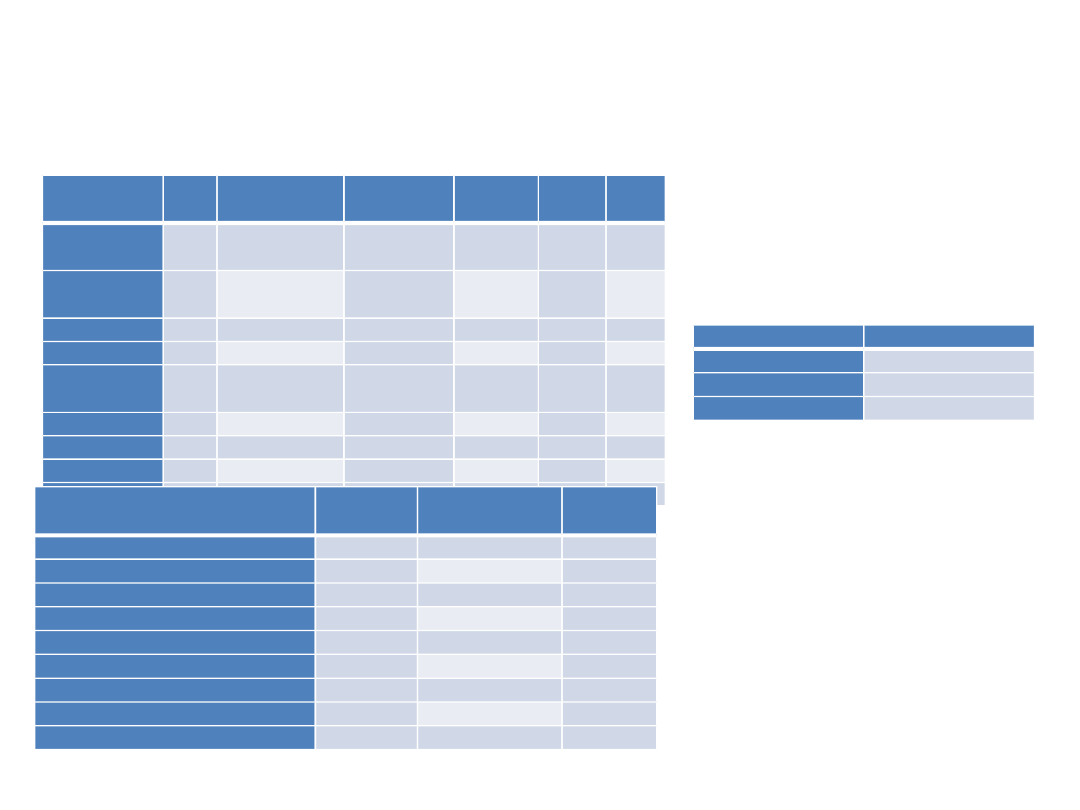
Model z powiązaniami między

predyktorami

 

 

 

Estimat

e

S.E.

C.R.

P

malzenstw
o

<--- dzieci

,590

,015 39,412

***

malzenstw
o

<--- finanse

,099

,007 14,523

***

osiagniecia

<--- finanse

,306

,008 39,864

***

osiagniecia

<--- malzenstwo

,154

,012 13,121

***

osiagniecia

<--- dzieci

,047

,014 3,236

,

001

zycie

<--- finanse

,127

,007 17,628

***

zycie

<--- zdrowie

,057

,007 8,034

***

zycie

<--- malzenstwo

,322

,009 34,729

***

zycie

<--- osiagniecia

,143

,010 14,789

***

Regression Weights:

 

 

 

Estima

te

malzenstwo

<---

dzieci

,469

malzenstwo

<---

finanse

,130

osiagniecia

<---

finanse

,392

osiagniecia

<---

malzenstwo

,149

osiagniecia

<---

dzieci

,036

zycie

<---

finanse

,176

zycie

<---

zdrowie

,074

zycie

<---

malzenstwo

,340

zycie

<---

osiagniecia

,155

Standardized Regression Weights:

 

Estimate

malzenstwo

,237

osiagniecia

,197

zycie

,250

Squared Multiple Correlations:

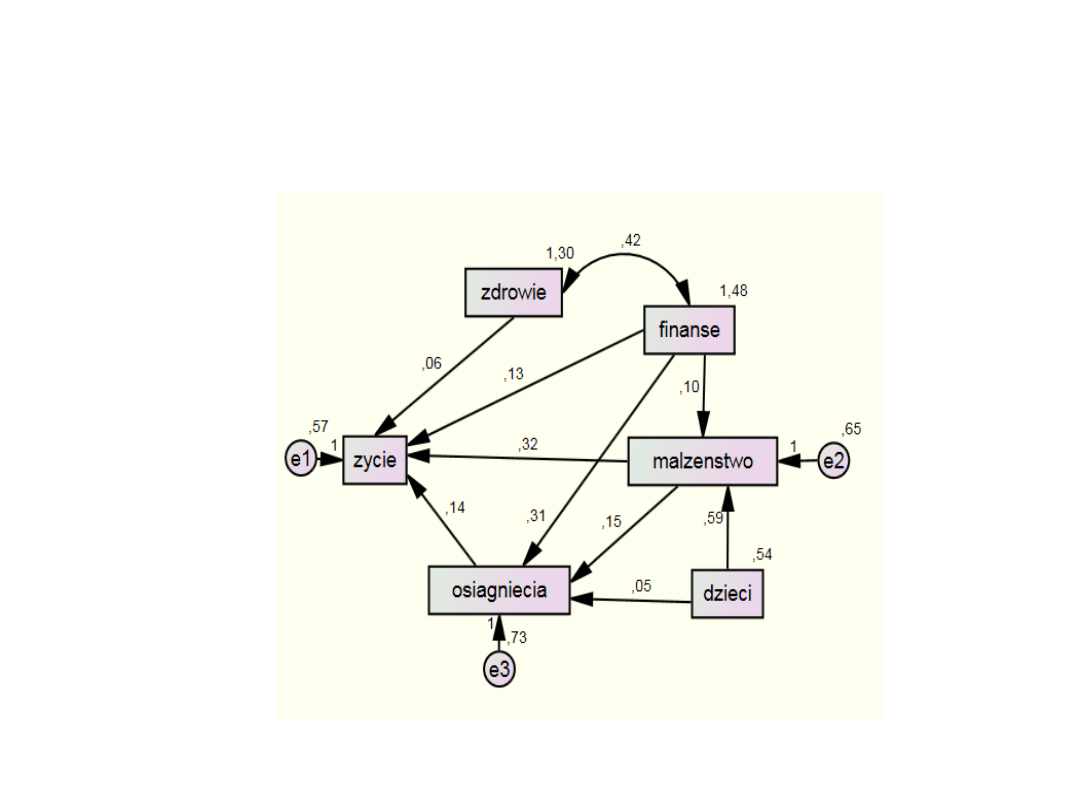
Model z powiązaniami między

predyktorami

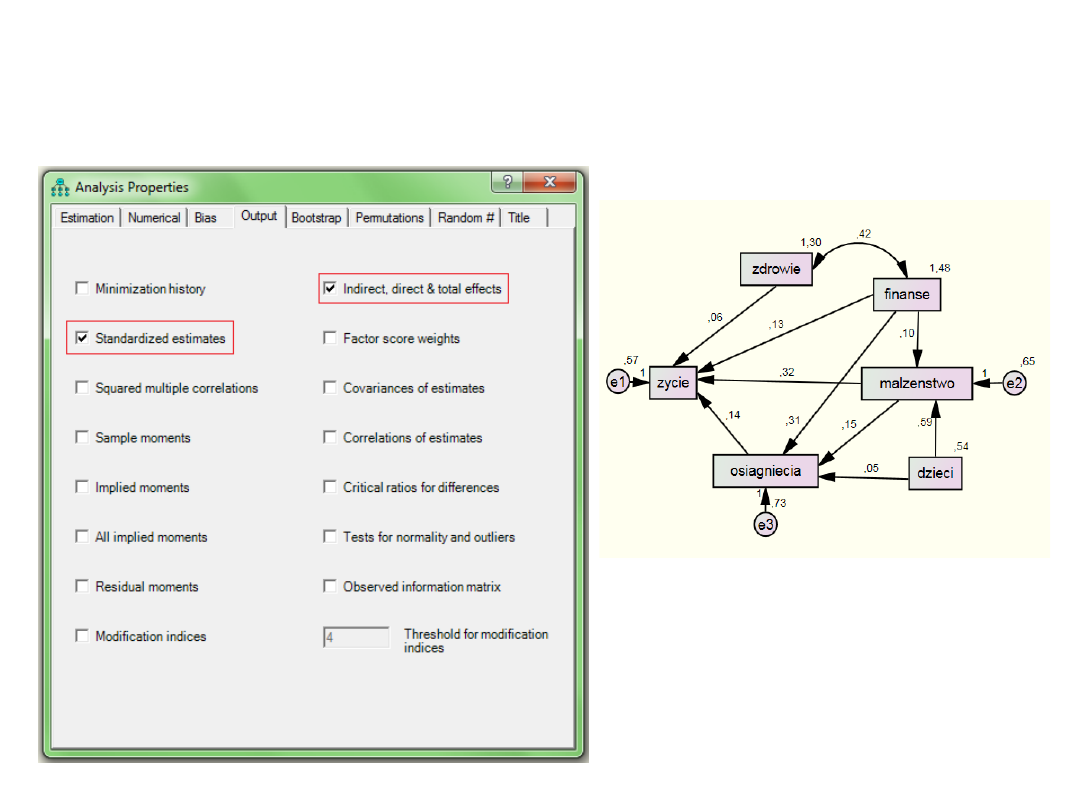
Efekty pośrednie i

bezpośrednie

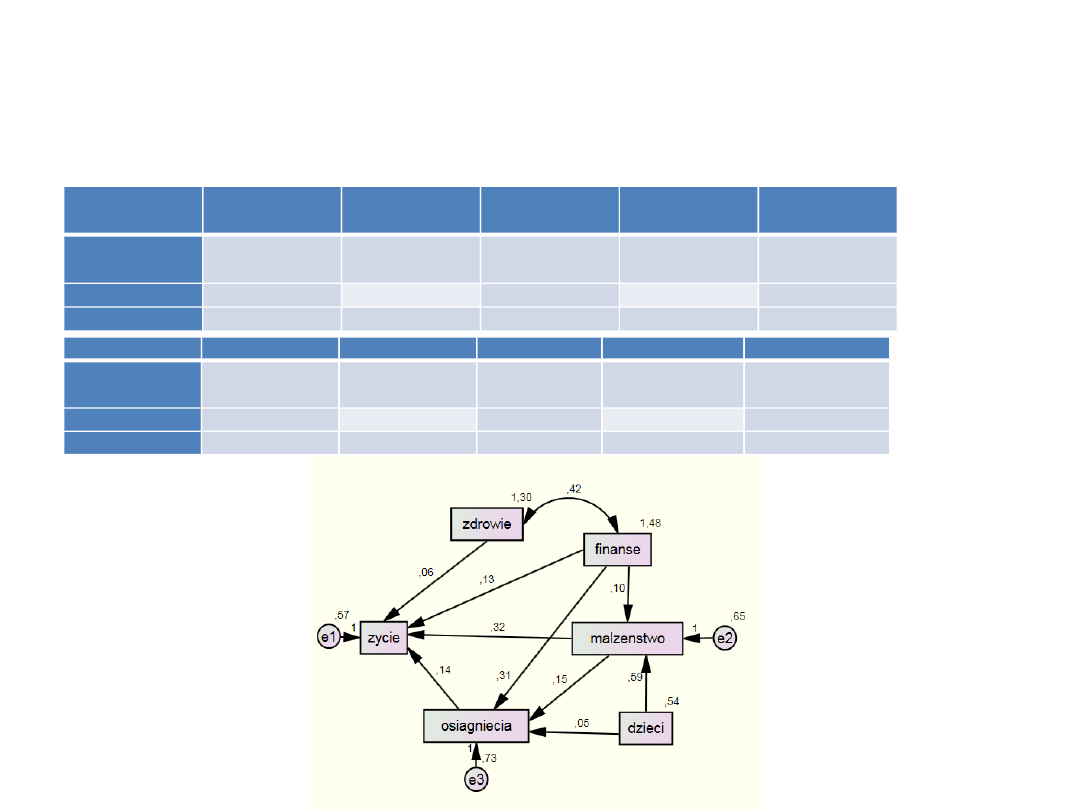
Efekty pośrednie i

bezpośrednie

 

dzieci

zdrowie

finanse

malzenstwo

osiagniecia

malzenstw
o

,000

,000

,000

,000

,000

osiagniecia

,070

,000

,019

,000

,000

zycie

,176

,000

,108

,023

,000

Standardized Indirect Effects

 

dzieci

zdrowie

finanse

malzenstw

o

osiagniecia

malzenstw
o

,469

,000

,130

,000

,000

osiagniecia

,036

,000

,392

,149

,000

zycie

,000

,074

,176

,340

,155

Standardized Direct Effects

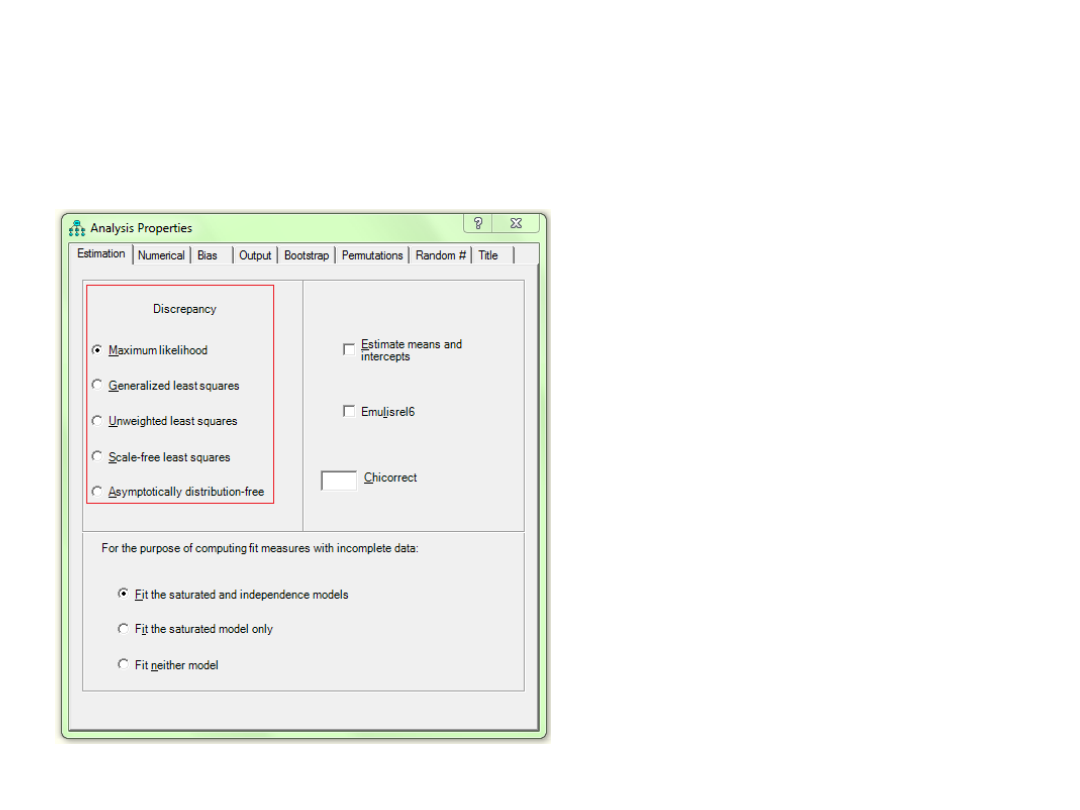
Metody modelowania

Najczęściej stosowana jest
Metoda Największej
Wiarygodności (Maximum
Likelihood, ML). Dopuszcza się jej
użycie, gdy rozkład odbiega od
normalnego, ale próba jest duża.
Metoda Uogólnionych
Najmniejszych Kwadratów
(Generalized Least Squares, GLS)
wymaga dużych prób, zakłada
wielowymiarowy rozkład normalny
zmiennych obserwowalnych. Gdy
próba powyżej 2500 obserwacji,
rozkłąd może odbiegać od
normalnego
Metoda Asymptotycznie Wolna
od Rozkładu (Asymptotically
Distribution-Free, ADF) nie
wymaga założenia
wielowymiarowego rozkładu
normalnego, stosowane tylko przy
dużych próbach.

Miary dopasowania

Mnogość miar dopasowania ale najczęściej stosowane to:
• CFI (comparative fit index) (szczególnie wrażliwa na błędy w

części pomiarowej modelu) - <0, 1> dobre dopasowanie CFI>
0,95

• RMSEA (Root Mean Squared Error of Approximation) dobre

dopasowanie RMSEA< 0,05

• GFI (Goodness of Fit Index) – analogiczny do R – kwadrat <0,

1> dobre dopasowanie GFI> 0,95

• NNFI (szczególnie wrażliwa na błędy w części pomiarowej

modelu) (nonnormed fit index) <0, 1> dobre dopasowanie
NNFI> 0,95– pochodna od NFI ale niezależna od liczby
zmiennych w modelu (jego złożoności)

• NFI (normed fit index) <0, 1> dobre dopasowanie NFI> 0,95–

wada im bardziej złożony model tym wyższa

Miary dopasowania - wydruk

Model

RMSEA

LO 90

HI 90

PCLOSE

Default
model

,168

,161

,174

,000

Independe
nce model

,279

,276

,283

,000

Model

NFI

Delta

1

RFI

rho1

IFI

Delta2

TLI

rho2

CFI

Default
model

,880

,640

,880

,640

,880

Saturated
model

1,000

 

1,000

 

1,000

Independen
ce model

,000

,000

,000

,000

,000

Odczytujemy miary z wiersza default model

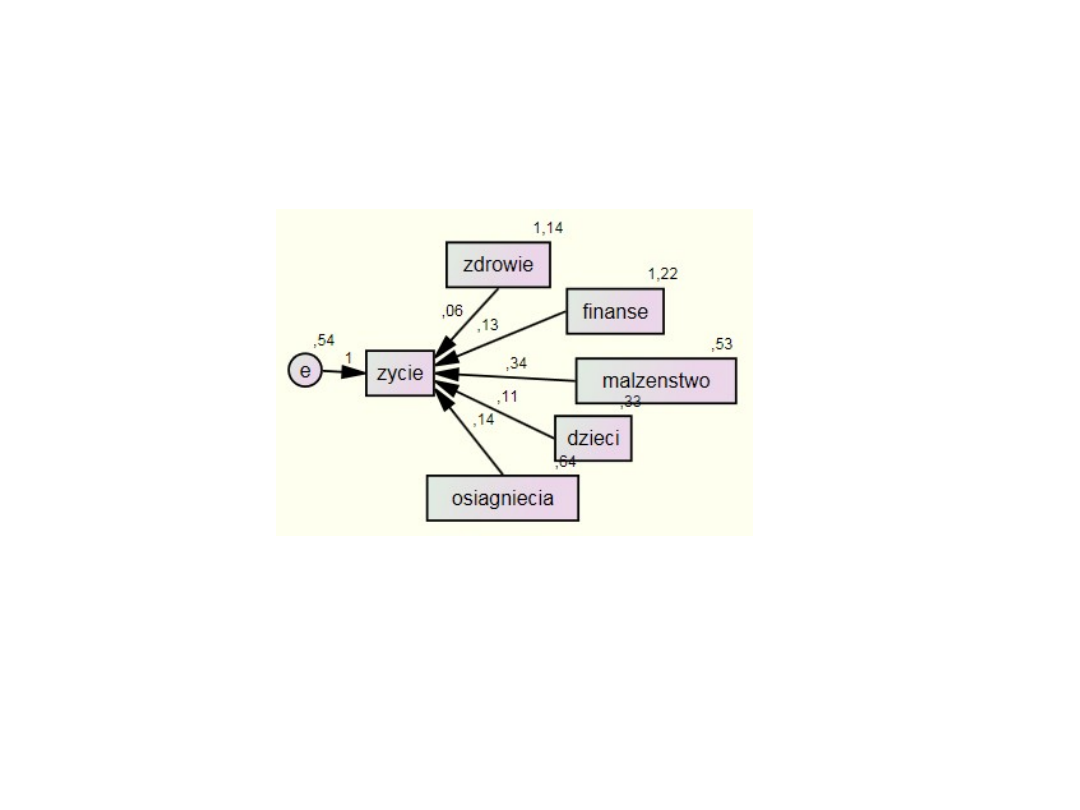
Modyfikowanie modelu

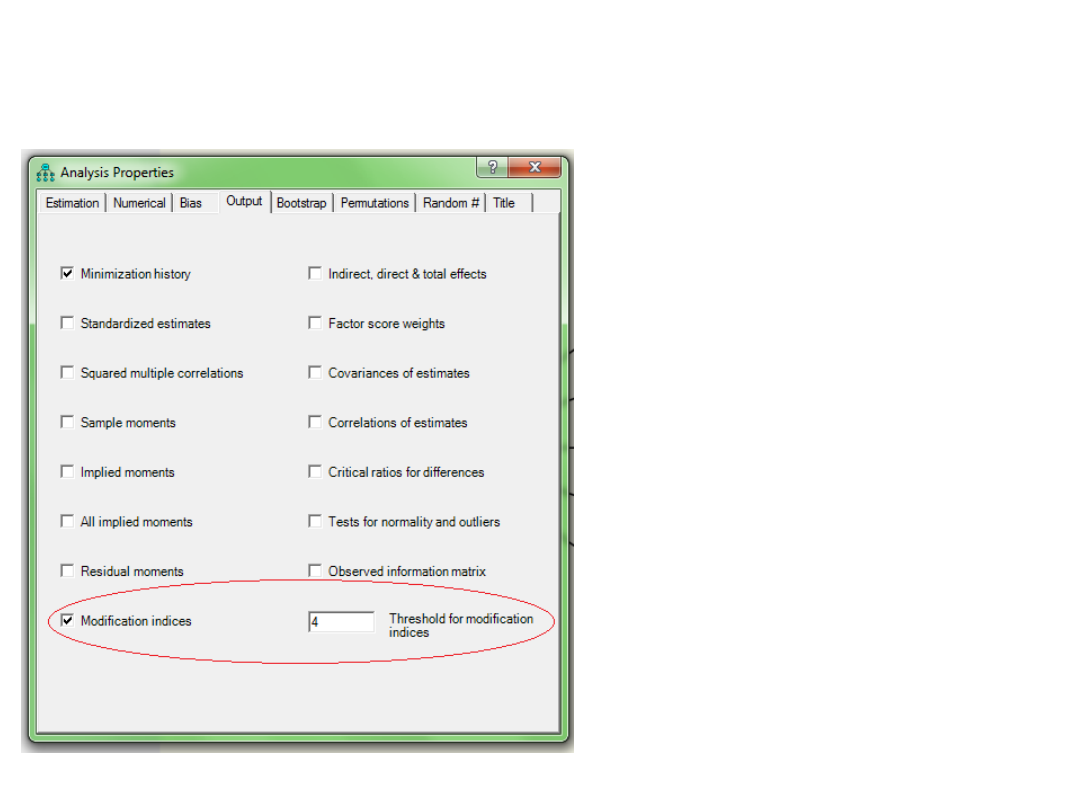
Modyfikowanie modelu

• Redukcja modelu -

Usunięcie
nieistotnych
ścieżek na
podstawie ich
poziomu istotności

• Rozbudowanie

modelu - Indeksy
modyfikacji – jakie
zależności warto
jeszcze uwzględnić

Informacja jakie kowariancje warto

wprowadzić

 

 

 

M.I.

Par

Change

osiagnieci
a

<-->

dzieci

778,483

,202

malzenst
wo

<-->

dzieci

3717,930

,415

malzenst
wo

<-->

osiagniecia 1250,317

,308

zdrowie

<-->

dzieci

473,832

,184

zdrowie

<-->

osiagniecia 2230,500

,512

zdrowie

<-->

malzenstw
o

522,008

,233

finanse

<-->

dzieci

364,008

,165

finanse

<-->

osiagniecia 2352,502

,537

finanse

<-->

malzenstw
o

627,009

,261

finanse

<-->

zdrowie

1331,647

,473

Covariances:

Par change informuje ile
wynosiłaby kowariancja
między dwiema
zmiennymi gdyby ją
dorysować.
Niestety nie ma
podpowiedzi, czy
zależność ta to tylko
korelacja czy zależność
kierunkowa
(przyczynowo-skutkowa).
Trzeba to sprawdzić
testując różne modele

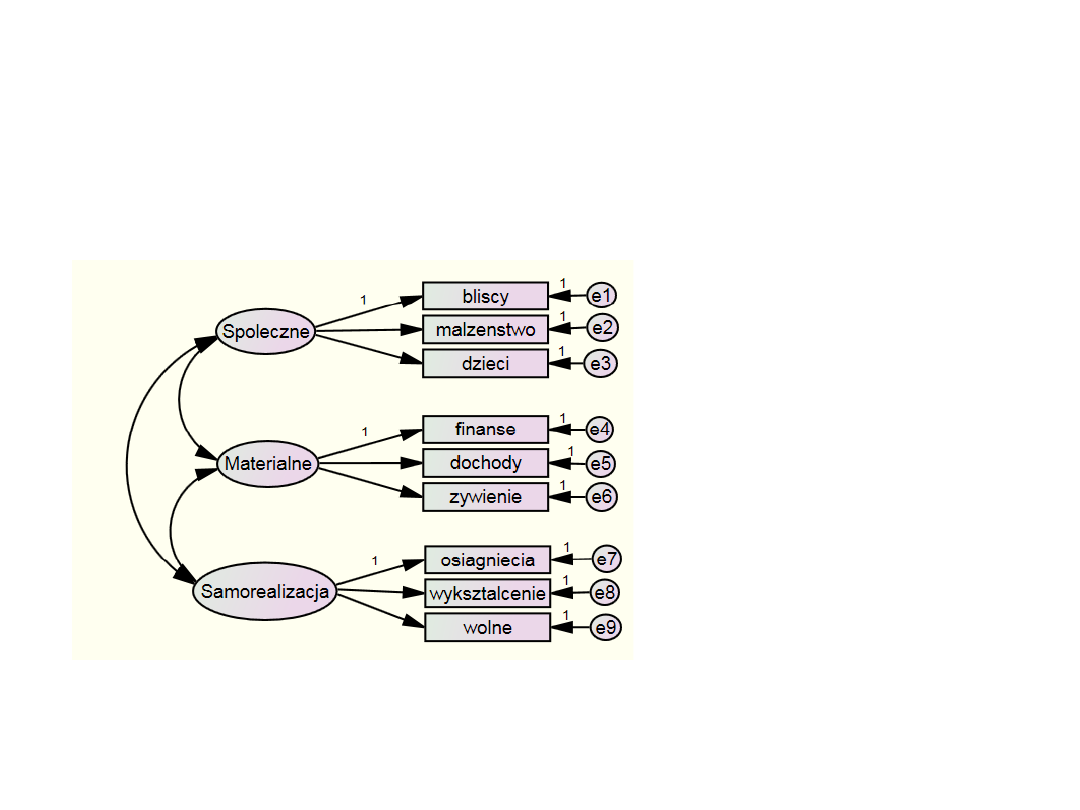
Zastosowania SEM – konfirmacyjna

analiza czynnikowa

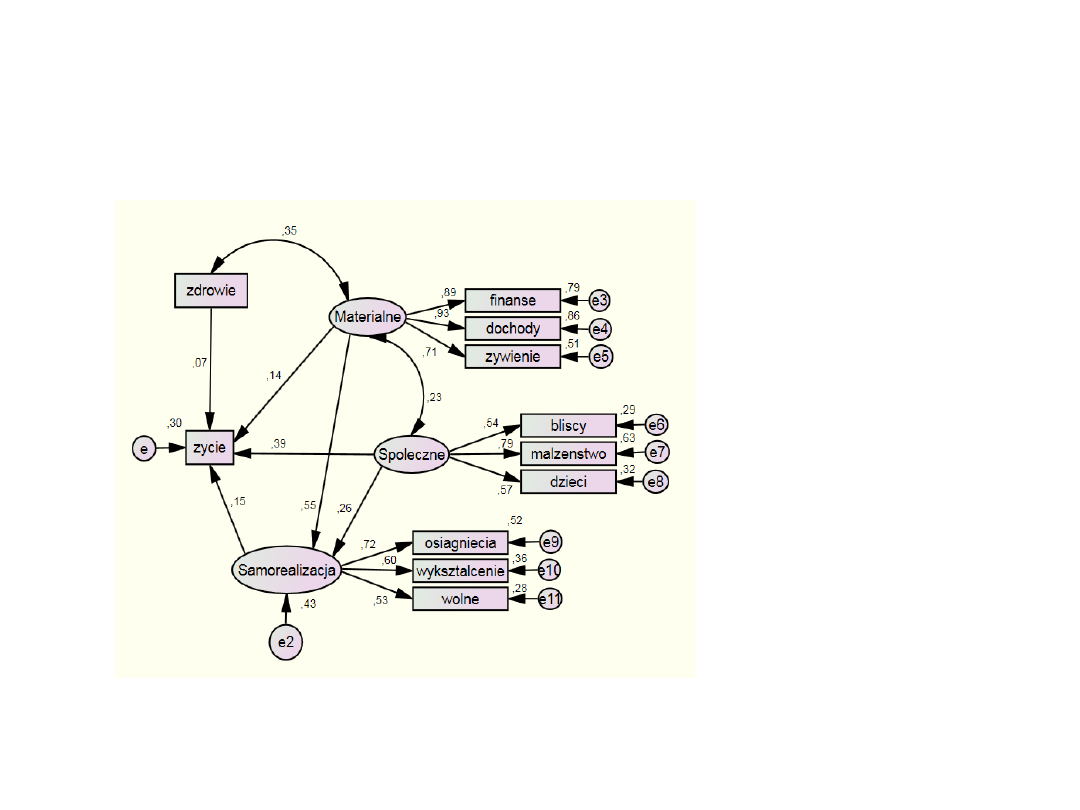
Model ścieżkowy +

czynnikowa

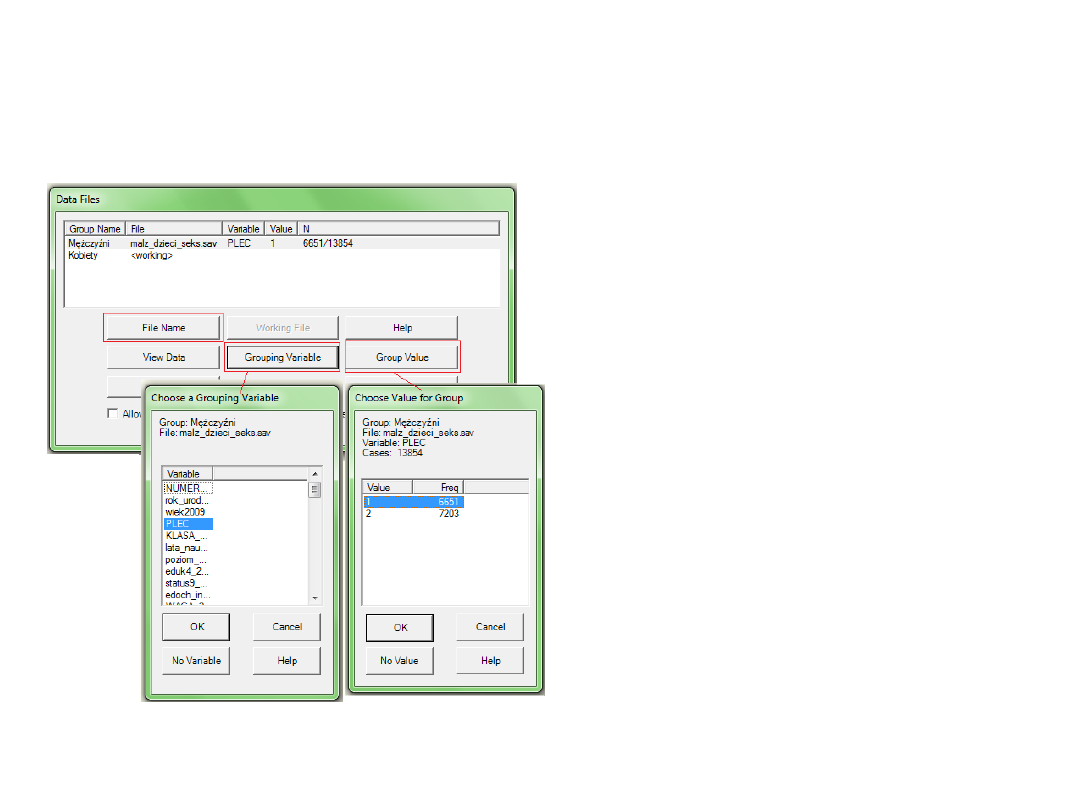
Zastosowania SEM – modelowanie w

podgrupach - interakcja