Wykład 9

*

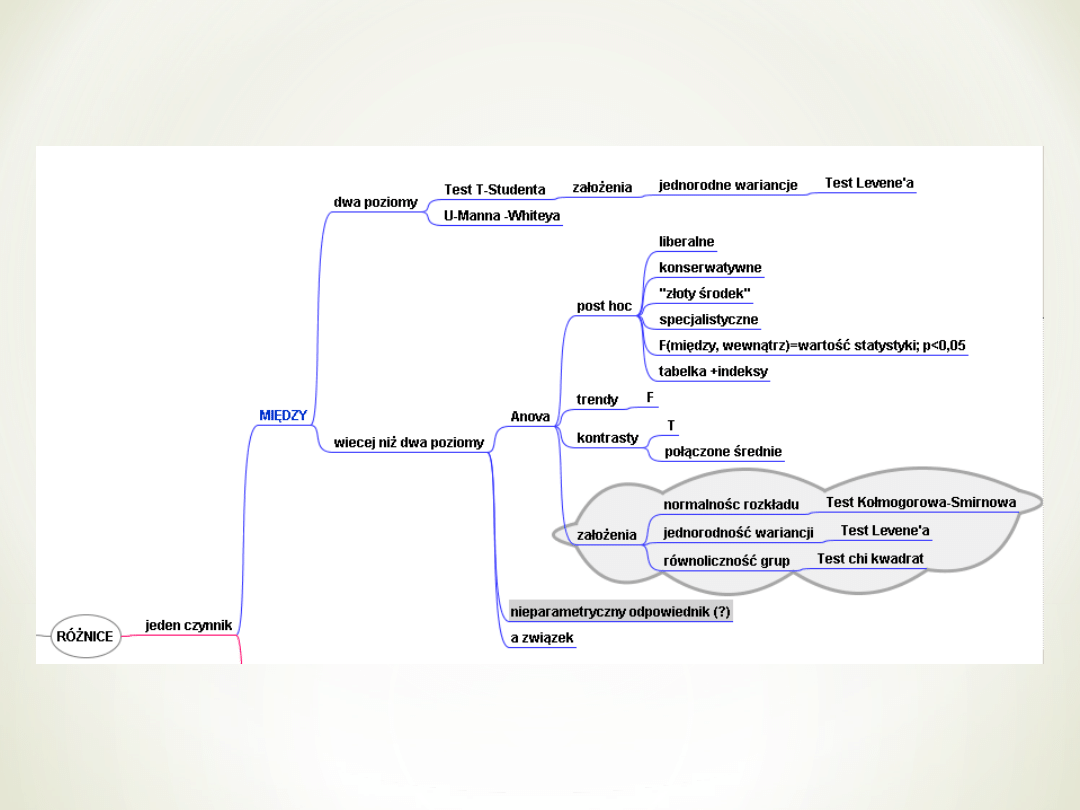
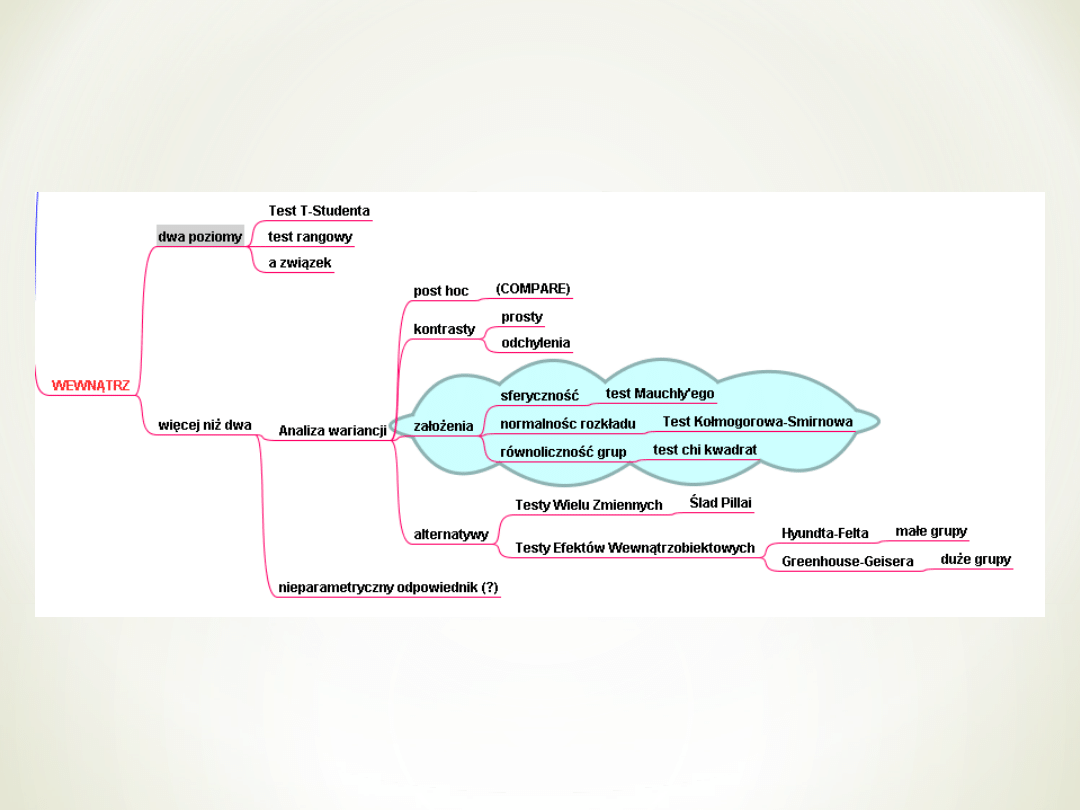
Dotychczas szukaliśmy różnic między
pewnymi grupami (zmienna niezależna
jakościowa)

*

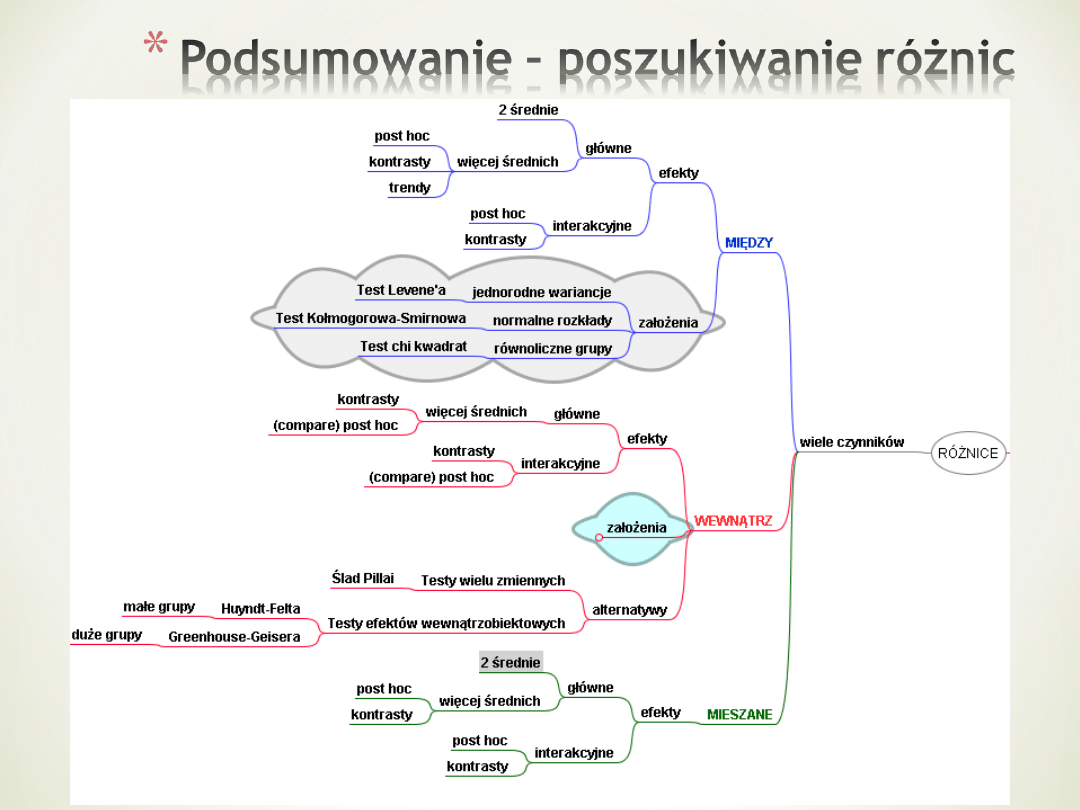
Podsumowanie – poszukiwanie różnic

*

Oprócz różnic chcemy także poszukiwanie
związku pomiędzy zmiennymi – metody
regresyjne

*

Zaczniemy od najprostszej postaci –
związek między dwiema zmiennymi
ilościowymi

*

Przewidywanie

*

Spojrzenie na średnie zarobki.

*

Dowiadujemy się, ile zarabiają przeciętnie Polacy i to jest wtedy przewidywana kwota jaką zarobimy.

*

Jeśli znamy predyktory zarobków np. poziom wykształcenia to możemy przewidzieć zarobki znając
średnią grupową.

*

Skoro osoby z wykształceniem średnim zarabiają przeciętnie 4400 złotych brutto to my też
powinniśmy

*

Jeśli mamy dwie zmienne ilościowe to
posługiwanie się średnią jest mało
dokładne.

*

Znacznie lepsze jest użycie do
przewidywania modelu uzyskanego w
wyniku analizy regresji

*

Pozwala na przewidywanie poziomu

jednej zmiennej na podstawie poziomu

drugiej zmiennej.

*

Nie ma sensu przeprowadzać prostej

analizy regresji, kiedy nie ma korelacji

między zmiennymi

*

Im silniejsza korelacja między zmiennymi,

tym lepsza możliwość przewidywania

*

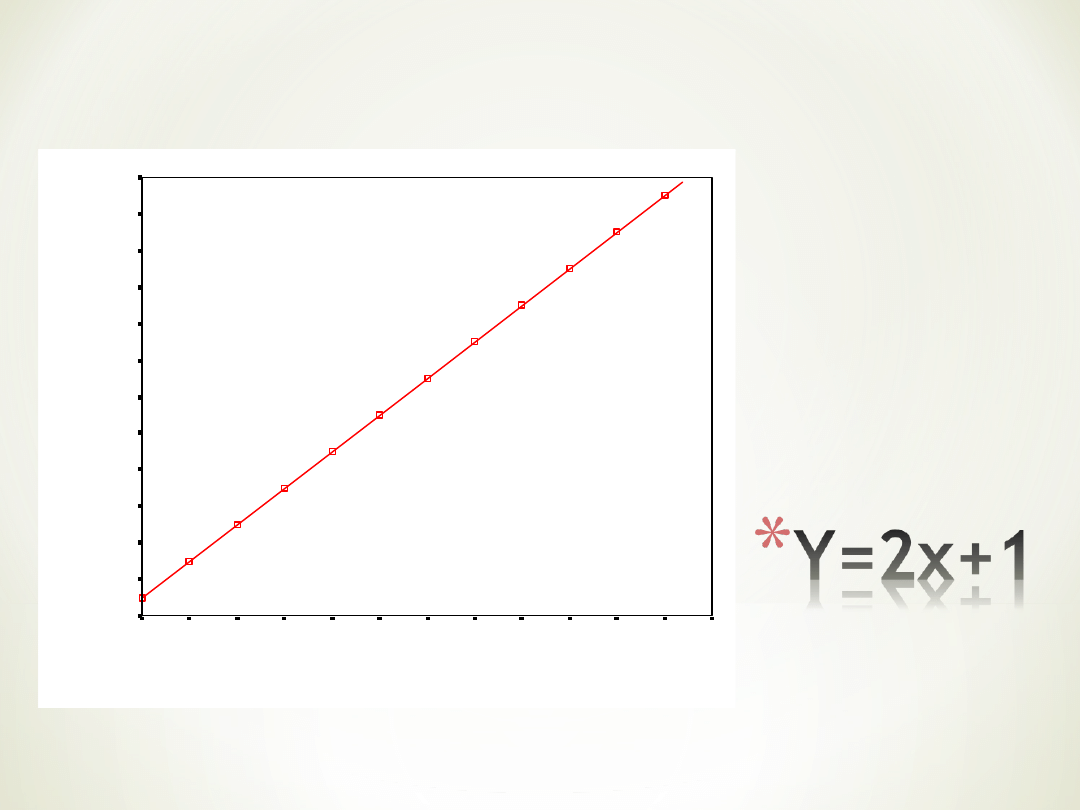
Analiza regresji prostoliniowej –

posługujemy się do przewidywania

matematycznym modelem linii prostej

stala

nachylenia

ˆ

B

X

B

Y





stala

nachylenia

ˆ

A

X

B

Y





X

12

11

10

9

8

7

6

5

4

3

2

1

0

Y

24

22

20

18

16

14

12

10

8

6

4

2
0

*

Jak wzrasta
wartość X o 1,
wartość Y
wzrasta o 2

*

Idealna
predykcja, w
większości
przypadków
mamy do
czynienia z
błędem predykcji

*

Pytanie badawcze: Czy wielkość

stresu kierownika jest

powiązana z liczbą podległych

mu pracowników?

*

Obie zmienne ilościowe

*

Pytanie badawcze o związek

między zmiennymi

*

Uznajemy, że zależność ta jest

proporcjonalna więc linia prosta

będzie dobrym modelem ją

opisującym.

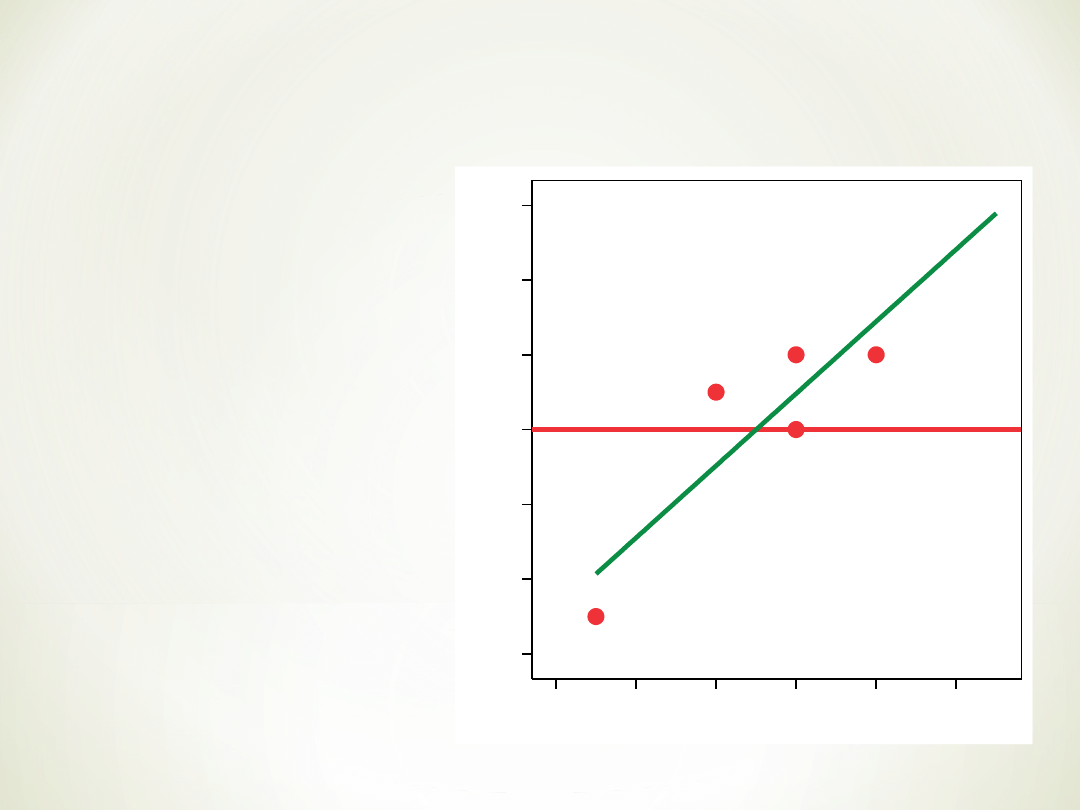
Aby opisać dane
posługujemy się
modelem linii prostej.

Szukamy takiej linii,
której odległość od
wszystkich wyników
jest minimalna.
Określamy to za
pomocą Metody
Najmniejszych
Kwadratów
odległości punktów
od linii.

2,00

4,00

6,00

8,00

10,00

12,00

os X - liczba pracowników

0,00

2,00

4,00

6,00

8,00

10,00

12,00

o

s

Y

-

p

o

zi

o

m

s

tr

es

u

R kwadrat dla Liniowej

= 0,766

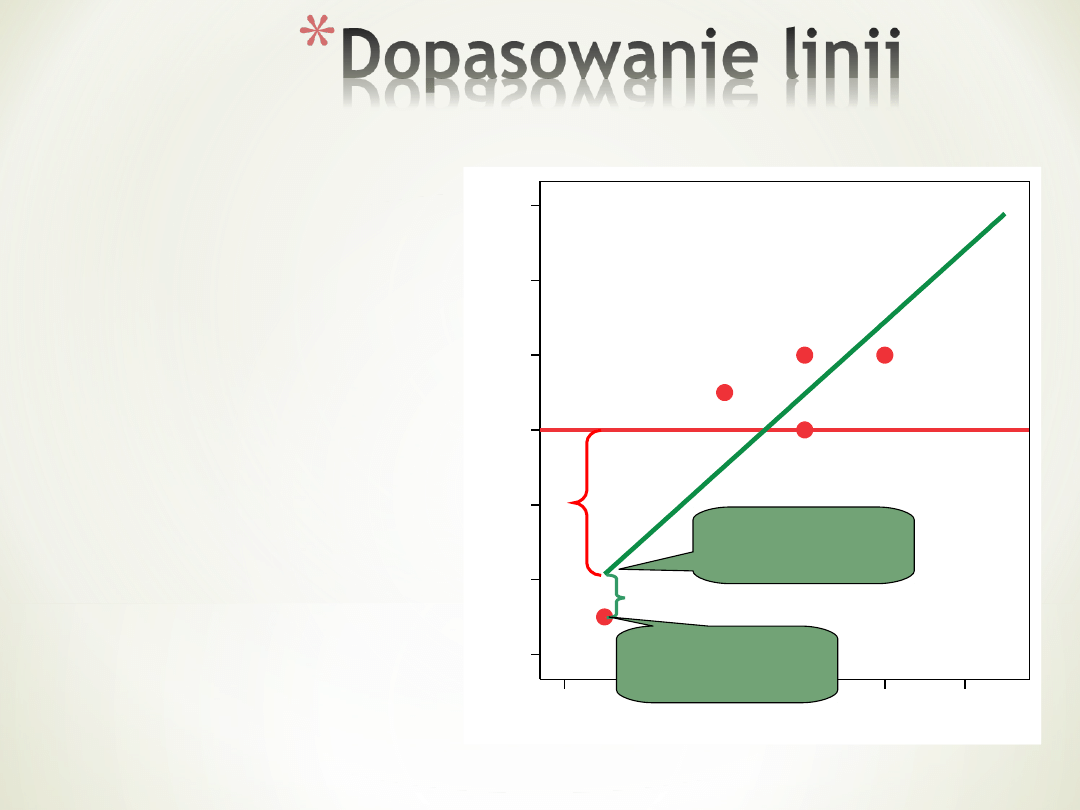
Porównanie
kwadratów odległości
punktów od

linii regresji

oraz

odległości punktu
przewidywanego od
średniej

2,00

4,00

6,00

8,00

10,00

12,00

os X - liczba pracowników

0,00

2,00

4,00

6,00

8,00

10,00

12,00

o

s

Y

-

p

o

zi

o

m

s

tr

es

u

R kwadrat dla Liniowej

= 0,766

.

Wyniki

rzeczywisty

Wyniki

przewidywan

y

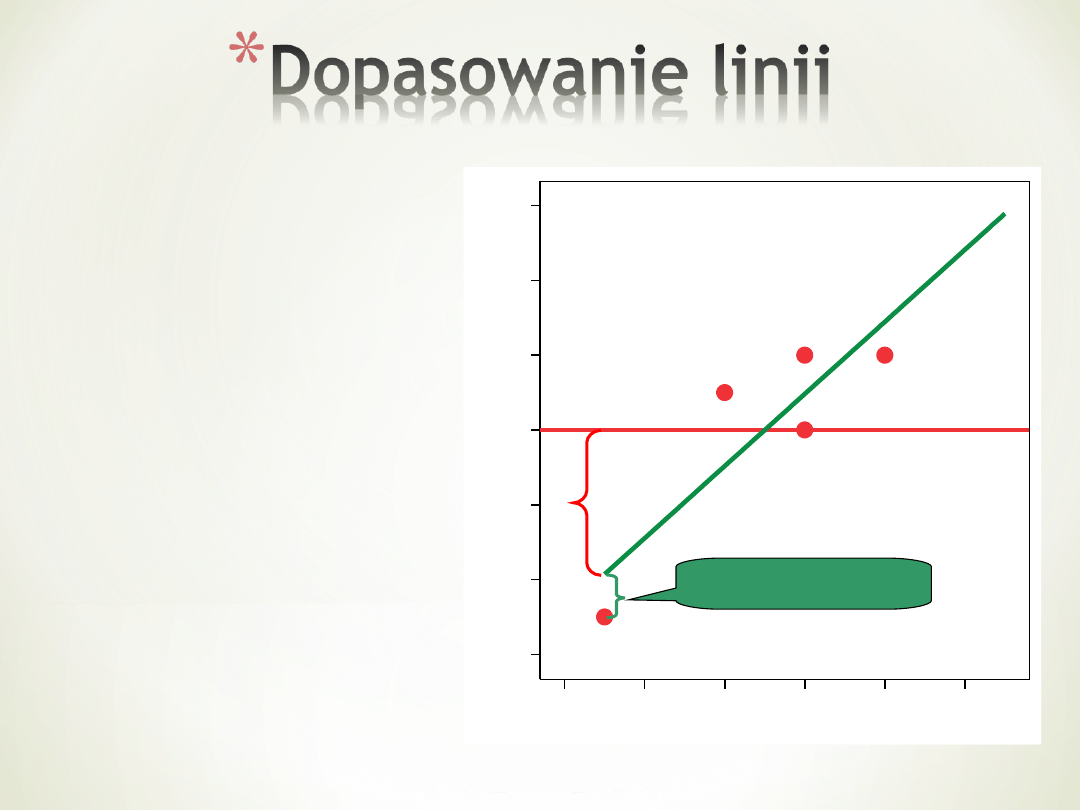
Kwadraty odległości
punktów to………

Jaka statystyka?

2,00

4,00

6,00

8,00

10,00

12,00

os X - liczba pracowników

0,00

2,00

4,00

6,00

8,00

10,00

12,00

o

s

Y

-

p

o

zi

o

m

s

tr

es

u

R kwadrat dla Liniowej

= 0,766

Reszta regresji

Aby sprawdzić, czy
linia regresji jest
dobrym modelem
wykonywana jest

analiza wariancji

porównująca średni
kwadrat regresji (to
co regresja wyjaśnia)
w stosunku do
średniego kwadratu
reszt (to czego
regresja nie
wyjaśnia)

*

Istotna analiza wariancji informuje nas, że

odległości przewidywanych wyników są większe
w porównaniu do reszt.

*

A tak po ludzku?

Analiza wariancji

b

26,036

1

26,036

9,807

,049

a

7,964

3

2,655

34,000

4

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), pracow

a.

Zmienna zależna: stres

b.

*

Wzór linii (dla danych surowych):

stres=0,964*liczba pracowników - 0,75
Na podstawie tego wzoru możemy przewidywać poziom stresu

innych kierowników

Na przykład – jeśli kierownik ma 40 podwładnych to zgodnie ze

wzorem 0,964*50-0,75=47,45

Oznacza to, że przewidywany poziom stresu powinien osiągnąć

około 47 punktów w kwestionariuszu. Nie musimy więc już go

mierzyć 

Współczynniki

a

-,750

2,275

-,330

,763

,964

,308

,875

3,132

,049

(Stała)
pracow

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: stres

a.

*

Interpretacji zależności dokonujemy na podstawie

współczynnika standaryzowanego beta. Jest to odpowiednik

współczynnika korelacji R-Pearsona

*

Siła i kierunek zależności

*

Istotność testu t informuje nas o tym czy beta=0

*

Jeśli beta jest równa zero, to nie ma zależności prostoliniowej

*

Jeśli istotnie różni się od zera to znaczy, że mamy zależność –

wtedy interpretujemy betę

Współczynniki

a

-,750

2,275

-,330

,763

,964

,308

,875

3,132

,049

(Stała)
pracow

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: stres

a.

*

Jaka jest zatem zależność między liczbą

podległych pracowników a poziomem stresu?

*

silna ? słaba

*

dodatnia ? ujemna

Współczynniki

a

-,750

2,275

-,330

,763

,964

,308

,875

3,132

,049

(Stała)
pracow

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: stres

a.

*

Aby się dowiedzieć, czy predyktor jest

dobrym predyktorem – wyjaśnia duży
procent wariancji zmiennej
przewidywanej patrzymy na wartość r
kwadrat

Model - Podsumowanie

,875

a

,766

,688

1,62934

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), pracow

a.

ogolem

regresja

SS

SS

R 

2

Model - Podsumowanie

,875

a

,766

,688

1,62934

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), pracow

a.

Analiza wariancji

b

26,036

1

26,036

9,807

,049

a

7,964

3

2,655

34,000

4

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), pracow

a.

Zmienna zależna: stres

b.

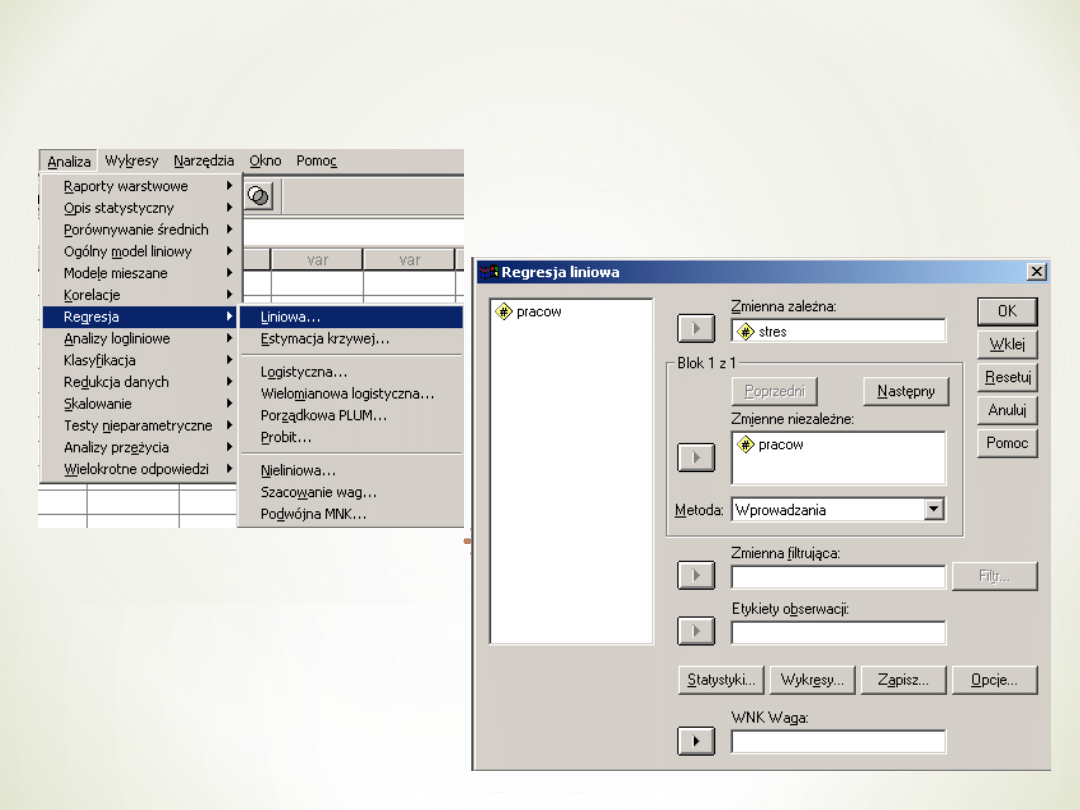
Kolejne kroki analizy regresji:

1.

Sprawdzamy czy model linii regresji

dobrze pasuje do danych (analiza

wariancji)

2.

Sprawdzamy, czy istnieje zależność

między predyktorem a zmienną zależną

(istotność współczynnika beta)

3.

Interpretujemy współczynnik beta (siła i

kierunek zależności)

4.

Zapisujemy wzór linii dla danych

surowych

Współczynniki

a

3,002

1,124

2,670

,026

,500

,118

,816

4,239

,002

(Stała)
x3

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: y3

a.

Analiza wariancji

b

27,470

1

27,470

17,972

,002

a

13,756

9

1,528

41,226

10

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), x3

a.

Zmienna zależna: y3

b.

4,00

6,00

8,00

10,00

12,00

14,00

x3

6,00

8,00

10,00

12,00

y3

R kwadrat dla Liniowej

= 0,666

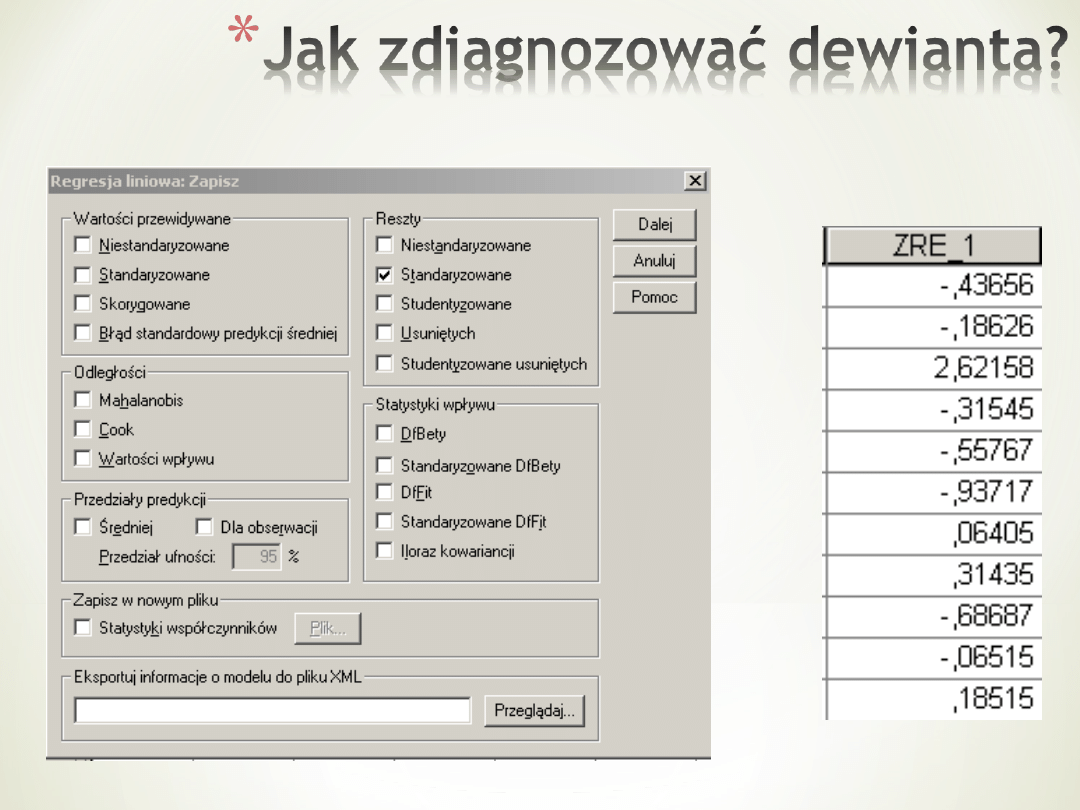
Gdy

większe

niż jeden

Statystyki opisowe

7,5009

2,03058

11

9,0000

3,31662

11

y4
x4

Średnia

Odchylenie

standardowe

N

Współczynniki

a

3,002

1,124

2,671

,026

,500

,118

,817

4,243

,002

(Stała)
x4

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: y4

a.

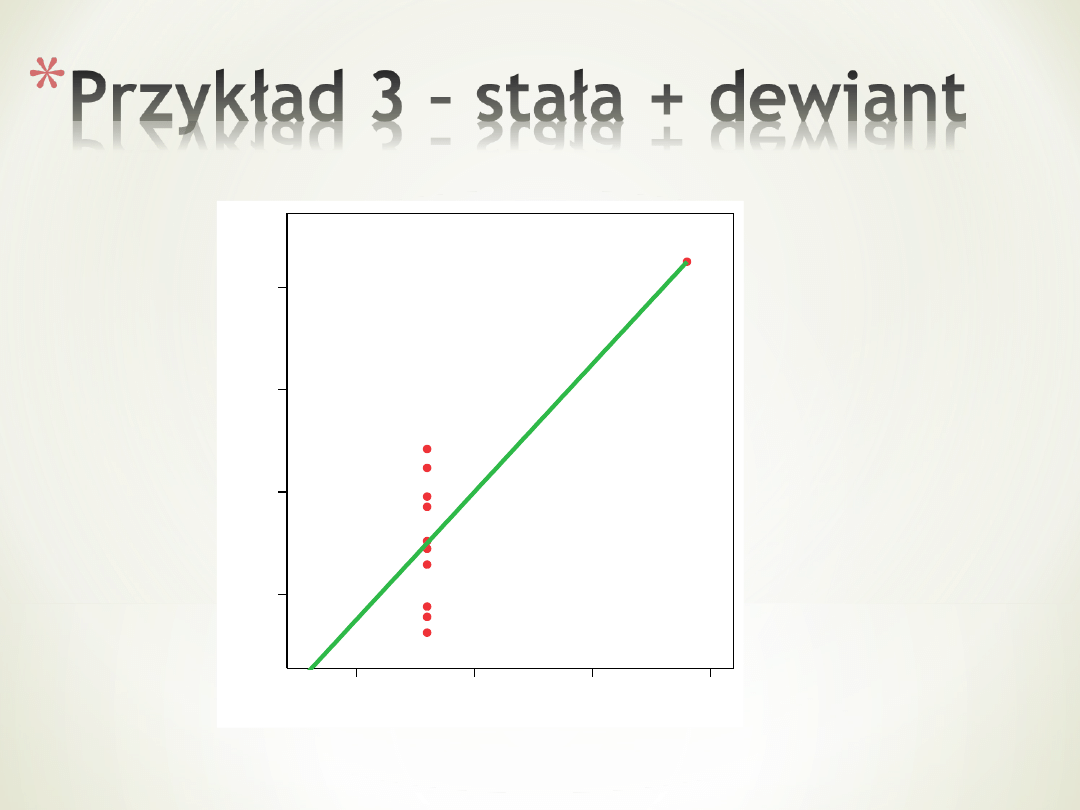
5,00

10,00

15,00

20,00

x4

6,00

8,00

10,00

12,00

y4

R kwadrat dla Liniowej

= 0,667

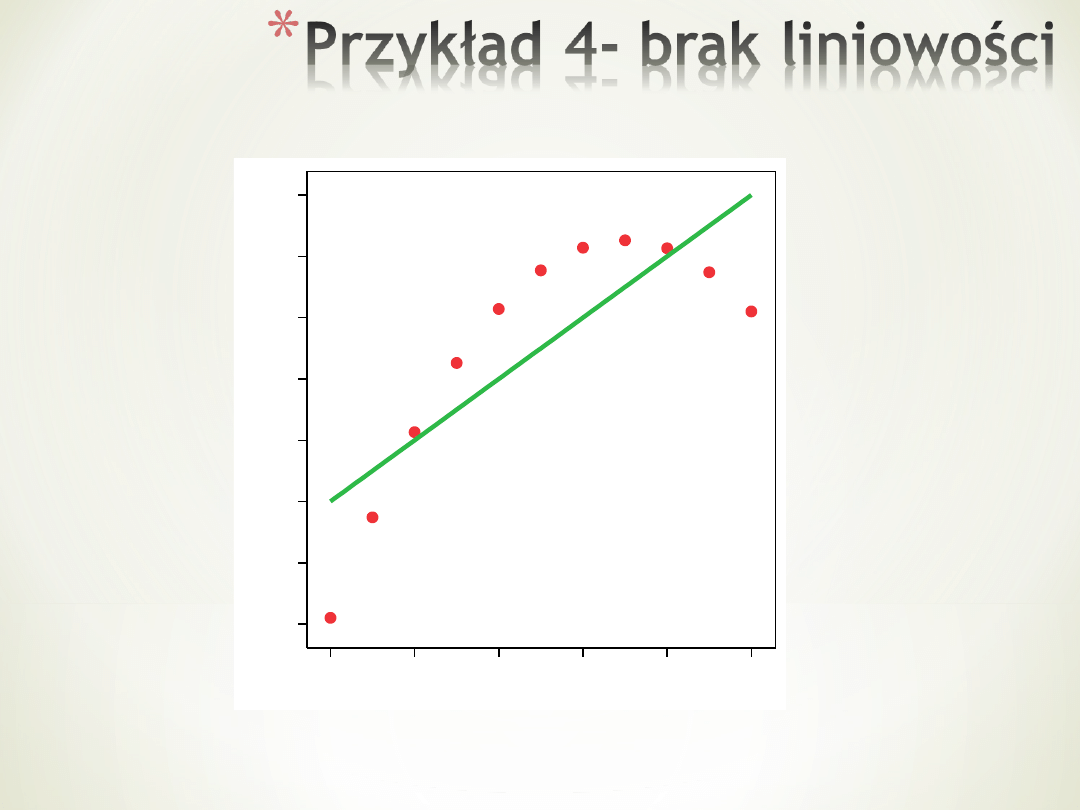
4,00

6,00

8,00

10,00

12,00

14,00

x2

3,00

4,00

5,00

6,00

7,00

8,00

9,00

10,00

y2

R kwadrat dla Liniowej

= 0,666

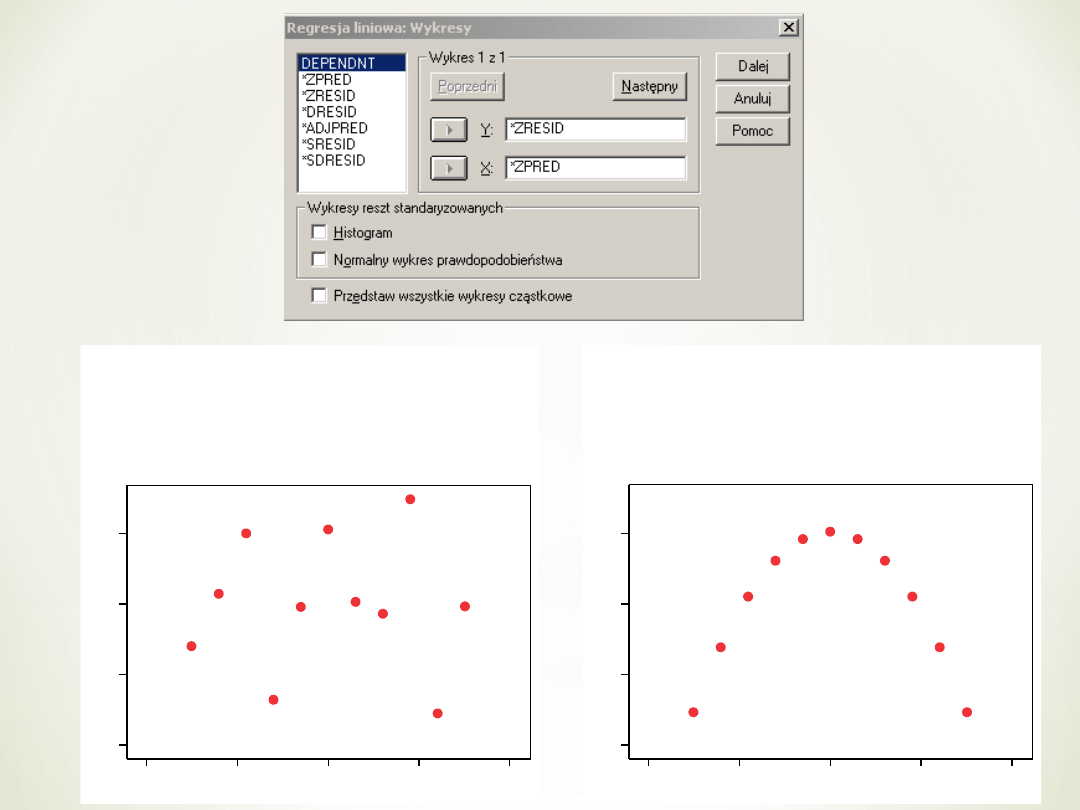
-2

-1

0

1

2

Regresja Standaryzowana wartość przewidywana

-2

-1

0

1

R

eg

re

sj

a

R

es

zt

a

st

an

d

ar

yz

o

w

an

a

Zmienna zależna: y2

Wykres rozrzutu

-2

-1

0

1

2

Regresja Standaryzowana wartość przewidywana

-2

-1

0

1

R

eg

re

sj

a

R

es

zt

a

st

an

d

ar

yz

o

w

an

a

Zmienna zależna: y1

Wykres rozrzutu

*

Odpowiednia liczba osób badanych. Ale co

to znaczy? Tabachnick i Fidel podają, że

musi to być 50 osób plus 8 na każdy

predyktor. Jeśli mamy jedną zmienną

niezależną to powinniśmy mieć w zbiorze

danych 58 osób badanych.

*

Zmienna zależna musi mieć rozkład

normalny

*

Zmienne niezależne powinny być liniowo

powiązane ze zmienną zależną

*

Przypadki odstające i ekstremalne powinny

zostać znalezione i wyeliminowane

*

Jak dobry rozmiar ramy?

*

Wysokość ramy musi zapewniać
dostateczny dystans pomiędzy górną
rurą ramy a kroczem. Ma on
pozwolić na bezpieczne zeskoczenie
z pedałów bez przykrych
konsekwencji. W rowerze górskim
rowerzysta, kiedy stoi okrakiem nad
ramą, musi mieć możliwość
uniesienia przedniego koła co
najmniej 15 cm nad ziemię.

*

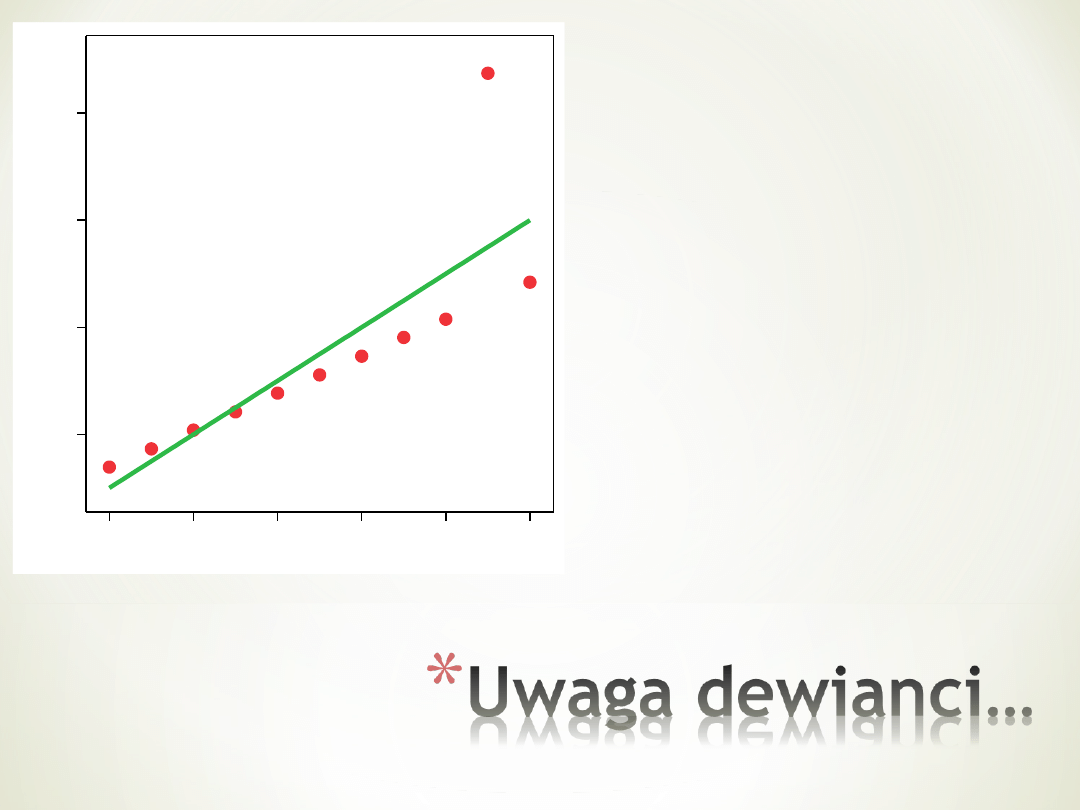
Wykres wygląda

mało
zachęcająco, ale
nie widać
żadnych
dewiantów ani
zależności
krzywoliniowej

0

1

2

3

4

5

6

7

L.KSIAZEK W DOM BIBLIOTECE R (OBECNIE)

0

20

40

60

80

100

W

Y

N

IK

W

T

E

S

C

IE

A

L

F

A

B

E

T

F

U

N

K

C

/1

99

9/

0-

10

0

Analiza wariancji

b

188548,096

1 188548,1

234,958

,000

a

768772,778

958

802,477

957320,874

959

Regresja
Reszta
Ogółem

Model
1

Suma

kwadratów

df

Średni

kwadrat

F

Istotność

Predyktory: (Stała), q163 L.KSIAZEK W DOM BIBLIOTECE R (OBECNIE)

a.

Zmienna zależna: alfa WYNIK W TESCIE ALFABET FUNKC/1999/0-100

b.

Model jest dobrze dopasowany do danych F(1,
958)=234,9; p<0,001

*

Jeśli osoba badana ma zero książek to

uzyskuje ….. punktów w teście.

*

Wraz z zakupem każdej kolejnej książki

osoba badana zyskuje 7,8 punktu w teście

*

Zależność jest dość silna i dodatnia

Współczynniki

a

25,851

1,591

16,247

,000

7,847

,512

,444

15,328

,000

(Stała)
q163 L.KSIAZEK W
DOM BIBLIOTECE
R (OBECNIE)

Model
1

B

Błąd

standardowy

Współczynniki

niestandaryzowane

Beta

Współczynniki

standaryzowa

ne

t

Istotność

Zmienna zależna: alfa WYNIK W TESCIE ALFABET FUNKC/1999/0-100

a.

*

Zmienna liczba książek pozwala wyjaśnić prawie

20% zmienności zmiennej analfabetyzm funkcjonalny

Model - Podsumowanie

,444

a

,197

,196

28,328

Model
1

R

R-kwadrat

Skorygowane

R-kwadrat

Błąd

standardowy

oszacowania

Predyktory: (Stała), q163 L.KSIAZEK W DOM BIBLIOTECE R
(OBECNIE)

a.

*

Regresja dopasowuje linię prostą –

metoda najmniejszych kwadratów –

analiza wariancji

*

Dowiadujemy się jak silny jest związek i

jaki jest jego kierunek (współczynnik

beta)

*

Dzięki wzorowi linii możemy przewidywać

wielkość zmiennej przewidywanej znając

tylko wielkość predyktora.

*

Uwaga na dewiantów i krzywoliniowość