Bazując na przykładzie

zaprezentowanym na wykładzie

wykonać poniższe ćwiczenie

WYZNACZENIE NIEZBĘDNEJ LICZBY

POMIARÓW W OKREŚALNIU

NORMY CZASOWEJ

TRWANIA CZYNOŚCI

TECHNOLOGICZNEJ

Załóżmy,

że

wyniku

przeprowadzenia badania wstępnego,
stwierdzono następujące czasy trwania
określonej czynności w minutach.

[135, 136+n∙3, 136, 138, 142,

142, 143+n∙5, 151, 155, 159,
160 162, 163-n∙5, 163, 165,]

Pytanie:

Ile należy wykonać pomiarów

aby oszacować średni czas wykonywania
badanej czynności z błędem nie większym
niż 3 minut przy poziomie ufności
wynoszącym (1-α) = 0,95.

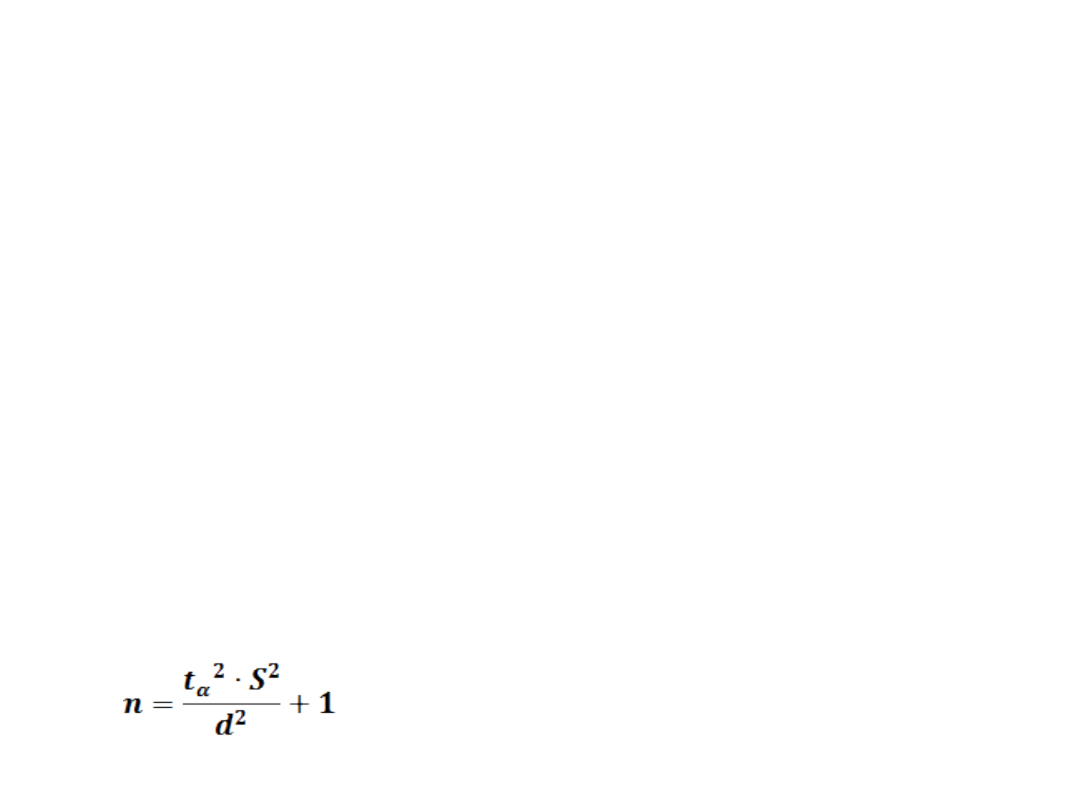
OBLICZENIA

Wartość średnia 2250 ÷ 5 = 150

OBLICZENIA

Wartość średnia 2250 ÷ 5 = 150

135, 136, 136, 138, 142,

-15 -14 -14 -12 -8

142, 143, 151, 155, 159,

-8 -7 +1 +5 +9

160 162, 163, 163, 165

+10 +12 +13 +13 +15 ∑ = 0

∑ vv = 1852 V(x) = S

= 132,3 σ = 11,5 3σ =

34,5

Z kolei, z tablicy do wyznaczania obszaru krytycznego dla
testów statystycznych opartych na rozkładzie t-Studenta,
przy uwzględnieniu obszaru krytycznego jednostronnego i
czternastu stopni swobody, wypisujemy t

= 1,8

n = [(1,8

∙ 132,3): 3

]

+ 1 = 47,6+1 =49

DZIĘKUJĘ

ETAPY EKSPERYMENTU

Wyznaczana, w realizowanym programie

przedmiotu „normowanie i
kosztorysowanie”, norma pracy bazuje na
ocenie przeprowadzonych pomiarów czasu
trwania określonej czynności
technologicznej. To działanie można
określić pojęciem „przeprowadzaniem
eksperymentu”.

Eksperyment taki, przed jego badaniem,

musi:

- być jednoznacznie określony co do
początku i końca
trwania badanej czynności (co będziemy
badali),

- mieć określone miejsce i warunki, w
których zostanie
przeprowadzone badanie,

- posiadać określone wymogi dokładności z
jaką ma być
określony wynik badania.

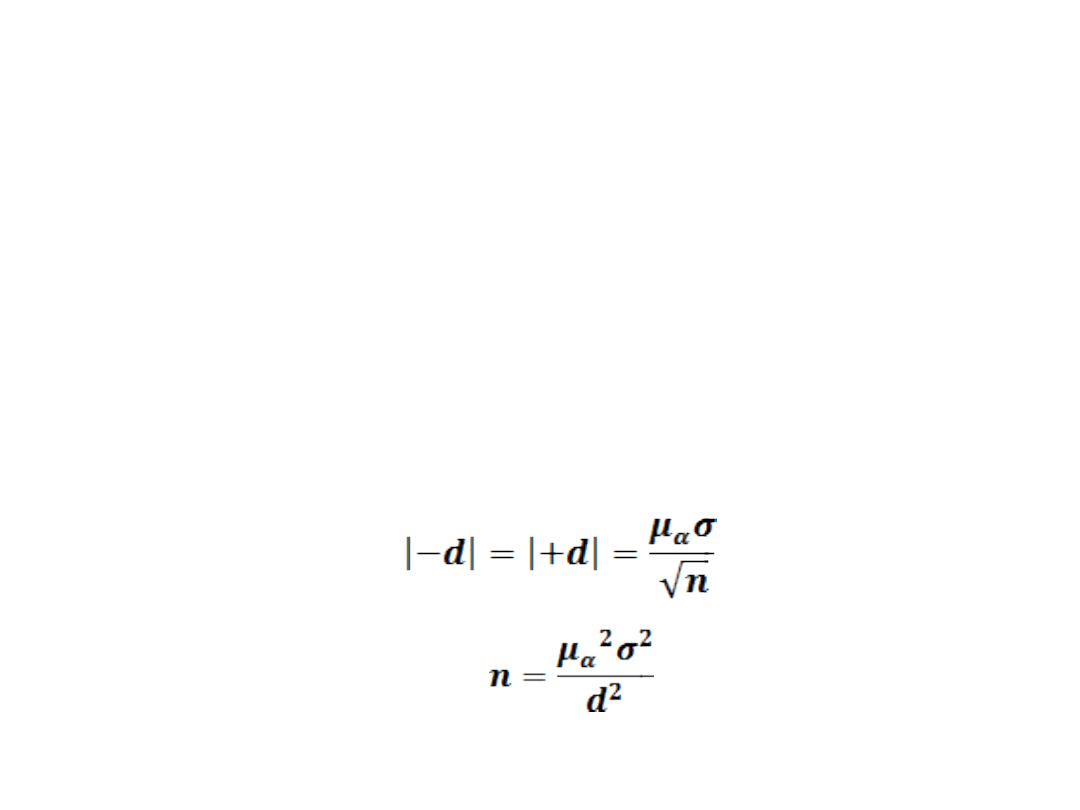
USTALANIE NIEZBĘDNEJ LICZBY

OBSERWACJI

PRZYPADEK 1.

Najprostszy przypadek

występuje wówczas, gdy znane jest

odchylenie standardowe σ zastosowanej

metody

pomiaru

przy

założonym

poziomie ufności (1-α). Wówczas długość

dopuszczalnej odchyłki d od wartości

średniej

wyniku

(dopuszczalny

błąd

wartości średniej) obliczymy z zależności

skąd

(1)

Na bazie tych danych, pierwszą
analizą eksperymentu jest określenie
niezbędnej

liczby

pomiarów

dla

osiągnięcia

zadanych

wymagań

dokładnościowych.

współczynnik, który po pomnożeniu go przez

wyznacza
granicę nieprzekroczenia dopuszczalnego błędu
d przy zadanym
poziomie ufności (1-α),
- odchylenie standardowe.

PRZYKŁAD do przypadku 1

Założenie:

znane jest odchylenie

standardowe pojedynczego pomiaru czasu
wykonywania danej czynności roboczej
wynoszące σ = ±30 s.

Pytanie:

Ile należy wykonać pomiarów aby

oszacowany czas wykonywanej czynności
był określony z dokładnością d = ±20 s
przy poziomie ufności (1-α) = 0,95.

Zgodnie z zależnością

otrzymujemy:

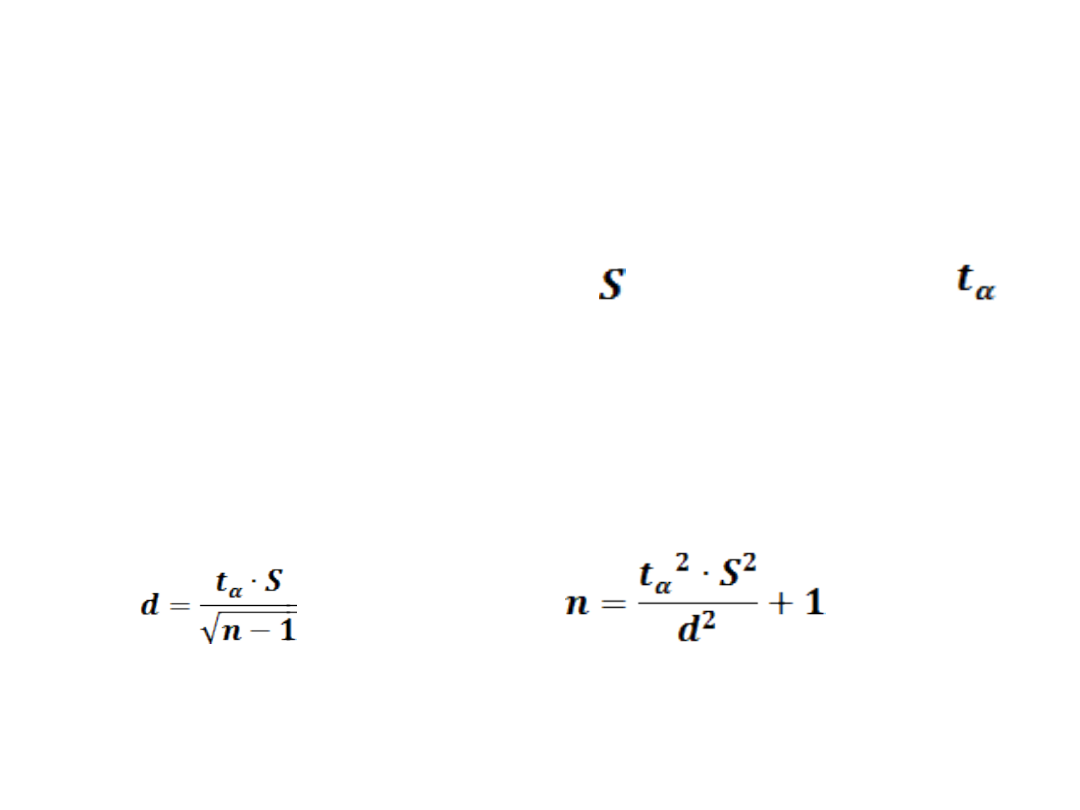
PRZYPADEK 2.

Na ogół nie jest znane

odchylenie standardowe σ dla przyjętej
metody pomiaru. Z tego względu
należy

określić

wstępnie

przeprowadzonej

próbnej

serii

pomiarów,

np.

liczności

(oznaczymy je ). Współczynnik ,
wyznaczający granicę nieprzekroczenia
błędu dopuszczalnego przy zadanym
poziomie ufności (1-α), określa się na
podstawie tablic, np. Studenta.
Dopuszczalny błąd wyniku wyznacza
zależność

skąd:

(2)

Jeżeli znalezione z tej zależności n > n

to należy dodatkowo

zaobserwować (n – n

) danych.

PRZYKŁAD DO REALIZACJI NA

ĆWICZENIACH

PRZYKŁAD do przypadku 2

Założenie:

nie jest znane odchylenie

standardowe

wykonywania

pojedynczego pomiaru czasu danej
czynności roboczej.

Pytanie:

Ile należy wykonać pomiarów

aby

oszacować

średni

czas

wykonywania badanej czynności z
błędem nie większym niż 3s przy
poziomie ufności wynoszącym (1-α) =
0,95.

Z treści zadania wynika, że
mamy do czynienia z
jednostronnym

obszarem

krytycznym, gdyż błąd mniejszy od
3s wolno nam popełnić, a jedynie
nie wolno popełnić błędu większego
od 3s.

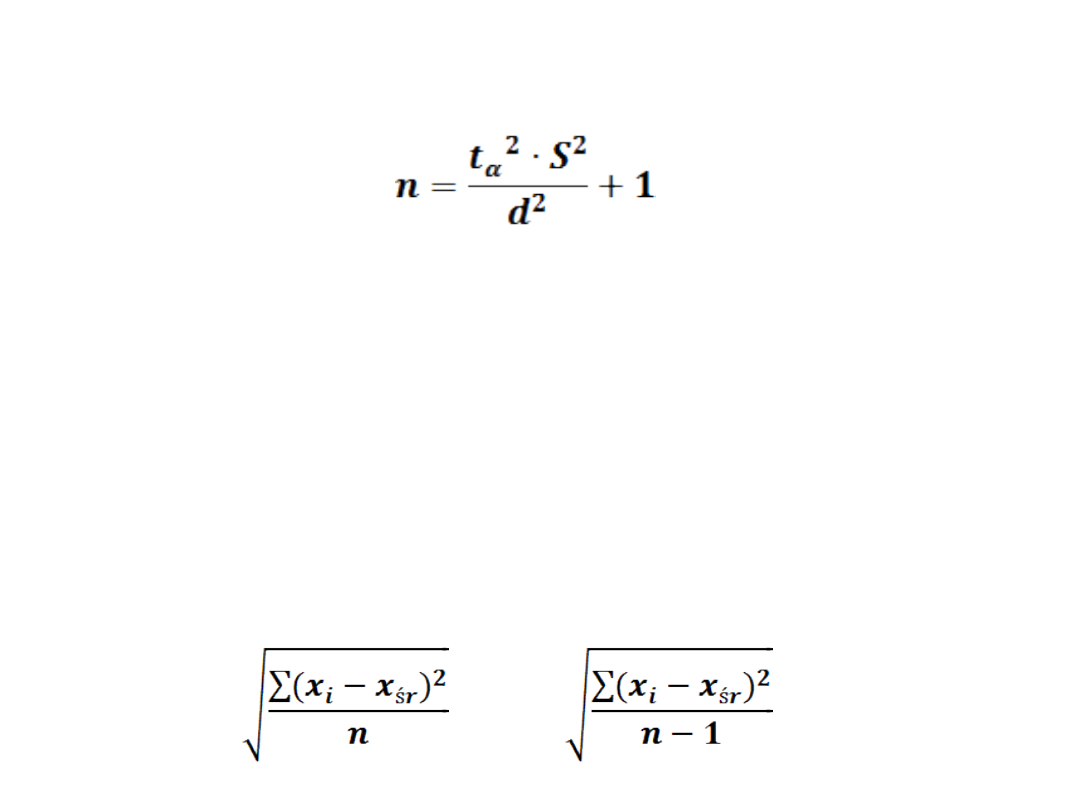
Zgodnie

procedurą

określoną

zależnością (2)

należy w pierwszej kolejności określić
odchylenie

standardowe

pojedynczego

pomiaru

ustalonym

sprzętem. W tym celu posiadanym
chronometrem

wykonano

próbny

pomiar, z którego wyniki w
sekundach zawiera poniższa macierz:
x

≡ │ 210; 212; 212; 216;

210 │

Odchylenie standardowe oblicza się z
zależności

lub

Wybieramy

Odchylenie standardowe jest
definiowane jako pierwiastek z
wariancji, zatem poszukiwane S

jest

wariancją zmiennej losowej, którą
jest wynik pomiaru. Jej obliczenie
daje.

 odchylenia od średniej, ich
kwadraty i sumy:
X-x ≡ │ +2; 0; 0;
-4; +2 │ = 0
(X-x)

≡ │ 4; 0; 0;

16; 4 │ = 24

 wartość średnia: X = 212

gdyż wzór ten odnosi się do „małej
próby”.

skąd wariancja (kwadrat odchylenia
standardowego) pojedynczej
obserwacji S

= 6

Z kolei, z tablicy do
wyznaczania obszaru krytycznego
dla testów statystycznych opartych
na

rozkładzie

t-Studenta,

przy

uwzględnieniu obszaru krytycznego
jednostronnego i czterech stopni
swobody, wypisujemy t

= 2,13185

kwantyl

rozkładu

0.9

0.95

0.975

0.98

0.99

0.995

0.999

0.9995

obszar

krytyczny
jednostro

nny,

0.1

0.05

0.025

0.02

0.01

0.005

0.001

0.0005

obszar

krytyczny

dwustron

0.2

0.1

0.05

0.04

0.02

0.01

0.002

0.001

n=1

3.07768 6.31375 12.7062 15.8945 31.8205 63.6568 318.306 636.627

1.88562 2.91999 4.30265 4.84873 6.96456 9.92484 22.3272 31.5990

1.63774 2.35336 3.18245 3.48191 4.54070 5.84091 10.2145 12.9240

1.53321 2.13185 2.77644 2.99853 3.74695 4.60409 7.17318 8.61031

1.47588 2.01505 2.57058 2.75651 3.36493 4.03214 5.89344 6.86884

1.43976 1.94318 2.44691 2.61224 3.14267 3.70743 5.20763 5.95880

1.41492 1.89458 2.36462 2.51675 2.99795 3.49948 4.78528 5.40787

1.39682 1.85955 2.30600 2.44898 2.89646 3.35539 4.50079 5.04130

1.38303 1.83311 2.26216 2.39844 2.82144 3.24984 4.29681 4.78092

1.37218 1.81246 2.22814 2.35931 2.76377 3.16927 4.14370 4.58691

Tablica t

do wyznaczania obszaru krytycznego dla

testów statystycznych opartych na rozkładzie t-Studenta
o danej liczbie n stopni swobody.

skąd wariancja (kwadrat odchylenia
standardowego) pojedynczej
obserwacji S

= 6

Z kolei, z tablicy do
wyznaczania obszaru krytycznego
dla testów statystycznych opartych
na

rozkładzie

t-Studenta,

przy

uwzględnieniu obszaru krytycznego
jednostronnego i czterech stopni
swobody, wypisujemy t

= 2,13185

Podstawiając te dane do
zależności (2)
, otrzymujemy n = 3
+ 1 = 4.
Odpowiedź: wystarczą cztery
obserwacje (pomiary).

POWYŻSZE ZADANIE OBLICZAMY

NA OBECNYCH ĆWICZENIACH

KONIEC

Badanie istotności wpływu czynników na
czas produkcyjny
Uzyskany „rozstęp wyników” w próbie [R = x

max

– x

min

]

porównujemy z wartością dopuszczalną [R

= w

∙ Δ

dop

∙

śr

]

Gdzie: Δ

dop

- dopuszczalny błąd względny czasu realizacji

zadania liczony względem wartości czasu przeciętnego.
Jego wartość w robotach budowlanych przyjmuje się w
granicach (7-15)% .
w

Dla obliczanego przykładu
X

śr

= 150 ; x

max

= 165; x

min

=135 ; R = 30

Przyjmując Δ

dop

= 12% otrzymujemy kolejno R

= w

∙ 0,12

∙

150 = 18

Stąd dla dwustronnej odchyłki od wartości średniej przedział
akceptowalnych wyników obserwacji wynosi 2∙ 18 i jest większy
od stwierdzonego. Oznacza to, że uzyskane wyniki pomiarów są
wiarygodne.

Tablica do wyznaczania obszaru krytycznego dla testów statystycznych opartych na rozkładzie t-Studenta o danej liczbie n stopni swobody.