WYKRESY I ICH

PREZENTACJA

Wykresy

stanowią

graficzną

interpretację

zależności

pomiędzy

dwiema lub wieloma zmiennymi. Jedną
zmienną jest zawsze wartość liczbowa
zjawiska, pozostałymi mogą być miary
czasu, powierzchni odniesienia, wieku,
liczebności danej populacji itp.

W zależności od przyjętego układu
współrzędnych mówimy o:
- wykresach prostokątnych, gdy
budowane są w układzie współrzędnych
prostokątnych,
- wykresach biegunowych, gdy
budowane są w układzie współrzędnych
biegunowych.

Wykresy prostokątne można podzielić
na:
- wykresy liniowe (proste i złożone),
- wykresy słupkowe,
- wykresy kropkowe.

Wykresy

liniowe

proste

przedstawiają zmienność tylko jednej
funkcji. Mogą być one rysowane w
układzie

arytmetycznym

lub

semilogarytmicznym.

Na

jednym

wykresie można wrysować wykresy
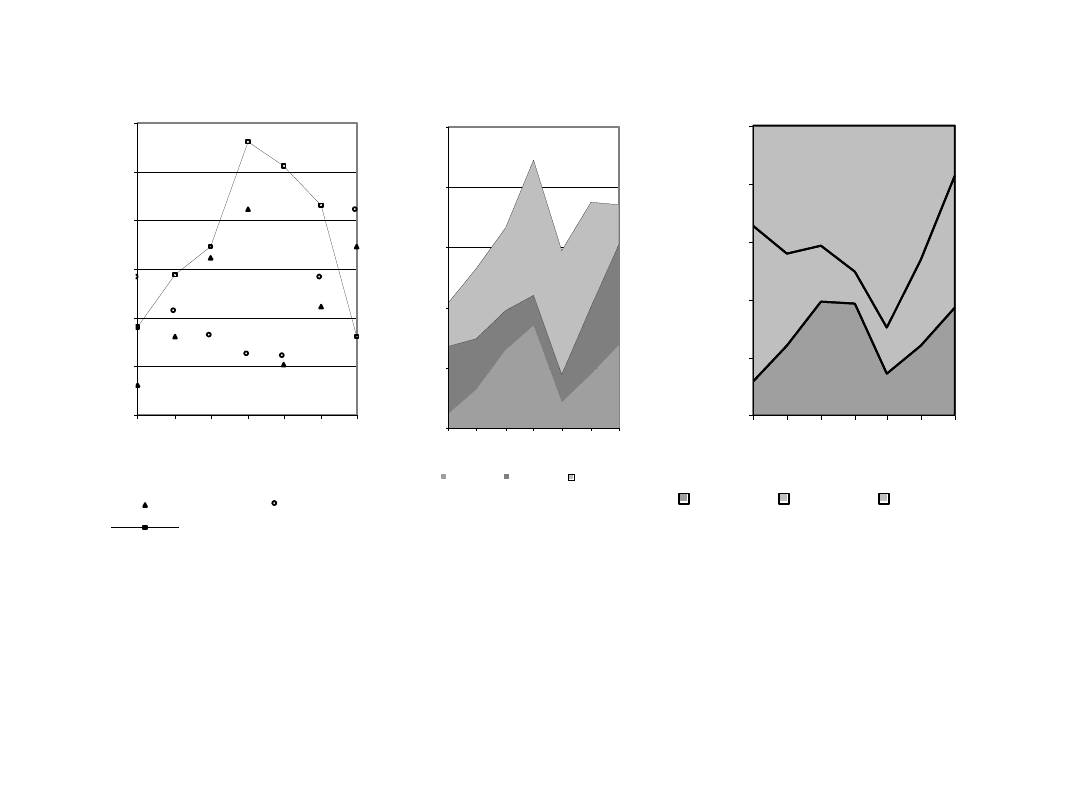
kilku funkcji tworząc „wykresy liniowe
złożone”. Zależnie od wzajemnego
stosunku tych funkcji tworzą one:
- wykres liniowy równoważny,
- wykres liniowy sumaryczny,
- wykres liniowy strukturalny.

W

układzie

semilogarytmicznym

oś

pionowa określająca wielkość zjawiska jest
wyskalowana w podziale logarytmicznym, a
oś pozioma w podziale arytmetycznym.

0

20

40

60

80

100

120

1

2

3

4

5

6

7

tygodnie

sz

tu

k

zjawisko A

zjawisko B

zjawisko C

0

50

100

150

200

250

1

2

3

4

5

6

7

tygodnie

sz

tu

k

zjawisko A

zjawisko B

zjawisko C

0%

20%

40%

60%

80%

100%

1

2

3

4

5

6

7

tygodnie

u

d

zi

ał

p

ro

ce

n

to

w

y

zjawisko A

zjawisko B

zjawisko C

Wykresy słupkowe różnią się od wykresów

liniowych formą graficzną i dyskretnym
(nieciągłym)

zobrazowaniem

zjawiska.

Podobnie jak wykresy liniowe, wykresy
słupkowe mogą być:
- proste (słupki stojące, leżące, schodkowe)
-

złożone

(grupowane,

sumaryczne,

strukturalne)
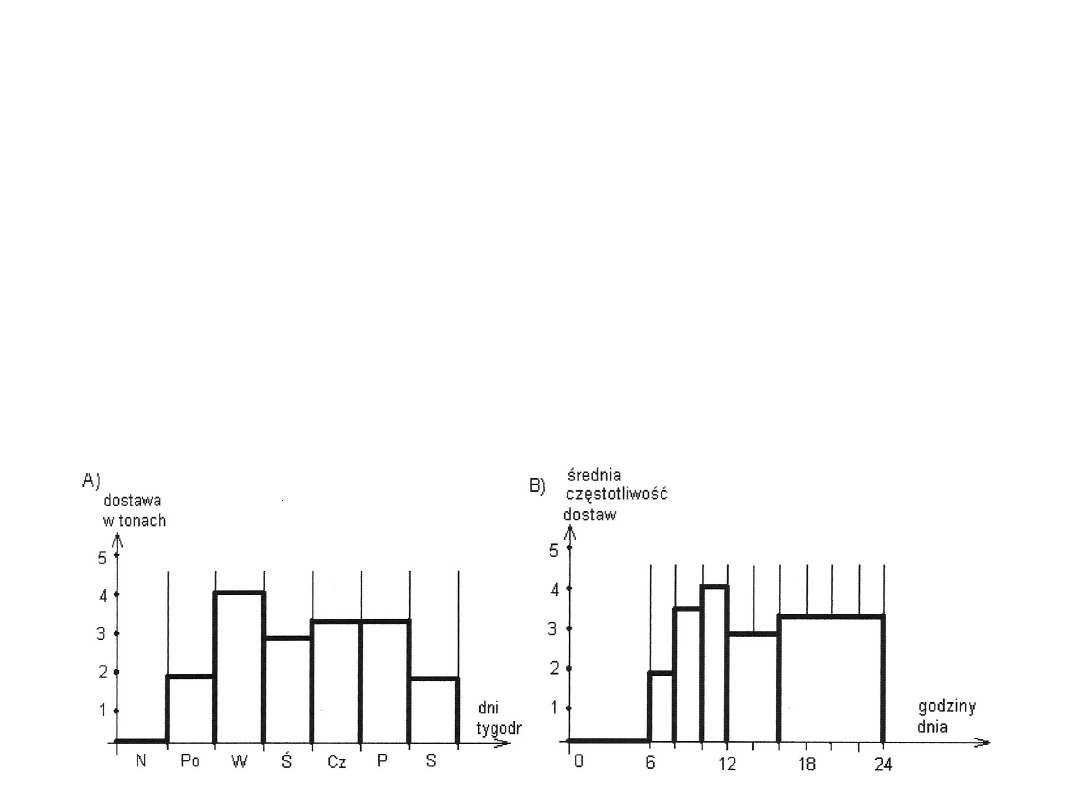
Na poniższych rysunkach przedstawiono tzw.

histogramy,

które są odpowiednikiem

wykresów częstotliwości i mogą być
budowane według równych lub różnych
przedziałów klasowych.

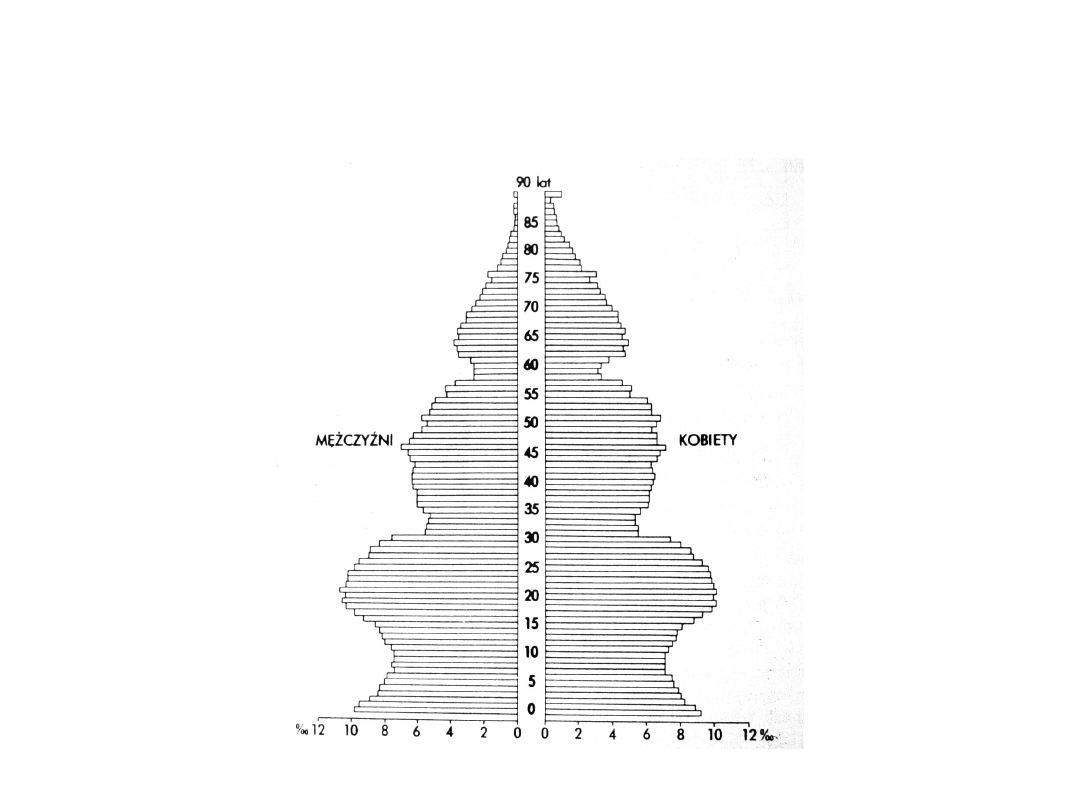
Często budowanym histogramem
porównawczym jest tzw. histogram
parzysty.

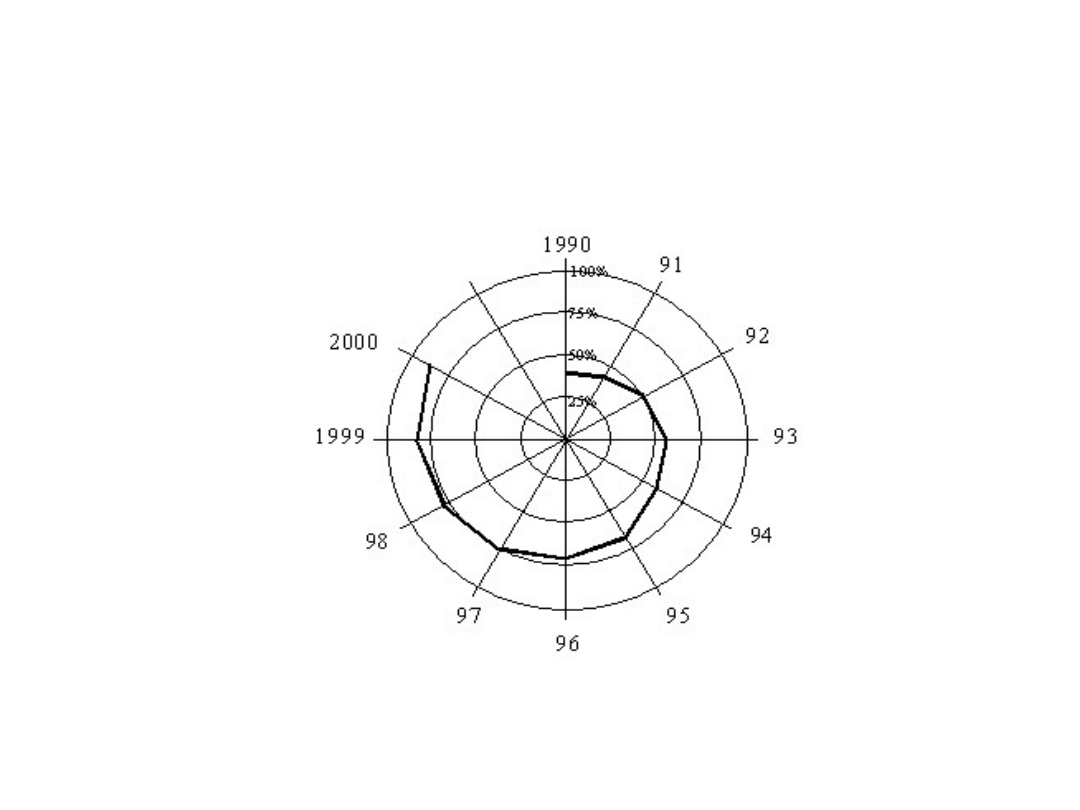
Inna formą wykresów są wykresy

biegunowe.

Wartości

jednej

zmiennej

mierzone są długością promienia, wartości
drugiej zmiennej - odległością kątową,
liczoną w prawo od promienia początkowo
(najczęściej skierowanego w górę.

Wykres biegunowy procentowej zmiany udziałów

wybranego zdarzenia w całości rozpatrywanych

zdarzeń w kolejnych latach

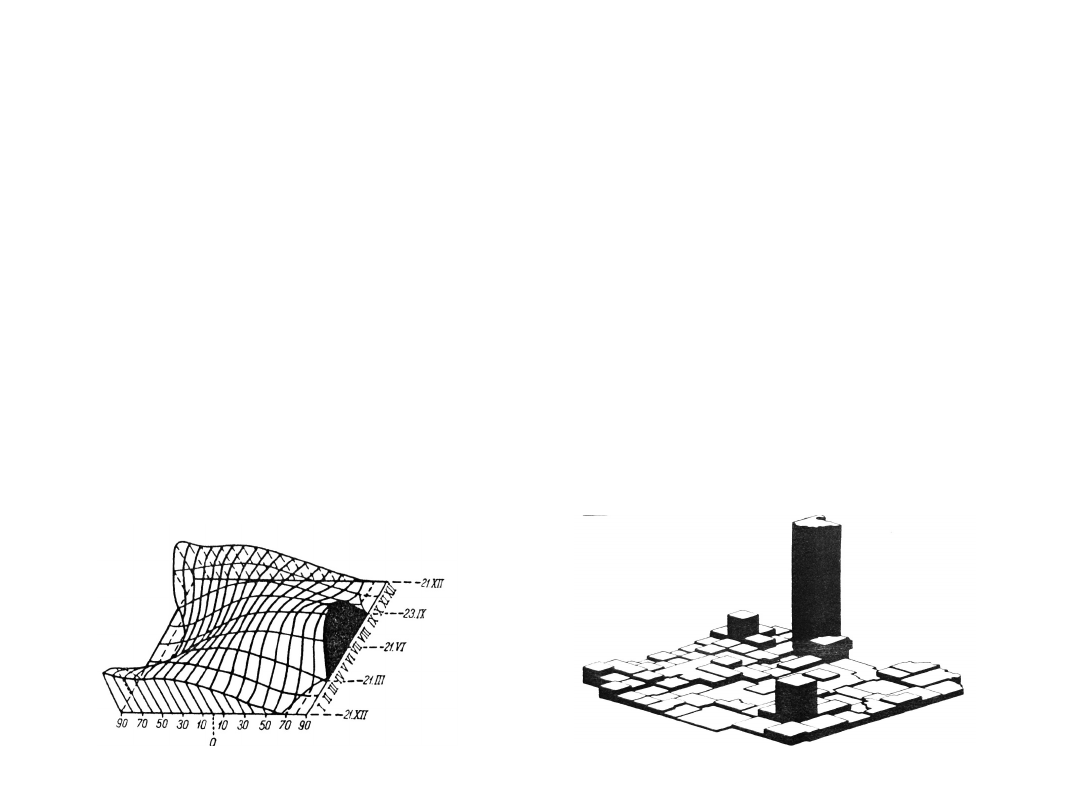
Wykresy bryłowe
Wykresy bryłowe budowane są w układzie

trzech współrzędnych prostokątnych. Osie x i
y określają położenie punktu na płaszczyźnie,
a oś z wartość jego potencjału. Ich celem
jest opisanie przestrzennego rozmieszczenia
opisywanego zjawiska, a ich położenie może
być prezentowane wrysowaną mapą na
płaszczyźnie x,y.

Graficzne opracowanie wykresów ułatwiają

bardzo odpowiednie programy komputerowe.
Wśród specjalistycznych należy wymienić
„Mathcad” i „Surface”, a wśród popularnych
„Microsoft Excel”.

Diagram
przestrzenny

Blokdiagram
przestrzenny

 

DIAGRAMY

Diagramy

stanowią

zwarte

figury

geometryczne o wyraźnie
zaznaczonych elementach konstrukcyjnych,
takich jak długość, wysokość i szerokość,
które łatwo jest wyróżnić z rysunku i
pomierzyć. Potrzeba prostoty pomiaru tych
elementów wynika z faktu, że diagramy
przedstawiają wielkość zjawiska poprzez
wskazywanie elementów do pomiaru oraz
podanie

zależności

funkcyjnej,

według

której należy obliczyć wartość opisywanego
zjawiska.

Obowiązującym

opisem

umożliwiającym

obliczenie

wartości

wynikowej, jest legenda diagramów.

Ze względu na swoją budowę, diagramy

dzielimy na liniowe, powierzchniowe i
bryłowe oraz na jedno-, - dwu- i
trójparametrowe.

Diagramy jednoparametrowe są

figurami lub bryłami foremnymi,
które określone są tylko jednym
parametrem, np. bokiem kwadratu,
średnicą lub promieniem koła, bokiem
trójkąta

foremnego,

krawędzią

sześcianu, średnicą kuli itd.

Diagramy

wieloparametrowe

opracowuje się dla opisu zjawisk, w
których wartość wynikowa zależy od
dwóch

lub

trzech

wzajemnie

niezależnych parametrów.

W obu przypadkach wyróżnia się

diagramy płaskie i diagramy bryłowe.
W swoim rysunku diagramy takie
wyróżniają jednoznacznie wielkości
podlegające

pomiarowi.

Diagramy

płaskie zawierają w sobie trzy
informacje, bryłowe – pięć.

Rozpatrzmy dla przykładu diagram
prostokątny. Informacja liczbowa może
być reprezentowana przez każdy z
boków oraz przez jego powierzchnię.
Skutkiem tego treść merytoryczna musi
być dobrana odpowiednio do tych
możliwości. Ma ona spełniać warunek
. Załóżmy, że: bok a przedstawia
średni plon z 1 ha w q, bok b – wielkość
zasianej powierzchni w ha. Wartość P
przedstawi efekt produkcyjny, czyli
uzyskany zbiór . Legenda dla tego typu
diagramu może wyglądać następująco:
m

1

– 1 mm podstawy  100 ha ;

m

2

– 1 mm wysokości  5q

/ ha.
W wyniku otrzymamy efekt produkcyjny
P, którego skalę możemy określić jako:
m

3

– 1 mm

2

powierzchni

odpowiada

500 q plonów.

b

a

P





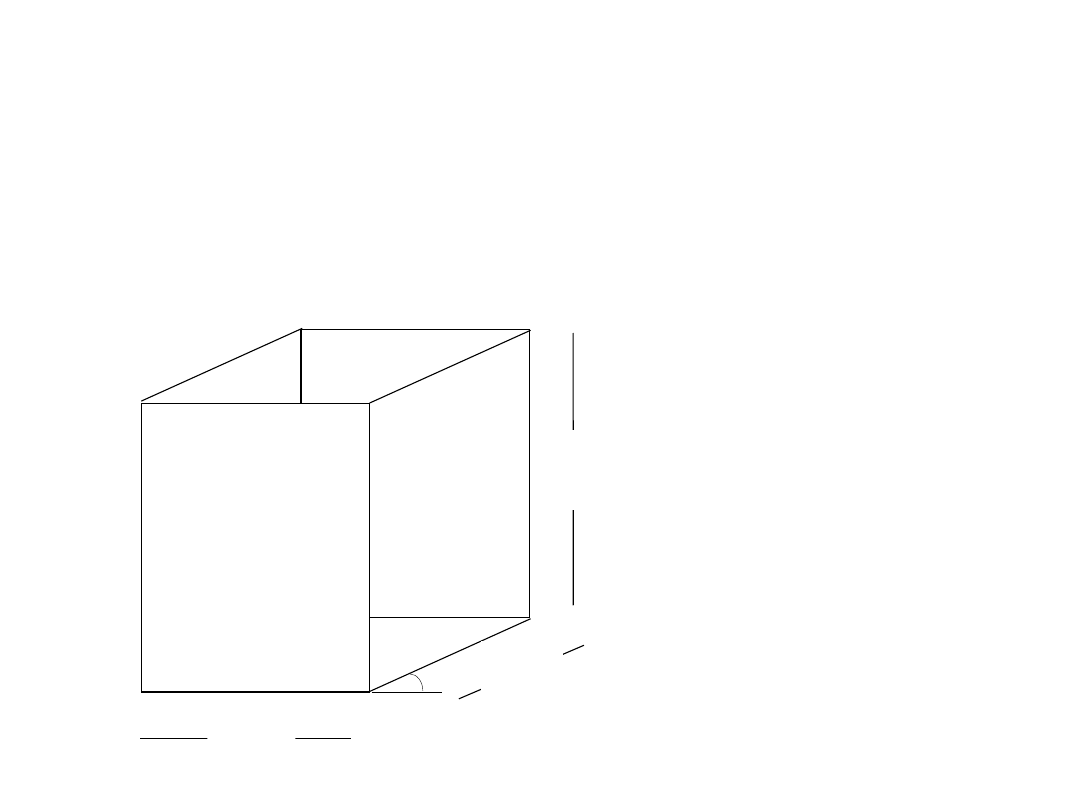
Diagramy bryłowe rysujemy w
perspektywie równoległej w taki
sposób, aby równoległe do siebie
boki miały tę samą długość
natomiast
boki podstawy rysujemy pod kątem
45

o

.

a

a

h

45

o

Przykład
diagramu
bryłowo
dwuparametro
wego

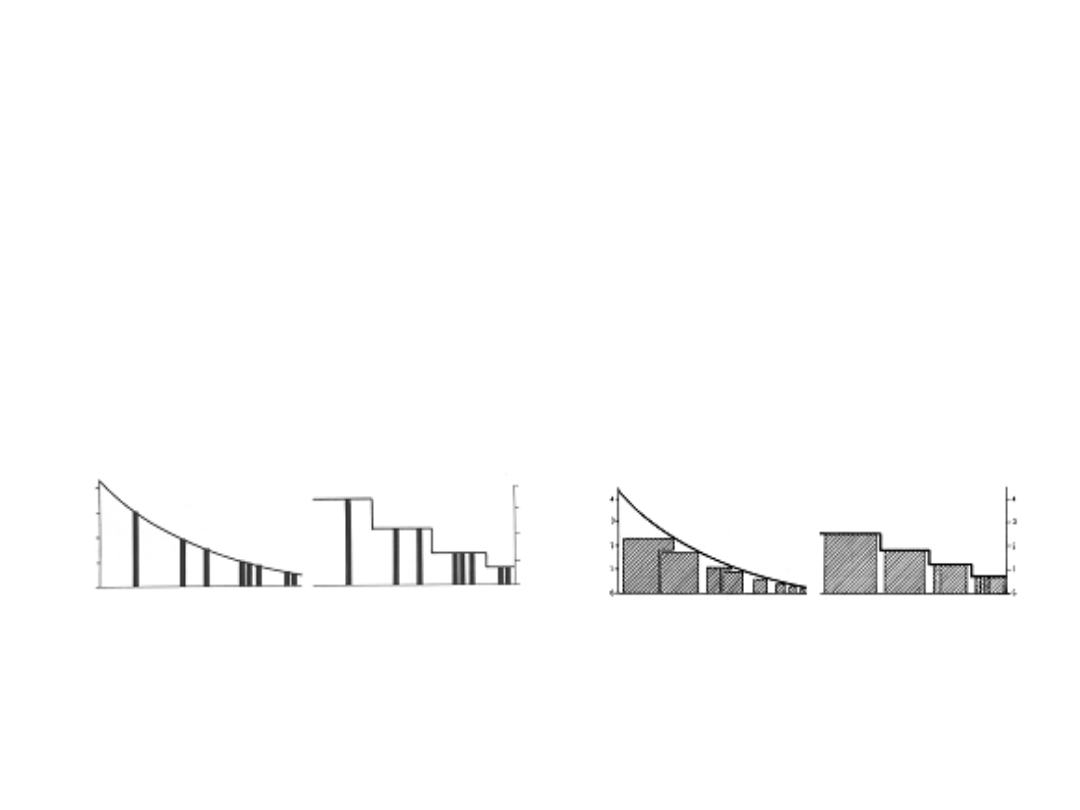
Skale diagramów
 

Z

założenia

metodycznego

diagramu wynika, że jedyną cechą
reprezentującą

ilość

jest

jego

wysokość, powierzchnia lub objętość.
Wielkość tę możemy wyrazić w ciągłej
lub skokowej skali wartości.

a) b) a) b)

Skala wartości: a) – ciągła, b) – skokowa

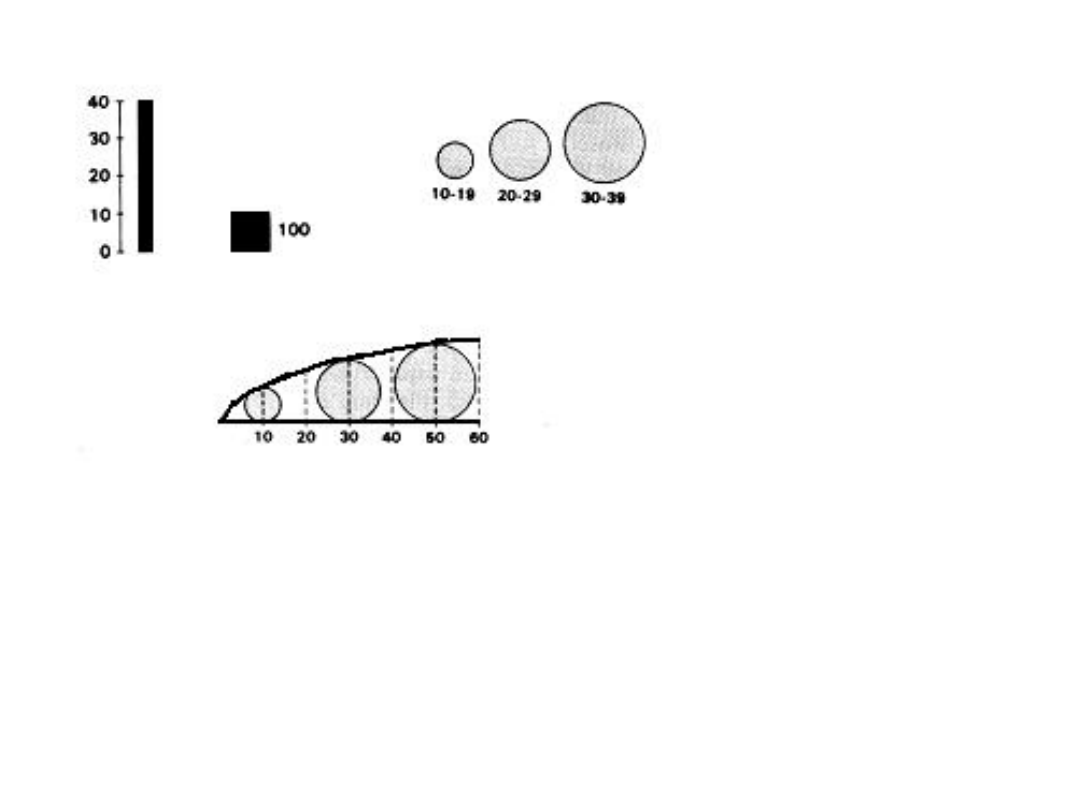
Przykłady legend
diagramów:
a) – słupkowego,
b) – kołowego
skokowego,
c) – kołowego
ciągłego

a
)

b
)

c
)

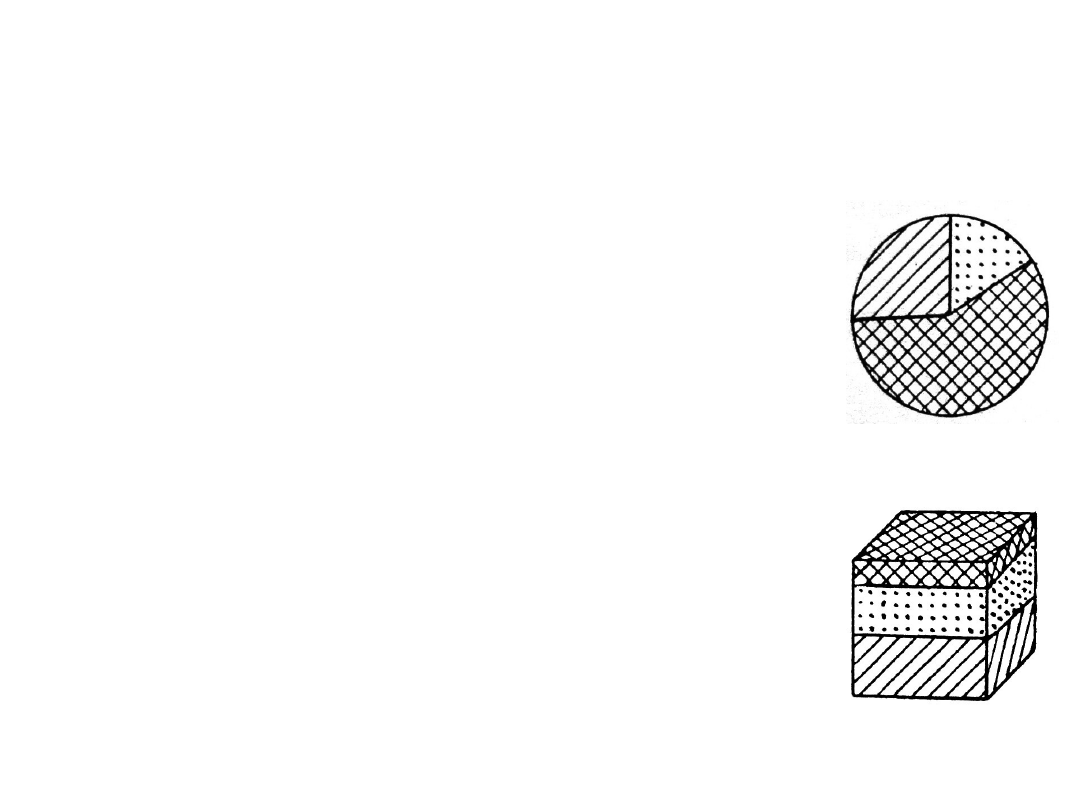
Rozbudowa treści
diagramów.

 

W celu zaprezentowania na

danym

diagramie

większej

liczby faktów (zjawisk) to
można go rozbudować zarówno
wewnętrznie jak i zewnętrznie.
Podział wewnętrzny stosowany
jest dla pokazania struktury
zjawisk – wówczas mówimy o
diagramach

strukturalnych.

Rozbudowa

zewnętrzna

następuje przez połączenie ze
sobą kilku diagramów. Ich
budowa odpowiada konstrukcji
sumarycznej i ma na celu
ukazanie

dynamiki

rozwoju

zjawiska.

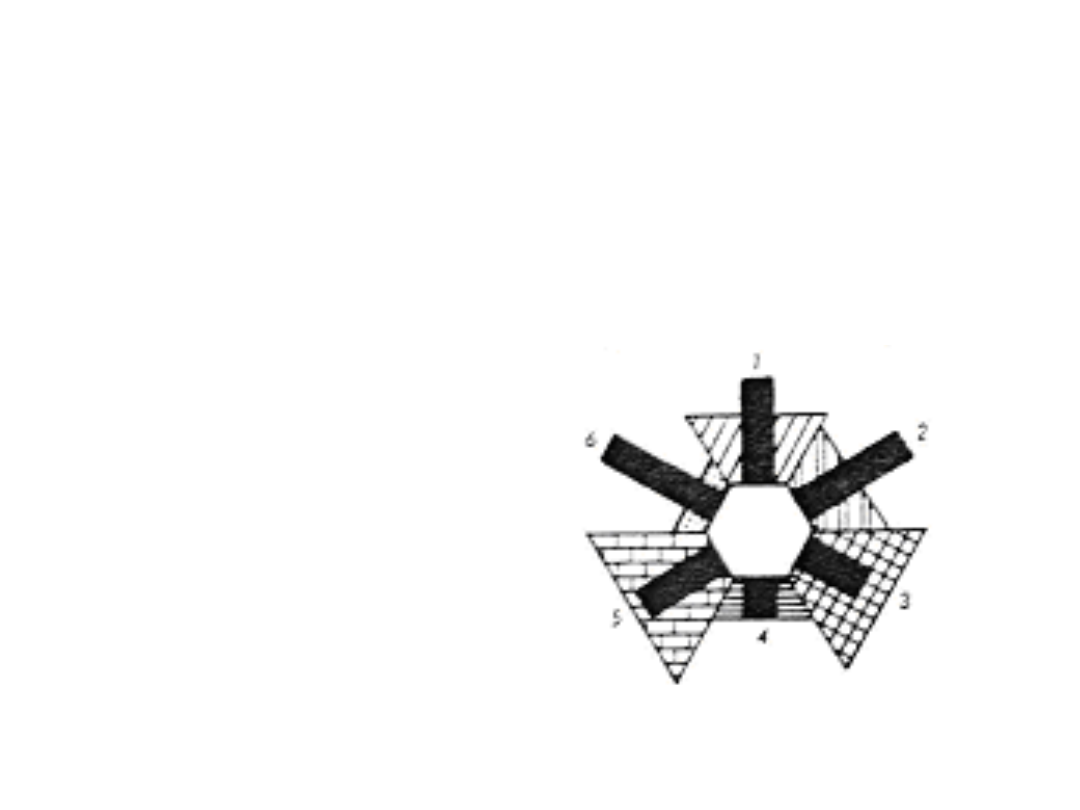
Specjalnym rodzajem diagramów

złożonych są diagramy centryczne,
nazywane też centrogramami. W tych
diagramach wartości odkładane są na
osiach rozchodzących się promieniście
z

centrum

diagramu

wskazując

dodatkowo

kierunek

geograficzny

działania zjawiska, np.
wiatrogram lub diagram
ilustrujący kierunki i siłę
ekspansji analizowanego
działania.

Przykład centrogramu

prezentującego kierunki,

rodzaj (szrafura)

i wielkość (pola trójkątów)

działań