Elektrochemia
obejmuje badania reakcji
przeniesienia elektronu
Reakcje przeniesienia elektronu to reakcje redoks –
- stanowią podstawę wytwarzania energii elektrycznej w
reakcji chemicznej
- dają możliwość badania reakcji chemicznej za pomocą
pomiarów wielkości elektrycznych
- leżą u podstaw wielu procesów biologicznych
( przekazywanie sygnału w neuronach) i przemysłowych
Urządzenie,
w którym dzięki reakcji chemicznej lub procesowi
fizykochemicznemu powstaje różnica potencjałów
umożliwiająca wykonanie pracy elektrycznej (praca
przeniesienia ładunku) nazywa się
ogniwem
elektrochemicznym
OGNIWA ELEKTROCHEMICZNE
ogniwa galwaniczne – reakcja chemiczna
ogniwa stężeniowe – proces fizykochemiczny wyrównywania stężeń,
ogniwa paliwowe – reakcja spalania,
ogniwa fotowoltaiczne – konwersja światła w prąd
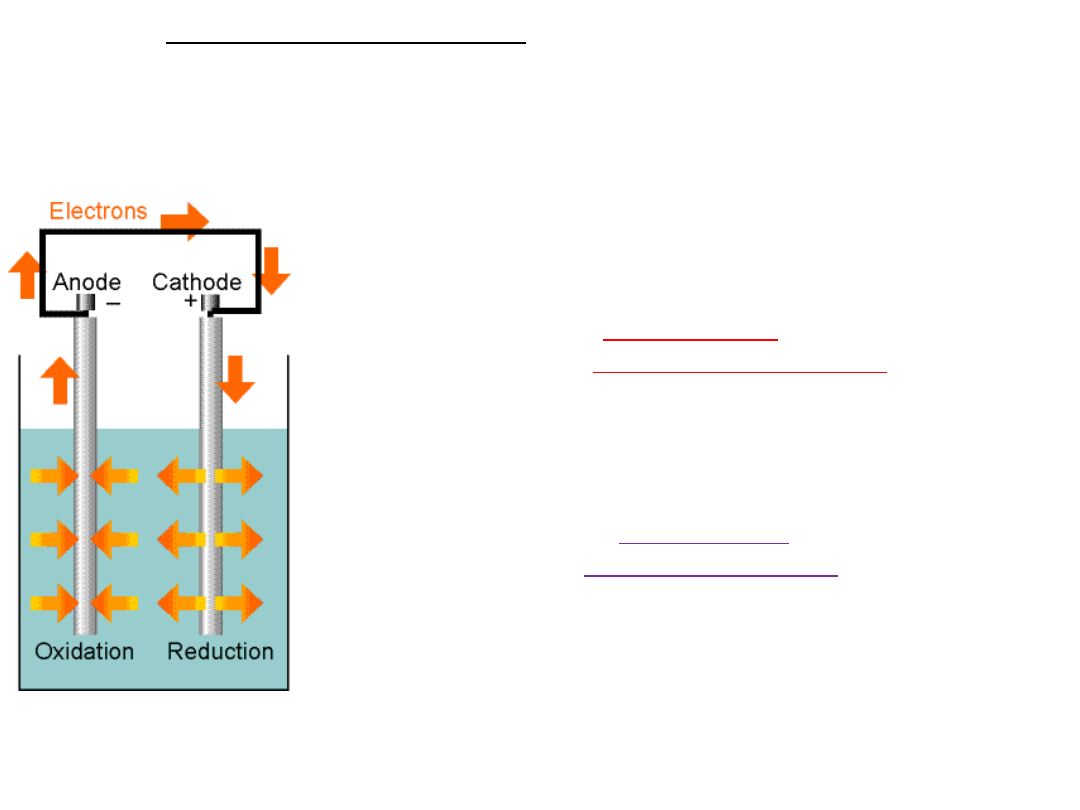
OGNIWO GALWANICZNE
to urządzenie zamieniające pracę reakcji chemicznej na pracę
przeniesienia ładunku.
Ogniwo to układ dwóch elektrod zanurzonych
w roztworze (roztworach ) elektrolitu,
po połączeniu przewodnikiem metalicznym
płynie w nim prąd.
Lewa elektroda:
ANODA – ⊖
-zachodzi na niej
proces UTLENIANIA
M
(s)
→ M
z+
+ z e (-)
X
z-
→ ½ X
2
+ z e (-)
Prawa elektroda:
KATODA –⊕
-zachodzi na niej
proces REDUKCJI
M
z+
+ z e → M
(s)
(+)
X
2
+ 2z e → 2X
z-
(+)
Potencjał elektrody prawej φ
pr
jest większy od
potencjału elektrody lewej φ
lew
, a ich różnica
jest dodatnia:
0
φ
φ
U
lew
pr
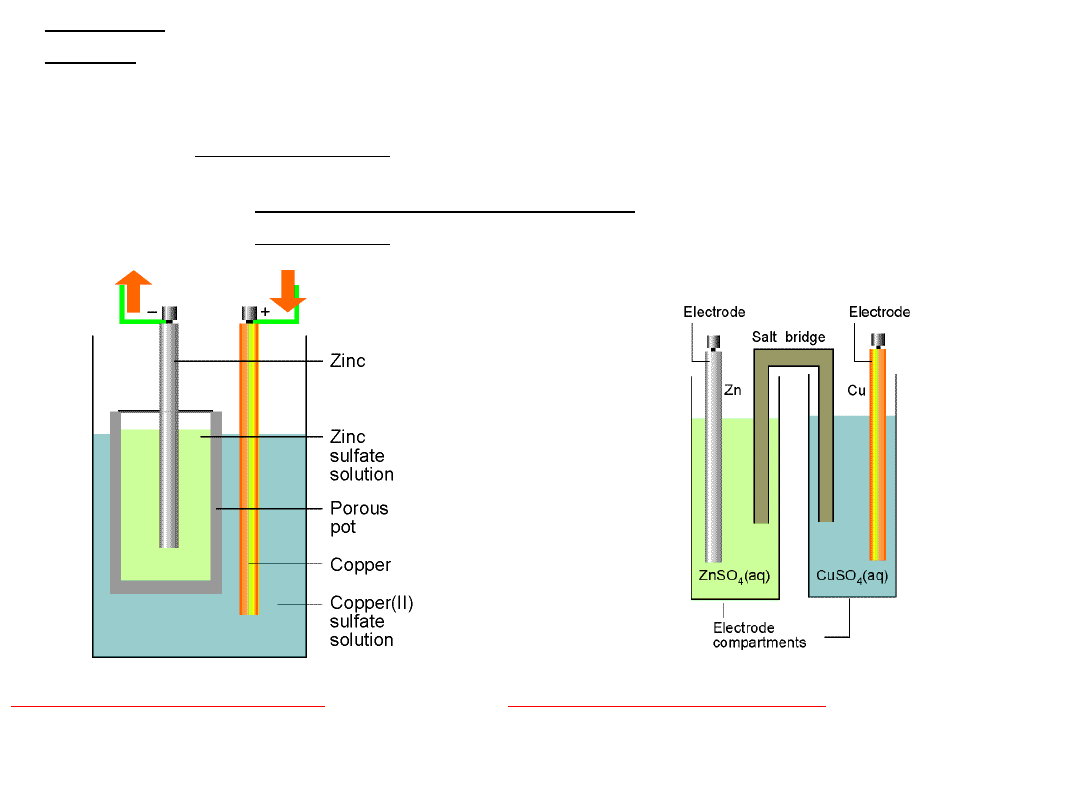
Budowa
ogniw
Elektrody mogą być zanurzone w jednym roztworze lub
każda z elektrod może być zanurzona w innym
roztworze elektrolitu.
Roztwory półogniw mogą być rozdzielone porowatą przegrodą lub
połączone kluczem elektrolitycznym
r-r
ZnSO
4
Porowata przegroda ⋮
przepuszczalna dla jonów
pojawia się na niej potencjał
dyfuzyjny E
d
wynikający z różnej
ruchliwości jonów
r-r CuSO
4
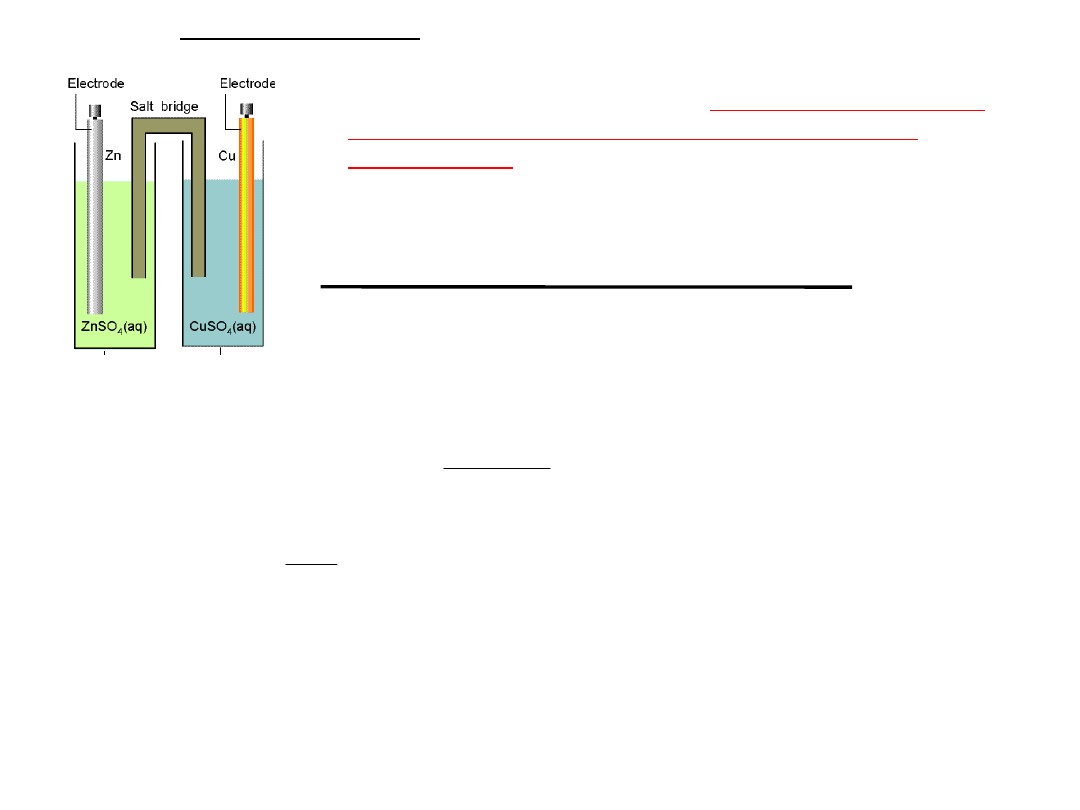
Schemat budowy ogniwa
Daniella:
Klucz elektrolityczny ∥
ośrodek
przewodzący jonowo
U-rurka napełniona stężonym
roztworem soli
w żelatynie. ośrodek przewodzący
jonowo
Zn
(s)
∣ZnSO
4(aq)
⋮CuSO
4(aq)
∣Cu
(s)
Zn
(s)
∣ ZnSO
4(aq)
∥
CuSO
4(aq)
∣Cu
(s)
Układ jaki tworzy elektroda wraz z roztworem, w którym jest zanurzona,
nazywamy
półogniwem.
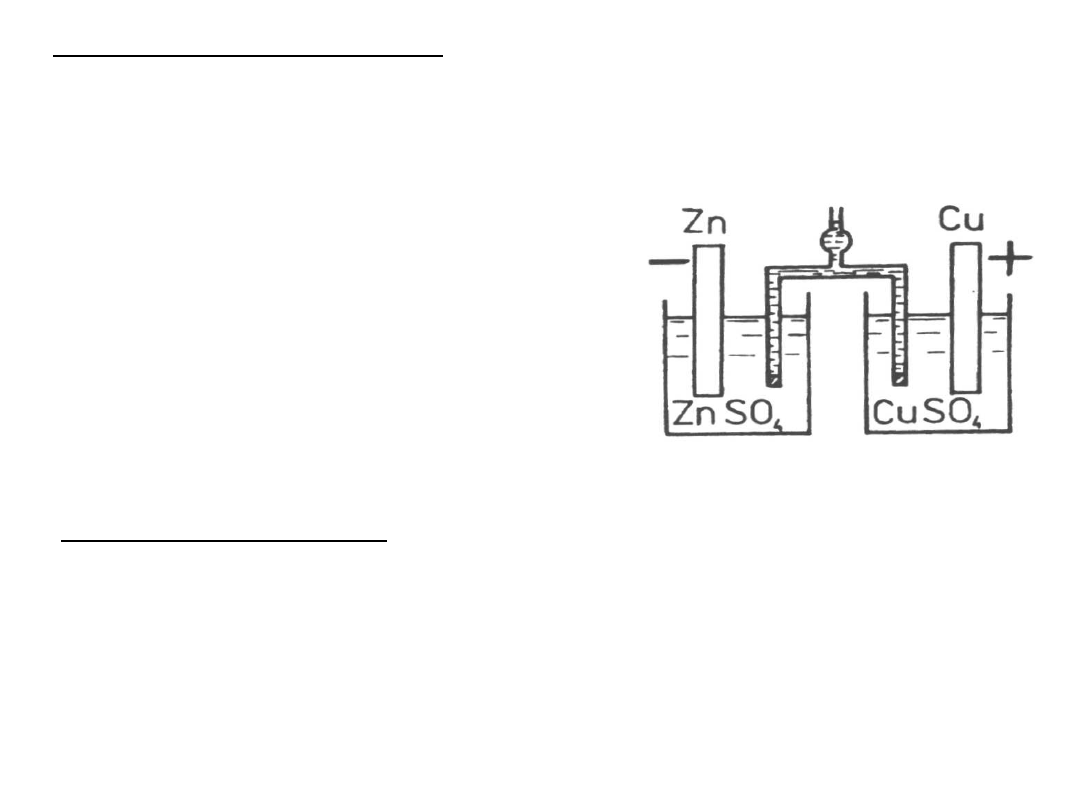
Konwencja zapisu ogniwa
lewa elektroda
utlenianie
- anoda
prawa
elektoda
redukcja
+ katoda
kolejne składniki ogniwa rozdziela się znakami:
∣ granica faz ⋮ porowata przegroda ∥ klucz elektrolityczny
Zn ∣Zn
2+
∥ Cu
2+
∣ Cu
Zn
(s)
→ Zn
2+
+ 2e Cu
2+
+ 2e → Cu
(s)
Reakcja w ogniwie:
Zn
(s)
+ Cu
2+
⇄ Zn
2+
+ Cu
(s)
Klucz elektrolityczny
to odwrócona U – rurka napełniona nasyconym roztworem elektrolitu o
zbliżonych liczbach przenoszenia jonów : t
+
~ t
-
~ 0,5.
Np. KCl
KNO
3
NH
4
NO
3
Na obu końcach klucz powstają potencjały dyfuzyjne o jednakowych
wartościach bezwzględnych lecz przeciwnych znakach, które znoszą się
wzajemnie.
SEM - siła elektromotoryczna ogniwa
(E)
Pomiędzy elektrodami ogniwa występuje różnica potencjałów,
którą nazywa się
napięciem ogniwa - E.
Gdy elektrody ogniwa połączymy zewnętrznym metalicznym
przewodnikiem,
to w ogniwie przebiega samorzutna reakcja chemiczna ( ∆
r
G <
0),
a w przewodniku zewnętrznym płyną elektrony (prąd).
Jeżeli przebieg tej samorzutnej reakcji chemicznej zostanie
zatrzymany przez przyłożenie do elektrod takiego napięcia z
zewnętrznego źródła, że układ jako całość znajdzie się w stanie
równowagi, to prąd przestanie płynąć, a reakcja zachodząca w
ogniwie osiągnie stan równowagi i będzie przebiegać w sposób
odwracalny. ⇄ . ( ∆
r
G = 0),
Różnica potencjałów elektrod takiego ogniwa niepracującego
nosi nazwę siły elektromotorycznej ogniwa SEM,
(E), lub napięcia w
warunkach bezprądowych.
Zgodnie z umową (UPAC)
siła elektromotoryczna ogniwa to różnica
potencjałów elektrody prawej i lewej.
E = φ
pr
- φ
lew
0
I
gdy
φ
-
φ
E
limU
E
lew
pr
0
I
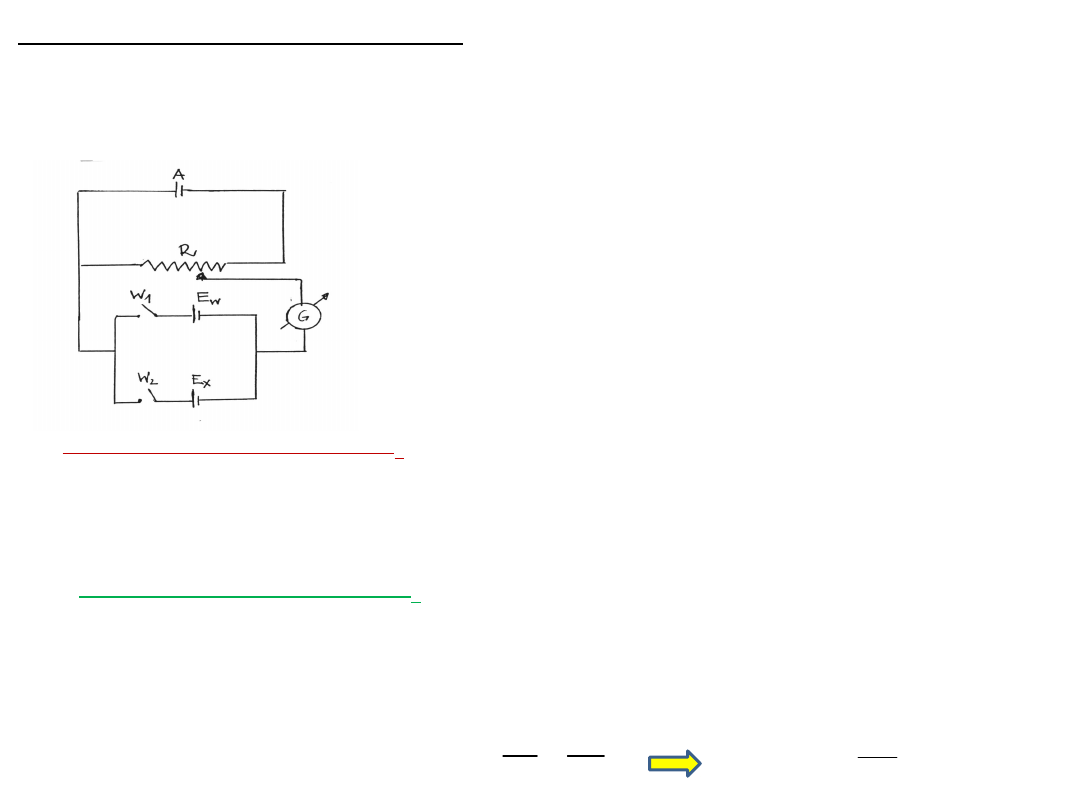
Wyznaczanie SEM ogniwa
Siła elektromotoryczna (E) ogniwa, lub napięcie ogniwa w warunkach
bezprądowych,
to napięcie ogniwa, przez które nie płynie prąd.
A - źródło prądu stałego o napięciu U
Z
E
w
- ogniwo wzorcowe (ogniwo Westona , E
W
= 1,018 V)
E
x
- ogniwo badane
R - opornik suwakowy
G - galwanometr
w
1
i w
2
– przełączniki zamykające dwa
obwody: z ogniwem wzorcowym E
W
i z
ogniwem badanym E
x
Schemat układu do potencjometrycznego pomiaru SEM
ogniwa
W
X
W
X
R
R
E
E
W
X
W
X
R
R
E
E
metoda kompensacyjna Poggendorfa
-
-
zrównoważenie napięcia ogniwa badanego U
X
zewnętrznym źródłem napięcia U
Z
1 zamknięty przełącznik w
1
gdy galwanometr nie wykazuje przepływu prądu spadek napięcia
U
w
na oporze R
w
kompensuje SEM ogniwa wzorcowego E
w
:
E
w
= U
w
= I R
w
2 zamknięty przełącznik w
2
gdy galwanometr nie wykazuje przepływu prądu spadek napięcia
U
x
na oporze R
x
kompensuje SEM ogniwa badanego E
x
:
E
x
= U
x
= I R
x
I- jest szczątkowym prądem w obwodzie, mniejszym od czułości
galwanometru.
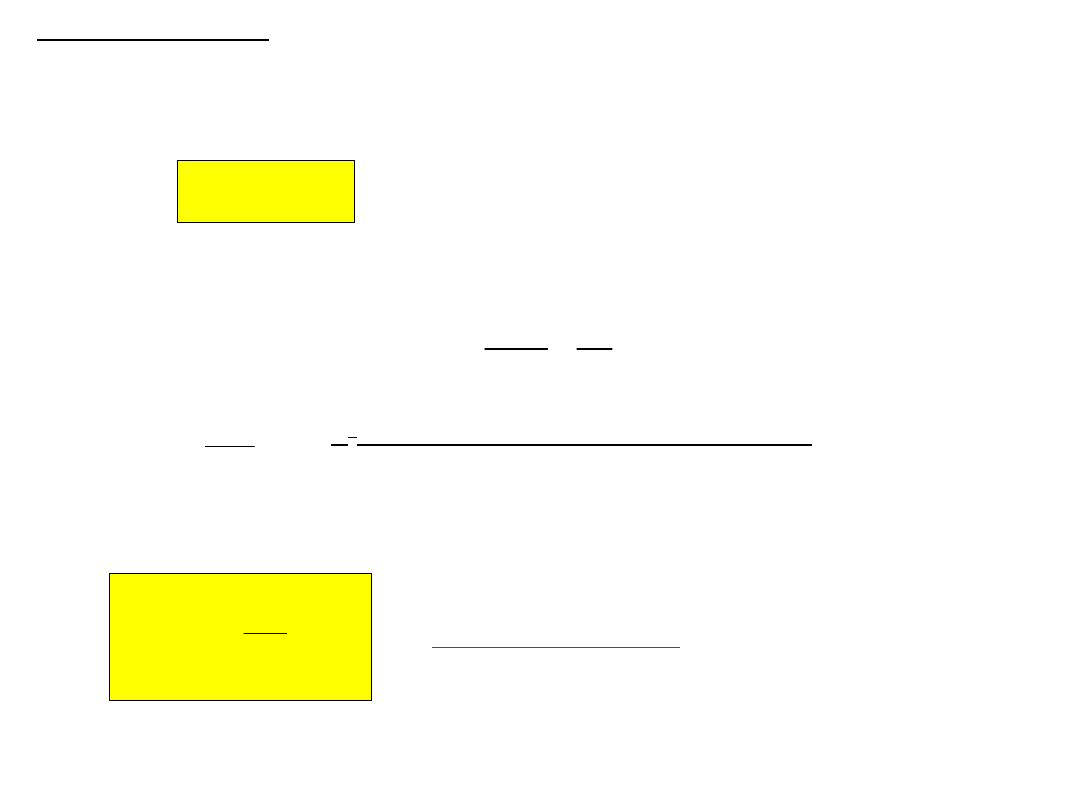
Dzieląc równania stronami otrzymujemy:
Obliczanie SEM - równanie
Nernsta
Zn ∣Zn
2+
∥ Cu
2+
∣ Cu
Zn
(s)
→ Zn
2+
+ 2e
Cu
2+
+ 2e →
Cu
(s)
Zn
(s)
+ Cu
2+
⇄ Zn
2+
+ Cu
(s)
E – różnica potencjałów między elektrodami
q – ładunek elektronów , który przepływa między
elektrodami q = - z F
z – liczba e wymienianych w reakcji
F – stała Faraday’a = ładunek 1 mola elektronów = e
N
A
= 96485 Cmol
-1
(s)
2
(s)
2
Zn
Cu
Cu
Zn
0
r
r
a
a
a
a
RTln
G
Δ
G
Δ
Jeżeli elektrody zbudowane są z
substancji czystych, to ich
aktywności a
(s)
= 1
Q - iloraz reakcji
zachodzącej w
ogniwie
W ogniwie galwanicznym
energia wytwarzana
w reakcji chemicznej zamienia się w pracę
elektryczną
przeniesienia ładunku w polu
elektrycznym określonym różnicą potencjałów
E
RTlnQ
G
Δ
G
Δ
a
a
RTln
G
Δ
G
Δ
0
r
r
Cu
Zn
0
r
r
2
2
lub
Praca elektryczna w
el
to praca przeniesienia ładunku q w polu
określonym różnicą potencjałów E
Dla procesu izotermiczno- izobarycznego użyteczna
praca elektryczna
,
którą układ może wykonać jest równa
G
r
w
el
= q E = -zFE
Obliczanie SEM - równanie
Nernsta
RTlnQ
G
Δ
zFE
0
r
lnQ
zF
RT
zF
G
Δ
E
0
r
∆
r
G = - z F E
Równanie Nernsta
– zależność napięcia ogniwa (SEM) od jego
składu
lnQ
zF
RT
E
E
0
Entalpia swobodna reakcji chemicznej zachodzącej w ogniwie
zamienia się w pracę elektryc
zną
w
el
= -zFE
RTlnQ
G
Δ
G
Δ
0
r
r
E
0
- standardowe napięcie ogniwa czyli napięcie
ogniwa przy zerowym prądzie, gdy wszystkie
reagenty (substraty i produkty) znajdują się w
swych stanach standardowych: a
i
= 1, Q = 1, ln Q =
0
zF
ΔG
E
0
0
Siła elektromotoryczna ogniwa, SEM
SEM ogniwa zależy od standardowego napięcia ogniwa
E
0
= φ
0
pr
– φ
0
lew
i od aktywności jonów (Q) stężenia roztworów w półogniwach
.
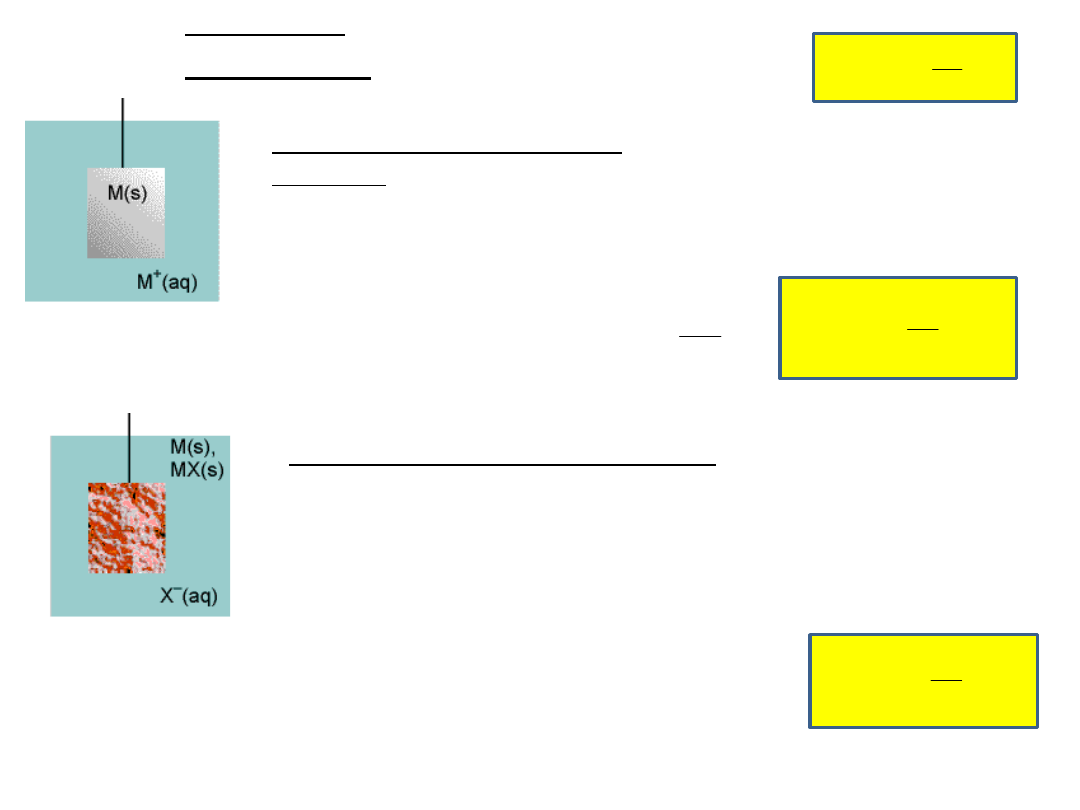
Rodzaje
półogniw
Półogniwa pierwszego
rodzaju
metal zanurzony w roztworze
swoich jonów
np. półogniwo srebrowe:
Ag
(s)
Ag
+
(aq)
Ag
+
(aq)
+ e → Ag
(s)
Półogniwa drugiego rodzaju
metal pokryty warstwą swojej trudno rozpuszczalnej
soli i zanurzony w elektrolicie o anionie wspólnym z
anionem trudno rozpuszczalnej soli
np. półogniwo chlorosrebrowe:
Ag
a
1
Q
Ag
(s)
AgCl
(s)
Cl
-
(aq)
AgCl
(s)
+ e → Ag
(s)
+ Cl
-
(aq)
Cl
a
Q
lnQ
zF
RT
Φ
Φ
0
Potencjał półogniwa
Ag
0
lna
F
RT
Φ
Φ
-
Cl
0
lna
F
RT
Φ
Φ
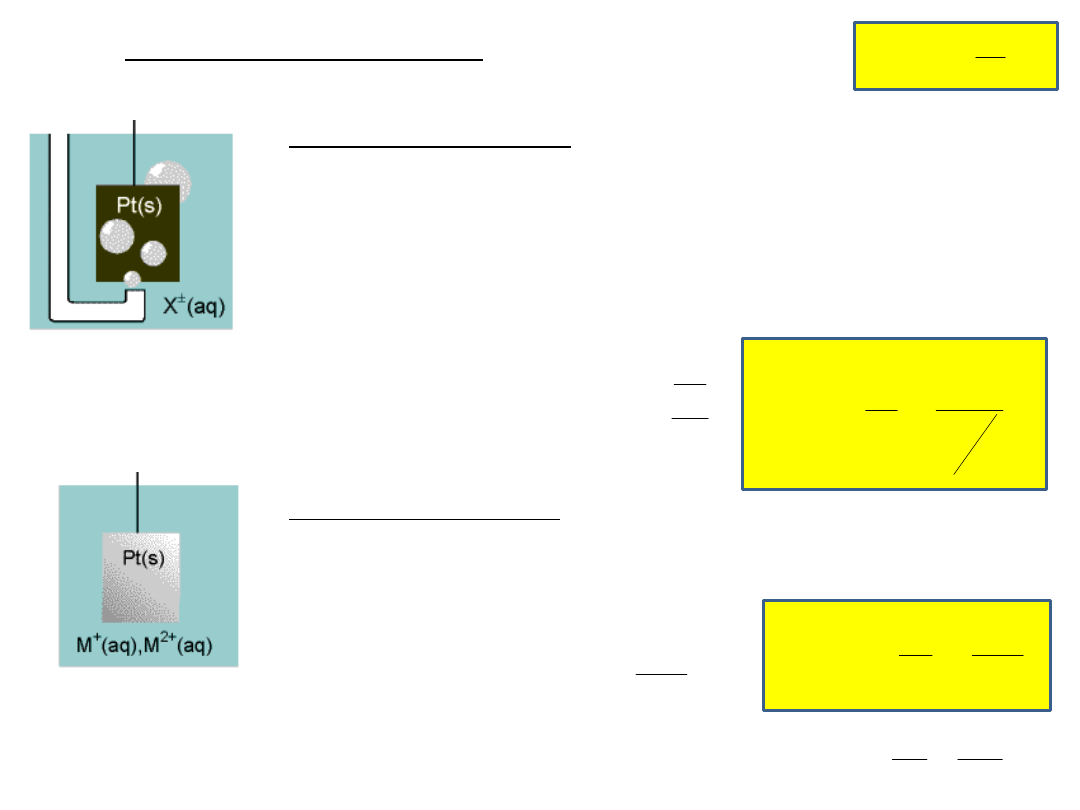
Rodzaje półogniw
Półogniwa gazowe
Elektroda z metalu chemicznie biernego( Pt) jest
omywana przez gaz i zanurzona w roztworze jonów tego
gazu
M
(s)
G
2(g)
G
+
(aq)
lub M
(s)
G
2(g)
G
-
(aq)
np. półogniwo wodorowe:
Pt
(s)
H
2(g)
H
+
(aq)
2H
+
(aq)
+ 2 e → H
2(g)
2
H
0
2
H
a
p
p
Q
Półogniwa redoks
Elektroda z metalu chemicznie biernego jest
zanurzona w roztworze zawierającym jony o różnych
stopniach utleniania:
Pt
(s)
Fe
2+
(aq)
, Fe
3+
(aq)
Fe
3+
(aq)
+ e → Fe
2+
(aq)
3
2
Fe
Fe
a
a
Q
3
2
Fe
Fe
0
a
a
ln
F
RT
Φ
Φ
0
H
2
H
0
p
p
a
ln
2F
RT
Φ
Φ
2
red
utl
0
a
a
ln
zF
RT
Φ
Φ
Potencjały elektrod zależą od aktywności jonów w roztworze.
lnQ
zF
RT
Φ
Φ
0
Potencjał półogniwa
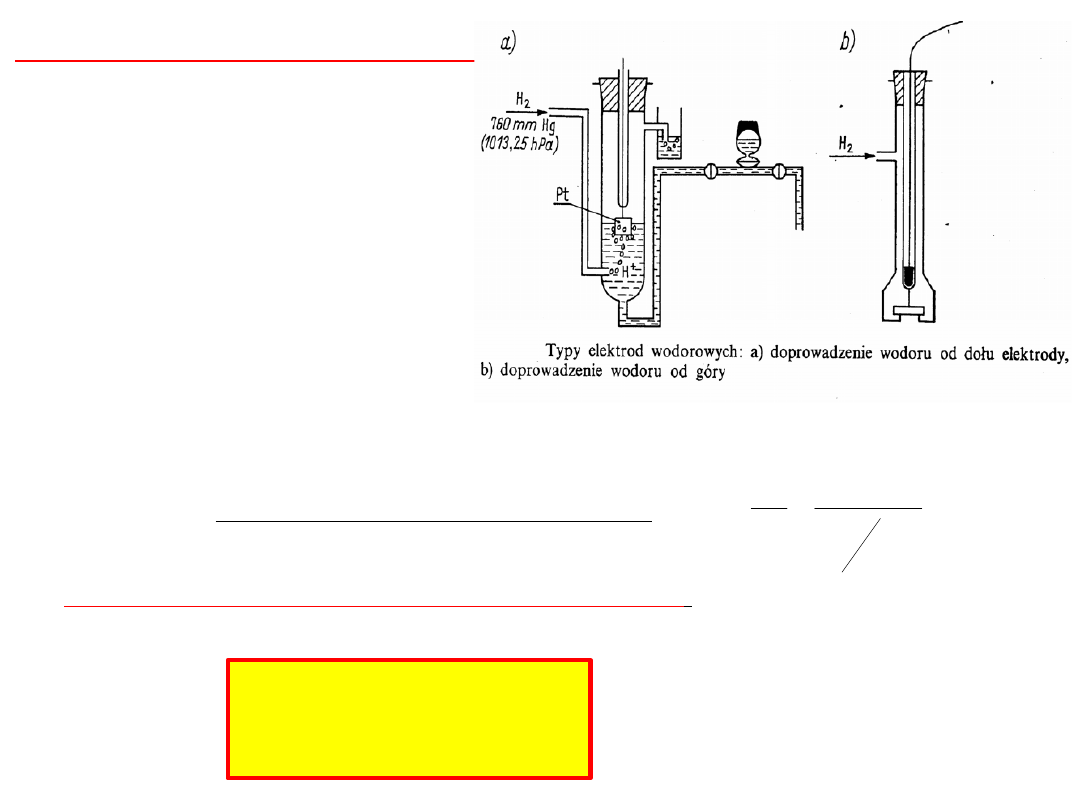
Standardowa elektroda wodorowa
blaszka platynowa pokryta
czernią platynową zanurzona w
roztworze kwasu, w którym
aktywność jonów wodorowych
a
H+
= 1 i opłukiwana gazowym
wodorem pod ciśnieniem p =
1,013 x 10
5
Pa.
Zgodnie z konwencją
sztokholmską IUPAC potencjał
dowolnej elektrody określa się
względem elektrody
wodorowej
Pt
(s)
H
2(g)
H
+
(aq)
na której przebiega reakcja
utleniania:
½ H
2(g)
→ H
+
(aq)
+ e
1/2
0
0
2
H
H
p
p
a
ln
F
RT
Φ
Φ
Potencjał elektrody wodorowej :
Potencjał standardowej elektrody wodorowej
:
0
0
Φ
Φ
1
a
Pa
5
10
1,013
p
H
2
H
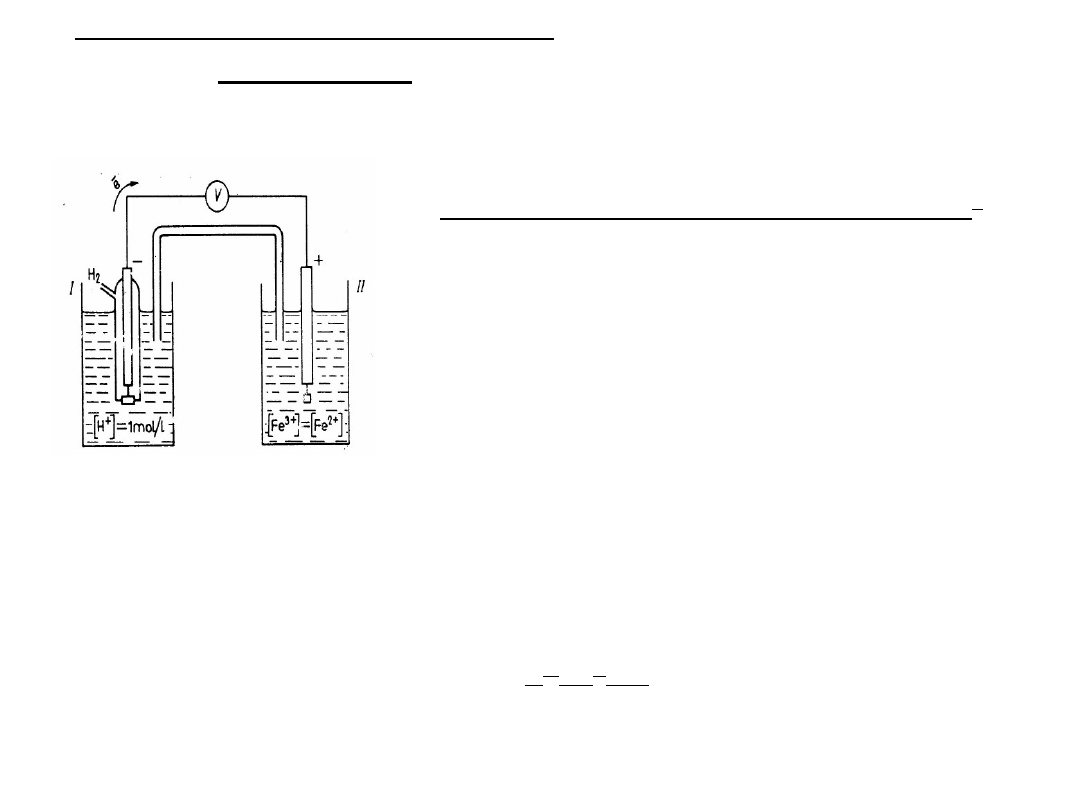
Potencjał standardowy
elektrody
Do wyznaczania potencjału elektrod jako układ odniesienia
przyjęto półogniwo wodorowe.
Potencjał standardowy elektrody E
0
to
SEM ogniwa złożonego z
elektrody
wodorowej jako anody
i
elektrody
badanej jako katody
.
Aktywności wszystkich reagentów w
standardowym ogniwie są równe 1.
E
0
= φ
praw
– φ
lew
=
φ
el
-
φ
0
el. wodor.
Potencjał standardowy elektrody
może przyjmować wartości dodatnie lub
ujemne
do zdefiniowania potencjału standardowego
elektrody wykorzystuje się reakcje
REDUKCJI :
X
+
+ e X
E
0
(X
+
/X)
Potencjał standardowy
elektrody
Na
+
/ Na Na
+
+ e → Na
- 2,714 V
Zn
2+
/ Zn Zn
2+
+ 2e → Zn
- 0,763 V
H
+
/ H
2
H
+
+ e → ½ H
2
0
Cu
2+
/ Cu Cu
2+
+ 2e → Cu
+ 0,337 V
Ag
+
/ Ag Ag
+
+ e → Ag
+ 0,799 V
E
0
< 0 oznacza,
że na tej elektrodzie zachodzi
UTLENIANIE, a na wodorowej
redukcja
E
0
> 0 oznacza,
że na tej elektrodzie zachodzi
REDUKCJA, a na wodorowej
utlenianie
Ujemna wartość potencjału standardowego (E
0
< 0 ΔG
0
= - z F
E
0
> 0)
wskazuje, że
na elektrodzie samorzutnie zachodzi
reakcja przeciwna do
założonej,
czyli na elektrodzie zachodzi
reakcja utleniania
,
a
na elektrodzie wodorowej zachodzi reakcja redukcji.
zF
ΔG
E
0
0
E
0
(X
+
/X)
Zastosowanie potencjałów standardowych par
redoks E
0
(X
+
/X)
Substancje o
niskich potencjałach redoks są silnymi
reduktorami
, a te o
wysokich potencjałach redoks – silnymi
utleniaczami.
Substancja o wyższym potencjale redoks zdolna jest utlenić
każdą substancję o niższym potencjale redoks.
Potencjał redoks
jest miarą zdolności do pobierania lub
oddawania elektronów przez układ i decyduje o
kierunku
samorzutnej reakcji redoks
.
Reakcja redoks może przebiegać samorzutnie , gdy utleniaczem
będzie forma utleniona pary redoks o wyższym potencjale,
natomiast reduktorem będzie forma zredukowana pary
redoks o niższym potencjale redoks
r
G
0
=-zFE
0
r
G
0
- zależy od zapisu równania stechiometrycznego reakcji
zachodzącej w ogniwie.
Potencjał standardowy ogniwa czy półogniwa nie zależy od zapisu
równania stechiometrycznego reakcji zachodzącej w ogniwie
zF
G
Δ
E
0
r
0
Określenie kierunku reakcji na podstawie E
0
reagentów
Proces korozji ()
)
c
(
aq
)
g
(
aq
)
s
(
O
H
Fe
O
H
Fe
2
2
2
2
1
2
Reakcja będzie przebiegać samorzutnie gdy
r
G
0
< 0,
czyli potencjał
standardowy reakcji E
0
> 0
Połówkowe reakcje redukcji:
0,44V
/Fe
Fe
E
Fe
2e
Fe
(a)
2
0
(s)
2
aq
1,23V
O)
/H
(O
E
O
H
2e
O
2
1
2H
(b)
2
2
0
(c)
2
2(g)
aq
() = (b) – (a) =
r
G
0
() =
r
G
0
(b) -
r
G
0
(a)
r
G
0
= - zFE
0
-zFE
0
() = - zFE
0
(b) + zFE
0
(a)
E
0
()
= E
0
(b) - E
0
(a) = 1,23V +0,44V =
+1,67 V
r
G
0
() = -2F (1,67V) < 0 K>1
reakcja () przebiega w kierunku tworzenia produktów
r
G
0
=-zFE
0
(s)
(c)
2
2
aq
2(g)
aq
Fe
O
H
2e
Fe
2e
O
2
1
2H
Wyznaczanie standardowego potencjału pary redoks na
podstawie innych wartości E
0
Mając dane:
E
0
(Cu
2+
/Cu) = +0,340 V i E
0
(Cu
+
/Cu) = +0,522 V
obliczyć
E
0
(Cu
2+
/Cu
+
)
0,522V
F
(b)
G
Δ
0,522V
/Cu)
(Cu
E
Cu
e
Cu
(b)
0,340V
2F
(a)
G
Δ
0,340V
/Cu)
(Cu
E
Cu
2e
Cu
(a)
0
r
0
(s)
aq
0
r
2
0
(s)
2
aq
?
)
/Cu
(Cu
E
Cu
e
Cu
(c)
2
0
aq
2
aq
(c) = (a) - (b)
r
G
0
(c) =
r
G
0
(a) -
r
G
0
(b)
r
G
0
= -zFE
0
-F E
0
(Cu
2+
/Cu
+
) = -2F E
0
(Cu
2+
/Cu) +F E
0
(Cu
+
/Cu)
- E
0
(Cu
2+
/Cu
+
) = -2(+0,340V) + (0,522V)
E
0
(Cu
2+
/Cu
+
) = +0,16V
Na
r
G
0
można wykonywać proste działania matematyczne takie
jak na równaniach stechiometrycznych natomiast nie można tego
robić bezpośrednio na E
0
Związek między SEM ogniwa
a funkcjami termodynamicznymi reakcji zachodzącej w ogniwie
lnQ
zF
RT
E
E
0
a
0
lnK
zF
RT
E
RT
zFE
lnK
0
a
∆
r
G
0
= - z F E
0
Jeżeli reakcja chemiczna w ogniwie osiągnie stan
równowagi to Q = K
a
i E = 0
ΔS
T
)
G
(
p
p
p
T
E
zF
T
G
0
0
)
(
p
r
T
E
zF
S
0
0
Zależność entropii reakcji od
SEM ogniwa
Zależność entalpii swobodnej reakcji od SEM ogniwa
G = H -
TS
∆
r
H = ∆
r
G + T∆
r
S
T
E
T
E
zF
T
E
zF
T
zFE
H
r
0
0
0
0
0
T
E
T
E
zF
H
r
0
0
0
Zależność entalpii reakcji od SEM ogniwa
współczynnik
temperaturowy
napięcia ogniwa
Pomiary elektryczne standardowego napięcia ogniwa E
0
mogą być
wykorzystywane do wyznaczania standardowych funkcji
termodynamicznych reakcji zachodzących w ogniwie.
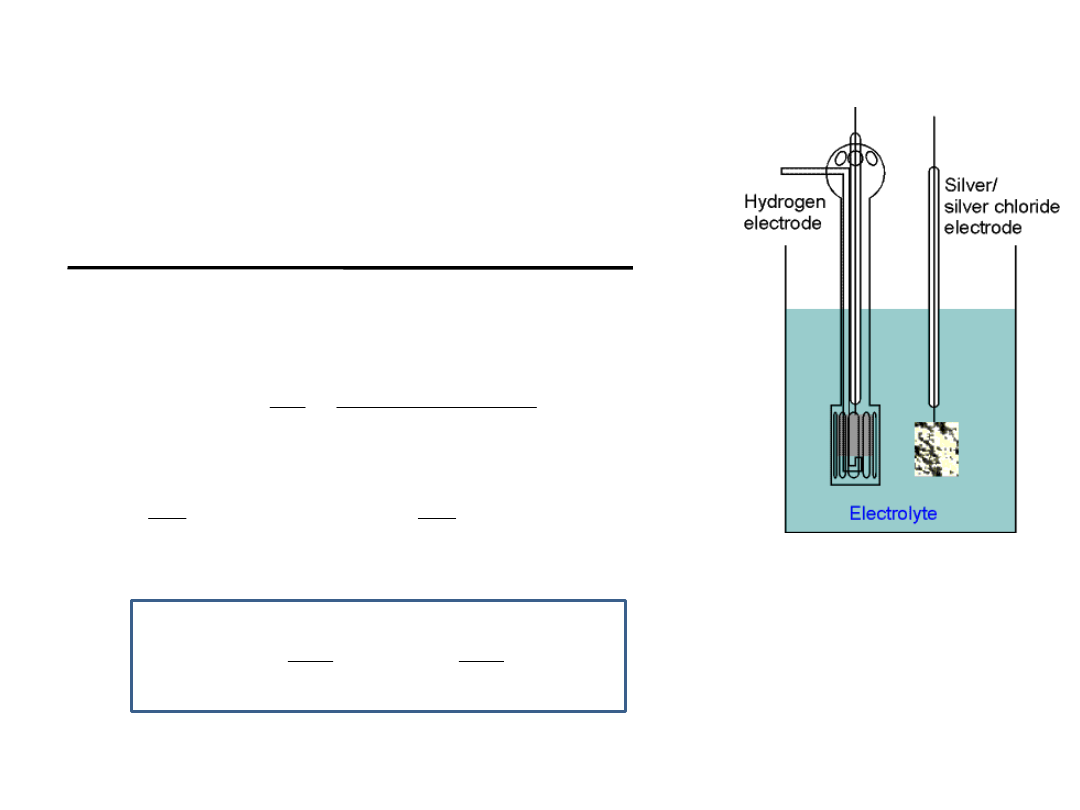
Wyznaczanie standardowej SEM
( E
0
)
Pt
(s)
H
2(g)
HCl
(c)
AgCl
(s)
,Ag
(s)
⊖
½ H
2
→ H
+
+ e
⊕
AgCl + e → Ag
(s)
+ Cl
-
½ H
2
+ AgCl
(s)
= Ag
(s)
+ H
+
+Cl
-
AgCl
1/2
0
H
Ag
Cl
H
0
a
)
/p
(p
a
a
a
ln
F
RT
E
E
2
)
γ
γ
m
ln(m
F
RT
E
)
a
ln(a
F
RT
E
E
_
Cl
H
Cl
H
Cl
H
0
0
2
2
0
)
ln(γ
F
RT
ln(m
F
RT
E
E
)
dla elektrolitu 1:1 m
+
=m
-
=m,
+
=
-
=
, moc
jonowa I = m
)
ln(γ
F
2RT
ln(m)
F
2RT
E
E
0
Jeżeli I < 0,01, to
ln
= - A I z
+
z
-
I I
0,5
= - A m
0,5
(graniczne prawo D-H)
)
m
A
(
F
2RT
lnm
F
2RT
E
E
0
m
b
E
lnm
F
2RT
E
0
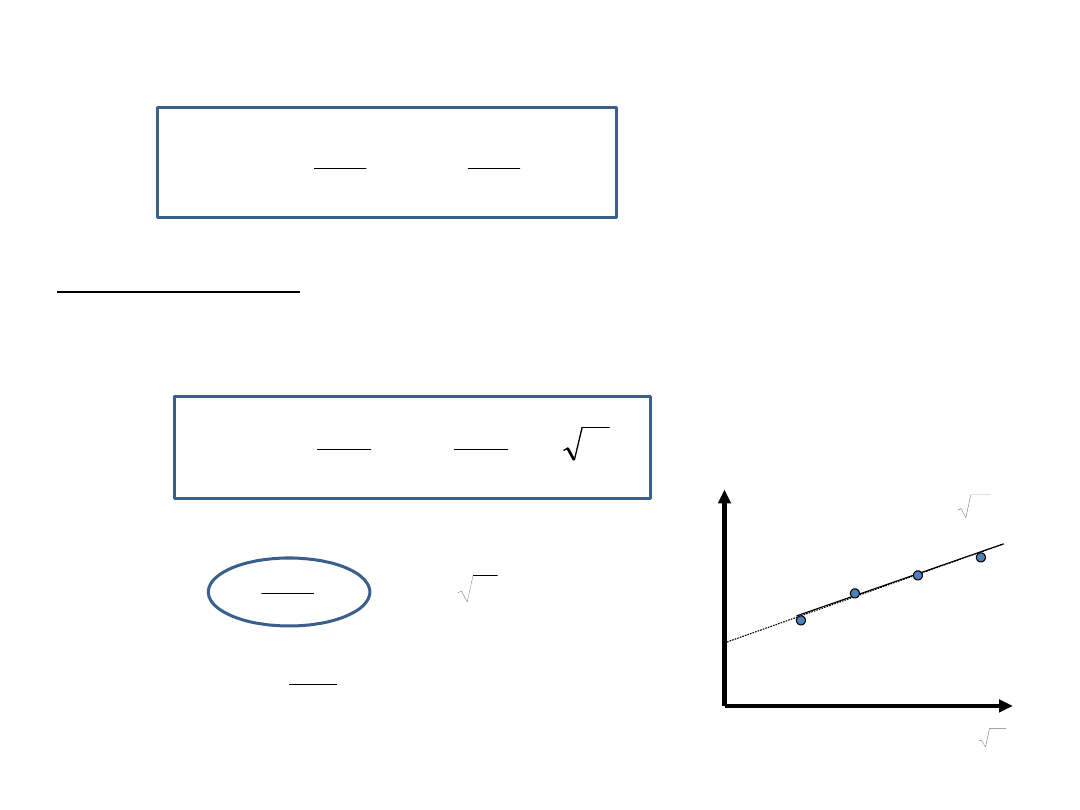
zmierzona SEM ogniwa dla określonej wartości
stężenia molarnego elektrolitu m jest liniową
funkcją m
0,5
.
lnm
F
2RT
E
y
y
m
E
0
m
b
E
y
0
Wyznaczanie standardowej SEM
( E
0
)
Zastosowanie pomiarów SEM
1.
Wyznaczanie stałej równowagi reakcji zachodzącej
w ogniwie
oraz funkcji termodynamicznych
charakteryzujących tę reakcję
:
RT
zFE
lnK
0
a
T
E
T
E
zF
H
Δ
0
0
0
r
T
E
zF
S
Δ
0
0
r
∆
r
G
0
= - z F E
0
Zastosowanie pomiarów SEM
2. Wyznaczanie średniego jonowego współczynnika aktywności
Pt
(s)
H
⃒
2(g)
HCl
⃒
(c)
AgCl
⃒
(s)
, Ag
(s)
½ H
2
+ AgCl
(s)
= Ag
(s)
+ H
+
+Cl
-
średni jonowy współczynnik aktywności
kwasu solnego o stężeniu m [molkg
-1
]
)
2
2
0
0
γ
ln(m
F
RT
E
)
a
ln(a
F
RT
E
E
Cl
H
lnm
2RT
F
E
E
lnγ
0
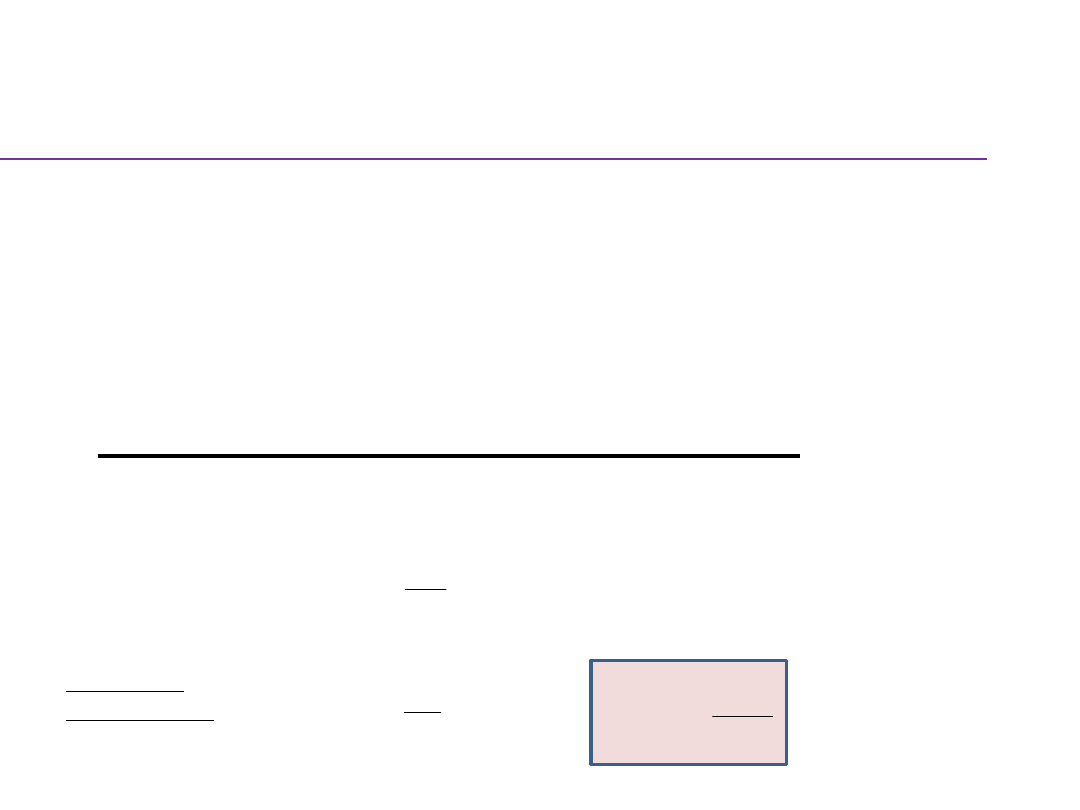
Zastosowanie pomiarów SEM
3. Wyznaczanie iloczynu rozpuszczalności soli trudno rozpuszczalnych
2
2
2
S
Zn
s
2
(aq)
2
(aq)
O
H
(s)
a
a
K
S
Zn
ZnS
Zn
(s)
l Zn
2+
(aq)
ll S
2-
(aq)
l ZnS
(s)
, Zn
(s)
⊖ utl. Zn
(s)
→ Zn
2+
+ 2 e ⊕ red. ZnS
(s)
+ 2 e → Zn
(s)
+ S
2-
(aq)
2
(aq)
2
(aq)
(s)
S
Zn
ZnS
2
S
2
Zn
a
a
ln
2F
RT
E
E
0
W stanie
równowagi:
E = 0, a Q =
K
s
= IR
s
0
lnK
2F
RT
E
RT
2FE
ln(IR)
0
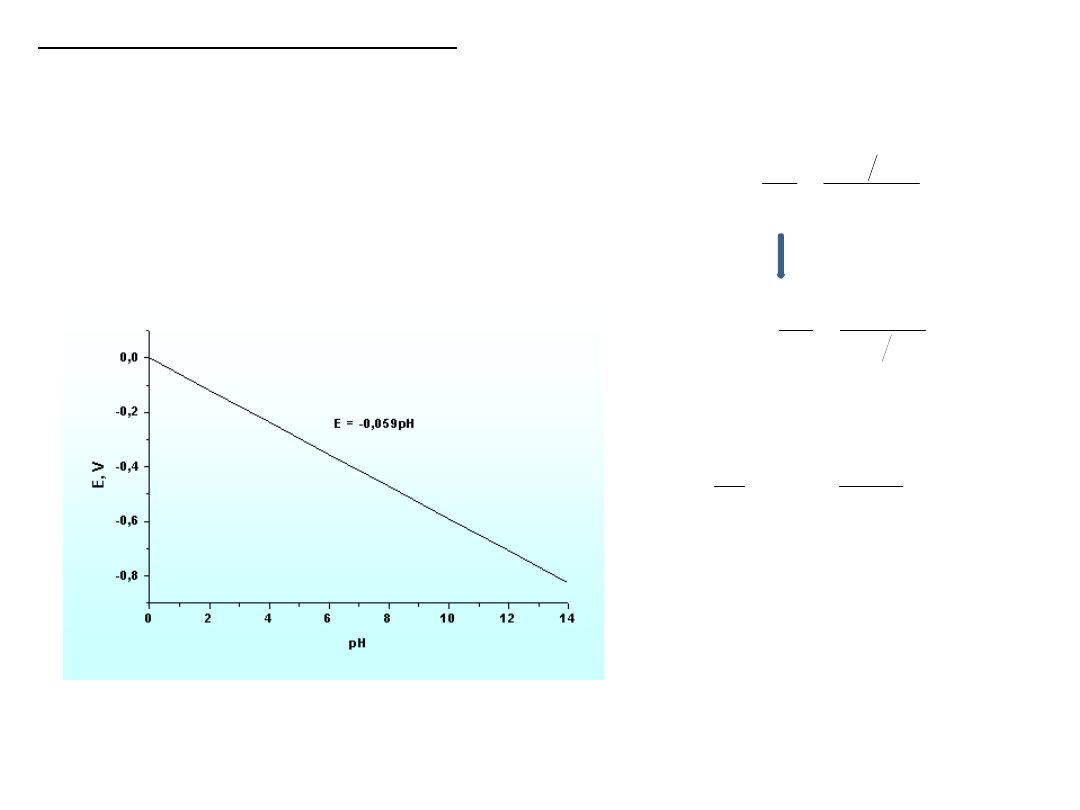
Wyznaczanie pH roztworów
W elektrochemicznym pomiarze pH wykorzystuje się liniową zależność
potencjału niektórych elektrod od pH roztworu.
pH
b
pH
F
2,3RT
lna
F
RT
E
H
/H
H
)
p
p
(
a
ln
2F
RT
E
E
0
H
2
H
0
/H
H
/H
H
2
2
H
2e
2H
Dla elektrody wodorowej
zależność ta wynika z
równania Nernsta
Zależność potencjału elektrody wodorowej od pH
2
H
0
H
0
/H
H
/H
H
a
)
p
p
(
ln
2F
RT
E
E
2
Document Outline