PODSTAWY

OBLICZEŃ

PRZEKŁADNI

ZĘBATYCH

Prowadzący:

Wykonała:

Monika Marciniak

Prof. dr hab. inż. Romuald
Będziński

Przekładnia:
Mechanizm służący do przenoszenia ruchu
obrotowego z wału czynnego (napędzającego) na
wał bierny (napędzany).

Przekładnia zębata:
Przekładnia mechaniczna, w której ruch obrotowy
jednego wału jest przenoszony na drugi, w wyniku
zazębienia się koła zębatego czynnego z kołem
zębatym biernym.

P

R

Z

E

K

Ł

A

D

N

I

E

Z

Ę

B

A

T

E

C

Z

O

Ł

O

W

E

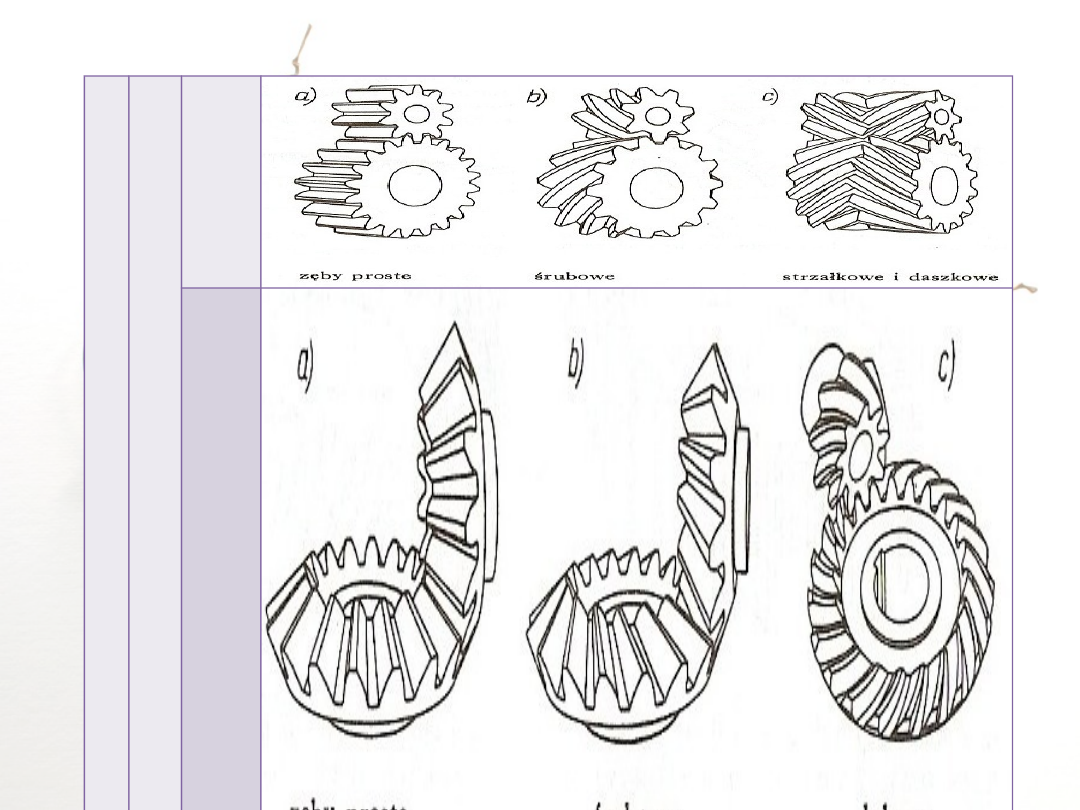
Wal

cow

e

(ró

wno

legł

e)

Sto

żko

we

(kąt

owe

)

P

R

Z

E

K

Ł

A

D

N

I

E

Z

Ę

B

A

T

E

Ś

R

U

B

O

W

E

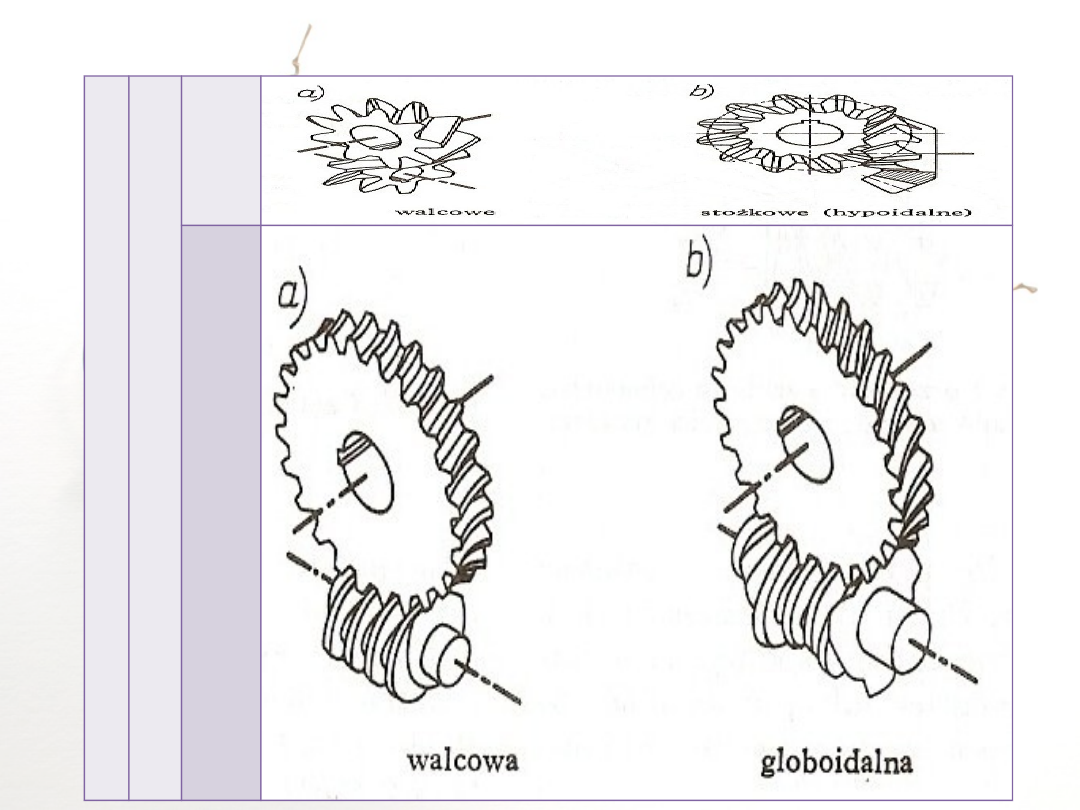
Hyp

erb

oloi

dal

ne

Śli

mak

owe

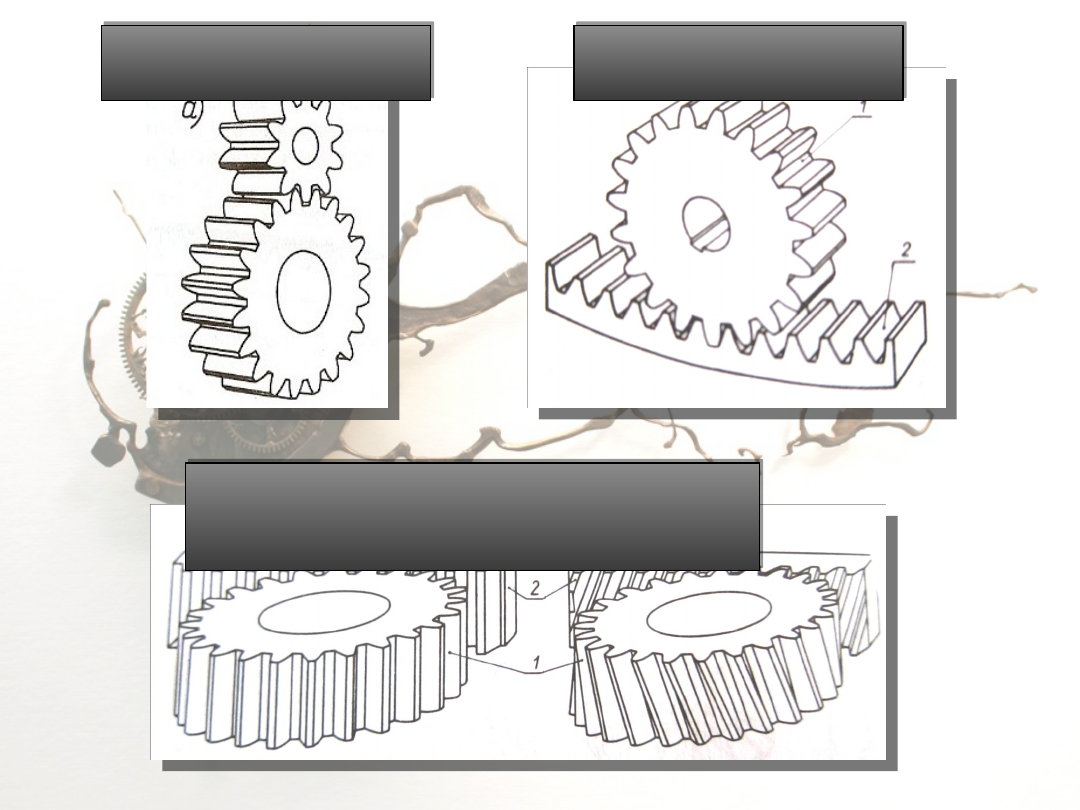
Zazębienie

zewnętrzne

Zazębienie

zewnętrzne

Zazębienie

wewnętrzne

Zazębienie

wewnętrzne

Zazębienie walcowego koła z zębatką

prostą o uzębieniu prostym lub

śrubowym

Zazębienie walcowego koła z zębatką

prostą o uzębieniu prostym lub

śrubowym

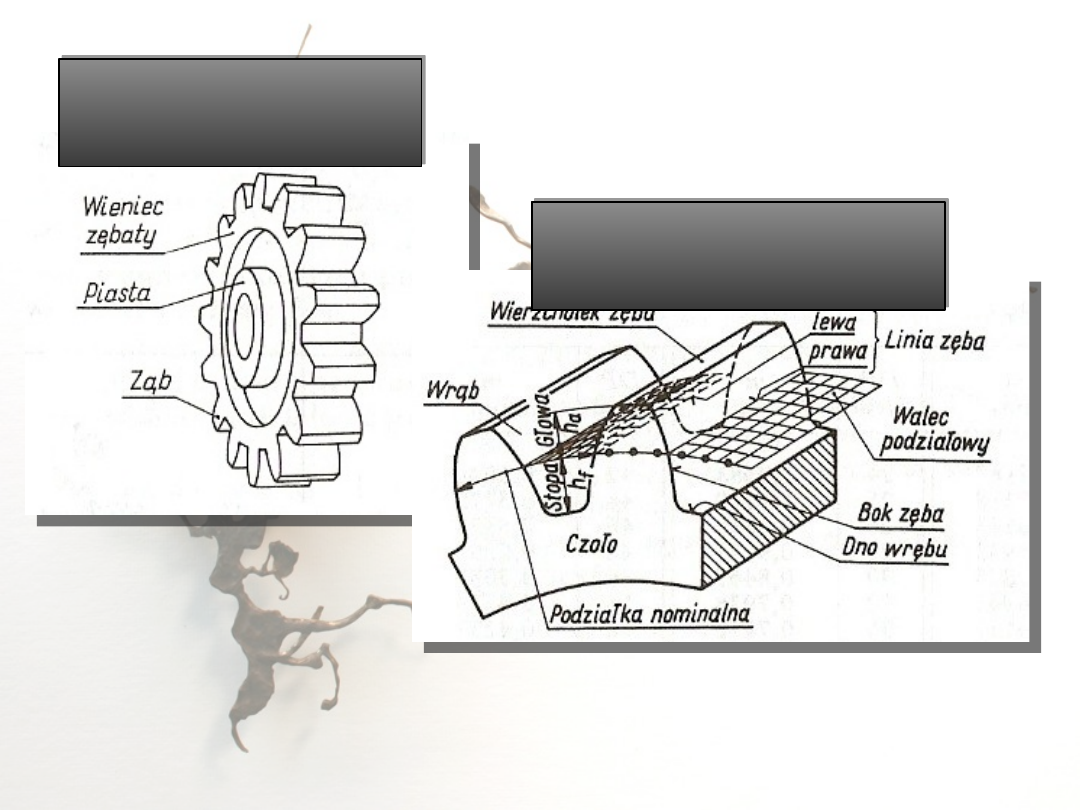
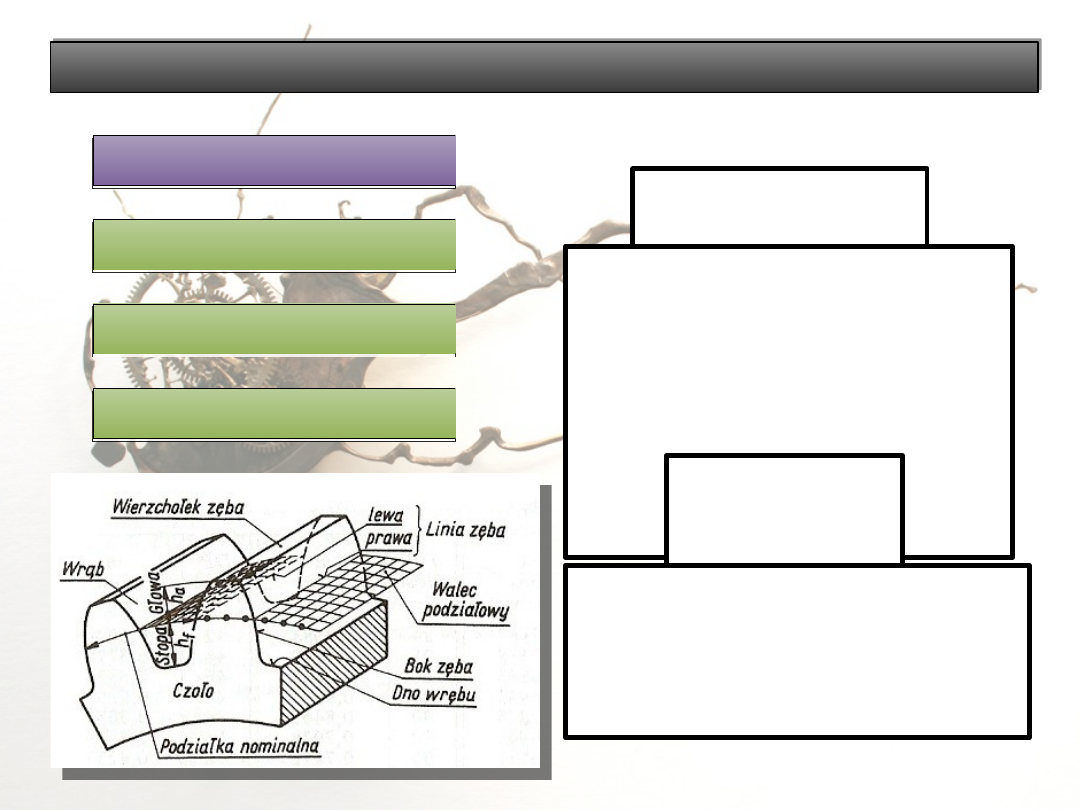
Części składowe

walcowego koła

zębatego

Części składowe

walcowego koła

zębatego

Zasadnicze wielkości

określające uzębienie koła

zębatego

Zasadnicze wielkości

określające uzębienie koła

zębatego

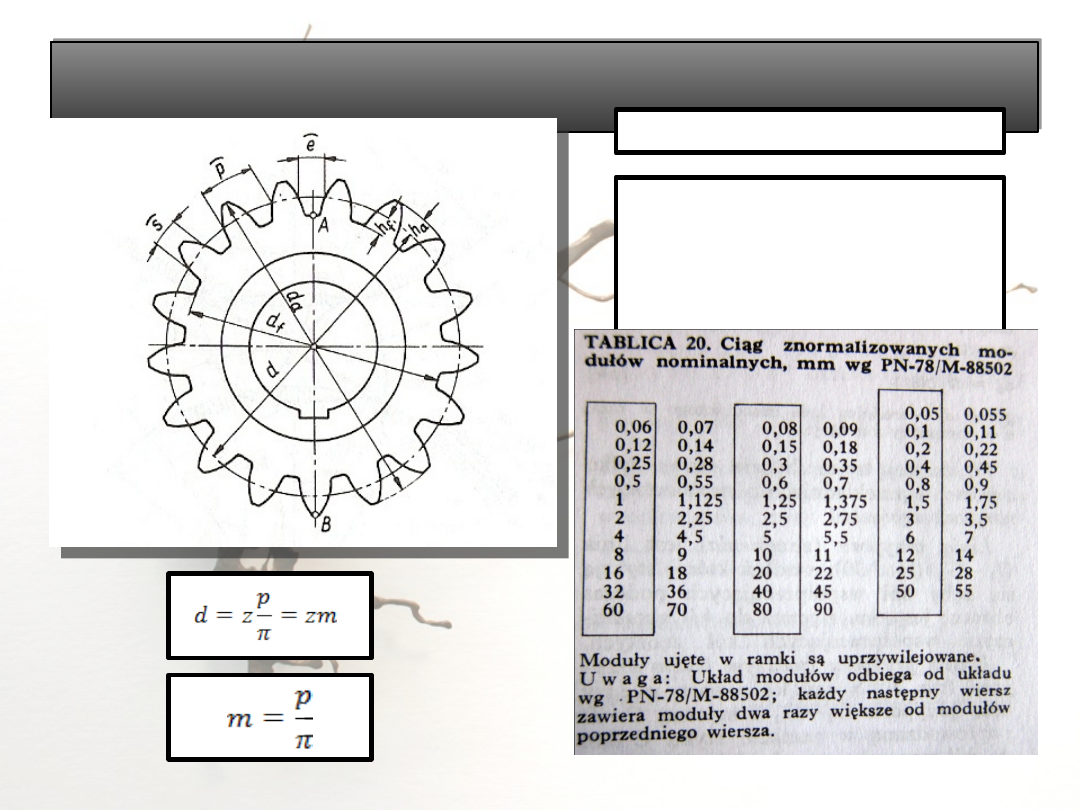
Podstawowe wymiary uzębienia i koła zębatego

walcowego

Podstawowe wymiary uzębienia i koła zębatego

walcowego

d – średnica podziałowa
[mm],
p – podziałka nominalna
[mm],
z – liczba zębów w kole,
m – moduł nominalny.

KOŁO PODZIAŁOWE

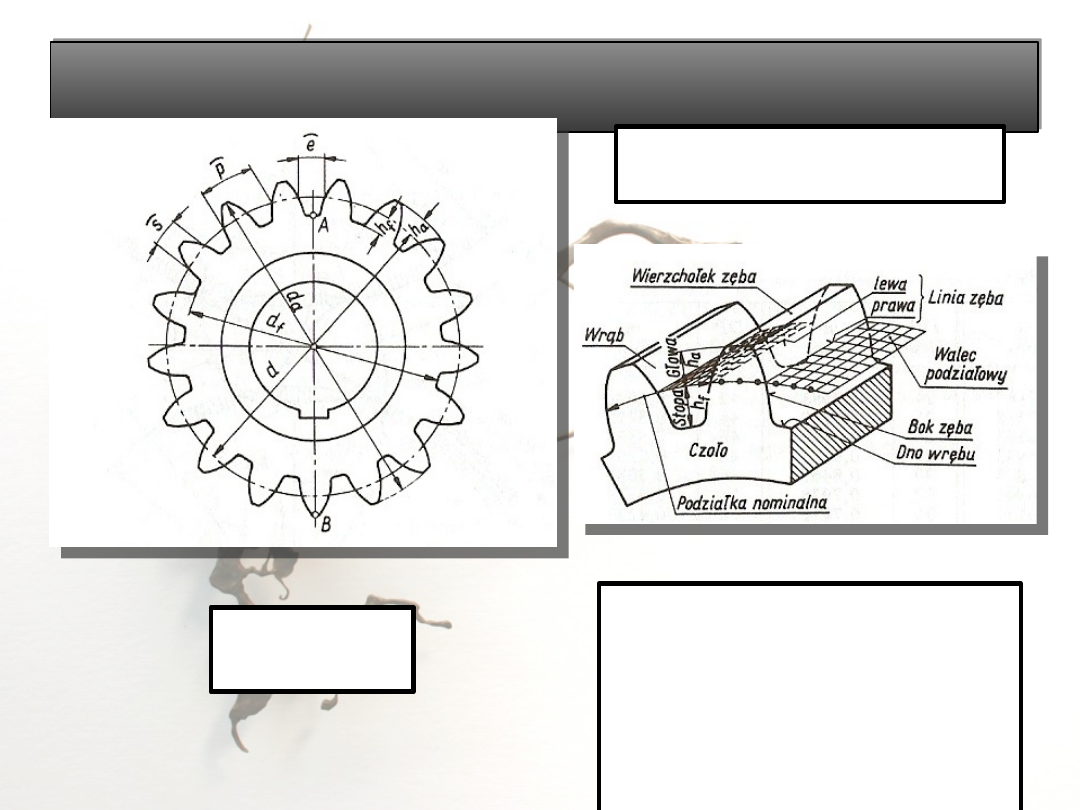
Podstawowe wymiary uzębienia i koła zębatego

walcowego

Podstawowe wymiary uzębienia i koła zębatego

walcowego

d

a

= d + 2h

a

d

f

= d – 2h

f

KOŁO WIERZCHOŁKOWE I

DNA WRĘBÓW

d

a

– średnica wierzchołkowa

[mm],
h

a

– wysokość głowy

zęba[mm],
d

f

– średnica dna wrębów

[mm],
h

f

– wysokość stopy zęba

[mm].

Zarysy boków zębów

Zarysy boków zębów

cykloidalne

cykloidalne

ewolwentowe

ewolwentowe

specjalne

specjalne

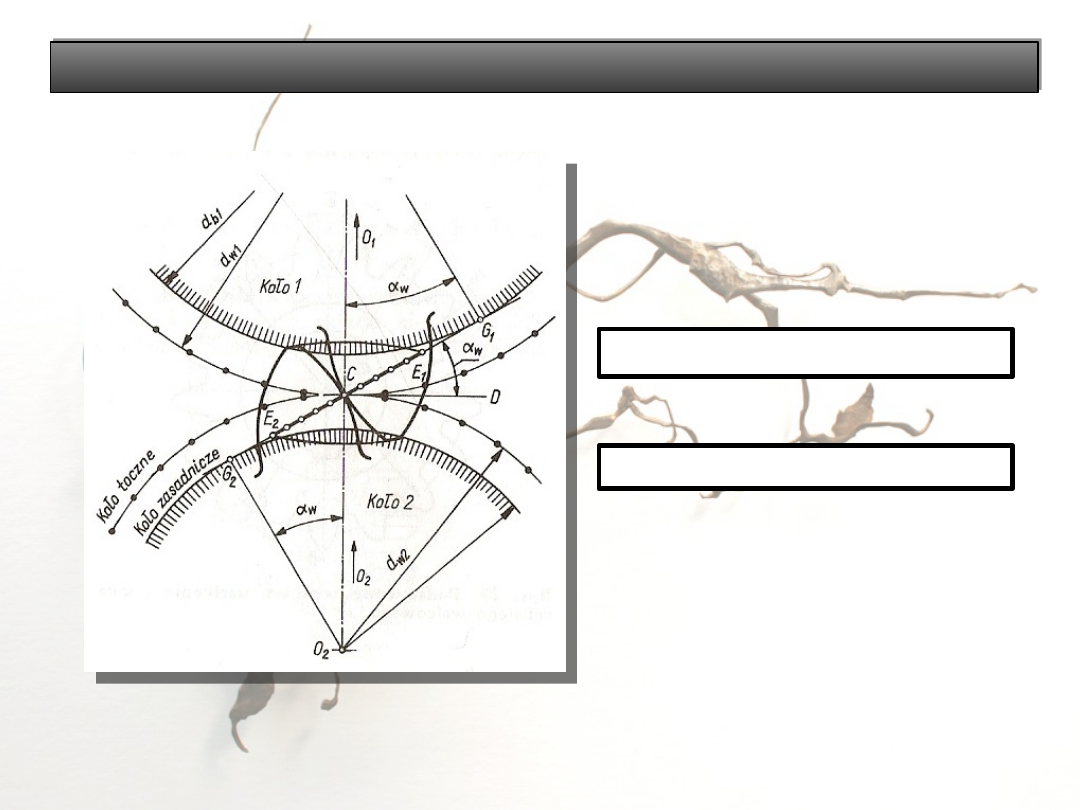
Ewolwentą jest krzywa, którą otrzymuje się przez

odwijanie nici z koła zasadniczego, którego średnicę

oblicza się ze wzoru:

d

b

= d cosα

d

b

- średnica koła zasadniczego

[mm],
α – nominalny kąt zarysu

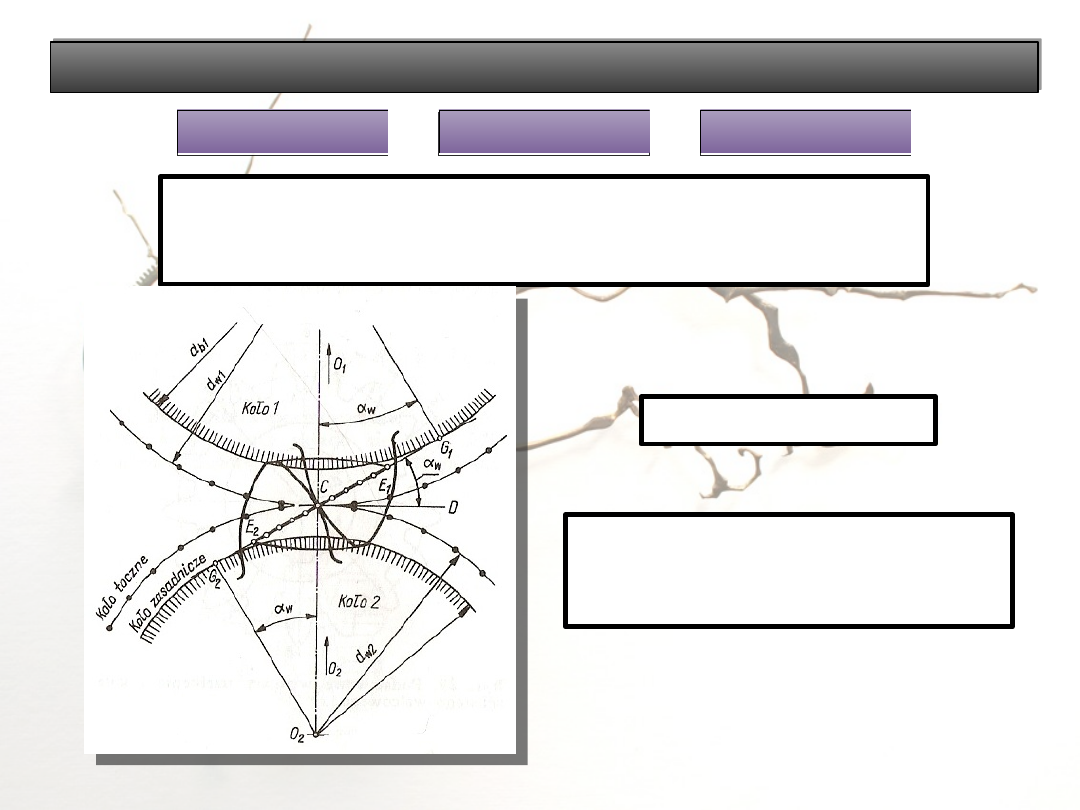
Zarysy boków zębów

Zarysy boków zębów

Linia przyporu: linia G

1

– G

2

Kąt przyporu: α

Klasyfikacja uzębienia

Klasyfikacja uzębienia

Typy zębów

Typy zębów

normalne

normalne

niskie

niskie

wysokie

wysokie

h = h

a

+ h

f

= 2ym

+ c

h – całkowita wysokość zęba
[mm],
h

a

– wysokość głowy zęba

[mm],
h

f

– wysokość stopy zęba

[mm],
c – luz wierzchołkowy,
y – współczynnik wysokości
zęba.

c = (0,1 –
0,3)m
średnio c

m

=

0,2m

Gdy:
y = 1  zęby normalne, h = (2,1
– 2,3)m
y < 1  zęby niskie
y > 1  zęby wysokie

Klasyfikacja uzębienia

Klasyfikacja uzębienia

Odmiany zębów

Odmiany zębów

zerowa

zerowa

korygowana

korygowana

dzika

dzika

Wysokość

Odmiana zęba

Zerowy

Korygowany

Dziki

Głowy zęba

h

a

= ym

h

ak

= (y +

x)m

h

ad

= (y + x -

k)m

Stopy zęba

h

f

= ym + c

h

fk

= (y - x)m

+ c

h

fd

= (y - x)m

+ c

Całkowita

zęba

h = h

a

+ h

f

= h

ak

+ h

fk

= 2ym

+ c

h

d

= (2y –

k)m + c

Klasyfikacja uzębienia

Klasyfikacja uzębienia

Graniczna liczba zębów:
Najmniejsza liczba zębów w kole nie wykazujących podcięcia
podczas obróbki obwiedniowej.

Graniczna liczba zębów:
Najmniejsza liczba zębów w kole nie wykazujących podcięcia
podczas obróbki obwiedniowej.

z

g

– teoretyczna graniczna liczba zębów,

z

g

‘

– praktyczna graniczna liczba zębów (z nieszkodliwym

podcięciem zęba u podstawy),

Korelacja uzębienia:
Jest potrzebna w przypadku, gdy w kole o liczbie zębów z < z

g

chce się uniknąć podcięcia zęba u podstawy.

Korelacja uzębienia:
Jest potrzebna w przypadku, gdy w kole o liczbie zębów z < z

g

chce się uniknąć podcięcia zęba u podstawy.

Wielkość przesunięcia v zarysu zęba:
v = xm lub v

‘

= x

‘

m

Klasyfikacja uzębienia

Klasyfikacja uzębienia

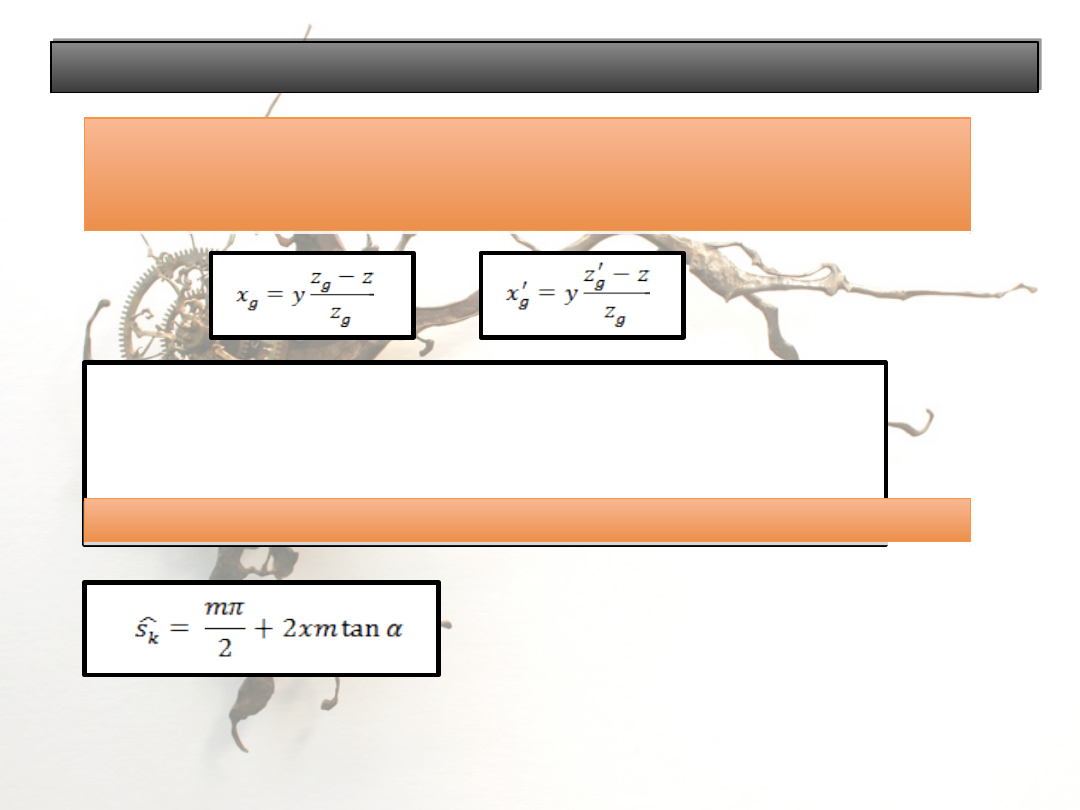
Współczynnik granicznego przesunięcia x

g

zarysu:

Najmniejsza wartość liczbowa współczynnika, przy której już
nie występuje podcięcie zęba.

Współczynnik granicznego przesunięcia x

g

zarysu:

Najmniejsza wartość liczbowa współczynnika, przy której już
nie występuje podcięcie zęba.

x

g

– współczynnik teoretycznego granicznego

przesunięcia zarysu zęba,
x’

g

– współczynnik praktycznego granicznego

przesunięcia zarysu zęba (z nieznacznym podcięciem
zęba)

Grubość zęba:

Grubość zęba:

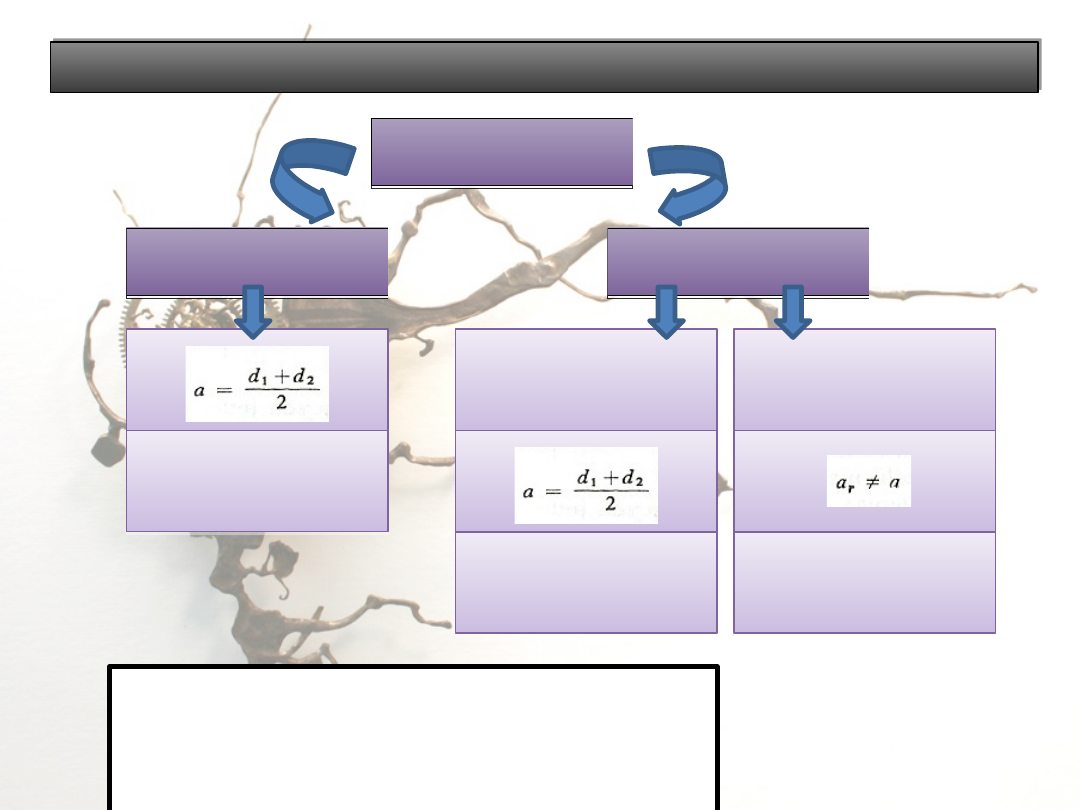
Rodzaje zazębień

Rodzaje zazębień

Zazębienie

Zazębienie

Zerowe

Zerowe

Korygowane

Korygowane

Zęby zerowe w

obu kołach

Zęby zerowe w

obu kołach

P - 0

P - 0

P

P

Zęby

korygowane

x

1

= - x

2

Zęby

korygowane

x

1

= - x

2

Zęby

korygowane

Zęby

korygowane

a

– zerowa odległość osi,

a

r

– rzeczywista odległość osi

x – współczynnik przesunięcia zarysu zęba
(korekcji)

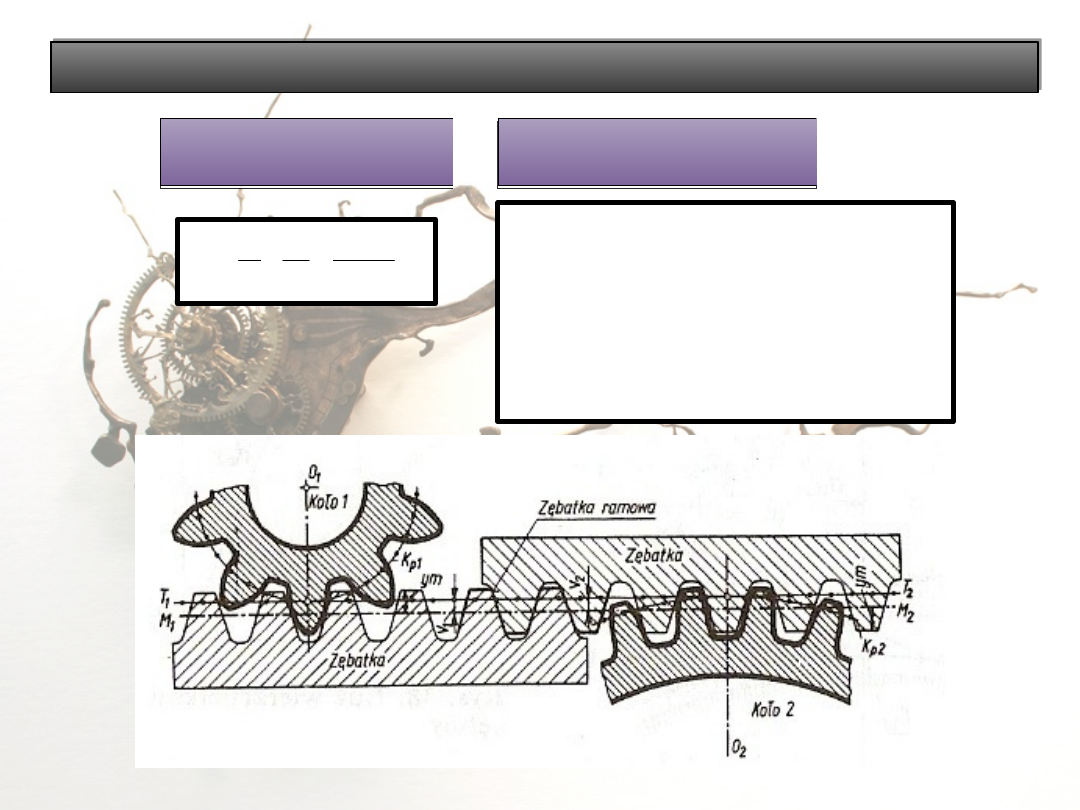
Klasyfikacja zazębienia

Klasyfikacja zazębienia

Zerowa odległość

osi a

Zerowa odległość

osi a

Korelacja

zazębienia P - 0

Korelacja

zazębienia P - 0

m

z

z

d

d

2

2

2

2

1

2

1







a =

Polega na przesunięciu
narzędzia zębatkowego w
jednym kole na zewnątrz o taką
samą wielkość, o jaką w drugim
kole – ku wnętrzu.
!WARUNEK: z

1

+ z

2

≥ 2z

g

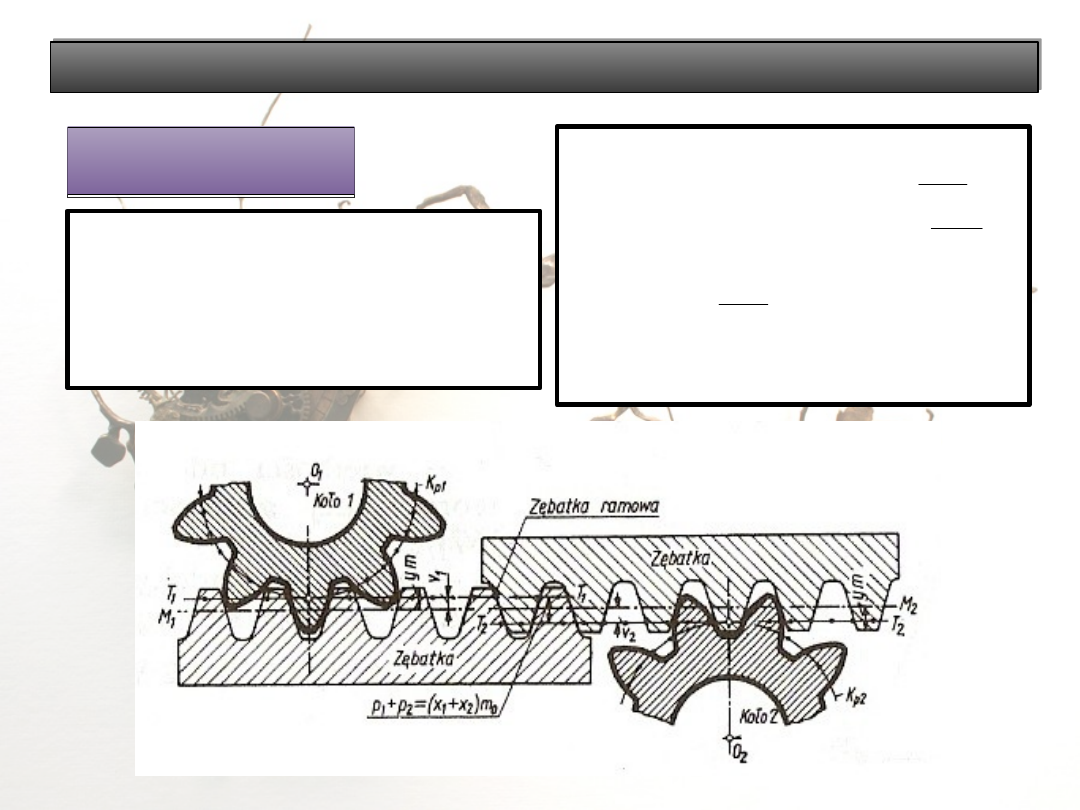
Klasyfikacja zazębienia

Klasyfikacja zazębienia

Korelacja

zazębienia P

Korelacja

zazębienia P

Stosowana gdy:
- warunek określony wzorem z

1

+ z

2

≥ 2z

g

nie może być

spełniony,
- z góry zakłada się a

r

≠ a

Pozorna odległość osi: a

p

= a +

(x

1

+x

2

)m,

Rzeczywista odległość osi: a

r

=

Średnica koła tocznego: d

w1

= 2a

r

Toczny kąt przyporu:
tgα

w

- α

w

= 2

Skrócenie zęba od wierzchołka:
km = a

p

- a

r

x

a





cos

cos

2

1

1

z

z

z


)

(

2

1

2

1















tg

tg

z

z

x

x

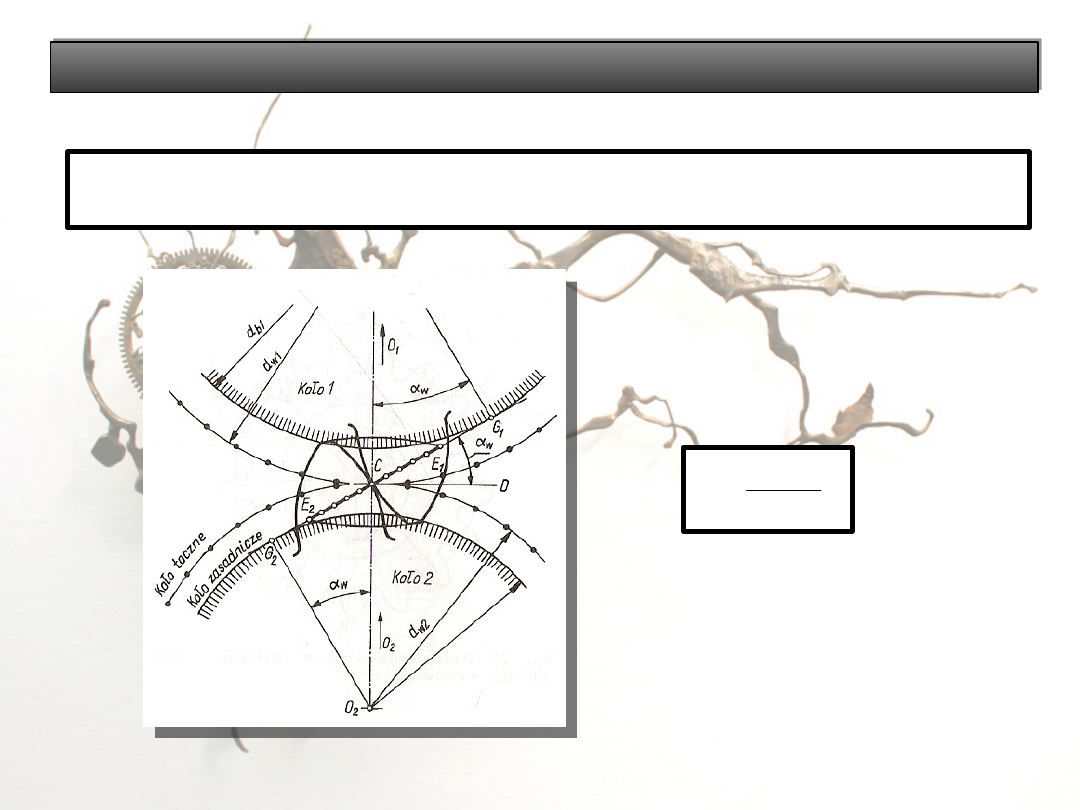
Stopień pokrycia

Stopień pokrycia

ε

α

=



cos

2

1

p

E

E

Stopień pokrycia - określa liczbę zębów pozostających
jednocześnie w zazębieniu.

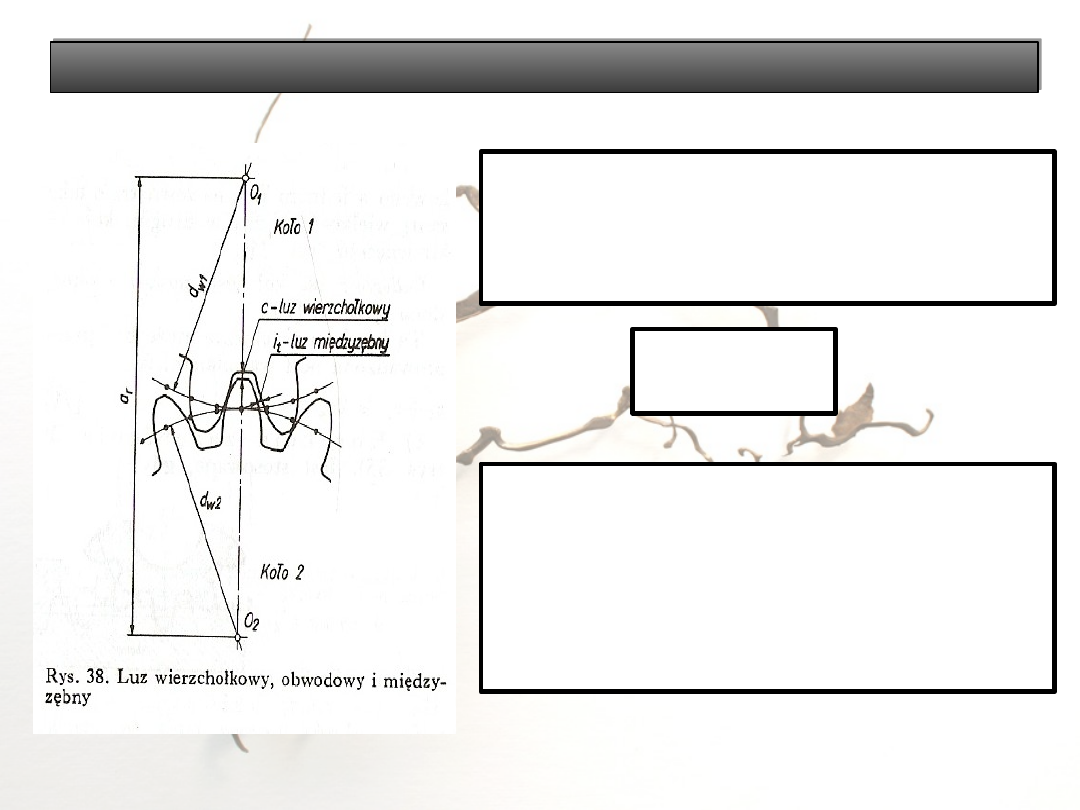
Luz obwodowy i międzyzębny

Luz obwodowy i międzyzębny

Luz obwodowy j – mierzy się wzdłuż
okręgu kół tocznych (podziałowych).
Luz międzyzębny j

n

– mierzy się

wzdłuż linii przyporu.

j

n

= j

t

cosα

w

Luz obwodowy j zależy od:
- wielkości odchyłek Δs

1

i Δs

2

od

teoretycznej grubości zębów

- wielkości odchyłki odległości Δa i
oblicza się wg wzoru: j

t

= -(Δs

1

+ Δs

2

) +

2 Δα tg α

w

Obliczenia wytrzymałościowe

Obliczenia wytrzymałościowe

Działanie sił na koła zębate powoduje:
- zginanie zębów,
- naciski na boki zębów z miejscu ich
zetknięcia.

Obciążenie działające na ząb koła oblicza się ze wzoru: P

zast

=

PC

p

C

d

N ,

gdzie:
P

zast

– zastępcze obciążenie [N],

P – obciążenie wynikające z mocy ustalonej [N],
C

p

- współczynnik przeciążenia,

C

d

– współczynnik nadwyżek dynamicznych.

Obciążenie wynikające z mocy ustalonej: P =
gdzie:
M

o

– moment obrotowy [N · mm],

N – moc ustalona [kW],
n – prędkość obrotowa koła [obr/min]

dn

N

d

M

9550000

*

2

2

0



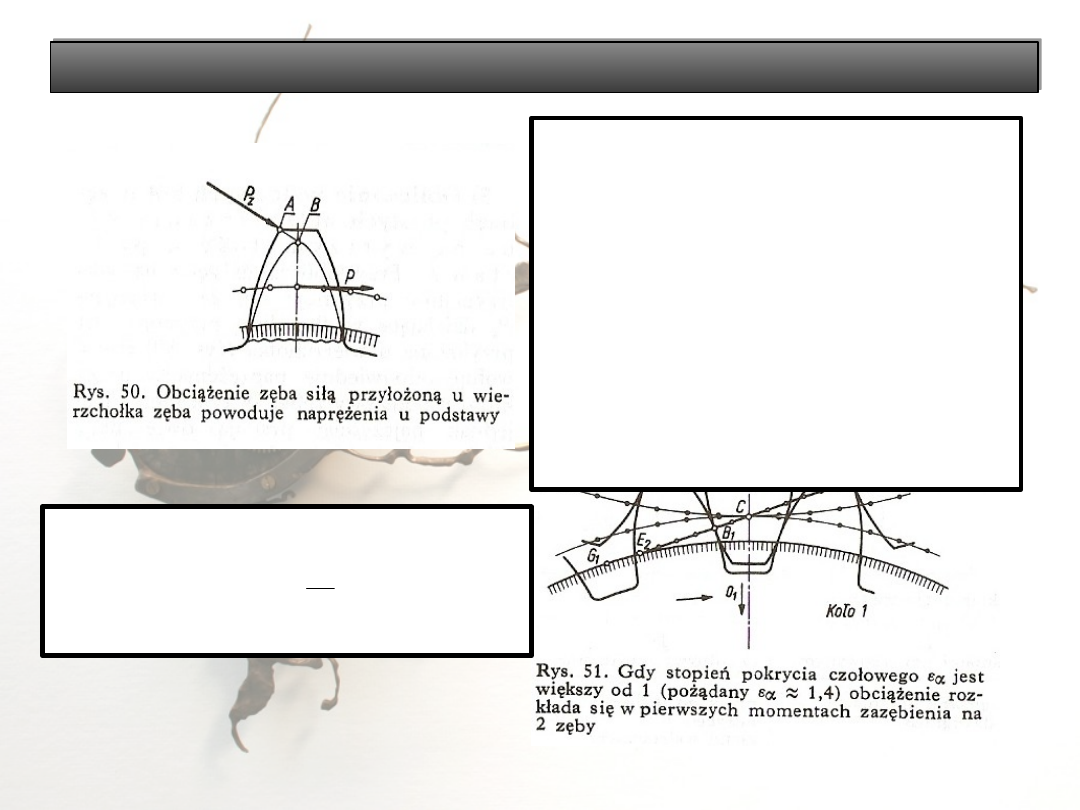
Obliczanie zęba na wytrzymałość u podstawy

Obliczanie zęba na wytrzymałość u podstawy

Przy

obliczaniu

zęba

na

wytrzymałość przyjmuje się, że
obciążenie P

z

działające wzdłuż

linii przyporu jest przyłożone u
wierzchołka

i

wywołuje

odpowiednie

naprężenia

w

przekroju u podstawy zęba. W
tym momencie jednak najczęściej
pracują dwie pary zębów, gdy
stopień pokrycia jest większy od
jedności.

Przyjmuje się tzw. obciążenie
obliczeniowe P

obl

określane z

dużym przybliżeniem za pomocą
wzoru: P

ob

l =

N

P

zast





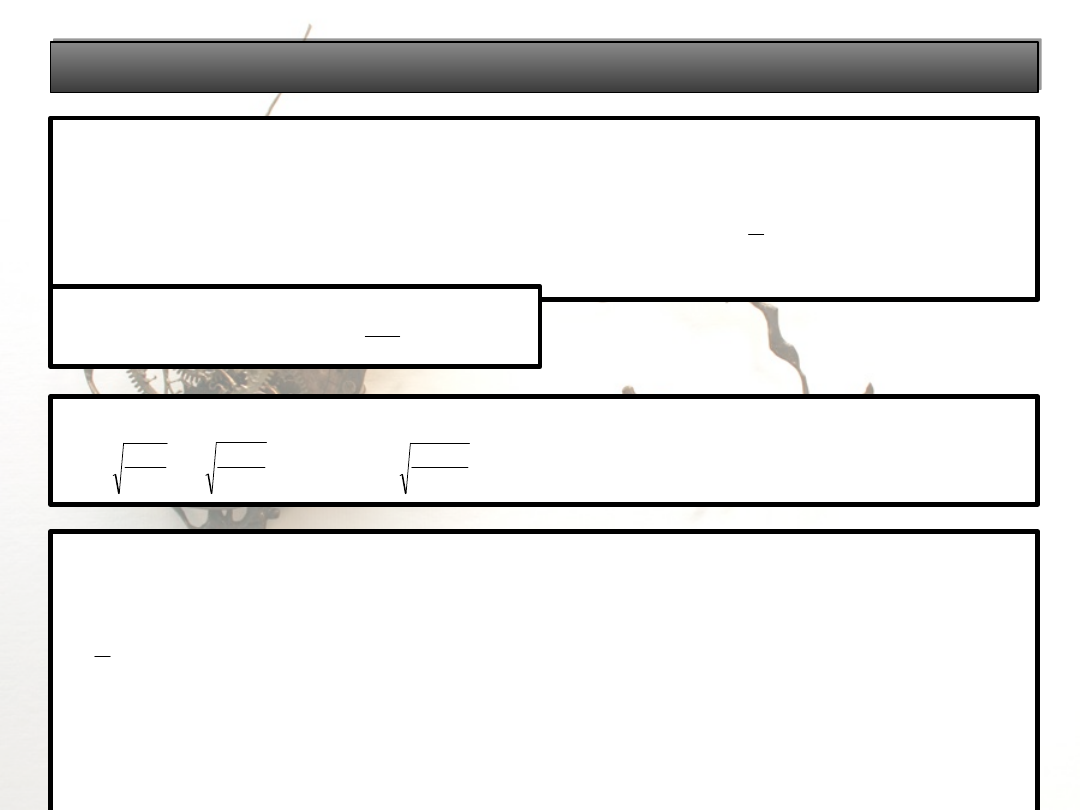
Obliczanie zęba na wytrzymałość u podstawy

Obliczanie zęba na wytrzymałość u podstawy

Istnieją dwa przypadki obliczeniowe:
- gdy znane są z, m, b oraz P

zast

, a szukamy materiału lub stosujemy

jako obliczanie kontrolne
- gdy mamy P

1

, M

0

( lub N ), materiał koła, z, współczynnik

, a

szukamy m

W pierwszym przypadku:
P

obl

= lub σ

gzast

=

m

b





g

mbk



g

obl

k

bm

P





W drugim przypadku:
 
m =

= 1,26 = 267

g

k

P



3

0

g

zk

M



3

g

znk

N



M

0

– moment obrotowy [N*mm]

N – moc przenoszona [kW]
n – prędkość obrotowa rozpatrywanego koła[obr/min]
- współczynnik odczytywany z tabel
λ – współczynnik wytrzymałości zęba u podstawy
σ

gzast

= zastępcze naprężenie zginające [MPa]

k

g

– naprężenie dopuszczalne dla danego materiału i warunków pracy

[MPa]

m

b





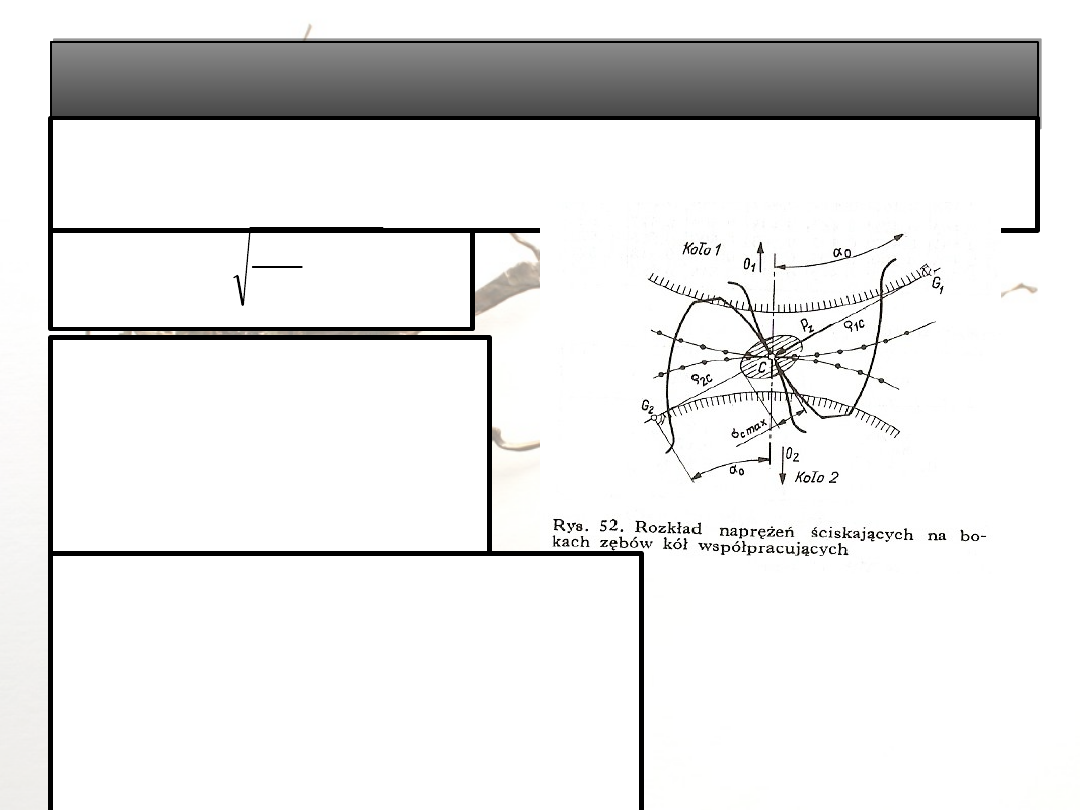
Obliczanie zęba na nacisk powierzchniowy wg wzorów

Hertza

Obliczanie zęba na nacisk powierzchniowy wg wzorów

Hertza

Najniebezpieczniejszym momentem jest przypadek, gdy całkowite
obciążenie P

zast

jest przenoszone tylko przez jeden ząb. Występuje to w

okolicy koła tocznego.

m

b





P

zast

- zastępcze obciążenie w N

- współczynnik uzależniony od
zestawu materiałów i kąta
przyporu kół
współpracujących
i

r

- przełożenie przekładni

b- szerokość wieńca

H

r

zast

m

H

k

i

l

bd

P

C







)

(

1

,

max





Naprężenie dopuszczalne kH oblicza się
wg wzoru:
k

H

= 0,9Z

H

C

0

lub k

H

= 0,9σ

H

C

0

 

Z

H

- wytrzymałość trwała na zmęczenie

naciskiem
σ

H

- wytrzymałość okresowa na zmęczenie

naciskiem
C

0

- współczynnik lepkości oleju

KONIE

C

KONIE

C