Parametry statystyczne

Wzory i właściwości

Charakterystyka podstawowych parametrów statystycznych

 

Parametry statystyczne - są to wielkości liczbowe, które służą do
opisu struktury zbiorowości statystycznej w sposób systematyczny

  

Miary położenia

 

Miary pozycyjne

Miary przeciętne

modalna

kwantyle:

kwartyl pierwszy

mediana (kwartyl

drugi)

kwartyl trzeci

decyle

charakteryzują średni lub typowy poziom

wartości cechy, wokół których skupiają

się wszystkie pozostałe wartości

analizowanej cechy

średnia arytmetyczna

średnia harmoniczna

średnia geometryczna

modalna

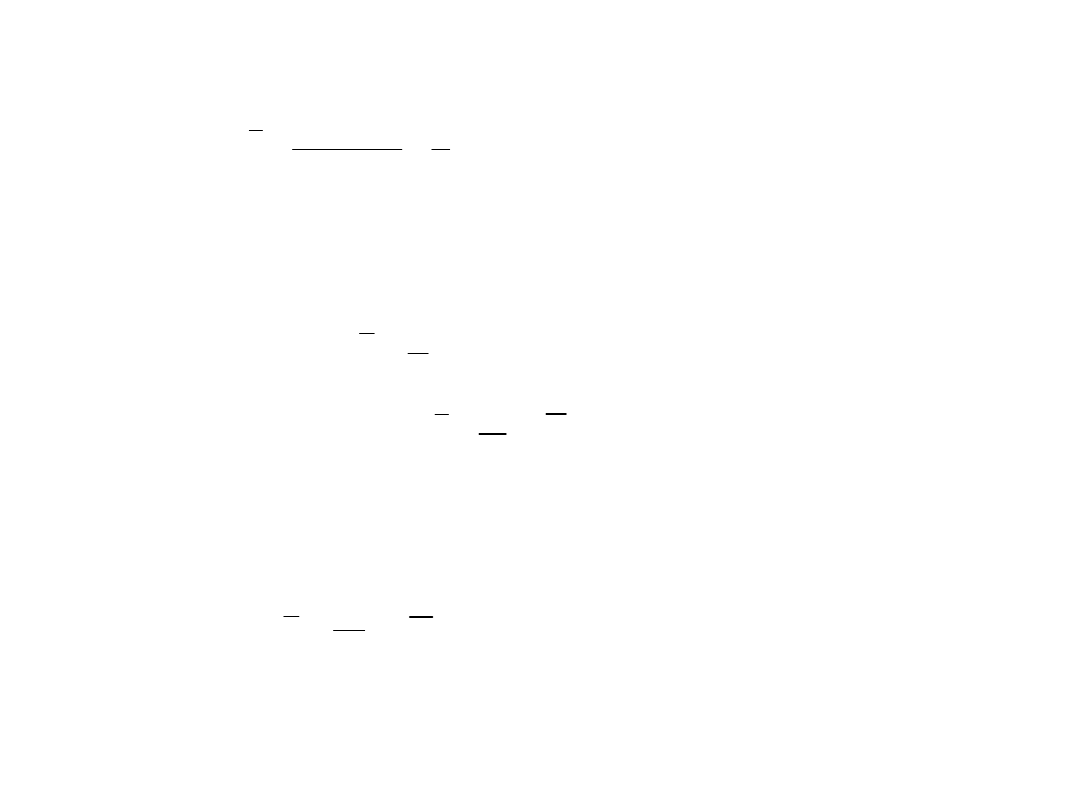
Średnia arytmetyczna

Średnią arytmetyczną - definiuje się jako sumę wartości cechy mierzalnej podzieloną przez

liczbę jednostek skończonej zbiorowości statystycznej. 

szereg szczegółowy (eq.1)
 
gdzie: n - liczebność zbiorowości próbnej (próby),
x

i

- wariant cechy.

Jest to tzn. średnia nieważna (prosta) - stosowana dla szeregów szczegółowych.
 
Średnia arytmetyczna ważona

szereg rozdzielczy punktowy (eq.2)

szereg rozdzielczy z przedziałami klasowymi (eq.3)
 

gdzie: oznacza środek przedziału klasowego

Średnia arytmetyczna (średnia ważona) dla r-grup łącznie oraz średnich arytmetycznych

cząstkowych i liczebności i-tej grupie n

i

:

(eq.4)

gdzie: jest sumą liczebności we wszystkich r-grupach

.















n

i

i

x

n

n

x

x

x

x

n

1

1

...

2

1

n

x

i

k

i

i

n

x







1

1

n

x

i

r

i

i

N

x







1

1



x

n

x

i

r

i

i

N

x







1

1







r

i

i

n

N

1

Podstawiając w miejsce n

i

wskaźnik struktury w

i

otrzymamy zależności:

lub

Wybrane właściwości średniej arytmetycznej

• suma wartości cechy jest równa iloczynowi średniej arytmetycznej i

liczebności

• zbiorowości: lub dla szeregu rozdzielczego,

• średnia arytmetyczna spełnia warunek:
• suma odchyleń poszczególnych wartości cechy od średniej równa się zero:
lub ,

• Suma kwadratów odchyleń poszczególnych wartości cechy od średniej jest

minimalna: lub ,

• średnią arytmetyczną można liczyć w zasadzie dla szeregów o zamkniętych

przedziałach klasowych; jeżeli liczebność w otwartym przedziale klasowym
stanowi niewielki odsetek, (praktycznie do 5%) możliwe jest domknięcie
przedziałów klasowych oraz obliczenie średniej w innym przypadku do
określenia zjawiska stosuje się parametry pozycyjne,

• średnia arytmetyczna jest wrażliwa na skrajne wartości cechy,
• średnia arytmetyczna z próby jest dobrym przybliżeniem wartości przeciętnej.







k

i

i

i

x

x

1











k

i

i

i

x

x

1









k

i

i

x

x

n

1

n

x

i

k

i

i

x

n







1









n

i

i

i

n

x

x

1

0

)

(









n

i

i

x

x

1

0

)

(









n

i

i

i

n

x

x

1

0

)

(









n

i

i

x

x

1

2

min

)

(









n

i

i

i

n

x

x

1

2

min

)

(

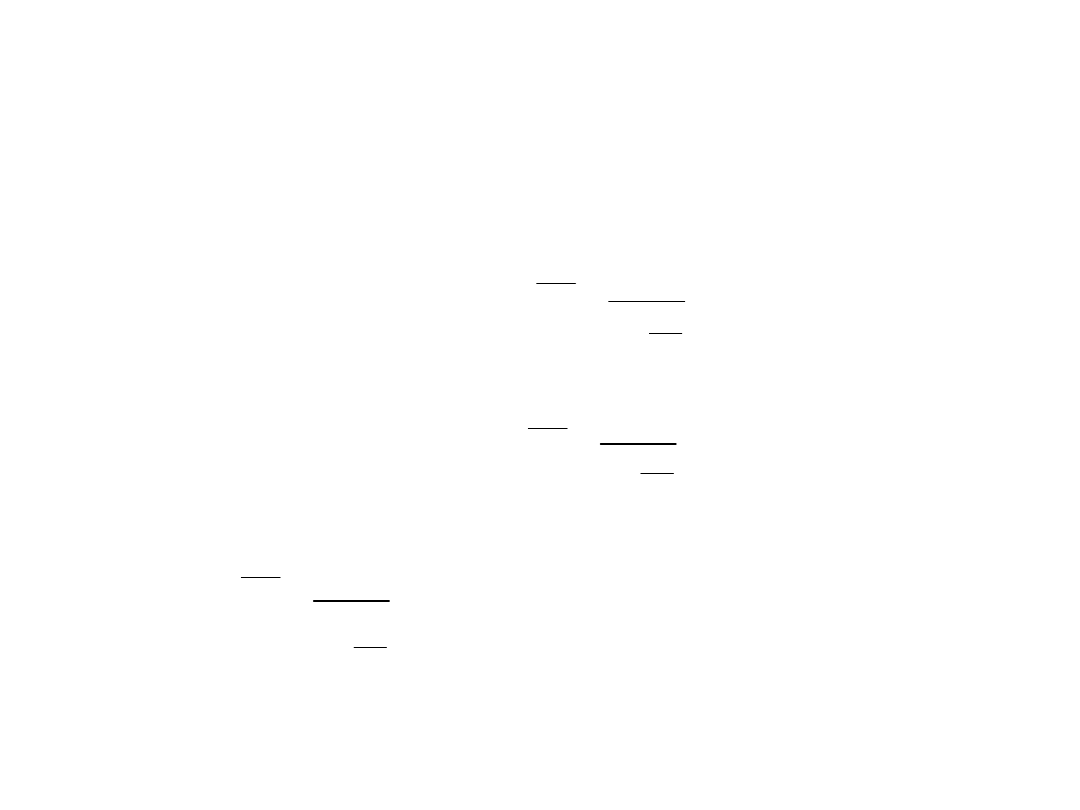
Średnia harmoniczna

 

Średnią harmoniczną - stosuje się wtedy, gdy wartości

cechy są podane w przeliczeniu na stałą jednostkę  innej
zmiennej, czyli w postaci wskaźników natężenia, wagi
natomiast w jednostkach liczników tych cech, np. prędkość
pojazdu w km/h.

• szereg szczegółowy

• szereg rozdzielczy

Przyjmując, że waga oraz

:







n

i

i

H

x

x

n

1

1











k

i

i

i

k

i

i

H

x

n

n

x

1

1

n

x

w

i

i

i









k

i

i

w

W

1







k

i

i

i

H

x

n

x

W

1

Średnia geometryczna

Średnią geometryczną - stosuje się w badaniach
średniego tempa zmian zjawisk, a więc gdy zjawiska są
ujmowane dynamicznie.

 

Modalna

•   Modalna Mo (dominanta D, moda, wartość

najczęstsza - jest to wartość cechy statystycznej, która w
danym rozdziale empirycznym występuje najczęściej

•  Dla szeregów szczegółowych oraz szeregów rozdzielczych

punktowych modalna odpowiada wartości cechy o
największej liczebności (częstości).

• W szeregach rozdzielczych z przedziałami klasowymi

bezpośrednio można określić tylko przedział, w którym
modalna występuje, jej przybliżoną wartość wyznacza się
graficznie z histogramu liczebności (częstości) lub ze wzoru
interpolacyjnego:

gdzie: m - numer przedziału (klasy), w którym występuje modalna,
- dolna granica przedziału, w którym występuje modalna,
n

m

- liczebność przedziału modalnej, tzn. klasy o numerze m,

n

m-1

; n

m+1

- liczebność klas poprzedzającej i następnej, o

numerach m – 1

i m + 1,
h

m

- rozpiętość przedziału klasowego, w którym występuje

modalna.

Kwantyle

Kwantyle - definiuje się jako wartości cechy badanej zbiorowości,
przedstawionej w postaci szeregu statystycznego, które dzielą
zbiorowość na określone części pod względem liczby jednostek,
części te pozostają do siebie w określonych proporcjach.

 

Kwartyl pierwszy Q

1

dzieli zbiorowość na dwie części w ten sposób, że 25% jednostek
zbiorowości ma wartości cechy niższe bądź równe kwartylowi
pierwszemu Q

1

, a 75% równe bądź wyższe od tego kwartyla

Kwartyl drugi (mediana Me)

dzieli zbiorowość na dwie równe części; połowa jednostek ma
wartości cechy mniejsze lub równe medianie, a połowa wartości
cechy równe lub większe od Me; stąd nazwa wartość środkowa

Kwartyl trzeci Q

3

dzieli zbiorowość na dwie części w ten sposób, że 75% jednostek
zbiorowości ma wartości cechy niższe bądź równe kwartylowi
pierwszemu Q

3

, a 25% równe bądź wyższe od tego kwartyla

Decyle

np. decyl pierwszy oznacza, że 10% jednostek ma wartości
cechy mniejsze bądź równe od decyla pierwszego, a 90%
jednostek wartości cechy równe lub większe od decyla
pierwszego

Kwartyl drugi (mediana Me)

Dla szeregu szczegółowego 

Dla szeregu rozdzielczego (graficznie lub analitycznie)

gdzie:
m - numer przedziału (klasy), w które występuje mediana,
dolna granica przedziału, w którym występuje mediana

n

m

- liczebność przedziału mediany, tzn. klasy o

numerze m, 

suma liczebności przedziałów poprzedzających przedział mediany, czyli liczebność
skumulowana,

h

m

- rozpiętość przedziału klasowego, w którym jest mediana,

N

Me

- pozycja mediany, czyli