PARAMETRY
STATYSTYCZNE

to wielkości liczbowe, które

służą do opisu struktury

zbiorowości statystycznej w

sposób systematyczny

Zadania parametrów
statystycznych



Określenie przeciętnego rozmiaru i

rozmieszczenia wartości zmiennej- za

pośrednictwem miar położenia



Określenie granic obszaru zmienności

wartości zmiennej- za pośrednictwem miar

zmienności



Określenie skupienia i spłaszczenia (w

stosunku do krzywej normalnej) oraz stopnia

zmiany od idealnej asymetrii- za

pośrednictwem miar asymetrii i koncentracji

MIARY POŁOŻENIA



MIARY POZYCYJNE



MIARY PRZECIĘTNE

MIARY POZYCYJNE



modalna



kwartyl pierwszy



mediana (kwartyl drugi)



kwartyl trzeci



decyle

MIARY PRZECIĘTNE



średnia arytmetyczna



średnia harmoniczna



średnia geometryczna



inne

Miary przeciętne

charakteryzują średni lub typowy

poziom wartości cechy, wokół których

skupiają się wszystkie pozostałe

wartości analizowanej cechy

Średnią arytmetyczną



definiuje się jako sumę wartości
cechy mierzalnej podzieloną przez
liczbę jednostek skończonej
zbiorowości statystycznej. 

ŚREDNIA NIEWAŻNA STOSOWANA DLA
SZEREGÓW SZCZEGÓŁOWYCH

gdzie:
n - liczebność zbiorowości próbnej
(próby),
x

i

- wariant cechy

Dwóch pracowników wykonuje detale tego samego typu.
Przeprowadzono obserwację czasu wykonania pięciu detali przez
robotnika A i dziesięciu detali przez robotnika B i otrzymano
następujące szeregi szczegółowe opisujące czas wykonania detalu:
dla robotnika A: 12, 15, 15, 18, 20
dla robotnika B: 10, 10, 12, 12, 15, 15, 18, 20, 21, 21



Korzystając z wzoru na
obliczenie średniej :

min

16

5

80

5

20

18

15

15

12















A

x

min

4

,

15

10

154

10

21

21

20

18

15

15

12

12

10

10

























B

x

W pewnym doświadczeniu

medycznym bada się czas snu

pacjentów leczonych na pewną

chorobę. Zmierzono u n=12

losowo wybranych pacjentów czas

snu

i otrzymano następujące wyniki

(w minutach):

435,389,533,324,561,395,416,500

,499,397,356,398.

Należy obliczyć średni czas snu:

583

,

433



x

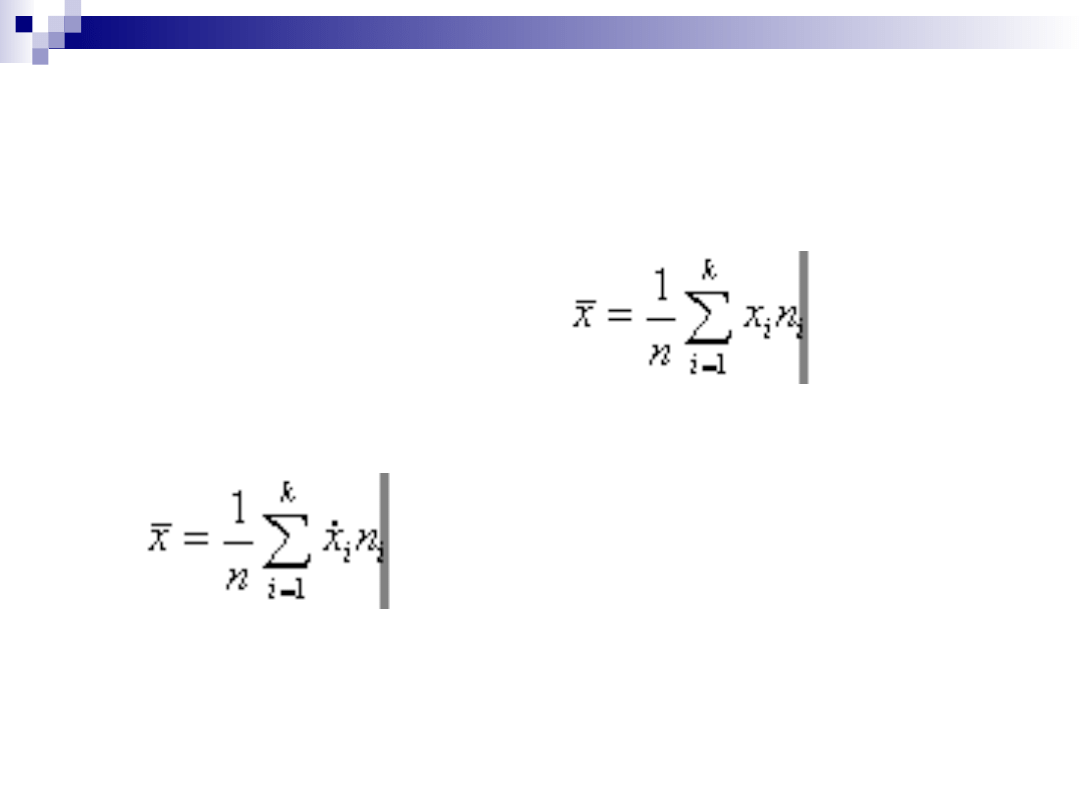
ŚREDNIA ARYTMETYCZNA
WAŻONA-

wyznacza się w szeregach rozdzielczych

punktowych i w szeregach rozdzielczych z przedziałami
klasowymi

SZEREG ROZDZIELCZY
PUNKTOWY

SZEREG ROZDDZIELCZY Z
PRZEDZIAŁAMI KLASOWYMI

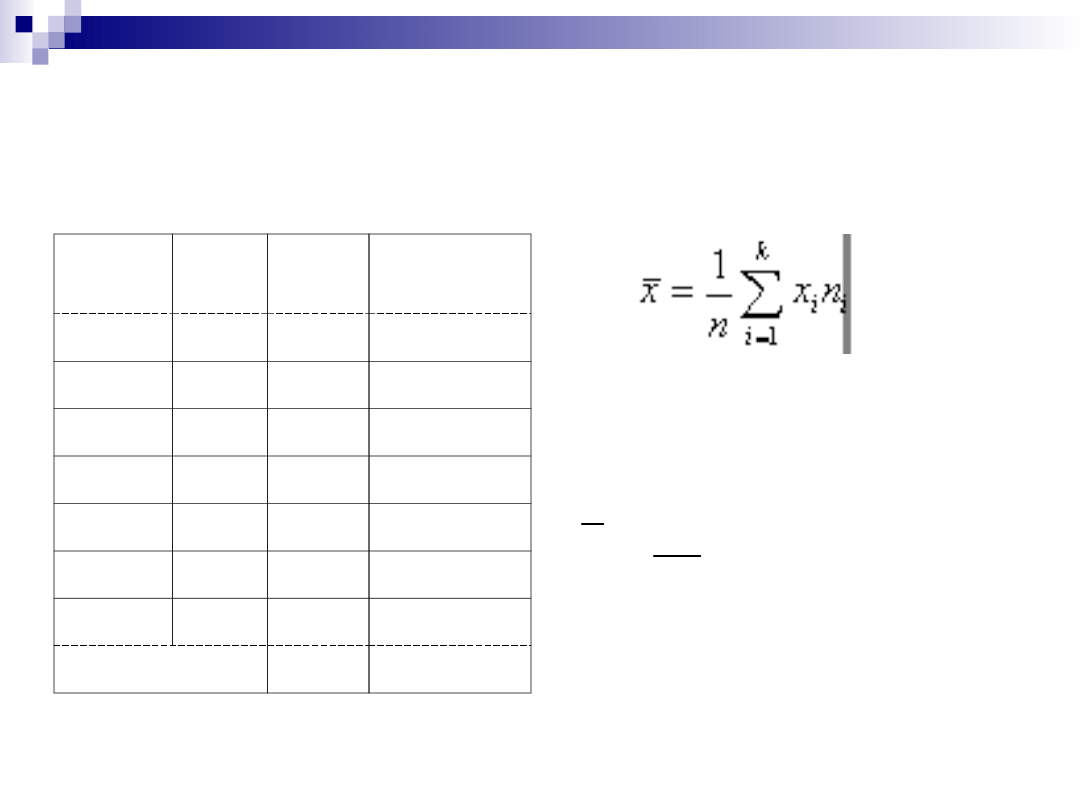
Przykład: W tabeli poniżej zestawiono wyniki badań czasu
pracy wykonania 15 detali. Jest to szereg szczegółowy
punktowy. Średnia arytmetyczną czasu wyznaczymy na
podstawie wzoru:

Numer

klasy

Czas w

mi

n

Liczba

det

ali

Obliczenia

pomocnic

ze

i

x

i

n

i

x

i

*n

i

1

10

2

20

2

12

3

36

3

15

4

60

4

18

2

36

5

20

2

40

6

21

2

42

RAZEM

15

234

min

6

,

15

234

*

15

1





x

Ćwiczenie



Dziesięć osób czekających przed
gabinetami lekarskimi w przychodni
zapytano, ile razy korzystały z
porad lekarskich w ciągu ubiegłego
roku kalendarzowego. Uzyskane
informacje przedstawiono w postaci
następującego szeregu
rozdzielczego

Oblicz ile razy w roku
przeciętnie korzystały z
porad lekarza badane
osoby?

Liczba

porad

Liczba

osób

0

1
2

3
4

6

1

1
2

2
3

1

Razem

10

Oblicz średni czas reakcji na nowy lek:

Obliczenia pomocnicze

i

X



i

i

n

X



Numer

Klasy

Przedział
Klasowy

Liczebność

klasy

n

i

1

2

3

4

5

1

2

3

4

5

6

7

8-12

13-17

18-22

23-27

28-32

33-37

38-42

4

29

38

80

35

9

5

ŁĄCZNIE

200

24

200

4800





x

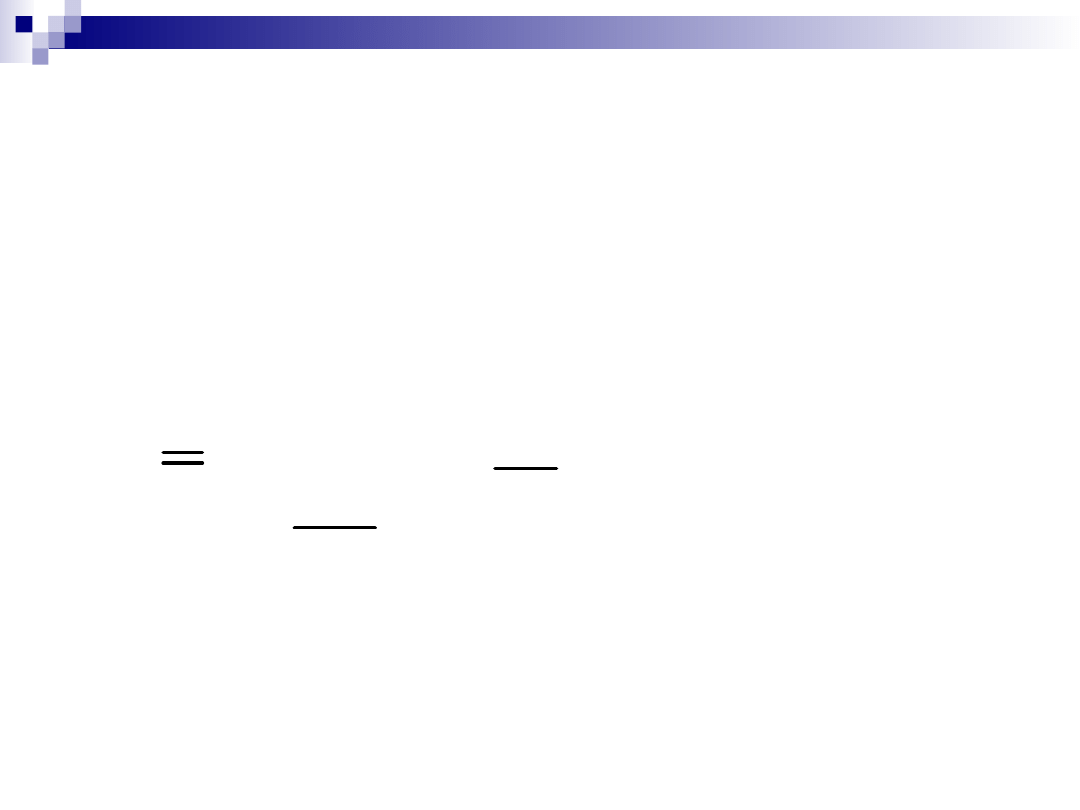
Jeżeli znamy średnie arytmetyczne dla
pewnych
r-grup i na tej podstawie chcemy wyznaczy
średnią arytmetyczną dla wszystkich grup
łącznie wykorzystujemy wówczas
następujący wzór:

i

r

i

i

n

x

N

x







1

1

Korzystając z powyższego wzoru możemy obliczy
średni czas wykonania detalu przez robotnika A i B.
Obliczona w ten sposób średnia nazywa się średnią
ważona, wyznaczona na podstawie
średnich cząstkowych :

min

6

,

15

15

4

,

15

x

10

16

x

5







x

B

A

x

x ;

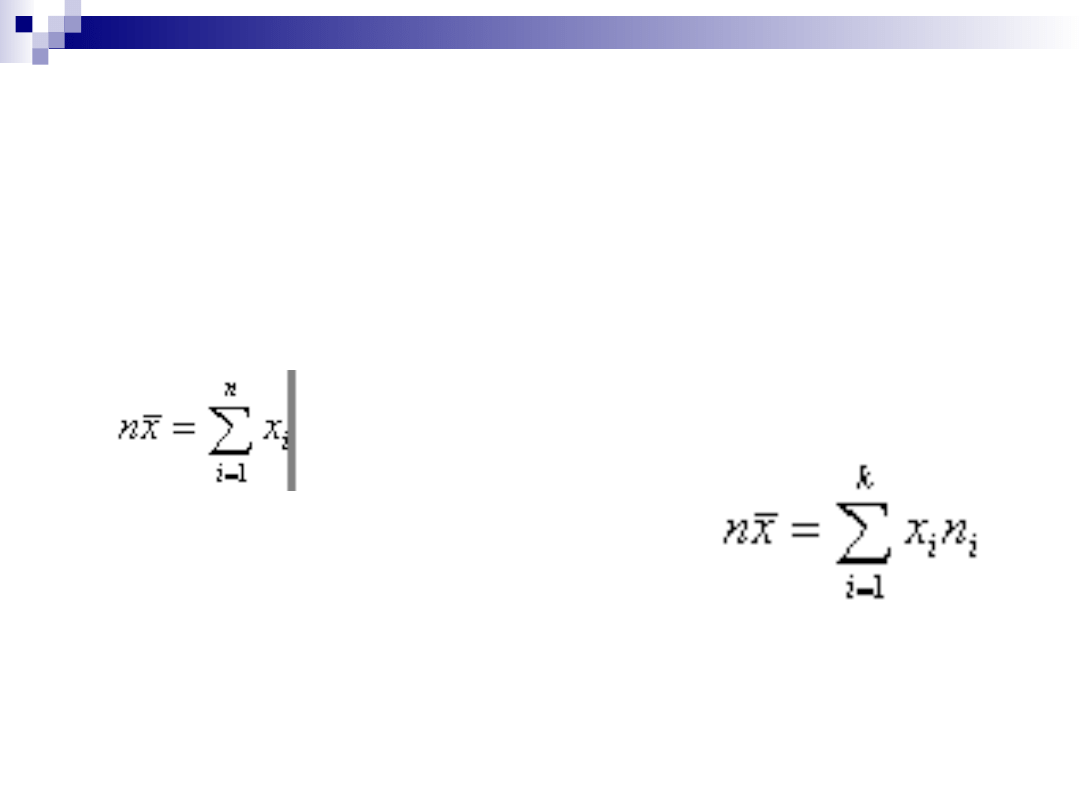
Wybrane właściwości średniej
arytmetycznej 



suma wartości cechy jest równa
iloczynowi średniej i liczebności
zbiorowości:

lub dla szeregu rozdzielczego ,



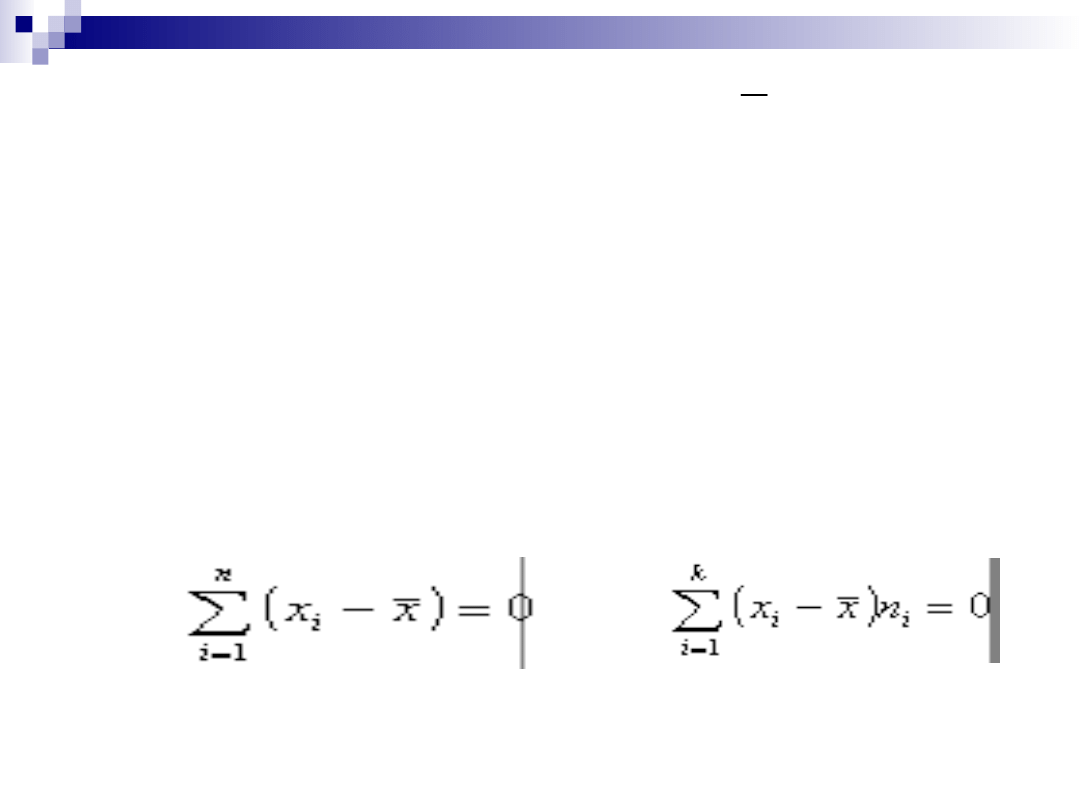
średnia
arytmetyczna
spełnia warunek:



suma odchyleń
poszczególnych
wartości cechy od
średniej równa się
zero

max

min

x

x

x







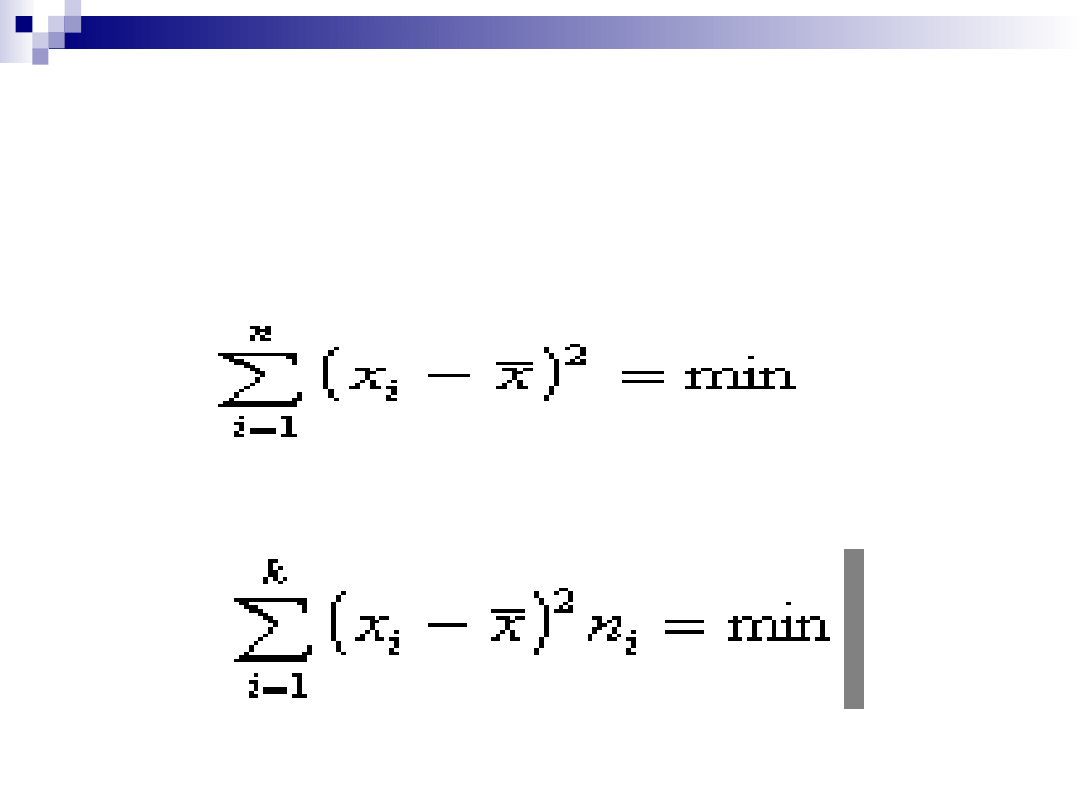
Suma kwadratów odchyleń
poszczególnych wartości cechy od
średniej jest minimalna

lub



średnia arytmetyczna jest wrażliwa na skrajne

wartości cechy, a więc np. na wartości cechy

jednostek przypadkowo włączonych do próby



średniej arytmetycznej nie można obliczać w

szeregach, w których udział liczebności

(częstości) w przedziałach klasowych

otwartych jest duży, do określenia przeciętnego

poziomu zjawiska stosuje się wówczas

parametry pozycyjne.



średnia arytmetyczna z próby, przy zachowaniu

warunków że próba jest reprezentacyjna jest

dobrym przybliżeniem wartości przeciętnej.

Średnia arytmetyczna jest miarą

prawidłową jedynie w odniesieniu
do zbiorowości jednorodnych, o
niewielkim zróżnicowaniu wartości
zmiennej. Średniej tej nie należy
stosować w przypadku rozkładów
skrajnie asymetrycznych,
bimodalnych i wielomodalnych.

Średnią harmoniczną



stosuje się wtedy, gdy wartości cechy
są podane w przeliczeniu na stałą
jednostkę  innej zmiennej, czyli w
postaci wskaźników natężenia, np.
prędkość pojazdu w km/h ;
pracochłonność w szt/min. ; gęstość
zaludnienia w osobach / km

2

.

Średnia harmoniczna jest

odwrotnością średniej arytmetycznej z
odwrotności wartości zmiennych. W
przypadku szeregów szczegółowych
(wyliczających) średnią harmoniczną
liczy się ze wzoru:







n

i

i

h

x

n

x

1

1

Dla szeregów rozdzielczych

przedziałowych średnią harmoniczną
liczy się następująco:











n

i

i

i

k

i

i

h

n

x

n

x

1

1

1

Średnią geometryczną



stosuje się w
badaniach
średniego tempa
zmian zjawisk, a
więc gdy zjawiska
są ujmowane
dynamicznie.

n

n

G

x

x

x

x









...

2

1

Przykład:



Z danych o ludności pewnego miasta

wynika, że w trzech kolejnych okresach

liczba ludności wynosiła odpowiednio :

5000, 7500, 8250. Obliczmy średni

przyrost względny ludności:



Wartości cechy (współczynniki względne)

w tym zadaniu będą następujące:



Zgodnie z wzorem na obliczenie średniej

geometrycznej średni przyrost ludności w

trzech kolejnych latach wynosił:

5

,

1

5000

7500

1





X

1

,

1

7500

8250

2





X

28

,

1

1

,

1

5

,

1







G

X

Modalna Mo (dominanta D,
moda, wartość najczęstsza)



jest to wartość cechy statystycznej,
która w danym rozdziale
empirycznym występuje najczęściej



Dla szeregów szczegółowych oraz
szeregów rozdzielczych punktowych
modalna odpowiada wartości cechy o
największej liczebności (częstości).



W szeregach rozdzielczych z
przedziałami klasowymi bezpośrednio
można określić tylko przedział, w
którym modalna występuje, jej
przybliżoną wartość wyznacza się
graficznie z histogramu liczebności
(częstości)

Określimy za pomocą modalnej
przeciętną liczbę przyjmowanych w
ciągu dnia przez pacjentów leków

Liczba przyjmowanych

leków

%

pacjent

ów

0
1

2
3

4
5 i więcej

4
19

21
32

17
7

RAZEM

100

gdzie:



m - numer przedziału (klasy), w którym występuje modalna,



X

0m

dolna granica przedziału, w którym występuje modalna,



n

m

- liczebność przedziału modalnej, tzn. klasy o numerze m,



n

m-1

; n

m+1

- liczebność klas poprzedzającej i następnej, o numerach

m – 1 i m + 1,



h

m

- rozpiętość przedziału klasowego, w którym występuje modalna

Kwantyle



definiuje się jako wartości cechy
badanej zbiorowości, przedstawionej
w postaci szeregu statystycznego,
które dzielą zbiorowość na określone
części. Pod względem liczby
jednostek, części te pozostają do
siebie w określonych proporcjach.

KWARTYL DRUGI – MEDIANA Me



dzieli zbiorowość na dwie równe
części; połowa jednostek ma wartości
cechy mniejsze lub równe medianie,
a połowa wartości cechy równe lub
większe od Me; stąd nazwa wartość
środkowa

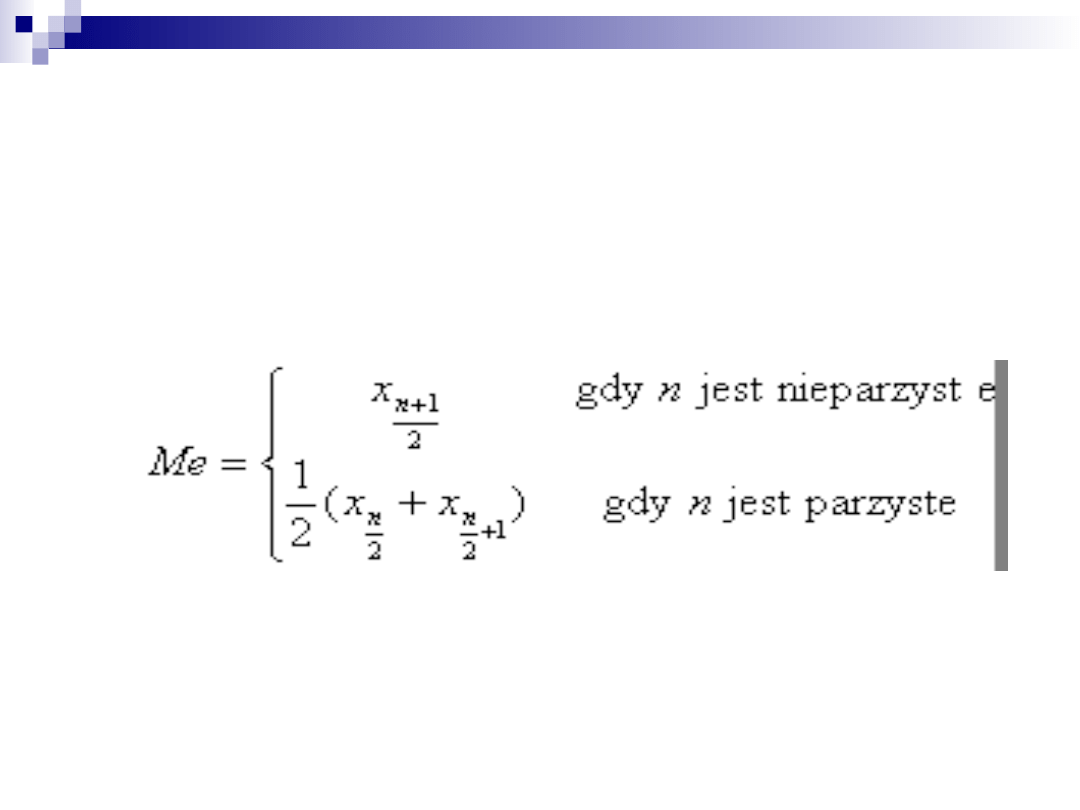
MEDIANA – SZEREG
SZCZEGÓŁOWY

Przykład:



wiek kobiet przyjętych w październiku 1999 na oddział

położniczy z przyczyn nagłych można przedstawić w

postaci następującego szeregu statystycznego:

18, 57, 34, 32, 29, 31, 19, 19, 27, 26, 26,

22, 23, 26, 26, 34, 26,



Teraz należy ten szereg uporządkować:

18, 19, 19, 22, 23, 26, 26, 26, 26, 26,27, 29,

31, 32, 34, 34, 57.



Szereg ten składa się z

17

wartości zmiennych.

Wartością środkową – medianą- w tym przypadku
będzie wartość znajdująca się na pozycji

9,

czyli

Me

=26

Przykład:



Weźmy pod uwagę tym razem wiek kobiet

przyjętych w październiku 1999 roku na oddział

położniczy w sposób zaplanowany.



Po uporządkowaniu szereg opisujący wiek tych

kobiet przedstawia się następująco:

19,21,22,28,28,29



Jak widać tym razem mamy 6 przypadków, czyli

ilość parzystą. Wartościami środkowymi będą

wielkości z pozycji 3 i 4 , czyli 22 i 28. Medianą

zatem będzie średnia arytmetyczna z tych dwóch
liczb, czyli

25

.



Wyznaczyć medianę dla wzrostu
podanego poniżej:

165,
166,167,170,172,173,175,175,18
1



Podejrzewano, że pewna choroba wiąże się z
podwyższonym poziomem białych krwinek.
W grupie pacjentów leczonych z powodu tej
choroby zbadano liczbę białych krwinek
w 1 mm3 krwi. Otrzymano następujące
wyniki; 6400, 6700, 6900, 7300, 7400, 7500,
7800, 8000, 15900, 16300.



Należy wyznaczyć medianę dla tego
szeregu

W przypadku szeregu

rozdzielczego przedziałowego medianę
wyznacza się metodą graficzną lub
rachunkową. W metodzie graficznej
wykorzystuje się wykres krzywej
liczebności skumulowanej.

Jeżeli dane są przedstawione za

pomocą szeregu rozdzielczego
punktowego (cecha skokowa) – medianą
jest pierwsza wartość, której odpowiada
co najmniej połowa skumulowanej
liczebności.

MEDIANA – SZEREG
ROZDZIELCZY

GDZIE



m - numer przedziału (klasy), w
którym występuje mediana,



X

0m

dolna granica przedziału, w

którym występuje mediana



n

m

- liczebność przedziału mediany,

tzn. klasy o numerze m, 

suma liczebności przedziałów

poprzedzających przedział mediany,
czyli liczebność skumulowana,

h

m

- rozpiętość przedziału klasowego, w

którym jest mediana,
N

Me

- pozycja mediany, czyli 

Zastosowanie mediany



W mikrobiologii do ustalenia przeciętnej liczby
drobnoustrojów.



W hematologii – do ustalania przeciętnej
wartości erytrocytów lub leukocytów we krwi.



Przy ustalaniu przeciętnej przeżywalności
pooperacyjnej oraz dożywalności po leczeniu
wielu nieuleczalnych dotychczas chorób (np.
po operacjach nowotworów złośliwych).

KWARTYL PIERWSZY Q

1



dzieli zbiorowość na dwie części w
ten sposób, że 25% jednostek
zbiorowości ma wartości cechy niższe
bądź równe kwartylowi pierwszemu
Q1, a 75% równe bądź wyższe od
tego kwartyla

KWARTYL TRZECI Q

3



dzieli zbiorowość na dwie części w
ten sposób, że 75% jednostek
zbiorowości ma wartości cechy niższe
bądź równe kwartylowi trzeciemu Q3,
a 25% równe bądź wyższe od tego
kwartyla

DECYLE



Np. decyl pierwszy oznacza, że 10%
jednostek ma wartości cechy
mniejsze bądź równe od decyla
pierwszego, a 90% jednostek
wartości cechy równe lub większe od
decyla pierwszego

Miary zmienności
(rozproszenia,
dyspersji)

MIARY KLASYCZNE
MIARY POZYCYJNE

MIARY ZMIENNOŚCI

Na zjawiska masowe oddziałują

dwa rodzaje przyczyn:

1.

Główne (wywołujące zmienność
systematyczną)

2.

Uboczne (wywołujące zmienność
przypadkową)

Przybliżonym miernikiem

składnika systematycznego zbiorowości
są miary przeciętne (średnie).
Odchylenia wartości poszczególnych
jednostek zbiorowości od wartości
średniej powstają pod wpływem
przyczyn przypadkowych (ubocznych).

Do pomiaru tych odchyleń

wykorzystuje się miary zmienności

(zróżnicowania, dyspersji,

rozproszenia).

Dyspersja to zróżnicowanie jednostek

badanej zbiorowości ze względu na

wartość badanej cechy statystycznej. Siłę

dyspersji można oceniać

za pomocą miar:

1.

Klasycznych

2.

Pozycyjnych.

Punktem odniesienia w miarach

klasycznych jest średnia arytmetyczna,

zaś miary pozycyjne wyznaczane są

przede wszystkim na podstawie kwartyli.

Miary klasyczne:

1.

Wariancja

2.

Odchylenie standardowe

3.

Odchylenie przeciętne (dewiata)

4.

Współczynnik zmienności*.

* - jeśli do jego wyliczenia

wykorzystywana jest średnia
arytmetyczna oraz odchylenie
standardowe)

Miary pozycyjne:

1.

Empiryczny obszar zmienności
(rozstęp, amplituda wahań, pole
rozsiania)

2.

Odchylenie ćwiartkowe

3.

Współczynnik zmienności**.

** - jeśli do jego wyliczenia

wykorzystywana jest mediana oraz
odchylenie ćwiartkowe)

Najczęściej stosowane miary

rozproszenia:

1.

Obszar zmienności

2.

Wariancja

3.

Odchylenie standardowe

4.

Współczynnik zmienności.

Obszarem zmienności

określa się różnicę pomiędzy największą a

najmniejszą wartością zmiennej, tzn.:

Miara ta ma niewielką wartość poznawczą,

gdyż obszar zmienności uzależniony jest

od wartości skrajnych, które często różnią się

istotnie od wszystkich pozostałych wartości

zmiennej. Na obszar zmienności wpływają

tylko wartości skrajne, pozostałe zaś

nie mają żadnego wpływu na wynik.

Obszar zmienności wykorzystywany jest

jedynie przy wstępnej ocenie rozproszenia.

min

max

x

x

R





Wariancją określa się średnią

arytmetyczną z sumy kwadratów
odchyleń poszczególnych wartości
cechy statystycznej od średniej
arytmetycznej całej zbiorowości
statystycznej. Wariancję wyznacza
się z następujących wzorów:

- dla szeregu szczegółowego:















n

i

i

x

x

n

s

1

2

2

1

2

s

-

dla szeregu rozdzielczego
punktowego:

-

dla szeregu rozdzielczego
przedziałowego:





i

n

i

i

n

x

x

n

s











1

2

2

1

i

n

i

i

n

x

x

n

s













 











1

2

2

1

Podstawowe właściwości wariancji:

1.

Jest zawsze liczbą nieujemną

2.

Jest zawsze wielkością
mianowaną, tzn. wyrażoną w
jednostkach badanej cechy
statystycznej. Miano wariancji
zawsze jest kwadratem jednostki
fizycznej, w jakiej mierzona jest
badana cecha

3.

Im zbiorowość statystyczna jest
bardziej zróżnicowana, tym wartość
wariancji jest wyższa

Odchylenie standardowe
s



jest to pierwiastek kwadratowy z
wariancji. Stanowi miarę
zróżnicowania o mianie zgodnym z
mianem badanej cechy, określa
przeciętne zróżnicowanie
poszczególnych wartości cechy od
średniej arytmetycznej.

Odchylenie standardowe jest

pierwiastkiem kwadratowym z
wariancji:

gdzie:
- odchylenie standardowe
- wariancja.
Odchylenie standardowe określa,

o ile wszystkie jednostki
statystyczne danej zbiorowości różnią
się średnio od wartości średniej
arytmetycznej badanej zmiennej.

2

s

s 

s

2

s



Odchylenie standardowe jest obok
średniej arytmetycznej najczęściej
stosowanym parametrem
statystycznym



Jest wielkością obliczoną na podstawie
wszystkich obserwacji danego szeregu



Im zbiorowość jest bardziej
zróżnicowana, tym większa jest
wariancja i oczywiście odchylenie
standardowe

Z odchyleniem standardowym

łączy się pojęcie zmiennej
standaryzowanej (unormowanej) dla
rozkładu empirycznego cechy
mierzalnej :

is

x

s

x

x

x

i

is





W statystyce odchylenie

standardowe wykorzystywane jest do

tworzenia typowego obszaru zmienności

statystycznej. W obszarze takim mieści

się około 2/3 wszystkich jednostek

badanej zbiorowości statystycznej.

Typowy obszar zmienności określa wzór:

Użyteczność kategorii typowego obszaru

zmienności sprowadza się przede

wszystkim do rozdziału jednostek

statystycznych

na typowe (tzn. występujące

stosunkowo często) i nietypowe (tzn.

występujące stosunkowo rzadko).

s

x

x

s

x

typ









Z odchyleniem standardowym wiąże się tzw.

Reguła trzech sigm, oparta na nierówności

Czybyszewa, która mówi, że wystąpienie

obserwacji o wartości cechy poza

przedziałem

)

3

;

3

(

s

x

s

x





Odchylenie standardowe spełnia regułę trzech

sigm w przypadku rozkładu normalnego lub

zbliżonego do normalnego ponad 2/3 wszystkich

zaobserwowanych wartości zmiennej (68,28%)

różni się od średniej nie mniej niż o wartość

odchylenia standardowego (+-s), 95,45%

obserwacji różni się od średniej maksymalnie o

dwa odchylenia standardowe, natomiast 99,73%

obserwacji mieści się w przedziale średnia do +-3

odchylenia standardowe

Jest mało

Jest mało

prawdopodobne

prawdopodobne

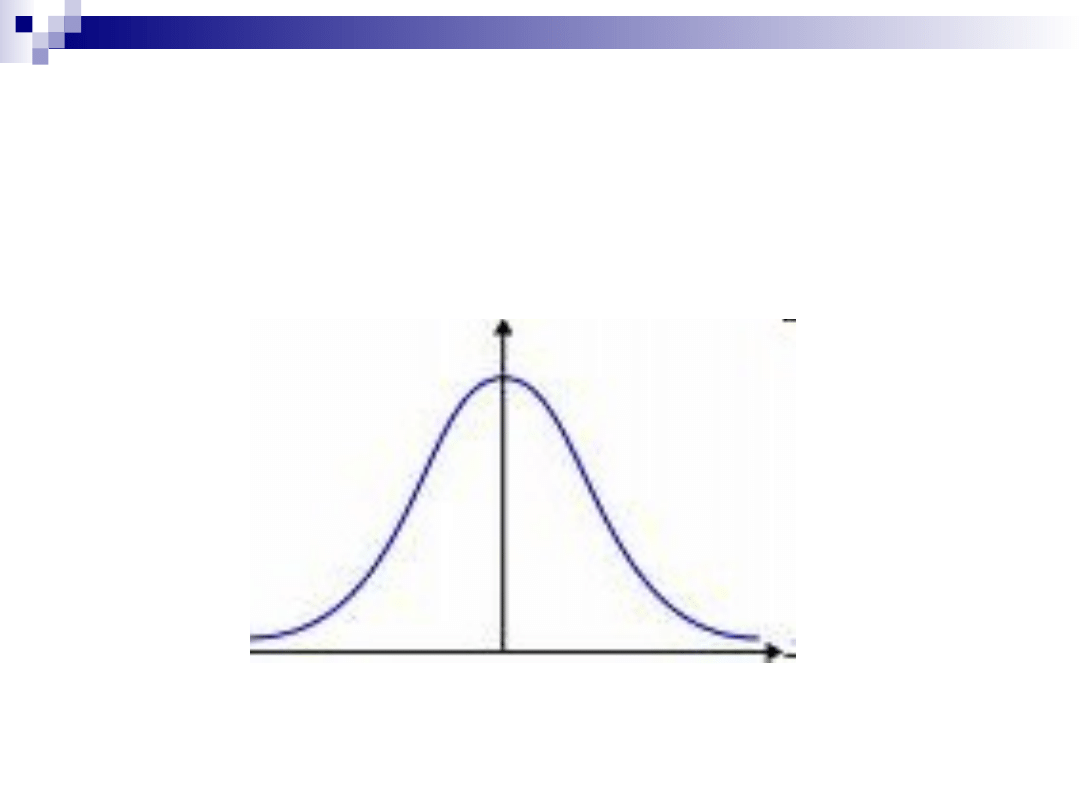
Rozkład normalny

Własności rozkładu
normalnego



Jest symetryczny



Ma kształt dzwonu



Jego średnia arytmetyczna, mediana
i modalna wypadają w tym samym
miejscu krzywej



Dwa końce krzywej praktycznie nigdy
nie dotykają osi poziomej

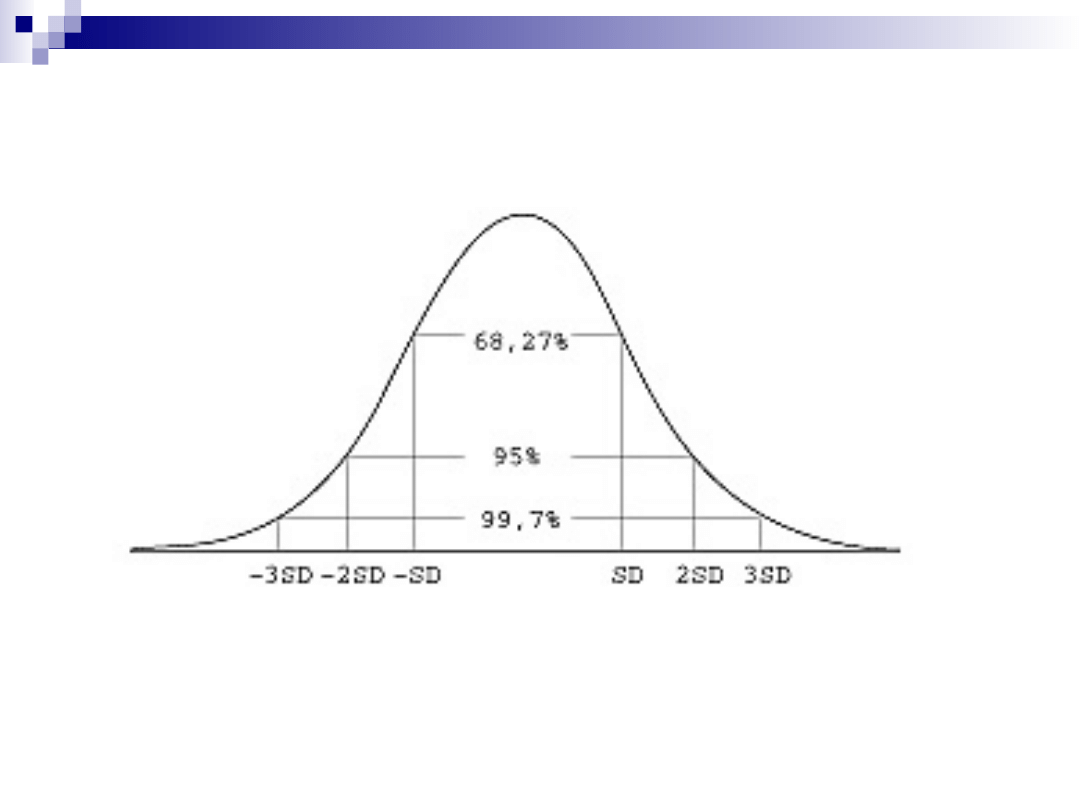
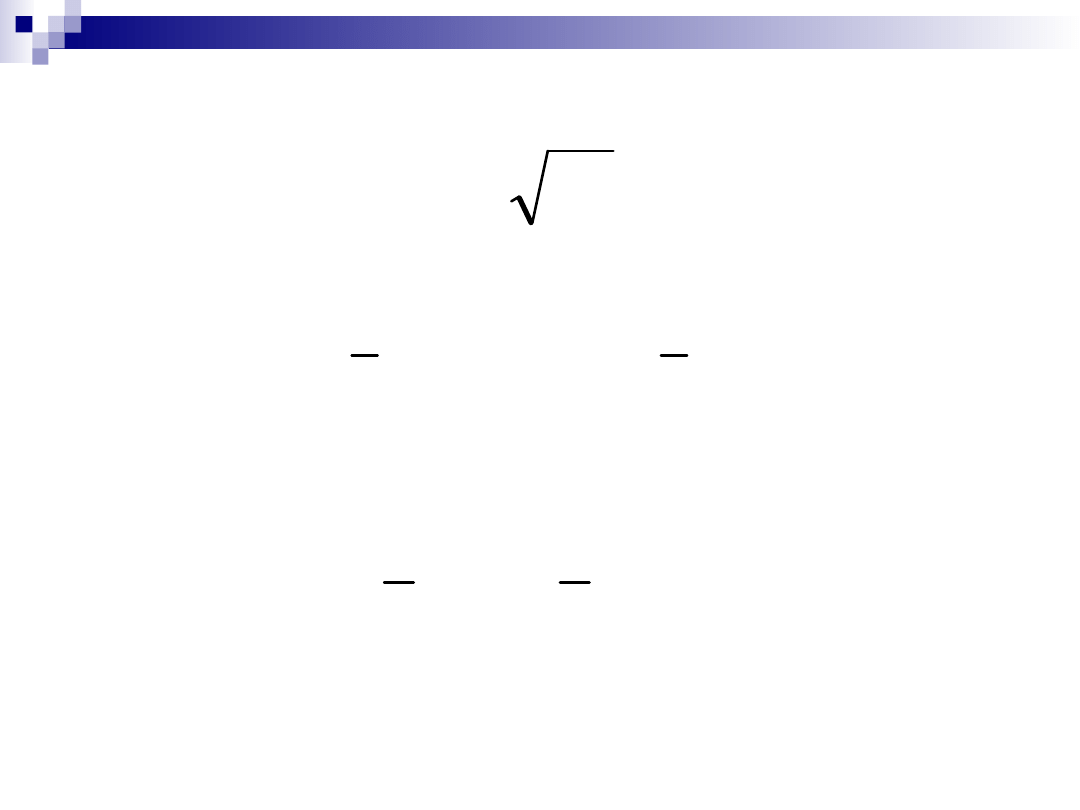
Odchylenie standardowe

Typowy obszar zmienności cechy

Reguła trzech sigm

2

s

s 

s

x

x

s

x

typ









)

3

;

3

(

s

x

s

x





Odchylenie przeciętne d



Określa o ile jednostki danej
zbiorowości różnią się średnio, ze
względu na wartość cechy, od
średniej arytmetycznej.

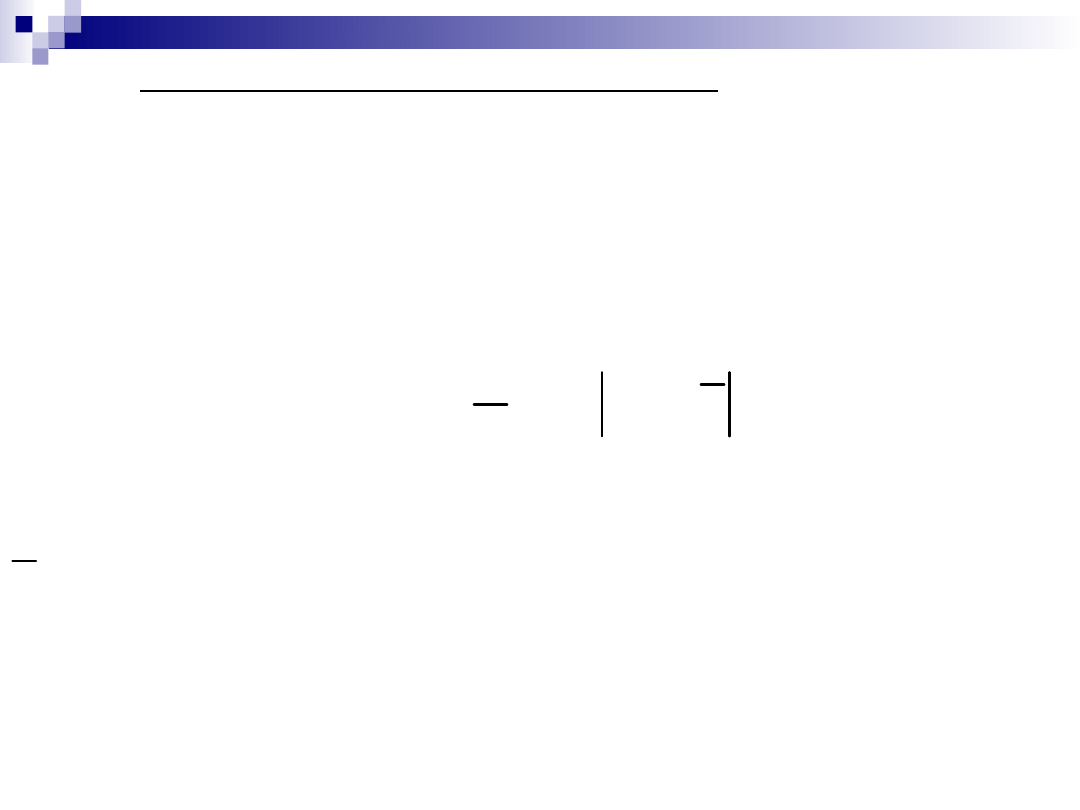
Odchyleniem przeciętnym d nazywa

się średnią arytmetyczną z

bezwzględnych odchyleń wartości zmiennej

x od średniej arytmetycznej. Odchylenie

przeciętne wyznaczamy z

następujących wzorów:

-

dla szeregu szczegółowego:

gdzie:
n - liczebność badanej zbiorowości
- wartości przyjmowane przez cechę mierzalną
- średnia arytmetyczna badanej zbiorowości











n

i

i

x

x

n

d

1

1

i

x

x

-

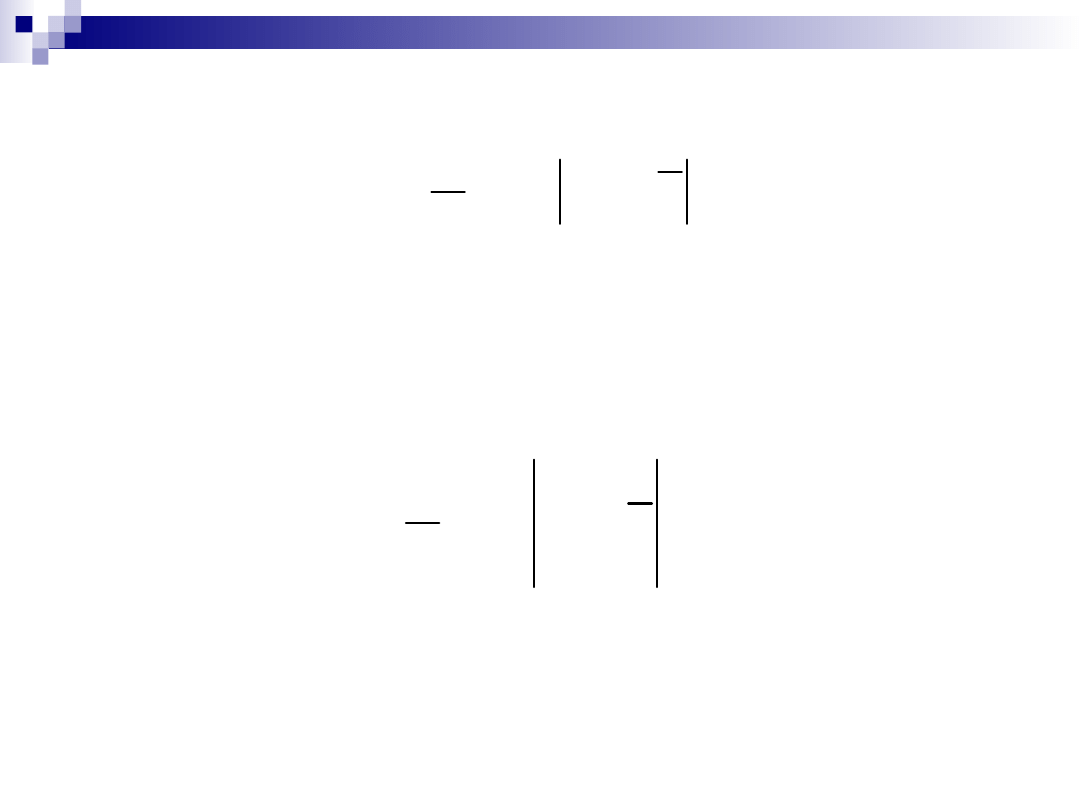
dla szeregu rozdzielczego punktowego:

-

dla szeregu rozdzielczego
przedziałowego:

gdzie:
- środek i-tego przedziału klasowego

i

k

i

i

n

x

x

n

d











1

1

i

k

i

i

n

x

x

n

d















1

1

i

x



Wariancja ogólna



Jeżeli całą zbiorowość podzielimy według

określonych kryteriów na r grup, to wariancja

dla całej zbiorowości, tzw. wariancja ogólna,

będzie sumą dwóch składników:



średniej arytmetycznej wewnątrzgrupowych

wariancji wartości cechy tzw. wariancji

wewnątrzgrupowej,



wariancji średnich grupowych wartości tej

zmiennej, tzw. wariancji międzygrupowej.

Wariancja ogólna nosząca
nazwę równości
wariancyjnej wyraża się
wzorem :

)

(

2

2

2

i

i

x

s

s

s





Gdzie:

i

r

i

i

i

i

r

i

i

i

n

x

x

N

x

s

oraz

n

s

N

s



















2

1

2

1

2

2

)

(

1

)

(

1

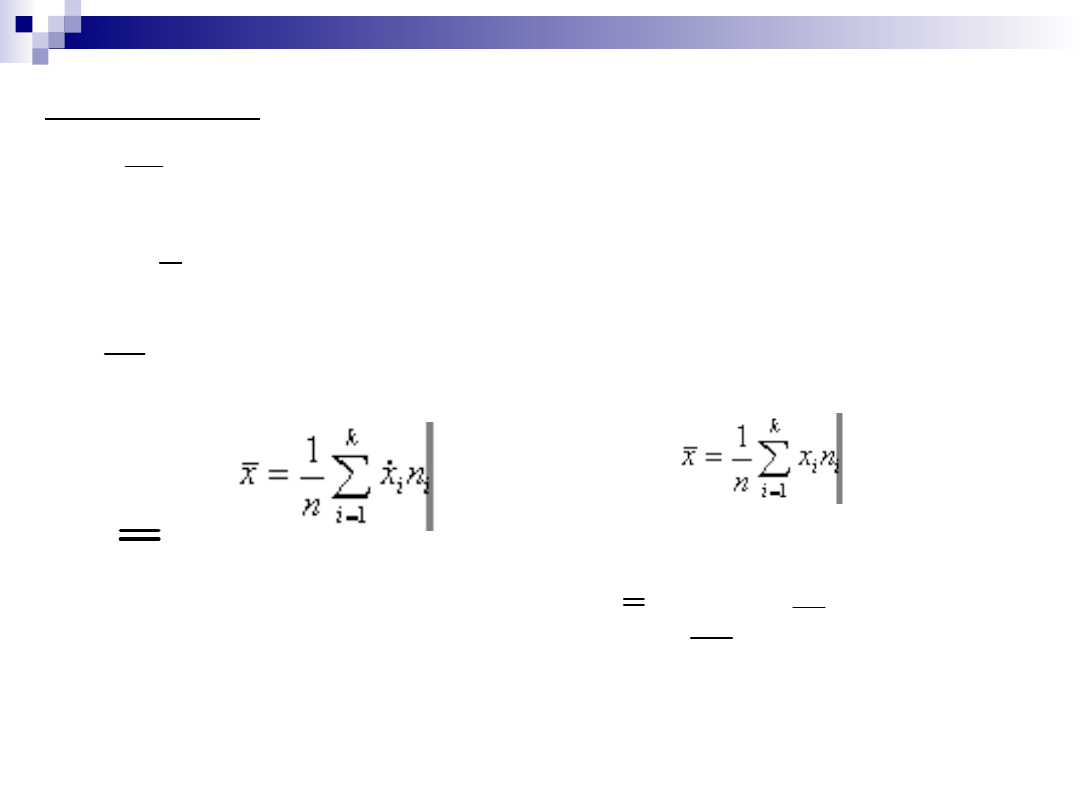
2

i

s

)

(

2

i

x

s

i

x

x

i

r

i

i

n

x

N

x







1

1

Przy czym:

- wariancja wewnątrzgrupowa

- wariancja międzygrupowa

- średnie cząstkowe wyznaczone na podstawie

- średnia arytmetyczna próby lub

populacji
wyznaczona na podstawie

N – suma liczebności we wszystkich r-
grupach.

Przykład



Właściciel zakładu zatrudniający dwóch

pracowników, dokonał pomiarów czasu wykonywania

detali. Okazało się, że robotnik A pracował przy

wykonaniu detalu średnio 16 min, a zróżnicowanie

mierzone wariancją wynosiło 7,6 minuty, wartości te

zostały wyznaczone na podstawie obserwacji n

A=

5

detali. Robotnik B na podstawie obserwacji czasów n

B

= 10 detali, miał średni czas równy 15,4 min, a

wariancję 17,24.Należy wyznaczy zróżnicowanie

czasu wykonania detali w tym zakładzie.



Średni czas wykonania detalu w zakładzie wynosi

15,6 min.



Wariancja
wewnątrzgrupowa czasu
wykonania detalu
wynosi



Wariancja
międzygrupowa



Wariancja ogólna jest
sumą dwóch
powyższych składników

03

,

14

15

4

,

210

)

10

24

,

17

5

6

,

7

(

15

1

2













i

s





08

,

0

15

2

,

1

10

)

6

,

15

4

,

15

(

5

)

6

,

15

16

(

15

1

)

(

2

2

2

















i

x

s

76

,

3

11

,

14

;

11

,

14

08

,

0

03

,

14

2











s

s

Miary dyspersji (rozproszenia),

jak i wartości średnie są liczbami
mianowanymi. Fakt ten umożliwia
bezpośrednie porównywania miar dyspersji
obliczonych dla różnych szeregów.

Jeżeli badane zjawisko mierzone

jest w różnych jednostkach miary lub
kształtuje się na niejednakowym
poziomie, wówczas do oceny
rozproszenia należy stosować
współczynnik zmienności.

Współczynnik zmienności jest ilorazem

odchylenia przeciętnego lub odchylenia
standardowego oraz średniej:

lub

(zamiast może być inna średnia, np.

mediana)

Współczynnik zmienności może

być wyrażony w procentach. Współczynnik
ten zastępuje bezwzględne miary
dyspersji.

x

s

V 

x

d

V 

x

Współczynnik zmienności

stosuje się zwykle w

porównaniach, gdy chcemy

ocenić zróżnicowanie:



Kilku zbiorowości pod względem tej
samej cechy,



Tej samej zbiorowości pod względem
kilku różnych cech.

Województwa Polski scharakteryzowano

przez dwie cechy: powierzchnię X i

liczbę ludności Y.

Należy obliczy dla powyższych cech

współczynniki zmienności



Wyznaczone dla
cechy X parametry
przedstawiają się
następująco:



Wyznaczone dla
cechy Y parametry
przedstawiają się
następująco:

24

,

2

;

28

,

6





s

x

590

;

784 



s

y

Obliczone współczynniki zmienności wskazują, że
zarówno pod względem powierzchni jak i liczby
ludności województwa są silnie zróżnicowane, przy
czym różnią się one znacznie bardziej pod
względem liczby mieszkańców

%

7

,

35

100

28

,

6

24

,

2







X

V

Powierzchnia

%

3

,

75

100

784

590







Y

V

Liczba ludności

Współczynnik zmienności
charakteryzuje stosunek nasilenia
przyczyn ubocznych do przyczyn
głównych



Wartości liczbowe współczynników
zmienności najczęściej są podawane w
procentach. Przyjmuje się, że jeżeli
współczynnik zmienności jest poniżej 10%,
to cechy wykazują zróżnicowanie nieistotne
statystycznie. Duże wartości tego
współczynnika świadczą o zróżnicowaniu a
więc niejednorodności zbiorowości.

MIARY ASYMETRII

wskaźnik skośności
współczynnik skośności

W wielu sytuacjach badanie średniego
poziomu cechy i rozproszenia jej
wartości nie wykazuje istnienia różnic
między analizowanymi zbiorowościami.
Obserwacja rozkładów empirycznych
tych cech wyklucza natomiast
podobieństwo struktury rozważanych
zbiorowości.

Szczegółowa analiza statystyczna

powinna zawierać nie tylko

poziom przeciętny i wewnętrzne

zróżnicowanie zbiorowości. Istotne

jest również określenie, czy

przeważająca liczba jednostek

znajduje się powyżej czy poniżej

przeciętnego poziomu badanej cechy.

Należy dokonać zatem oceny

asymetrii rozkładu. W związku z

tym określa się charakter (kierunek)

oraz natężenie (rozmiar) skośności.

W tabeli przedstawiono
strukturę płac pracowników
trzech zakładów
produkcyjnych

Stawka

godzinowa w zł

Odsetek pracowników
Zakład I

Zakład II

Zakład III

10-20

10

5

10

20-30

20

35

25

30-40

40

25

25

40-50

20

25

35

50-60

10

10

5

RAZEM

100

100

100

średnia

35

35

35

odchylenie

stand

120

120

120

mediana

35

34

36

modalna

35

27,5

42,5

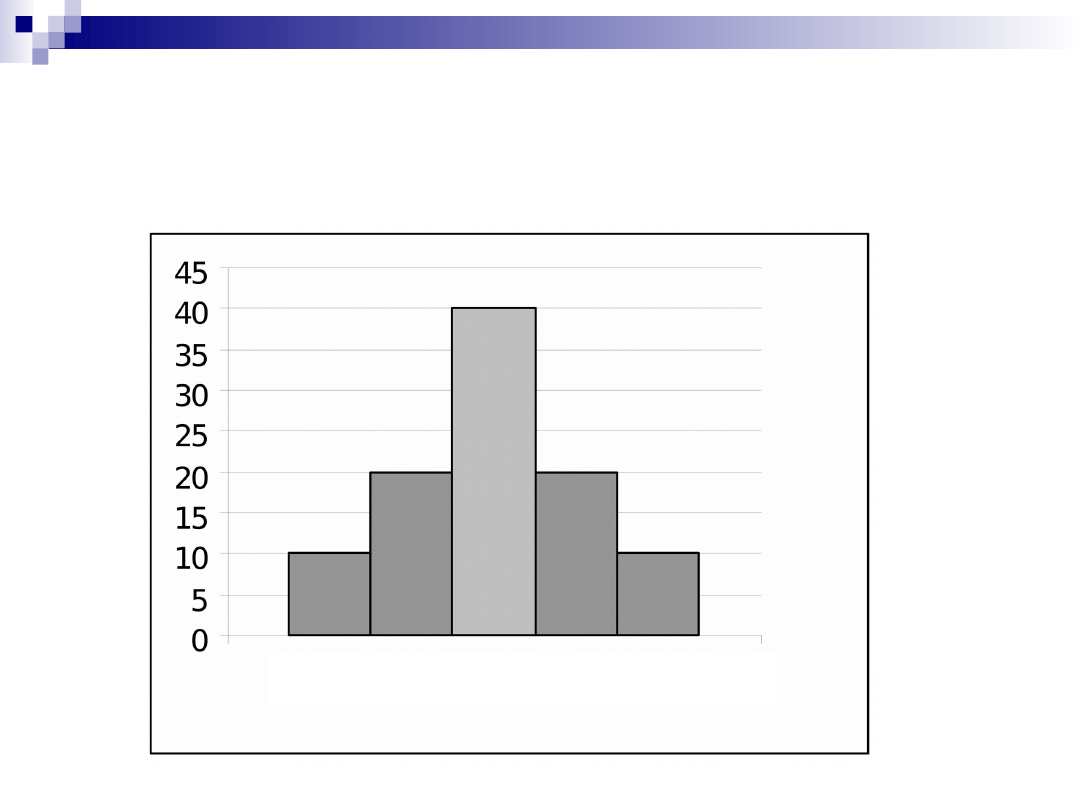
Zakład I

10 20 30 40 50

60

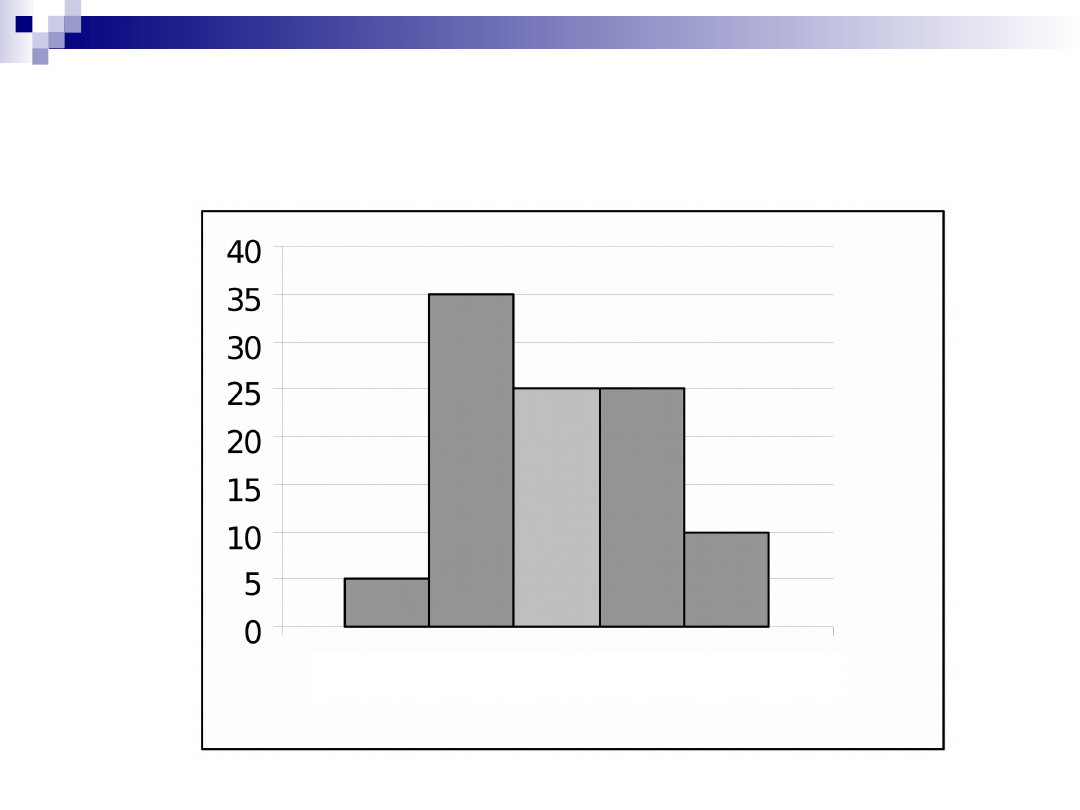
ZAKŁAD II

10 20 30 40 50

60

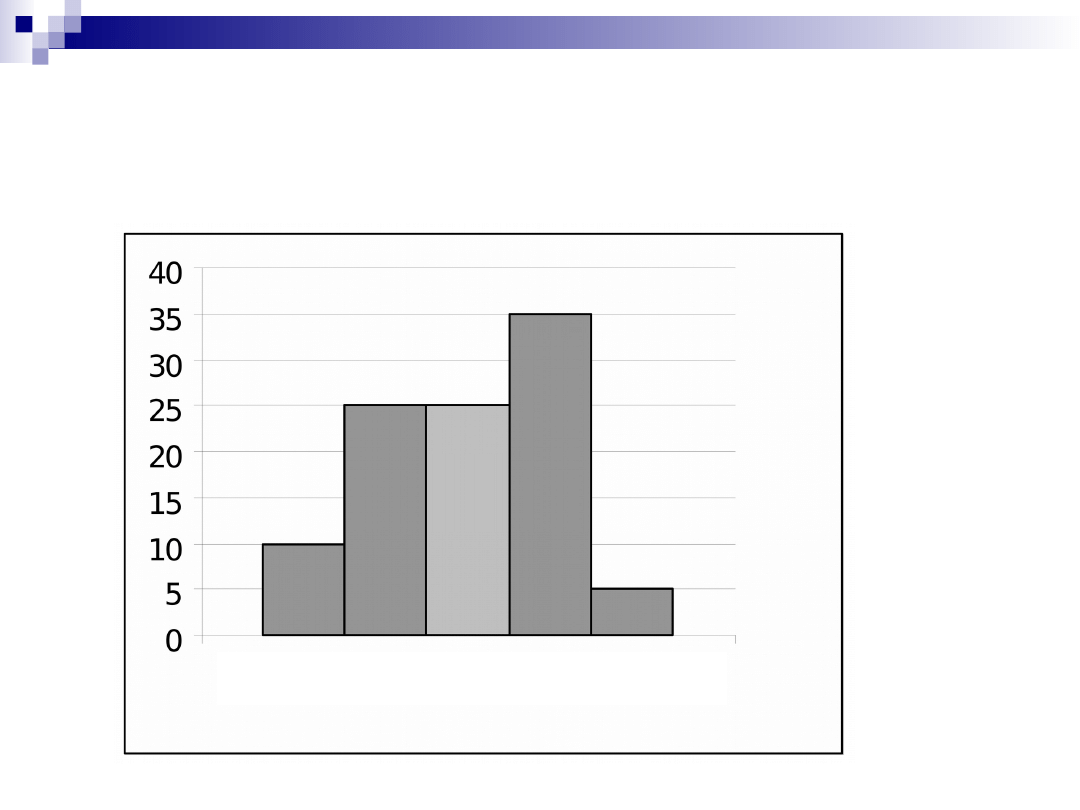
ZAKŁAD III

10 20 30 40 50

60



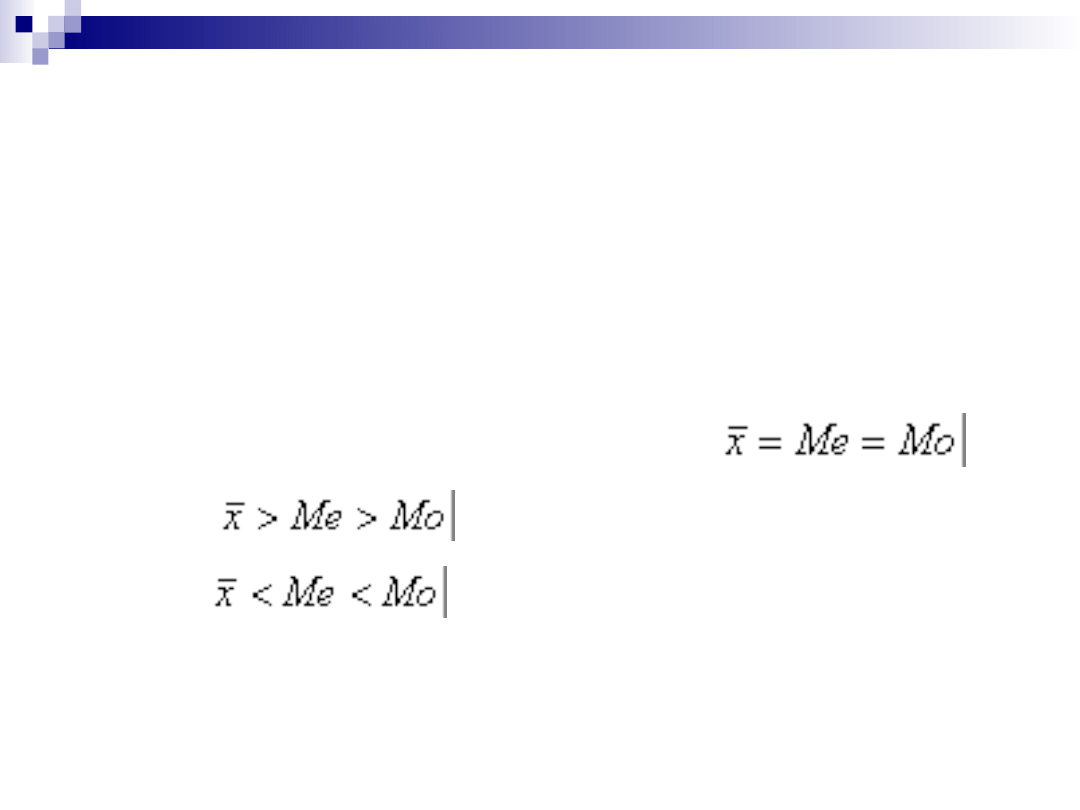
Rozkłady różnią się między sobą kierunkiem
i siłą asymetrii (miary klasyczne):



dla szeregów symetrycznych



jeżeli asymetria prawostronna



jeżeli asymetria lewostronna.

Im większe są różnice pomiędzy
średnią arytmetyczną a modalną, tym
bardziej asymetryczny jest rozkład
badanej cechy.

Skośność dodatnia

(prawostronna) ma miejsce
wówczas, gdy dłuższe ramię
krzywej charakteryzującej rozkład
liczebności szeregu znajduje
się po prawej stronie średniej.

Jeżeli dłuższe ramię krzywej

znajduje się po lewej stronie
średniej, wówczas można mówić o
skośności ujemnej (lewostronnej).

Jednym z mierników skośności jest

wskaźnik skośności (inaczej:
bezwzględna miara skośności):

Wskaźnik ten jest bezwzględną

miarą asymetrii posiadającą miano
badanej cechy. Z tego względu
ma on ograniczone zastosowanie
w analizie porównawczej. Poza tym,
wskaźnik skośności określa jedynie
kierunek asymetrii (prawo-, czy
lewostronna) nie wskazując jej siły.

Mo

x

Ws







W szeregach asymetrycznych
wskaźnik asymetrii może być większy
lub mniejszy od zera. Wówczas
mówimy o asymetrii prawostronnej
lub lewostronnej. I tak:



asymetria prawostronna



- asymetria lewostronna

Mo

Me

x

czyli

Mo

x









0

Mo

Me

x

czyli

Mo

x









0

Współczynniki skośności

(asymetrii)

są stosowane w porównaniach, do określenia

siły oraz kierunku asymetrii,



Wielkość różnicy pomiędzy średnią
arytmetyczną a wartością modalną jest jednak
zależna od wielkości jednostek statystycznych .



Aby otrzymać miarę asymetrii, niezależną od
wielkości obserwacji, a zależną tylko od
struktury zbiorowości statystycznej, różnicę
pomiędzy średnią i modalną dzielimy przez
odchylenie standardowe i w ten sposób
otrzymujemy współczynnik asymetrii,

Współczynnik ten przyjmuje

zazwyczaj wartości z przedziału:
<-1;1>. Jedynie przy bardzo
silnej asymetrii wartość
współczynnika może wykroczyć
poza w/w przedział.

s

Mo

x

As





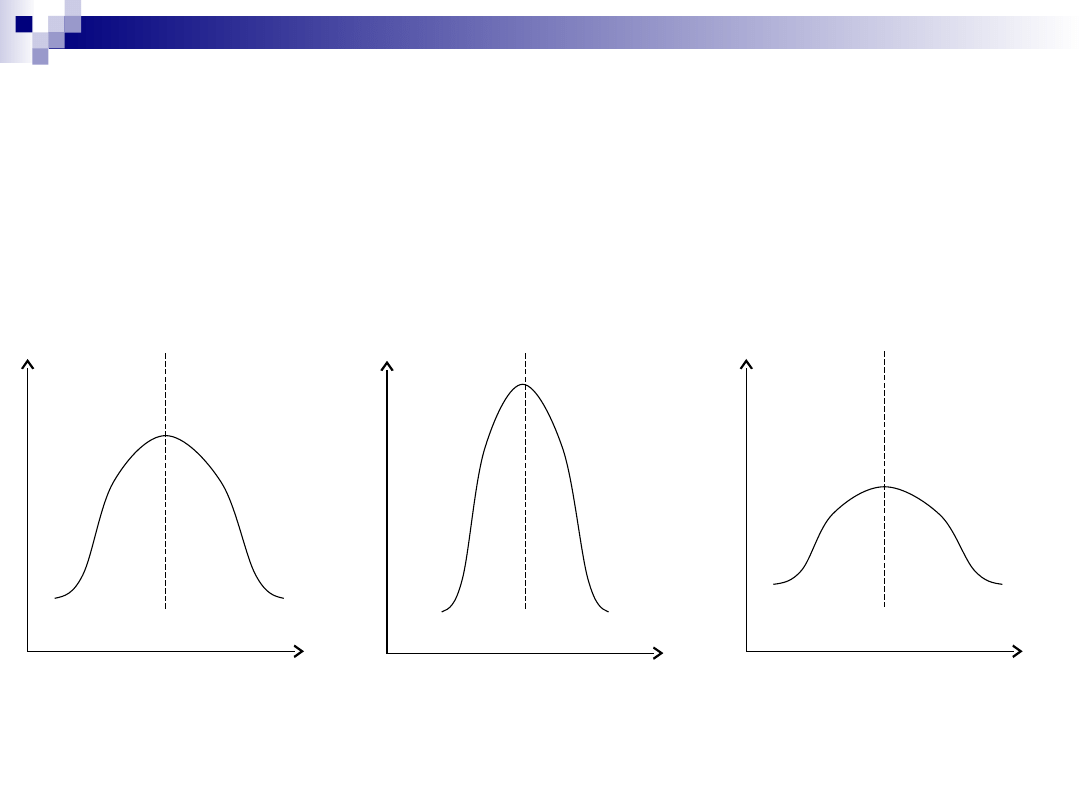
Rozkłady symetryczne (mają oś symetrii a
po obu jej stronach rozkład ilości jest taki
sam); rozkłady symetryczne można podzielić
na normalne, spłaszczone i wysmukłe

n

i

x

i

n

i

x

i

n

i

x

i

r. normalny

r. wysmukły

r. spłaszczony

Współczynnik
koncentracji



to wielkość
statystyczna zwana
inaczej kurtozą lub
współczynnikiem
skupienia. Jest to
miara skupienia, którą
możemy wyliczyć ze
wzoru:

4

4

s

m

K 

gdzie:



a) dla szeregu
punktowego



b) dla szeregu
rozdzielczego

4

1

4

)

(

1

x

x

n

m

n

i

i









i

k

i

i

n

x

x

n

m











4

1

4

)

(

1

Kurtoza



jest miarą skupienia wartości jednostki badanego

szeregu wokół ich wartości średniej. Im gęściej te

wartości są skupione wokół średniej , tym większe jest K,

a krzywa ilustrująca rozkład jest bardziej wysmukła od

rozkładu normalnego (K>0) Natomiast wartości K<0

świadczą o bardzo słabej koncentracji cechy wokół

średniej a co za tym idzie spłaszczeniu rozkładu bardziej

niż rozkład normalny. Przyjmuje się , że jeżeli zbiorowość

ma rozkład normalny, to K=3, bardziej spłaszczony

rozkład od normalnego ma K<3, a bardziej wysmukły od

normalnego ma K>3. Z tego właśnie względu

współczynnik koncentracji K podaje się w postaci:

3

4

4

'





s

m

K

To już

naprawdę

koniec !!!

!

Wskaźnik podobieństwa
struktur



Do pomiaru podobieństwa struktur stosuje się

różne miary, Jedną z nich jest wskaźnik

podobieństwa struktur określany wzorem:



Im ω

p

jest bliższe jedności, tym struktury

badanych zbiorowości są bardziej podobne.

1

0

)

,

min(

2

1

1











p

i

k

i

i

p

czym

przy









WSKAŹNIKI NATĘŻENIA



Są to wielkości stosunkowe, wyrażające
kształtowanie się wielkości jednego
zjawiska na tle innego, logicznie z nim
związanego. Częsta prawidłowa ocena
rozmiarów badanego zjawiska jest
uwarunkowana uprzednim obliczeniem
odpowiedniego wskaźnika natężenia.

Zaliczamy tu:



-stopę bezrobocia (stosunek liczby

bezrobotnych do liczby ludności czynnej

zawodowo)



-gęstość zaludnienia (liczba ludności

przypadająca na 1 km2 powierzchni)



- wskaźnik umieralności (liczba zmarłych do

średniej liczby ludności)



- wskaźnik zachorowalności (liczba zachorowań

na daną chorobę do liczby ludności)