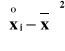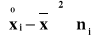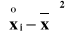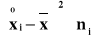Zadanie 1

Badano zawartość nikotyny w dwóch gatunkach papierosów. W próbie liczącej 50 papierosów gatunku A zaobserwowano średnią arytmetyczną zawartości nikotyny
mg przy odchyleniu standardowym s₁ = 1,2 mg. W próbie liczącej 40 papierosów gatunku B zaobserwowano
mg, s₂ = 1,4 mg.

1. na poziomie istotności α = 0,01 zweryfikować hipotezę, że wariancja zawartości nikotyny w obu gatunkach papierosów są jednakowe,

2. czy można uważać, że na poziomie istotności α = 0,05, że przeciętna zawartość nikotyny w papierosach gatunku A jest niższa niż w papierosach gatunku B?

UWAGA! Test do punkty b) dobrać w zależności od weryfikacji hipotezy z punktu a).

a) Gatunek A Gatunek B

n₁ = 50 n₂ = 40

próba duża próba duża

S₁ = 1,2 S₂ = 1,4

α = 0,01 1 - α = 0,99 z_α = 2,58

Testy dla dwóch wariancji - testy od 11 - 13

Korzystam z testu 13 dla prób dużych.

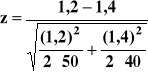
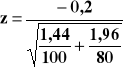
z = - 1,01 wartość statystyki należy porównać z wartością krytyczną z_α = - 2,58

Statystyka nie wpada do obszaru krytycznego. Nie ma podstaw do odrzucenia hipotezy H₀, mówiącej o tym, że wariancje zawartości nikotyny w obu gatunkach papierosów są jednakowe.

b) α = 0,05

Należy zweryfikować układ hipotez o równości wariancji, co wykazałam w podpunkcie a)

Korzystam z testów dla dwóch średnich arytmetycznych, czyli testy od 4 do 8.

Gatunek A Gatunek B

n₁ = 50 n₂ = 40

próba duża próba duża

S₁ = 1,2 S₂ = 1,4

Wybieram test nr 5, dla próby dużej:

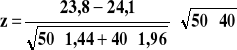
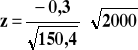
obszar krytyczny lewostronny

Zwiększam poziom istotności o 2!

Statystyka nie wpada do obszaru krytycznego. Nie ma podstaw do odrzucenia hipotezy H₀, mówiącej o tym, że przeciętna zawartość nikotyny w papierosach gatunku A jest niższa niż w papierosach gatunku B.

Zadanie 2

Na pudełkach zapałek jest napisane „średnio 64 zapałki”. Celem zweryfikowania hipotezy zerowej mówiącej o tym, że średnia liczba zapałek w pudełku jest równa zadeklarowanej, przeliczono zapałki w n = 100 przypadkowo wybranych pudełkach i okazało się, że
, a
. Czy otrzymane wyniki przeczą hipotezie zerowej przy poziomie istotności α = 0,01?

α = 0,01 α = 0,99 z_α = 2,58

n = 100 n duże

S = 5

σ - nieznane

Test dla średniej arytmetycznej dla n dużego, czyli test 2.

z = 2

Statystyka nie wpada do obszaru krytycznego. Nie ma podstaw do odrzucenia hipotezy H₀ mówiącej o tym, że średnia liczba zapałek w pudełku jest równa zadeklarowanej.

Zadanie 3

Pomiary prędkości samochodów osobowych na pewnym odcinku autostrady dały wyniki:

Prędkość w km/h	Liczba samochodów
poniżej 80	7
80-90	30
90-100	40
100-110	69
110-120	48
powyżej 120	6

1. na poziomie istotności α = 0,01, że przeciętna prędkość wynosi poniżej 105 km/h,

2. na poziomie istotności α = 0,01, że odchyleni standardowe jest większe niż 10 km/h.

a)

(xi0,xi1>	ni
70-80	7	75	525	726,3025	5084,1175
80-90	30	85	2550	287,3025	8619,075
90-100	40	95	3800	48,3025	1932,1
100-110	69	105	7245	9,3025	641,8725
110-120	48	115	5520	170,3025	8174,52
120-130	6	125	750	531,3025	3187,815
Σ	200	X	20390	X	27639,5

Testy dla średniej arytmetycznej, czyli test nr 2 dla n dużego.

α = 0,01 1 - α = 0,99 z_α = 2,58

n = 200

Podwajam poziom istotności.

Statystyka wpada do obszaru krytycznego. Odrzucam hipotezę H₀ na rzecz H₁ mówiącej o tym, że przeciętna prędkość wynosi poniżej 105 km/h.

b) α = 0,01

σ₀ = 10

n = 200

S = 11,76

Test dla wariancji, czyli test 11 dla n dużego, σ nieznana.

Podwajam poziom istotności:

Statystyka wpada do obszaru krytycznego. Odrzucam hipotezę H₀ na rzecz hipotezy alternatywnej, która mówi o tym, że odchylenie standardowe jest większe niż 100.

Zadanie 4

Rejestrując straty czasu na skutek przestoju maszyn i urządzeń otrzymano dla wydziału A pewnego zakładu następujące wyniki:

Straty czasu w minutach	0-10	10-20	20-30	30-40
Liczba stanowisk	8	11	14	8

1. zweryfikować hipotezę, że przeciętna strata na tym wydziale wynosi 25 min, α = 0,01.

2. dla wydziału B otrzymano dla losowo wybranych 36 stanowisk
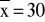
   min i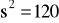
   . Czy można uważać, że wariancja strat czasu na obydwu wydziałach jest taka sama? Poziom istotności α = 0,01.

3. zweryfikować hipotezę o równości wartości przeciętnych strat czasu na obydwu wydziałach, α=0,01.

UWAGA! Test do punktu c) dobrać w zależności od weryfikacji hipotezy z punktu b).

a)

(xi0,xi1>	ni
0-10	8	5	40	236,2369	1889,8952
10-20	11	15	165	28,8369	317,2059
20-30	14	25	350	21,4369	300,1166
30-40	8	35	280	214,0369	1712,2952
Σ	41	X	835	500,5476	4219,5129

n = 41 n duże

α = 0,01 1 - α = 0,99 z_α = 2,58

Test dla średniej arytmetycznej, test 2, dla n dużego, σ nieznane.

S=10,14

z = - 2,92 z_α = 2,58

Statystyka wpada do obszaru krytycznego. Odrzucam hipotezę H₀ na rzecz H₁ mówiącej o tym, że przeciętna strata na tym wydziale nie wynosi 25 minut.

b) WYDZIAŁ A WYDZIAŁ B

n₁ = 41 n duże n₂ = 36 n duże

minut

S₁ = 10,14 S₂ = 10,95

α = 0,01 1 - α = 0,99 z_α = 2,58

Testy dla dwóch wariancji, czyli test 13.

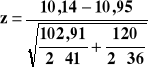
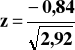
Statystyka nie wpada do obszaru krytycznego. Nie ma podstaw do odrzucenia hipotezy H₀ mówiącej o tym, że wariancja strat czasu na obydwu wydziałach jest taka sama.

c)

WYDZIAŁ A WYDZIAŁ B

n₁ = 41 n duże n₂ = 36 n duże

S₁ = 10,14 S₂ = 10,95

α = 0,01 1 - α = 0,99 z_α = 2,58

Testy dla dwóch średnich arytmetycznych, czyli test nr 5, dla n dużego,

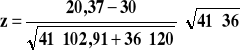
z = - 4,00

Statystyka wpada do obszaru krytycznego. Odrzucam hipotezę H₀ na rzecz H₁ mówiącej o tym, że przeciętne wartości strat czasu na obydwu wydziałach są różne.

Zadanie 5

Badając odruchy warunkowe u psa otrzymano następujące ilości śliny wydzielające się przy bodźcu (w cm³): 0,76; 0,54; 0,65; 0,40; 0,27; 0,65; 0,16; natomiast przy drugim bodźcu otrzymano: 0,32; 0,40; 0,20; 0,09; 0,38; 0,50; 0,15; 0,28.

Na poziomie istotności α = 0,05 zweryfikować hipotezę, że przy drugim bodźcu ilość wydzielającej się śliny psa jest mniejsza, zakładając, że badana cecha ma rozkład N (m, σ). Jaką hipotezę należy najpierw zweryfikować?

Bodziec pierwszy

Bodziec drugi

n₁ = 7 n małe n₂ = 8 n małe

α = 0,05 1 - α = 0,95

Testy dla dwóch średnich arytmetycznych., czyli testy od 4 do 8.

Przed wyborem statystyki testowej, należy zweryfikować układ hipotez o równości wariancji, czyli testy od 11 do 13.

Test 11 dla prób małych, σ₁ i σ₂ nieznane

gdy

F = 2,5

Odczytuję wartość z tablicy:

Statystyka nie wpada do obszaru krytycznego. Nie ma podstaw do odrzucenia hipotezy H_o mówiącej o tym, że wariancje są równe.

Powracam do:

Wybieram test nr dla dwóch średnich arytmetycznych, czyli test nr 6, dla prób małych i

v = n₁ + n₂ - 2

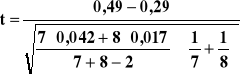
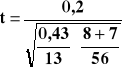
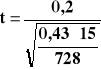
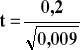
α = 0,05

Odczytuję wartość t z tablicy, podwajam poziom istotności.

Statystyka wpada do obszaru krytycznego. Odrzucamy hipotezę H₀ na rzecz hipotezy alternatywnej, która mówi o tym, że przy drugim bodźcu ilość wydzielającej się śliny psa jest mniejsza.

Zadania dotyczące testowania hipotez parametrycznych

9

z_α = -2,58

z_α = - 1,01

INTERPRETACJA:

z = - 1,09

INTERPRETACJA:

z_α=2,58

z=2

INTERPRETACJA:

Zakładając, że prędkość samochodów osobowych na tym odcinku ma rozkład N (m, σ), zweryfikować hipotezy:

z_α = 2,33

Z = - 3,67

INTERPRETACJA:

z_α = 2,33

z = 3,6

INTERPRETACJA:

z_α = -2,58

z = - 2,92

INTERPRETACJA:

z_α = 2,58

z = - 0,49

INTERPRETACJA:

z_α = −2,58

z = - 4,00

INTERPRETACJA:

3,87

2,5

INTERPRETACJA:

INTERPRETACJA:

z_α = 2,58

z_α = 1,64

z_α = 2,58

---