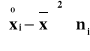Zadanie 1
Ze wszystkich wybudowanych w roku 2002 w Warszawie mieszkań wybrano w sposób losowy 120 i otrzymano dla nich następujący rozkład powierzchni mieszkalnej:
Powierzchnia w m2 |
35-45 |
45-55 |
55-65 |
65-75 |
75-85 |
85-95 |
Razem |
Liczba mieszkań |
10 |
25 |
40 |
30 |
10 |
5 |
120 |
Na poziomie istotności α=0,05 sprawdzić, czy rozkład powierzchni mieszkań jest rozkładem normalnym.
Test zgodności ![]()
n = 120 liczebność duża
Test ten sprawdza, czy badany rozkład jest zgodny z rozkładem teoretycznym.
α = 0,05
PROCEDURA POSTĘPOWANIA
Wyznaczamy parametry, które charakteryzują rozkład normalny, czyli m - średnia arytmetyczna, σ - odchylenie standardowe.
Obliczam średnią arytmetyczną i odchylenie standardowe.
![]()
![]()
![]()
![]()
W ostatnim przedziale, liczebność jest mniejsza od 8, więc łączymy ostatni przedział z przedostatnim.
Wyznaczamy górne wartości przedziałów xi1.
Standaryzujemy:
Odczytujemy dystrybuantę
Obliczamy prawdopodobieństwo
, czyli
Wyznaczamy liczebność teoretyczną
Wyznaczam wartość statystyki
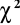
Porównuję z wartość krytyczną.
Wyznaczamy parametry, które charakteryzują rozkład normalny, czyli m - średnia arytmetyczna, σ - odchylenie standardowe.
W pierwszym i ostatnim przedziale, liczebność jest mniejsza od 8, więc łączymy ostatni przedział z przedostatnim., natomiast pierwszy drugim.
Wyznaczamy górne wartości przedziałów xi1.
Standaryzujemy:
Odczytujemy dystrybuantę
Obliczamy prawdopodobieństwo
, czyliWyznaczamy liczebność teoretyczną
Wyznaczam wartość statystyki
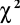
Porównuję z wartość krytyczną.
Tworzymy tablicę asocjacji.
Określić, która z badanych cech wykazuje największą zmienność
Obliczyć kowariancje między cechami X i Y, X i Z oraz Y i Z
Obliczyć współczynniki korelacji między wymienionymi w punkcie b) parami cech
Zbadać statystyczną istotność każdego z trzech wyżej wymienionych związków, zakładając prawdopodobieństwo popełnienia błędu I rodzaju na poziomie 0,05
Obliczyć współczynniki korelacji rang Spearmana między cechami X i Y, X i Z oraz Y i Z
Określić kolejność uczniów ze względu na wszystkie badane cechy.
Pomiędzy zmiennymi występuje dość silna korelacja dodatnia, co oznacza, że wraz ze wzrostem wartości jednej zmiennej wartość drugiej zmiennej wzrasta i odwrotnie.
Odrzucam hipotezę H0 na rzecz H1 na poziomie istotności α=0,05 współczynnik korelacji pomiędzy zmiennymi jest statystycznie istotny, czyli zależność między nimi jest istotna.
Nie ma podstaw do odrzucenia hipotezy H0 na poziomie istotności α=0,05 współczynnik korelacji pomiędzy zmiennymi jest statystycznie nieistotny, czyli zależność między nimi jest nieistotna.
Odrzucam hipotezę H0 na rzecz H1 na poziomie istotności α=0,05 współczynnik korelacji pomiędzy zmiennymi jest statystycznie istotny, czyli zależność między nimi jest istotna.
(xi0, xi1> |
ni |
|
|
|
(xi0, xi1> |
ni |
xi1 |
|
F(Zi1) |
pi=F(Zi)−F(Zi-1) |
|
|
|
|
35-45 |
10 |
40 |
400 |
4840 |
35-45 |
10 |
45 |
−1,42 |
0,0778 |
0,0778 |
9,6 |
10 |
0 |
0 |
45-55 |
25 |
50 |
1250 |
3600 |
45-55 |
25 |
55 |
−0,58 |
0,281 |
0,2032 |
24,384 |
24 |
1 |
0,04 |
55-65 |
40 |
60 |
2400 |
160 |
55-65 |
40 |
65 |
0,25 |
0,5987 |
0,3177 |
38,124 |
38 |
2 |
0,11 |
65-75 |
30 |
70 |
2100 |
1920 |
65-75 |
30 |
75 |
1,08 |
0,86 |
0,2613 |
31,356 |
31 |
−1 |
0,03 |
75-85 |
10 |
80 |
800 |
3240 |
75-95 |
15 |
95 |
2,75 |
|
0,14 |
16,8 |
17 |
−2 |
0,24 |
85-95 |
5 |
90 |
450 |
3920 |
Razem: |
120 |
X |
X |
X |
1,00 |
X |
120 |
|
0,42 |
Razem: |
120 |
X |
7400 |
17680 |
![]()
![]()
Wartość statystyki ![]()
F(−1,42) = 1 − F(1,42) = 1 − 0,922196 = 0,077804
F(−0,58) = 1 − F(0,58) = 1 − 0,719043 = 0,280957
F(0,25) = 0,598706
F(1,08) = 0,859929
F(2,75) = 0,997020
![]()
α = 0,05
k - liczba przedziałów po złączeniu
r - liczba szacowanych parametrów, dla rozkładu normalnego
k = 5
r = 2 ![]()
stopnie swobody
![]()
![]()
![]()
Nie ma podstaw do odrzucenia hipotezy H0, która mówi o tym, że rozkład powierzchni mieszkań jest rozkładem normalnym.
Zadanie 2
W celu oszacowania średniej wytrzymałości na ściskanie pewnego typu betonu, dokonano n = 80 niezależnych pomiarów wytrzymałości tego betonu i otrzymano następujące wyniki (w KG/cm2):
Wytrzymałość |
190-194 |
194-198 |
198-202 |
202-206 |
206-210 |
210-214 |
Razem |
Liczba pomiarów |
6 |
12 |
26 |
20 |
11 |
5 |
80 |
Zweryfikować na poziomie istotności α = 0,05 hipotezę, że rozkład wytrzymałości na ściskanie badanego betonu jest normalny.
Test zgodności ![]()
n = 80 liczebność duża α = 0,05
Test ten sprawdza, czy badany rozkład jest zgodny z rozkładem teoretycznym.
PROCEDURA POSTĘPOWANIA
Obliczam średnią arytmetyczną i odchylenie standardowe.
![]()
![]()
![]()
![]()
(xi0, xi1> |
ni |
|
|
|
(xi0, xi1> |
ni |
xi1 |
|
F(Zi1) |
pi=F(Zi)−F(Zi-1) |
|
|
|
|
190-194 |
6 |
192 |
1152 |
600 |
190-198 |
18 |
198 |
−0,8 |
0,2119 |
0,2119 |
16,952 |
17 |
1 |
0,0588 |
194-198 |
12 |
196 |
2352 |
432 |
198-202 |
26 |
202 |
0 |
0,5 |
0,2881 |
23,048 |
23 |
3 |
0,3913 |
198-202 |
26 |
200 |
5200 |
104 |
202-206 |
20 |
206 |
0,8 |
0,7881 |
0,2881 |
23,048 |
23 |
−3 |
0,3913 |
202-206 |
20 |
204 |
4080 |
80 |
206-214 |
16 |
214 |
2,4 |
|
0,2119 |
16,952 |
17 |
−1 |
0,0588 |
206-210 |
11 |
208 |
2288 |
396 |
Razem: |
80 |
X |
X |
X |
1,00 |
X |
80 |
|
0,9002 |
210-214 |
5 |
212 |
1060 |
500 |
||||||||||
Razem: |
80 |
X |
16132 |
2112 |
![]()
![]()
Wartość statystyki ![]()
F(−0,8) = 1 − F(0,8) = 1 − 0,788145 =0,211855
F(0) = 0,5
F(0,8) = 0,788145
F(2,4) = 0,991802
![]()
α = 0,05
k - liczba przedziałów po złączeniu
r - liczba szacowanych parametrów, dla rozkładu normalnego
k = 4
r = 2 ![]()
stopień swobody
![]()
![]()
![]()
Nie ma podstaw do odrzucenia H0, która mówi o tym, że rozkład wytrzymałości na ściskanie badanego betonu jest normalny.
Zadanie 3
W celu sprawdzenia hipotezy, że „zarwanie” nocy przed egzaminem powoduje jego niezdanie, wylosowano próbę 200 studentów, którym zadano pytanie: „Czy spał/a Pan/Pani w noc poprzedzającą najtrudniejszy egzamin w sesji?”. Otrzymane odpowiedzi zestawiono w tablicy:
|
Noc przed egzaminem |
|
|
przespana |
nieprzespana |
zdany |
115 |
45 |
niezdany |
26 |
14 |
Test niezależności ![]()
PROCEDURA Postępowania (uproszczona)
wynik egzaminu |
noc przespana |
noc nieprzespana |
Σ |
zdany |
115 a |
45 b |
160 |
niezdany |
26 c |
14 d |
40 |
Σ |
141 |
59 |
|
Statystyka ![]()
ma postać
![]()
![]()
![]()
![]()
![]()
porównuję z wartością krytyczną dla rozkładu ![]()
.
liczba stopni swobody
![]()
![]()
Nie ma podstaw do odrzucenia H0, która mówi o tym, że wyniki egzaminu nie zależą od sposobu spędzenia nocy poprzedzającej egzamin.
Zadanie 4
Pewien produkt można wytwarzać trzema metodami. Wysunięto hipotezę, że wadliwość produkcji nie zależy od metody produkcji. Pobrano próbkę o liczebności n = 400 sztuk i otrzymano następujące wyniki badania jakości dla poszczególnych metod:
Jakość |
|
||
|
I |
II |
III |
Sztuki dobre |
100 |
140 |
100 |
Sztuki wadliwe |
10 |
30 |
20 |
Test niezależności ![]()
.
Test nr 5
Tworzymy tablicę asocjacji.
jakość |
Metoda produkcji |
|
||
|
I |
II |
III |
|
sztuki dobre |
100 |
140 |
100 |
340 |
sztuki wadliwe |
10 |
30 |
20 |
60 |
|
110 |
170 |
120 |
400 |
|
|
|
|
100 |
93,5 |
6,5 |
0,4519 |
140 |
144,5 |
−4,5 |
0,1401 |
100 |
102 |
−2 |
0,0392 |
10 |
16,5 |
−6,5 |
2,5606 |
30 |
25,5 |
4,5 |
0,7941 |
20 |
18 |
2 |
0,2222 |
400 |
400 |
|
4,2081 |
Wartość statystyki ![]()
dla 100 ![]()
dla 140 ![]()
dla 100 ![]()
dla 10 ![]()
dla 30 ![]()
dla 20 ![]()
![]()
porównuję z wartością krytyczną dla rozkładu ![]()
.
liczba stopni swobody
k - liczba kolumn
l - liczba wierszy ![]()
![]()
![]()
Nie ma podstaw do odrzucenia H0, która mówi o tym, że jakość produkcji nie zależy od metody produkcji.
Zadanie 5
Na podstawie danych dotyczących wyników egzaminu wstępnego na wyższą uczelnię (Y, w punktach), ilorazu inteligencji (X) i liczby godzin poświęcanych tygodniowo na naukę (Z) grupy 12 osób wybranych w sposób losowy utworzono poniższą tabelę:
Numer |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Y |
83 |
77 |
95 |
49 |
63 |
80 |
91 |
79 |
36 |
58 |
93 |
84 |
X |
112 |
115 |
129 |
103 |
117 |
115 |
124 |
113 |
106 |
114 |
136 |
127 |
Z |
9 |
6 |
14 |
4 |
8 |
12 |
10 |
9 |
5 |
7 |
8 |
3 |
Y - wyniki egzaminu wstępnego na wyższą uczelnię w punktach
X - iloraz inteligencji
Z - liczba godzin poświęcanych tygodniowo na naukę
|
|
|
|
|
|
|
|
|
|
|
112 |
83 |
9 |
-6 |
9 |
1 |
36 |
81 |
1 |
-54 |
-6 |
115 |
77 |
6 |
-3 |
3 |
2 |
9 |
9 |
4 |
-9 |
-6 |
129 |
95 |
14 |
11 |
21 |
6 |
121 |
441 |
36 |
231 |
66 |
103 |
49 |
4 |
-15 |
-25 |
-4 |
225 |
625 |
16 |
375 |
60 |
117 |
63 |
8 |
-1 |
-11 |
0 |
1 |
121 |
0 |
11 |
0 |
115 |
80 |
12 |
-3 |
6 |
4 |
9 |
36 |
16 |
-18 |
-12 |
124 |
91 |
10 |
6 |
17 |
2 |
36 |
289 |
4 |
102 |
12 |
113 |
79 |
9 |
-5 |
5 |
1 |
25 |
25 |
1 |
25 |
-5 |
106 |
36 |
5 |
-12 |
-38 |
-3 |
144 |
1444 |
9 |
456 |
36 |
114 |
58 |
7 |
-4 |
-16 |
-1 |
16 |
256 |
1 |
64 |
4 |
136 |
93 |
8 |
18 |
19 |
0 |
324 |
361 |
0 |
342 |
0 |
127 |
84 |
3 |
9 |
10 |
-5 |
81 |
100 |
25 |
90 |
-45 |
1411 |
888 |
95 |
X |
X |
X |
1027 |
3788 |
113 |
1615 |
104 |
![]()
![]()
![]()
|
|
|
|
ranga xi |
ranga yi |
ranga zi |
di=xi−yi |
|
di=xi−zi |
|
di=yi−zi |
|
|
112 |
83 |
9 |
9 |
3 |
8 |
8,5 |
-5 |
25 |
-5,5 |
30,25 |
-0,5 |
0,25 |
|
115 |
77 |
6 |
6 |
6,5 |
5 |
4 |
1,5 |
2,25 |
2,5 |
6,25 |
1 |
1 |
|
129 |
95 |
14 |
126 |
11 |
12 |
12 |
-1 |
1 |
-1 |
1 |
0 |
0 |
|
103 |
49 |
4 |
100 |
1 |
2 |
2 |
-1 |
1 |
-1 |
1 |
0 |
0 |
|
117 |
63 |
8 |
0 |
8 |
4 |
6,5 |
4 |
16 |
1,5 |
2,25 |
-2,5 |
6,25 |
|
115 |
80 |
12 |
24 |
6,5 |
7 |
11 |
-0,5 |
0,25 |
-4,5 |
20,25 |
3 |
9 |
|
124 |
91 |
10 |
34 |
9 |
10 |
10 |
-1 |
1 |
-1 |
1 |
0 |
0 |
|
113 |
79 |
9 |
5 |
4 |
6 |
8,5 |
-2 |
4 |
-4,5 |
20,25 |
-2,5 |
6,25 |
|
106 |
36 |
5 |
114 |
2 |
1 |
3 |
1 |
1 |
-1 |
1 |
-2 |
4 |
|
114 |
58 |
7 |
16 |
5 |
3 |
5 |
2 |
4 |
0 |
0 |
-2 |
4 |
|
136 |
93 |
8 |
0 |
1 |
11 |
6,5 |
-10 |
100 |
-5,5 |
30,25 |
4,5 |
20,25 |
|
127 |
84 |
3 |
-50 |
10 |
9 |
1 |
1 |
1 |
9 |
81 |
8 |
64 |
|
1411 |
888 |
95 |
384 |
X |
X |
X |
X |
156,5 |
X |
194,5 |
X |
115 |
|
![]()
![]()
![]()
S(x) = 9,2511 ≈ 9 S(y) = 17,767 ≈ 18 S(z) = 3,0687 ≈ 3
KOWARIANCJA
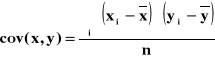
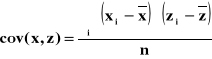
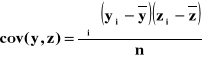
![]()
![]()
![]()
Korelacja dodatnia Korelacja dodatnia Korelacja dodatnia
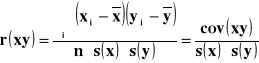
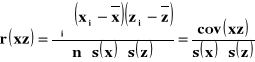
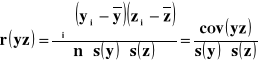
![]()
![]()
![]()
Test istotności współczynnika korelacji liniowej Pearsona
H0: ![]()
H1: ![]()
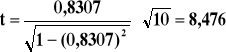
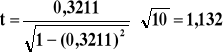
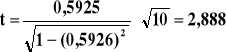
![]()
WSPÓŁCZYNNIK KORELACJI RANG SPEARMANA
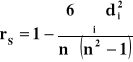
![]()
![]()
![]()
![]()
![]()
![]()
Zadania dotyczące testowania hipotez nieparametrycznych
1
Zadania dotyczące testowania hipotez nieparametrycznych
10
H0: F(X) = F0(X)
H1: F(X) ≠ F0(X)
H0: F(X) = F0(X)
H1: F(X) ≠ F0(X)
Na poziomie istotności α=0,05 sprawdzić hipotezę o niezależności wyniku egzaminu od sposobu spędzenia nocy poprzedzającej egzamin.
H0: wyniki egzaminu nie zależą od nocy przed egzaminem
H1: wyniki egzaminu zależą od nocy przed egzaminem
n
γ = (k − 1) (l −1) = 1
Przyjmując poziom istotności α=0,05, zweryfikować hipotezę o niezależności jakości produkcji od metod produkcji.
H0: jakość produkcji nie zależy od metody produkcji
H1: jakość produkcji zależy od metody produkcji
γ = (k − 1) (l − 1)
![]()
tα,γ
tα,γ
tα,γ
t
t
t
Wyszukiwarka
Podobne podstrony:
Rozwiązania z testowania hipotez nieparametrycznych 3, statystyka
Rozwiązania z testowania hipotez parametrycznych 2, statystyka
06 Testowanie hipotez statystycznychid 6412 ppt
statystyka, Przedzial ufnosci dla m. Testowanie hipotezy dla m., PRZEDZIAŁ UFNOŚCI DLA WARTOŚCI OCZE
Ogólne zasady testowania hipotez statystycznych
Statystyka #6 Testowanie hipotez
testowanie hipotez, Statystyka i metodologia(1)
Zajęcia 7 Teoria testowania hipotez statystycznych
etapy testowania hipotez statystycznych, statystyka
5 Testowanie hipotez statystycznych
TESTOWANIE HIPOTEZ STATYSTY, szkoła
06 Testowanie hipotez statystycznychid 6412 ppt
Testowanie hipotez statystycznych
Metodologia z elelmentami statystyki dr Izabela Krejtz wyklad 5 Testowanie hipotez Test T
statystyka egzaminy rozwiązane, UTP, II semestr, STATYSTYKA
hipotezy nieparametryczne 13 01 Nieznany
Metody testowania hipotez ewolucyjnych, Psychologia, biologia, ewolucyjna
więcej podobnych podstron