Wydział : Inżynierii Lądowej	Dzień/godz.: Poniedziałek 14-17	Data: 29.10.2001	Nr zespołu: 15
Nazwisko i Imię	Ocena z przygotowania:	Ocena ze sprawozdania:	Ocena:
1. Głódź Katarzyna
2. Szutkiewicz Joanna
3. Szczepaniak Paweł
Prowadzący:		Podpis prowadzącego:

1. TEMPERATUROWA ZALEŻNOŚĆ OPORNOŚCI ELEKTRYCZNEJ METALU I PÓŁPRZEWODNIKA.

Celem przeprowadzonego przez nas ćwiczenia było zbadanie temperaturowej zależności oporności elektrycznej metalu i półprzewodnika oraz ukazanie charakterystycznych cech tej zależności dla obu materiałów. Dla porównania badaliśmy również wpływ zmiany oporności właściwej konstantu ( Cu₆₀Ni₄₀ ) na zmianę temperatury. Jego opór właściwy powinien nieznacznie zmieniać się wraz ze zmianą temperatury.

a) metale:

W przypadku metali analizując wzór r(T) ~ 1/( n(T)μ(T) ) , gdzie r(T) - oporność właściwa, n(T) - koncentracja nośników prądu, μ(T) - ruchliwość nośników prądu; stwierdzamy, że oporność właściwa metalu ( r(T) ) jest odwrotnie proporcjonalna do ruchliwości nośników prądu ( μ(T) ). Koncentracja nośników prądu ( n(T) ) nie ma wpływu na oporność właściwą gdyż nie zmienia się wraz ze zmianą temperatury n(T)=const. Ruchliwość nośników prądu wyraża się wzorem: μ=( eτ )/m, gdzie e - ładunek elektronu, m - masa elektronu, τ - czas relaksacji, który w przybliżeniu jest równy stosunkowi drogi swobodnej (λ) do wartości średniej prędkości V_śr. : τ ≈ λ/ V_śr. .

W modelu klasycznym λ powinna być porównywalna ze stałą sieciową, która od temperatury nie zależy, czyli powinna być stała, a czas relaksacji ( τ ) powinien być zależny od V_śr.. Związek V_śr. ze średnią energią kinetyczną drgań sieci ( im wyższa temperatura tym wyższa energia drgań sieci ) wyraża się w przybliżeniu wzorem : ( mv_sr²)/2 ≈ E_{k śr.}= kT, gdzie k - stała Boltzmana, E_{k śr.} - średnia energia kinetyczna drgań, stąd czas relaksacji ( τ ) jest proporcjonalny do 1/T^0.5 ,a więc opór właściwy :

r(T) ~ T^0.5

W modelu kwantowym decydujący wpływ na przewodnictwo elektryczne mają elektrony, których stany znajdują się w pobliżu energii Fermiego, a ponieważ zakładamy, że na tym poziomie energia Fermiego jak i prędkość nie zależą od temperatury, więc czas relaksacji ( τ ) będzie zależny od drogi swobodnej ( λ ). W modelu kwantowym temperaturowa zależność drogi swobodnej ( λ ) określona jest rozproszeniem na drganiach sieci krystalicznej. Prawdopodobieństwo rozproszenia wzrasta proporcjonalnie do kwadratu amplitudy drgań ( A² ), a ponieważ energia drgań jest również proporcjonalna do tejże amplitudy, stąd wynika że λ ~ 1/T. Wnioskujemy stąd, że oporność właściwa w kwantowym ujęciu jest proporcjonalna do temperatury:

r(T) ~ T.

Postaramy się dowieść, że powyższa zależność lepiej odzwierciedla rzeczywistość niż zależność wyprowadzona na bazie modelu klasycznego.

b) półprzewodniki:

W przypadku metali pasmo walencyjne jest zawsze zapełnione ( niezależnie od temperatury ), więc przewodnictwo odbywa się tylko w paśmie przewodnictwa. Odmiennie sytuacja wygląda w przypadku półprzewodników gdzie pasmo walencyjne zapełnione jest tylko w temperaturze T=O⁰K . W tej temperaturze półprzewodniki zachowują się jak izolatory, bo w paśmie przewodnictwa nie ma elektronów, a pasmo walencyjne mają całkowicie zapełnione. Dzięki temu pasmo zabronione ( przerwa energetyczna ) w półprzewodnikach jest dużo „cieńsze” niż w izolatorach ( półprzewodnik - 1eV, izolator - 10eV ) podczas ogrzewania część elektronów walencyjnych przedostaje się do pasma przewodnictwa stwarzając warunki do przepływu prądu. Powstają dwa poziomy częściowo zapełnione przez które może następować transport elektronów. W wyniku przejścia części elektronów walencyjnych do pasma przewodnictwa w paśmie walencyjnym powstają „dziury” ( stany nie obsadzone ), wobec tego przewodnictwo w półprzewodnikach zależy zarówno od „dziur” jak i od elektronów.

σ = neμ_e + peμ_d

, gdzie n i μ_e - koncentracja i ruchliwość elektronów, a p i μ_d - koncentracja i ruchliwość „dziur”.

Koncentracja nośników prądu bardzo silnie wzrasta wraz ze wzrostem temperatury : n ~ e ^-(ΔE)/(2kT) , gdzie ΔE jest przerwą energetyczną lub energią jonizacji domieszek.

Podsumowując w odróżnieniu od metali, w półprzewodnikach decydującym czynnikiem o zmianach oporu ze zmianą temperatury jest koncentracja nośników prądu. Temperaturową zależność ruchliwości nośników możemy zaniedbać ze względu na bardzo silny ( wykładniczy ) wzrost koncentracji nośników prądu wraz ze wzrostem temperatury, a wiec w przybliżeniu :

σ = σ₀e ^-(ΔE)/(2kT)

, logarytmując obydwie strony równania otrzymamy:

lnσ = lnσ₀ - (ΔE)/(2kT),

wykresem tej funkcji jest linia prosta. Z nachylenia tej prostej ( w temperaturze 20 - 90⁰ C) możemy odczytać współczynnik (ΔE)/(2kT), a przekształcając go - przerwę energetyczną lub energie jonizacji nośników domieszkowych.

2. WYNIKI POMIARÓW.

podczas ogrzewania				podczas ochładzania
Temp [stC]±0.5	Cu [] ±0.05	Konstantan []±0.01	Termistor [	Temp [stC]	Cu [	Konstantan [	Termistor [
41	5,25	6,37	-	41	-	-	-
42	5,1	6,36	-	42	-	-	-
43	4,95	6,35	-	43	6	5,5	-
44	5,05	6,35	-	44	6,05	5,48	-
45	5,05	6,38	-	45	6,05	5,45	-
46	5,02	6,38	-	46	6,05	5,47	-
47	5,25	6,39	-	47	6,05	5,49	-
48	5,3	6,33	-	48	6,1	5,49	-
49	5,4	6,33	40,1	49	6,2	5,45	-
50	5,55	6,31	39,5	50	6,4	5,42	-
51	5,5	6,35	37,7	51	6,4	5,4	-
52	5,4	6,34	35,7	52	6,4	5,4	-
53	5,4	6,34	35,3	53	6,45	5,4	-
54	5,4	6,33	33,5	54	6,45	5,4	-
55	5,4	6,34	31,2	55	6,45	5,4	-
56	5,4	6,34	30,8	56	6,45	5,42	-
57	5,5	6,32	30	57	6,45	5,4	-
58	5,6	6,32	29,1	58	6,45	5,4	-
59	5,7	6,32	28,1	59	6,45	5,38	-
60	5,8	6,32	26,5	60	6,45	5,38	24,3
61	5,37	6,3	25,4	61	6,45	5,38	26,6
62	5,8	6,3	25	62	6,8	5,38	25,5
63	5,8	6,3	24,8	63	6,8	5,4	24,7
64	5,8	6,28	23,5	64	6,8	5,4	23,8
65	5,7	6,25	22,8	65	6,8	5,51	22,9
66	5,8	6,25	21,9	66	6,8	5,58	22,1
67	5,85	6,25	21,3	67	6,8	5,6	21,6
68	6	6,31	20,6	68	6,8	5,74	20,8
69	5,8	6,32	19,6	69	6,8	5,74	19,9
70	5,8	6,33	19,1	70	7,2	5,74	19,5
71	5,9	6,33	18,6	71	7,2	5,75	18,8
72	6	6,32	17,9	72	7,2	5,73	18,1
73	6,05	6,31	17,4	73	7,2	5,73	17,7
74	6,1	6,3	16,7	74	7,2	5,73	16,9
75	6,2	6,3	16,2	75	7,2	5,71	16,4
76	6,2	6,3	15,5	76	7,25	5,69	16
77	6,2	6,3	14,9	77	7,2	5,69	15,2
78	6,25	6,3	14,6	78	7,4	5,69	14,8
79	6,3	6,3	14,3	79	6,6	5,71	14,3
80	6,35	6,27	13,7	80	6,4	5,71	13,8
81	6,3	6,27	13,3	81	5,6	5,71	13,4
82	6,4	6,2	12,8	82	5,45	5,71	12,9
83	6,4	6,24	12,3	83	6,4	5,76	12,5
84	6,45	6,24	11,9	84	6,45	5,76	12,2
85	6,45	6,17	11,5	85	6,45	5,79	11,8
86	6,5	6,19	11,2	86	6,45	5,79	11,4
87	6,55	6,2	10,9	87	6,45	5,82	11
88	6,55	6,2	10,5	88	6,45	5,88	10,7
89	6,55	6,15	10,2	89	6,45	5,8	10,4
90	6,6	6,07	10	-	-	-	-

3. WYKRESY ZALEŻNOŚCI OPORNOŚCI ELEKTRYCZNEJ OD TEMPERATURY

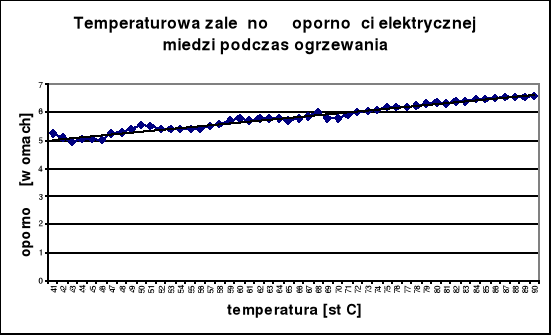
MIEDŹ

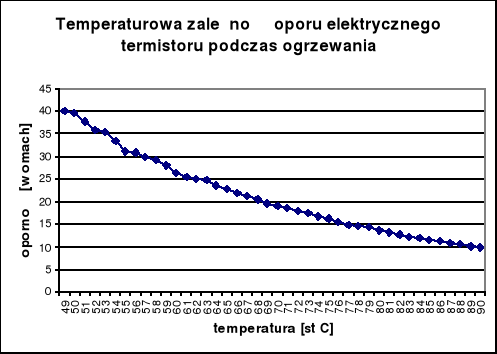
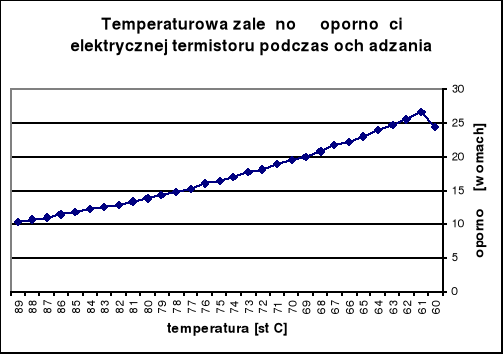
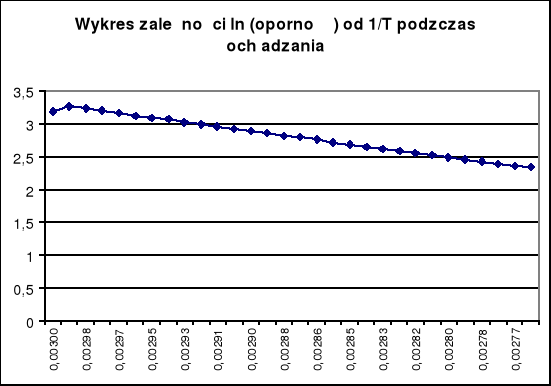
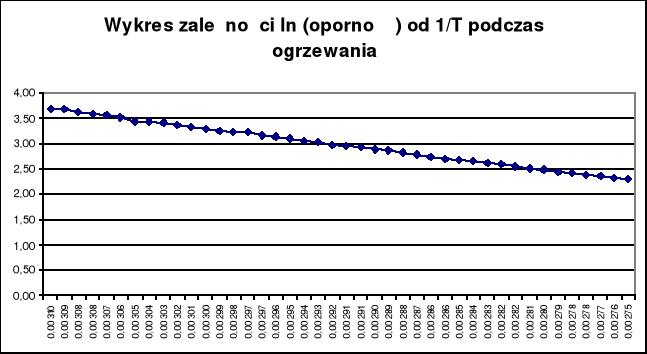
TERMISTOR

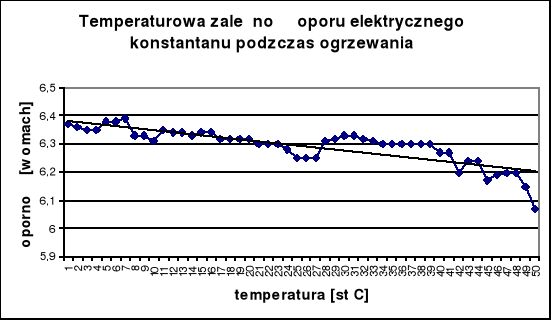
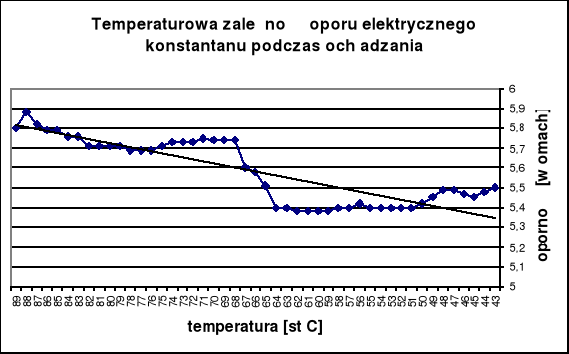
KONSTANTAN

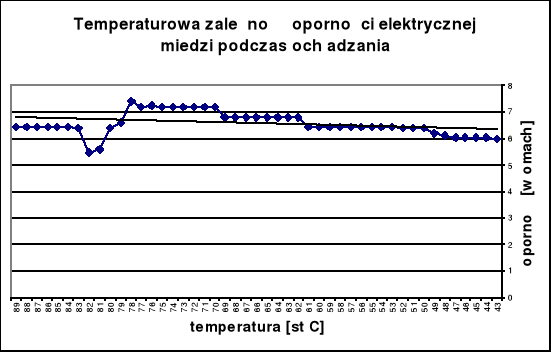
TERMISTOR

4. OBLICZENIA.

a) wyznaczenie stałej α dla miedzi:

Z równania R=R_o+ R_oαt wyznaczamy a=R_oα i b= R_o , gdzie a - współczynnik nachylenia prostej widocznej na dołączonym wykresie ,a b - punkt przecięcia się prostej z osią OY. Współczynniki a i b zostały wyznaczone za pomocą metody najmniejszych kwadratów i wynoszą a = 0,0321666 , b = 6,85498. Przekształcając powyższe wzory otrzymujemy α= a/b, czyli α= 4,68*10^-3, błąd pomiaru tej wielkości oszacowaliśmy na S_a =0,000233 porównując α z wartością tablicową wynoszącą α=4,33*10^-3, otrzymujemy błąd pomiaru tej wielkości wynoszący ± 0,000363, oznacza to, że błąd pomiaru wyznaczony przez nas w rzeczywistości jest trochę większy. Błąd względny mierzonej stałej wynosi: Δα_wz=7,73[%]. Ostatecznie wynik pomiaru tej wielkości możemy zapisać jako :

α= (4,68 ± 0,36)* 10^-3 [K^-1].

b) wyznaczanie przerwy energetycznej lub energii jonizacji domieszek (ΔE).

Do równania ln(Term.) = ln(Term.₀) + ΔE/(2kT), gdzie k - stała Boltzmana równa k=1,38*10^-3 podstawiamy a=ΔE/(2k), a - współczynnik nachylenia prostej widocznej na dołączonym wykresie. Korzystając z metody najmniejszych kwadratów obliczony współczynnik wyniósł a=39998,4 ± 17,75, a więc ΔE=2ka=(1,104±0,005)* 10^-3 [eV]. Po przeliczeniu na dżule ( 1 [eV] =1,60219*10^-3 [J] ) ΔE=0,6889 ± 0,0030 [J]. Błąd względny mierzonej energii wyniósł : Δ(ΔE)_wz= 0,44[%] Błąd obliczenia energii obliczyliśmy korzystając z metody różniczki zupełnej. Ostateczny wynik pomiaru :

ΔE=(1,087±0,005)* 10^-3 [eV].

4. WNIOSKI.

Na podstawie wyników otrzymanych podczas pomiaru oporności miedzi, stwierdzamy, że zależność r(T) ~T wyprowadzona na bazie modelu kwantowego w zakresie temperatur (20 - 90 [⁰C]) dobrze charakteryzuje rzeczywiste wyniki.

Początkowo podczas ogrzewania w miedzi zaobserwowaliśmy występowanie znacznych wahań oporności co mogło być spowodowane niejednakową prędkością ogrzewania, natomiast drobne skoki w oporności mogą być spowodowane niedokładnością przyrządów oraz błędami w odczycie.

W przypadku pomiaru oporności elektrycznej konstantanu podczas ogrzewania odstępstwa mogą być spowodowane zawirowaniami oleju, w którym znajduje się próbka (fluktuacja). Podczas ochładzania nastąpił brak indukowania prądu co jest przyczyną znacznych różnic w pomiarze oporu próbki w stosunku do pomiaru w czasie ogrzewania.

Sądząc po otrzymanych wynikach i błędach obliczeń stwierdzamy, że zastosowana metoda pomiarowa jest w miarę dokładna. Jedyne zastrzeżenia można mieć do pomiaru oporności konstantu, duże błędy pomiaru spowodowane zostały niemożnością dokładnego odczytania mierzonego oporu.

2

---