1. Wprowadzenie teoretyczne
Gaz wypływający przez otwór (lub dyszę zbieżną) w ścianie zbiornika rozpręża się według przemiany adiabatycznej, tzn. bez wymiany ciepła z otoczeniem. Aby określić parametry przepływu gazu w tej przemianie korzystamy z równań: Bernoulliego, adiabaty, Clapeyrona, ciągłości. Prędkość wypływu gazu przez otwór w ścianie zbiornika obliczamy ze wzoru Saint-Venanta-Wantzela lub ze wzoru na krytyczną prędkość. Skorzystanie z jednego albo drugiego wzoru uzależnione jest od następujących warunków:
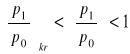
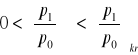
gdzie:
p1 - ciśnienie panujące na zewnątrz zbiornika,
p0 - ciśnienie panujące wewnątrz zbiornika.
Jeżeli spełniony jest pierwszy warunek to stosujemy wzór Saint-Venanta-Wantzela, a jeżeli warunek drugi to wzór na krytyczną prędkość.
Rys. 1.1. - Schemat stanowiska
W skład stanowiska pomiarowego wchodzą:
dmuchawa powietrza z pierścieniem wodnym,
separator wody,
zbiornik,
dysza wylotowa,
manometr sprężysty,
termometr,
rurka spiętrzająca Prandtla,
manometr różnicowy,
zawór zasilający z sieci wodociągowej,
zawór rozprężny,
zawór spustowy,
odbiornik wody,
czujnik temperatury,
miernik.
2. Wzory i obliczenia do ćwiczenia
Dane do obliczeń:
Ciśnienie panujące w pomieszczeniu:
p1 = pa = 0,1002 MPa
Ciśnienie w zbiorniku ze sprężonym powietrzem:
pnzb = pn0 = 0,055 MPa
Suma obydwu ciśnień:
p0 = pn0 + p1 = 0,055 + 0,1002 = 0,1552 MPa
Z tablic odczytujemy stosunek ciśnień dla χ = 1,4:
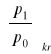
= 0,5283
W naszym przypadku:
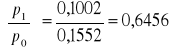
, stąd
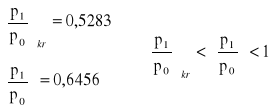
Do dalszych obliczeń będziemy stosowali wzór Saint-Venanta-Wantzela, dzięki któremu obliczymy teoretyczną prędkość wypływu gazu v1.
Wzór Saint-Venanta-Wantzela:
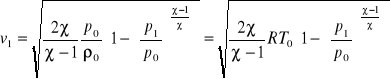
gdzie:
![]()
T0 = 273,15 + 27 = 300,15 K (temperatura gazu wewnątrz zbiornika)
Znając wartości nadciśnienia pn0 i temperatury spiętrzenia powietrza w zbiorniku oraz ciśnienia atmosferycznego p1=pa wyliczymy teoretyczną prędkość wypływu gazu v1:
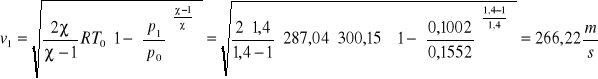
![]()
.
Rozkład prędkości wzdłuż osi strumienia powietrza wypływającego z dyszy:
Prędkość lokalną możemy obliczyć ze wzoru:
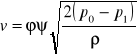
,
gdzie:
ϕ - współczynnik prędkości, dla rurki Prandtla w doświadczeniu wynosi ϕ = 0,99;
ψ - współczynnik uwzględniający wpływ ściśliwości gazu (powierza), wynoszący dla odległości większej od 30 [mm] - 1,0.
ρ - gęstość gazu w strudze, wyznaczamy z równania Clapeyrona;
p0-p1 - różnica ciśnienia całkowitego i statycznego,
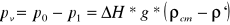
;ρcm - gęstość cieczy manometrycznej = gęstości wody;
ρ`- gęstość gazu nad cieczą manometryczną;
Uwzględniając, że gęstość gazu ρ` jest daleko mniejsza od gęstości wody ( ρ`<<ρH2O), otrzymujemy wzór:
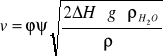
,
![]()
![]()
Prędkość strumienia w odległości 4,2 cm od otworu wylotowego wynosi:
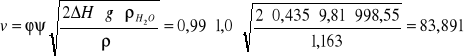
Dalsze obliczenia zestawione są w tabelach na stronach 4, 5, 6 i 7.
Objętościowe natężenie przepływu.
Aby policzyć objętościowe natężenie przepływu w określonym przekroju poprzecznym, należy podzielić ten przekrój na pierścienie. Znając średnią prędkość w danym pierścieniu, obliczoną z różnicy wskazań na manometrze, pomierzoną w czterech punktach na danym promieniu i znając pole pierścienia, możemy policzyć objętościowe natężenie przepływu w danym pierścieniu. Zsumowane wartości objętościowego natężenia przepływu we wszystkich pierścieniach dadzą całkowitą wartość objętościowego natężenia przepływu w danym przekroju poprzecznym.
Objętościowe natężenie przepływu liczymy ze wzoru:
![]()
![]()
![]()
gdzie:
- ![]()
- uśredniona prędkość w środku pierścienia ![]()
w odległości ![]()
od osi strumienia;
- ![]()
- pole i-tego pierścienia o szerokości ![]()
w przekroju poprzecznym strumienia;
Dla przekroju j=i (L=4,2cm), dla pierścienia nr. 0:
![]()
![]()
![]()
gdzie ![]()
to średnia prędkość strumienia dla danego pierścienia
Dalsze obliczenia zestawione są w tabelach na stronach 4, 5, 6 i 7.
3. Zestawienie wyników.
Tab. 3.1. - Rozkład prędkości wzdłuż osi strumienia
Nr. Serii |
lp. |
L [cm] |
H1[m] |
H2[m] |
Hśr[m] |
1 |
1 |
4,2 |
0,350 |
-0,085 |
0,435 |
|
2 |
8,2 |
0,165 |
0,040 |
0,125 |
|
3 |
12,2 |
0,120 |
0,070 |
0,050 |
|
4 |
16,2 |
0,104 |
0,082 |
0,022 |
|
5 |
20,2 |
0,098 |
0,085 |
0,013 |
|
6 |
24,2 |
0,096 |
0,086 |
0,010 |
|
7 |
28,2 |
0,094 |
0,090 |
0,004 |
2 |
1 |
4,2 |
0,350 |
-0,086 |
0,436 |
|
2 |
8,2 |
0,166 |
0,041 |
0,125 |
|
3 |
12,2 |
0,120 |
0,071 |
0,049 |
|
4 |
16,2 |
0,106 |
0,079 |
0,027 |
|
5 |
20,2 |
0,100 |
0,082 |
0,018 |
|
6 |
24,2 |
0,098 |
0,085 |
0,013 |
|
7 |
28,2 |
0,094 |
0,089 |
0,005 |
Lp - liczba porządkowa
L - odległość rurki Prandla od otworu dyszy
H1 - odczyt pierwszej wysokości z manometru
H2 - odczyt drugiej wysokości z manometru
Hśr - różnica wskazań manometru
Tab. 3.2. - Rozkład prędkości wzdłuż osi strumienia - dalsze obliczenia
L [cm] |
ΔH1[mm] |
ΔH2[mm] |
Hśr[mm] |
v[m/s] |
4,2 |
435 |
436 |
435,5 |
24,934 |
8,2 |
125 |
125 |
125 |
13,359 |
12,2 |
50 |
49 |
49,5 |
8,406 |
16,2 |
22 |
27 |
24,5 |
5,914 |
20,2 |
13 |
18 |
15,5 |
4,704 |
24,2 |
10 |
13 |
11,5 |
4,052 |
8,2 |
4 |
5 |
4,5 |
2,535 |
L - odległość rurki Prandla od dyszy
H1 - różnica wskazań manometru dla pierwszego pomiaru
H2 - różnica wskazań manometru dla drugiego pomiaru
Hśr - średnia różnica wskazań manometru
V - obliczona prędkość strugi powietrza
Rozkład prędkości w przekroju poprzecznym strumienia powietrza, temperatura strumienia w określonych punktach oraz objętościowe natężenie przepływu.
Tab. 3.3.1 - Rozkład prędkości w przekroju poprzecznym strumienia, wzdłuż osi poziomej:
Seria |
L[cm] |
L0[cm] |
H1[m] |
H2[m] |
ΔH1[m] |
1 |
8,550 |
-1,050 |
0,090 |
0,090 |
0,000 |
|
8,700 |
-0,900 |
0,092 |
0,088 |
0,004 |
|
8,850 |
-0,750 |
0,100 |
0,084 |
0,016 |
|
9,000 |
-0,600 |
0,128 |
0,065 |
0,063 |
|
9,150 |
-0,450 |
0,180 |
0,030 |
0,150 |
|
9,300 |
-0,300 |
0,270 |
-0,040 |
0,310 |
|
9,450 |
-0,150 |
0,036 |
-0,092 |
0,128 |
|
9,600 |
0,000 |
0,350 |
-0,085 |
0,435 |
|
9,750 |
0,150 |
0,300 |
-0,050 |
0,350 |
|
9,900 |
0,300 |
0,217 |
0,012 |
0,205 |
|
10,050 |
0,450 |
0,150 |
0,050 |
0,100 |
|
10,200 |
0,600 |
0,105 |
0,078 |
0,027 |
|
10,350 |
0,750 |
0,095 |
0,085 |
0,010 |
|
10,500 |
0,900 |
0,092 |
0,088 |
0,004 |
|
10,650 |
1,050 |
0,090 |
0,090 |
0,000 |
2 |
8,550 |
-1,050 |
0,091 |
0,090 |
0,001 |
|
8,700 |
-0,900 |
0,093 |
0,087 |
0,006 |
|
8,850 |
-0,750 |
0,101 |
0,085 |
0,016 |
|
9,000 |
-0,600 |
0,130 |
0,070 |
0,060 |
|
9,150 |
-0,450 |
0,182 |
0,032 |
0,150 |
|
9,300 |
-0,300 |
0,270 |
-0,042 |
0,312 |
|
9,450 |
-0,150 |
0,362 |
-0,092 |
0,454 |
|
9,600 |
0,000 |
0,350 |
-0,085 |
0,435 |
|
9,750 |
0,150 |
0,301 |
-0,050 |
0,351 |
|
9,900 |
0,300 |
0,220 |
0,015 |
0,205 |
|
10,050 |
0,450 |
0,152 |
0,050 |
0,102 |
|
10,200 |
0,600 |
0,103 |
0,078 |
0,025 |
|
10,350 |
0,750 |
0,093 |
0,085 |
0,008 |
|
10,500 |
0,900 |
0,092 |
0,088 |
0,004 |
|
10,650 |
1,050 |
0,090 |
0,085 |
0,005 |
L - położenie rurki Prandla względem miarki umieszczonej na modelu
L0 - odległość od punktu „0”
H1 - odczyt pierwszej wysokości z manometru
H2 - odczyt drugiej wysokości z manometru
ΔH - różnica wskazań manometru
Tab. 3.3.2 - Rozkład prędkości w przekroju poprzecznym strumienia, wzdłuż osi poziomej - dalsze obliczenia
pierścień |
ΔH1[mm] |
ΔH2[m] |
Hśr[m] |
v[m/s] |
7 |
0,000 |
0,001 |
0,001 |
2,844 |
6 |
0,004 |
0,006 |
0,005 |
8,994 |
5 |
0,016 |
0,016 |
0,016 |
16,089 |
4 |
0,063 |
0,060 |
0,062 |
31,543 |
3 |
0,150 |
0,150 |
0,150 |
49,262 |
2 |
0,310 |
0,312 |
0,311 |
70,933 |
1 |
0,128 |
0,454 |
0,291 |
68,615 |
0 |
0,435 |
0,435 |
0,435 |
83,891 |
1 |
0,350 |
0,351 |
0,351 |
75,303 |
2 |
0,205 |
0,205 |
0,205 |
57,590 |
3 |
0,100 |
0,102 |
0,101 |
40,423 |
4 |
0,027 |
0,025 |
0,026 |
20,510 |
5 |
0,010 |
0,008 |
0,009 |
12,067 |
6 |
0,004 |
0,004 |
0,004 |
8,045 |
7 |
0,000 |
0,005 |
0,003 |
6,360 |
Tab. 3.3.3 - Rozkład prędkości w przekroju poprzecznym strumienia, wzdłuż osi poziomej - obliczenia końcowe
pierścień |
v[m/s] seria1 |
v[m/s] seria 2 |
vśr[m/s] |
0 |
- |
83,891 |
83,891 |
1 |
75,303 |
68,615 |
71,959 |
2 |
57,590 |
70,933 |
64,262 |
3 |
40,423 |
49,262 |
44,843 |
4 |
20,510 |
31,543 |
26,026 |
5 |
12,067 |
16,089 |
14,078 |
6 |
8,045 |
8,994 |
8,519 |
7 |
6,360 |
2,844 |
4,602 |
Tab. 3.4.1 - Rozkład prędkości w przekroju poprzecznym strumienia, wzdłuż osi pionowej
Seria |
L[cm] |
L0[cm] |
H1[m] |
H2[m] |
ΔH2[m] |
1 |
50,050 |
-1,050 |
0,091 |
0,088 |
0,003 |
|
50,200 |
-0,900 |
0,095 |
0,088 |
0,007 |
|
50,350 |
-0,750 |
0,105 |
0,079 |
0,026 |
|
50,500 |
-0,600 |
0,148 |
0,053 |
0,095 |
|
50,650 |
-0,450 |
0,221 |
0,005 |
0,216 |
|
50,800 |
-0,300 |
0,310 |
-0,062 |
0,372 |
|
50,950 |
-0,150 |
0,375 |
-0,103 |
0,478 |
|
51,100 |
0,000 |
0,380 |
-0,108 |
0,488 |
|
51,250 |
0,150 |
0,308 |
-0,050 |
0,358 |
|
51,400 |
0,300 |
0,198 |
0,018 |
0,180 |
|
51,550 |
0,450 |
0,130 |
0,060 |
0,070 |
|
51,700 |
0,600 |
0,103 |
0,080 |
0,023 |
|
51,850 |
0,750 |
0,093 |
0,088 |
0,005 |
|
52,000 |
0,900 |
0,091 |
0,088 |
0,003 |
|
52,150 |
1,050 |
0,090 |
0,090 |
0,000 |
2 |
50,050 |
-1,050 |
0,091 |
0,089 |
0,002 |
|
50,200 |
-0,900 |
0,095 |
0,088 |
0,007 |
|
50,350 |
-0,750 |
0,105 |
0,079 |
0,026 |
|
50,500 |
-0,600 |
0,148 |
0,053 |
0,095 |
|
50,650 |
-0,450 |
0,221 |
0,006 |
0,215 |
|
50,800 |
-0,300 |
0,310 |
-0,062 |
0,372 |
|
50,950 |
-0,150 |
0,380 |
-0,103 |
0,483 |
|
51,100 |
0,000 |
0,385 |
-0,108 |
0,493 |
|
51,250 |
0,150 |
0,305 |
-0,055 |
0,360 |
|
51,400 |
0,300 |
0,200 |
0,020 |
0,180 |
|
51,550 |
0,450 |
0,135 |
0,060 |
0,075 |
|
51,700 |
0,600 |
0,102 |
0,080 |
0,022 |
|
51,850 |
0,750 |
0,093 |
0,089 |
0,004 |
|
52,000 |
0,900 |
0,092 |
0,090 |
0,002 |
|
52,150 |
1,050 |
0,091 |
0,090 |
0,001 |
L - położenie rurki Prandla względem miarki umieszczonej na modelu
L0 - odległość od punktu „0”
H1 - odczyt pierwszej wysokości z manometru
H2 - odczyt drugiej wysokości z manometru
ΔH - różnica wskazań manometru
Tab. 3.4.2 - Rozkład prędkości w przekroju poprzecznym strumienia, wzdłuż osi pionowej - dalsze obliczenia
pierścień |
ΔH1[m] |
ΔH2[m] |
Hśr[m] |
v[m/s] |
7 |
0,003 |
0,002 |
0,003 |
6,360 |
6 |
0,007 |
0,007 |
0,007 |
10,642 |
5 |
0,026 |
0,026 |
0,026 |
20,510 |
4 |
0,095 |
0,095 |
0,095 |
39,204 |
3 |
0,216 |
0,215 |
0,216 |
59,047 |
2 |
0,372 |
0,372 |
0,372 |
77,579 |
1 |
0,478 |
0,483 |
0,481 |
88,169 |
0 |
0,488 |
0,493 |
0,491 |
89,082 |
1 |
0,358 |
0,360 |
0,359 |
76,211 |
2 |
0,180 |
0,180 |
0,180 |
53,964 |
3 |
0,070 |
0,075 |
0,073 |
34,248 |
4 |
0,023 |
0,022 |
0,023 |
19,079 |
5 |
0,005 |
0,004 |
0,005 |
8,533 |
6 |
0,003 |
0,002 |
0,003 |
6,360 |
7 |
0,000 |
0,001 |
0,001 |
2,844 |
Tab. 3.4.3 - Rozkład prędkości w przekroju poprzecznym strumienia, wzdłuż osi pionowej - obliczenia końcowe
pierścień |
v[m/s] seria1 |
v[m/s] seria 2 |
vśr[m/s] |
0 |
- |
89,082 |
89,082 |
1 |
76,211 |
88,169 |
82,190 |
2 |
53,964 |
77,579 |
65,771 |
3 |
34,248 |
59,047 |
46,647 |
4 |
19,079 |
39,204 |
29,142 |
5 |
8,533 |
20,510 |
14,521 |
6 |
6,360 |
10,642 |
8,501 |
7 |
2,844 |
6,360 |
4,602 |
ΔH1 - różnica wskazań manometru dla pierwszego pomiaru
ΔH2 - różnica wskazań manometru dla drugiego pomiaru
ΔHśr - średnia różnica wskazań manometru
V - obliczona prędkość strugi powietrza
Vśr - średnia prędkość strugi powietrza
A - pole powierzchni pierścienia
Q - objętościowe natężenie przepływu w danym pierścieniu
Tab. 3.5. - średnie prędkości strugi powietrza, pole powierzchni pierścienia oraz objętościowe natężenie przepływu.
pierścień |
vśr[m/s] poziomo |
vśr[m/s] pionowo |
vśr[m/s] |
r[m] |
A[m2] |
Q[m3/s] |
0 |
83,89 |
89,08 |
86,49 |
0,0015 |
0,00001414 |
0,001223 |
1 |
71,96 |
82,19 |
77,07 |
0,003 |
0,00002827 |
0,002179 |
2 |
64,26 |
65,77 |
65,02 |
0,0045 |
0,00004241 |
0,002757 |
3 |
44,84 |
46,65 |
45,75 |
0,006 |
0,00005655 |
0,002587 |
4 |
26,03 |
29,14 |
27,58 |
0,0075 |
0,00007069 |
0,00195 |
5 |
14,08 |
14,52 |
14,30 |
0,009 |
0,00008482 |
0,001213 |
6 |
8,52 |
8,50 |
8,51 |
0,0105 |
0,00009896 |
0,000842 |
7 |
4,60 |
4,60 |
4,60 |
0,012 |
0,00011310 |
0,00052 |
|
|
|
|
|
ΣA |
ΣQ |
|
delta ri |
0,0015 |
m |
|
0,00050894 |
0,013272 |
Pole powierzchni pierścienia - A oraz objętościowe natężenie przepływu w danym pierścieniu - Q, zestawione w tabeli 3.5., zostały wyliczone na podstawie wzorów zamieszczonych na stronie 4!!
Znając średnicę otworu dyszy d = 2 mm oraz vt, możemy wyliczyć Qt - teoretyczne natężenie przepływu:
![]()
![]()
Z powyższego wykresu rozpływu strumienia wnioskujemy, że w osi wypływu powietrza, czyli dla pierścienia zerowego prędkość powietrza jest największa. Natomiast na granicach strumienia i otaczającej go cieczy występuje duża różnica prędkości między sąsiednimi strugami. W obszarze tym burzliwość ruchu jest największa.
4. Wnioski
Na podstawie otrzymanych wyników możemy wnioskować, że prędkości na poszczególnych pierścieniach, nie zależnie od położenia punktu pomiarowego na poszczególnym pierścieniu są porównywalne. Doświadczenia pokazało również, że na zewnętrznych pierścieniach zarówno prędkość średnia jak i objętościowe natężenie przepływu jest mniejsze niż na tych wewnętrznych.
Tak, więc z policzonych wartości objętościowego natężenia przepływu można wywnioskować, że w miarę wzrastania odległości od otworu wylotowego ta wartość maleje, mimo iż teoretycznie powinna być stałą. Najprawdopodobniej przyczyną tego jest dobrany zbyt mały promień przekroi poprzecznych i w związku z tym zewnętrzna część strumienia powietrza nie została w ogóle wzięta pod uwagę w doświadczeniu.
Zarówno prędkość wypływu gazu obliczona metodą teoretyczna oraz metoda doświadczalną, jaki i natężenie przepływu wyliczone tymi dwoma metodami znacznie się od siebie różni, co w pewnym stopniu spowodowane jest błędami grubymi, popełnionymi podczas wykonywania ćwiczenia. Jednak w głównym stopniu na tę różnicę wpłynęły zawirowaniami powietrza, które występowały tuż za wylotem dyszy. Jest to zjawisko, które nie zależnie od naszej dokładności zawsze wpłynie na wynik końcowy i spowoduje dość znaczną różnicę pomiędzy wynikami teoretycznymi i doświadczalnymi.
- 9 -
Wyszukiwarka
Podobne podstrony:
tabela do spr nr 17 wypływ adiabatyczny powietrza poprawa
Wypływ adiabatyczny powietrza doc
Cussler Clive Zaginione miasto [poprawiona] DOC
Powierzcgnia wirująca DOC
Opis poprawiony doc
~$chanika płynów N9 poprawne doc
poprawiony (3) doc
Badanie napięcia powierzchniowego cieczy DOC
Lab Hih wypływ cieczy ze zbiornika DOC
POPRAWKI DOC
tabela do spr nr 17 wypływ adiabatyczny powietrza
RAPORT UNIPEDE, PO POPRAWK DOC
~$ojekt z żelbetu poprawiony doc
Fazy kształtowania powierzchni Ziemi doc
poprawa (5) doc
więcej podobnych podstron




