1. PROJEKT POMOSTU TECHNOLOGICZNEGO

O KONSTRUKCJI STALOWEJ

1.1. ZAŁOŻENIA

1.1.1. Wymiary pomostu w osiach systemowych - 9,00x24,00 m.

1.1.2. Wysokość użyteczna pod pomostem - 4,00 m.

1.1.3. Wypełnienie pomostu - płyta żelbetowa o grubości 10 cm.

1.1.4. Obciążenie technologiczne - p = 10,0 kN/m².

5. Gatunki stali St3SX, St3SY.

2. OPIS TECHNICZNY

1.2.1. Opis stropu pomostu

Pomost zaprojektowano wewnątrz hali produkcyjnej o wymiarach osiowych rzutu poziomego 24,50x45,00 m. Konstrukcję nośną pomostu zaprojektowano jako stalową. Na belkach stalowych B-1 oparto monolityczną płytę żelbetową, o grubości 10 cm. Na płycie żelbetowej ułożono na wylewce cementowej o grubości 2,5 cm płytki posadzkowe z terakoty. Dolną powierzchnię płyty otynkowano zaprawą wapienno cementową o grubości 2 cm. Łączna grubość stropu wynosi 15 cm.

2. Opis konstrukcji stalowej

Konstrukcję nośną stropu stanowią belki B-1 z dwuteowników walcowanych IPE 300, rozmieszczone w odstępach 3,00 m, swobodnie oparte na podciągach: środkowym P-1 i skrajnych P-2. Poziom stopek górnych belek stropowych + 4,64 m. Podciągi P-1 i P-2 (poprzeczne do osi symetrii hali), zaprojektowano jednolicie z dwuteowników HEA 650. Podciągi oparto na słupach ram poprzecznych hali i dodatkowo podparto w środku rozpiętości na słupach stalowych wahadłowych S-1, realizując schemat belki dwuprzęsłowej. Podciągi podzielono na trzy elementy wysyłkowe o jednakowych długościach ∼8,00 m.

Styki montażowe podciągów zaprojektowano jako uniwersalne, kategorii C, na śruby sprężające klasy 8.8, a połączenia rusztowe belek stropowych z podciągami na śruby zwykłe klasy 4.8, kategoria połączenia A.

3. Obciążenia

Na konstrukcję działają obciążenia stałe od ciężaru własnego konstrukcji i stropu oraz obciążenia technologiczne o wartości charakterystycznej p = 10,0 kN/m².

4. Obliczenia

1. Materiały konstrukcyjne

Belki stropowe B-1 i słupy S-1 zaprojektowano ze stali St3SX. Podciągi P-1 oraz P-2 zaprojektowano ze stali St3SY, a żebra poprzeczne, usztywniające środnik oraz elementy styków montażowych ze stali St3SX. Elektrody przyjęto EA 1.46.

2. Wytrzymałości obliczeniowe stali

- na ściskanie i zginanie: f_d = 215 MPa dla elementów o grubości ścianek t ≤ 16 mm

oraz f_d = 205 MPa dla dla elementów o grubości ścianek t > 16 mm

- na ścinanie: 0,58f_d,= 124,7 MPa,

Rys. 1.1

1.2.4.3. Wytrzymałość charakterystyczna śrub

- dla śrub klasy 8.8 wytrzymałość doraźna R_m = 800 MPa oraz umowna granica

plastyczności R_e = 640 MPa

- dla śrub klasy 4.8 wytrzymałość doraźna R_m = 420 MPa oraz granica plastycz-

ności R_e = 340 MPa

1.3. OBLICZENIA STATYCZNE

Schemat konstrukcji stalowej stropu przedstawiono na rys.1.1.

1.3.1. Obciążenia

- Obciążenia charakterystyczne na 1m² stropu wynoszą

płytki posadzkowe 0,010*22,0 = 0,220 kN/m²

wylewka cementowa 0,025*21,0 = 0,525 kN/m²

płyta żelbetowa 0,100*25,0 = 2,500 kN/m²

tynk 0,015*19,0 = 0,285 kN/m²

razem obciążenia stałe g_k = 3,530 kN/m²

obciążenia technologiczne p_k = 10,00 kN/m²

- Obciążenia obliczeniowe na 1m² stropu wynoszą

płytki posadzkowe 1,2*0,220 = 0,264 kN/m²

wylewka cementowa 1,3*0,525 = 0,683 kN/m²

płyta żelbetowa 1,1*2,500 = 2,750 kN/m²

tynk 1,3*0,285 = 0,371 kN/m²

razem obciążenia stałe g = 4,018 kN/m²

obciążenia technologiczne p = 1,2*10,00 = 12,00 kN/m²

2. Belka stropowa B-1

1.3.2.1.Zestawienie obciążeń

Obciążenia na 1 mb belki wynoszą

- Wartości charakterystyczne

ciężar własny belki IPE 300 0,0098*42,2 = 0,41 kN/m

obciążenie stałe ze stropu 3,530*3,00 = 10,59 kN/m

obciążenie technologiczne 10,00*3,00 = 30,00 kN/m

obciążenia charakterystyczne łącznie q_k = 41,00 kN/m

- Wartości obliczeniowe

ciężar własny belki IPE 300 1,1*0,41 = 0,45 kN/m

obciążenie stałe ze stropu 4,018*3,00 = 12,05 kN/m

obciążenie technologiczne 12,00*3,00 = 36,00 kN/m

obciążenia obliczeniowe łącznie q = 48,50 kN/m

2. Obliczenie wielkości statycznych

Oddziaływania podpór i moment maksymalny

V = 0,5*48,50*4,50 = 109,1 kN

M = 0,125*48,50*4,50² = 122,8 kNm

3. Wymiarowanie

a) Stan graniczny nośności

Warunek nośności belki zginanej

Przyjęto dwuteownik IPE 300, dla którego wskaźnik wytrzymałości W_x = 557 cm³ oraz moment bezwładności J_x = 8360 cm⁴. Kryterium smukłości środnika oraz stopki ściskanej przekroju według normy PN-90/B-03200

b/t = (30,0 - 2*2,57)/0,71 = 35,0 < 66 → klasa 1

b/t = (15,0 - 3,71)/2*1,07 = 5,3 < 9 → klasa 1

kwalifikuje przekrój IPE 300 do klasy 1, dla której dopuszcza się plastyczną redystrybucję naprężeń. Dla momentu statycznego połówki przekroju S₁ = 314 cm³, obliczeniowy współczynnik rezerwy plastycznej wynosi

α_p = (557 + 2*314)/2*557 = 1,064

Nośność obliczeniowa przekroju przy jednokierunkowym zginaniu wynosi

M_R = 1,064*557*215*10^-3 = 127,4 kNm

Belka jest zabezpieczona przed zwichrzeniem przez połączenie jej pasa ściskanego z płytą żelbetową stropu, zatem warunek nośności na zginanie

= 0,964 < 1,000

Warunek nośności przekroju ścinanego

Smukłość środnika ze względu na ścinanie

b/t = 30,0/0,71 = 42,3 < 70

zatem środnik nie jest podatny na utratę stateczności przy czystym ścinaniu.

Nośność przekroju ścinanego wynosi

V_R = 0,58*30,0*0,71*215*10^-1 = 265,6 kN

Warunek nośności przekroju podporowego belki

= 0,411 < 1,000

b) Stan graniczny użytkowania

f =
*
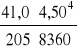
*10⁴ = 1,28 cm <
= 1,80 cm

c) Połączenie przegubowe belki B-1 z podciągiem P-1 (P-2)

Przyjęto 3 śruby M16 klasy 4.8 w układzie pokazanym na rys.1.2.

Pole przekroju przy ścinaniu trzpienia śruby

A_v = 3,14*1,6²/4 = 2,01 cm²

Nośność śruby M16 w połączeniu dla

S_Rv = 0,45*420*2,01*10^-1 = 38,0 kN

S_Rb = 2,5*215*1,6*0,7*10^-1 = 60,2 kN

wynosi

S_R = min(S_Rv, S_Rb) = 38,0 kN

Siła działająca na każdą ze śrub

V₁ =
= 36,4 kN < S_R

jest mniejsza od ich nośności.

Rys.1.2

3. Podciąg P-1

1. Zestawienie obciążeń

Obciążenia skupione przekazywane przez belki B-1 i ciężar własny podciągu (przyjęty szacunkowo dla dwuteownika szerokostopowego HEA 650)

- wartości charakterystyczne

od obciążeń technologicznych

P_k = 30,0*4,50 = 135,0 kN

od obciążeń stałych i zmiennych

Q_k = 41,0*4,50 + 6,0 ≅ 191,0 kN

od obciążeń stałych

G_k = 191,0 - 135,0 = 56,0 kN

- wartości obliczeniowe

od obciążeń technologicznych

P = 36,0*4,50 = 162,0 kN

od obciążeń stałych i zmiennych

Q = 48,5*4,50 + 1,1*6,0 ≅ 225,0 kN

od obciążeń stałych

G = 225,0 - 162,0 = 63,0 kN

2. Obliczenie wielkości statycznych

Przyjęto dwuteownik HEA 650, dla którego kryterium smukłości środnika oraz stopki ściskanej przekroju według normy PN-90/B-03200

b/t = (64,0 - 2*5,3)/1,35 = 39,6 < 66
= 67,6 → klasa 1

b/t = (30,0 - 6,65)/2*2,4 = 4,86 < 9
= 9,2 → klasa 1

kwalifikuje przekrój do klasy 1, dla której dopuszcza się plastyczną redystrybucję naprężeń w przekrojach, a także obliczenia statyczne belki ciągłej z uwzględnieniem plastycznego wyrównania momentów zginających:

- od obciążeń stałych według schematu pokazanego na rys.1.3/a

0,469Gl - ΔM = 0,266Gl + 0,5ΔM → ΔM = 0,135Gl

M = (0,469-0,135) = 0,334Gl

- od obciążeń zmiennych według schematu pokazanego na rys.1.3/b

Rys.1.3

0,469Pl - ΔM = 0,383Pl + 0,5ΔM → ΔM = 0,057Pl

M = (0,469 - 0,057)Pl = 0,412Pl

Momenty wyrównane w przęśle i nad podporą pośrednią wynoszą

M_AB = |M_B| = (0,334*63,0 + 0,412*162,0)*12,0 = 1053,4 kNm

Ekstremalna siła poprzeczna i reakcje podpór

|V_Bl| = (3,0 - 1,167)Q = 1,833*225,0 = 412,4 kN

maxR_A = (1,032 + 0,135)G + (1,266 + 0,057)P

= 1,167 63,0 + 1,323*225,0 = 287,8 kN

maxR_B = (6,0 - 2*1,167)Q + Q = 4,666*225,0 = 1049,9 kN

Moment zginający i siła poprzeczna w przekroju x = 8,00 m

M = (1,167*63,0 + 1,323*162,0) 8,00 - 225,0*7,00 = 727,8 kNm

V = 1,167*63,0 + 1,323*162,0 - 2*225,0 = 162,2 kN

1.3.3.3. Wymiarowanie

a) Stan graniczny nośności

Warunki nośności belki zginanej

Dla dwuteownika HEA 650, wskaźnik wytrzymałości W_x = 5470 cm³ oraz moment bezwładności J_x = 175200 cm⁴. Pole przekroju czynne przy ścinaniu według normy PN-90/B-03200 wynosi

A_v = 1,35*64,0 = 86,4 cm²

Wartość obliczeniowa współczynnika rezerwy plastycznej

α_p = (5470 + 6140)/2*5470 = 1,061

Nośność przekroju HEA 650 w prostych stanach zginania i ścinania

M_R = 1,061*5470*205*10^-3 = 1189,8 kNm

V_R = 0,58*86,4*205*10^-1 = 1027,3 kN

Warunek nośności na ścinanie przekroju podpory skrajnej A i C

= 0,280 < 1,000

Warunek nośności na zginanie przekrojów: przęsłowego AB i podpory pośredniej B

= 0,885 < 1,000

Warunek nośności na ścinanie przekroju podpory pośredniej B

= 0,401 < 0,600

zatem zgodnie z p.4.5.2 normy PN-90/B03200 interakcja M - V nie zachodzi (sprawdzenie warunku nośności wzorem (45) jest zbędne).

Warunki nośności prętów nie są miarodajne ponieważ podciąg jest zabezpieczony przed zwichrzeniem poprzez połączenie pasa ściskanego z płytą żelbetową stropu.

Żebra usztywniające

Przyjęty przekrój żeber podporowych skrajnych o wymiarach 2x10*140 mm przedstawiono na rys.1.4/a. Powierzchnia przekroju żebra z uwzględnieniem współpracy środnika

A = 2*14,0*1,0 + (10,0 + 15*1,35)*1,35 = 28,0 + 40,8 = 68,8 cm²

Moment bezwładności i promień bezwładności przekroju żebra względem osi środnika

J_s = 1,0*29,35³/12 = 2107 cm⁴

i_s =
= 5,53 cm

Warunek sztywności żebra dla współczynnika

k = 1,5*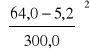
= 0,058 < 0,75

J_s = 2700 cm⁴ > 0,75*(64,0 - 5,2)*1,35³ = 108,5 cm⁴

Sprawdzenie żebra na ściskanie

λ = 0,8*58,8/5,53 = 8,5

λ_p = 84*
= 86,0

λ/λ_p = 8,5/86,0 = 0,099

ϕ =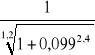
= 0,997

N_Rc = 68,8*205*10^-1 = 1410 kN

= 0,205 < 1,000

Sprawdzenie żebra na docisk

N_Rb = 1,25*215*28,0*10^-1 = 752,5 kN

= 0,382 < 1,000

Żebro ze środnikiem połączono spoinami pachwinowymi ciągłymi o grubości 4 mm. Naprężenia w spoinie wynoszą

τ =
*10 = 45,0 MN/m² < 0,8*205 = 164,0 MPa

Rys.1.4

Przyjęty przekrój żeber podporowych pośrednich o wymiarach 2x14x140 mm przedstawiono na rys.1.4/b. Powierzchnia przekroju żebra z uwzględnieniem współpracy środnika

A = 2*14,0*1,4 + 30*1,35*1,35 = 39,2 + 54,7 = 93,9 cm²

Moment bezwładności i promień bezwładności przekroju żebra względem osi środnika

J_s = 1,4*29,35³/12 = 2950 cm⁴

i_s =
= 5,605 cm

Warunek sztywności żebra dla współczynnika k = 0,75 jest spełniony.

Sprawdzenie żebra na ściskanie

λ = 0,8*58,8/5,605 = 8,4

λ/λ_p = 8,4/86,0 = 0,098

ϕ =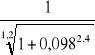
= 0,997

N_Rc = 93,9*205*10^-1 = 1925,0 kN

= 0,547 < 1,000

Sprawdzenie żebra na docisk

N_Rb = 1,25*215*39,2*10^-1 = 1053,5 kN

= 0,997 < 1,000

Żebro połączono z środnikiem spoinami pachwinowymi ciągłymi o grubości 5 mm. Naprężenia w spoinie wynoszą

τ =
*10 = 105,0 MN/m² < 0,8*205 = 164,0 MPa

Przyjęty przekrój żeber pośrednich o wymiarach 2x8*140 mm. Z uwagi na stosunkowo nieduże siły, przekazywane przez belki stropowe na żebro, sprawdzenie żebra pośredniego pominięto.

Stateczność miejscowa środnika i pasów

Stopki i środnik dwuteownika HEA 650 spełniają normowe kryterium klasy 1 przekroju, co wykazano w p.1.3.2.3, równocześnie smukłość środnika spełnia warunek:

b/t = 39,6 < 70
= 71,7

co oznacza, że ścianka jest odporna na miejscową utratę stateczności przy czystym ścinaniu. Sprawdzenie warunków stateczności w stanach prostych jest zbędne.

W stanie złożonym naprężenia środnika, w polu przyległym do podpory pośredniej:

J_w =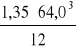
= 29491 cm⁴

W_w =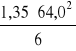
= 921,6 cm³

M_w = (1053,4 - 412,4*0,32)*
= 155,1 kNm

M_Rw = 921,6*205*10^-3 = 188,9 kNm

warunek stateczności miejscowej

+
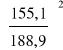
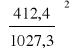
= 0,835 < 1,000

b) Stan graniczny użytkowania według przybliżonych wzorów PN-90/B-03200

f = 0,5f_G + 0,75f_P

- strzałka ugięcia belki wolno podpartej obciążonej trzema siłami Q_k = 191,0 kN

f_Q =
*
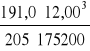
*10⁴ = 4,62 cm

f_G = 4,62*56,0/191,0 = 1,35 cm, f_P = 4,62 - 1,35 = 3,27 cm

f = 0,5*1,35 + 0,75*3,27 = 3,13 cm < fgr =
= 3,43 cm

Ugięcie belki ciągłej obliczone dokładniej

- strzałka ugięcia belki swobodnie podpartej obciążonej momentem

|M_Bk| = (0,469*56,0 + 0,234*135,0)*12,0 = 694,2 kNm

f_Q =
*
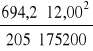
*10⁴ = 1,79 cm

- strzałka ugięcia łącznie

f = 4,62 - 1,79 = 2,83 cm < fgr =
= 3,43 cm

c) Styk montażowy

Konstrukcję styku montażowego zaprojektowano w sposób przedstawiony na rys. 1.5. Przyjęto dla przykładek śruby sprężające M16, a dla nakładek śruby M24 klasy 8.8, w otworach średniodokładnych, dla których współczynnik otworu α_s = 1,0.

Założono przygotowanie powierzchni styku przez metalizowanie natryskowe aluminium po śrutowaniu, stąd współczynnik tarcia μ = 0,50. Pole przekroju czynnego rdzenia śruby M16, według tablicy Z2-2 PN wynosi A_s = 1,57 cm². Nośność obliczeniowa śruby w stanie granicznym zerwania trzpienia

S_Rt = min {0,65*800*1,57*10^-1; 0,85*640*1,57*10^-1} = 81,6 kN

Nośność obliczeniowa śruby w stanie granicznym poślizgu przykładek

S_Rs = 1,0*0,50*81,6*2 = 81,6 kN

Nośność obliczeniową śrub w stanie granicznym zerwania trzpienia można odczytać bezpośrednio z tablicy Z2-2 PN, np. dla śrub M24: S_Rt = 190,0 kN. Nośność obliczeniowa śruby w stanie granicznym poślizgu nakładek

S_Rs = 1,0*0,50*190,0 = 95,0 kN

Warunki nośności śrub

Momenty bezwładności brutto przekroju elementów kryjących styk wynoszą

- nakładek

J_n = 2*2,0*30,0*33,0² = 130680 cm⁴

- przykładek

J_p = 2*0,8*48,0³/12 = 14746 cm4

Moment działający w przekroju grupy śrub przykładek

M* = 727,8 + 162,2*0,08 = 740,8 kNm

Rys. 1.5

Moment zginający przypadający na przykładki i nakładki

M_p = 740,8
= 75,1 kNm

M_n = 740,8 - 75,1 = 665,7 kNm

Przyjmując układ osi współrzędnych (x,y) o początku w środku obrotu A, przyjętej na rys. 1.5 grupy śrub sprężających M16, dla x_max = 4,0 cm, y_max = 20,0 cm oraz

= 10*4,0² + 4*20,0² + 4*10,0² = 2160 cm²

dla najbardziej obciążonej śruby skrajnej, wyznaczamy siły:

- od działania siły poprzecznej V

N_Vy = 162,2/10 = 16,2 kN

- od działania momentu M_p

N_My = 75,1
*10,0² = 13,9 kN

N_Mx = 75,1
*10,0² = 69,5 kN

- siła wypadkowa

N_max =
= 75,7 kN < S_Rs = 81,6 kN

Obliczenie potrzebnej liczby śrub sprężających M24 w nakładkach. Siła osiowa rozciągająca nakładkę wynosi:

H =
*10,0² = 1008,6 kN

stąd potrzebna liczba śrub

n = 1008,6/95,0 = 10,6

przyjęto 2*6 = 12 śrub sprężających M24 po każdej stronie styku w nakładkach.

Warunki nośności nakładek i przykładek

Pole przekroju nakładek netto

A_n = 30,0*2,0 - 2*2,0*2,4 = 60,0 - 9,60 = 50,4 cm²

Sprowadzone pole przekroju nakładek

A_ψ = 50,4
= 67,2 cm² > 60,0 cm²

Nośność nakładki rozciąganej

N_Rt = 60,0*205*10^-1 = 1230 kN

Siła zredukowana w przekroju śrub skrajnych

H_a = 1008,6(1 - 0,4
) = 941,4 kN < N_Rt = 1230 kN

spełnia warunek nośności.

4. Podciąg P-2

1.3.4.1. Zestawienie obciążeń

Obciążenia skupione przekazywane przez belki B-1 i ciężar własny podciągu stanowią około 50% obciążeń według p.1.3.3.1.

1.3.4.2. Obliczenie wielkości statycznych

Przyjęto dwuteownik IPE 550, dla którego kryterium smukłości środnika oraz stopki ściskanej przekroju według normy PN-90/B-03200

b/t = (55,0 - 2*4,1)/1,11 = 42,2 < 66
= 67,6 → klasa 1

b/t = (21,0 - 5,91)/2*1,72 = 4,39 < 9
= 9,2 → klasa 1

kwalifikuje przekrój do klasy 1, czyli siły przekrojowe można oszacować jako 50% wartości obliczonych według p.1.3.3.2.:

M_AB = |M_B| = 0,5*1053,4 = 526,7 kNm

Reakcje podpór skrajnych i środkowej

R_A = 143,9 kN, V_Bl = 206,2 kN, R_B = 525,0 kN

1.3.4.3. Wymiarowanie

Warunki nośności belki zginanej

Dla dwuteownika IPE 550, wskaźnik wytrzymałości W_x = 2440 cm³ oraz moment bezwładności J_x = 67120 cm⁴. Pole przekroju czynne przy ścinaniu według normy PN-90/B-03200 wynosi

A_v = 1,11*55,0 = 61,1 cm²

Wartość obliczeniowa współczynnika rezerwy plastycznej

α_p = (2440 + 2780)/2*2440 = 1,070

Nośność przekroju IPE 550 w prostych stanach zginania i ścinania

M_R = 1,070*2440*205*10^-3 = 535,2 kNm

V_R = 0,58*61,1*205*10^-1 = 726,5 kN

Warunek nośności na zginanie przekrojów: przęsłowego AB i podpory pośredniej B

= 0,984 < 1,000

Warunek nośności na ścinanie przekroju podpory pośredniej B

= 0,284 < 0,600

czyli interakcja M-V w przekroju podpory pośredniej nie zachodzi.

Można wykazać, że konstrukcja podciągu P-2 o przekroju IPE 550, spełnia warunki sztywności, a także pozostałe wymagania bezpieczeństwa według normy PN-90/B-03200. Jednak ze względu na ujednolicenie konstrukcji pomostu, podciągi skrajne zaprojektowano z dwuteowników HEA 650.

5. Słup S-1

1. Zestawienie obciążeń

Siła osiowa działająca na słup:

oddziaływanie podciągu P-1 1049,9 kN

ciężar własny szacunkowo 5,1 kN

razem obciążenie słupa N = 1055,0 kN

2. Wymiarowanie słupa

Obliczenie trzonu

Przyjęto przekrój HEA 240, dla którego A = 76,8 cm², i_x = 10,11 cm, i_y = 6,00 cm. Długości wyboczeniowe słupa o schemacie pokazanym na rys.1.1, przy przegubowo-nieprzesuwnym zamocowaniu obu końców wynoszą: l_x = l_y = 420 cm. Smukłości względne i współczynniki wyboczeniowe

λ_x = 420/10,11 = 41,5
_x = 41,5/84 = 0,494 → krzywa b

λ_y = 420/6,00 = 70,0
_y = 70,0/84 = 0,833 → krzywa c

ϕ_x =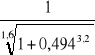
= 0,940

ϕ_y =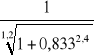
= 0,660

Warunek nośności trzonu, dla

b/t = (24,0 - 4,95)/2*1,2 = 7,94 < 9 → klasa przekroju 1

N_Rc = 76,8*215*10^-1 = 1651,2 kN

= 0,968 < 1,000

Obliczenie stopy słupa

Przyjętą konstrukcję stopy przedstawiono na rys.1.6. Dla blachy podstawy o wymiarach rzutu poziomego 300x320 mm, naprężenia pod blachą wynoszą

σ =
10 = 11,0 MN/m²

stąd wymagana minimalna klasa betonu użytego na fundamenty: B20, dla której wytrzymałość obliczeniowa na ściskanie według normy PN-84/B-03264 wynosi R_b = 11,5 MPa.

Rys. 1.6

Momenty zginające blachę podstawy, obliczone wzorem Galerkina, dla płyty zastępczej podpartej na trzech krawędziach, wynoszą:

b/a = 11,6/20,6 = 0,563 → α = 0,063

M = 0,063*11,0*0,206²*10³ = 29,4 kNm/m

Potrzebna grubość blachy podstawy

t ≥
= 0,0293 m

przyjęto t = 30 mm. Blachę podstawy połączono z trzonem słupa spoinami pachwinowymi o wymiarach pokazanych na rys. 1.6/a.

Obliczeniowe pole przekroju spoin wynosi

A_s = 0,6*(2*24,0 +4*9,5) + 2*0,5*16,5 = 68,1 cm²

Naprężenie w spoinach

τ =
*10 = 154,9 MN/m² < 0,8*205 = 164 MPa

Obliczenie głowicy słupa

Konstrukcję głowicy zaprojektowano w sposób przedstawiony na rys.1.6/b.

Nacisk liniowy na płytkę centrującą z podciągu

p =
*10² = 3500 kN/m

Przyjęto promień krzywizny r = 50,0 cm, stąd warunek docisku płytki centrującej według Hertza

σ_bH = 0,42*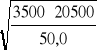
= 503,1 MN/m² < f_dbH = 3,6*205 = 738 MPa

Powierzchnia docisku płytki centrującej na trzon słupa wynosi

A_b = 0,75*(23,0 - 2*1,2) + 2*1,2*(12,0 + 2*2,0) = 53,85 cm²

Warunek nośności na docisk

*10^-1 = 0,729 < 1,000

Moment zginający płytkę centrującą na długości jednostkowej

M =
= 52,5 kNm/m

Uwzględniając nośność blachy poziomej głowicy o wartości

M_R = 1,0*2,0²*205*10^-1/6 = 13,7 kNm/m

obliczamy wymaganą grubość płytki centrującej

t ≥
= 0,0337 m

przyjęto t = 40 mm. Płytkę centrującą dopasowano do blachy poziomej przez frezowanie i przyspawano spoinami o grubości 6 mm, zatem połączenie można sprawdzić na 25 % siły:

τ =
*10^-1 = 72,9 MN/m² < 0,8*205 = 164 MPa

Rysunek roboczy konstrukcji stalowego pomostu oraz wykaz stali zamieszczono we wkładce do skryptu (rys. nr 1).

---