X WOJEWÓDZKI KONKURS MATEMATYCZNY
UCZNIÓW GIMNAZJÓW

27 marca 2010 r.

etap wojewódzki

GRATULACJE - zakwalifikowałaś / zakwalifikowałeś się do etapu wojewódzkiego
X Wojewódzkiego Konkursu Matematycznego. Do rozwiązania masz test składający się z 19 zadań zamkniętych i otwartych za które możesz uzyskać 50 punktów. W każdym z zadań zamkniętych tylko jedna z czterech podanych odpowiedzi jest poprawna. Zaznacz ją na karcie odpowiedzi. Na rozwiązanie wszystkich zadań masz 90 minut.

POWODZENIA!

1. 
   
   
   
   (1 pkt.) Pewna liczba dzieli się przez 3 i przez 5. Znaczy to, że dzieli się również przez :

8 15 10 20

2. 
   
   
   
   (1 pkt.) Jeżeli dzielną zmniejszymy o dzielnik to iloraz zmniejszy się o :

dzielnik 2 1 nie zmieni się

3. 
   
   
   
   (1 pkt.) Jeżeli x + y = 12 i x² + y² = 126 to x ∙ y ma wartość :

9 10 11 13

4. (1 pkt.) Rozwiązaniem równania
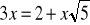
   jest liczba :

5. (1 pkt.) Promień okręgu wpisanego w kwadrat o przekątnej d = 6 ma długość :

3

6. 
   
   
   
   (1 pkt.) Odległość z Warszawy do Medyki wynosi 36 km. Pan Nowak pokonał ją w czasie 4,5h. Ile wyniósł łączny czas jego podróży, jeśli w drodze powrotnej jechał z prędkością
   o 12,5 % większą.

8,5h 7,5h 8h 9h

7. (1 pkt.) Wartość wyrażenia 4% ∙ 4% jest równa :
   
   
   
   

0,0016% 0,16% 1,6% 16%

8. (1 pkt.) Liczba
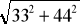
   jest równa :

55 66 77

9. 
   
   
   
   (1 pkt.) Prędkość rozchodzenia się światła jest równa 1 080 000 000 000 m/h. Światło zatem rozchodzi się z prędkością :

3 ∙10 km/s 3 ∙10³ km/s 3 ∙10⁵ km/s 3 ∙10⁷ km/s

10. 
    
    
    
    (1 pkt.) Powierzchnia dużego sześcianu jest równa 216 cm². Jaka jest łączna powierzchnia dwóch mniejszych sześcianów, jeśli każda z krawędzi ma długość równa połowie krawędzi dużego sześcianu ?

108 cm² 216 cm² 54 cm² 72 cm²

11. 
    
    
    
    (1 pkt.) Wyrażenie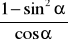
    po uproszczeniu jest równe :

cosα 1 sinα tgα

12. (1 pkt.) Powierzchnia boczna stożka jest wycinkiem kołowym o promieniu 10 i długości łuku 10π. Wysokość tego stożka wynosi:

13. 
    
    
    
    (1 pkt.) Ile wynosi a jeśli liczba 14¹⁴ - a jest podzielna przez 10 ?

6 5 4 3

14. 
    
    
    (1 pkt.) Ile osi symetrii ma figura złożona z prostej i punktu, który do niej nie należy ?
    

2 1 3,3 nieskończenie wiele

15. (1 pkt.) W loterii zawierającej 100 losów pięć pozwala wybrać pierwszą nagrodę,
    20 - drugą nagrodę i 30 - trzecią. Jakie jest prawdopodobieństwo wygrania nagrody ?

0,55 0,05

16. (7 pkt.) Inżynier ma postawić słupy telegraficzne między dwoma miejscowościami.

Obliczył, że jeśli ustawi po jednym słupie w skrajnych punktach i co 50m między tymi

punktami, to zabraknie mu 21 słupów; jeśli zaś będzie je ustawiać co 55m, to zabraknie mu

tylko jednego słupa. Ile było słupów i jaka była odległość między tymi miejscowościami ?

17. (9 pkt.) Dany jest okrąg o środku O, a w nim kąt wpisany o mierze 60^o oparty na łuku AB.

Długość cięciwy AB wynosi
. W punktach A i B poprowadzono styczne do okręgu,

które przecięły się w punkcie M. Oblicz pole czworokąta AMBO.

18. (7 pkt.) Na graniastosłupie prawidłowym trójkątnym, którego pole podstawy wynosi
    36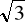
    cm² opisano walec. Oblicz objętość i pole powierzchni całkowitej walca, jeżeli przekątna ściany bocznej graniastosłupa tworzy z krawędzią boczną kąt 30^o.

19. (12 pkt.) Dla jakich wartości parametrów m i k układ równań:

kx + y + 4 = 0

2x + y + m = 0

nie ma rozwiązania i stosunek pół trójkątów wyznaczonych przez wykresy tych równań
i osie układu współrzędnych wynosi 1:4

---