POLITECHNIKA LUBELSKA w LUBLINIE		LABORATORIUM MATERIAŁOZNASTWA Ćwiczenie 5
Nazwisko : WALCZYSZYN	Imię : RAFAŁ	Semestr 3	Grupa EZ 3	Rok akadem. 2008/2009
Temat ćwiczenia: Badanie podstawowych właściwości dielektryków stałych.			Data wykonania 05-02-2009	Ocena

Cel ćwiczenia:

Celem ćwiczenia było zapoznanie się z metodami pomiaru rezystancji skrośnej i powierzchniowej.

Układy pomiarowe:

1.Pomiar rezystancji skrośnej.

2.Pomiar rezystancji powierzchniowej.

3.Pomiar podstawowych właściwości dielektryków stałych ( R, C, tgδ)

Tabela nr.1

Pomiar rezystancji skrośnej i powierzchniowej

próbka	rezystancja skrośna Rv [Ω]	rezystancja powierzchniowa Rs [Ω]
1	2217*10^8	4027*10^8
2	1940*10^8	4250*10^8
3	1367*10^8	3740*10^8
4	1787*10^8	4360*10^8
5	1507*10^8	2870*10^8

1. Teflon

2. Laminat

3. Getynaks

4.Pleksa

5.Tekstolit

Tabela nr.2

Wymiary geometryczne próbek.

próbka		średnica zewn. d [m]	Grubość h [m]	średnica szczeliny g [m]	A [ ]	B [ ]
1		0,05	0,001	0,005		0,172
2								0,0015
3								0,0015
4								0,001
5								1, 0,0005

A-efektywna powierzchnia

B-efektywna długość elektrody pomiarowej

Przykładowe obliczenia:

A=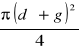

A=

B=

B=3,14(0,05+0,005)=0,172

Tabela nr.3

Obliczenia rezystywności skrośnej i powierzchniowej

próbka	rezystywność skrośna v [Ω*m]	rezystywność powierzchniowa s [Ω*m]
1	5,254*10^11
2	3,065*10^11	1,46*10^13
3	2,159*10^11	1,28*10^13
4	2,823*10^11	1,49*10^13
5	7,143*10^11	9,87*10^12

Rezystywność skrośną oblicza się ze wzoru:

R_v-Rezystancja skrośna

h- grubość próbki

5,254*10¹¹ Ω*m

Rezystywność powierzchniową oblicza się ze wzoru:

Ω*m

Tabela nr.4

Pomiar rezystancji, pojemności oraz tg δ - kąta stratności pojedynczych próbek

L.p	Średnica d	Rezystancja R	Pojemność C 1kHz	Pojemność C 120Hz	Kąt stratności tg δ 1kHz	Kąt stratności tg δ 120Hz
		[m]	[MΩ]	[pF]	[pF]		-
Pleksiglas	0,069	Więcej niż10	139	150	0,055	0,114
Tekstolit 1			3,33	370	456	0,128	0,226
Tekstolit 2			4,17	233	303	0,162	0,294
Getynaks 1			7,48	220	254	0,096	0,187
Getynaks 2			8,95	134	163	0,131	0,261

Tabela nr 5 Obliczone wartości przenikalności względnej próbek.

Lp.	Grubość x	Przenikalność próżni ε0	Powierzchnia próbki S	Przenikalność względna przy ε01kHz	Przenikalność względna przy ε0120Hz
		(m)	(F/m)	(m^2)	-	-
Pleksiglas	0,001	8,842x10^-12		8,05	8,69
Tekstolit 1	0,0005				10,72	13,21
Tekstolit 2	0,001				13,5	17,56
Gerynaks 1	0,001				12,75	14,72
Gerynaks 2	0,002				15,53	19,13

Do obliczenia wartości przenikalności elektrycznej ε w tabeli 5 stosuje się wzór:

;

Gdzie: C - pojemność z tabeli 4 dla 1kHz i dla 120Hz

Przykładowe obliczenia:

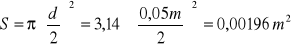
Przenikalność elektryczna dla 1 kHz

Tabela 6.Pomiar Rezystancji, pojemności oraz tgδ-kąt stratności próbek przy podwójnym uwarstwieniu szeregowym.

Lp.	Rezystancja R	Pojemność C Przy 1kHz	Pojemność C Przy 120Hz	Kąt stratności tgδ 1kHz	Kąt stratności tgδ120Hz
		[MΩ]	[pF]	[pF]	-	-
Pleksiglas Tekstolit 2	Więcej niż 10	106	124	0,101	0,185
Getynaks 2 Tekstolit 1	Więcej niż 10	113	139	0,139	0,274

Obliczone wartości tg δ - kąta stratności próbek przy podwójnym uwarstwowieniu szeregowym

L.p	tg δ 1kHz	tg δ 120Hz
		-	-
Pleksiglas Tekstolit 2	0,094	0,173
Getynaks 2 Tekstolit 1	0,130	0,251

Przykładowe obliczenia:

Do obliczeń tgδ należy wykorzystać wzór:

tgδ=

Wnioski

Po wykonaniu pomiarów można dostrzec, że największe rezystancje mają dielektryki: pleksiglas i gentynaks próbka druga. Wartości nie można było odczytać, ponieważ miernik nie miał tak dużego zakresu. Najmniejszą rezystancję miał teksolit próbka pierwsza. Pojemność dielektryków badanych jest większa przy częstotliwości 120Hz niż przy 1kHz. Największą pojemność przy obu częstotliwościach ma teksolit 1. Najmniejszą wartość przenikalności względnej przy obu częstotliwościach ma pleksiglas a największą getynaks próbka 2. Przy połączeniu próbek szeregowo pojemności są mniejsze niż w pojedynczych próbkach analogicznie jak dla kondensatorów szeregowo łączonych, wartości obliczone kąta stratności są przybliżone dla 120Hz, a różne dla 1kHz. Rezystywność zależy od wymiarów próbki i rodzaju materiału. Rezystywność skrośna może być większa dla grubszych próbek a rezystywność powierzchniowa dla próbek o większej powierzchni między punktami przyłożenia napięcia

---