Niestacjonarne czerwiec 2014

1. Na linii SML leżą portfele:

   1. Efektywne CAPM

   2. Nieefektywne CAPM

   3. będące w równowadze

   4. niedowartościowane

   5. żadne z powyższych

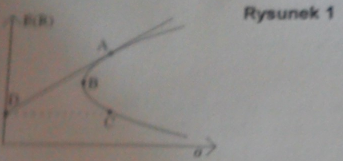
2. Na rysunku 1 aktywa wolne od ryzyka reprezentują:

   1. A+D posiadają inst. Wolne od ryzyka

   2. odcinek CD

   3. łuk CB

   4. D

   5. żadne z powyższych

3. Stopa zwrotu z portfela aktywów jest równa:

   1. średniej stóp zwrotu z aktywów

   2. średniej ważonej stóp zwrotu z aktywów

   3. sumie stóp zwrotu z aktywów

   4. sumie ważonej stóp zwrotu z aktywów

   5. żadne z powyższych

4. Wyrażenie 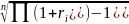reprezentuje stopę zwrotu:

   1. geometryczną dla n lat

   2. geometryczną dla n stóp

   3. geometryczną dla i stóp

   4. nie reprezentuje żadnej stopy zwrotu

   5. żadne z powyższych

5. Model APT to inaczej model:

   1. średniej A- wariancji P

   2. diagonalny macierzy

   3. arbitrażu cenowego

   4. taki model nie istnieje

   5. żadne z powyższych

6. Ryzyko całkowite akcji mierzymy:

   1. betą

   2. odchyleniem standardowym składnika losowego

   3. odchyleniem standardowym stopy zwrotu

   4. ekierką

   5. ksi

   6. żadne z powyższych

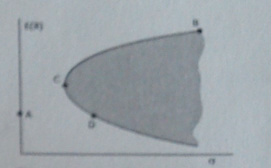
7. Na rysunku 2 portfel A jest portfelem:

   1. nieefektywnym

   2. efektywnym

   3. ze zbioru możliwości inwestycyjnych

   4. spoza zbioru możliwości inwestycyjnych

   5. żadne z powyższych

8. Wariancja uwzględnia odchylenia standardowe od wartości oczekiwanej:

   1. tylko ujemne

   2. tylko dodatnie

   3. ujemne i dodatnie

   4. ani ujemne, ani dodatnie ponieważ...

   5. żadne z powyższych

9. Kowariancja:

   1. mierzy kierunek związku

   2. mierzy siłę związku

   3. mierzy kierunek oraz siłę związku... korelacja

   4. kowariancja dotyczy rozproszenia...

   5. kowariancja to wariancja podniesiona...(do kwadratu?)

10. Jeżeli można inwestować w aktywa (......) to portfel rynkowy jest portfelem:

    1. nieefektywnym

    2. efektywnym

    3. zdominowanym

    4. pozbawionym ryzyka

    5. nie ma wówczas portfela rynkowego

11. Inwestor konstruując portfel dwuskładnikowy powinien wybierać akcje:

    1. dodatnio skorelowane

    2. ujemnie skorelowane

    3. nieskorelowane

    4. o ujemnej korelacji pomiędzy .....

    5. o ujemnej korelacji między ws......

12. Jeżeli udział akcji A w budowanym...... wynosić -0.2, to znaczy że należy...

    1. nabyć

    2. krótko sprzedać

    3. nic nie robić

    4. ......

13. Premię za ryzyko obliczamy pomniejszając oczekiwaną stopę zwrotu o:

    1. R_m

    2. R_f

    3. βR_m

    4. σ

    5. wszystkie oprócz a)

14. Dla portfela 2 składnikowego warunek: W₁>0, W₂>0 oznacza, że:

    1. krótka sprzedaż jest dozwolona

    2. krótka sprzedaż jest zabroniona

    3. to nie ma związku z krótką sprzedażą

    4. należy nabywać pojedyncze akcje

    5. żadne z powyższych

15. W modelu Sharpe`a bessa na rynku akcji wpływa na stopę zwrotu z akcji A poprzez:

    1. α

    2. β

    3. R_m

    4. ξ

    5. żadne z powyższych

16. Portfel złożony wyłącznie z akcji A o parametrach β>0, α>0, σ²>0 jest obciążony ryzykiem:

    1. wyłącznie specyficznym

    2. wyłącznie systematycznym

    3. systematycznym i specyficznym

    4. ani systematycznym ani specyficznym

    5. żadne z powyższych

17. Siłę związku liniowego między zmiennymi mierzy:

    1. Kowariancja- tylko kieunek

    2. wariancja

    3. współczynnik korelacji

    4. odchylenie standardowe

    5. żadne z powyższych

18. Portfel rynkowy jest obciążony ryzykiem:

    1. wyłącznie specyficznym

    2. wyłącznie systematycznym

    3. systematycznym i specyficznym

    4. ani systematycznym ani specyficznym

    5. żadne z powyższych

19. Stosując model Sharpe`a inwestor powinien dobierać do portfela spółki o α:

    1. wysokim

    2. niskim

    3. 0

    4. poziom α nie ma tu znaczenia

    5. żadne z powyższych

20. W modelu Sharpe`a korelacja pomiędzy akcjami wynika z istnienia:

    1. składnika losowego

    2. parametru alfa

    3. indeksu rynkowego

    4. w modelu Sharpe`a korelacja nie występuje

    5. ...

21. Linia SML ......... stopą zwrotu z akcji a:

    1. σ²_m

    2. σ²

    3. β

    4. λ

    5. żadna z powyższych

22. W równaniu Hamady

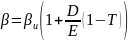współczynnik β_{u to:}

1. beta lewarowana

2. beta nielewarowana

3. beta długu

4. to nie jest równanie Hamady

5. żadna z powyższych

23. Rynkowa premia za ryzyko w modelu CAPM:

    1. zależy wyłącznie od stopy zwrotu dowolnej obligacji na rynku

    2. zależy wyłącznie od stopy zwrotu z indeksu giełdowego

    3. zależy wyłącznie od stopy inflacji

    4. zależy od stopy zwrotu indeksu giełdowego i stopy zwrotu wolnej od ryzyka

    5. zależy od kursu pary walutowej EUR/USD

24. Akcje niedowartościowane w modelu CAPM

    1. znajdują się na linii SML

    2. znajdują się pod linią SML przewart.

    3. znajdują się nad linią SML

    4. znajdują się tylko w IV ćwiartce układu współrzędnych

    5. znajdują się nad linią CML

25. Czy CAPM był laureatem Nagrody im. Nobla z ekonomii?

    1. tak, samodzielnie

    2. nie

    3. tak, ale razem z SHARPE`M

    4. był laureatem nagrody, ale nie Nobla

    5. dopiero będzie

26. Dywidenda:

    1. jest wypłacana z zysku brutto

    2. o jej wypłacie decyduje zarząd wspólników(?)

    3. jeżeli występuje zysk w roku obrotowym to musi być wypłacona

    4. jeżeli nie ma zysku to nie może być wypłacona

    5. żadna z powyższych

27. Współczynnik korelacji Pearsona:

    1. dostarcza informacji o sile zależności pomiędzy występującymi zmiennymi

    2. wskazuje na kierunek powiązania liniowego pomiędzy stopami zwrotu akcji

    3. przyjmuje wartości z domkniętego przedziału -1 do 1

    4. wartość jego modelu wyraża zależności

    5. wszystkie powyższe odpowiedzi są prawidłowe

28. Premię za czas stanowi:

    1. R_m-R_f premia za ryzyko

    2. β_i

    3. R_f

    4. β_iR_m

29. Ze wzoru na wariancję stopy zwrotu portfela wynika, że ryzyko portfela zależy od:

1. Tylko od ryzyka akcji wchodzących w skład portfela

2. Ryzyka akcji wchodzących w skład portfela oraz od współczynnika kreacji tych akcji

3. Tylko od współczynnika korelacji akcji wchodzących w skład portfela

4. Żadne z powyższych

30. Przyjmując, że ryzyko powinno być określane tylko na podstawie elementów niepożądanych dla inwestora, za miarę ryzyka można uznać:

1. Odchylenie standarowe

2. Semiodchylenie

3. Współczynnik zmienności

4. Żadne z powyższych

31. Logarytmiczna stopa zwrotu w skali rocznej

1. Zawsze daje ten sam wynik jak w przypadku stopy zwrotu prostej

2. Zakłada kapitalizację ciągłą

3. Zakłada kapitalizację w okresach rocznych

4. Zakłada brak kapitalizacji

32. Który współczynnik wskazuje, o ile procent w przybliżeniu wzrośnie stopa zwrotu akcji, gdy stopa zwrotu z indeksu wzrośnie o 1%:

1. Alfa

2. Współczynnik korelacji

3. Beta

4. Żaden z powyższych

33. Ryzyko portfela dwuskładnikowego (bez krótkiej sprzedaży) przy odpowiednim szacunku udziałów można wyeliminować w sytuacji, gdy:

1. P12=1

2. P12=-1

3. P12=0

4. Żadne z powyższych

34. Które ryzyko można zmniejszyć poprzez zwiększenie ilości akcji w portfelu?

1. Ryzyko systematyczne

2. Ryzyko płynności

3. Ryzyko specyficzne

4. Żadne z powyższych

35. Inwestor dwa lata temu zakupił akcję, której cena w tym okresie wzrosła trzykrotnie. Ile zarobił inwestor za cały okres przetrzymania akcji w ujęciu stopy dochodu?

1. 50%

2. 100%

3. 200%

4. 300%

36. Jeśli w portfelu odchylenie standardowe stopy zwrotu akcji A wynosi 5%, a odchylenie standardowe stopy zwrotu akcji B wynosi 10%, to odchylenie standardowe portfela:

1. Będzie zawsze zawierać się pomiędzy 5% a 10%

2. Może przyjąć minimalnie wartość 0, a maksymalnie 10% przy założeniu nieujemności udziałów akcji w portfelu

3. Może przyjąć tylko wartości poniżej 5%

4. Może przyjąć tylko wartości od 2,5% do 7,5% przy założeniu nieujemności udziałów akcji w portfelu

37. Portfel o minimalnym ryzyku:

1. Należy do granicy efektywnej

2. Nie należy do granicy efektywnej

3. Jest portfelem zdominowanym

4. Nie istnieje

38. Arytmetyczna stopa zwrotu w skali rocznej

1. Zawsze daje wynik jako stopa średnia roczna

2. Zakłada brak kapitalizacji

3. Zakłada kapitalizację ciągłą

4. Zakłada kapitalizację w okresach rocznych

39. Linia rynku kapitałowego (CML) opisywana równaniem R=Rf+(Rm-Rf/m )*σ :

1. Odzwierciedla zbiór portfeli efektywnych w danych warunkach rynkowych

2. Odzwierciedla zbiór portfeli zdominowanych w danych warunkach rynkowych

3. Opisuje zależność pomiędzy stopami zwrotu dwóch spółek

4. Opisuje zależność pomiędzy stopą zwrotu danej spółki a stopą zwrotu z portfela rynkowego

40. Linia charakterystyczna akcji dana wzorem r=a + βrm + Ɛ:

1. Zależy od zmienności kurów walut Ɛ

2. Jest wykorzystywana w modelu zdyskontowanych dywidend

3. Służy do prognozowania zmian stopy zwrotu z akcji w zależności od zmian derywatów pogodowych

4. Służy do prognozowania zmian stopy zwrotu z akcji w zależności od zmian stopy zwrotu rynku w modelu Sharpa (jednowskaźnikowym)

41. Portfel o minimalnym ryzyku dla współczynnika korelacji równego 1 i dla nieujemnych udziałów w portfelu dwuskładnikowym:

1. Składa się w równych udziałach z akcji obu spółek tworzących portfel

2. Składa się wyłącznie z akcji o mniejszym ryzyku

3. Składa się wyłącznie z akcji o wyższym ryzyku

4. Zawsze tworzony jest przynajmniej z jedną akcją znajdującą się w krótkiej sprzedaży

42. Stopa zwrotu akcji reaguje z taką samą skalą ale przeciwnie niż indeks, gdy:

1. Β=1

2. -1<β<0

3. Β= -1

4. Żadne z powyższych, gdyż według tego parametru nie można określić reakcji akcji na zmiany indeksu

43. Model Wyceny Aktywów Kapitałowych to inaczej model:

1. Diagonalny Sharpe’a

2. CAPM

3. Markowitza

4. APT

44. W doskonale zdywersyfikowanym portfelu ryzyko specyficzne:

1. Decyduje o ryzyku całkowitym portfela

2. Jest nieistotne dla ryzyka całkowitego portfela

3. Jest większe od ryzyka systematycznego

4. Nie zostało obniżone w procesie dywersyfikacji

45. Ryzyko specyficzne:

1. Mierzone jest w modelu Sharpa za pomocą współczynnika β

2. Może zostać zmniejszone poprzez zwiększenie liczby papierów wartościowych w portfelu

3. Może zostać zmniejszone poprzez zmniejszenie liczby papierów wartościowych w portfelu

4. Jest związane ze zmianami stóp procentowych banku centralnego

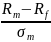46. może być określone jako:

1. Cena jednostki ryzyka (premii za ryzyko rynkowe przypada na jednostkę ryzyka rynkowego)

2. Cena czasu

3. Cena prowizji maklera obracającego portfelem akcji

4. Cena, jaką inwestor musi zapłacić za portfel z udziałem instrumentów wolnych od ryzyka