20. Model atomu wodoru według Bohra.
Wybór i opracowanie zadań – Jadwiga Mechlińska-Drewko.
Więcej zadań na ten temat znajdziesz w II części skryptu.
20.1.
Opierając się na teorii Bohra znaleźć:
a/
promień n-tej orbity elektronu w atomie wodoru,
b/
prędkość elektronu na tej orbicie,
c/
jego
całkowitą energię na n-tej orbicie.
20.2.
Wyznaczyć długość fali promieniowania emitowanego przez atom wodoru przy przejściu
elektronu z orbity n na orbitę k.
20.3.
Przejście elektronu z n-tej orbity na orbitę k=1 zachodzi z emisją fotonu o długości λ=1,026
10
-7
m. Znaleźć promień n-tej orbity.
20.4.
Znaleźć dla dwóch pierwszych orbit atomu wodoru wartość siły przyciągania
kulombowskiego między elektronem i jądrem oraz natężenie pola elektrycznego
wytworzonego przez jądro w odległości równej promieniowi pierwszej i drugiej orbity.
20.5.
Ile razy zwiększy się promień orbity elektronu w atomie wodoru będącego w stanie
podstawowym (n=1) przy wzbudzeniu go kwantem o energii E
ν
=12,09 eV ?
20.6.
W atomie wodoru elektron przeskakuje z drugiej orbity na pierwszą. Wyznaczyć zmianę
wartości pędu elektronu oraz zmianę jego energii kinetycznej przy tym przeskoku.
20.7.
Seria linii wodorowych z zakresu światła widzialnego (tzw. seria Balmera) powstaje przy
przejściu elektronu z wyższych orbit na drugą. Znaleźć granice serii Balmera.
20.8.
Wykazać, że częstotliwość fali świetlnej emitowanej przez atom wodoru przy przejściu
elektronu z n+1 na n-tą orbitę dąży, przy dużych n, do częstotliwości obiegu elektronu na
n-tej orbicie.
20.9.
Obliczyć minimalne liniowe rozmiary pozytonium oraz jego energię jonizacji. Pozytonium
jest układem złożonym z pozytonu i elektronu krążących wokół wspólnego środka masy.
20.10.
Obliczyć wartość orbitalnego momentu magnetycznego elektronu w atomie wodoru w stanie
podstawowym.
Rozwiązania:
20.1.R.
Korzystając z równań:
2
2
0
2
4
1
2
n
n
n
n
n
r
e
r
mV
i
h
n
r
V
m
πε
π
=
=
,
gdzie:
m- masa elektronu,
r
n
- promień n-tej orbity,
V
n
- prędkość elektronu na n-tej orbicie,
h- stała Plancka,
e- ładunek elektronu,
ε
0
- przenikalność elektryczna próżni,
wyznaczamy:
n
h
e
V
i
n
e
m
h
r
n
n
1
2
0
2
2
2
2
0
ε
π
ε
=
=
.
Całkowita energia elektronu jest sumą energii kinetycznej
2
2
n
kn
mV
E
=
i energii potencjalnej oddziaływania elektronu z jądrem
n
pn
r
e
E
2
0
4
1
πε
−
=
czyli
.
10
09
,
1
8
,
1
8
1
7
3
2
0
4
2
2
2
2
0
4
−
⋅
=
=
−
=
−
=
+
=
m
c
h
me
R
gdzie
n
Rhc
n
h
me
E
E
E
pn
kn
n
πε
πε
R - stała Rydberga.
20.2.R.
2
2
k
Rhc
n
Rhc
E
E
c
h
h
k
n
+
−
=
−
=
=
λ
υ
.
−
=
+
−
=
2
2
2
2
1
1
1
1
1
n
k
R
k
n
R
λ
.
20.3.R.
Z poprzednich zadań mamy zależności:
(1)
−
=
2
2
1
1
1
n
k
R
λ
(2)
2
2
2
0
n
e
m
h
r
n
π
ε
=
.
Po wstawieniu n
2
wyznaczonego z równania (1) do równania (2) mamy:
.
10
75
,
4
)
(
10
2
2
2
2
0
m
k
R
e
m
k
R
h
r
n
−
⋅
=
−
=
λ
π
λ
ε
.
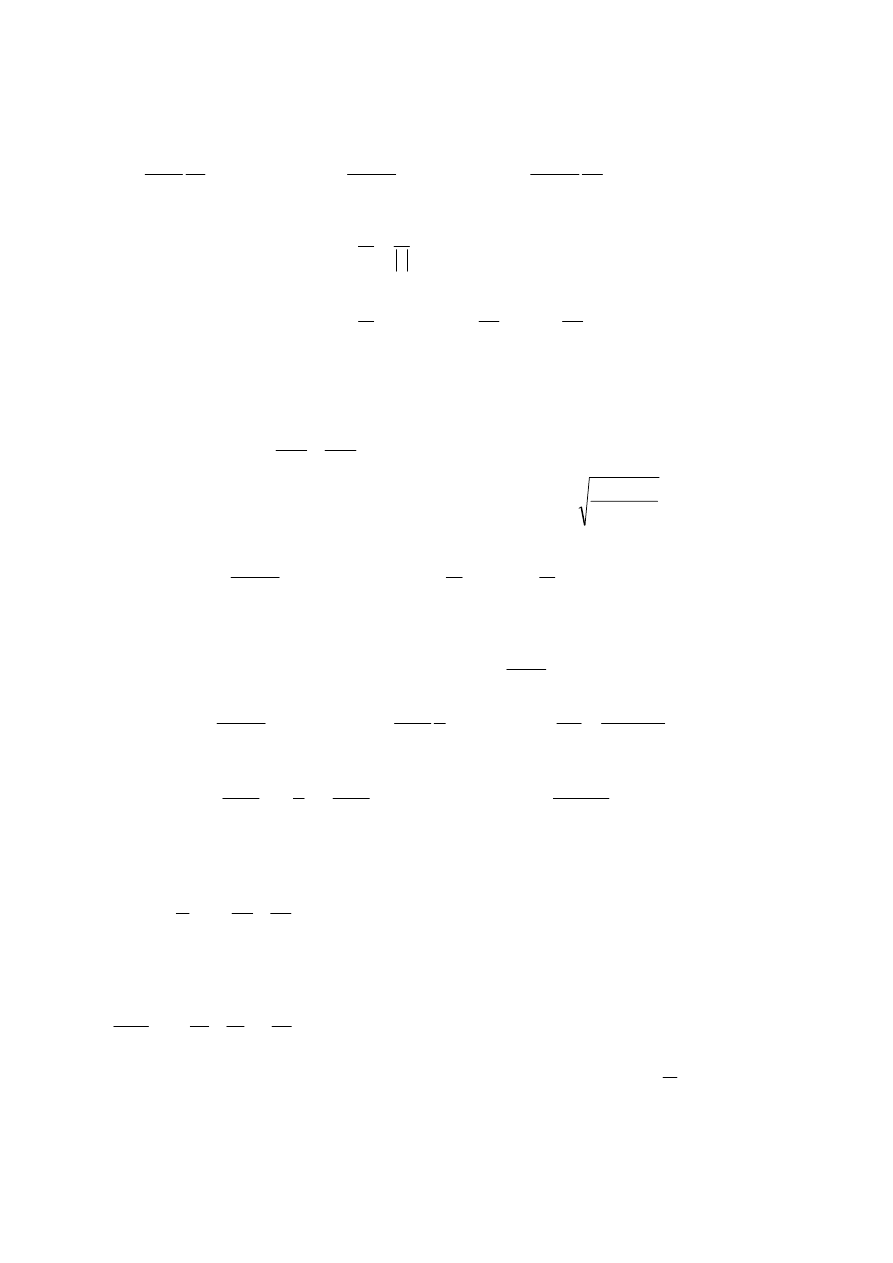
20.4.R.
Ponieważ
2
2
0
4
1
n
n
r
e
F
πε
=
oraz
2
2
2
0
n
e
m
h
r
n
π
ε
=
to
4
3
0
4
6
2
1
4
n
h
e
m
F
n
ε
π
=
.
Natężenie pola elektrycznego
e
F
q
F
E
=
=
.
Wynik obliczeń:
4
1
2
4
1
2
11
1
8
1
2
,
2
10
13
,
5
,
10
22
,
8
E
E
F
F
oraz
m
V
E
N
F
=
=
⋅
=
⋅
=
−
.
20.5.R.
W wodorze, przy przejściu elektronu z orbity n-tej na pierwszą orbitę następuje emisja
kwantu o energii:
2
2
1
1
Rhc
n
Rhc
E
E
h
E
n
+
−
=
−
=
=
υ
υ
.
Znając wartość energii kwantu można wyznaczyć wartość n :
3
=
−
=
υ
E
Rhc
Rhc
n
.
Elektron w procesie opisanym w zadaniu został wzbudzony na poziom trzeci.
Ponieważ :
2
2
2
0
n
e
m
h
r
n
π
ε
=
i
r
to
2
1
n
r
n
=
9
3
2
1
3
2
1
=
=
=
r
r
i
n
r
r
n
.
20.6.R.
Z postulatu Bohra wynika:
n
n
n
n
r
nh
p
i
h
n
r
V
m
π
π
2
=
=
2
.
Ponieważ
2
2
2
0
n
e
m
h
r
n
π
ε
=
to
2
2
2
0
4
2
0
2
8
2
1
2
n
h
me
m
p
E
oraz
n
h
me
p
n
kn
n
ε
ε
=
=
=
.
Z powyższych zależności wynika, że:
2
2
0
4
2
1
0
2
0
2
2
1
32
3
4
2
1
1
2
h
me
E
E
E
oraz
h
me
h
me
p
p
p
ε
ε
ε
=
−
=
∆
=
−
=
−
=
∆
.
20.7.R.
Przy przejściu elektronu z n-tej orbity na
k-tą następuje emisja światła o długości spełniającej
równanie
−
=
2
2
1
1
1
n
k
R
λ
. Dla serii Balmera
k=2.
Przy przejściu z
n=3 na k=2 nastąpi emisja kwantu o najmniejszej energii (i największej
długości fali) w serii Balmera. Jest to długofalowa granica serii przy czym:
.
660
36
5
3
1
2
1
1
max
2
2
.
max
nm
czyli
R
R
=
=
−
=
λ
λ
Krótkofalowa granica odpowiada przejściu z
∞
=
n
na
k=2 i wynosi
nm
R
367
4
.
min
=
=
λ
.
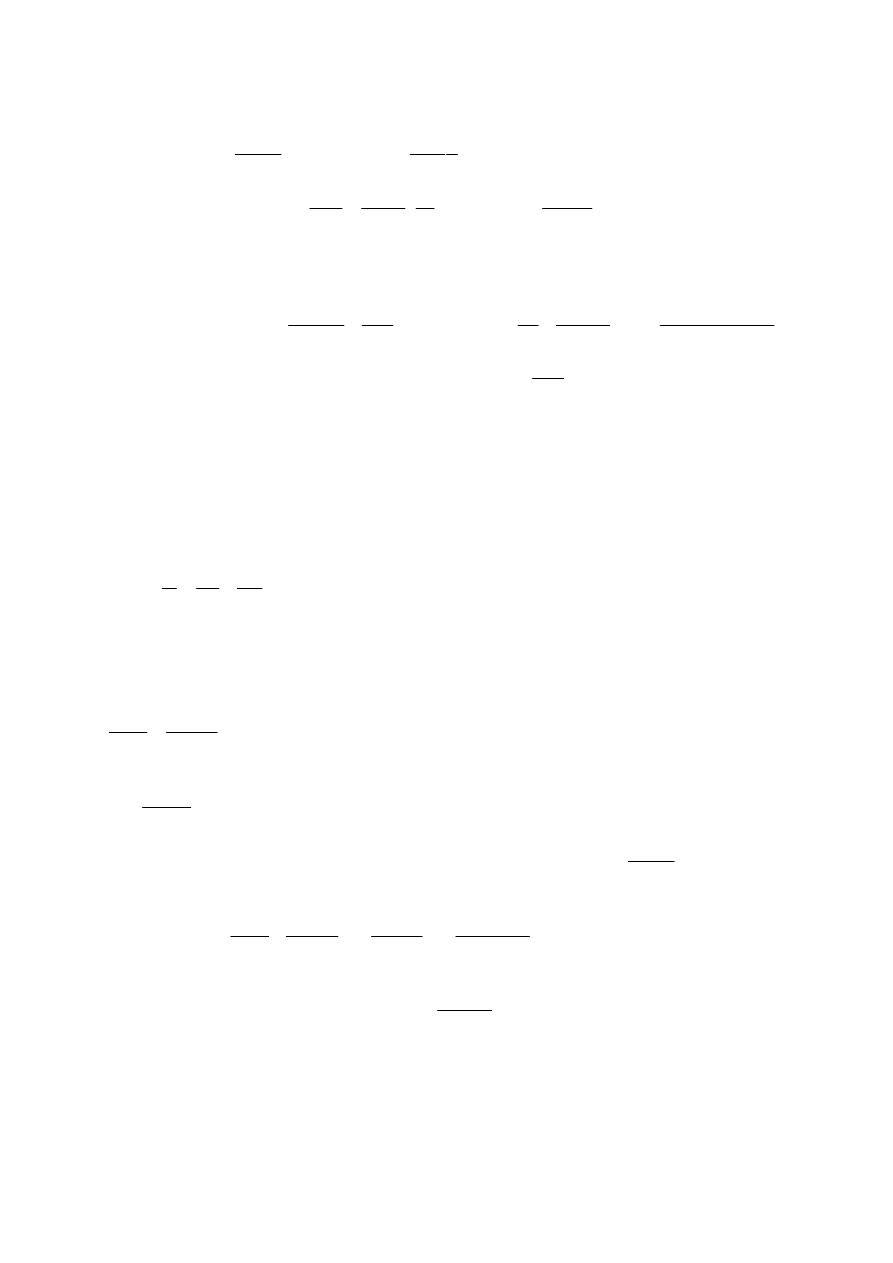
20.8.R.
Ponieważ
n
h
e
V
i
n
e
m
h
r
n
n
1
2
0
2
2
2
2
0
ε
π
ε
=
=
częstotliwość obiegu elektronu w atomie
wodoru jest równa:
3
3
2
0
4
1
4
2
n
h
me
r
V
n
n
n
⋅
=
=
ε
π
υ
.
8
3
2
0
4
c
h
me
R
ε
=
Przy przejściu elektronu z orbity
n+1 na orbitę n następuje emisja kwantu o energii:
(
)
(
)
2
2
2
2
2
2
2
2
1
1
1
2
1
1
1
)
1
(
n
n
n
n
n
Rc
n
n
Rc
czyli
n
Rhc
n
Rhc
E
E
h
E
n
n
+
−
+
+
=
+
−
=
+
+
−
=
−
=
=
+
υ
υ
υ
Dla n>>1 częstotliwość kwantu dąży do wartości
3
2
n
Rc
n
=
υ
co jest równe częstotliwości
obiegu elektronu.
20.9.R.
Pozyton jest cząstką o masie równej masie elektronu. Ładunek pozytonu jest równy co do
wartości bezwzględnej ładunkowi elektronu i wynosi 1,6
⋅10
-19
C.
Uwzględniając ruch elektronu i pozytonu wokół wspólnego środka masy wprowadzamy masę
zredukowaną
µ układu elektron-pozyton:
p
e
m
m
1
1
1
+
=
µ
gdzie
m
e
i
m
p
odpowiednio masy elektronu i pozytonu.
Korzystając z układu równań:
h
n
r
V
n
n
=
µ
π
2
i
2
0
2
2
4
n
n
n
r
e
r
V
πε
µ
=
,
przyjmując, że
m
e
=m
p
=m wyznaczamy
2
2
2
0
2
n
e
m
h
r
n
π
ε
=
.
Minimalne rozmiary pozytonium określa promień pierwszej orbity:
2
2
0
1
2
e
m
h
r
π
ε
=
.
Energia wiązania pozytonium wynosi:
2
2
2
0
4
0
2
0
2
2
16
8
4
2
n
h
me
r
e
r
e
V
E
E
E
n
n
n
p
k
w
ε
πε
πε
µ
−
=
−
=
−
=
+
=
Energia jonizacji z poziomu pierwszego
eV
h
me
E
j
8
,
6
16
2
2
0
4
=
=
ε
.
20.10.R.
Moment magnetyczny obwodu z prądem
IS
=
µ
I natężenie prądu jaki daje ruch elektronu po orbicie kołowej,
S powierzchnia obejmowaną przez ten obwód z prądem.
n
T
e
I
=
T
n
–okres obiegu elektronu na
n-tej orbicie
2
2
n
n
n
n
r
S
V
r
T
π
π
=
=
n
n
m
eh
r
eV
r
r
eV
B
n
n
n
n
n
n
n
n
µ
π
µ
µ
π
π
µ
=
=
=
=
4
2
2
2
µ
B
=0,93
⋅10
-23
J/T -magneton Bohra.