Wszechnica Popołudniowa

Algorytmika Internetu

Prof. dr hab. Krzysztof Diks

prof. dr hab. acie ysło

eszyt dydaktyczny opracowany w ramach pro ektu edukacy nego

— ponadregionalny program rozwi ania kompetenc i

uczniów szkół ponadgimnaz alnych w zakresie technologii
informacy no komunikacy nych I

.

Warszawska Wyższa zkoła Informatyki

ul. ewartowskiego

Warszawa

Pro ekt graficzny

I WI

A

Warszawa

opyright © Warszawska Wyższa zkoła Informatyki

Publikac a nie est przeznaczona do sprzedaży.

Instytut Informatyki

niwersytet Warszawski

diks mimuw.edu.pl

< 4 > 

Informatyka + 

W sieci Internet zna du e się blisko

stron liczba adresów IP zbliża się do

. ak

to est możliwe że pomimo olbrzymiego rozmiaru Internetu esteśmy w stanie niezmiernie szybko odnaleźć
interesu ące nas informac e dzielić się filmami i muzyką zdobywać przy aciół w mie scach do których nigdy
nie dotarlibyśmy osobiście kazu e się że okiełznanie sieci wymagało wynalezienia i zaimplementowania
odpowiednich algorytmów. niektórych z nich est mowa na t ym wykładzie.

1. Wstęp

.................................................................................................................................................

2. Autorska, bardzo krótka historia algorytmów ..............................................................................................

3. Trzy proste problemy algorytmicz e i ich rozwiąza ia .................................................................................

. . ider

.................................................................................................................................................

. . nożenie macierzy przez wektor ...........................................................................................................
. . ilnie spó ne składowe ..........................................................................................................................

. Autorska, bardzo krótka historia

ter etu ..................................................................................................

.

harakteryst yka

ter etu .........................................................................................................................

. Algorytm age a k ....................................................................................................................................

odsumowa ie ...............................................................................................................................................

iteratura

...............................................................................................................................................

..........

.....

.........

> Algorytmika Internetu 

< 5 >

Algorytmika est działem informatyki który za mu e się pro ektowaniem i analizowaniem algorytmów. Kom
putery bez algorytmów zapisanych w postaci programów okazu ą się bezużyteczne. Żeby ednak zaprząc
komputery do realizowania pożądanych przez nas zadań musimy być przekonani że wykorzystywane algo
rytmy są poprawne tzn. że dla danych spełnia ących określone kryteria po wykonaniu algorytmu otrzymamy
oczekiwane wyniki oraz że są one możliwe do wykonania na dostępnym sprzęcie – wykorzystywane kom
putery dysponu ą pamięcią o wystarcza ące po emności a obliczenia zakończą się w akceptowanym przez
nas czasie. atem główne aspekty analizy algorytmów to ich poprawność i wyda ność. Analizy algorytmów
dokonu emy abstrahu ąc od sprzętu na którym będą wykonywane. Powszechnie przy mu e się że algorytmy
szybkie to takie które wykonu ą się w czasie wielomianowym ze względu na rozmiar danych. kazu e się
że w dobie Internetu nawet algorytmy liniowe mogą być nie do wykorzystania na współczesnych kompute
rach z powodu olbrzymich rozmiarów danych które muszą być przetwarzane. A ednak potrafimy wyszukiwać
w tak monstrualne sieci aką est Internet oraz poznawać e strukturę. ak to est możliwe en wykład to pró
ba naszkicowania odpowiedzi na te pytania.

istoria algorytmów sięga starożytności. koło

lat przed naszą erą po awił się powszechnie dziś uczony

w szkole algorytm uklidesa służący do obliczania na większego wspólnego dzielnika dwóch liczb natural
nych. W roku

rancuz abriel amé udowodnił że liczba dzieleń wymagana w pesymistycznym przypad

ku do znalezienia na większego wspólnego dzielnika dwóch liczba algorytmem uklidesa est nie większa
niż pięć razy liczba cyfra w zapisie dziesiętnym mnie sze z tych liczb co oznacza że działa on w czasie wie
lomianowym ze względu na rozmiar danych. Wynik amé możemy traktować ako pierwszą analizę złożoności
czasowe algorytmu uklidesa i początek teorii złożoności obliczeniowe .

Po ęcie algorytmu choć w obecnych czasach intuicy nie oczywiste wymagało formalizac i po to żeby algo
rytmy mogł y być badane precyzy nymi matematycznymi metodami. W roku

Alan uring zaproponował

teoretyczny model maszyny liczące znane od tego czasu ako maszyna uringa. imo swe prostot y moc
obliczeniowa maszyny uringa rozumiane ako zdolność rozwiązywania problemów algorytmicznych przy
zadanych zasobach pamięci i czasie odpowiada współczesnym komputerom.

W roku

harles oare zaproponował na popularnie szy dziś algorytm sortowania – uick ort. Algorytm

uick ort działa pesymistycznie w czasie kwadratowym ale znakomicie zachowu e się dla przeciętnych lo

sowych danych. nie więce w tym samym czasie ack dmonds za mu ący się algorytmami grafowymi zde
finiował klasę P tych problemów algorytmicznych które można rozwiązać w czasie wielomianowym. edno
cześnie okazało się że dla wielu ważnych problemów optymalizacy nych nie można było znaleźć algorytmów
działa ących w czasie wielomianowym. Wytłumaczenie tego z awiska po awiło się w roku

kiedy to te

phen ook podał pierwszy tak zwany problem P zupełny wykazu ąc że eśli potrafilibyśmy sprawdzać w cza
sie wielomianowym czy dana formuła logiczna zdaniowa ma wartościowanie dla którego przy mu e wartość
prawda to wiele innych problemów dla których poszukiwano bezskutecznie wielomianowego rozwiązania
dałoby się także rozwiązać w czasie wielomianowym. W tym samym roku ichard Karp wskazał osiem innych
problemów P zupełnych. becnie lista takich problemów liczy tysiące pozyc i. o czy problemy P zupełne
ma ą wielomianowe rozwiązanie est ednym z siedmiu tzw. problemów mileni nych. a rozwiązanie każdego
z nich zaoferowano milion dolarów. eden z tych problemów – hipoteza Poincaré – został uż rozwiązany. edyne
znane algorytmy dla problemów P zupełnych działa ą w czasie wykładniczo zależnym od rozmiaru danych.

znacza to że dla danych dużych rozmiarów ale wciąż spotykanych w praktyce nie zawsze est możliwe znale

zienie rozwiązania z pomocą współczesnych komputerów ze względu na nieakceptowalnie długi czas obliczeń.

Dzisia nie znamy algorytmu służącego do rozkładania liczby na czynniki będące liczbami pierwszymi w cza
sie wielomianowo zależnym od długości e komputerowe reprezentac i. akt ten est podstawą protokołu
kryptograficznego

A wynalezionego w roku

. drugie strony w roku

wykazano że to czy licz

ba naturalna est liczbą pierwszą można sprawdzić w czasie wielomianowym. zy powinniśmy się obawiać
o protokół

A

< 6 > 

Informatyka + 

W tym rozdziale omówimy trzy proste problemy algorytmiczne podamy ich rozwiązania oraz zanalizu emy
złożoność obliczeniową zaproponowanych rozwiązań.

Dane:

dodatnia liczba całkowita n oraz ciąg liczb całkowitych a

a

… a n .

Wynik: liczba całkowita x która po awia się w ciągu a więce niż połowę razy czyli taka liczba x

że i a i x n

o ile takie x istnie e w przeciwnym przypadku dowolny element z ciągu a.

ozwiązanie które proponu emy wykorzystu e następu ące spostrzeżenie. iech u, v będą dwoma różnymi

elementami ciągu a. eśli x est liderem w a to est także liderem w ciągu a z usuniętymi elementami u i v.
Innymi słowy eśli x est liderem i każdy element w ciągu a o wartości różne od x sparu emy z elementem
o wartości różne od w to pozostaną t ylko niesparowane elementy o wartościach równych x. to algorytm
wykorzystu ący powyższą ideę.

Algorytm ider

pierwszy element ciągu

licz

mamy licz niesparowanych elementów o wartości

while nie koniec ciągu do

y kole ny element ciągu

i licz the

y licz

else i y the

licz licz

else

licz licz

parowanie

retur

Proponu emy zastanowienie się dlaczego ten algorytm est poprawny. kupmy się na ego złożoności. a roz
miar zadania w tym przypadku przy mu emy n – długość ciągu a. W każdym obrocie pętli pobieramy eden
element ciągu i wykonu emy na nim stałą liczbę operac i. atem złożoność czasowa est liniowa co w notac i
asymptotyczne wyraża się formułą

n .

auważmy że algorytm nie gwarantu e tego że wynik x est liderem. Żeby to stwierdzić potrzebny est esz

cze eden przebieg przez dane i policzenie liczby wystąpień x w ciągu. W niektórych zastosowaniach do prze
twarzania danych w Internecie drugi przebieg nie est możliwy.

Dane:

liczba naturalna n kwadratowa macierz liczb rzeczywistych A ..n ..n
wektor liczb rzeczywisty x ..n .

Wynik: wektor y ..n Ax gdzie y i A i

x

A i

x

… A i n x n .

Algorytm mnożenia macierzy przez wektor wynika wprost z opisu wyniku.

Algorytm

acierz

Wektor

or i to n do

y i
or to n do
y i y i A i

retur y

> Algorytmika Internetu 

<   >

analizu my teraz czas działania powyższego algorytmu. a droższą operac ę w tym algorytmie est ope

rac a mnożenia dwóch liczb rzeczywistych. Wykonu emy n takich mnożeń. eśli za rozmiar zadań przy mie
my właśnie n to nasz algorytm działa w czasie liniowym ze względu na rozmiar danych – liczbę elemen
tów macierzy A. Algorytm liniowe są uważane za szybkie. ozważmy czas działania naszego algorytmu dla
n

. Dale się okaże że nie est to rozmiar „ wzięty z sufitu”. Przy mi my dodatkowo że w ciągu

edne sekundy możemy wykonać

mnożeń. Wówczas czas potrzebny na wykonanie wszystkich mnożeń

w naszym algorytmie wyniósłby

sekund czyli około

dni est eszcze eden problem. dy

byśmy na zapisanie edne liczby rzeczywiste przeznaczyli ba tów to musielibyśmy mieć pamięć o rozmia
rze

ba tów czyli więce niż petaba t ak więc używa ąc konwenc onalnych komputerów nie bylibyśmy

w stanie realnie rozwiązać tego zadania.

W praktyce często po awia ą się macierze w których wiele elementów to zera. auważmy że eżeli A i
to wykonanie instrukc i y i y i A i

x nie zmienia wartości y i . żywa ąc technik listowych można

pominąć mnożenia przez . Wówczas liczba mnożeń i dodawań est proporc onalna do liczby niezerowych
elementów macierzy A. znaczmy liczbę niezerowych elementów macierzy A przez

A . zas działania al

gorytmu w tym przypadku wynosi

ma n

A co gdy

A est liniowe ze względu na n da e algorytm

mnożenia macierzy w czasie liniowo zależnym od n. Wówczas nawet dla n

można się spo

dziewać wyniku w rozsądnym czasie. acierz które liczba niezerowych elementów est liniowa ze wzglę
du na wymiar macierzy nazywamy macierzą rzadką. żywa ąc technik listowych macierze rzadkie można
reprezentować w pamięci o rozmiarze proporc onalnym do liczby niezerowych elementów macierzy co dla
n

est znacząco mnie niż petaba t.

Powiemy że graf skierowany est silnie spó ny eśli dla każde pary węzłów u i v istnie ą skierowane ścieżki
z u do v i v do u. ilnie spó ną składową skierowanego grafu nazywamy każdy ego maksymalny w sensie
zwierania silnie spó ny podgraf. ilnie spó nymi składowymi w grafie z rysunku są podgrafy rozpięte na wę
złach identyfikowanych przez pierwsze liczby w parach

.

10,1

2,9

3,6

5,3

4,5

6,2

8,1

1,10

12,1

11,2

9,2

y unek 
raf skierowany

pecyfikac a zadania ilnie spó ne składowe est następu ąca

Dane:

– graf skierowany.

Wynik: funkc a

…

taka że dla każde pary węzłów u v u v wtedy i tylko wtedy gdy ist

nie ą ścieżki w grafie    u do v i z v do u.

<   > 

Informatyka + 

łożoność algorytmów zna dowania silnie spó nych składowych w grafie zależy od reprezentac i grafu.
ą dwie zasadnicze reprezentac e tablicowa w które w tablicy kwadratowe A indeksowane węzłami mamy

A u v gdy istnie e krawędź z u do v natomiast A u v gdy takie krawędzi nie ma. iezależnie od liczby
krawędzi w grafie rozmiar takie reprezentac i wynosi

. Ponieważ liczba krawędzi w grafie skierowanym

waha się od do

×

–

reprezentac ą uwzględnia ącą ten fakt są listy sąsiedztwa. W te reprezentac i

dla każdego węzła przechowu emy listę sąsiadów do których prowadzą krawędzie z tego węzła – tzw. listę
„ w przód” oraz listę sąsiadów od których prowadzą krawędzie do tego węzła – tzw. listę „ w tył”. ozmiar
reprezentac i grafu w postaci list sąsiedztwa wynosi

i est ona szczególnie wygodna i oszczędna

w przypadku grafów rzadkich to znaczy takich w których liczba krawędzi liniowo zależy od liczby węzłów.
W algorytmie wyznaczania silnie spó nych składowych opisanym poniże przy miemy tę drugą reprezentac ę.

Przedstawimy teraz krótko algorytm którego pełny opis wraz z dowodem poprawności można znaleźć w książ
ce

. a potrzeby opisu załóżmy że zbiór węzłów to

…

. W celu znalezienia silnie spó nych skła

dowych przeszuku emy graf dwukrotnie w głąb. a pierwszym razem wykorzystu emy listy w przód gdy
w następnym przeszukiwaniu korzystamy z list w tył. Przeszuku ąc graf w przód numeru emy węzł y w kole
ności odwiedzania i dla każdego węzła liczymy liczbę węzłów w poddrzewie przeszukiwania o korzeniu w tym
węźle. a rysunku pierwsze liczby w parach odpowiada ą numerom w kole ności przeszukiwania tuta iden
t yfiku emy e z węzłami a drugie liczby w parach mówią o rozmiarach poddrzew przeszukiwania w przód.
Krawędzie lasu przeszukiwania w przód są narysowane ciągłą pogrubioną kreską. auważmy że numerac a
i liczba węzłów w poddrzewach pozwala na łatwe stwierdzenie czy węzeł v est w poddrzewie przeszukiwa
nia o korzeniu w u. Wystarczy sprawdzić czy numer v est nie mnie szy od numeru u ale mnie szy od numeru
u plus liczba węzłów w poddrzewie o korzeniu u. Dla przykładu węzeł o numerze est w poddrzewie węzła
o numerze ponieważ ≤ węzeł o numerze

nie est w poddrzewie węzła o numerze ponieważ

≥

.

Podczas przeszukiwania grafu po listach w tył wykrywamy silnie spó ne składowe. Ident yfikatorem silnie
spó ne składowe będzie węzeł o na mnie szym numerze z te składowe . Dlatego w drugie fazie przegląda
my węzły w kole ności rosnących numerów. dy napotkamy węzeł który nie był eszcze widziany w drugie
fazie to rozpoczynamy z niego przeszukiwanie w tył ale t ylko po węzłach które są w poddrzewie przeszuki
wania w przód o korzeniu w węźle od którego rozpoczęliśmy przeszukiwanie właśnie wykrywane składowe .
Wszystkie napotkane w ten sposób węzły będą należał y do silnie spó ne składowe które identyfikatorem
będzie węzeł od którego rozpoczynaliśmy przeszukiwanie. ozważmy eszcze raz graf z rysunku . ozpo
czynamy od węzła i idziemy po krawędziach w tył. W ten sposób dochodzimy do węzła

i ponieważ est on

w poddrzewie w przód węzła to zaliczamy go do silnie spó ne składowe o numerze . węzła

próbu e

my węzeł i też zaliczamy go do silnie spó ne składowe o numerze . węzła próbu emy prze ść do węzła

ale nie est on w poddrzewie w przód węzła więc nie należy do silnie spó ne składowe o ident yfikato

rze . Kole ny węzeł odwiedzany z węzła to i zaliczamy go do silnie spó ne składowe węzła numer . W ten
sposób wykry emy całą silnie spó ną składową zawiera ącą węzeł . Wszystkie e węzł y są zaznaczone ako
odwiedzone. Przegląda ąc kole no węzł y docieramy do węzła ako pierwszego nieodwiedzonego w tył i te
raz z niego odkrywamy silnie spó ną składową o identyfikatorze węzły . astępnie zostanie wykryta
składowa o identyfikatorze węzł y

a na koniec o identyfikatorze

węzł y

i

.

to formalny zapis omówionego algorytmu.

Algorytm il ie pó e kładowe

aza

W przód

węzeł

ost nr ost nr nr

ost nr

ost nr – ostatnio nadany numer

wezly ost nr

porządkowanie węzłów według numerów

or each u – węzeł na liście w przód węzła do
i nr u the

W przód u

nr u oznacza że węzeł nie został odwiedzony

w poddrzewie

ost nr – nr

rozmiar poddrzewa w przód

> Algorytmika Internetu 

<   >

Przeszukiwanie w przód
ost nr
or each węzeł do nr

or each węzeł do
i nr

the W przód

aza

W t ył

węzeł id s ..

id s – id aktualnie wykrywane składowe

s

id s

or each węzeł u na liście w tył węzła do
i s u

u nie był eszcze odwiedzony

A D

oraz

nr id s nr u nr id s w poddrzewie id s

est w poddrzewie id s

the W tył u id s

Przeszukiwanie w tył
or each węzeł do s

s

oznacza że nie był odwiedzony

or i to

do

i s wezly

the W t ył wezly

wezly

ważny czytelnik dostrzeże że złożoność czasowa powyższego algorytmu wynosi

i est on liniowy

ze względu na rozmiar grafu. en algorytm bardzo dobrze zachowu e się dla grafów z bardzo dużą liczbą wę
złów i liniową względem nie liczbą krawędzi.

W następnych rozdziałach przekonamy się że trzy przedstawione problemy ma ą silny związek z Internetem.

Internet to ogólnoświatowa sieć komputerowa która z punktu widzenia przeciętnego użytkownika est ed
norodną siecią logiczną w które węzły komputery są ednoznacznie identyfikowane przez swó adres. Po
czątki Internetu sięga ą końca lat sześćdziesiątych

wieku kiedy to powsta e sieć A PA

łącząca cztery

ednostki naukowe w Kalifornii i w stanie tah. ieć A PA

była poletkiem doświadczalnym dla powstania

i rozwo u powszechnie dziś używane rodziny protokołów komunikacy nych w sieci Internet –

P IP. W roku

powsta e firma icrosoft które rozwiązania przyczyniły się i nadal przyczynia ą do upowszechniania

świata komputerów wśród zwykłych ludzi. W roku

po awił się system operacy ny ni – dziadek sys

temów operacy nych z rodziny inu . W tym też roku królowa lżbieta wysłała swó pierwszy e mail. W roku

powsta e

– protoplasta powszechnych dziś sieci społecznościowych. W roku

po awia

się komputer osobisty I

P . ez komputerów osobistych które możemy postawić na biurku i korzystać

z ich dobrodzie stw w domu globalizac a Internetu nie byłaby możliwa. W roku

wraz z ustaleniem pro

tokołów

P IP nazwa Internet z wielkie litery zaczyna się rozpowszechniać. W roku

liczba hostów

w Internecie przekracza

w roku

przekroczona zosta e granica

hostów w roku

liczba hostów sięga miliona. Według Internet ystem onsortium w lipcu

roku liczba hostów wynosiła

.

W roku

sieć A PA

przechodzi do historii. ok

to narodziny sieci WWW – ogólnoświatowe

sieci powiązanych stron zawiera ących różnorodne treści multimedialne. ieć WWW est rozwi ana z wy
korzystaniem Internetu a strony w sieci WWW są ident yfikowane poprzez tzw. adresy

niform  e o

ur e  o ator . W roku

po awia się

AI – pierwsza graficzna przeglądarka stron WWW a niedługo

po nie etscape. ok

to narodziny ahoo. a większy obecnie gracz w Internecie to firma oogle

która powstała w roku

. W roku

startu e acebook – na popularnie sza obecnie w świecie sieć

społecznościowa.

< 

 > 

Informatyka + 

polskie historii odnotu my udostępnienie w roku

komunikatora adu

adu powstanie w roku

serwisu gier Kurnik a w roku

– portalu społecznościowego asza Klasa.

zym charakteryzu e się Internet a z punktu widzenia zwykłego użytkownika – a sieć WWW akie problemy

algorytmiczne należy rozwiązać żeby zasoby sieci WWW stał y się łatwo i szybko dostępne Próbu emy odpo
wiedzieć na te pytania w następnym punkcie.

anim za miemy się problemami algorytmicznymi związanymi z Internetem zastanówmy się ak można opi

sać tę sieć. kupimy się tuta bardzie na sieci WWW z które na co dzień korzystamy. ieć WWW możemy
przedstawić ako graf skierowany którego węzłami są strony internetowe natomiast dwie strony W są po
łączone krawędzią eśli na stronie istnie e dowiązanie link do strony W. W roku

grupa naukowców

z Alta ista ompany I

Almaden esearch enter i ompa ystems esearch enter opisała strukturę

sieci WWW na podstawie danych zebranych przez szperacze ang.  rawler firmy Alta ista

. zperacze

odwiedził y ponad

milionów stron przechodząc po więce niż pół tora miliarda łączach. W wyniku analizy

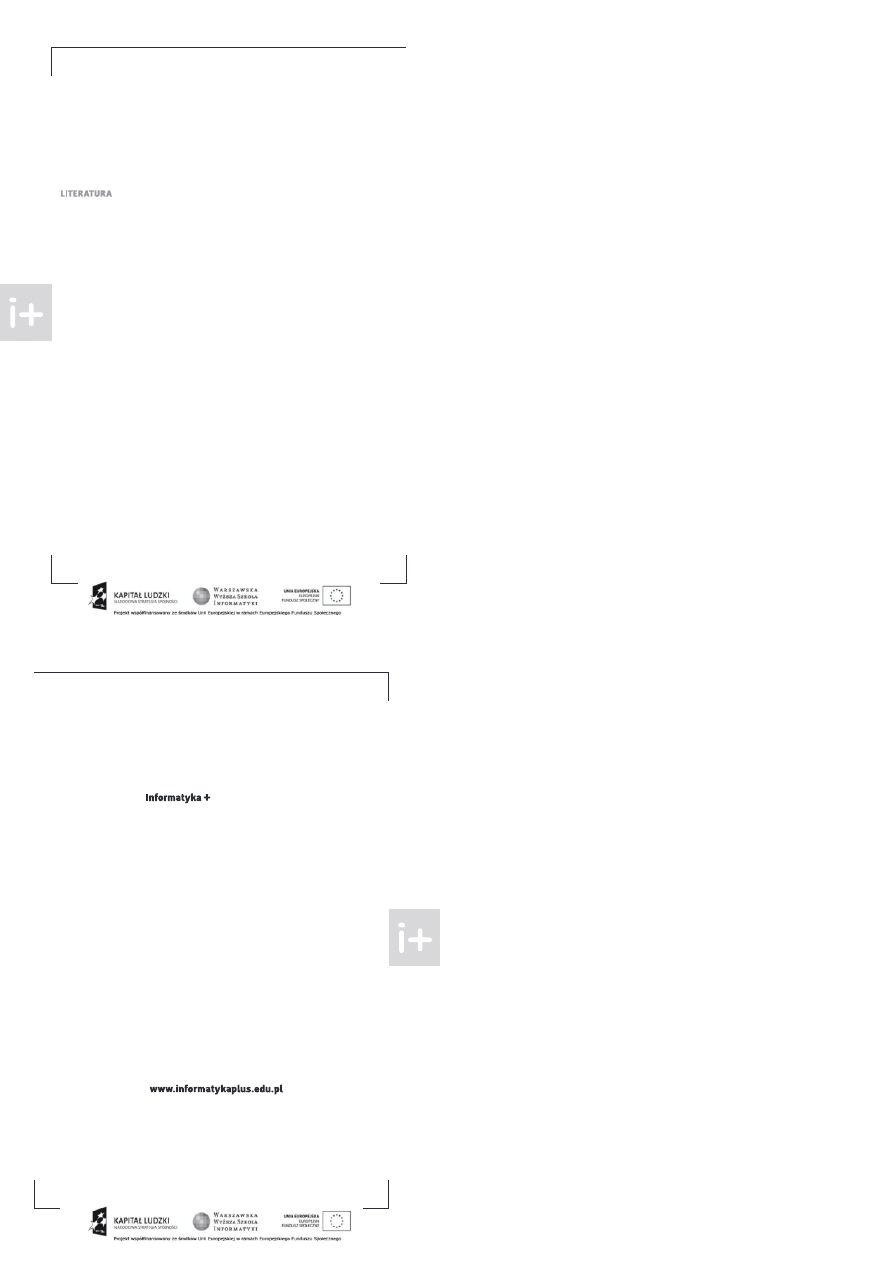
ustalono że graf sieci WWW ma strukturę przedstawioną na rysunku .

IN

SCC

Tendrils
44 Million nodes

44 Million nodes

56 Million nodes

44Million nodes

Disconnected components

Tubes

OUT

y unek 
ieć WWW

o możemy wyczytać z tego rysunku dybyśmy zapomnieli o orientac ach krawędzi to prawie wszystkie

strony należał yby do edne spó ne składowe . ieć ednak est grafem skierowanym. kłada ą się na nią
cztery główne części. a większa est część środkowa

– silnie spó na składowa. W składowe

z każ

de strony możemy do ść do każde inne wykonu ąc być może wiele kliknięć. dowolne strony części I
można prze ść przez

do dowolne strony części

. części I wychodzącą tzw. wici ang  ten ril

czyli

strony które są osiągalne z pewnych stron w I . Podobnie wici prowadzą do

– strony z których można

dostać się do stron w

. zęść stron z

est bezpośrednio osiągalna ze stron I za pomocą tzw. rur

ang.  tu e . Po zanalizowaniu próbki sieci roder i inni doszli do ważnych wniosków

■

sieć WWW est skierowanym grafem rzadkim tzn. liczba e krawędzi liniowo zależy od liczby węzłów

badana sieć zawierała

×

stron adresów

i

×

dowiązań

> Algorytmika Internetu 

< 

 >

■

odległości w sieci są małe w sieci zbadane przez rodera średnia długość ścieżki skierowane wynosiła

– tyle kliknięć wystarczy żeby dotrzeć do pożądane osiągalne strony gdybyśmy zapomnieli o

orientac i krawędzi to średnia długość ścieżki wyniosłaby .

becnie rozmiar Internetu est dużo większy niż w roku

. ak uż wspomnieliśmy w lipcu

roku

zare estrowano

hostów. grudnia

w użyciu było

adresów IP obe mu ących

kra ów. zacu e się że na dzień stycznia

liczba stron poindeksowanych przez firmę oogle wyno

siła ponad

miliardów. aki stąd wniosek Pro ektu ąc algorytmy dla sieci WWW musimy wiedzieć że dzia

łamy na sieci o miliardach węzłów która szczęśliwie est rzadka. ie est to zaskaku ące. W sieci są miliardy
stron ale na każde stronie może być od kilku do kilkudziesięciu dowiązań.

ieć WWW niesie z sobą wiele wyzwań algorytmicznych. Wyzywa ących zarówno ze względu na ogrom Inter

netu ale także dlatego że Internet est w pełni rozproszony i bez centralne administrac i. Do podstawowych
problemów algorytmicznych związanych z siecią WWW można zaliczyć

■

wyszukiwanie i składowanie stron zawartości

■

indeksowanie stron i przetwarzania zapytań

■

odpowiadanie na zapytania w sposób zadowala ący użytkownika

■

zgłębianie i analiza sieci WWW.

W następnym punkcie przedstawimy algorytm Page ank który służy do nadawania rang stronom w taki spo
sób żeby po znalezieniu stron w odpowiedzi na pytanie użytkownika wymienić e w kole ności od na waż
nie szych do na mnie ważnych. ważny czytelnik nat ychmiast spostrzeże trudności w tak sformułowanym
problemie. trona która est ważna dla ednego użytkownika może być mnie ważna dla innego. zy istnie e

akiś w miarę obiektywny ranking stron który byłby akceptowalny przez większość użytkowników Internetu

akie pytanie zadali sobie twórcy firmy oogle ergiey rin i ary Page. dpowiedzią na nie był algorytm

Page ank który przyczynił się do powstania i rozwo u oogle.

Przedstawiony poniże opis algorytmu Page ank został przygotowany uż wcześnie i ukazał się w czasopi
śmie Delta nr

pod tytułem „

iara ważności”

.

Każdy z nas choć raz w życiu użył wyszukiwarki oogle. zy zastanawialiśmy się dlaczego wyszukiwarka

oogle poda e adresy stron będących odpowiedzią na zapytanie właśnie w takie a nie inne kole ności.

Autor przeprowadził eksperyment i zanotował co oogle.pl dała w odpowiedzi na zapytanie matematyka.

to pierwszych adresów do stron które autor otrzymał .

.

godz.

.

. www.matematyka.pl
. www.matematyka.pisz.pl
. pl.wikipedia.org wiki

atematyka

. matematyka.org
. www.math.edu.pl.

Przeglądarka oogle podała że wybrała e spośród

kandydatów. Dlaczego właśnie te strony

uznano za na ważnie sze aka est miara ważności ranga strony kazu e się że podstawą analizy waż
ności stron w oogle est analiza połączeń w sieci WWW. Przypomni my że sieć WWW est grafem skiero
wanym w którym węzłami są strony a krawędzie odpowiada ą dowiązaniom pomiędzy stronami – strona
zawiera ąca adres internetowy inne strony est początkiem krawędzi a strona o danym adresie est e
końcem. zy można na podstawie samego grafu powiązań stron powiedzieć które strony są ważnie sze
a które mnie

trona ważna to strona interesu ąca. trona interesu ąca to taka do które łatwo dotrzeć ponieważ wiele in

nych stron na nią wskazu e. a dodatek wiele spośród stron wskazu ących na ważną stronę też est ważnych
i interesu ących itd. ergey rin i arry Page wyrazili to matematycznie w następu ący sposób.

< 

 > 

Informatyka + 

ałóżmy że mamy n stron

…

n

. iech w

i

będzie liczbą rzeczywistą dodatnią mierzącą ważność

strony

i

. Wówczas określamy

w

i

∑

 

∈We

i

gdzie We

i 

to zbiór stron zawiera ących adres strony

i

czyli zbiór początków krawędzi prowadzących

do

i

zaś Wy

 

est liczbą odnośników wychodzących ze strony czyli krawędzi prowadzących do stron

ze zbioru Wy

 

. Wzór ten oznacza że ważność strony mierzy się ważnością stron na nią wskazu ących.

eżeli przy miemy na początek że wszystkie strony są ednakowo ważne i dla każde z nich w

i 

n gdzie

n to liczba wszystkich stron to ważność stron można obliczyć za pomocą następu ące metody iteracy ne

proces

w

k

i

∑

 

∈We

i

a powyższy proces można spo rzeć ak na błądzenie losowe po sieci WWW. ozpoczynamy z dowolne stro

ny a następnie z każde oglądane strony ruszamy losowo do edne ze stron do których adresy umieszczono
na te stronie. eżeli nasz proces będziemy powtarzali bardzo długo to pewne ze stron będziemy oglądali
częście niż inne. trony oglądane częście są ważnie sze.

iestety może się zdarzyć że przemieszcza ąc się po stronach natrafimy na takie z których nie ma wy ścia

np. strony zawiera ące zd ęcia. W takim przypadku zakładamy że w następnym kroku wybierzemy losowo
dowolną ze stron w Internecie. eraz nasz proces iteracy ny ma następu ącą postać proces

w

k

i 

∑

 

∈We

i

∑

 

∈

gdzie oznacza zbiór wszystkich stron końcowych czyli takich które nie zawiera ą dowiązań do żadnych innych
stron. esteśmy uż blisko algorytmu a racze ego idei firmy oogle służącego do ustalania ważności stron.

rin i Page obserwu ąc zachowanie użytkowników Internetu zauważyli że czasami porzuca ą oni bieżące

przeszukiwanie i rozpoczyna ą nowe od losowo wybrane strony. Dlatego zmodyfikowali swó proces ite
racy ny wprowadza ąc parametr α o wartości z przedziału

. W każde iterac i z prawdopodobieństwem

α aktualne przeszukiwanie est kont ynuowane natomiast z prawdopodobieństwem – α rozpoczynane

est nowe przeszukiwanie. statecznie postać każde iterac i est następu ąca proces

w

k

i 

α ∑

 

∈We

i

∑

 

∈   

 

        

– α) ∑

.

ardzie doświadczeni czytelnicy pewnie uż spostrzegli że nasz proces iteracy ny est procesem stochastycz

nym zbieżnym do stac onarnego rozkładu prawdopodobieństwa. elem kole nych modyfikac i procesu było
zapewnienie właśnie takie zbieżności. Końcowy rozkład prawdopodobieństwa odpowiada ważności stron.

astanówmy się teraz aki est związek opisanego procesu iteracy nego z mnożeniem macierzy przez wektor.
ieć WWW na potrzeby tego procesu możemy opisać za pomocą macierzy o rozmiarach n n i zdefiniowane

następu ąco

,i

znaczmy przez w

k

..n wektor ważności stron po k te iterac i tzn. w

k

i est ważnością strony

i

po k te

iterac i. godnie z opisaną konwenc ą na początku wszystkie strony są ednakowo ważne. atem dla każde
strony

i

mamy w i n. Przy takie notac i proces możemy zapisać następu ąco

w

k

w

k

est tak dlatego ponieważ i ty wiersz macierzy zawiera odwrotności liczby dowiązań na stronach z których

prowadzą łącza do strony

i

.

w

 

Wy

 

w

k

 

W

y

 

.

w

k

 

W

y

 

w

k

 

n

w

k

 

 

w

k

 

n

n

w

k

 

n

W

i 

eśli istnie e dowiązanie z

i

do

w przeciwnym razie.

> Algorytmika Internetu 

< 

 >

Proces uwzględnia fakt że są strony nie zawiera ące żadnych dowiązań. W macierzy kolumny odpowia
da ące takim stronom zawiera ą same . takich stron do dalszego przeszukiwania wybieramy dowolną stro
nę z prawdopodobieństwem

n. W notac i macierzowe wystarczy zatem zastąpić w macierzy wszystkie

kolumny zawiera ące same przez kolumny w których na każde pozyc i est wartość

n. znaczmy tak

powstałą macierz przez . Wówczas proces ma postać

.

w

k

w

k

.

Proces to zmodyfikowany proces w którym z prawdopodobieństwem α kont ynuu emy przeszukiwanie
sieci z dane strony a z prawdopodobieństwem – α przechodzimy do losowe strony. znacza to nastę
pu ącą modyfikac ę macierzy każdą pozyc ę macierzy mnożymy przez α i doda emy do tego – α n.

ak otrzymaną macierz oznaczmy przez . ak więc iteracy ny proces obliczania rang stron w macierzowe

reprezentac i zapisu e się następu ąco

w

k

w

k

.

o est zwykłe mnożenie macierzy przez wektor. Wiemy uż że macierz reprezentu e sieć składa ącą się

z ponad

miliardów węzłów. iestety chociaż sieć est rzadka zawiera kilkaset miliardów krawędzi

to macierz nie est rzadka – do każdego elementu macierzy dodaliśmy bowiem – α n. zczęśliwie uży
wa ąc przekształceń algebraicznych możemy każdą iterac ę zapisać ako mnożenie rzadkie macierzy przez
wektor plus dwie modyfikac e otrzymanego wektora

. w

k+

w

k

.

. pomnóż każdy element wektora w

k+  

przez α w

k+

αw

k

. oblicz wartość β

k

równą n sumy –α oraz sumy tych elementów wektora w

k

które odpowiada ą stronom nie zawiera ącym dowiązań do innych stron pomnożone przez α

βk – α ∑

i∈k

α w

k

i

. do każdego elementu wektora w

k+

doda β

k

.

est eszcze wiele pytań które pozosta ą bez odpowiedzi. ak szybko powyższy proces zbiega do końcowego

rozkładu ak dobierać parametr α Parametr α dobrany w oogle wynosi .

. acierz z takim parametrem

nosi nazwę macierzy oogle. kazu e się że w tym przypadku wystarczy kilkanaście iterac i aby policzyć
wektor rang. Ale każda iterac a to setki miliardów operac i arytmetycznych i przetwarzanie olbrzymiego grafu.
W aki sposób możemy przyśpieszyć proces obliczeń auważmy że mnożąc macierz przez wektor można nie
zależnie pomnożyć każdy wiersz macierzy przez ten wektor. A gdyby zrobić to równolegle o uż ednak inna
historia.

ainteresowanych dokładną analizą algorytmu Page ank odsyłam do wspaniałe książki autorstwa Amy

. ang ille i arla D. eyera oogle’  Page ank an   eyon : 

e 

ien e of  ear

  ngine  anking

.

Przedstawiliśmy trzy problemy algorytmiczne które zna du ą bezpośrednie zastosowanie w przetwarzaniu
danych w Internecie. Algorytm obliczania silnie spó nych składowych może posłużyć do analizy sieci WWW.

nożenie macierzy przez wektor wykorzystu e się do obliczania rang stron w sieci WWW t ylko na podsta

wie struktury sieci. o zadziwia ące również ider zna du e zastosowanie. Wyobraźmy sobie ruter który
steru e ruchem pakietów w bardzo ruchliwe sieci. Administratorów sieci często interesu e akie pakiety
generu ą na większy ruch a dokładnie pod które adresy est dostarczana na większa liczba komunikatów.

eśli pakietów są miliardy to nie esteśmy w stanie zapamiętać danych o wszystkich z nich a następnie

przet worzyć e. Algorytm przedstawiony w t ym opracowaniu est tak zwanym algorytmem strumieniowym
– na bieżąco przet warzany est strumień danych i nie ma możliwości powrotu do historii. ak się okazało
można w ten sposób wskazać adres który na bardzie obciąża sieć eśli t ylko generu e on ponad połowę

n

<  4 > 

Informatyka + 

ruchu. iewielka modyfikac a przedstawionego algorytmu umożliwia wskazywanie pakietów z których
każdy generu e np. co na mnie edną dziesiątą ruchu.

aki morał pł ynie z naszych rozważań Warto się uczyć algorytmiki. awet wydawałoby się dziwne proble

my po awia ą się w tak gorących zastosowaniach ak przetwarzanie Internetu. iestety nie każdy algorytm
który wyda e się dobry w konwenc onalnych zastosowaniach np. działa w czasie wielomianowym nada e
się do przetwarzania takiego ogromu danych akie niesie ze sobą Internet. awet algorytmy liniowe mogą
wymagać wielodniowych obliczeń. W przetwarzaniu danych w Internecie może pomóc równoległość algoryt
my strumieniowe i statystyczne. Algorytm Page ank pokazu e też że bardzo dobre efekty z punktu widzenia
użytkowników da ą algorytmy które naśladu ą ich naturalne zachowanie. achęcam czytelników do poszu
kiwania naturalnych problemów związanych z Internetem i rozwiązywaniu ich w st ylu algorytmu Page ank.

. anachowski . Diks K. ytter W. Algorytmy i  truktury  any

, W

Warszawa

. roder A. Kumar . aghoul . agha an P. a agopalan . tata . omkins A. Wiener . . ra

 

tru ture in t e We . omputer etworks

. Diks K. iara ważnoś i Delta

. ang ille A. . eyera .D. oogle’  Page ank an   eyon : 

e 

ien e of  ear

  ngine  anking , 

Princeton ni ersity Press

> Algorytmika Internetu 

<  5 >

W pro ekcie

poza wykładami i warsztatami

przewidziano następu ące działania

■

godzinne kursy dla uczniów w ramach modułów tematycznych

■

godzinne kursy metodyczne dla nauczycieli przygotowu ące

do pracy z uczniem zdolnym

■

nagrania

wykładów informatycznych prowadzonych

przez wybitnych spec alistów i nauczycieli akademickich

■

konkursy dla uczniów trzy w ciągu roku

■

udział uczniów w pracach kół naukowych

■

udział uczniów w konferenc ach naukowych

■

obozy wypoczynkowo naukowe.

zczegółowe informac e zna du ą się na stronie pro ektu

<  6 >  otatki 

Informatyka +