Combustion, Explosion, and Shock Waves, Vol. 37, No. 6, pp. 626–633, 2001

Nonequilibrium Thermodynamics of Autowaves

of Laminar Combustion

UDC 536.46

A. P. Gerasev

1

Translated from Fizika Goreniya i Vzryva, Vol. 37, No. 6, pp. 13–21, November–December, 2001.
Original article submitted November 9, 2001.

Within the framework of the Zel’dovich–Frank-Kamenetskii theory of thermal prop-
agation of flame, thermodynamic properties of an open nonlinear system are consid-
ered, and nonequilibrium entropy of a steady combustion wave is constructed. The
nonequilibrium dynamic system is analyzed qualitatively and quantitatively, and the
distribution functions of local entropy production in terms of the spatial variable are
constructed. It is shown that total entropy production in the system is a functional
on integral curves that possess extreme properties, and its minimum corresponds to
a unique physically sustainable solution of the problem. The procedure of “cutting”
(vanishing) of the reaction rate is justified by methods of nonequilibrium thermody-
namics. A variational formulation of the problem is presented for calculation of a
steady combustion wave.

INTRODUCTION

For the first time during many years, attention of

physicists, mathematicians, and chemists is focused on
the same key notion, which is an autowave [1]. Prob-
lems of propagation of nonlinear waves in active kinetic
systems have been studied almost simultaneously in the
combustion theory and biology [2–5]. One of the fun-
damental places in science on autowave processes be-
longs currently to the theory of combustion [1]. The
problems of existence, stability, and destruction of or-
ganized structures in nonequilibrium systems of differ-
ent natures are of interest for versatile fields of science.
The general theory of self-organization in open, strongly
nonequilibrium systems is developed in thermodynam-
ics of irreversible processes [6]. Onsager was the first
to find expressions that reflect irreversibility and for-
mulated a new generic principle, namely, the principle
of the least dissipation of energy [7, 8]. As was shown
in [9], Prigogine’s principle of minimum entropy pro-
duction [6], which was assumed to be a new variational
principle for a long time, is not independent of On-
sager’s principle but is only an alternative formulation.

1

Boreskov Institute of Catalysis, Siberian Division,
Russian Academy of Sciences, Novosibirsk 630090.

The variational problem of phenomenological thermo-
dynamics of irreversible processes and extreme princi-
ples of Onsager, Prigogine, Zigler, Biot, and Dyarmati
are analyzed in [10, 11]. Thermodynamic systems de-
scribed by nonlinear kinetic equations were also consid-
ered (see, e.g., [12]). Moreover, the principle of min-
imum entropy production was extended to autowave
processes in a stationary catalytic bed both for a first-
order reversible reaction [13, 14] and for a reaction with
a nonlinear mechanism [15]. The effectiveness of using
the principle of minimum entropy production for deter-
mining the velocity of a steady combustion wave was
shown to be doubtful in [16], but the present study was
stimulated by the results of [13–15].

The objective of the present work is to study the

properties of an open nonlinear distributed thermody-
namic system, to construct nonequilibrium entropy of
a steady combustion wave, to study the problem of ex-
istence of autowaves and their thermodynamic justifi-
cation, and to compare the results obtained with the
theory developed by Ya. B. Zel’dovich and D. A. Frank-
Kamenetskii.

626

0010-5082/01/3706-0626 $25.00 c

2001

Plenum Publishing Corporation

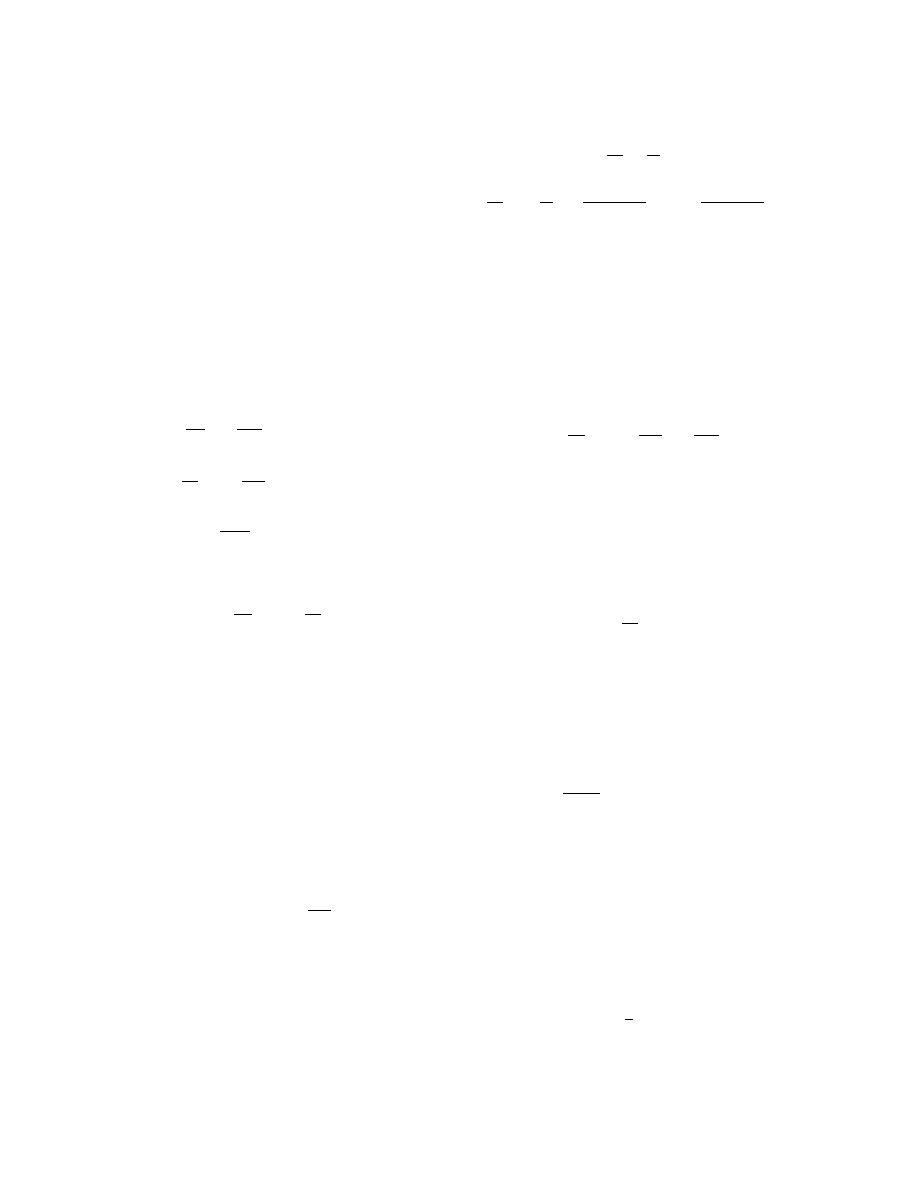
Nonequilibrium Thermodynamics of Autowaves of Laminar Combustion

627

ENTROPY-BALANCE EQUATION
IN A STEADY COMBUSTION WAVE

Steady propagation of a combustion wave is an

asymptotic characteristic of the dynamic process, which
makes sense only for open systems of infinite length at
rather large times. The mathematical model of thermal
propagation of laminar flame in the simplest formula-
tion takes into account the processes of heat and mass
transfer described by the Fourier and Fick linear laws,
chemical transformation of substances described by the
Arrhenius nonlinear law, and convective gas flow. The
model is constructed under the assumption that the re-
action mixture obeys the law of ideal gases, and the
gas pressure is constant. In the case of one irreversible
chemical reaction of the type A

→ B in a coordinate sys-

tem propagating with the combustion-wave velocity, the
mathematical model has the following form [4, 5, 17]:

mc

p

dT

dx

= λ

d

2

T

dx

2

+ Qv(a, T ),

(1)

m

da

dx

= ρD

d

2

a

dx

2

− v(a, T ),

(2)

p =

ρRT

M

= const,

(3)

x

→ −∞: T → T

0

,

a

→ 1,

(4)

x

→ +∞: λ

dT

dx

= 0,

da

dx

= 0.

Here a = ρ

A

/ρ is the mass fraction of the component A,

ρ

0

and ρ are the initial and current densities of the

mixture, ρ

A

is the density of the component A, D is the

diffusion coefficient, x

0

= x + u

n

t + const is the spatial

variable (hereinafter, the prime is omitted in formulas),
u

n

is the normal burning rate, t is the time, m = ρu =

ρ

0

u

n

is the mass velocity of the combustion wave, c

p

is

the heat capacity of the mixture, M is the molar weight
of the mixture, Q is the thermal effect of the reaction per
unit mass, v is the reaction rate, R is the universal gas
constant, p is the pressure, T

0

and T are the initial and

current temperatures, and λ is the thermal conductivity.

The rate of the first-order chemical reaction in mass

units is

v(a, T ) = k

0

ρ

A

exp

−

E

RT

,

(5)

where E is the activation energy and k

0

is the preexpo-

nent.

The mass velocity of flame propagation m is the

eigenvalue of the boundary problem (1)–(4).

If the

temperature and concentration distributions are similar
(which occurs for the Lewis number Le = ρc

p

D/λ = 1),

the problem reduces to a system of two first-order non-
linear ordinary differential equations [17], which are re-
duced to the form

dθ

dx

=

c

p

λ

y,

(6)

dy

dx

= m

c

p

λ

y

−

k

1

(1

− θ)

T

0

+ θT

ad

exp

−

β

T

0

+ θT

ad

,

(7)

x

→ −∞: θ → 0,

y

→ 0,

(8)

x

→ +∞: θ → 1,

y

→ 0,

where θ = (T

− T

0

)/T

ad

is the dimensionless tempera-

ture equal to the fractional conversion of the key com-
ponent (θ = 1

−a), T

ad

= Q/c

p

is the adiabatic temper-

ature, β = E/R, y = (λ/Q)(dT /dx), and k

1

= k

0

ρ

0

T

0

.

Multiplying (2) by Q and adding it to (1), we ob-

tain an equation that does not include the chemical re-
action rate explicitly:

m

dh

dx

− QρD

d

2

a

dx

2

= λ

d

2

T

dx

2

.

(9)

Here h = (ρ

A

h

A

+ ρ

B

h

B

)/ρ is the total specific en-

thalpy of the gas, h

A

(T ) = h

0
A

+ c

p

(T

− T

0

) and

h

B

(T ) = h

0
B

+ c

p

(T

− T

0

) are the partial enthalpies of

the components A and B per unit mass. For Le = 1,
the heat flux is exactly compensated by the flux of the
“chemical” part of the total enthalpy transferred by
the diffusion flux of reagents (λdT /dx =

−QρD da/dx).

Therefore, Eq. (9) takes the simple form

m

dh

dx

= 0.

(10)

It follows from Eq. (10) that the total specific enthalpy
of the mixture remains constant for all values of x.

Thermodynamics of nonequilibrium dynamic sys-

tems is based on two generic postulates: the principle
of local equilibrium and the second law of thermody-
namics according to which irreversible processes always
lead to an increase in entropy [6, 9, 18]:

∂ (ρs)

∂ t

=

− div J

S,Σ

+ σ.

(11)

Here s is the entropy per unit mass, J

S,Σ

= ρus + J

S

is

the total flux of entropy (with regard for the convective
component) per unit surface in unit time, and σ is the
local entropy production (per unit volume in unit time).

It should be noted that the notion of local equilib-

rium should be referred not to a continuum point but to
a certain elementary cell for which the Gibbs equation
is valid [6, 9, 18], which unites the first and second laws
of thermodynamics for specific (in terms of mass) local
quantities:

T ds = dh

−

1

ρ

dp

−

n

X

k=1

µ

k

da

k

.

(12)

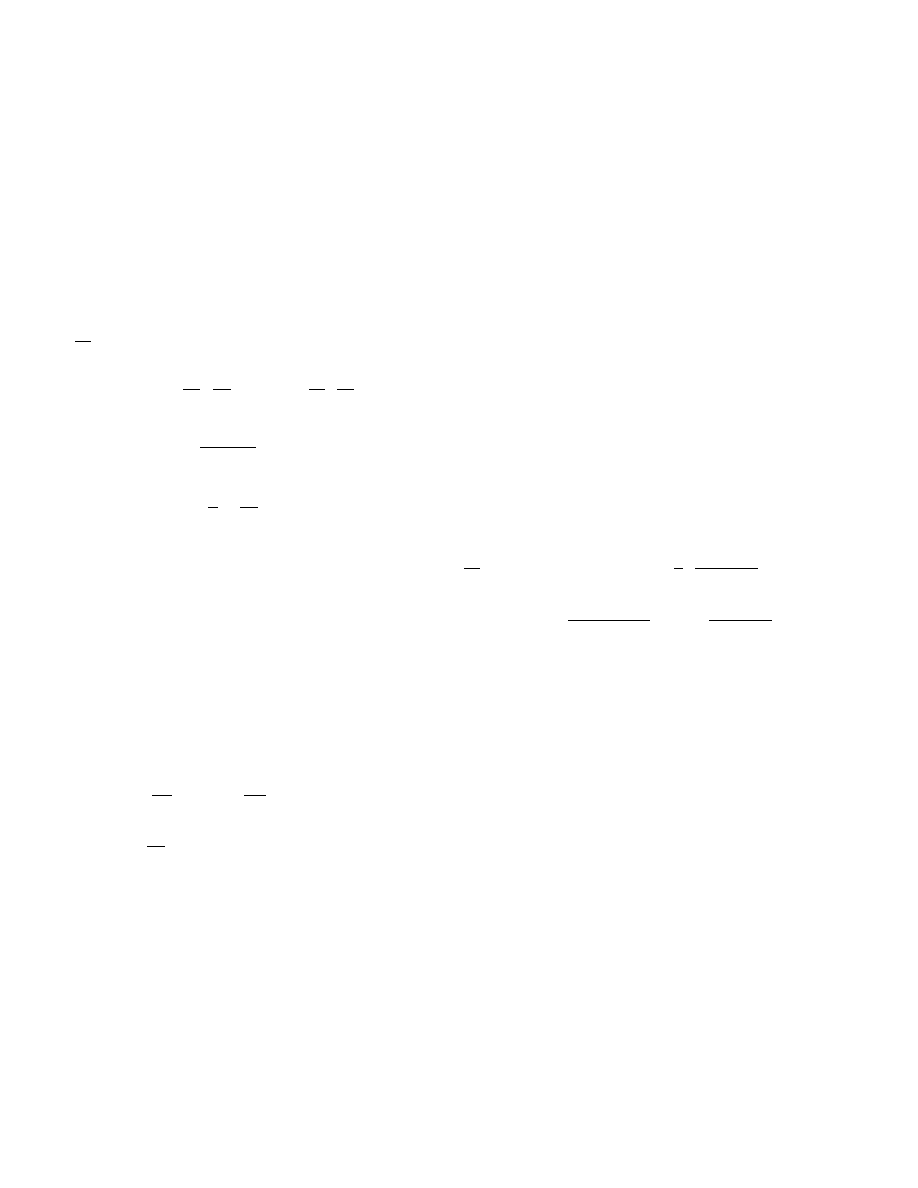
628

Gerasev

Here µ

k

= µ

0
k

(p, T ) + RT /M

k

ln a

k

, a

k

, and M

k

are the

chemical potential, mass fraction, and molar weight of
the kth component.

Production of entropy can be always represented

as a sum of products of the corresponding number of
fluxes and conjugate forces (σ =

P

i

J

i

X

i

> 0) or, in the

case of linear constitutive equations, in a quadratic form
σ =

P

i,k

L

ik

X

i

X

k

> 0.

Using Eqs. (11) and (12) and thermodynamic re-

lations [6, 9, 18], we can pass from the balance of en-
thalpy (9) to the balance of entropy and identify terms
corresponding to local entropy production:

d

dx

(ms + J

S

)

= σ =

λ

T

2

dT

dx

2

+

X

k

J

k

d

dx

µ

k

T

+

Av(a, T )

T

= σ

q

+ σ

d

+ σ

ch

> 0. (13)

Here

J

S

=

−

1

T

λ

dT

dx

+

X

k

µ

k

J

k

is the flux of entropy, J

k

is the diffusion flux of the sub-

stance of the kth component, A is the chemical affinity
of the reaction per unit mass, and σ

q

, σ

d

, and σ

ch

are

the local entropy productions due to thermal conduc-
tion, diffusion, and chemical reaction, respectively. The
terms that take into account cross effects (thermodiffu-
sion and diffusive thermal conduction) are omitted in
Eq. (13), since these terms are insignificant and are ig-
nored in the combustion theory [17].

In thermodynamics, chemical reactions are as-

sumed to be necessarily reversible, and the chemical
affinity of the reaction per mole of the reagent for c

p

=

const is determined by the expression [19]

A

mole

=

−

∂G

∂ξ

T ,p

=

−

∂H

∂ξ

T ,p

+ T

∂S

∂ξ

T ,p

=

−∆H

0

T

+ T ∆S

0

T

− RT ln

Y

k

p

ν

k

k

,

where ξ is the coordinate of the reaction, ∆H

0

T

and ∆S

0

T

are the enthalpy and entropy of the reaction at standard
pressure, and ν

k

are stoichiometric coefficients.

The

thermal effect of combustion reactions is usually rather
large (

−∆H

0

T

T |∆S

0

T

|); therefore, it yields a good

approximation of chemical affinity in a wide range of
compositions of the mixture in the course of the reac-
tion for entropies of mixing of reagents close to zero
[s

mix,k

=

−R ln(p

k

/p)] [19]. For the same reason, the

equilibrium concentration of the initial deficient reagent
takes a very small value, which is still different from
zero. However, the kinetic equation of the reaction (5)
has no reversibility term, and in the traditional formula-
tion of problem (1)–(4), the mass (molar) fraction of the
reagent varies from unity to zero. Taking into account
this formulation of the problem and also the possibility
of idealization in the method of mathematical simula-
tion, we assume that chemical affinity of the reaction for
all admissible concentrations of the reagents is equal to
the thermal effect of the reaction:

A =

−∆H

0

T

/M = Q.

(14)

Since the composition of the mixture changes not only
in the course of the reaction but also as a result of diffu-
sion of the reagents, we have to eliminate entropy pro-
duction due to diffusion from subsequent consideration
owing to the above assumption. Such strong idealiza-
tion is a consequence of the traditional description of
the reaction rate by Eq. (5), which is not in agreement
with thermodynamics. Transition to consideration of a
reversible reaction does not involve the above assump-
tions, but this is outside the scope of the present work
and is the subject of future studies. With allowance for
(5), (14), and the assumption accepted above, Eq. (13)
in dimensionless variables takes the form

d

dx

(ms + J

S

) = σ = σ

q

+ σ

ch

=

1

λ

Qy

T

0

+ θT

ad

2

+

Q(1

− θ)k

1

(T

0

+ θT

ad

)

2

exp

−

β

T

0

+ θT

ad

. (15)

Note that Eqs. (1) and (9) correspond to the energy

approach and Eq. (15) to the entropy approach. At the
same time, the right part of Eq. (15), the source of
entropy, contains qualitatively new information.

PRINCIPLE OF MINIMUM
ENTROPY PRODUCTION
IN A STEADY COMBUSTION WAVE

For low temperatures, the Arrhenius law yields a

finite rate of chemical transformation; therefore, the
notion of a steady combustion wave is approximate
[17, 20–22]. To find the unique solution of problem (6)–
(8), we use an artificial method of “cutting” (vanishing)
of the chemical reaction rate at low temperatures. This
procedure is considered to be physically correct only
if the results are independent of an arbitrarily chosen
value of the “cutting” temperature in a wide range of
initial temperatures [17, 20–22]. It should be noted that
the “cutting” procedure of the source is introduced as
an axiom that does not rest on any physical law, and

Nonequilibrium Thermodynamics of Autowaves of Laminar Combustion

629

the belonging of the process of flame propagation to
autowave processes is always related to the notion of
“intermediate asymptotics.”

From the theory of dynamic system on the plane

[23, 24], it is known that the autowave structure corre-
sponds to a mathematical image, which is a separatrix
trajectory connecting singular (stationary) points of the
system of equations. Therefore, the problem of exis-
tence of a steady combustion wave reduces to investiga-
tion of singular points of the dynamic system (6), (7).

Case A: T

0

= 0.

An important feature of the

method of mathematical simulation is the construction
and analysis of idealized models with different degrees
of detalization of the processes and phenomena under
study. Since no restrictions are imposed on the values
of parameters in the mathematical model, the temper-
ature range may be extended to 0 K from the mathe-
matical viewpoint. The use of methods and techniques
of the qualitative study of dynamic systems [23, 24]
shows that system (6), (7) has two singular points.
One of them, which is determined by the conditions
at r

→ +∞, is a saddle point; this is a point of inter-

section of zero isoclines of system (6), (7) [y = 0 and
y = k

1

λ(1

− θ)/(mc

p

(T

0

+ θT

ad

)) exp(

−β/(T

0

+ θT

ad

)),

respectively]. The saddle point corresponds to condi-
tions of completion of the irreversible reaction, which
are determined by system parameters. The second sin-
gular point is independent of system parameters; it is
located at 0 K, where the chemical reaction rate rigor-
ously vanishes. This is an unstable node with degenera-
tion; the matrix of the linearized system of equations in
the vicinity of this singular point has zero and positive
eigenvalues (characteristic values). Hence, system (6),
(7) may have a one-parameter family of solutions with
the parameter m.

It is of interest to note that Kolmogorov et al. [3],

who studied possible autowave regimes in problems of
the class considered, proved that it is possible to con-
struct an infinite number of solutions, but only the front
moving with the minimum wave velocity is asymptoti-
cally stable.

The case T

0

= 0 is of interest only from the math-

ematical point of view. Therefore, we consider a physi-
cally realistic case T

0

6= 0; moreover, we will come back

to the behavior of separatrix trajectories.

Case B: T

0

6= 0. If T

0

6= 0, then the point for

x

→ −∞ is not stationary. Nevertheless, for an ar-

bitrarily chosen value of m, it is possible to construct
numerically a separatrix trajectory entering the equi-
librium point (1,0) by integrating system (6), (7) in
the direction opposite to the vector-field direction (in
the “reverse” time). The resultant separatrix trajec-
tory connects the saddle-type singular point (1,0) with

Fig. 1. Trajectories of system (6), (7) on the phase
plane for T

0

= 300 K and mass burning rate m =

1.0 (1), 1.4621184 (2), and 2.0 kg/(m

2

· sec) (3);

curves 1

0

, 2

0

, and 3

0

are zero isoclines of Eq. (7) for

the corresponding values of m.

the unstable node located at 0 K, since the boundary
condition for x

→ −∞ is not used in integration in

the “reverse” time, and no restriction is imposed on the
initial temperature T

0

. The problem of using bound-

ary conditions for x

→ −∞ has to be clarified. Sys-

tem parameters specified formally for x

→ +∞ acquire

physical meaning only for fixed input parameters for
x

→ −∞.

Figures 1 and 2 show the separatrix trajectories of

the system in the phase plane (θ, y); the correspond-
ing profiles of θ versus x for an input temperature
T

0

= 300 K are plotted in Fig. 3. Numerical integration

of system (6), (7) was performed with a doubled accu-
racy by the fourth-order explicit Runge–Kutta–Merson
method with an automatically chosen step.

The al-

lowable error varied within 10

−8

–10

−16

. The charac-

teristic values of parameters were borrowed from [16]:
c

p

= 1 kJ/(kg

· K), E = 100 kJ/mole, Q = 10

3

kJ/kg,

k

0

= 5

· 10

10

sec

−1

, R = 8.314 J/(mole

· K), p = 10

5

Pa,

λ = 0.05 W/(m

· K), and M = 0.0249 kg/mole.

The numerical experiment shows that all separatrix

trajectories located in the upper half-plane of the phase
space reach the straight line corresponding to 0 K. For
small values of the parameter m, the trajectories reach
0 K for y > 0 (curve 1 in Fig. 1) and approach the
zero isocline of Eq. (7) at low temperatures as m in-
creases. Each separatrix trajectory corresponds to its
own zero isocline, which is an asymptotic curve at low
temperatures (see Fig. 2). The trajectories lie along the
corresponding zero isoclines but cannot intersect them
at low temperatures, as it follows from the vector-field

630

Gerasev

Fig. 2. Trajectories of system (6), (7) on the phase
plane near the point (0, 0) for T

0

= 300 K and mass

burning rate m = 1.46211 (1), 1.4621184 (2), and
1.46213 kg/(m

2

· sec) (3); curve 4 shows the zero iso-

clines of Eq. (7).

analysis. The greater m, the higher the temperature at
which the separatrix trajectory is located near the zero
isocline (see Fig. 1). A typical feature of all trajectories
is the “slow” motion of the image point in the vicinity of
the zero isocline at low temperatures. At high temper-
atures, the separatrices intersect zero isoclines with the
maximum value of the gradient, which rigorously follows
from the analysis of system (6), (7). With increasing m,
the maximum value of the gradient decreases. Note, for
the above-given characteristic values of parameters and
temperatures θ < 0.3, the zero isoclines of Eq. (7) are
located in the vicinity of the abscissa axis.

In the theory of dynamic systems [23, 24], part of

the total trajectory including one of the singular points
is called a half-trajectory. For half-trajectories in the
interval 0

≤ θ < 1 (x

0

≤ x < +∞), we calculated the

integral material balance

m =

+

∞

Z

x

0

v[θ(x)] dx,

(16)

where x

0

is determined by the condition θ = 0. The

analysis of the results obtained shows that the material
balance (16) is fulfilled with a high accuracy for half-
trajectories that approached the zero isoclines for θ

≥ 0

(curves 2 and 3 in Figs. 1 and 2). If the trajectory inter-
sects the straight line θ = 0 far from the zero isocline,
the material balance (16) on the half-trajectory is not
fulfilled. The amount of the substance burning out in
the reaction zone is greater than that added, which has
no physical sense.

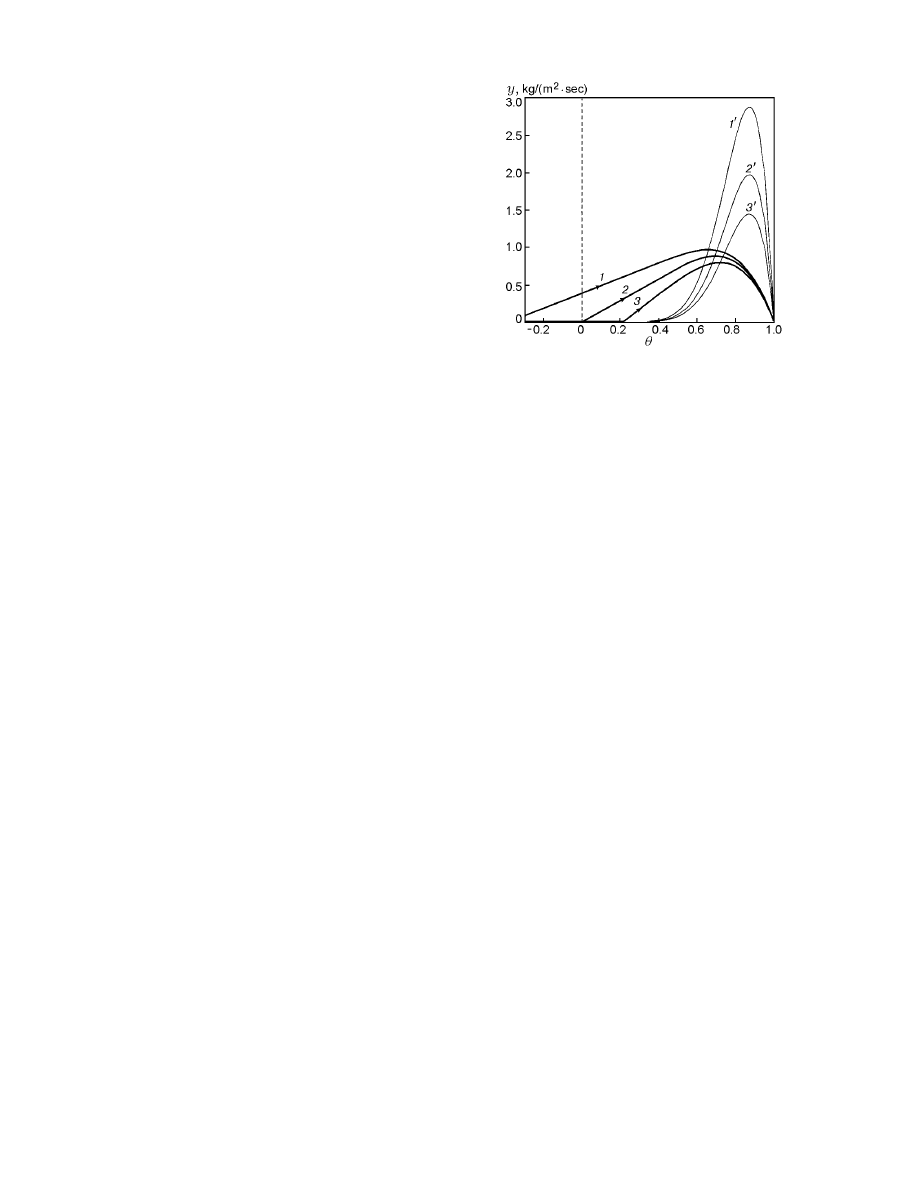
Fig. 3. Profiles of the dimensionless temperature
(fractional conversion) and distribution functions σ
(bold solid curves), σ

q

(thin solid curves), and σ

ch

(dotted curves) versus the spatial variable (curve
numbers correspond to the numbers of trajectories
shown in Fig. 1).

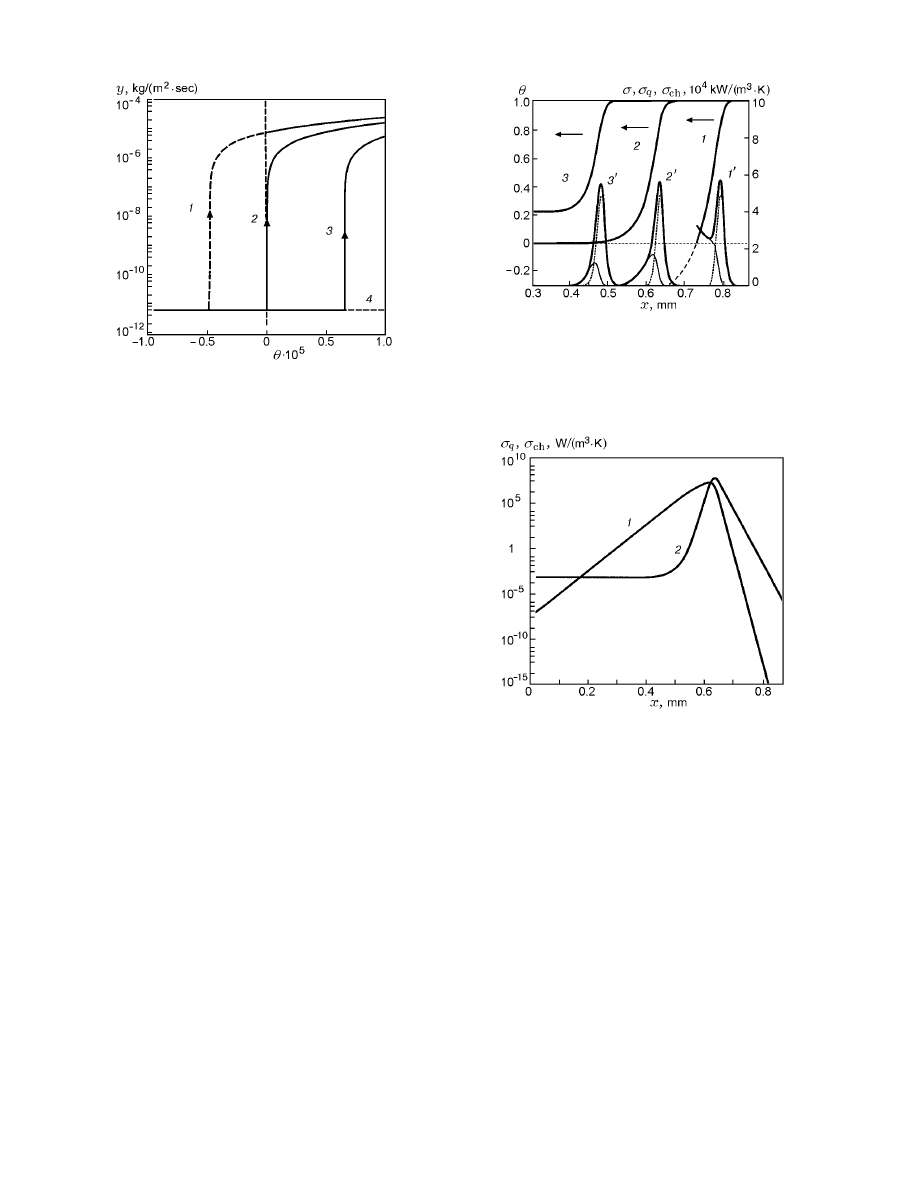
Fig. 4. Distribution functions σ

q

(curve 1) and

σ

ch

(2) versus the spatial variable for m

1

=

1.4621184 kg/(m

2

· sec).

The total production of entropy in the system is

the integral P =

Z

V

σ dV . For a one-dimensional prob-

lem, P is the integral of (15) in terms of the spatial
variable x:

P =

+

∞

Z

−∞

σ[θ(x), y(x)] dx.

(17)

For all half-trajectories in the interval x

0

≤ x <

+

∞, using Eqs. (15) and (17), we calculated the val-

ues of σ, σ

q

, σ

ch

, and P . If the half-trajectories reach

the vicinity of the zero isocline at θ

≥ 0, the distri-

Nonequilibrium Thermodynamics of Autowaves of Laminar Combustion

631

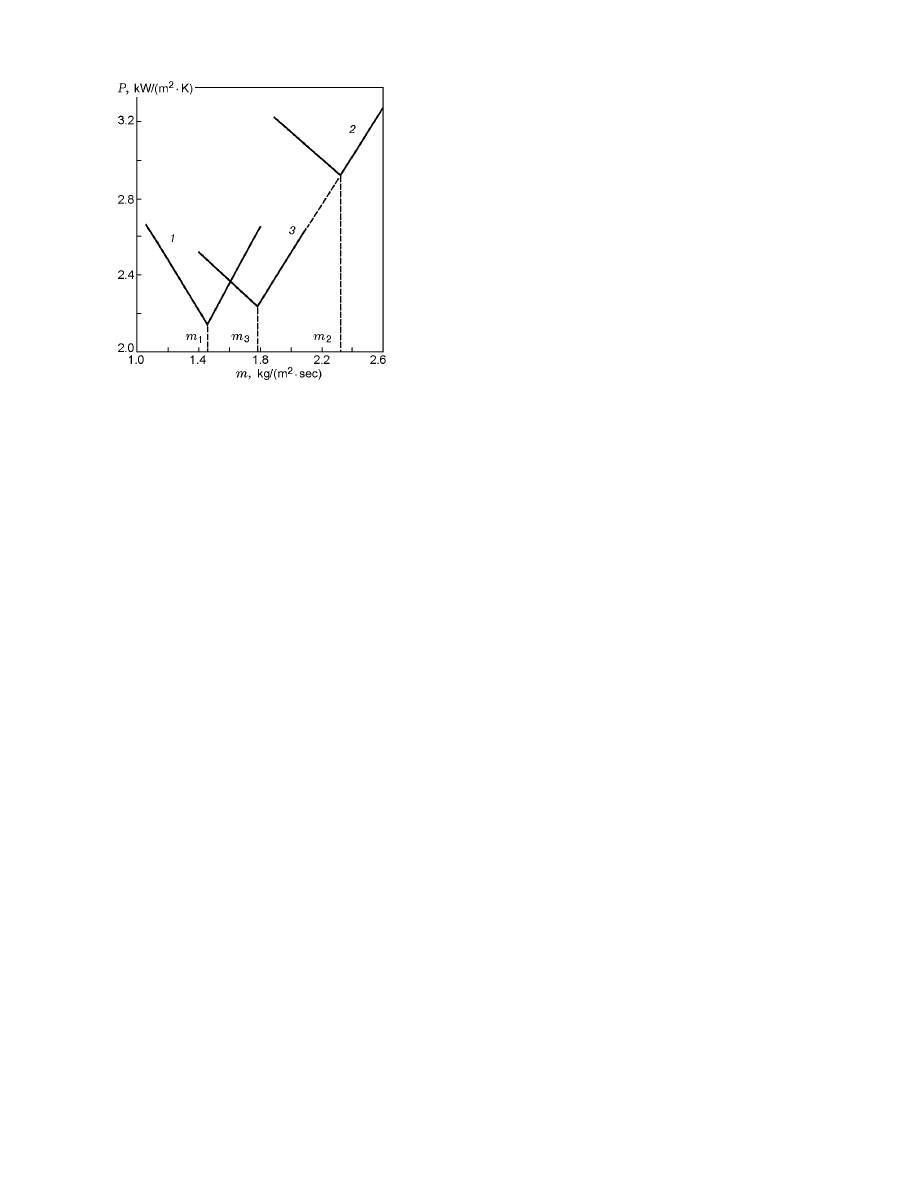
Fig. 5. Total entropy production in the system as a func-
tion of the mass burning rate for E = 100 kJ/mole
and T

0

= 300 K (curve 1), E = 100 kJ/mole and

T

0

= 400 K (curve 2), and E = 105 kJ/mole and T

0

=

400 K (curve 3): m

1

= 1.4621184 kg/(m

2

· sec), m

2

=

2.3172451 kg/(m

2

· sec), and m

3

= 1.77805 kg/(m

2

· sec).

bution functions of σ and its components σ

q

and σ

ch

along x have explicit maxima (Figs. 3 and 4). An anal-
ysis of Eq. (15) with regard for Eq. (8) shows that σ

q

and σ

ch

are equal to zero at singular points of sys-

tem (6), (7). With increasing m, the maximum value
of σ

max

decreases, but the zone of reaching the ini-

tial temperatures θ = 0 becomes significantly extended
thereby. Note, a finite-length zone is revealed, where
the necessary amount of the substance “burns out” at
low velocities of chemical transformation (curve 3 in
Figs. 1–3). The calculation of the total entropy produc-
tion in the system shows (Fig. 5) that P is a functional
on half-trajectories of the system, which possesses ex-
treme properties. In the numerical search of the min-
imum of P (m), the combustion-wave velocity was var-
ied with a high accuracy.

Thus, for the combustion

wave represented by curve 2 in Figs. 1–3, we confined
ourselves by the value m

1

= 1.4621184 kg/(m

2

· sec).

The functional reaches the minimum value for the only
half-trajectory that can be found by an artificial proce-
dure of “cutting” the reaction rate at low temperatures
[17, 20–22]. Without this procedure, the image point
cannot reach the point (0, 0), which is demonstrated in
Fig. 2. Zero isoclines cut off all trajectories from the
abscissa axis. The reaction rate vanishing, the zero iso-
clines merge with the abscissa axis, and all points lying
on this axis lower than the “cutting” temperature are
“stationary” points. The trajectories enter these points
along the straight line dy/dθ = m.

An analysis of the reasons for the extreme behav-

ior of the functional P shows that the temperature and
concentration gradients increase with decreasing m (see
Fig. 1); therefore, the values of both σ

max

and P in-

crease. If the trajectory approaches the zero isocline,
the temperature gradient and, hence, the value of σ

q

tend to zero, and the contribution of σ

ch

to the local

entropy production becomes determining (see Fig. 4).
With increasing m, beginning from a certain value, the
length of the part of the trajectory located near the
zero isocline for θ

≥ 0 increases. For this reason, P in-

creases as an integral quantity. The dependences P (m)
of different character lead to extreme properties of the
functional, which allows one to find a physically con-
sistent solution of the problem — a steady combustion
wave. The linear dependences of the functional P (m)
obtained by numerical integration stimulated the search
for the proof of an auxiliary theorem.

The following lemma is valid.
Lemma 1.

The total entropy production in a

nonequilibrium system is determined by the product of
the mass burning rate and the difference in specific en-
tropies of the reaction mixture under input and output
conditions.

Proof. Substituting (15) into (17), we find

P =

+

∞

Z

−∞

d(ms + J

S

) = ms

|

+

∞

−∞

+ J

S

|

+

∞

−∞

.

(18)

It follows from the boundary conditions (8) that the
flux of entropy J

S

caused by thermal conduction and

diffusion of the reagents equals zero for x

→ ±∞. Since

the specific entropy of the mixture is a function of the
parameters of state s(T, p, ξ) only, from (18) we obtain

P = m[s(T

b

, p, 1)

− s(T

0

, p, 0)] = m∆s,

(19)

where T

b

= T

0

+ T

ad

is the temperature behind the

combustion front.

Corollary 1. System parameters responsible for

the state of the reaction mixture under boundary condi-
tions being fixed, the increment of specific entropy re-
mains unchanged. Variation of the remaining param-
eters of the system leads to different solutions of the
problem, for which the linear dependence P (m) is the
same by virtue of (19), i.e., these solutions lie on one
straight line.

One set of the parameters of state in Fig. 5 cor-

responds to dependences 2 and 3.

It is seen from

the figure that the right branches of dependences 2
and 3 are rather accurately described by the equation
P = mc

p

ln(T

b

/T

0

) = 1.253m [kW/(m

2

· K)]. Note, for

T

0

6= 0, the point (0,0) of system (6), (7) is not sta-

tionary, and numerical integration is performed in the
interval x

0

≤ x < +∞. An increase in temperature of

632

Gerasev

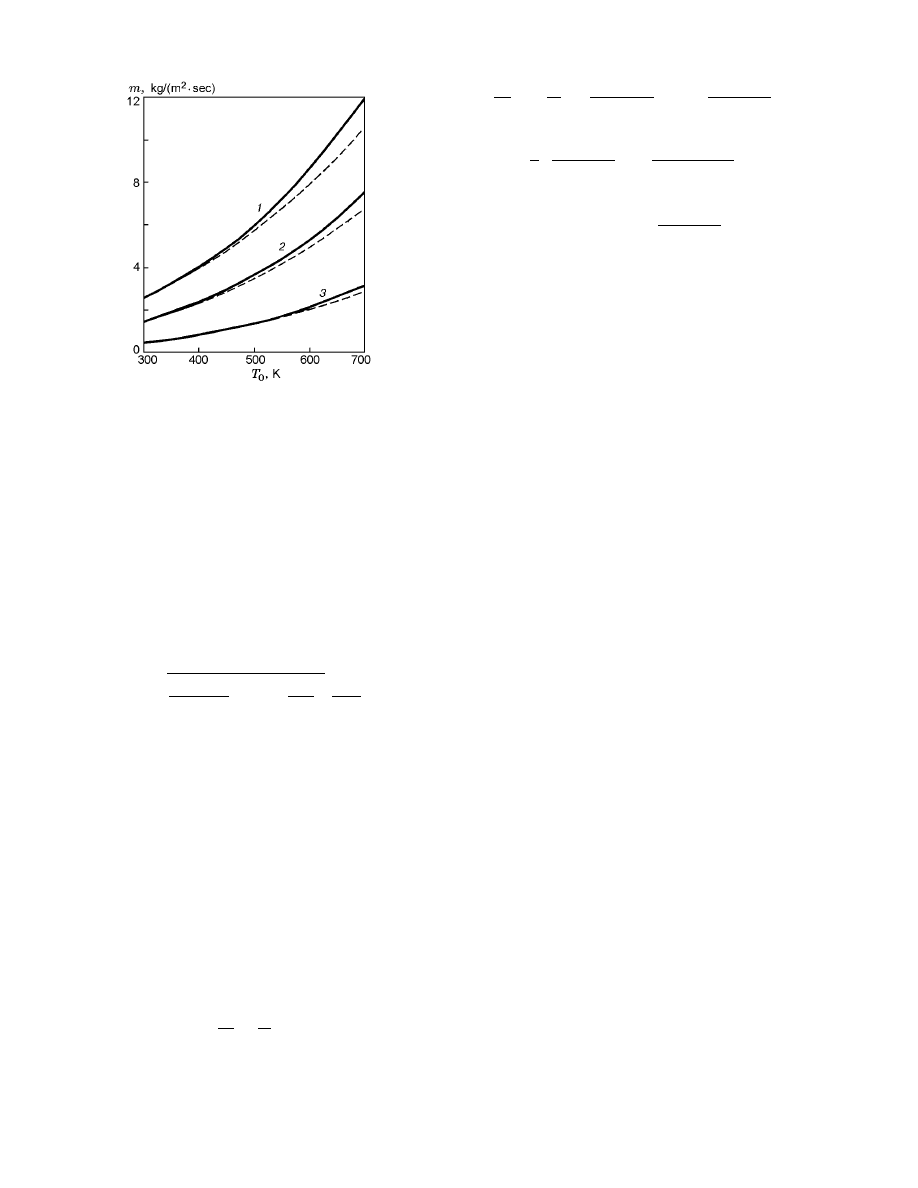
Fig. 6. Mass burning rate versus the temperature of
the initial reaction mixture for reaction activation en-
ergies of 90 (curve 1), 100 (curve 2), and 120 kJ/mole
(curve 3): the solid and dashed curves refer to the
calculations by model (6)–(8) and estimate (20), re-
spectively.

the initial reaction mixture leads to an increase in the
combustion-wave velocity and total entropy production
in the system, whereas an increase in activation energy
leads to a decrease in these parameters (see Fig. 5).

Approximate formulas for the combustion-wave ve-

locity are known for simple kinetic equations of chemical
reactions. Thus, for the first-order reaction [5, 17], we
have

m =

s

2λk

0

ρ

0

T

0

c

p

T

2

ad

T

b

exp

−

E

RT

b

RT

2

b

E

.

(20)

Therefore, it is of interest to compare the results for m
calculated by model (6)–(8) and estimate (20). As is
seen from Fig. 6, the accuracy of the estimate is high
for low input temperatures and different values of the
reaction activation energy and decreases with increas-
ing input temperature and activation energy. It should
also be noted that the exact values of the mass burning
rate calculated in [16] are in agreement with the results
plotted in Fig. 6. The reasons for the disagreement of
the results of thermodynamic calculations of [16] and
the data presented above are obvious, and their analy-
sis presents no difficulties for an interested reader.

Thus, the extreme properties of the functional al-

low us to give a variational formulation of the problem
for calculation of a steady combustion wave:

dθ

dx

=

c

p

λ

y,

dy

dx

= m

c

p

λ

y

−

k

1

(1

− θ)

T

0

+ θT

ad

exp

−

β

T

0

+ θT

ad

,

P =

+

∞

Z

x

0

1

λ

Qy

T

0

+ θT

ad

2

+

Q(1

− θ)k

1

(T

0

+ θT

ad

)

2

× exp

−

β

T

0

+ θT

ad

dx

→ min,

x = x

0

:

θ = 0,

x

→ +∞: θ → 1,

y

→ 0.

The unique solution of this system is found without us-
ing the procedure of “cutting” the reaction rate, which
is preferable from the computational point of view.

CONCLUSIONS

Within the framework of postulates of the com-

bustion theory, a thermodynamic description of a dis-
tributed open system is considered and nonequilibrium
entropy is constructed. The process of flame propaga-
tion is described by an unsteady mathematical model,
but the transition to self-similar variables allows one
to reduce the problem to a steady system (system of
two nonlinear ordinary differential equations). An aux-
iliary theorem is proved, and it is confirmed by numer-
ical methods that the total entropy production in an
open distributed nonequilibrium system is a functional
on integral curves of the mathematical model. Among
the one-parameter family of integral curves, the mini-
mum of the functional corresponds to the unique phys-
ically consistent solution of the problem — a steady
combustion wave (spatial–temporal dissipative struc-
ture). Generally speaking, the total entropy produc-
tion in the system (increment of entropy) may be used
as the Lyapunov function possessing potential proper-
ties [11]. Note, however, that the transitional processes
of wave capturing are not considered, and we may speak
only of stability of autowaves to perturbations of the
mass burning rate. Among the limited range of solu-
tions that do not contradict the laws of conservation of
mass and energy, the stable solution had the minimum
wave velocity.

This conclusion is in good agreement

with the Kolmogorov–Petrovskii–Piskunov theory [3],
where similar problems were studied. It is shown that
only the integral form of the variational principle is ful-
filled (P = min), whereas its local form (σ = min) is
not satisfied.

Hence, the process of steady propaga-

tion of the combustion wave is accompanied by exact
compensation of thermodynamic fluxes inside the sys-
tem on a limited interval, i.e., it is structurally stable.
This may be considered as thermodynamic justification

Nonequilibrium Thermodynamics of Autowaves of Laminar Combustion

633

of the “cutting” procedure of the reaction rate. The
Arrhenius (nonlinear) law of the chemical reaction rate
does not impose restrictions on the principle of the min-
imum total entropy production in a wide range of tem-
peratures. It is worth emphasizing that the extreme
principles of nonequilibrium thermodynamics are prin-
cipally equivalent [11]; at the same time, the form of
representation of the variational principle is very im-
portant in solving particular problems.

Thus, a steady combustion autowave arises as a re-

sult of the loss of stability of a uniform state and is a
consequence of fulfillment of the second law of thermo-
dynamics in a nonequilibrium formulation.

This work was supported by the Russian Foun-

dation for Fundamental Research (Grant No. 00–03–
32465).

REFERENCES

1. V. A. Vasil’ev, Yu. M. Romanovskii, and V. G. Yakhno,

Autowave Processes [in Russian],

Nauka,

Moscow

(1987).

2. R. A. Fisher, “The wave of advance of advantageous

genes,” Ann. Eugenics, 7, 335–369 (1937).

3. A. N. Kolmogorov, I. G. Petrovskii, and N. S. Piskunov,

“Investigation of the diffusion equation combined with

an increase in the amount of the substance, and the use

of this equation in one biological problem,” Byul. Mosk.

Gos. Univ., 1, Ser. A, No. 6, 1–26 (1937).

4. Ya. B. Zel’dovich and D. A. Frank-Kamenetskii, “The-

ory of uniform propagation of flame,” Dokl. Akad. Nauk

SSSR, 19, No. 9, 693–697 (1938).

5. Ya. B. Zel’dovich and D. A. Frank-Kamenetskii, “The-

ory of thermal propagation of flame,” Zh. Fiz. Khim.,

12, No. 1, 100–105 (1938).

6. P. Glansdorff and I. Prigogine, Thermodynamic Theory

of Structure, Stability, and Fluctuations, Wiley Inter-

sciences, New York (1971).

7. L. Onsager, “Reciprocal relations in irreversible pro-

cesses. I,” Phys. Rev., 37, 405–426 (1931).

8. L. Onsager, “Reciprocal relations in irreversible pro-

cesses. II,” Phys. Rev., 38, 2265–2279 (1931).

9. I. Dyarmati, Non-Equilibrium Thermodynamics. Field

Theory and Variational Principles, Springer-Verlag,

Berlin–Heidelberg–New York (1970).

10. I. P. Vyrodov, “Variational principles of phenomeno-

logical thermodynamics of irreversible processes in the

aspect of a closed system of axioms,” Zh. Fiz. Khim.,

56, No. 6, 1329–1342 (1982).

11. I. P. Vyrodov, “Extreme properties of nonequilibrium

thermodynamic systems and their dissipative function-

als,” Zh. Fiz. Khim., 62, No. 4, 865–882 (1988).

12. I. P. Vyrodov, “Generalization of the Onsager theorem

and construction of nonequilibrium entropy in nonlinear

phenomenological thermodynamics of irreversible pro-

cesses,” Zh. Fiz. Khim., 72, No. 2, 225–228 (1998).

13. A. P. Gerasev, “Nonequilibrium thermodynamics of

propagation of heat waves in a catalytic bed,” Dokl.

Ross. Acad. Nauk, 359, No. 4, 495–498 (1998).

14. A. P. Gerasev, “Nonequilibrium thermodynamics of

heat waves in a catalytic bed. Functional of an au-

towave solution,” Fiz. Goreniya Vzryva, 36, No. 3, 51–

59 (2000).

15. A. P. Gerasev, “Propagation of heat waves in a catalytic

bed upon oxidation of sulphur dioxide,” Zh. Fiz. Khim.,

74, No. 7, 1174–1180 (2000).

16. A. I. Karpov, “Minimal entropy production as an ap-

proach to the prediction of the stationary rate of flame

propagation,” J. Non-Equilib. Thermodyn., 17, No. 1,

1–9 (1992).

17. Ya. B. Zel’dovich, G. I. Barenblatt, V. B. Librovich,

and G. M. Makhviladze, The Mathematical Theory of

Combustion and Explosions, Plenum, New York (1985).

18. S. R. de Groot and P. Mazur, Non-Equilibrium Ther-

modynamics, North-Holland, Amsterdam (1962).

19. I. Prigogine and R. Defei, Chemical Thermodynamics,

Longmans–Green, London–New York–Toronto (1954).

20. A. P. Aldushin, V. D. Lugovoi, A. G. Merzhanov, and

B. I. Khaikin, “Degeneration conditions for a steady

combustion wave,” Dokl. Akad. Nauk SSSR, 243, No. 6,

1434–1437 (1978).

21. A. G. Merzhanov and B. I. Khaikin, Theory of Com-

bustion Waves in Homogeneous Media [in Russian],

Inst. of Struct. Macrokinetics, Russian Acad. of Sci.,

Chernogolovka (1992).

22. A. P. Aldushin, Ya. B. Zel’dovich, and S. I. Khudyaev,

“Numerical investigation of flame propagation in a mix-

ture reacting at the initial temperature,” Fiz. Goreniya

Vzryva, 15, No. 6, 20–27 (1979).

23. A. A. Andronov, E. A. Leontovich, I. I. Gordon, and

A. G. Maier, Qualitative Theory of Second-Order Dy-

namic Systems [in Russian], Nauka, Moscow (1966).

24. N. N. Bautin and E. A. Leontovich, Methods and Proce-

dures of Qualitative Investigation of Dynamic Systems

on a Plane [in Russian], Nauka, Moscow (1976).