BANK I KREDYT czerwiec 2004

46

Rynki i Instytucje Finansowe

Wprowadzenie

Wiele Êwiatowych banków tworzy strategie zabezpie-
czajàce stosujàc opcje egzotyczne, wycenia te instru-
menty oraz prowadzi aktywny handel nimi. Definiuje
si´ je jako kontrakty opcyjne, które gwarantujà odmien-
nà struktur´ dochodu ni˝ standardowe opcje kupna
i sprzeda˝y

1

. Cz´sto nazywa si´ je instrumentami po-

chodnymi drugiej generacji.

Wprowadzenie tych instrumentów by∏o odpowie-

dzià wspomnianych instytucji finansowych na zapo-
trzebowanie rynku. Opcje egzotyczne nie sà nowym in-
strumentem na rynkach finansowych. Niektóre zacz´∏y
funkcjonowaç nawet kilka lat przed za∏o˝eniem pierw-
szej oficjalnej gie∏dy, na której by∏ prowadzony obrót
opcjami – the Chicago Board of Options Exchange
(CBOE). Podmioty gospodarcze, chcàc ograniczyç po-
noszone przez siebie ryzyko musia∏y zabezpieczaç swo-

je pozycje na rynku derywatów. Ponadto wzrost zmien-
noÊci cen wielu aktywów stwarza∏ szerokie mo˝liwoÊci
osiàgania zysków. Przyczyni∏o si´ to do powstania po-
pytu na te instrumenty.

Obrót wi´kszoÊcià opcji egzotycznych odbywa si´ na

rynku pozagie∏dowym (g∏ównie mi´dzybankowym), choç
niektóre znajdujà si´ na gie∏dach. Na przyk∏ad na New
York Mercantile Exchange (NYMEX) znajdujà si´ w obro-
cie opcje spreadowe. Jednak handel tymi opcjami to zale-
dwie niewielki procent wolumenu wszystkich opcji egzo-
tycznych. Z powodu ma∏ej przejrzystoÊci rynku pozagie∏-
dowego opcje egzotyczne nadal pozostajà egzotyczne dla
wielu inwestorów, nawet tych, dla których opcje standar-
dowe nie majà tajemnic. Choç wi´kszoÊç instrumentów
pochodnych znajduje si´ w obrocie na rynkach regulowa-
nych, opcje egzotyczne stanowià tu wyjàtek. Przyczyna
tkwi w ich unikalnym charakterze, co uniemo˝liwia stan-
daryzacj´ produktu i wprowadzenie go na rynek gie∏do-
wy. W przeciwieƒstwie do derywatów znajdujàcych si´
w obrocie gie∏dowym opcje egzotyczne mogà byç dowol-
nie dopasowywane do potrzeb inwestorów.

Zastosowanie wybranych opcji
egzotycznych i zasady ich wyceny

I z a b e l a P r u c h n i c k a - G r a b i a s

1 M. Kuêmierkiewicz: Ewolucja rynku opcji ku pozagie∏dowym opcjom egzo-
tycznym i ich klasyfikacja. „Bank i Kredyt” nr 3/1999, s. 18.

47

BANK I KREDYT czerwiec 2004

Rynki i Instytucje Finansowe

Ta b e l a Rodzaje opcji uwarunkowanych

èród∏o: opracowanie w∏asne na podstawie: M. Ong: Exotic options: the market and their taxonomy. W: I. Nelken: The handbook of exotic options: instruments,

analysis and applications. New York 1996, Mc Graw-Hill Book Company, s. 25.

Opcje egzotyczne uwarunkowane (Path-dependent exotic options)

Grupa opcji uwarunkowanych

Rodzaje opcji uwarunkowanych

Barrier (barierowe)

Partial

Outside

Multiple

Curvilinear

Lookback (wsteczne)

Partial

Modified

Ratchet (zapadkowe)

Ratchet

Ladder (drabinowe)

Modified

Step-lock

Shout (okrzykowe)

Simple

Modified

Average (azjatyckie)

Average rate

Average strike

Inverse average rate

Partial average

Flexible average

Geometric

Capped (z czapkà)

Capped

Caps and floors

Cap

Floor

Collar (korytarzowe)

Collar

Potencjalni inwestorzy

Stron´ popytowà opcji egzotycznych tworzà nast´pujà-
ce grupy podmiotów:

– inwestorzy zarzàdzajàcy aktywami,
– dealerzy instrumentów pochodnych,
– instytucje finansowe nie prowadzàce dzia∏alno-

Êci dealerskiej,

– instytucje niefinansowe (na przyk∏ad przedsi´-

biorstwa).

Pierwszà z wymienionych grup mo˝na podzieliç na

inwestorów profesjonalnych i detalicznych. Profesjona-
liÊci zarzàdzajàcy aktywami sp´dzajà ca∏e dnie przed
ekranami Reutersa i na bie˝àco orientujà si´ w sytuacji
rynkowej. NieprofesjonaliÊci sà bardziej pasywnymi
uczestnikami rynku. Zajmujà si´ raczej notowaniami
wybranych aktywów znajdujàcych si´ w ich portfelu.
Produkty dostosowane sà do omówionych typów inwe-
storów i dzielimy je na aktywne i bierne. Aktywne wy-
magajà Êledzenia rynku na bie˝àco; w przypadku bier-
nych nie jest to konieczne. Produkty aktywne sà kre-
owane specjalnie dla zarzàdzajàcych aktywami i nie
mogà byç sprzedawane inwestorom indywidualnym.

Dealerzy instrumentów pochodnych zainteresowa-

ni sà przede wszystkim premiami opcyjnymi. Sà one
wi´ksze w przypadku opcji egzotycznych ni˝ na przy-
k∏ad opcji typu vanilla. Obrót egzotycznymi opcjami

oko∏o 15% ich wolumenu, podczas gdy zysk osiàgni´ty
z tego rodzaju transakcji to oko∏o 50% zysków ogó∏em.
Warto zatem handlowaç tymi instrumentami, gdy˝ –
jak widaç – w wielu bankach sà wyjàtkowo zyskowne.

Instytucje finansowe nieprowadzàce dzia∏alnoÊci

dealerskiej (jak banki komercyjne czy fundusze ubezpie-
czeniowe) mogà wykorzystaç opcje egzotyczne do zarzà-
dzania ryzykiem niedopasowania po stronie aktywów
i pasywów. JeÊli chodzi o instytucje ubezpieczeniowe,
pieniàdze ze sk∏adek wp∏ywajà wczeÊniej, a dopiero
w okresie póêniejszym powstajà ewentualne zobowiàza-
nia z tytu∏u roszczeƒ ubezpieczonych. W zwiàzku z tym
zak∏ad ubezpieczeƒ musi prowadziç odpowiednià strate-
gi´ zarzàdzania aktywami i pasywami, do czego z powo-
dzeniem mo˝e wykorzystaç omawiane instrumenty.

Bank komercyjny zbiera natomiast pieniàdze od

klientów. P∏aci swoim deponentom wed∏ug krótkoter-
minowej stopy procentowej. W tym samym czasie in-
westuje te same Êrodki w instrumenty d∏ugoterminowe.
Wynika z tego, ˝e bank po˝ycza wed∏ug krótkotermino-
wej stopy procentowej, a lokuje wed∏ug d∏ugotermino-
wej, co przynosi mu zyski. Gdy nastàpià niekorzystne
zmiany stóp procentowych, mo˝e dojÊç do powa˝nych
strat. Przed tym ryzykiem mo˝na si´ zabezpieczyç, u˝y-
wajàc w∏aÊnie opcji egzotycznych.

Przedsi´biorstwa z kolei mogà stosowaç opcje

egzotyczne do budowy strategii hedgingowych ograni-

BANK I KREDYT czerwiec 2004

48

Rynki i Instytucje Finansowe

czajàcych ponoszone ryzyko dzia∏alnoÊci. Za∏ó˝my, ˝e
pewna firma sprzedaje swoje produkty w ró˝nych kra-
jach i nagle chce wejÊç na nowe rynki w paƒstwach,
w których do tej pory nie sprzedawa∏a swoich wyro-
bów. JeÊli b´dà to rynki krajów o niestabilnej sytuacji
gospodarczej (np. kraje Europy Wschodniej czy by∏e
kraje komunistyczne, jak Polska) to korporacja b´dzie
nara˝ona na silne oddzia∏ywanie ryzyka walutowego,
stóp procentowych itp. Przed tym ryzykiem mo˝na si´
chroniç stosujàc opcje egzotyczne.

Jednà z odmian opcji egzotycznych majàcych sze-

rokie zastosowanie w hedgingu sà instrumenty wysta-
wiane na stopy procentowe, takie jak caps, floors, i tzw.
collar. Instrumenty to stanowià grup´ opcji uwarunko-
wanych (path-dependent options), co przedstawia tabe-
la. Opcjom tym, a w szczególnoÊci ich wycenie zdecy-
dowa∏am si´ poÊwi´ciç pozosta∏à cz´Êç niniejszego
opracowania. Wycenia si´ je za pomocà formu∏y Blac-
ka-Scholesa.

ZmiennoÊç stóp procentowych

Najwa˝niejszym i jednoczeÊnie najtrudniejszym eta-
pem przy wycenie opcji jest w∏aÊciwe oszacowanie
zmiennoÊci instrumentu bazowego. Problem tkwi
w tym, ˝e historyczna jej wartoÊç wcale nie musi si´
pokrywaç z bie˝àcà, wskutek czego mo˝e dojÊç do ma-
∏o precyzyjnej kalkulacji ceny opcji. ZmiennoÊç ceny
instrumentu jest miarà niepewnoÊci co do kszta∏towa-
nia si´ przysz∏ych zmian jej wartoÊci

2

. ZmiennoÊç ceny

akcji jest odchyleniem standardowym stopy zwrotu
z tej akcji dla jednego roku, przy czym stopa zwrotu jest
kapitalizowana w sposób ciàg∏y

3

. Bazuje si´ tu na od-

chyleniach dochodów z akcji, a nie ich cen rzeczywi-
stych. W przeciwnym wypadku otrzymalibyÊmy wyni-
ki ma∏o wiarygodne, gdy˝ odchylenie standardowe
zmienia si´ wraz ze wzrostem ceny. Odchylenie stan-
dardowe jest natomiast pierwiastkiem kwadratowym
z wariancji, która okreÊla stopieƒ rozrzutu (zró˝nicowa-
nia) wartoÊci zmiennej losowej wokó∏ wartoÊci oczeki-
wanej

4

.

JeÊli wzrasta zmiennoÊç, roÊnie prawdopodobieƒ-

stwo, ˝e dany instrument finansowy znacznie zmieni
swojà cen´ w przysz∏oÊci. Mo˝e to byç zarówno zmia-
na korzystna, jak i niekorzystna z punktu widzenia po-
siadacza takiego instrumentu.

Istnieje równie˝ zmiennoÊç implikowana, którà

szacujemy na podstawie danych cen opcji

5

. Do modelu

Blacka–Scholesa podstawiamy cen´ rynkowà opcji

i przy reszcie parametrów danych uzyskujemy wartoÊç
zmiennoÊci implikowanej. Nale˝y jednak pami´taç, ˝e
przy takim kwotowaniu zmiennoÊci, równie˝ pojawia-
jà si´ pewne problemy. Modele wyceny sà bowiem nie-
doskona∏e, na ceny opcji wp∏ywa prawo popytu i poda-
˝y, a ceny te zawierajà w sobie mar˝´ zysku, czyli b´dà
wy˝sze, ni˝ w rzeczywistoÊci wynika∏oby to z ich
zmiennoÊci. JeÊli chodzi o zmiennoÊç, to nale˝y pami´-
taç, ˝e w d∏ugim okresie wyst´puje tzw. zjawisko po-
wrotu do Êredniej. W przypadku stóp procentowych
(b´dàcych instrumentem bazowym dla omawianych tu
opcji cap czy floor) oznacza to, ˝e jeÊli sà one w danym
momencie stosunkowo wysokie, to istnieje du˝e praw-
dopodobieƒstwo, ˝e spadnà. I na odwrót: jeÊli sà niskie,
to prawdopodobne jest, ˝e w najbli˝szym okresie doj-
dzie do ich wzrostu. Zasada ta sugeruje, ˝e tradycyjny
sposób przeliczania zmiennoÊci z krótszych na d∏u˝sze
okresy prowadzi do przeszacowania tego parametru
i tym samym wartoÊci opcji w modelu Blacka-Scholesa.
OczywiÊcie im d∏u˝szy jest termin, na który
wystawiono opcje, tym zagro˝enie to ma wi´ksze zna-
czenie. Ponadto, wspomniany model zak∏ada sta∏oÊç te-
go parametru, co jest jednà z przyczyn jego krytyki.
Tymczasem wartoÊç zmiennoÊci zmienia si´ i wp∏yw
na nià ma nie tylko metoda szacowania, lecz równie˝
przedzia∏ czasowy, który weêmiemy do obliczeƒ, czyli
d∏ugoÊç okresu, za który szacuje si´ ten parametr.

Najbardziej popularnà miarà zmiennoÊci jest

wspomniane ju˝ odchylenie standardowe. Wprawdzie
metoda ta zach´ca swà prostotà, jednak nie uwzgl´dnia
zjawiska „powrotu do Êredniej”, wi´c jej stosowanie
jest ograniczone.

Oprócz odchylenia standardowego istniejà inne

modele pomiaru zmiennoÊci. Do powszechnie stosowa-
nych nale˝à

6

:

– prosta kwadratowa Êrednia ruchoma,
– metoda percentyli (symulacja historyczna),
– wyk∏adniczo wa˝ona Êrednia ruchoma zmiennoÊci,
– GARCH.

Je˝eli chodzi o prostà kwadratowà Êrednià rucho-

mà, to pomiar zmiennoÊci przy jej zastosowaniu jest
podobny jak przy u˝yciu odchylenia standardowego
z wyjàtkiem za∏o˝enia, ˝e Êrednia ma wynosiç zero. Je-
˝eli przyjmiemy, ˝e Êrednia wi´kszoÊci szeregów ceno-
wych jest bliska zera, to Êrednia ruchoma da wynik po-
dobny do odchylenia standardowego.

Równanie Êredniej ruchomej dla kalkulacji zmien-

noÊci ma postaç

7

:

(1)

σ =

=

=

∑

(

)

X

n

t

t n

t

2

1

2 K. Piontek: Prognozowanie zmiennoÊci instrumentów finansowych - cz. I.
„Rynek Terminowy” nr 3/2001, s. 114-121.
3 J. Hull: Kontrakty terminowe i opcje. Warszawa 1998 Wig Press, s. 294.
4 J. Jóêwiak, J. Podgórski: Statystyka od podstaw. Warszawa 2000 PWE, s. 105.
5 T. Garliƒski, R. Weron: Krótka historia VOLAX-u – czyli jak próbowano han-

dlowaç implikowanà zmiennoÊcià. „Rynek Terminowy” nr 6/1999, s. 52-56.

6 P. Best: WartoÊç nara˝ona na ryzyko. Kraków 2000 Oficyna Ekonomiczna,
s. 85.
7 Tam˝e, s. 85.

49

BANK I KREDYT czerwiec 2004

Rynki i Instytucje Finansowe

gdzie:

X

t

– procentowa zmiana ceny dla t–ego dnia (t = 1 ozna-

cza zmian´ ceny w poprzednim dniu, t = 2 oznacza
zmian´ ceny dwa dni wczeÊniej itd.)

n – liczba dni, dla których mierzona jest Êrednia

ruchoma.

W przypadku metody percentyli (symulacji histo-

rycznej) szereg procentowych zmian cen jest porzàdko-
wany rosnàco. Wskaênik zmiennoÊci wyznacza zmiana
ceny odpowiadajàca kwantylowi równemu wymagane-
mu poziomowi ufnoÊci. Zaletà tej metody jest to, ˝e nie
przyjmuje si´ ˝adnych za∏o˝eƒ co do rozk∏adu badane-
go szeregu. Stosuje si´ jà w przypadku, gdy nie mo˝na
przyjàç za∏o˝enia o normalnoÊci rozk∏adu. Zak∏ada to,
˝e przysz∏y rozk∏ad stóp zwrotu b´dzie taki sam, jak
w przesz∏oÊci, co równie˝ nie musi byç prawdziwe

8

.

W modelu zmiennoÊci tworzonym za pomocà wyk∏ad-

niczo wa˝onej Êredniej ruchomej (EWMA) ostatnim anali-
zowanym dniom przypisuje si´ wi´ksze wagi ni˝ wcze-
Êniejszym. Nie zak∏ada si´, ˝e zmiany cen majà rozk∏ad nor-
malny. Metoda ta jest stosowana przez bank inwestycyjny
JP Morgan (obecnie przej´ty przez Chase). Równanie osza-
cowania zmiennoÊci za pomocà EWMA ma postaç

9

:

(2)

gdzie:

λ

– czynnik starzenia si´ informacji; okreÊla on

wysokoÊç wag dla ostatnich dochodów, a tak˝e szyb-
koÊç, z jakà miara zmiennoÊci powróci do ni˝szego po-
ziomu po zanotowaniu du˝ego dochodu,

n – liczba dni wykorzystywana do wyprowadzenia

zmiennoÊci,

µ

– wartoÊç przeci´tna w rozk∏adzie; zazwyczaj za-

k∏ada si´, ˝e wynosi ona zero.

Na rynkach finansowych szeroko stosowanym mo-

delem jest GARCH, jednak szacowanie parametrów tym
sposobem nie jest proste. Na ogó∏ wymaga to dost´pu
do danych za trzy lata. Parametry powinny byç przeli-
czane raz w miesiàcu. W przypadku du˝ej liczby in-
strumentów oznacza to koniecznoÊç przeprowadzenia
wielu obliczeƒ

10

. Najbardziej u˝ytecznà cechà modelu

GARCH wydaje si´ to, ˝e obejmuje on zjawisko powro-
tu do Êredniej, o którym wczeÊniej pisa∏am.

Niezale˝nie od przyj´tej metody szacowania

zmiennoÊci bardzo wa˝ny jest wybór okresu, dla które-
go obliczamy t´ wielkoÊç. J. Hull zaleca, by braç pod
uwag´ ceny zamkni´cia dla danych dziennych z 90 –
180 dni

11

.

PoÊród przyczyn zmiennoÊci cen akcji zwolennicy

hipotezy efektywnoÊci rynku wymieniajà przypadko-
wo docierajàce do inwestorów informacje wp∏ywajàce
na przysz∏e stopy zwrotu z instrumentów. Inni teorety-
cy twierdzà, ˝e zmiennoÊç jest przede wszystkim efek-
tem rynkowego obrotu walorami. Fama i French prze-
prowadzili empiryczne testy, by sprawdziç, czy zmien-
noÊç jest taka sama w dniach sesyjnych i w dniach, gdy
nie ma notowaƒ. Po obliczeniu wariancji stopy zwrotu
z akcji pomi´dzy zamkni´ciem dwóch kolejnych sesji,
kiedy nie wyst´powa∏y mi´dzy nimi dni wolne oraz
wariancji stopy zwrotu z akcji pomi´dzy zamkni´ciem
sesji w piàtek a zamkni´ciem sesji w poniedzia∏ek, do-
szli do wniosku, ˝e zmiennoÊç jest znacznie wy˝sza,
gdy gie∏da jest czynna, ni˝ wtedy, gdy jest zamkni´ta.
Wynika z tego, ˝e jeÊli do pomiaru zmiennoÊci wyko-
rzystywane sà dane dzienne, to dni, w których nie ma
sesji, mogà byç zignorowane.

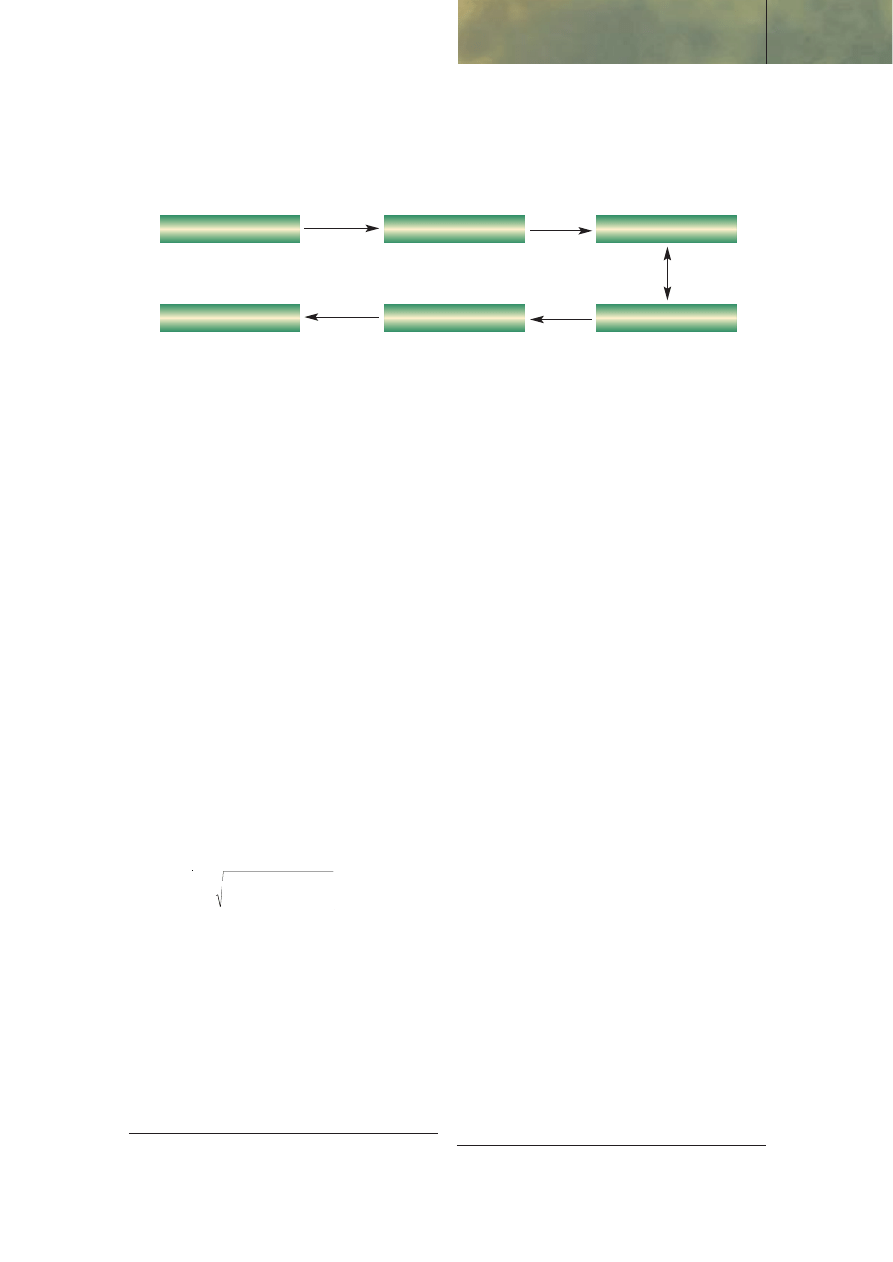
Dopasowanie zmiennoÊci rzeczywistej i impliko-

wanej przedstawione na schemacie wyst´puje tylko
w teorii. W rzeczywistoÊci parametry te mogà byç rów-
ne jedynie wtedy, gdy rynkowa cena opcji jest taka sa-
ma jak cena wynikajàca z modelu, co w praktyce jest
ma∏o prawdopodobne. Przyczyn takiego stanu rzeczy
nale˝y upatrywaç w ograniczeniach modelu wyceny

σ

λ

λ

µ

=

−

−

=

=

∑

(

)

(

)

1

2

1

t

t

t n

t

X

8 W.L. Jaworski, Z. Zawadzka: BankowoÊç – podr´cznik akademicki. Warsza-
wa 2002 Poltext, s. 622.
9 Tam˝e, s. 88.

10 P. Konieczny: Modele GARCH. Rynek terminowy nr 4/2000, s. 144.
11 J. Hull: Kontrakty..., op.cit., s. 296.

S c h e m a t Zale˝noÊç pomi´dzy zmiennoÊcià implikowanà a rzeczywistà

èród∏o: opracowanie w∏asne na podstawie R. Flavell: Swaps and other derivatives. Chichester John Wiley&Sons, Ltd, s. 275.

ZmiennoÊç rzeczywista

Model wyceny opcji

Cena wynikajàca z modelu

ZmiennoÊç implikowana

Model wyceny opcji

Cena rynkowa opcji

BANK I KREDYT czerwiec 2004

50

Rynki i Instytucje Finansowe

opcji. Opiera si´ on na za∏o˝eniach, z których nie
wszystkie sà spe∏nione w praktyce. Dlatego te˝ model
ten jest nierzadko krytykowany, jednak na razie lepsze-
go nie stworzono. Jedno z za∏o˝eƒ, które nie jest spe∏-
nione, to przyj´cie, ˝e zmiennoÊç jest wielkoÊcià sta∏à,
co oczywiÊcie nie jest prawdà. Ponadto model Blacka-
-Scholesa bazuje na nast´pujàcych za∏o˝eniach

12

:

– ceny akcji zachowujà si´ zgodnie z rozk∏adem

logarytmiczno – normalnym,

– wszystkie koszty transakcyjne oraz podatki sà po-

mijane, a papiery wartoÊciowe sà doskonale podzielne,

– w okresie wa˝noÊci opcji akcje bazowe dla dane-

go kontraktu nie przynoszà dywidend,

– nie istniejà mo˝liwoÊci pozbawionego ryzyka ar-

bitra˝u,

– obrót papierami wartoÊciowymi jest ciàg∏y,
– uczestnicy rynku mogà po˝yczaç i inwestowaç

Êrodki wed∏ug tej samej, wolnej od ryzyka stopy pro-
centowej,

– krótkoterminowa wolna od ryzyka stopa procen-

towa jest sta∏a.

W rzeczywistoÊci bardziej poprawnym rozk∏adem

opisujàcym zmiany cen jest rozk∏ad zawierajàcy tzw.
grube ogony. W zwiàzku z tym prawdopodobieƒstwo
realizacji wysokiego zysku jest wi´ksze, ni˝ zak∏ada
teoria. Oznacza to, ˝e rynkowe ceny opcji sà cz´sto
wy˝sze, ni˝ wynika to z modelu. To z kolei prowadzi
do obliczenia zmiennoÊci implikowanej na wy˝szym
poziomie ni˝ wynikajàca z modeli s∏u˝àcych do licze-
nia tego parametru.

Efekt „grubych ogonów” ma wi´ksze znaczenie

przy opcjach, które sà g∏´boko in-the-money

13

lub out-

-of-the-money

14

, najmniejsze natomiast dla instrumen-

tów, w przypadku których cena rynkowa instrumentu
bazowego jest równa cenie wykonania opcji (tzw. opcje
at-the-money). Jest to przyczyna tzw. uÊmiechu krzy-
wej zmiennoÊci. Poniewa˝ opcja typu cap jest strumie-
niem niezale˝nych opcji, znaczenie wyra˝enia at-the-
money jest inaczej interpretowane. Zwykle zak∏ada si´,
˝e cena ka˝dego pojedynczego instrumentu caplet musi
byç taka sama i równa sta∏ej stopie procentowej trans-
akcji spawowej, majàcej taki sam termin wygaÊni´cia
jak opcja cap

15

. WartoÊç kontraktu swapowego mo˝na

obliczyç z nast´pujàcego wzoru:

Fw (s,e) =

Σ

d

i

x

L

i

x

DF

i

/

Σ

d

i

x

DF

i

= (DF

s

- DF

e

)/(Q

e

- Q

s

) (3)

gdzie:

DF – wspó∏czynnik dyskontowy,
s – pierwszy dzieƒ obowiàzywania kontraktu swa-

powego,

e – dzieƒ wygaÊni´cia kontraktu swapowego,
i – dzieƒ wyceny kontraktu swapowego,
L – aktualna wartoÊç stopy procentowej forward,
d – d∏ugoÊç czasu ˝ycia swapu do momentu i.

Opcje typu

cap i ich wycena

Transakcja cap jest umowà pomi´dzy sprzedajàcym
a kupujàcym cap. Wynika z niej, ˝e w przypadku wzro-
stu rynkowej stopy procentowej ponad uzgodniony po-
ziom sprzedajàcy wyrówna posiadaczowi cap ró˝nic´
pomi´dzy uzgodnionà, granicznà stopà procentowà
a rynkowà stopà procentowà dla przyj´tej w umowie
wielkoÊci kapita∏u i za ustalony w umowie okres.

Na kszta∏towanie si´ ceny zakupu opcji cap wp∏y-

wajà ró˝norodne czynniki zewn´trzne, w tym przede
wszystkim:

– przewidywana wysokoÊç zmiennoÊci rynkowych

stóp procentowych; im wi´kszà zmiennoÊcià charakte-
ryzujà si´ stopy procentowe, tym trudniej przewidzieç
ich przysz∏y poziom, co z kolei wp∏ywa na wzrost ceny
kontraktu cap;

– obecny poziom stóp procentowych – cena kon-

traktu cap maleje wraz ze zwi´kszaniem si´ ró˝nicy po-
mi´dzy aktualnym poziomem stóp procentowych
a ustalonà cenà wykonania opcji;

– wysokoÊç kapita∏u b´dàcego przedmiotem umowy

– im wi´kszy kapita∏ dotyczy umowy, tym wy˝sza jest ce-
na opcji, gdy˝ zwi´ksza si´ ryzyko dla sprzedajàcego;

– czas trwania umowy – cena opcji roÊnie wraz ze

wzrostem d∏ugoÊci okresu, na który zawarto umow´.

Sprzedawca opcji cap liczy na spadek stopy pro-

centowej, dzi´ki czemu zarabia na premii zap∏aconej
przez nabywc´. W przypadku wzrostu stóp procento-
wych ponad ustalony w umowie poziom sprzedawca
opcji cap ponosi natomiast straty zale˝ne od wysokoÊci
tego wzrostu, teoretycznie w zasadzie nieograniczone.

Z matematycznego punktu widzenia cap jest serià

niezale˝nych opcji typu caplet. Dlatego te˝ wycena
opcji cap bazuje na wycenie tych pojedynczych instru-
mentów. Caplet to pojedyncza opcja typu call wysta-
wiona na stop´ procentowà forward F (t, T), majàca po-
czàtek w czasie t i wygasajàca w czasie T. JeÊli za∏o˝y-
my, ˝e opcja ma cen´ wykonania na poziomie K%,
a umowa cap dotyczy kapita∏u P, wtedy:

• W czasie t stopa procentowa F wynosi L%.
• JeÊli L > K, to wyp∏ata = [L – K] x (T – t) x P zwykle

wyp∏acana w czasie T.

• JeÊli L

≤

K, to wyp∏ata = 0.

12 Tam˝e, s.299.
13 Dla opcji typu call sytuacja taka wyst´puje, gdy cena rynkowa instrumen-
tu bazowego przekracza cen´ wykonania opcji, dla opcji typu put, gdy cena

wykonania opcji jest wy˝sza od ceny instrumentu bazowego.
14 Dla opcji typu put sytuacja taka wyst´puje, gdy cena rynkowa instrumentu
bazowego przekracza cen´ wykonania opcji, dla opcji typu call, gdy cena wy-

konania opcji jest wy˝sza od ceny instrumentu bazowego.
15 R. Flavell: Swaps and other derivatives. Chichester 2002, John Wiley&Sons,
Ltd, s. 276.

51

BANK I KREDYT czerwiec 2004

Rynki i Instytucje Finansowe

Ogólniej wyp∏at´ mo˝na wyraziç formu∏à:

max [0, L – K] x (T – t) x P

(4)

JeÊli wyp∏ata ma nastàpiç w czasie t, zgodnie z za-

sadà kontraktów FRA formu∏a przybierze nast´pujàcà
postaç:

(5)

Rozwa˝my nast´pnie opcj´ wystawionà na obliga-

cj´ sprzedawanà z dyskontem. Za∏ó˝my, ˝e p (t’, t, T)
jest szacowanà cenà obligacji dyskontowej w czasie t’,
którà instrument ten ma osiàgnàç w czasie t. Obligacja
ta wygasa w czasie T i wià˝e si´ to z przep∏ywem
pieni´˝nym w pewnej wysokoÊci. Wyp∏ata z tytu∏u po-
siadania S opcji typu put z cenà wykonania p

k

wygasa-

jàcych w czasie t definiowana jest jako:

max [0, – p

k

– p (t’, t, T) ]

x

S

(6)

Zgodnie z definicjà:

p (t’, t, T) = [1 + L

x

(T – t) ]

-1

(7)

p

k

= [1 + K

x

(T – t) ]

-1

Po podstawieniu powy˝szych równaƒ do wzoru na

wyp∏at´ otrzymujemy:

(8)

Podstawiajàc S = 1/p

k

, otrzymujemy identycznà

funkcj´ wyp∏aty jak w przypadku opcji caplet. Wynika
z tego zatem, ˝e opcj´ caplet mo˝na przedstawiç
w dwojaki sposób: albo jako opcj´ typu call wystawio-
nà na przysz∏à stop´ procentowà albo jako opcj´ typu
put wystawionà na obligacj´ dyskontowà.

Model Blacka-Scholesa dla opcji typu caplet wy-

stawionej na przysz∏à stop´ procentowà F(t,T) mo˝e zo-
staç przedstawiony w postaci:

C = P

x

DF

t

x

{F (t, T)

x

N (d

1

) – K

x

N (d

2

) }

x

(T – t) (9)

Oznaczajàc zmiennoÊç jako

σ

:

d

1

= {ln (F/K) + 0,5

x

σ

2

t } /

σ√

t

(10)

d

2

= d

1

–

σ√

t

(11)

gdzie:

N(x) – dystrybuanta standaryzowanej zmiennej x

majàcej rozk∏ad normalny,

DF – wspó∏czynnik dyskontowy.

Opcje typu

floor i ich wycena

Kontrakt floor jest odwrotnoÊcià kontraktu cap.
W kontrakcie tym okreÊla si´ kwot´ kapita∏u, okres
trwania zobowiàzania sprzedawcy i granicznà wyso-
koÊç stopy procentowej, poni˝ej której sprzedawca jest
zobowiàzany wyp∏acaç odsetki od kapita∏u obliczone
wed∏ug procentu b´dàcego nadwy˝kà stopy floor pod
bie˝àcà stop´ procentowà, za ka˝dy dzieƒ okresu,
w którym taka nadwy˝ka nastàpi∏a.

Sprzedawca opcji floor liczy na wzrost stopy pro-

centowej. W razie spe∏nienia si´ jego oczekiwaƒ, zara-
bia premi´, którà zap∏aci∏ nabywca opcji floor. W prze-
ciwnym razie, w przypadku spadku stóp procentowych
poni˝ej poziomu ustalonego w umowie, sprzedawca
opcji floor ponosi straty. WielkoÊç tych strat zale˝y od
zakresu zmiany stóp procentowych.

Opcja floor jest strumieniem opcji put wystawio-

nych na stopy procentowe forward. Opcje typu floor
wycenia si´ równie˝ zgodnie z modelem Blacka-Sch-
oelesa.

Za∏o˝enia:

• Oznaczamy stop´ procentowà forward F (t, T) jako

okreÊlanà w czasie od t do T.

• Zak∏adamy, ˝e opcja ma cen´ wykonania równà K%,

a umowa dotyczy kapita∏u P.

• W czasie t stopa procentowa F wynosi L%.
• Wyp∏ata pojedynczego floorletu wynosi:
max[0, K - L]

x

(T – t)

x

P.

U˝ywajàc tych samych oznaczeƒ co dotychczas,

wartoÊç pojedynczego przep∏ywu opcyjnego (zwanego
floorlet) kontraktu floor wystawionego na stop´ procen-
towà forward F (t, T) mo˝na zapisaç w modelu Blacka-
-Scholesa jako:

(12)

Poni˝ej podaj´ przyk∏adowà wycen´ przep∏ywu

floorlet wystawionego na 3-miesi´cznà stop´ procento-
wà forward

16

.

Dane:

Dzisiejsza data: 4 stycznia 2000 r.
Kapita∏: 100 mln USD
Stopa forwardowa: data poczàtkowa: 6 lipca 2001 r.

data koƒcowa: 8 paêdziernika
2001 r.

Cena wykonania

17

: 6%

ZmiennoÊç: 17% w skali rocznej.

Zgodnie ze wzorami 10, 11, 12:

Fl

P DF

K N

d

F t T

N

d

T

t

t

=

−

−

−

−

×

×

×

×

×

{

(

)

( ,

)

(

)} (

)

2

1

{max[ ,

] (

)

}

[

(

)]

0

1

L K

T

t

P

L

T

t

p

k

−

−

+

−

×

×

×

×

×

S

max[ ,

] (

)

[

(

)]

0

1

L K

T

t

P

L

T

t

−

×

− ×

+ ×

−

16 R. Flavell: Swaps and..., op.cit., s. 288.
17 Wyra˝ona procentem kapita∏u.

BANK I KREDYT czerwiec 2004

52

Rynki i Instytucje Finansowe

d

1

= {ln (7,106%/6%)+0,5

x

17%

x

17%

x

1,519}/17%

x

1,232 = -0,9123

d

2

= -0,0092 - 17%

x

1,232 = 0,7027

N (-d

1

) = 0,1808

N (-d

2

) = 0,2411

Fl = 100 mln USD

x

0,889113

x

{6%

x

0,2411 - 7.106%

x

0,1808}

x

0,261 = 37556 USD.

Opcje typu

collar i zasady ich wyceny

Kiedy inwestor ma ju˝ ochron´ swoich aktywów w po-
staci nabytej opcji typu cap, popularnà strategià jest jed-
noczesna sprzeda˝ opcji typu floor majàcej ni˝szà cen´
wykonania ni˝ cap. Strategia ta nazywa si´ w∏aÊnie ko-
rytarzem (collar). Opcje collar kupuje si´ na ogó∏ po to,
aby obni˝yç koszty opcji cap. Kupujàcy cap wyst´puje
jednoczeÊnie jako sprzedajàcy floor, a zatem ponosi on
w tym przypadku mniejsze koszty ni˝ przy inwestycji
jedynie w cap. P∏acàc za cap otrzymuje jednoczeÊnie za-
p∏at´ za floor. W ten sposób inwestor po˝yczajàcy Êrod-
ki ma zagwarantowanà stop´ procentowà le˝àcà pomi´-
dzy górnym poziomem okreÊlanym przez cap i dolnà
granicà wyznaczanà przez floor. Ca∏kowity koszt takiej
strategii uzale˝niony jest od kosztów obu tych instru-
mentów z osobna, które z kolei zale˝ne sà od wysokoÊci
cen wykonania. Dzia∏ajà tu jednak dwie regu∏y:

– koszt opcji cap zmniejsza si´ wraz ze wzrostem

ceny wykonania

– koszt opcji floor zwi´ksza si´ wraz ze wzrostem

ceny wykonania.

Mo˝liwe jest takie dobranie cen wykonania instru-

mentów cap i floor s∏u˝àcych do zbudowania danego
kontraktu collar, ˝e ca∏kowity koszt operacji wyniesie
zero.

Poniewa˝ opcje collar sà kombinacjami opcji cap

i floor, ich wycena przeprowadzana jest wed∏ug takich
samych modeli, jak wycena ka˝dego z tych instrumen-
tów z osobna, przedstawiona powy˝ej.

Podsumowanie

W ostatnich dziesi´cioleciach obserwujemy sta∏y
wzrost ryzyka finansowego. Proces ten przyczynia si´
do gwa∏townego rozwoju instrumentów pochodnych.
Wprowadzenie do obrotu opcji egzotycznych stanowi-

∏o kolejny etap tego procesu. Instrumenty te cieszà si´
niezwyk∏à popularnoÊcià wÊród inwestorów, poniewa˝
dajà du˝o wi´ksze mo˝liwoÊci ni˝ dajà standardowe
derywaty. W Polsce mamy jeszcze stosunkowo niewiel-
kà liczb´ opcji egzotycznych mo˝liwych do zrealizowa-
nia. Rozwin´∏y si´ jedynie opcje walutowe. Najbogat-
szà ofert´ rynkowà instrumentów zabezpieczajàcych
majà w Polsce nast´pujàce banki:

– BRE Bank SA,
– Citibank Handlowy,
– Millenium Bank SA,
– Société Générale.
Wprowadzenie do obrotu opcji egzotycznych na-

daje nowy wymiar rynkom derywatów poprzez stwo-
rzenie podmiotom gospodarczym i finansowym zupe∏-
nie nowych mo˝liwoÊci zarzàdzania ryzykiem. Jednak
rozwój tych instrumentów napotyka liczne bariery, do
których nale˝à m.in.:

• Brak podstawowej wiedzy o tych instrumentach

finansowych. Mam tu na myÊli zw∏aszcza ich wycen´
czy zastosowanie w hedgingu. Szczegó∏owà wiedz´ na
ten temat majà wy∏àcznie specjaliÊci zajmujàcy si´ tymi
instrumentami zawodowo. Brakuje natomiast tego ro-
dzaju wiedzy u osób zarzàdzajàcych korporacjami go-
spodarczymi.

• Obrót opcjami egzotycznymi charakteryzuje si´

niskà p∏ynnoÊcià ze wzgl´du na niewielkà liczb´ insty-
tucji finansowych, które je sprzedajà.

• Nie ma standaryzacji terminologii, zasad kwoto-

wania, obrotu opcjami oraz brakuje jednolitych zasad
wyceny.

• Podmioty gospodarcze i inwestorzy rzadko sto-

sujà opcje egzotyczne do zarzàdzania ryzykiem. S∏abo
rozwini´te jest stosowanie opcji egzotycznych przez
podmioty gospodarcze i inwestorów do zarzàdzania
ryzykiem.

Wynika z tego, ˝e dalszy rozwój opcji egzotycz-

nych zarówno w Polsce, jak i na Êwiecie uzale˝nio-
ny b´dzie od post´pów na wymienionych obsza-
rach. Powinno si´ to odbyç poprzez promowanie
tych instrumentów przez banki, które dokonujà
obrotu nimi, i zach´canie choçby eksporterów i im-
porterów do skorzystania np. z egzotycznych opcji
walutowych, które w Polsce ju˝ funkcjonujà. Chodzi
tu o uÊwiadamianie mened˝erom, ˝e racjonalne za-
rzàdzanie ryzykiem jest konieczne do podnoszenia
efektywnoÊci funkcjonowania korporacji.

Literatura podstawowa

1. P. Best: WartoÊç nara˝ona na ryzyko. Kraków 2000 Oficyna ekonomiczna.
2. S. Brady: Handle exotics with care. „Corporate Finance”, marzec 1994, s. 38-39.
3. E. Briys, M. Bellalah, H. M. Mai, F. de Varenne: Options, futures and exotic derivatives: theory, application and

practice. Chichester 1998 John Wiley & Sons.

53

BANK I KREDYT czerwiec 2004

Rynki i Instytucje Finansowe

4. N.A. Chriss: Black-Scholes and beyond: option pricing models. New York 1997 McGraw-Hill Book Company.
5. R. Flavell: Swaps and other derivatives. London 2002 John Wiley and Sons, Ltd.
6. T. Garliƒski, R. Weron: Krótka historia VOLAXu - czyli jak próbowano handlowaç zmiennoÊcià. „Rynek Termi-

nowy” nr 6/1999, s. 52-56.

7. J. Hull: Kontrakty terminowe i opcje. Wprowadzenie. Warszawa 1998 WIG Press.
8. W.L. Jaworski, Z. Zawadzka: BankowoÊç. Podr´cznik akademicki. Warszawa 2002 Poltext.
9. J. Jóêwiak, J. Podgórski: Statystyka od podstaw. Warszawa 2000 Polskie Wydawnictwo Ekonomiczne.
10. P. Konieczny: Modele GARCH. „Rynek Terminowy” nr 4/2000, s. 142-148.
11. M. Kuêmierkiewicz: Ewolucja rynku opcji ku pozagie∏dowym opcjom egzotycznym i ich klasyfikacja. „Bank

i Kredyt” nr 3/1999, s. 18.

12. I. Nelken: The handbook of exotic options: instruments, analysis and applications. New York 1996 Mc Graw-

-Hill Book Company.

13. K. Piontek: Prognozowanie zmiennoÊci instrumentów finansowych – cz. I. „Rynek Terminowy” nr 3/01, s. 114-121.
14. N. Taleb: Dynamic hedging: managing vanilla and exotic options. New York 1997 John Wiley&Sons.
15. P. Wilmott: Derivatives. The theory and practice of financial engineering. Chichester 2000 John Willey & Sons.