
POLITECHNIKA WROCŁAWSKA
WYDZIAŁ MECHANICZNO-ENERGETYCZNY
Kierunek:
Mechanika i budowa maszyn (MBiM)
Specjalność:
Inżynieria lotnicza (IL)
WYTRZYMALOŚĆ
KONSTRUKCJI
LOTNICZYCH
PROJEKT 2
Obliczenia dla zestawu nr 33
Autor:
Jan Słowik 163103
Prowadzący:
dr inż. Bogusław Mrozek
Ocena pracy:
WROCŁAW 2011

Spis treści
1
Dane zadania:
2
1.1
Dane zadania: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
1.2
Zależności geometryczne . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.3
Odległości od osi z . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
2
Obliczenie y
sc
5
2.1
∆S
i
z
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.2
P
11
i=1
∆S
i
z
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.3
P
11
i=1
A
i
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.4
y
sc
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
3
Obliczenie S
z
7
3.1
∆S
i
z
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
3.2
S
1,j
z
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
4
Obliczenie centralnego momentu bezwładności względem osi Z
9
5
Wydatek naprężeń stycznych wzdłuż obwodu q(s)
10
6
Wykres rozkładu naprężeń wydatku naprężeń stycznych
11

Rozdział 1
Dane zadania:
1.1
Dane zadania:
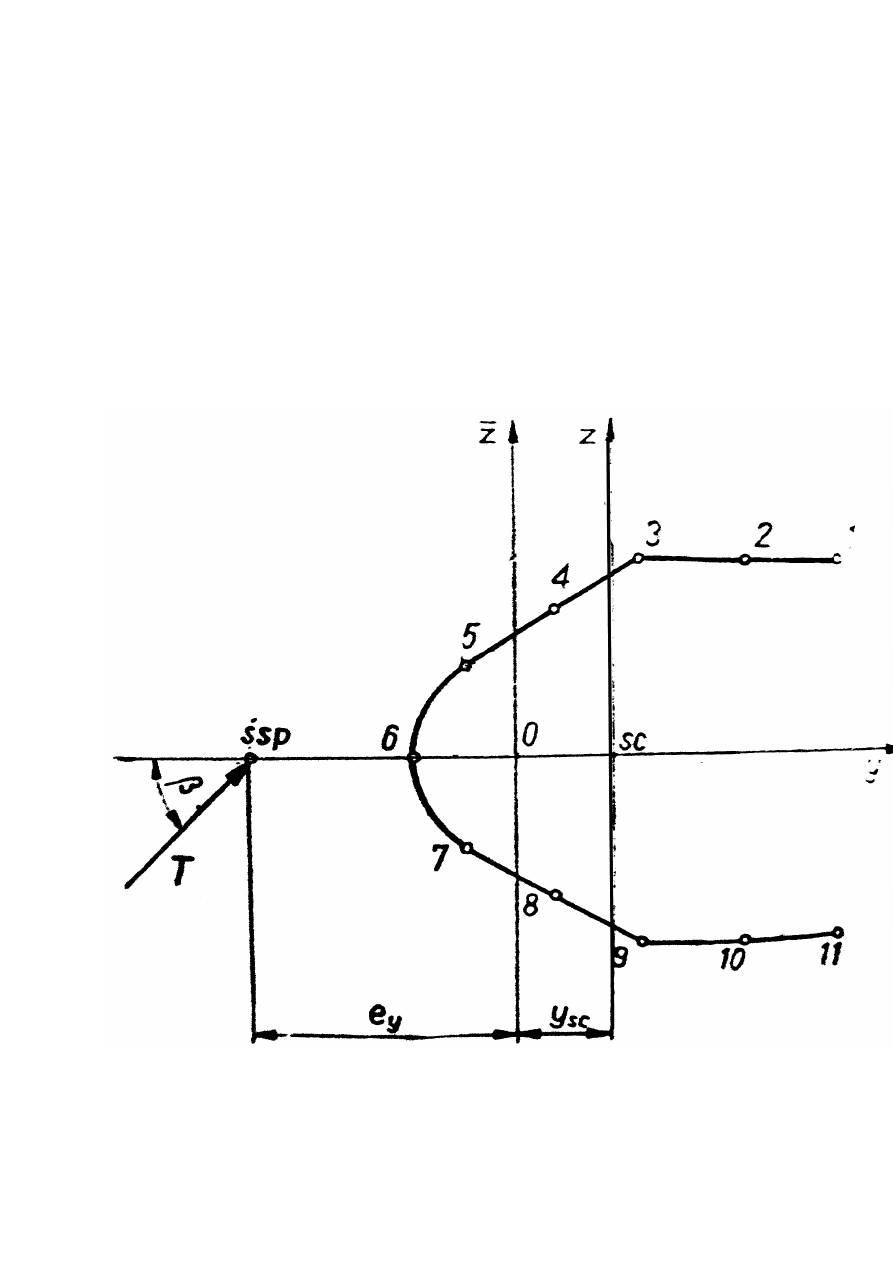
Dane pochodzą dla zestawu numer 33 i odnoszą się do rysunku 6
β
=
0
[
0
]
T
=
1230.769
[N]
a
=
180
[mm]
δ
=
3.606
[mm]
α
=
60
[
0
]
A
1
=
A
11
=
1
2
δa
A
2
=
A
10
=
δa
A
3
=
A
9
=
δa
A
4
=
A
8
=
δa
A
5
=
A
7
=
1
2
(1 +
π
3
)δa
A
6
=
1
3
πδa
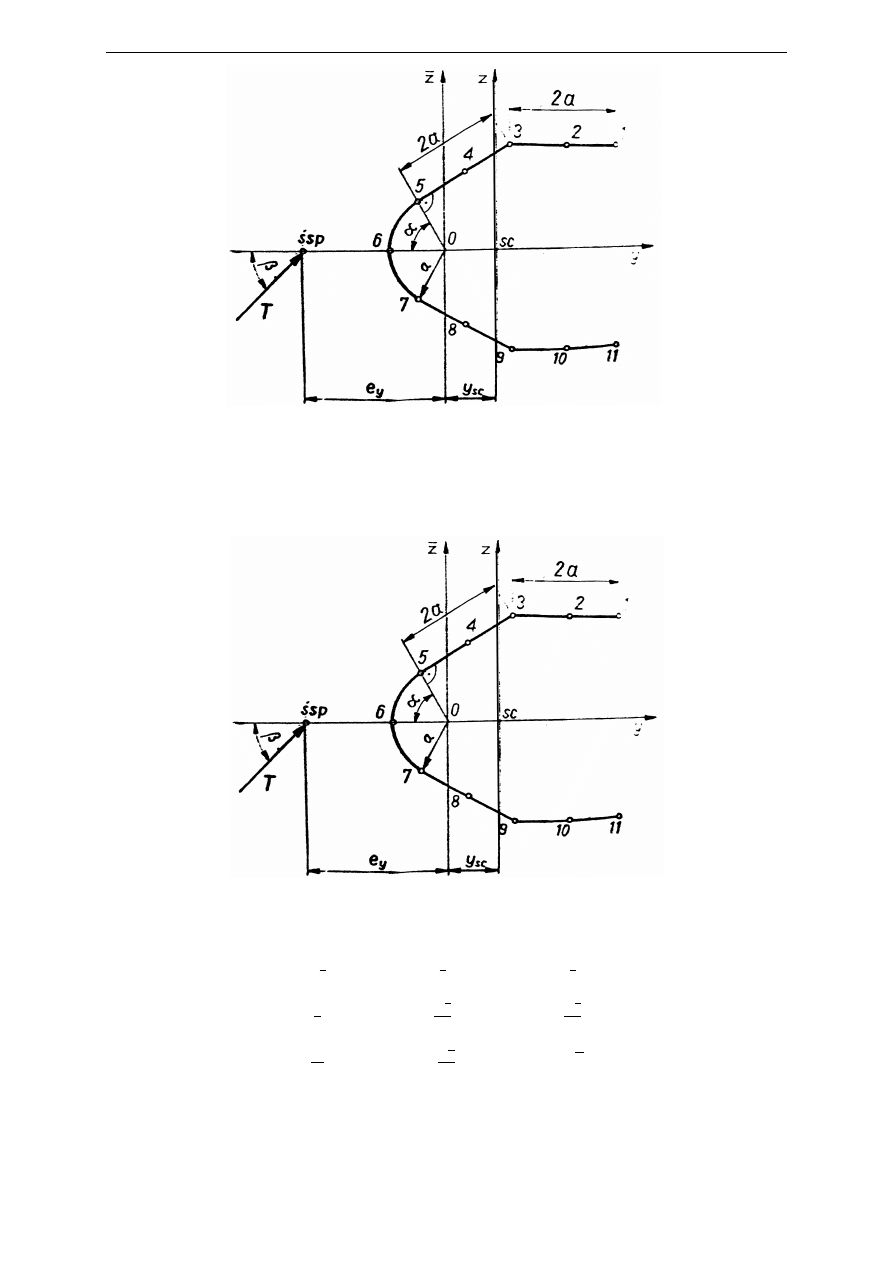
1. Dane zadania:
3
Rysunek 1.1 Rysunek dla zestawu 33
1.2
Zależności geometryczne
Rysunek 1.2 Zależności geometryczne
j
a
= cos(60
0
) =
1
2
−→
j = a
1
2
s
a
= cos(30
0
) =
√
3
2
−→
s = a
√
3
2
i
2a
= cos(30
0
) =
√
3
2
−→
i = a
√
3

1. Dane zadania:
4
1.3
Odległości od osi z
z
1
=
z
11
=
2
√
3+3
2
a
z
2
=
z
10
=
2
√
3+1
2
a
z
3
=
z
9
=
2
√
3−1
2
a
z
4
=
z
8
=
√
3−1
2
a
z
5
=
z
7
=
−
1
2
a
z
6
=
−a
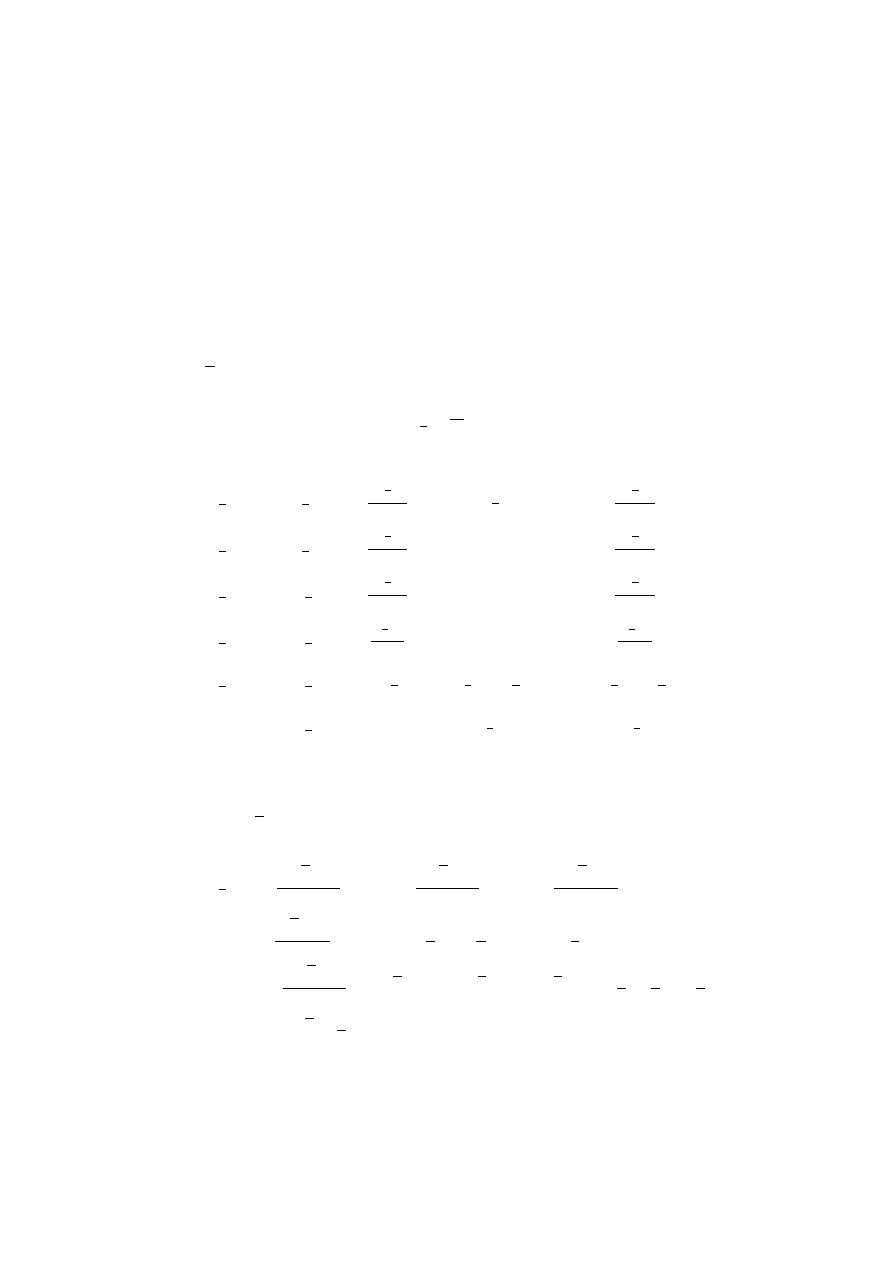
Rozdział 2
Obliczenie y
sc
2.1
∆S
i
z
∆S
i
z
= z
i
∗ A
i
∆S
1
z
=
∆S
11
z
=
2
√
3+3
2
a
*
1
2
δa
=
2
√
3+3
4
a
2
δ
∆S
2
z
=
∆S
10
z
=
2
√
3+1
2
a
*
δa
=
2
√
3+1
2
a
2
δ
∆S
3
z
=
∆S
9
z
=
2
√
3−1
2
a
*
δa
=
2
√
3−1
2
a
2
δ
∆S
4
z
=
∆S
8
z
=
√
3−1
2
a
*
δa
=
√
3−1
2
a
2
δ
∆S
5
z
=
∆S
7
z
=
−
1
2
a
*
1
2
(1 +
π
3
)δa
=
−
1
4
(1 +
π
3
)a
2
δ
∆S
6
z
=
−a
*
1
3
πδa
=
−
1
3
πa
2
δ
2.2
P
11
i=1
∆S
i
z
11
X
i=1
∆S
i
z
= 2 ∗
2
√
3 + 3
4
a
2
δ + 2 ∗
2
√
3 + 1
2
a
2
δ + 2 ∗
2
√
3 − 1
2
a
2
δ+
+ 2 ∗
√
3 − 1
2
a
2
δ + 2 ∗ (−
1
4
(1 +
π
3
)a
2
δ) + (−
1
3
πa
2
δ)
= a
2
δ(
2
√
3 + 3
2
+ 2
√
3 + 1 + 2
√
3 − 1 +
√
3 − 1 −
1
2
−
1
6
π −
1
3
π)
= a
2
δ(6
√
3 −
1
2
π)

2. Obliczenie y
sc
6
2.3
P
11
i=1
A
i
11
X
i=1
A
i
= 2 ∗
1
2
aδ + 6 ∗ aδ + 2 ∗ aδ
1
2
(1 +
pi
3
) + aδπ
1
3
= aδ(1 + 6 + 1 +
pi
3
+
pi
3
)
= aδ(8 +
2
3
π)
2.4
y
sc
y
sc
=
P
11
i=1
∆S
i
z
P
11
i=1
A
i
=
=
a
2
δ(6
√
3 −
1
2
π)
aδ(8 +
2
3
π)
=
= 0, 874 ∗ a
= 157, 32[mm]
Rozdział 3
Obliczenie S
z
3.1
∆S
i
z
∆S
i
z
= (z
i
− y
sc
) ∗ A
i
∆S
1
z
=
∆S
11
z
=
(
2
√
3+3
2
− 0, 874)a
*
1
2
δa
=
1, 179
a
2
δ
∆S
2
z
=
∆S
10
z
=
(
2
√
3+1
2
− 0, 874)a
*
δa
=
1, 358
a
2
δ
∆S
3
z
=
∆S
9
z
=
(
2
√
3−1
2
− 0, 874)a
*
δa
=
0.358
a
2
δ
∆S
4
z
=
∆S
8
z
=
(
√
3−1
2
− 0, 874)a
*
δa
=
−0, 508
a
2
δ
∆S
5
z
=
∆S
7
z
=
(−
1
2
− 0, 874)a
*
1
2
(1 +
π
3
)δa
=
−1, 406
a
2
δ
∆S
6
z
=
(−1 − 0, 874)a
*
1
3
πδa
=
−1, 961
a
2
δ

3. Obliczenie S
z
8
3.2
S
1,j
z
S
1,j
z
=
j
X
i=1
∆S
j
z
S
1,1
z
=
1, 179
a
2
δ
=
137748
[mm
3
]
S
1,2
z
=
2, 537
a
2
δ
=
296409
[mm
3
]
S
1,3
z
=
2, 895
a
2
δ
=
338236
[mm
3
]
S
1,4
z
=
2, 387
a
2
δ
=
278884
[mm
3
]
S
1,5
z
=
0, 981
a
2
δ
=
114615
[mm
3
]
S
1,6
z
=
−0, 981
a
2
δ
=
−114615
[mm
3
]
S
1,7
z
=
−2, 387
a
2
δ
=
−278884
[mm
3
]
S
1,8
z
=
−2, 895
a
2
δ
=
−338236
[mm
3
]
S
1,9
z
=
−2, 537
a
2
δ
=
−296409
[mm
3
]
S
1,10
z
=
−1, 179
a
2
δ
=
−137748
[mm
3
]
Rozdział 4
Obliczenie centralnego momentu
bezwładności względem osi Z
I
z
=
k
X
i=1
A
i
y
2
i
2
*
((
2
√
3+3
2
− 0, 874)a)
2
*
1
2
δa
=
5, 560
a
2
δ
2
*
((
2
√
3+1
2
− 0, 874)a)
2
*
δa
=
3, 688
a
2
δ
2
*
((
2
√
3−1
2
− 0, 874)a)
2
*
δa
=
0.256
a
2
δ
2
*
((
√
3−1
2
− 0, 874)a)
2
*
δa
=
0, 516
a
2
δ
2
*
((−
1
2
− 0, 874)a)
2
*
1
2
(1 +
π
3
)δa
=
3, 863
a
2
δ
+
1
*
((−1 − 0, 874)a)
2
*
1
3
πδa
=
3, 675
a
2
δ
17, 558
a
3
δ
I
z
= 17, 558 ∗ a
3
δ = 369248111[mm
4
]
Rozdział 5
Wydatek naprężeń stycznych wzdłuż
obwodu q(s)
q(s)
i
=
T
I
z
S
1,i
z
q
1
=
82,64
a
=
0, 459
[
N
mm
]
q
2
=
177,84
a
=
0, 988
[
N
mm
]
q
3
=
202,93
a
=
1, 127
[
N
mm
]
q
4
=
167,32
a
=
0, 930
[
N
mm
]
q
5
=
68,77
a
=
0, 382
[
N
mm
]
q
6
=
−68,77
a
=
−0, 382
[
N
mm
]
q
7
=
−167,32
a
=
−0, 930
[
N
mm
]
q
8
=
−202,93
a
=
−1, 127
[
N
mm
]
q
9
=
−177,84
a
=
−0, 988
[
N
mm
]
q
10
=
−82,64
a
=
−0, 459
[
N
mm
]
Rozdział 6
Wykres rozkładu naprężeń wydatku
naprężeń stycznych
Wyszukiwarka
Podobne podstrony:
jan slowik 163103 zadanie 3 ver 1 1
jan slowik 163103 zadanie 1 ver 1 3
Jan Nowak Jeziorański Zadanie wykonane
Ściąga wzory wytrzymałość, UTP-ATR, Mechanika dr. Sadowski Jan, Zadania wytrzymałość materiałów UTP
pierwiastki dobra i zla ver. 0.5, WYPRACOWANIA, ZADANIA
Zadania laboratoryjne 2 ver. 1
Zadania z metodologii, Z A D A N I E, ver. PL- 1.0, Z A D A N I E I
Zadania laboratoryjne 4 ver 1
Jasna Panna m Jan Maklakiewicz opr x Stanisław Ormiński (ver 3 gł)
Serca ludzkie się radują t Hanna Jarwicz muz Jan Maklakiewicz opr x A Hoffman SDB (ver 3 gł)
Ostojski Jan Zadania szkoły i organizacji paramilitarnych w kształtowaniu świadomości młodzieży w z
Zadania z treścia
Prezentacja 2 analiza akcji zadania dla studentow
więcej podobnych podstron