
POLITECHNIKA WROCŁAWSKA
WYDZIAŁ MECHANICZNO-ENERGETYCZNY
Kierunek:
Mechanika i budowa maszyn (MBiM)
Specjalność:
Inżynieria lotnicza (IL)
WYTRZYMALOŚĆ
KONSTRUKCJI
LOTNICZYCH
PROJEKT 1
Obliczenia dla zestawu nr 13
Autor:
Jan Słowik 163103
Prowadzący:
dr inż. Bogusław Mrozek
Ocena pracy:
WROCŁAW 2011

Spis treści
1
Dane zadania:
2
1.1
Funkcje odległości od osi y . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
2
Obliczenie momentów stycznych względem osi Y
4
2.1
S
AB
y
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
2.2
S
BD
y
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.3
S
DE
y
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.4
S
EF
y
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.5
S
F H
y
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2.6
S
HI
y
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2.7
S
y
w przekrojach od A do I
. . . . . . . . . . . . . . . . . . . . . . . . . .
9
3
Obliczenie centralnego momentu bezwładności względem osi Y
10
4
Obliczenie wydatku naprężeń stycznych wzdłuż obwodu q(s)
13
5
Obliczenie e
y
15
5.1
AB . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
5.2
BD . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
5.3
DE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
5.4
EF . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
16
5.5
FH . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
5.6
HI . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
5.7
R
S
C
0
S
y
(s)ρ(s)ds . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
5.8
e
y
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
6
Podsumowanie wyników
18
7
Wykres rozkładu naprężeń wydatku naprężeń stycznych
19
Rozdział 1
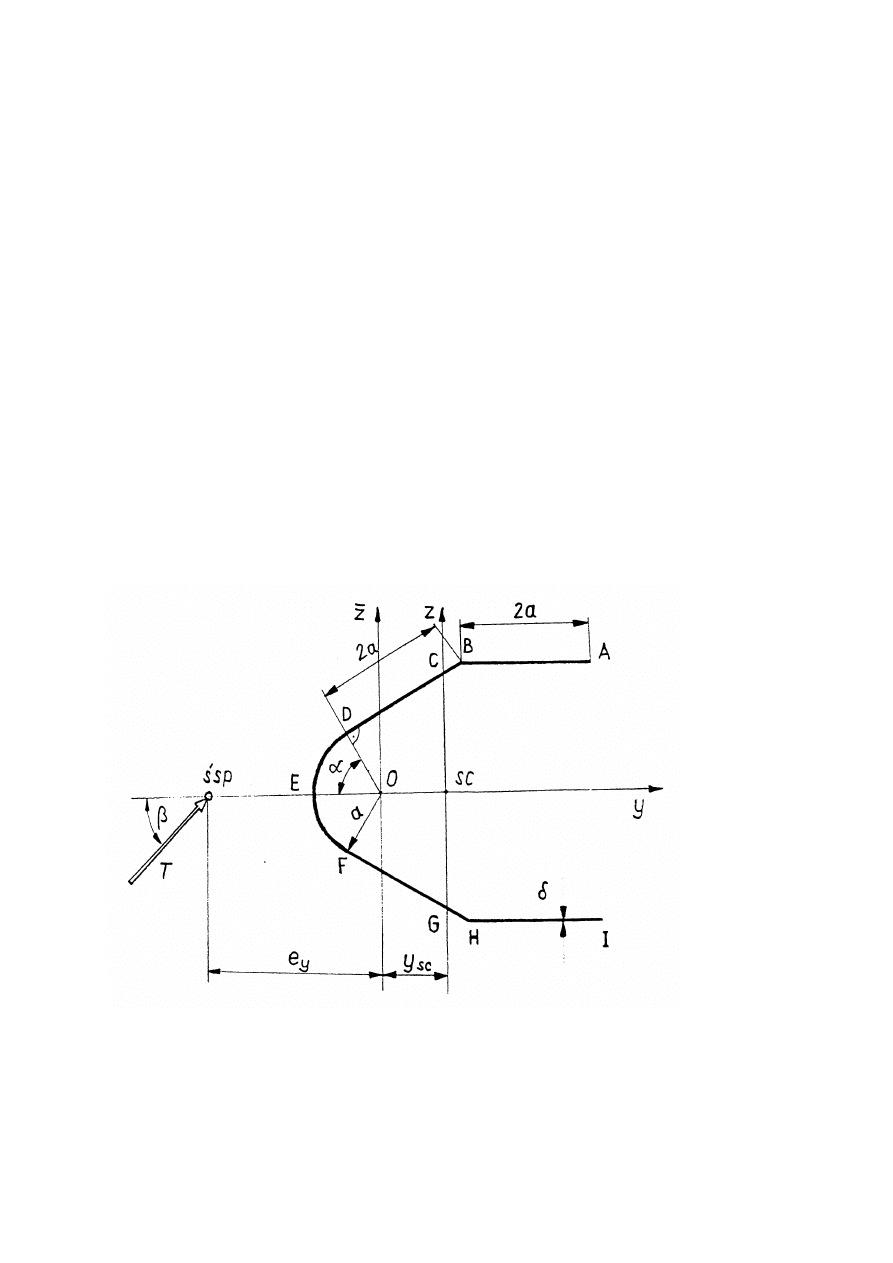
Dane zadania:
Dane pochodzą dla zestawu numer 13 i odnoszą się do rysunku 7
• β = 90 [
o
]
• T = 1230.769 [N ]
• a = 180 [mm]
• δ = 3.606 [mm]
• α = 60 [
o
]
1. Dane zadania:
3
1.1
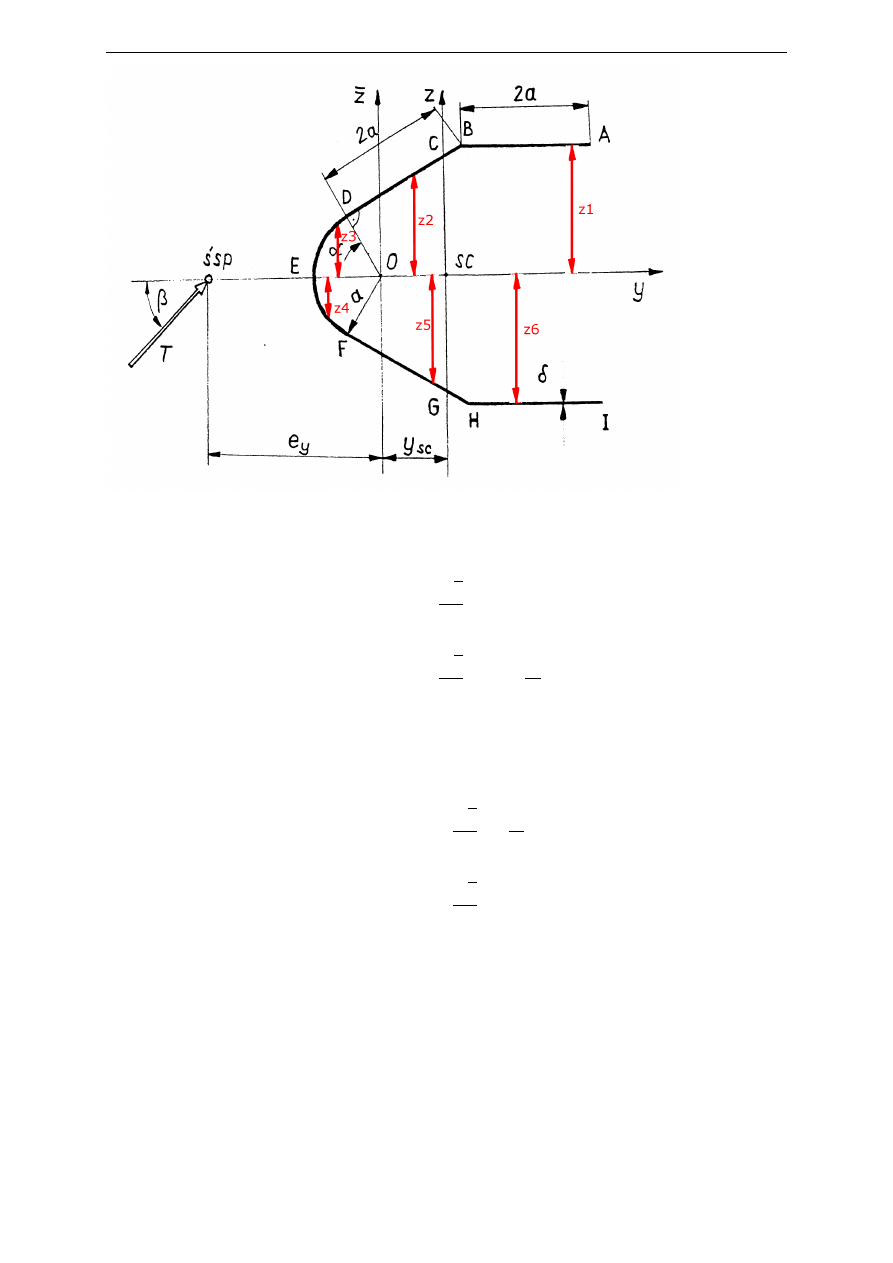
Funkcje odległości od osi y
z
1
(s
1
) = a(
√
3
2
+ 1)
(1.1)
z
2
(s
2
) = a(
√
3
2
+ 1) −
s
2
2
(1.2)
z
3
(α
3
) = sin(60
0
− α
3
)a
(1.3)
z
4
(α
4
) = −sin(α
4
)a
z
5
(s
5
) = −a(
√
3
2
) −
s
5
2
(1.4)
z
6
(s
6
) = −a(
√
3
2
+ 1)
(1.5)
(1.6)
Rozdział 2
Obliczenie momentów stycznych
względem osi Y
2.1
S
AB
y
S
AB
y
(s
1
) =
s
1
Z
0
z
1
(s)δds
1
=
=
s
1
Z
0
a(
√
3
2
+ 1)δds
1
=
= a(
√
3
2
+ 1)δs
1
|
s
1
0
=
= s
1
δa(
√
3
2
+ 1)
(2.1)
dla 0 ¬ s
1
¬ 2a
S
A
y
(s
1
= 0) = 0 ∗ δa(
√
3
2
+ 1) =
= 0
(2.2)
S
B
y
(s
1
= 2a) = 2a ∗ δa(
√
3
2
+ 1) =
= δa
2
(
√
3 + 2)
2. Obliczenie momentów stycznych względem osi Y
5
2.2
S
BD
y
S
BD
y
(s
2
) = S
B
y
+
s
2
Z
0
z
2
(s
2
)δds
2
=
= S
B
y
+
s
2
Z
0
(a(
√
3
2
+ 1) −
s
2
2
)δds
2
=
= S
B
y
+ δ(a(
√
3
2
+ 1)s
2
−
s
2
2
4
) |
s
2
0
=
= S
B
y
+ δ(a(
√
3
2
+ 1)s
2
−
s
2
2
4
) =
= δ(a
2
(
√
3 + 2) + a(
√
3
2
+ 1)s
2
−
s
2
2
4
)
(2.3)
dla 0 ¬ s
2
¬ 2a
S
B
y
(s
2
= 0) = δ(a
2
(
√
3 + 2) + a(
√
3
2
+ 1) ∗ 0 −
0
2
4
) =
= δa
2
(
√
3 + 2)
(2.4)
S
D
y
(s
2
= 2a) = δ(a
2
(
√
3 + 2) + a(
√
3
2
+ 1) ∗ 2a −
(2a)
2
4
) =
= δ(a
2
(
√
3 + 2) + a
2
(
√
3 + 2) −
4a
2
4
) =
= δa
2
(2
√
3 + 3)
(2.5)
2.3
S
DE
y
S
DE
y
(α
3
) = S
D
y
+
α
3
Z
0
0
z
3
(α
3
)δadα
3
=
= S
D
y
+
α
3
Z
0
0
sin(60
0
− α
3
)δa
2
dα
3
=
= S
D
y
+ (δa
2
cos(60
0
− α
3
)) |
α
3
0
0
=
= S
D
y
+ δa
2
(cos(60
0
− α
3
) −
1
2
) =
= δa
2
(2
√
3 + 3) + δa
2
(cos(60
0
− α
3
) −
1
2
) =
= δa
2
(2
√
3 +
5
2
+ cos(60
0
− α
3
))
(2.6)
dla 0
0
¬ α
3
¬ 60
0

2. Obliczenie momentów stycznych względem osi Y
6
S
D
y
(α
3
= 0
0
) = δa
2
(2
√
3 + 3 −
1
2
+ cos(60
0
− 0
0
)) =
= δa
2
(2
√
3 + 3 −
1
2
+ cos(60
0
)) =
= δa
2
(2
√
3 + 3 −
1
2
+
1
2
) =
= δa
2
(2
√
3 + 3)
(2.7)
S
E
y
(α
3
= 60
0
) = δa
2
(2
√
3 + 3 −
1
2
+ cos(60
0
− 60
0
)) =
= δa
2
(2
√
3 + 3 −
1
2
+ cos(0
0
)) =
= δa
2
(2
√
3 + 3 −
1
2
+ 1) =
= δa
2
(
7 + 4
√
3
2
)
(2.8)
2.4
S
EF
y
S
EF
y
(α
4
) = S
E
y
+
α
4
Z
0
0
z
4
(α
4
)δadα
4
=
= S
E
y
+
α
4
Z
0
0
−sin(α
4
)δa
2
dα
4
=
= S
E
y
+ δa
2
(cos(α
4
)) |
α
4
0
0
=
= S
E
y
+ δa
2
(cos(α
4
) − 1) =
= δa
2
(
7 + 4
√
3
2
) + δa
2
(cos(α
4
) − 1) =
= δa
2
(
7 + 4
√
3
2
+ cos(α
4
) − 1)
(2.9)
dla 0
0
¬ s
1
¬ 60
0
S
E
y
(α
4
= 0
0
) = δa
2
(
7 + 4
√
3
2
+ cos(0
0
) − 1) =
= δa
2
(
7 + 4
√
3
2
+ 1 − 1) =
= δa
2
(
7 + 4
√
3
2
)
(2.10)
S
F
y
(α
4
= 60
0
) = δa
2
(
7 + 4
√
3
2
+ cos(60
0
) − 1) =
= δa
2
(
7 + 4
√
3
2
+
1
2
− 1) =
= δa
2
(3 + 2
√
3)
(2.11)

2. Obliczenie momentów stycznych względem osi Y
7
2.5
S
F H
y
S
F H
y
(s
5
) = S
F
y
+
s
5
Z
0
z
5
(s
5
)δds
5
=
= S
F
y
+
s
5
Z
0
(−a(
√
3
2
) −
s
5
2
)δds
5
=
= S
F
y
+ δ(−a(
√
3
2
)s
5
−
s
2
5
4
) |
s
2
0
=
= S
B
y
+ δ(−a(
√
3
2
)s
5
−
s
2
5
4
) =
= δa
2
(2
√
3 + 3) + δ(−a(
√
3
2
)s
5
−
s
2
5
4
) =
= δ(a
2
(2
√
3 + 3) − a(
√
3
2
)s
5
−
s
2
5
4
)
(2.12)
dla 0 ¬ s
1
¬ 2a
S
F
y
(s
5
= 0) = δ(a
2
(2
√
3 + 3) − a(
√
3
2
) ∗ 0 −
0
2
4
) =
= δa
2
(2
√
3 + 3)
(2.13)
S
H
y
(s
5
= 2a) = δ(a
2
(2
√
3 + 3) − a(
√
3
2
) ∗ 2a −
(2a)
2
4
) =
= δa
2
(2
√
3 + 3 −
√
3 − 1) =
= δa
2
(
√
3 + 2)
(2.14)
2.6
S
HI
y
S
HI
y
(s
6
) = S
H
y
+
s
6
Z
0
z
6
(s
6
)δds
6
=
= S
H
y
+
s
6
Z
0
(−a(
√
3
2
+ 1))δds
6
=
= S
H
y
+ (−a(
√
3
2
+ 1)δs
6
) |
s
6
0
=
= S
H
y
+ (−a(
√
3
2
+ 1)δs
6
) =
= δa
2
(
√
3 + 2) − (a(
√
3
2
+ 1)δs
6
)
(2.15)

2. Obliczenie momentów stycznych względem osi Y
8
dla 0 ¬ s
6
¬ 2a
S
H
y
(s
6
= 0) = δa
2
(
√
3 + 2) − (a(
√
3
2
+ 1)δ ∗ 0) =
= δa
2
(
√
3 + 2)
(2.16)
S
I
y
(s
6
= 2a) = δa
2
(
√
3 + 2) − (a(
√
3
2
+ 1)δ ∗ 2a) =
= δa
2
(
√
3 + 2) −
√
3 − 2) =
= δa
2
∗ 0
= 0
(2.17)

2. Obliczenie momentów stycznych względem osi Y
9
2.7
S
y
w przekrojach od A do I
S
A
= 0[mm
3
]
(2.18)
S
B
= δa
2
(
√
3 + 2) =
= (3.606)(180)
2
(
√
3 + 2) =
= (116834.4)(
√
3 + 2) =
= 436031.9169[mm
3
]
' 4.36[10
−4
m
3
]
(2.19)
S
D
= δa
2
(3 + 2
√
3) =
= (3.606)(180)
2
(3 + 2
√
3) =
= (116834.4)(3 + 2
√
3) =
= 755229.4337[mm.
3
]
' 7.55[10
−4
m
3
]
(2.20)
S
E
= δa
2
(
7 + 4
√
3
2
) =
= (3.606)(180)
2
(
7 + 4
√
3
2
) =
= (116834.4)(
7 + 4
√
3
2
) =
= 813646.6337[mm.
3
]
' 8.14[10
−4
m
3
]
(2.21)
S
F
= δa
2
(3 + 2
√
3) =
= (3.606)(180)
2
(3 + 2
√
3) =
= (116834.4)(3 + 2
√
3) =
= 755229.4337[mm.
3
]
' 7.55[10
−4
m
3
]
(2.22)
S
H
= δa
2
(
√
3 + 2) =
= (3.606)(180)
2
(
√
3 + 2) =
= (116834.4)(
√
3 + 2) =
= 436031.9169[mm.
3
]
' 4.36[10
−4
m
3
]
(2.23)
S
I
= 0[mm.
3
]
(2.24)
Rozdział 3
Obliczenie centralnego momentu
bezwładności względem osi Y
I
y
=
k
X
i=1
A
i
z
2
i
= I
AB
y
+ I
BD
y
+ I
DE
y
+ I
EF
y
+ I
F H
y
+ I
HI
y
= 2(I
AB
y
+ I
BD
y
+ I
DE
y
)
(3.1)
I
AB
y
=
2a
Z
0
(z
1
(s
1
))
2
δds
1
=
=
2a
Z
0
(a(
√
3
2
+ 1))
2
δds
1
=
=
2a
Z
0
a
2
(
7 + 4
√
3
4
)δds
1
=
= δa
2
(
7 + 4
√
3
4
)s
1
|
2a
0
=
= δa
3
(
7 + 4
√
3
2
)
(3.2)

3. Obliczenie centralnego momentu bezwładności względem osi Y
11
I
BD
y
=
2a
Z
0
(z
2
(s
2
))
2
δds
2
=
=
2a
Z
0
(a(
√
3
2
+ 1) −
s
2
2
)
2
δds
2
=
=
2a
Z
0
(a
2
7 + 4
√
3
4
− as
2
(
√
3
2
+ 1) +
s
2
2
4
)δds
2
=
= δ(a
2
7 + 4
√
3
4
s
2
− a
s
2
2
2
(
√
3
2
+ 1) +
s
3
2
12
) |
2a
0
=
= δ(a
2
7 + 4
√
3
4
(2a) − a
(2a)
2
2
(
√
3
2
+ 1) +
(2a)
3
12
) =
= δ(a
3
7 + 4
√
3
2
− 2a
3
(
√
3
2
+ 1) +
2a
3
3
) =
= δa
3
13 + 6
√
3
6
(3.3)
I
DE
y
=
60
0
Z
0
(z
3
(α
3
))
2
aδdα
3
=
=
60
0
Z
0
(sin(60
0
− α3)a)
2
aδdα
3
=
=
60
0
Z
0
(sin
2
(60
0
− α3)a
2
aδdα
3
=
= δa
3
60
0
Z
0
sin
2
(60
0
− α3)dα
3
=
= δa
3
(
1
4
(2(α
3
− 60
0
) + sin(
2π
3
− 2α
3
))) |
60
0
=
π
3
0
= δa
3
[(
1
4
(2 ∗ (60
0
− 60
0
) + sin(120
0
− 2 ∗ 60
0
))) − (
1
4
(2 ∗ (0
0
− 60
0
) + sin(120
0
− 2 ∗ 0
0
)))]
= δa
3
[(
1
4
(2 ∗ (0) + sin(0
0
))) − (
1
4
(−120
0
+ sin(120
0
)))]
= δa
3
[0 − (
1
4
(−120
0
+
√
3
2
))]
= δa
3
[(
1
4
(120
0
−
√
3
2
))]
= δa
3
[(
1
4
(
2
3
π −
√
3
2
))]
= δa
3
(
2
12
π −
√
3
8
)
(3.4)

3. Obliczenie centralnego momentu bezwładności względem osi Y
12
I
y
= 2(I
AB
y
+ I
BD
y
+ I
DE
y
)
= 2(δa
3
(
7 + 4
√
3
2
) + δa
3
13 + 6
√
3
6
+ δa
3
(
2
12
π −
√
3
8
)) =
= δa
3
2 ∗
136 + 69
√
3 + 4π
24
=
= δa
3
136 + 69
√
3 + 4π
12
(3.5)
I
y
= (3.606)(180)
3
136 + 69
√
3 + 4π
12
=
= (21030192)
136 + 69
√
3 + 4π
12
=
= 469799602, 92[mm
4
]
' 469799603[mm
4
]
(3.6)

Rozdział 4
Obliczenie wydatku naprężeń stycznych
wzdłuż obwodu q(s)
q(s) =
T
z
S
y
(s)
I
y
(4.1)
q
A
=
T
z
S
A
y
I
y
=
(1230.769) ∗ (0)
469799603
= 0[
N
mm.
]
(4.2)
q
B
=
T
z
S
B
y
I
y
=
(1230.769) ∗ (436031.9169)
469799603
= 1.142305
' 1.14[
N
mm
]
(4.3)
q
D
=
T
z
S
D
y
I
y
=
(1230.769) ∗ (755229.4337)
469799603
= 1.978531
' 1.98[
N
mm
]
(4.4)

4. Obliczenie wydatku naprężeń stycznych wzdłuż obwodu q(s)
14
q
E
=
T
z
S
E
y
I
y
=
(1230.769) ∗ (813646.6337)
469799603
= 2.131571
' 2.13[
N
mm.
]
(4.5)
q
F
=
T
z
S
F
y
I
y
=
(1230.769) ∗ (755229.4337)
469799603
= 1.978531
' 1.98[
N
mm
]
(4.6)
q
H
=
T
z
S
H
y
I
y
=
(1230.769) ∗ (436031.9169)
469799603
= 1.142305
' 1.14[
N
mm
]
(4.7)
q
I
=
T
z
S
I
y
I
y
=
(1230.769) ∗ (0)
469799603
= 0[
N
mm
]
(4.8)

Rozdział 5
Obliczenie e
y
e
y
= −
1
I
y
Z
S
c
0
S
s
y
ρ(s)ds
(5.1)
ρ
1
(s
1
) = z
1
(1)
= a(
√
3
2
+ 1)
(5.2)
ρ
2
(s
2
) = a
(5.3)
ρ
3
(α
3
) = a
(5.4)
ρ
4
(α
4
) = a
ρ
5
(s
5
) = a
(5.5)
ρ
6
(s
6
) = z
6
(s
6
)
= a(
√
3
2
+ 1)
(5.6)
(5.7)
Z
S
C
0
S
y
(s)ρ(s)ds =
Z
2a
0
S
AB
y
(s
1
)ρ(s)ds
1
+
Z
2a
0
S
BD
y
(s
2
)ρ(s)ds
2
+
Z
60
0
0
S
DE
y
(s
3
)ρ(s)dα3
(5.8)
+
Z
60
0
0
S
EF
y
(s
4
)ρ(s)dα4 +
Z
2a
0
S
F H
y
(s
5
)ρ(s)ds
5
+
Z
2a
0
S
HI
y
(s
6
)ρ(s)ds
6
(5.9)
5. Obliczenie e
y
16
5.1
AB
Z
2a
0
S
AB
y
(s
1
)ρ(s)ds
1
=
Z
2a
0
s
1
δ(
√
3
2
+ 1) ∗ a(
√
3
2
+ 1)d
s
1 =
7 + 4
√
3
4
δa
2
Z
2a
0
s
1
ds
1
=
=
7 + 4
√
3
4
δa
2
s
2
1
2
|
2a
0
=
7 + 4
√
3
4
δa
2
(2a)
2
2
=
=
7 + 4
√
3
2
δa
4
(5.10)
5.2
BD
Z
2a
0
S
BD
y
(s
2
)ρ(s)ds
2
=
Z
2a
0
δ(a
2
(
√
3 + 2) + a(
√
3
2
+ 1)s
2
−
s
2
2
4
) ∗ ads
2
=
= δ(a
3
(
√
3 + 2)s
2
+
a
2
4
(
√
3
2
+ 1)s
2
2
−
as
3
2
12
) |
2a
0
=
= δ(a
3
(
√
3 + 2)(2a) +
a
2
4
(
√
3
2
+ 1)(2a)
2
−
a(2a)
3
12
) |
2a
0
=
= a
4
δ[2(2 +
√
3 +
2 +
√
3
4
4 −
8
12
] =
=
16 + 9
√
3
3
a
4
δ
(5.11)
5.3
DE
Z
60
0
0
S
DE
y
(s
3
)ρ(s)adα
3
=
Z
60
0
0
δa
2
(2
√
3 +
5
2
+ cos(60
0
− α
3
)) ∗ a
2
dα3 =
= a
4
δ(2
√
3α
3
+
5
2
α
3
+ cos(60
0
)sin(α
3
) − sin(60)cos(α
3
)) |
60
0
0
=
=
1
2
a
4
δ[(5 + 4
√
3)
π
3
+
√
3]
(5.12)
5.4
EF
Z
60
0
0
S
EF
y
(s
4
)ρ(s)adα4 =
Z
60
0
0
δa
2
(
5 + 4
√
3
2
+ cos(α
4
)) ∗ a
2
dα4 =
=
1
2
a
4
δ[(5 + 4
√
3)α
4
+ 2sin(α
4
)] |
60
0
0
=
=
1
2
a
4
δ[(5 + 4
√
3)
π
3
+
√
3]
(5.13)

5. Obliczenie e
y
17
5.5
FH
Z
2a
0
S
F H
y
(s
5
)ρ(s)ds
5
=
Z
2a
0
δ(a
2
(2
√
3 + 3) − a(
√
3
2
)s
5
−
s
2
5
4
) ∗ ads
5
=
= δ[(3 + 2
√
3)a
3
s
5
−
√
3
4
a
2
s
2
5
−
as
2
5
12
] |
2a
0
=
= δa
4
((3 + 2
√
3) ∗ 2 −
√
3 −
8
12
) =
=
16 + 9
√
3
3
a
4
δ
(5.14)
5.6
HI
Z
2a
0
S
HI
y
(s
6
)ρ(s)ds
6
=
Z
2a
0
(δa
2
(
√
3 + 2) − (a(
√
3
2
+ 1)δs
6
)) ∗ (a(
√
3
2
+ 1))ds
6
=
=
1
8
(7 + 4
√
3)a
2
δs
6
(4a − s
6
) |
2a
0
=
=
1
8
(7 + 4
√
3)a
2
δ(2a)(2a) =
=
7 + 4
√
3
2
δa
4
(5.15)
5.7
R
S
C
0
S
y
(s)ρ(s)ds
Z
S
C
0
S
y
(s)ρ(s)ds =
7 + 4
√
3
2
δa
4
+
16 + 9
√
3
3
a
4
δ
+
1
2
a
4
δ[(5 + 4
√
3)
π
3
+
√
3] +
1
2
a
4
δ[(5 + 4
√
3)
π
3
+
√
3]
+
16 + 9
√
3
3
δa
4
+
7 + 4
√
3
2
δa
4
=
= δa
4
(
53 + 33
√
3 + (5 + 4
√
3)π
3
(5.16)
Z
S
C
0
S
y
(s)ρ(s)ds = δa
4
(
53 + 33
√
3 + (5 + 4
√
3)π
3
)
(5.17)
= 1.862588184 ∗ 10
11
(5.18)
5.8
e
y
e
y
= −
1
I
y
Z
S
C
0
S
y
(s)ρ(s)ds = = −
1.862588184 ∗ 10
11
469799603
= −396.464[mm]
(5.19)
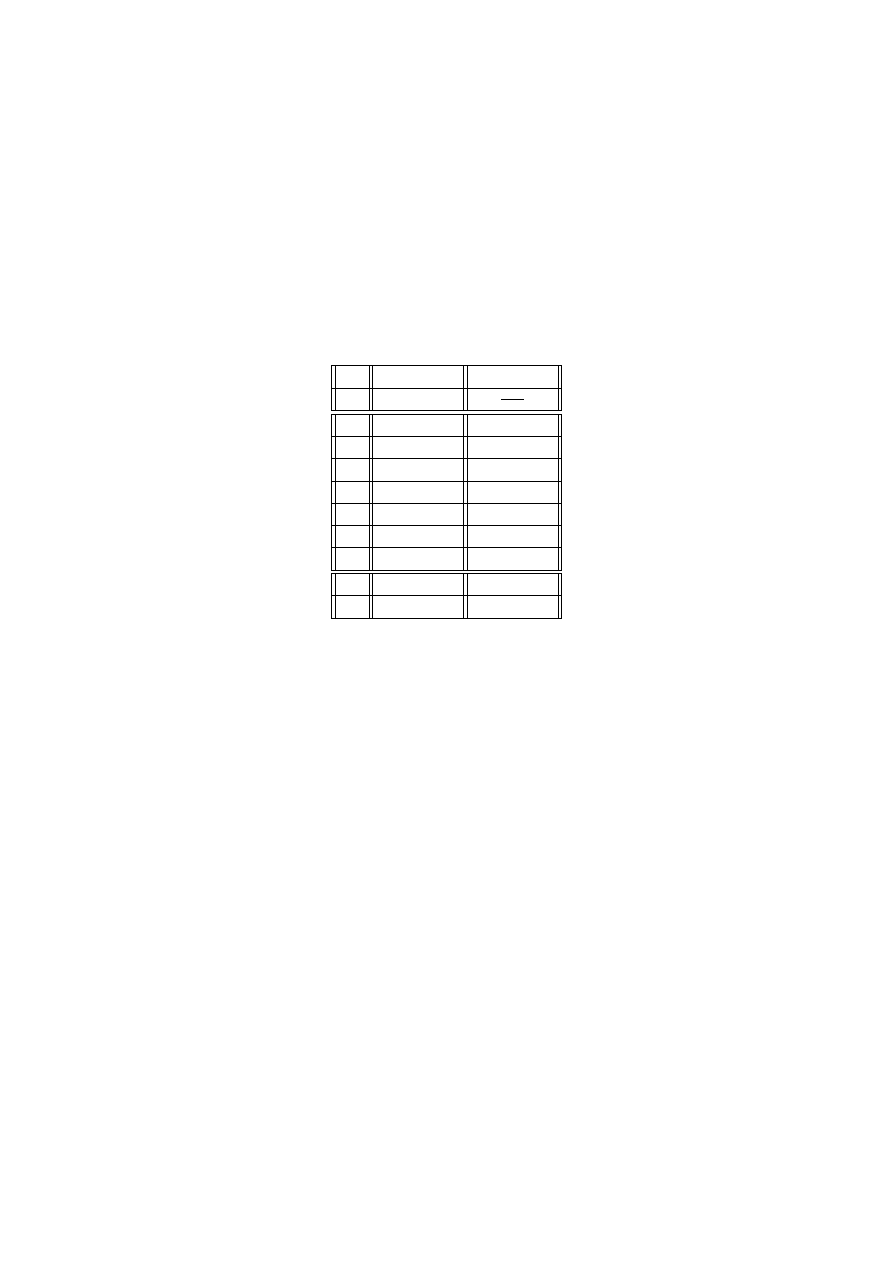
Rozdział 6
Podsumowanie wyników
i
S
i
y
q
i
−
[10
5
mm
3
]
[
N
mm
]
A
0
0
B
4.36
1.14
D
7.55
1.98
E
8.14
2.13
F
7.55
1.98
H
4.36
1.14
I
0
0
I
y
4.698
[10
8
mm
4
]
e
y
-396
[mm]
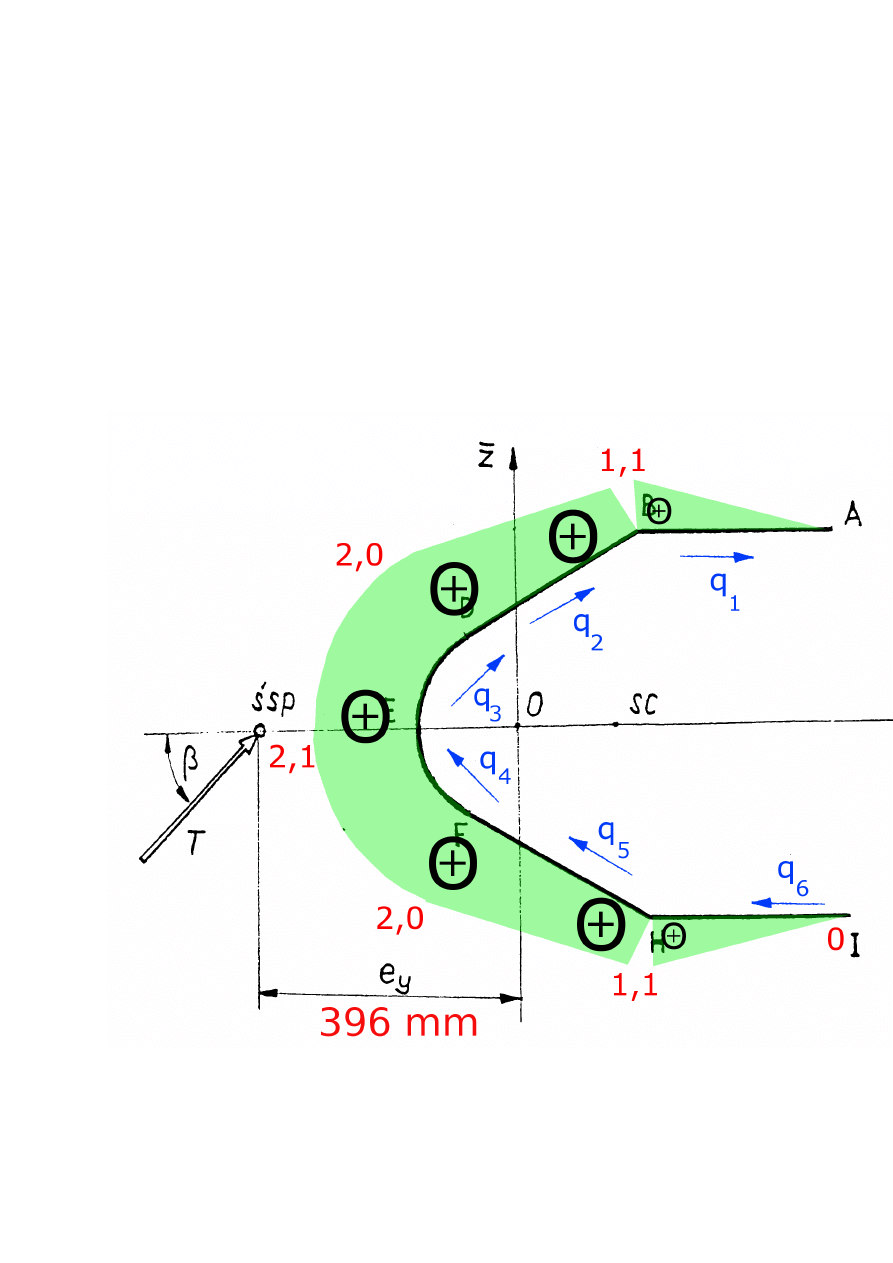
Rozdział 7
Wykres rozkładu naprężeń wydatku
naprężeń stycznych
Wyszukiwarka
Podobne podstrony:
jan slowik 163103 zadanie 2 ver 1 0
jan slowik 163103 zadanie 3 ver 1 1
Jan Nowak Jeziorański Zadanie wykonane
Ściąga wzory wytrzymałość, UTP-ATR, Mechanika dr. Sadowski Jan, Zadania wytrzymałość materiałów UTP
pierwiastki dobra i zla ver. 0.5, WYPRACOWANIA, ZADANIA
Zadania laboratoryjne 2 ver. 1
Zadania z metodologii, Z A D A N I E, ver. PL- 1.0, Z A D A N I E I
Zadania laboratoryjne 4 ver 1
Jasna Panna m Jan Maklakiewicz opr x Stanisław Ormiński (ver 3 gł)
Serca ludzkie się radują t Hanna Jarwicz muz Jan Maklakiewicz opr x A Hoffman SDB (ver 3 gł)
Ostojski Jan Zadania szkoły i organizacji paramilitarnych w kształtowaniu świadomości młodzieży w z
Zadania z treścia
Prezentacja 2 analiza akcji zadania dla studentow
więcej podobnych podstron