1. Cel ćwiczenia.

Celem ćwiczenia było zapoznanie się z różnymi rodzajami błędów pomiarowych, przyczynami ich powstawania oraz sposobami ich eliminacji z surowych wyników pomiarów.

Pojęcia podstawowe.

1. Błąd systematyczny jest to błąd, który przy wielokrotnym wykonywaniu pomiaru tej samej wartości wielkości mierzonej w tych samych warunkach ma wartość stałą lub zmienia się według określonego prawa. Błędy przypadkowe mają wartość zmieniającą się losowo, dla każdego pomiaru tej samej wielkości mają nieznaną przypadkową wartość. Błąd podstawowy jest to błąd w warunkach odniesienia, czyli przy umownie przyjętych stanach wielkości wpływających, w których określone są własności metrologiczne przyrządu (w tym błąd podstawowy).

2. Wyznaczanie charakterystyki.

Otrzymane wyniki wykorzystane zostały do aproksymacji charakterystyki wielomianami stopnia 2, 3 i 4-tego. Na wybranym odcinku charakterystyki wykonana została również aproksymacja liniowa.

3. Pomiary statystyczne dla jednego położenia rdzenia przetwornika.

przy czym wykorzystano tu następujące wzory:

• wartość średnia :
  

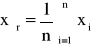
• odchylenie standardowe:
  

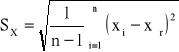
X_śr= -0,025

σ = 0,7980 - odchyłka standardowa

3.1. Eliminacja błędów grubych i oszacowanie wartości poprawnej.

W celu eliminacji błędów grubych przyjmujemy rozkład normalny błędów o parametrach: E(x)= x_śr i σ =S_X , oraz 3-sigmowy przedział ufności. Stąd dopuszczalny zakres wyników wejściowych wynosi:

[x_śr - 3 S_X , x_śr + 3 S_X] = [ -2,419 ; 2,369]

W naszych pomiarach wystąpił błąd gruby w jednym pomiarze dokonaliśmy eliminacji. Po eliminacji dopuszczalny zakres wyników wynosi:

[x_śr - 3 S_X , x_śr + 3 S_X] = [ -1,704 ; -3,084]

Zadaniem naszym było wyliczyć przedziały ufności dla trzech poziomów ufności

α=0,9

α=0,95

α=0,99

i dla różnej ilości próbek N

oraz wykazanie dla jakich α oraz N wzór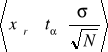
można zastąpić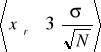

	0,9	0,95	0,99		[1]	[1]	[1]	[2]
N	tα(odczytane z tablic)			Sx	tα*Sx			3*Sx
2	2,92	4,303	9,925	0,543	1,586	2,337	5,391	1,630
5	2,015	2,571	4,032	0,344	0,692	0,883	1,385	1,031
10	1,812	2,228	3,169	0,243	0,440	0,541	0,770	0,729
20	1,725	2,086	2,831	0,172	0,296	0,358	0,486	0,515
30	1,697	2,042	2,75	0,140	0,238	0,286	0,386	0,421
40	1,684	2,021	2,704	0,121	0,205	0,245	0,328	0,364
60	1,671	2	2,66	0,099	0,166	0,198	0,264	0,298
120	1,658	1,98	2,617	0,070	0,116	0,139	0,184	0,210

Ponieważ w każdym przypadku X_śr było takie same wiec wystarczyło tylko sprawdzić jak zachowuje się człon ±
aby ocenić przedziały ufności.

Korzystając z testu „t” oszacujemy wartość poprawną na podstawie wzoru :

dla poziomów ufności : α = 0,90 , α = 0,95 dla którego odczytana z tablic wartość t_α wynosi t_α = 1,684 , t_α = 2,021.

-0,7362
-0,3888

-0,7709
-0,3541

W tych zakresach mieszczą się tylko wartości -0,5.

Obliczyliśmy również różnice między dwoma średnimi korzystając ze wzorów zawartych w protokole

X_śr1 = -0,562

X_śr2 = -0,401

S_x1,2 = 0,54

Badaliśmy czy dla poziomów ufności α = 0,90 , α = 0,95 zachodzi nierówność

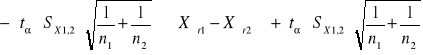
α = 0,90

-0,341≤-0,32≤0,341

α = 0,95

-0,409≤-0,32≤0,409

4. Uwagi i wnioski.

Charakterystyka została aproksymowana za pomocą wielomianów stopnia 2,3 i 4-tego.Tak jak można się było tego spodziewać im wyższy jest stopień wielomianu aproksymującego tym lepsze jest przybliżenie kształtu charakterystyki, wielomiany 2 i 3 stopnia znacznie odbiegają od kształtu wyznaczonej charakterystyki , natomiast kształt funkcje aproksymowanej wielomianem 4 stopnia prawie się pokrywa. załączone wykresy pokazują najlepiej jak ważny jest dobór odpowiedniej funkcji aproksymującej do przybliżenia otrzymanych wyników. Dodatkowo aproksymowaliśmy liniowa funkcje charakterystyki i współczynnik korelacji wyniósł 0,989. Błędny wybór daje tak duże odstępstwa iż praktycznie dyskwalifikuje przyjęte przybliżenie. Dokonaliśmy również wyznaczenia przedziału ufności z rozkładu studenta. Zauważyliśmy, że jest możliwe zastąpienie wzoru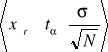
wzrorem

• jeżeli liczba próbek jest niewielka(N<3) i współczynnik poziomu ufności jest najmniejszy z zadanych w naszym ćwiczeniu

• oraz jeżeli liczba próbek jest większa (N>3) dla współczynnika α=0.99.

Dla serii 2*20 mieszczą się tylko wartości -0,5 w przedział wartości poprawnej obliczonej na podstawie wzoru.

Politechnika Śląska w Gliwicach

Laboratorium Podstaw Miernictwa

Błędy Systematyczne i Przypadkowe

Grupa : 5

Sekcja : 9

AEiI

Marcin Gala

Jarosław Pilch

Gliwice 03-12-2000

---