Marcin Łubik

Piotr Sroka

Krzysztof Witos

grupa nr 207

informatyka

Sprawozdanie z laboratorium z fizyki

Ćwiczenie nr 13

Temat ćwiczenia:

Wyznaczanie przyspieszenia ziemskiego przy pomocy wahadła rewersyjnego.

I Część teoretyczna

Przyspieszeniem ziemskim nazywamy przyspieszenie swobodnego spadku ciał pod wpływem ich ciężaru Q. Zgodnie z II Zasadą Dynamiki:

gdzie:

g - przyspieszenie ziemskie

m - masa ciała

Przyspieszenie ziemskie zmienia się w niewielkim zakresie w różnych punktach powierzchni ziemi ze względu na zmienność ciężaru. Ciężar jest wypadkową skierowanej do środka ziemi siły grawitacji oraz odśrodkowej siły bezwładności spowodowanej ruchem obrotowym ziemi wokół jej osi:

Q = F_g +F_b

Wartość siły bezwładności oraz jej kierunek względem kierunku siły grawitacji są zależne od szerokości geograficznej.

Natężenie pola grawitacyjnego:

Potencjał pola grawitacyjnego:

.

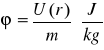
Moment siły

M- moment siły

F- przyłożona siła

R- ramię siły

Siła harmoniczna jest to siła proporcjonalna do przesunięcia ciała od początku układu i która jest skierowana ku początku układu. Jeżeli obierzemy oś x wzdłuż przesunięcia, to siła harmoniczna jest wyrażona równaniem F=-kx

gdzie x jest przesunięciem od położenia równowagi.

Równanie ruchu harmonicznego prostego przedstawia się następująco:

x(t)=Asin(ωt+ϕ) gdzie:

A-amplituda drgań

ω- częstość kątowa(związana z okresem drgań)

ϕ- faza początkowa.

Wahadłem rewersyjne jest wahadłem fizycznym o ustalonych osiach obrotu O₁ i O_2.

Położenie masy m₂ jest stałe, zaś masy m₁ - zmienne. Okres drgań wahadła fizycznego wyrażony jest wzorem :

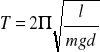
gdzie : I - moment bezwładności wahadła,

m - masa wahadła,

d - odległość osi obrotu wahadła od jego środka ciężkości.

Równanie to jest słuszne dla małych wychyleń wahadła z położenia równowagi. Zgodnie z Tw. Steinera:

I=I₀+md­²

gdzie :

I_{0 ­}- moment bezwładności wahadła wzgl. osi O, przechodzącej przez środek ciężkości wahadła.

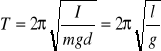
gdzie l - to jest długość zredukowana wahadła fizycznego i
.

Ze wzoru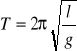
można obliczyć przyspieszenie ziemskie które będzie wynosiło

.

II Część laboratoryjna

t 1 [s]	t 2 [s]	t 3 [s]	t4 [s]	t 5 [s]	t 6 [s]	t 7 [s]	t 8 [s]	t 9 [s]	t 10 [s]	t [s]	S^'t [s]	tα,n	St [s]
16,03	17,61	17,76	17,76	17,82	17,70	17,76	17,79	17,75	17,73	17,57	0,16	2,26	0,36

Kn[cm]	5	10	15	20	25	30	35	40	45	50
t ' [s]	20,37	19,30	18,60	18,13	17,80	17,57	17,47	17,49	17,69	17,75
t '' [s]	20,08	19,68	19,32	19,09	18,98	18,97	18,76	18,77	18,81	18,87

Kn[cm]	55	60	65	70	75	80	85	90	95
t ' [s]	17,94	18,27	18,43	18,69	18,99	19,38	19,64	20,06	20,29
t '' [s]	18,85	19,03	19,13	19,32	19,51	19,75	19,95	20,13	20,41

to'[s]=19,9	to''[s]=20,9	to[s]=20,4	Δ to'[s]=0,1	Δ to[s]=0,4
To[s]=2	l[m]=1,00m	Δl[m]=0,01m	Δg[m/s^2]=9,48	g[m/s^2]=0,28

III Wzory i przykładowe obliczenia

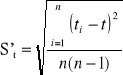
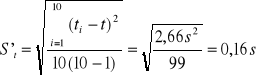
t_o=( t_o'+ t_o'')/2=(19,9s+20,9s)/2=20,4s

Δt₀=[(S_t²+(Δt₀')²]^0,5

Δt₀=(0,13s²+0,01s²)^0,5=0,37s

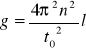
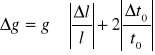
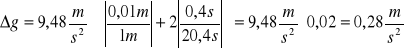
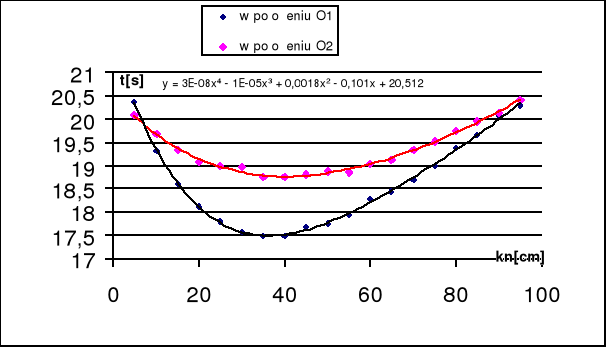
IV Wykres

Wynik końcowy

---