1. Cel ćwiczenia :

Określenie dla materiału użytkowego w doświadczeniu:

• Wytrzymałość na ściskanie (R_c),

• Moduł Younga (E).

Próbę statycznego ściskania stosuje się głównie przy badaniu materiałów kruchych, czyli nie wykazujących zdolności do znacznych odkształceń plastycznych (beton, cegła, skały). Materiały kruche mają znacznie większą wytrzymałość na ściskanie (R_c) niż wytrzymałość na rozciąganie (R_m).Cecha, która charakteryzuje materiały kruche jest właśnie wytrzymałość na ściskanie (R_c)

gdzie : P_c - największa wartość obciążenia ściskającego, przy którym następuje rozkruszenie próbki,

F₀ - pole początkowego przekroju próbki.

Jeżeli wykres ściskania l = f(P) ma część, w której skrócenie (l) jest wprost proporcjonalne do siły ściskającej (P), to na tej podstawie wyznaczamy dla tego materiału moduł Younga (E).

Wartość modułu Younga wyznacza się z prawa Hook'a:

gdzie : P - siła ściskająca,

Δl - skrócenie próbki odpowiadające sile (P)

l - początkowa wysokość próbki,

F₀ - pole powierzchni początkowej próbki, w naszym przypadku koło.

Ćwiczenie wykonałyśmy na dwóch próbkach. Pierwsza próbkę ściskałyśmy bez przeprowadzenia pomiarów jej skrócenia, zapisałyśmy tylko siłę przy której próbka uległa zniszczeniu, równą co do wartości 8100 [N]. Co pozwoliło nam określić, bezpieczną granice (około 60%) do której będziemy mogły wykonywać pomiary na drugiej próbce aby nie uszkodzić tensometrów. Pomiary drugiej próbki prowadziłyśmy co 200 [N].

2. Zestawienie pomiarów :

		próbka I	próbka II
siła, przy której nastąpiło zniszczenie próbki [N]	Pc	8100	6950
pole pierwotnego przekroju próbki [mm^2]	F0	1962,500	1962,500
wytrzymałość na ściskanie[MPa]	Rc	4,127	3,541
początkowa wysokość próbki [mm]	l	990	101

Pomiary uzyskane ze ściskania drugiej próbki :

Nr pomiaru	siła ściskająca [N]	Wielkość skrócenia próbki [mm]						Wartość modułu Younga [MPa]
				l1	Δl1	l2	Δl2		l3	Δl3
1	200	100,93	0,07	100,93	0,07	100,93	0,07	146,97
2	700	100,82	0,18	100,85	0,15	100,83	0,17	216,04
3	900	100,80	0,20	100,83	0,17	100,80	0,20	243,66
4	1100	100,78	0,22	100,81	0,19	100,77	0,23	265,23
5	1300	100,76	0,24	100,79	0,21	100,75	0,25	286,59
6	1500	100,74	0,26	100,77	0,23	100,73	0,27	304,57
7	1700	100,73	0,27	100,75	0,25	100,71	0,29	323,87
8	1900	100,72	0,28	100,74	0,26	100,70	0,30	349,05
9	2100	100,69	0,31	100,72	0,28	100,68	0,32	356,12
10	2300	100,68	0,32	100,70	0,30	100,66	0,34	369,72
11	2500	100,66	0,34	100,69	0,31	100,64	0,36	381,97
12	2700	100,66	0,34	100,67	0,33	100,62	0,38	396,81
13	2900	100,64	0,36	100,65	0,35	100,60	0,40	403,17
14	3100	100,60	0,40	100,64	0,36	100,59	0,41	408,87
15	3300	100,59	0,41	100,63	0,37	100,58	0,42	424,37

Wartość średnia modułu Younga:

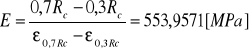
Wytrzymałość na ściskanie wyliczone

3. Wnioski :

Wykres ściskania l = f(P) ma część, w której skrócenie (l) jest wprost proporcjonalne do siły ściskającej (P), to na tej podstawie powinno się wyznaczyć dla badanej próbki materiału moduł Younga (E), jednak proporcjonalność na naszym wykresie może wynikać również z niedokładnego notowania pomiarów. Uzyskany przez nas wynik jest wyliczony z różnicy modułu dla wydłużenia równego 0,7 z pomiarów przeprowadzonych dla drugiej próbki, błędy które się pojawiły nie mają dużego wpływu na poprawność obliczeń, wynikać mogą jedynie z niedoskonałości oka obserwatora. Wynik jest zadawalający ponieważ niewiele różni się od danych tablicowych.

Jednak uzyskany wynik wytrzymałości na ściskanie (R_c) różni się dość znacznie od wartości tablicowy, wpływ na to mogła mieć jedynie wadliwość drugiej próbki, mogło się tak zdarzyć bo dane tablicowe są średnia arytmetyczną z wielu pomiarów, i być może gdybyśmy zrobiły pomiary większej ilości próbek, wynik uzyskany z pomiarów drugiej próbki odrzuciłybyśmy jako ten najmniejszy.

Z przeprowadzonego doświadczenia wynika, że materiały kruche (beton, szkło) mają mniejszy moduł sprężystości liniowej niż materiały plastyczne (stal), co za tym idzie betony dzięki zastosowaniu zbrojenia są doskonałym materiałem stosowanym w budownictwie. Wykazują również większą wytrzymałość na ściskanie niż na rozciąganie (beton od 5-20 razy większą).

POPRAWA :

		próbka I	próbka II
siła, przy której nastąpiło zniszczenie próbki [N]	Pc	8100	6950
pole pierwotnego przekroju próbki [mm^2]	F0	1962,500	1962,500
wytrzymałość na ściskanie[MPa]	Rc	4,127	3,541
początkowa wysokość próbki [mm]	l	990	101

Wartość średnia modułu Younga:

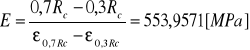
Wytrzymałość na ściskanie wyliczone

Wnioski :

Wnioski pozostają bez zmian, lecz wartość modułu Younga została policzona nie ze średniej arytmetycznej. Odrzuciłyśmy skrajne wartości które mogły zawyżać lub zaniżać uzyskaną wartość modułu Younga, dzięki temu wartość ta jest bardziej zbliżona do wartości oczekiwanej.

---