Publikacja opracowana podczas realizacji projektu „Plan Rozwoju Politechniki Częstochowskiej”

współfinansowanego przez Unię Europejską w ramach Europejskiego Funduszu Społecznego.

Jacek Przybylski

MECHANIKA

Materiały pomocnicze do wykładu
Przedmiot podstawowy w ramach kierunku Mechatronika– studia stacjonarne
inżynierskie. Semestr II.

Instytut Mechaniki i Postaw Konstrukcji Maszyn

POLITECHNIKA CZĘSTOCHOWSKA

Podstawowe pojęcia i prawa mechaniki

Mechanika klasyczna zwana także newtonowską jest nauką opisującą zagadnienia działania
sił i związane z tym problemy równowagi i ruchu ciał materialnych. Jakkolwiek historię
mechaniki tworzyli już Arystoteles (384-322 p.n. e.) i Archimedes (287-212 p.n. e.), to
dopiero Newton na przełomie XVII i XVIII wieku sformułował jej podstawowe prawa. Prawa
te wyrażone w zmodyfikowanej postaci przez d’Alemberta, Lagrange’a i Hamiltona są nadal
aktualne w odniesieniu do ciał materialnych poruszających się z prędkościami mniejszymi od
prędkości światła. Mimo poznanych ograniczeń mechaniki związanych z teorią względności
Einsteina i teorii kwantów Plancka, stanowi ona podstawę nauk inżynierskich.

Podstawowymi pojęciami mechaniki, które nie są jednoznacznie definiowalne są:
- przestrzeń
- czas
- masa
- siła.


Prawa Newtona

1. Jeżeli siła wypadkowa działająca na punkt materialny jest równa zeru, to punkt ten

pozostaje w spoczynku (jeśli był w spoczynku przed przyłożeniem sił) lub porusza się ze
stałą prędkością wzdłuż linii prostej (jeśli początkowo był w ruchu).

2. Jeżeli siła wypadkowa działająca na punkt materialny o masie m nie jest równa zeru, to

punkt ten będzie się poruszał z przyspieszeniem proporcjonalnym do wartości tej siły i
zgodnie z jej zwrotem i kierunkiem

m

F

a

=

3. Siły wzajemnego oddziaływania między ciałami znajdującymi się w kontakcie mają tę

samą wartość, linię działania i przeciwny zwrot.

Podział mechaniki klasycznej

1. Statyka. W ramach statyki bada się zagadnienia równowagi układów sił działających na

ciała pozostające w spoczynku.

2. Kinematyka. W kinematyce opisuje się ruch ciał bez uwzględniania sił wywołujących ten

ruch.

3. Dynamika. Dynamika dotyczy ruchu ciał powstającego na skutek działania określonego

układu sił.

W mechanice ciała materialne są aproksymowane modelami idealnymi takimi jak punkt
materialny lub ciało doskonale sztywne.
Punkt materialny to ciało o znikomo małych rozmiarach; w trakcie jego ruchu pomija się
zmiany położenia wywołane przez obrót. Ciało doskonale sztywne to ciało stałe, którego dwa
dowolne punkty nie zmieniają wzajemnej odległości pod wpływem przyłożonego obciążenia.

3

STATYKA
Elementy rachunku wektorowego

Wielkości występujące w naukach fizykalnych to wielkości skalarne (skalarowe) lub
wielkości wektorowe. Wielkości skalarowe są określane przez podanie ich wartości.
Wielkości wektorowe określa się przez podanie ich wartości, kierunku i zwrotu. Dodatkowo
w przypadku wektorów nieswobodnych należy podać ich punkt zaczepienia.


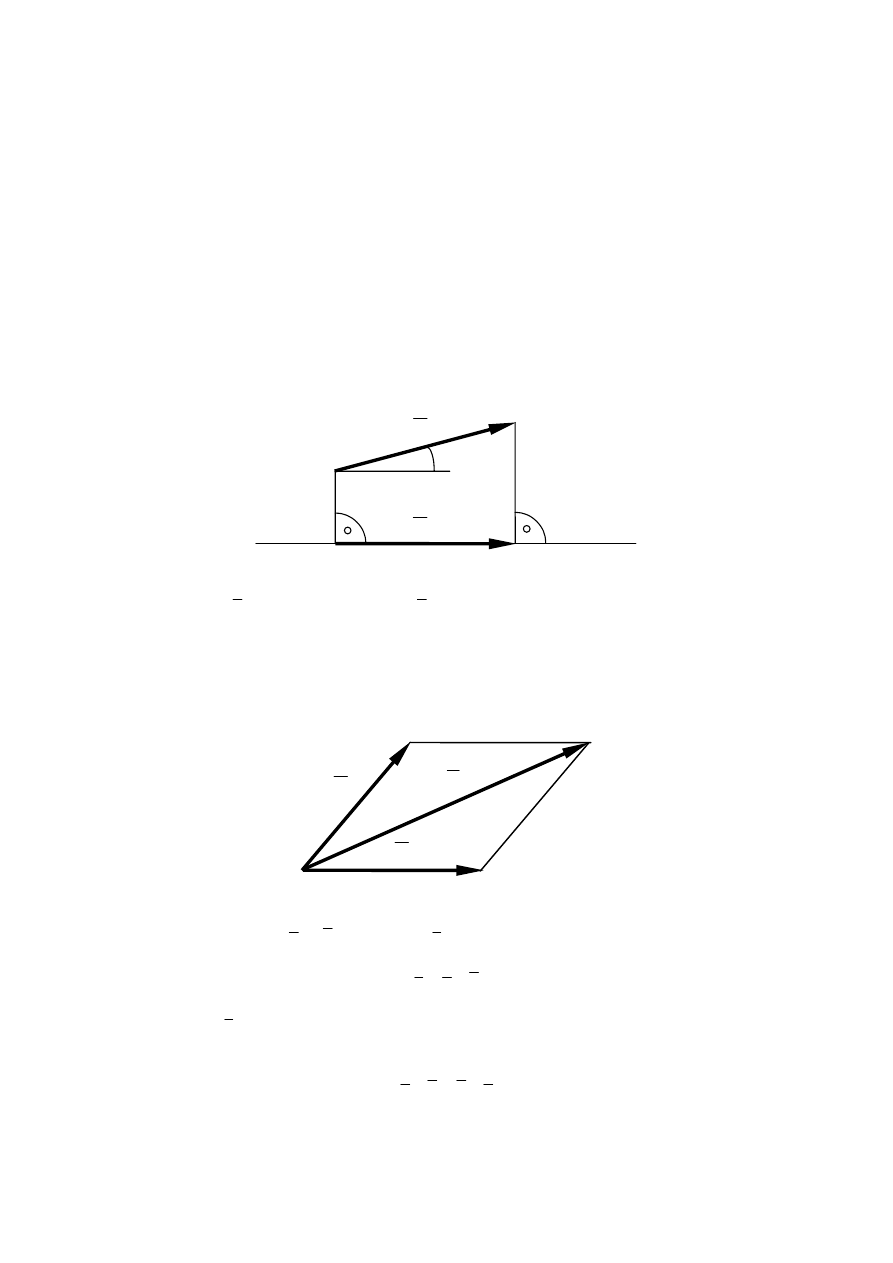
Rzut wektora na prostą

a

a′

l

α

Rzutem wektora

a na prostą l jest wektor

a′

leżący na tej prostej o module

α

cos

a

a

=

′

Suma dwóch wektorów

b

a

c

Sumą dwóch wektorów

a i b jest wektor c wychodzący z punktu przyłożenia i leżący na

przekątnej równoległoboku

b

a

c

+

=

Moduł wektora

c jest równy długości przekątnej równoległoboku.

Prawo przemienności dodawania wektorów

a

b

b

a

+

=

+

4

Odejmowanie wektorów

b

−

a

c

b

( )

b

a

b

a

c

−

+

=

−

=

Odejmowanie wektorów polega na dodawaniu wektora przeciwnego. Wektorem przeciwnym
do wektora

b jest wektor b

− o tym samym kierunku, module i przeciwnym zwrocie. Suma

wektora i wektora przeciwnego jest równa zeru, stąd takie dwa wektory noszą nazwę dwójka
zerowa.

( )

b

a

b

a

c

−

+

=

−

=

Mnożenie wektora przez liczbę

Przy mnożeniu wektora przez liczbę dodatnią kierunek i zwrot wektora pozostają nie
zmienione, natomiast zmianie ulega jego moduł.

O

b

a

0

>

k

a

k

b

=

Składowe wektora w prawoskrętnym kartezjańskim układzie współrzędnych

W układzie współrzędnych prostokątnych wektor może być rozłożony na trzy składowe o
kierunkach osi układu współrzędnych.

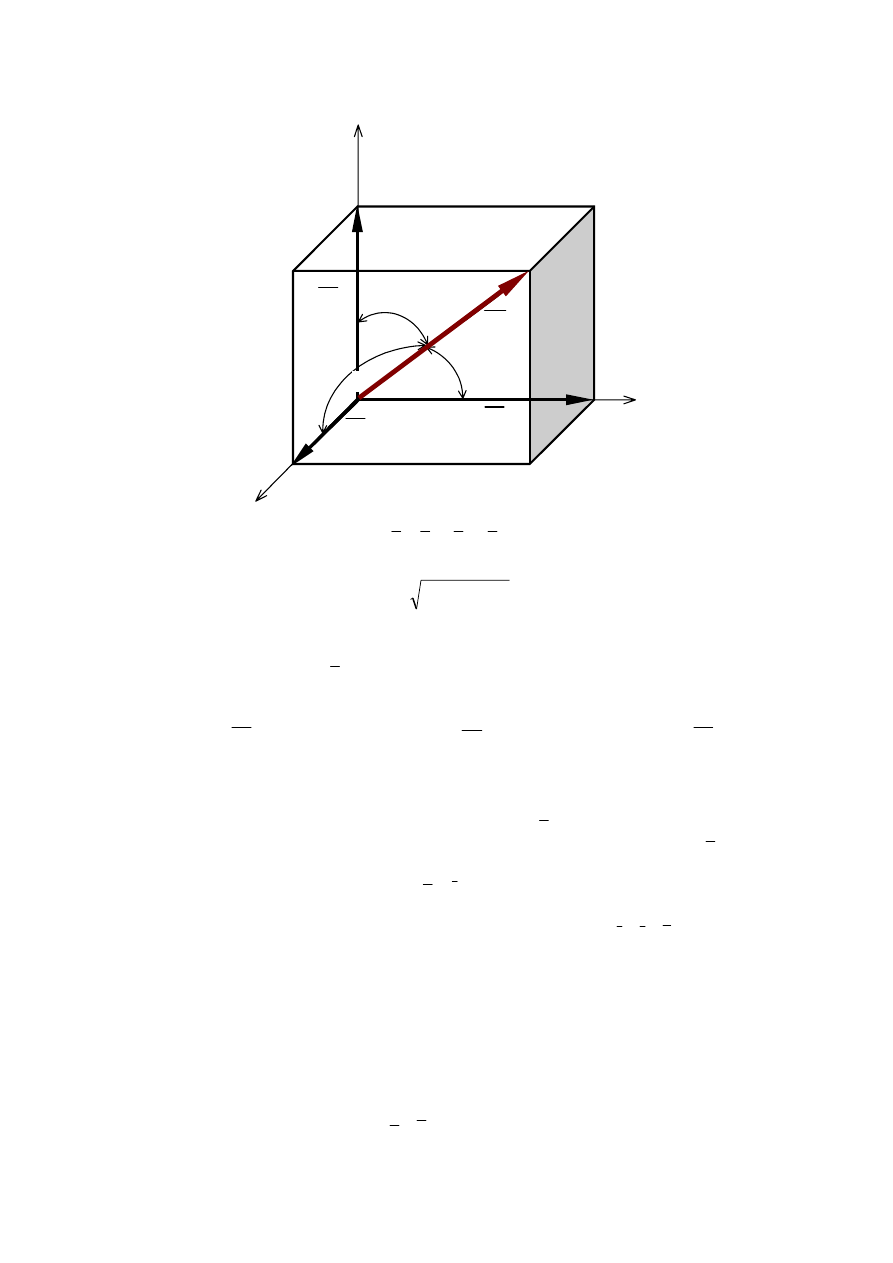
5

α

β

γ

a

y

a

x

a

z

a

x

y

z

z

y

x

a

a

a

a

+

+

=

2

2

2

z

y

x

a

a

a

a

+

+

=

Cosinusy kierunkowe wektora

a

a

a

x

=

α

cos

,

a

a

y

=

β

cos

,

a

a

z

=

γ

cos

Wektor jednostkowy (wersor)
Wersorem (wektorem jednostkowym) danego wektora a nazywamy wektor o module
równym jedności mającym kierunek i zwrot zgodny z modułem równym wektora

a .

a

i

a

=

Wersory osi układu współrzędnych x, y i z są oznaczane odpowiednio i ,

j

, k .

Iloczyn skalarny dwóch wektorów

Iloczynem skalarnym dwóch wektorów jest skalar o wartości iloczynu mnożonych wektorów
i cosinusa kąta zawartego między tymi wektorami

a

·

b = a b cos

α

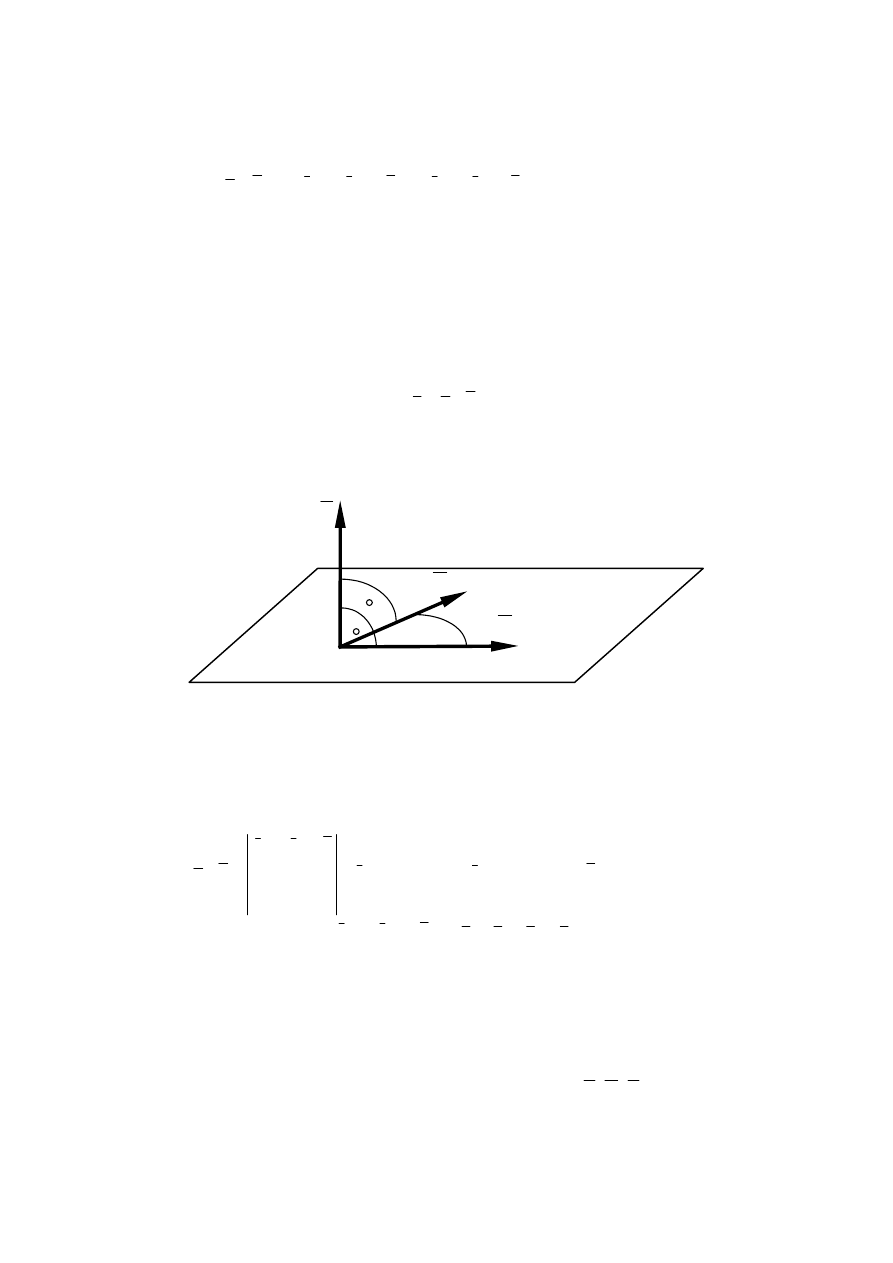
6

Wyrażając mnożone wektory przez sumy geometryczne ich składowych, iloczyn skalarny
będzie równy

a

·

b =

(

)

k

a

j

a

i

a

z

y

x

+

+

·

(

)

k

b

j

b

i

b

z

y

x

+

+

=

z

z

y

y

x

x

b

a

b

a

b

a

+

+

Iloczyn wektorowy dwóch wektorów

Iloczynem wektorowym dwóch wektorów niekolinearnych jest wektor prostopadły do
płaszczyzny utworzonej przez mnożone wektory i module równym iloczynowi modułów tych
wektorów przez sinus kąta zawartego między tymi wektorami

b

a

c

×

=

,

gdzie:

c = a b sin

α

α

a

b

c

π

Zwrot wektora w przypadku prawoskrętnego układu współrzędnych ustala reguła trzech
palców prawej dłoni.
Wykorzystując własności wyznacznika iloczyn wektorowy dwóch wektorów wyraża się
następująco:

(

)

(

)

(

)

=

−

+

−

+

−

=

=

×

x

y

y

x

z

x

x

z

y

z

z

y

z

y

x

z

y

x

b

a

b

a

k

b

a

b

a

j

b

a

b

a

i

b

b

b

a

a

a

k

j

i

b

a

c

c

c

c

c

k

c

j

c

i

z

y

x

z

y

x

=

+

+

=

+

+

=

Siła jako wektor liniowy

Podstawowym pojęciem wektorowym w mechanice jest siła. W tekstach drukowanych
wektory sił oznacza się dużymi literami z kreską u góry (

,...)

,

,

P

G

F

, bądź drukiem

wytłuszczonym (F, G, P,...). Zapis ten jest stosowany w dalszej części wykładu.

7

Siła jest wyrazem i miarą wzajemnego oddziaływania ciał na siebie, przy czym siły mogą być
wywierane bezpośrednio w wyniku kontaktu ciał, bądź mogą być wywierane na odległość.
Siły zewnętrzne to siły działające na punkty materialne danego układu wywołane działaniem
innego układu, siły wewnętrzne to siły oddziaływania między punktami materialnymi układu.
Siły czynne to siły, które dążą do wprowadzenia ciała w ruch; siły bierne wyrażają działanie
więzów.


Więzy

W statyce rolę więzów pełnią podpory.
Rodzaje podstawowych podpór podano w tabelach.

Podpory o znanych kierunkach reakcji

R

R

Podpora gładka

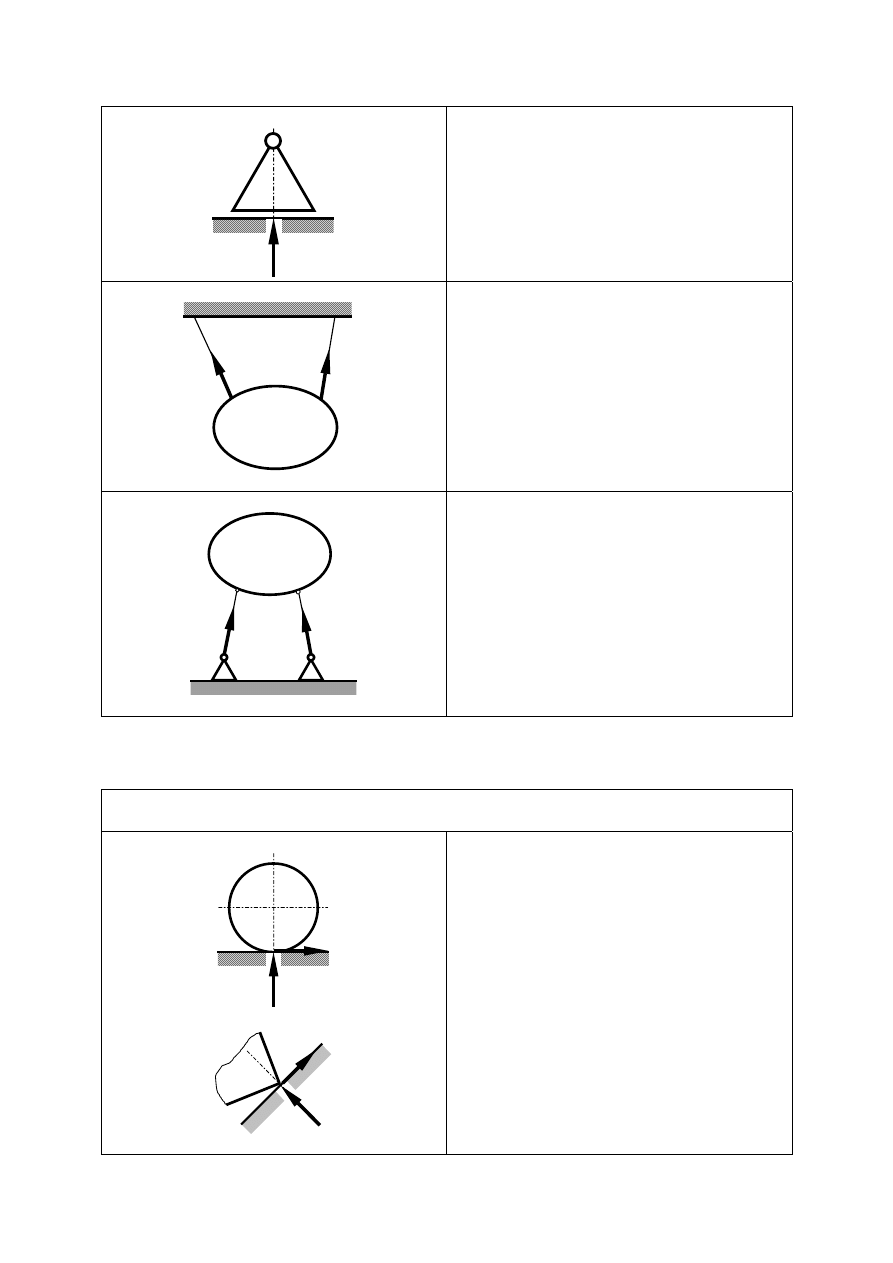
8

R

Podpora przegubowa przesuwna

R

1

R

2

Cięgno

R

1

R

2

Nieważkie pręty przegubowe

Podpory o nieznanych kierunkach reakcji

R

T

R

T

Podparcie szorstkie

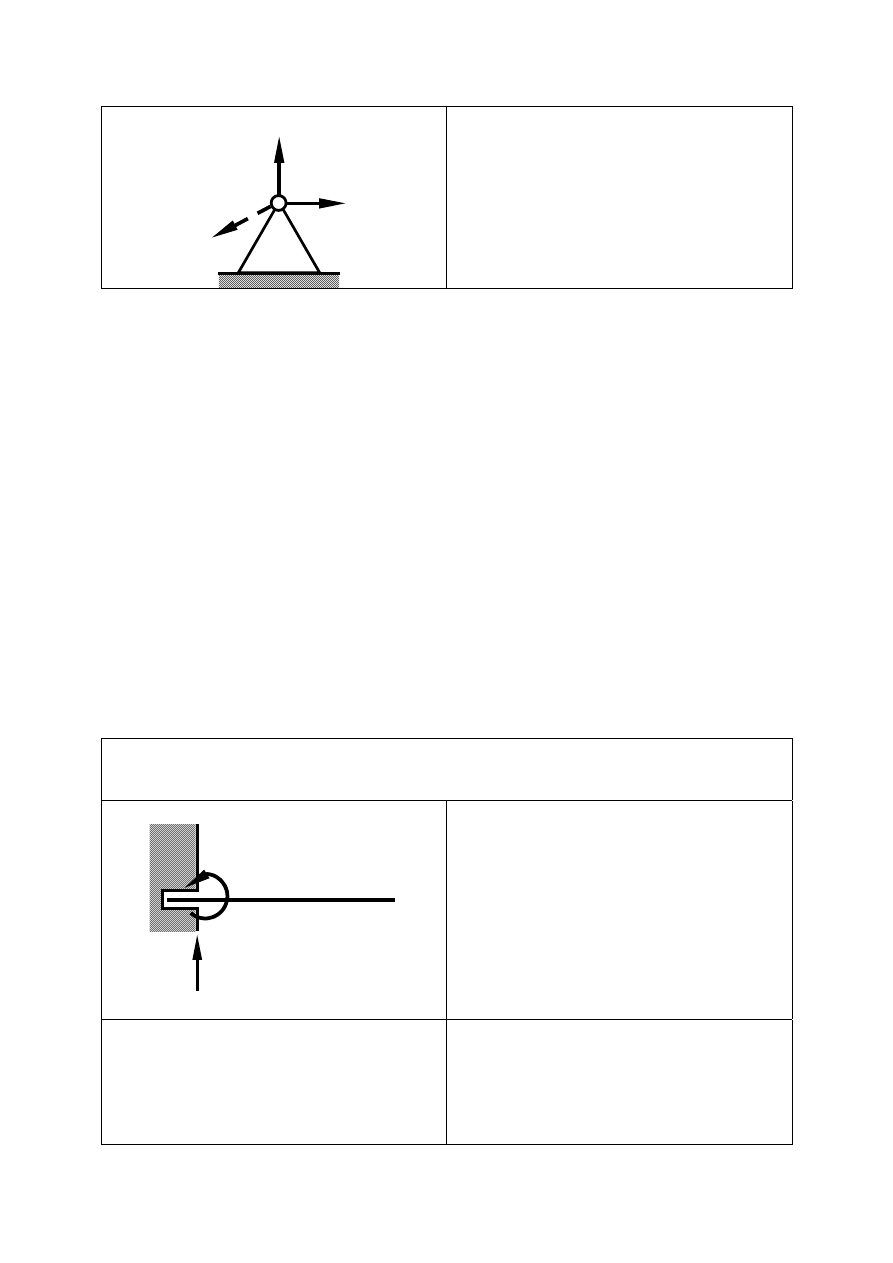
9

R

Ay

R

Ax

(R

Az

)

A

Podpora przegubowa przesuwna

(układ płaski – 2 składowe reakcji;

układ przestrzenny 3 składowe reakcji

)

Utwierdzenia

R

y

M

- przesuwne

(w układzie przestrzennym należy dodać

drugą składową reakcji i drugą składową

wektora momentu

)

- sztywne

(w układzie przestrzennym należy dodać

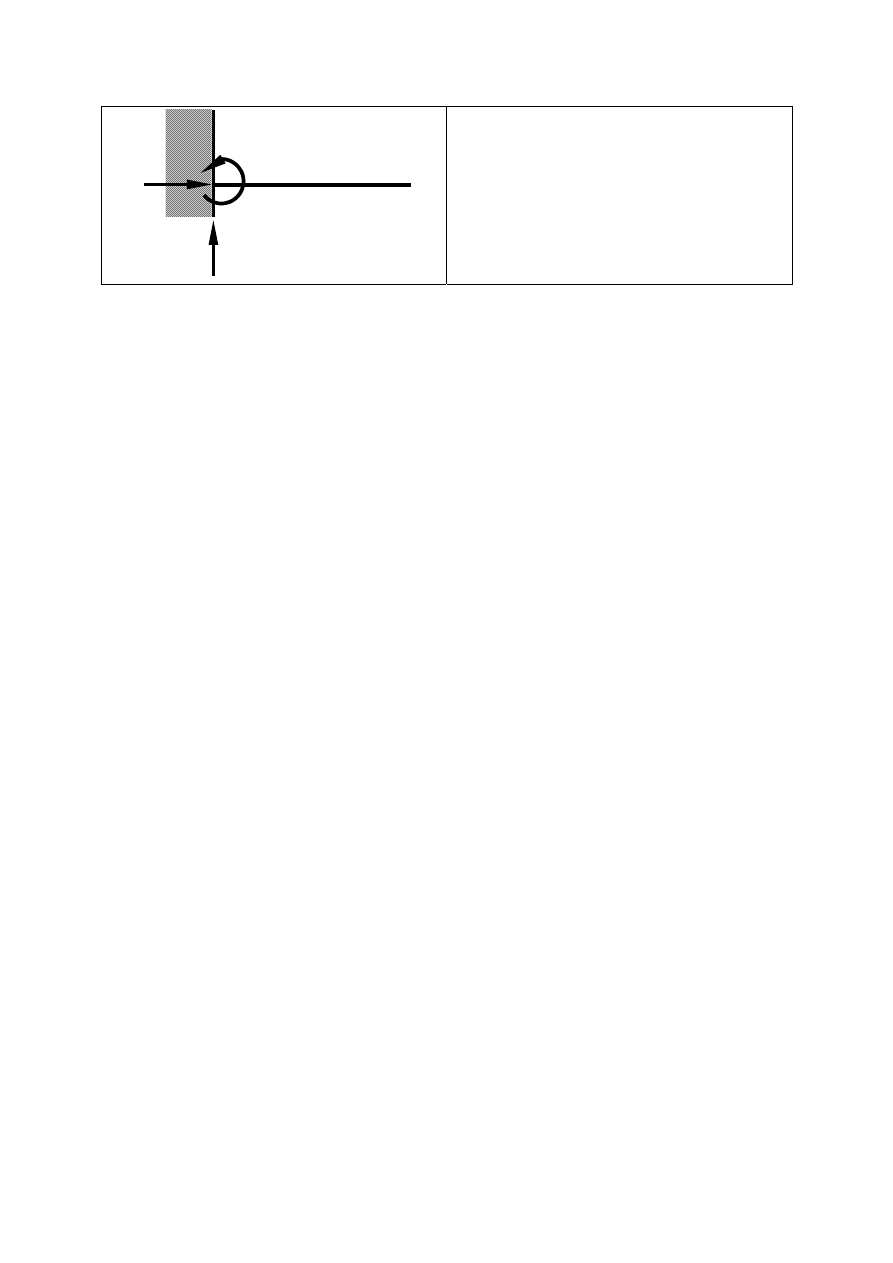
10

R

y

M

R

x

trzecią składową reakcji i dwie składowe

wektora momentu

)

Moment siły względem punktu i prostej

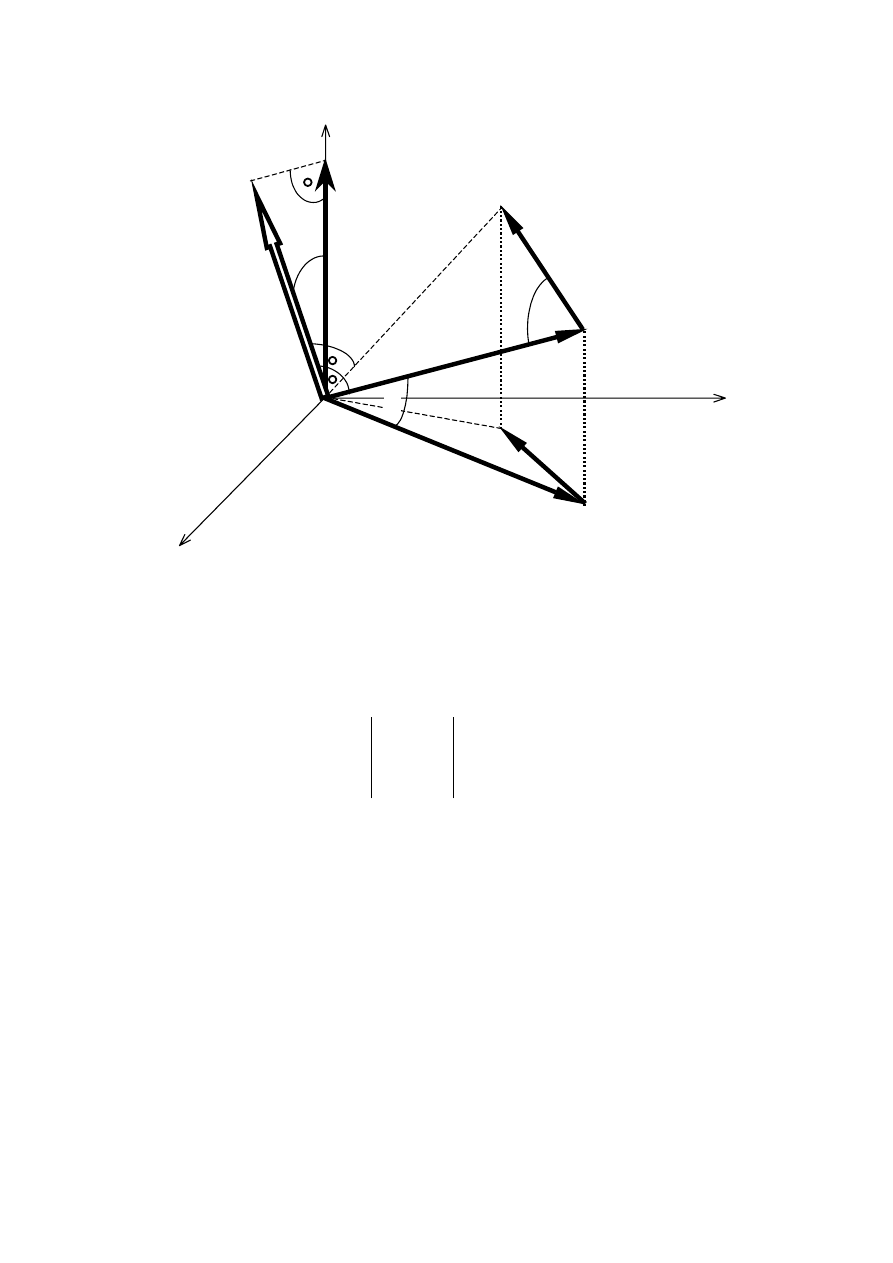
Moment siły względem punktu

Moment siły P względem punktu O jest wektorem otrzymanym w wyniku mnożenia
wektorowego promienia wektora r (ramienia) i siły P

M

O

= r

×

P

Ramię r jest wektorem poprowadzonym od punktu O do początku siły P, a moduł wektora
M

O

jest równy podwojonemu polu powierzchni trójkąta OAB:

M

O

= P r sin

ϕ

Moduł wektora momentu można przedstawiać jako iloczyn siły i ramienia poprowadzonego
od punktu O pod kątem prostym do linii działania siły:

M

O

= P h

Na podstawie podanego rysunku łatwo sprawdzić, że

h

= r sin (180 -

ϕ

) = r sin

ϕ

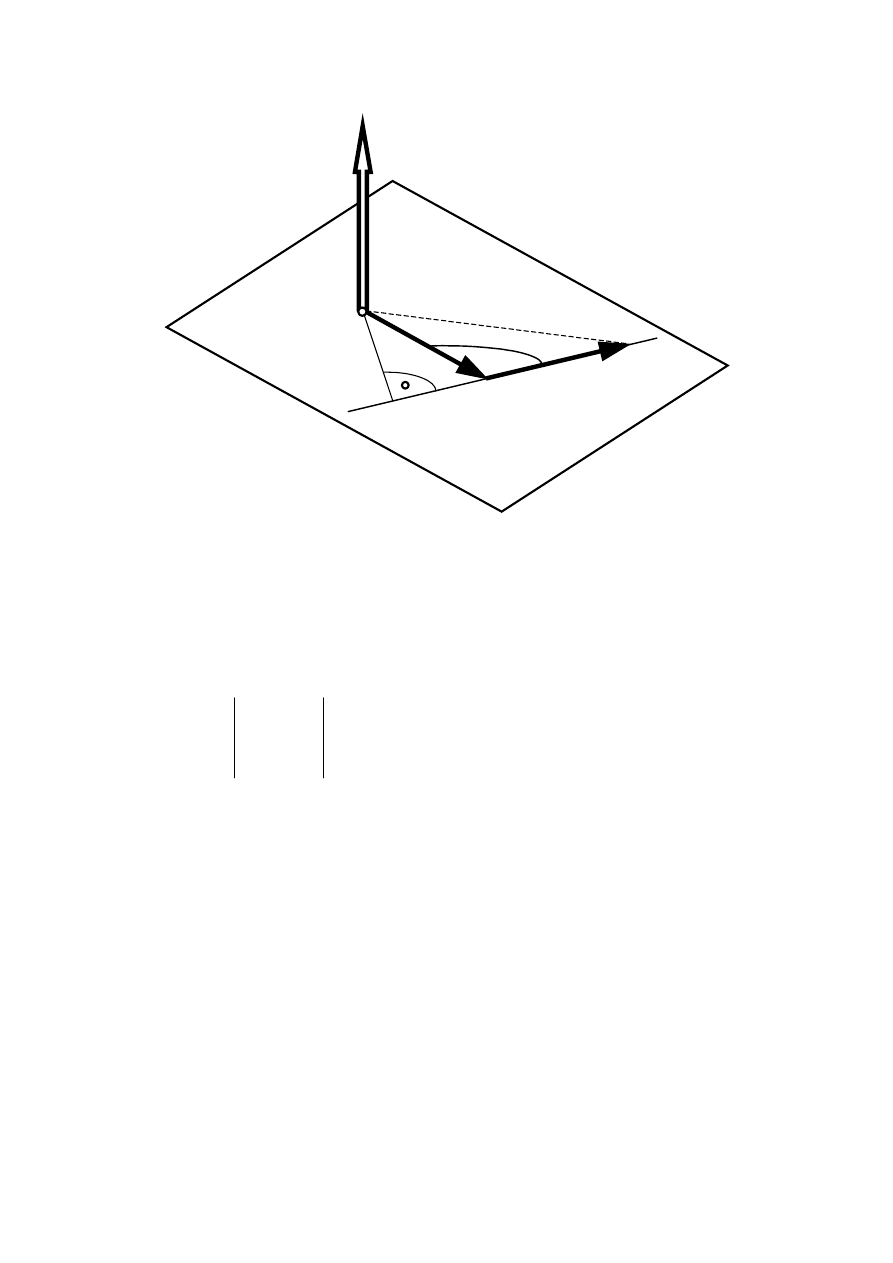
11

O

ϕ

M

O

P

r

h

A

B

Umieszczając wektory siły i ramienia w przestrzeni względem układu współrzędnych
kartezjańskich o początku w punkcie O i zapisując je jako sumy geometryczne rzutów na osie
tego układu, ich iloczyn wektorowy przyjmie postać

M

O

= r

×

P

= (i r

x

+ j r

y

+ k r

z

)

×

(i P

x

+ j P

y

+ k P

z

) =

=

z

y

x

z

y

x

P

P

P

r

r

r

k

j

i

=

(

)

(

)

(

)

x

y

y

x

z

x

x

z

y

z

z

y

P

r

P

r

P

r

P

r

P

r

P

r

−

+

−

+

−

k

j

i

=

=

(

)

(

)

(

)

x

y

y

x

z

x

x

z

y

z

z

y

P

r

P

r

P

r

P

r

P

r

P

r

−

+

−

+

−

k

j

i

=

=

z

y

x

M

M

M

k

j

i

+

+

=

M

x

+

M

y

+

M

z

Moment siły względem początku układu współrzędnych (punktu O) jest więc sumą
momentów względem osi

x, y i z. Z tego wyprowadzenia wynika definicja momentu siły

względem prostej.

12

x

y

z

O

A

B

ϕ

γ

γ

M

O

P

r

r'

P'

B'

A'

M

z

Moment siły względem prostej

Na podstawie rysunku moment siły

P względem prostej (osi) z można zdefiniować jako

moment rzutu tej siły (

P’) na płaszczyznę prostopadłą do tej prostej względem punktu

przebicia tej prostej z tą prostopadłą płaszczyzną, czyli

=

=

′

×

′

=

0

0

y

x

y

x

z

P

P

r

r

k

j

i

P

r

M

(

)

z

x

y

y

x

M

P

r

P

r

k

k

=

−

Moduł tego wektora można więc wyrazić następująco:

γ

cos

Ο

=

−

=

M

P

r

P

r

M

x

y

y

x

z

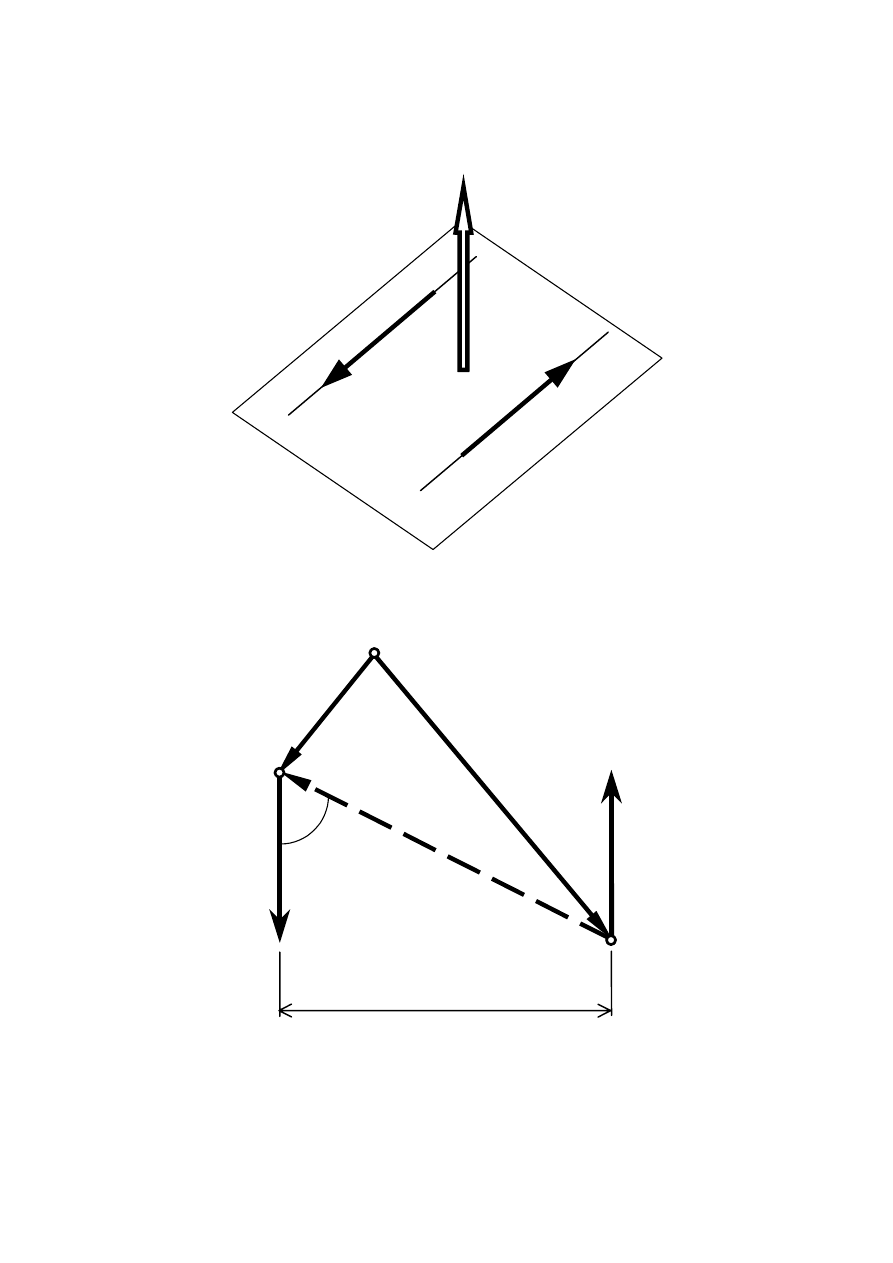
Para sił

Parą sił nazywamy układ dwóch sił równoległych o równych modułach i przeciwnych
zwrotach. Suma pary sił jest równa zeru, ale siły te nie równoważą się gdyż nie działają
wzdłuż jednej prostej.
Para sił jest elementarnym układem, który nie może być zastąpiony jedną siłą, ponieważ nie
ma wypadkowej.

13

Para sił jest równoważna wektorowi momentu M, którego kierunek jest prostopadły do
płaszczyzny wyznaczonej przez linie działania sił pary. Zwrot wektora momentu wynika z
reguły śruby prawoskrętnej.

M

P

-P

Moment pary sił względem bieguna O

O

ϕ

h

r

P

1

P

2

r

2

r

1

O

1

Przy założeniu, że P

1

= P, P

2

= - P, moment pary sił względem bieguna O jest równy:

M

O

= r

1

×

P

1

+ r

2

×

P

2

= r

1

×

P

-

r

2

×

P = (r

1

-

r

2

)

×

P = r

×

P

14

Ławo zauważyć, że ramię r

=

r

1

-

r

2

nie zależy od położenia punktu O. Stąd wynika

wniosek, że moment pary sił zależy jedynie od wartości tych sił i ich wzajemnej odległości.
Na podstawie rysunku moduł wektora momentu pary sił jest równy

h

P

P

r

M

sin

1

=

=

Ο

ϕ

Moment pary sił jest wektorem swobodnym, ponieważ nie zależy od punktu na płaszczyźnie,
względem którego jest obliczany. Parę sił można więc przenosić w płaszczyźnie jej działania.

Redukcja dowolnego przestrzennego układu sił

Redukcja układu sił polega na zastąpieniu go innym prostszym, którego skutek działania na
ciało materialne jest identyczny z tym jaki wynika z działania układu niezredukowanego.

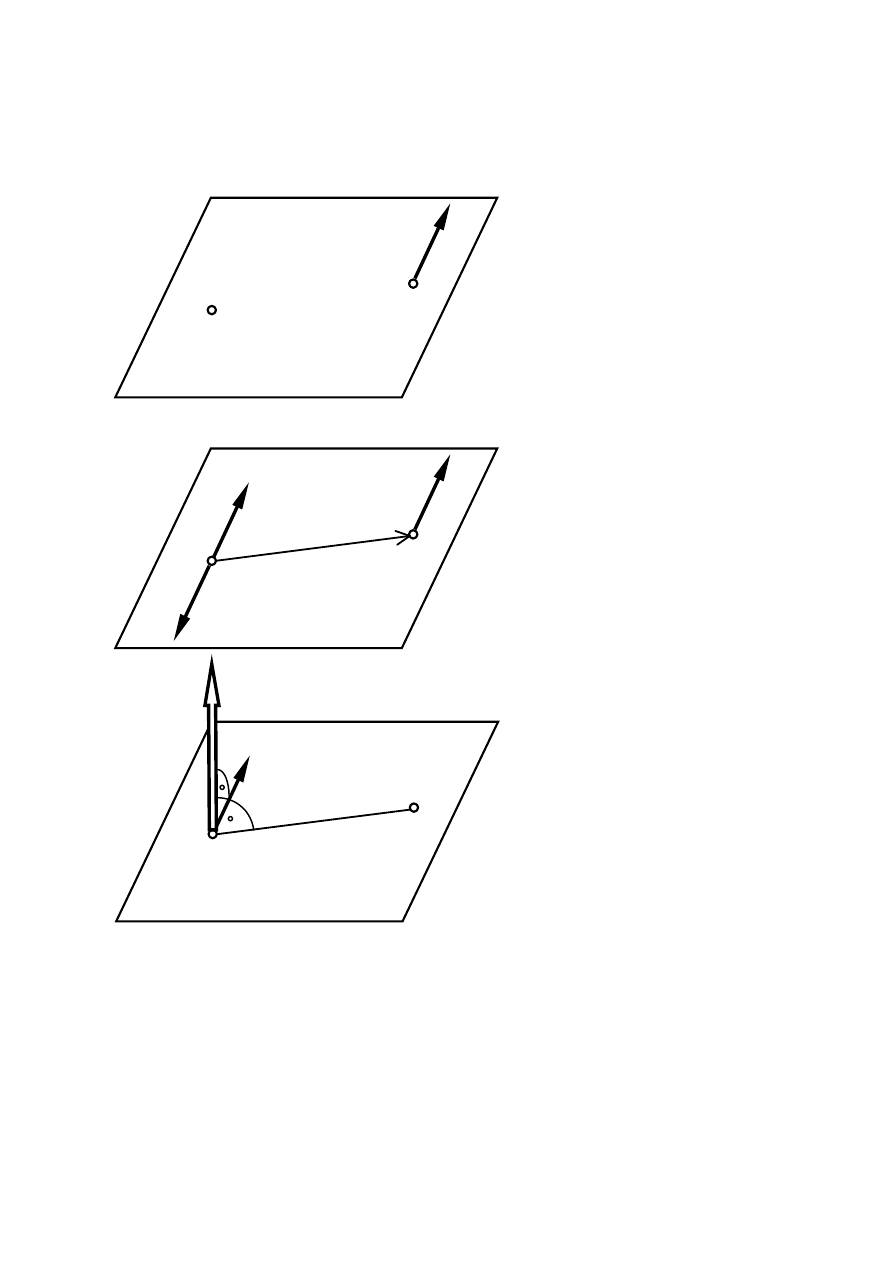
Redukcja siły do punktu

15

O

A

P

O

A

P

P

-P

r

O

A

P

M

O

Zadanie polega na przeniesieniu
siły P działającej w punkcie A do
punktu O bez zmiany efektu
oddziaływania tej siły na ciało
materialne.







W tym celu w punkcie O
przykładamy dwójkę zerową
złożoną z sił P i – P. Wektor
ramienia r wyznacza położenie
punktu A względem punktu O.
Siła P przyłożona w punkcie A
i siła -P zaczepiona w punkcie O
tworzą parę sił o momencie M

O

:

M

O

= r

×

P

Wniosek:
Przesunięciu siły z jednego
punktu do drugiego towarzyszy
dodanie momentu siły zależnego
od punktu końcowego przesu-
nięcia. Wektor momentu ma
kierunek prostopadły do
płaszczyzny odpowiedniej pary.

16

Redukcja układu n sił do punktu

x

y

z

O

β

M

O

P

1

M

1

P

2

M

2

P

n

M

n

P

Każda siła układu n sił jest przesuwana do
punktu O, który jest środkiem redukcji.
Przesunięciu siły P

i

towarzyszy dodanie

odpowiedniego wektora momentu M

i

, który

ma kierunek prostopadły do wektora siły
(M

i

⊥ P

i

).

Po geometrycznym dodaniu wszystkich
wektorów sił otrzymuje się główny wektor
siły

:

∑

=

=

n

i

i

1

P

P

Geometryczna suma wektorów momentów
daje wektor głównego momentu:

∑

=

=

n

i

i

1

O

M

M

Redukcja układu sił umożliwia więc zastąpienie go dwoma wektorami: głównym wektorem
siły P i wektorem głównego momentu M

O

. W ogólnym przypadku oba wektory mają linie

działania nachylone pod dowolnym kątem zaznaczonym na rysunku jako

β.

Niezmienniki układu sił

1. Główny wektor siły jest niezmiennikiem, ponieważ nie zależy on od położenia środka

redukcji (punktu O). Wektor głównego momentu nie jest niezmiennikiem – jego wielkość
jest zdeterminowana położeniem środka redukcji.

2. Iloczyn skalarny głównego wektora siły i wektora głównego momentu

P

·

M

O

= const = P M

O

cos

β

Analityczny warunek równowagi dowolnego przestrzennego układu sił

Dowolny przestrzenny układ sił redukuje się do wektora głównego i momentu głównego

∑

=

=

n

i

i

1

P

P

∑

=

=

n

i

i

1

O

M

M

Równowaga takiego układu sił możliwa jest tylko wtedy i tylko wtedy gdy suma
geometryczna wszystkich sił jest równa zeru oraz gdy suma geometryczna momentów od
wszystkich sił względem punktu O jest równa zeru

0

1

=

=

∑

=

n

i

i

P

P

0

1

O

=

=

∑

=

n

i

i

M

M

17

Wiedząc, że

0

1

1

1

1

=

+

+

=

=

∑

∑

∑

∑

=

=

=

=

n

i

iz

n

i

iy

n

i

ix

n

i

i

P

P

P

k

j

i

P

P

0

1

1

1

1

O

=

+

+

=

=

∑

∑

∑

∑

=

=

=

=

n

i

iz

n

i

iy

n

i

ix

n

i

i

M

M

M

k

j

i

M

M

powyższe równania mogą być spełnione tylko wtedy, gdy

0

1

=

∑

=

n

i

ix

P

0

1

=

∑

=

n

i

iy

P

0

1

=

∑

=

n

i

iz

P

0

1

=

∑

=

n

i

ix

M

0

1

=

∑

=

n

i

iy

M

0

1

=

∑

=

n

i

iz

M

Sześć powyższych równań tworzy analityczny warunek równowagi dowolnego
przestrzennego układu sił, który ma następujące brzmienie:

Przestrzenny dowolny układ sił jest w równowadze gdy sumy rzutów tych sił na osie układu

współrzędnych oraz sumy momentów tych sił względem osi układu współrzędnych są równe

zeru

Metody analityczne w statyce układów płaskich

Z płaskim układem sił mamy do czynienia gdy linie działania wszystkich sił układu leżą w
jednej płaszczyźnie. W tym przypadku wektor główny siły P znajduje się także w
płaszczyźnie układu, a wektor głównego momentu M

O

jest prostopadły do tej płaszczyzny.

x

y

z

O

M

O

P

18

Wektor główny ma więc dwie składowe w rzutach na osie układu współrzędnych, a wektor
głównego momentu ma jedną składową.
Wektorowy warunek równowagi płaskiego układu sił prowadzi do równań

0

1

1

1

=

+

=

=

∑

∑

∑

=

=

=

n

i

iy

n

i

ix

n

i

i

P

P

j

i

P

P

0

1

1

O

O

O

=

=

=

∑

∑

=

=

n

i

i

n

i

i

M

k

M

M

,

które będą spełnione gdy

0

1

=

∑

=

n

i

ix

P

0

1

=

∑

=

n

i

iy

P

0

1

=

∑

=

Ο

n

i

i

M

Płaski dowolny układ sił jest w równowadze gdy sumy rzutów wszystkich sił na osi x i y
układu współrzędnych oraz moment od wszystkich sił względem punktu O są równe zeru.



Alternatywne warunki równowagi kładu płaskiego dowolnego:
a)

0

1

=

∑

=

n

i

ix

P

0

1

=

∑

=

Α

n

i

i

M

0

1

=

∑

=

Β

n

i

i

M

,

przy czym punkty A i B nie mogą leżeć na prostej prostopadłej do osi x.

b)

0

1

=

∑

=

Α

n

i

i

M

0

1

=

∑

=

Β

n

i

i

M

,

0

1

C

=

∑

=

n

i

i

M

przy czym punkty A, B i C nie mogą leżeć na jednej prostej.

19

Układy płaskie zbieżne i złożone

Układ sił płaski zbieżny (środkowy) to taki układ, w którym wektorów sił leżących w jednej
płaszczyźnie przecinają się w jednym punkcie.
Warunek analityczny równowagi takiego układu jest następujący:

0

1

=

∑

=

n

i

ix

P

0

1

=

∑

=

n

i

iy

P

Układ płaski złożony tworzy kilka lub kilkanaście ciał materialnych połączonych ze sobą
więzami. Rozwiązanie układu złożonego polega na rozdzieleniu poszczególnych ciał
i zapisaniu warunków równowagi dla każdej z brył z osobna.

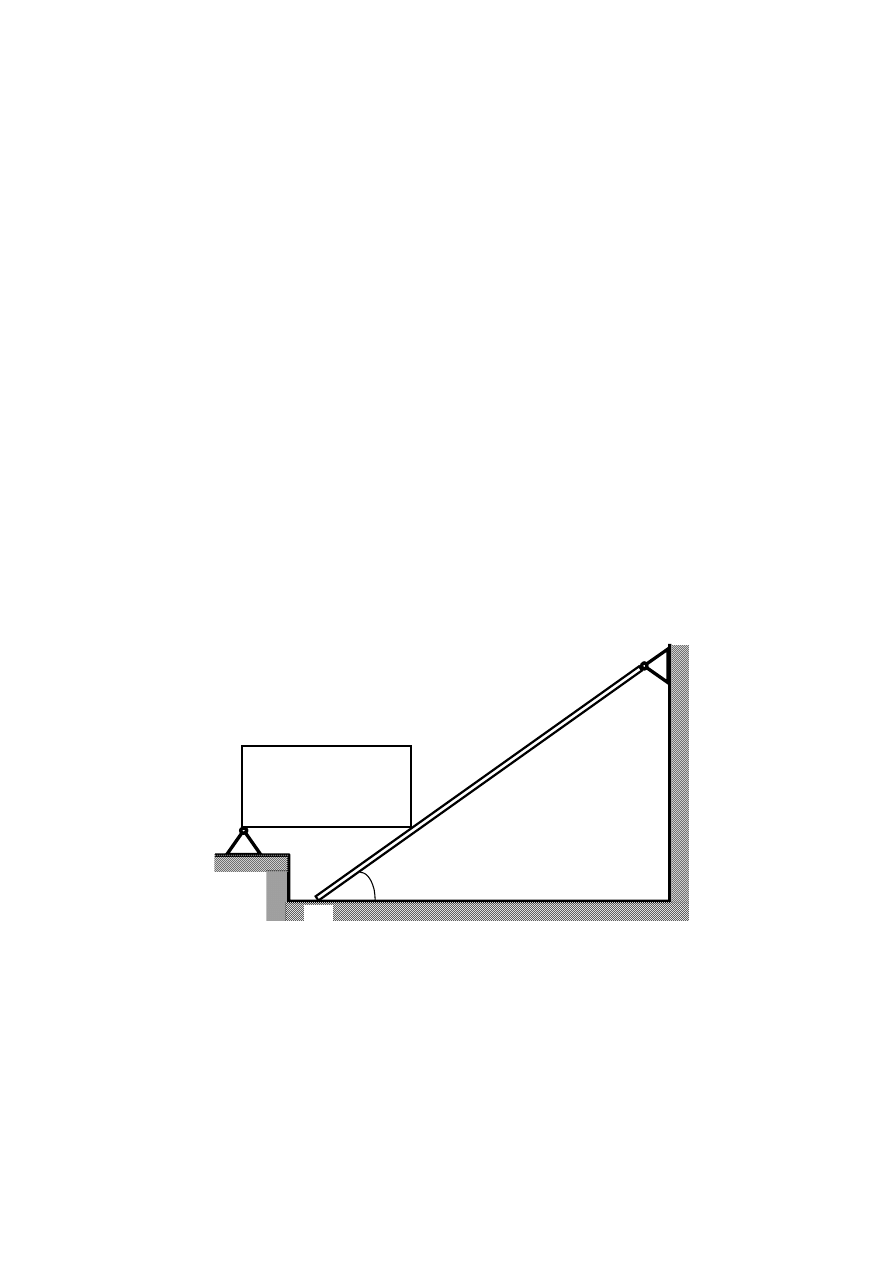
Poniżej zaprezentowany układ jest złożony z dwóch ciał materialnych: płyty i belki. Płyta
wsparta jest w punkcie A na podporze przegubowej stałej, natomiast w punkcie D opiera się o
belkę. Belka jest zamocowana na podporze przegubowej w punkcie B i jest oparta o płaskie
sztywne podłoże w punkcie C. Znając masy belki i płyty, kąt nachylenia belki do poziomu
oraz wymiary geometryczne obu elementów można, po rozdzieleniu obu ciał, wyznaczyć
reakcje we wszystkich wskazanych punktach zapisując sześć równań wynikających z
warunku równowagi dla układu płaskiego dowolnego.

A

B

D

α

C

Kratownice płaskie

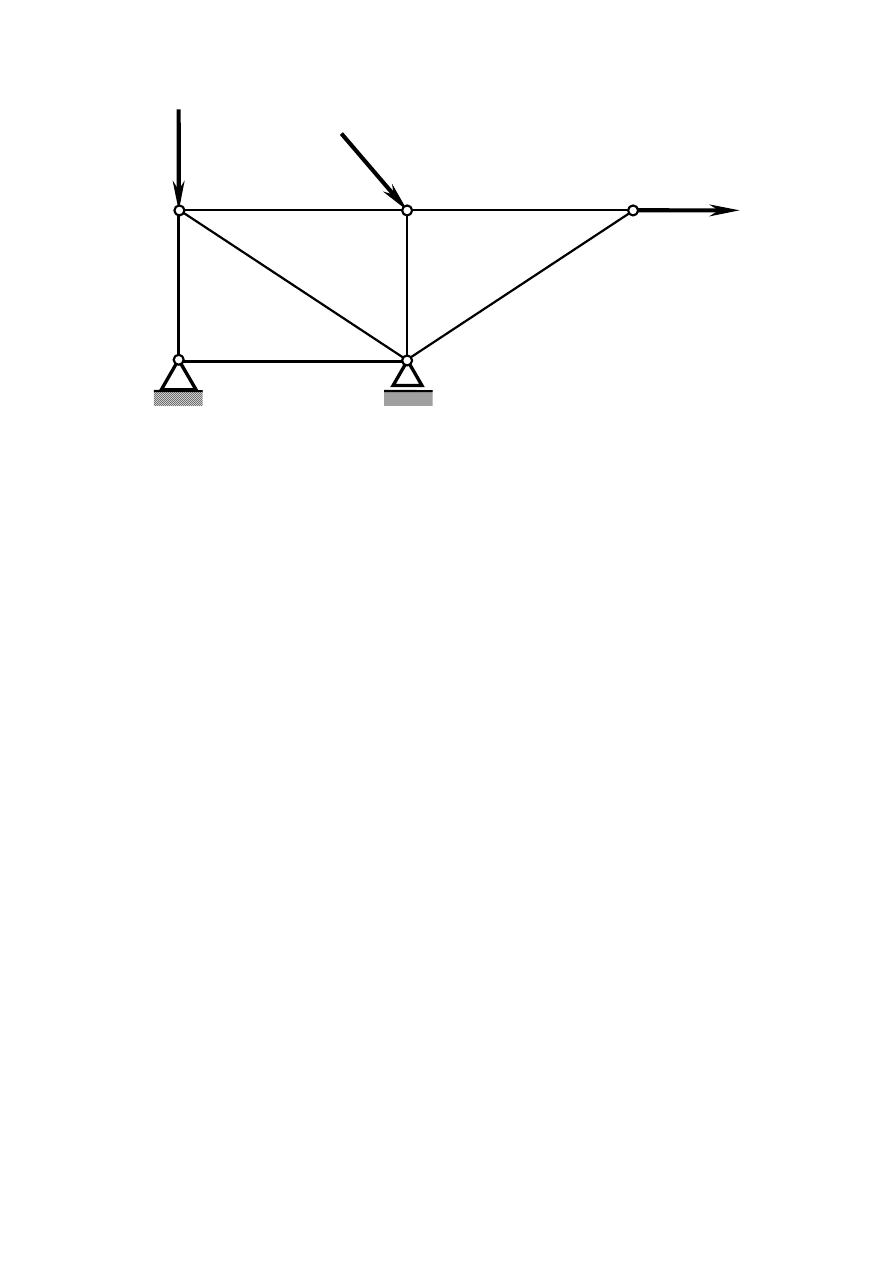
Kratownica jest układem złożonym z nieważkich sztywnych prętów połączonych ze sobą
przegubami i obciążanym siłami skupionymi w niektórych przegubach.

20

P

1

P

2

P

3

A

B

Warunkiem statycznej wyznaczalności kratownic jest by liczba prętów p spełniała warunek

p = 2 w - 3

gdzie w jest liczbą węzłów.

W podanym przykładzie mamy 7 prętów i 5 węzłów, czyli jest to kratownica statycznie
wyznaczalna.
Rozwiązanie kratownicy polega na obliczeniu reakcji podpór, a następnie obliczeniu sił
wzdłużnych w poszczególnych prętach.

Analitycznymi metodami rozwiązywania kratownic są metoda Rittera i metoda równoważenia
sił w węzłach.

Tarcie. Równowaga sił z uwzględnieniem sił tarcia

Tarcie zewnętrzne jest zjawiskiem fizycznym, jakie występuje na powierzchniach kontaktu
ciał materialnych. Natura sił tarcia, przeciwdziałających ruchowi względnemu stykających się
ciał, nie jest jeszcze poznana do końca, ale wynikają one z chropowatości powierzchni i
zjawiska adhezji.

Rozróżniamy dwa typy tarcia
- tarcie suche zwane tarciem Coulomba – badacza zjawiska tarcia
- tarcie płynne występujące między warstwami płynu poruszającego się z różnymi

prędkościami.

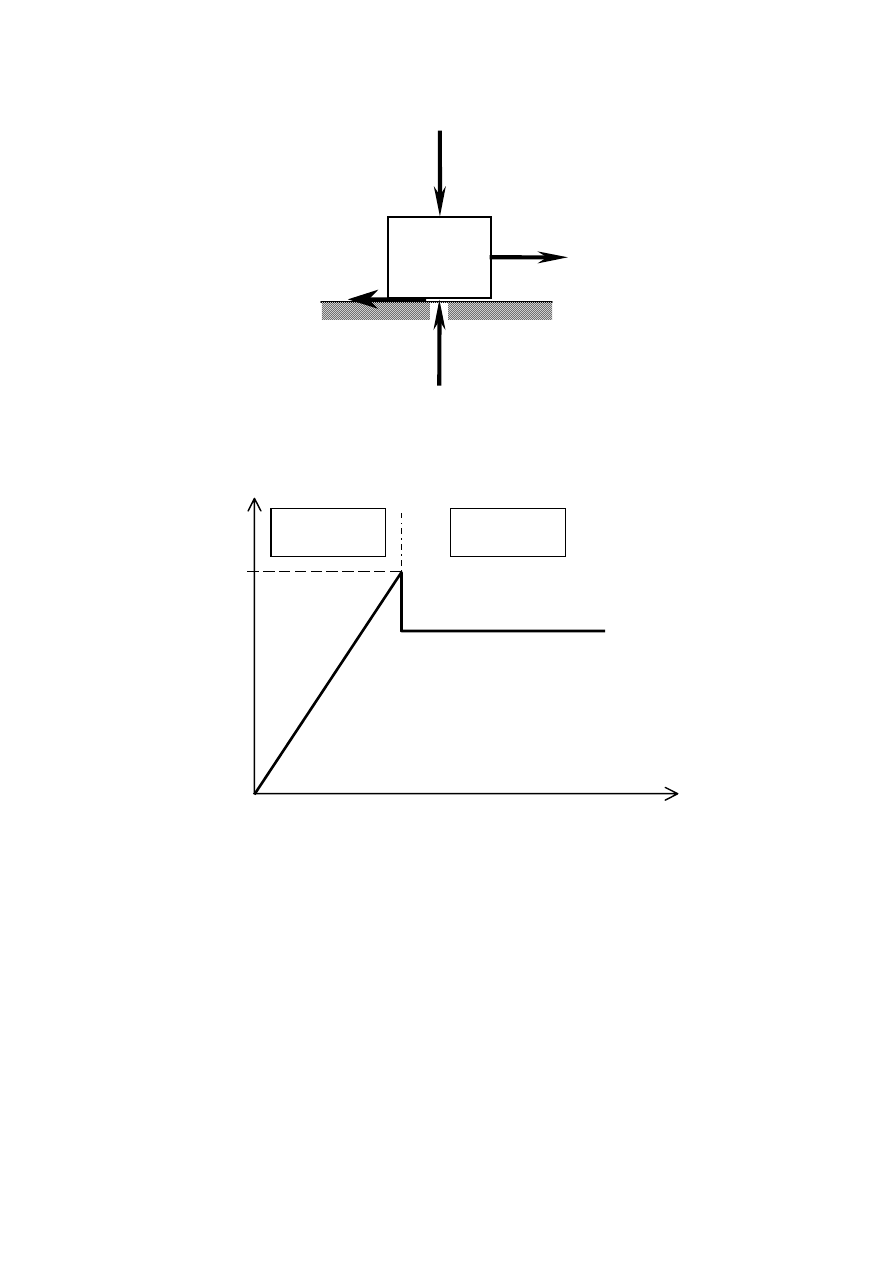
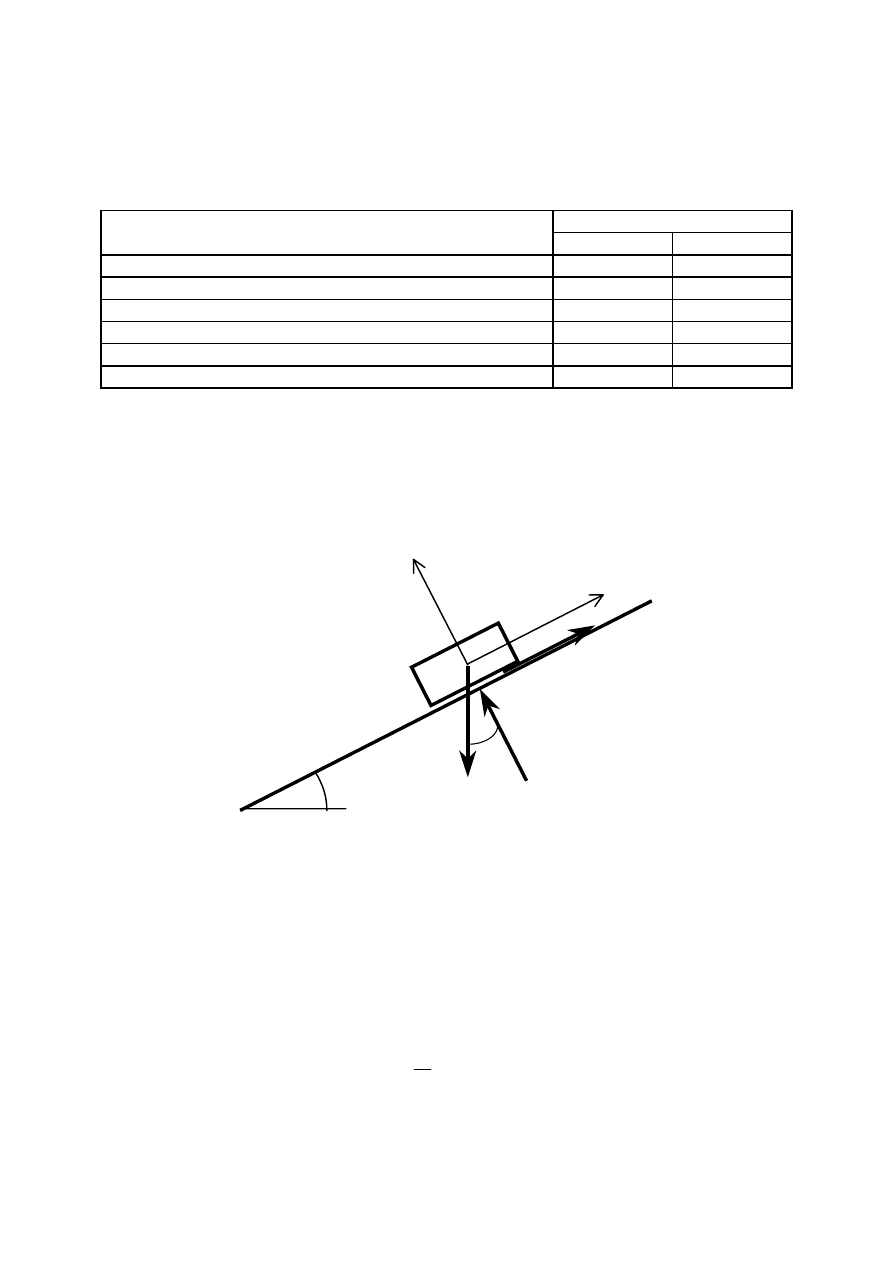
Jeśli do bryły stojącej na płaskiej powierzchni przyłożymy poziomą siłę P, to bryła będzie
pozostawała w spoczynku dopóki wartość tej siły nie przekroczy maksymalnej wartości siły
tarcia T.

21

P

G

T

N

Relację między poziomą wartością bezwzględną siły P a modułem siły tarcia T można
zobrazować na wykresie.

T

P

T

k

T

m

Równowaga

statyczna

Ruch bryły

Wzrost wartości siły czynnej P powoduje proporcjonalny wzrost siły tarcia aż do osiągnięcia
wartości maksymalnej T

m

, poczym bryła rozpoczyna ślizganie się względem podłoża. Wtedy

siła tarcia maleje do wartości T

k

– siły tarcia kinetycznego, jaką utrzymuje niezależnie od

wzrostu siły poziomej P i wzrostu prędkości ruchu.
Badania eksperymentalne wskazują, że siła tarcia statycznego jest równa

N

T

s

m

µ

=

natomiast siłę tarcia kinetycznego określa wzór

N

T

k

k

µ

=

gdzie: N to siła nacisku, a

µ

s

i

µ

k

to współczynniki tarcia statycznego i kinetycznego.

22

Siła tarcia, a także współczynniki tarcia, nie zależą od wielkości powierzchni kontaktu
między ciałami, zależą natomiast od rodzaju materiału z jakiego wykonane są ciała.


Tabela wartości współczynników tarcia

Współczynniki tarcia

Rodzaj materiałów ciał w kontakcie

statycznego kinematyczn.

guma/beton 0.9

0.75

szkło/szkło 0.94

0.4

metal/metal 0.4-0.6

0.3-0.5

metal/kamień 0.3-0.7

0.4-0.6

lód/lód 0.1

0.03

teflon/teflon 0.04

0.04

Ciało na równi pochyłej

Na ciało o ciężarze G znajdujące się na równi pochyłej nachylonej do poziomu pod kątem

α

działają także siła nacisku N oraz siła tarcia T.

α

G

T

N

α

x

y

Bryła będzie w równowadze statycznej jeśli sumy rzutów tych sił na osie układu
współrzędnych będą równe zeru:

0

1

=

∑

=

n

i

ix

P

T – G sin

α

= 0

0

1

=

∑

=

n

i

iy

P

N – G cos

α

= 0

Przenosząc składowe siły ciężkości na prawą stronę i dzieląc oba równania przez siebie
otrzymuje się:

α

tg

=

N

T

Na podstawie prawa tarcia wiadomo, że T =

µ

N, czyli

23

µ

= tg

α

Stąd można zauważyć, że ciało znajdujące się na równi pochyłej będzie w spoczynku jeśli kąt
nachylenia równi

α

będzie mniejszy lub równy kątowi tarcia

ρ

, co można zapisać

ρ

α

≤

≤

0

Zwiększenie kąta nachylenia równi ponad wartość kąta tarcia spowoduje zsunięcie bryły, co
jest możliwe do zaobserwowania na drodze prostego eksperymentu.

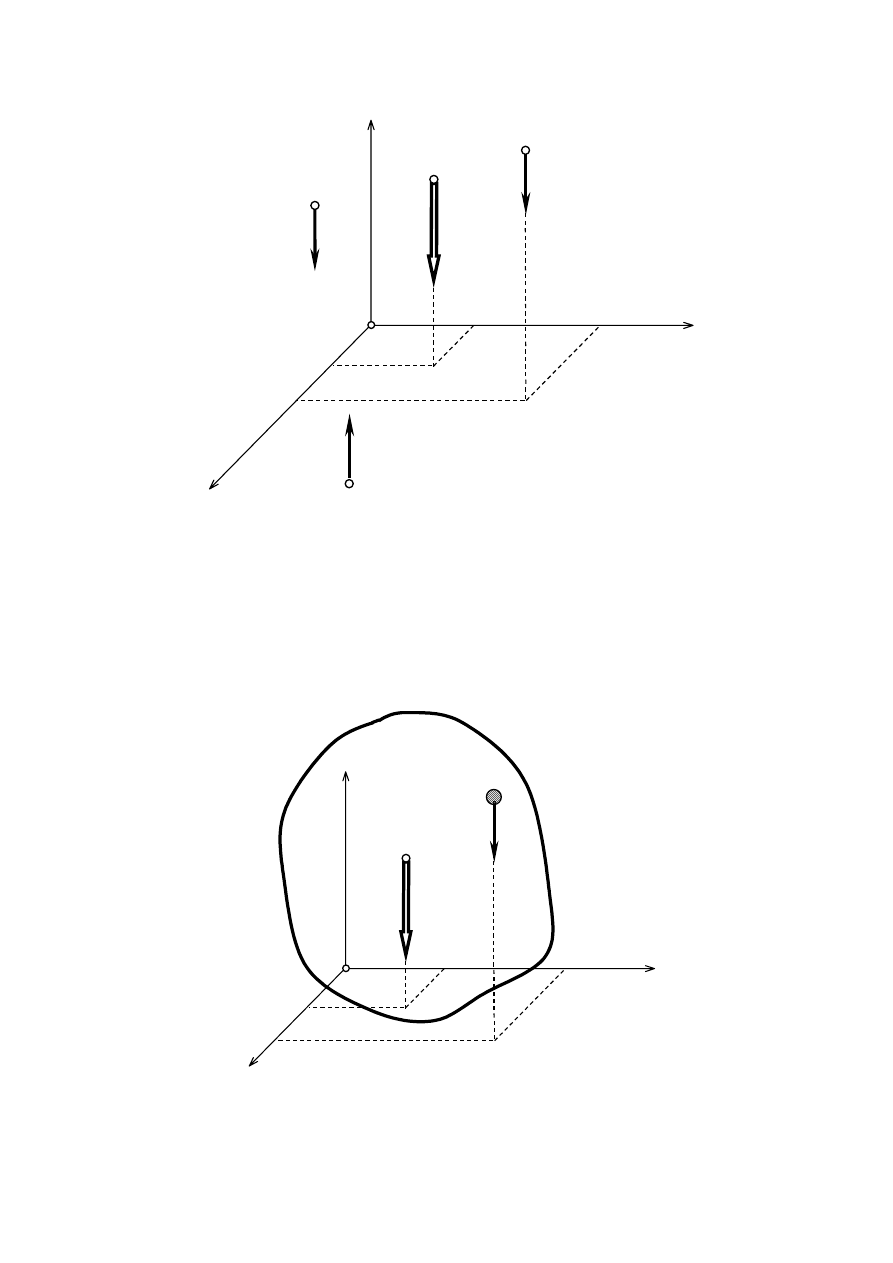
Przestrzenny układ sił równoległych. Środek ciężkości

Przestrzenny układ sił równoległych tworzą siły o równoległych kierunkach działania.
Wypadkową takiego układu znajdujemy sumując wszystkie siły składowe

∑

=

=

n

i

i

1

P

P

,

natomiast punkt przyłożenia wypadkowej jest wyznaczany na podstawie równań

∑

∑

=

=

=

n

i

i

n

i

i

i

C

P

x

P

x

1

1

,

∑

∑

=

=

=

n

i

i

n

i

i

i

C

P

y

P

y

1

1

,

∑

∑

=

=

=

n

i

i

n

i

i

i

C

P

z

P

z

1

1

gdzie: P

i

to moduł i-tej siły składowej; x

i

, y

i

, z

i

to współrzędne punktu zaczepienia i-tej siły

składowej.
Punkt C, przez który przechodzi wypadkowa układu sił równoległych jest nazywany środkiem
sił równoległych

.

24

P

i

A

i

x

y

z

O

z

i

x

i

y

i

P

1

A

1

P

2

A

2

P

C

z

C

x

C

y

C

Metody wyznaczania środków ciężkości figur płaskich i brył przestrzennych.
Twierdzenie Guldina

Podstawowym układem sił równoległych jest układ sił ciężkości.

G

i

x

y

z

O

z

i

x

i

y

i

G

C

z

C

x

C

y

C

Środek sił równoległych w odniesieniu do sił ciężkości jest nazywany środkiem ciężkości. Po
podzieleniu całej bryły na n elementarnych objętości o znanym ciężarze każdego z
elementów, położenie środka ciężkości jest wyznaczone przez następujące współrzędne:

25

∑

∑

=

=

=

n

i

i

n

i

i

i

C

G

x

G

x

1

1

,

∑

∑

=

=

=

n

i

i

n

i

i

i

C

G

y

G

y

1

1

,

∑

∑

=

=

=

n

i

i

n

i

i

i

C

G

z

G

z

1

1

gdzie:

G

G

n

i

i

=

∑

=1

jest ciężarem całej bryły, a

x

i

,

y

i

,

z

i

to współrzędne położenia

i-tej

objętości o ciężarze elementarnym

G

i

.

Gdy ciało materialne zostanie podzielone na nieskończenie wiele elementów

dG

o wymiarach i ciężarze bliskich zeru, to położenie środka ciężkości wyrażają następujące
wzory:

G

dG

x

x

G

C

∫

=

,

G

dG

y

y

G

C

∫

=

,

G

dG

z

z

G

C

∫

=

W jednorodnym polu ciężkości ciężar jest iloczynem masy

m i przyspieszenia ziemskiego g,

można więc zapisać, że

mg

G

=

,

dm

g

dG

=

Stąd:

m

dm

x

x

m

C

∫

=

,

m

dm

y

y

m

C

∫

=

,

m

dm

z

z

m

C

∫

=

czyli:

W jednorodnym polu ciężkości środek masy pokrywa się ze środkiem ciężkości

Dla ciał jednorodnych ich masa właściwa (gęstość) jak również ciężar właściwy to wielkości
stałe.
Po podstawieniu: m =

ρ

V i dm =

ρ

dV, gdzie

ρ

to gęstość materiału bryły,

dV to objętość jej

nieskończenie małego elementu, a

V to objętość całkowita, otrzymuje się wzory na środek

masy (ciężkości) bryły przestrzennej w postaci

V

dV

x

x

V

C

∫

=

,

V

dV

y

y

V

C

∫

=

,

V

dV

z

z

V

C

∫

=

W przypadku ciała, które jest

powierzchnią jednorodną o stałej grubości f, czyli jego masa

jest równomiernie rozłożona na całej powierzchni, prawdziwe są następujące relacje:

26

S

f

V

=

,

dS

f

dV

=

gdzie:

S to całkowite pole powierzchni, a dS to powierzchnia elementarna.

Środek masy takiej powierzchni wyrażają wzory:

S

dS

x

x

S

C

∫

=

,

S

dS

y

y

S

C

∫

=

,

S

dS

z

z

S

C

∫

=

Dla

płaskiej płyty leżącej na płaszczyźnie Oxy współrzędna środka masy z

C

= 0.

Niektóre ciała takie jak liny, druty, cięgna mogą być uważane z dostateczną dokładnością za
linie jednorodne o stałym polu powierzchni przekroju A. Objętości całkowita i elementarna
takiego ciała są równe

l

A

V

=

,

dl

A

dV

=

gdzie

l to długość całkowita linii, dl to długość elementarna.

Środek masy

linii elementarnej określają wzory:

l

dl

x

x

l

C

∫

=

,

l

dl

y

y

l

C

∫

=

,

l

dl

z

z

l

C

∫

=

Środki mas ciał złożonych

Przy wyznaczaniu położenia środka masy ciał złożonych dzieli się je na ciała podstawowe,
których położenia środków mas są znane, a następnie wykorzystuje się odpowiednie formuły
definiujące momenty statyczne poszczególnych ciał podstawowych.
Jeśli np. figurę płaską można podzielić na określoną liczbę figur prostych takich jak
prostokąty, trójkąty, koła, półkola itp., to współrzędne środka masy figury złożonej są
następujące:

S

x

S

x

n

i

i

i

C

∑

=

=

1

,

S

y

S

y

n

i

i

i

C

∑

=

=

1

gdzie:

∑

=

=

n

i

i

S

S

1

to pole powierzchni całej figury złożonej z

n figur podstawowych, S

i

- pole

powierzchni

i-tej figury, x

i

, y

i

– współrzędne środka masy i-tej figury.

Sumy iloczynów

∑

=

n

i

i

i

x

S

1

i

∑

=

n

i

i

i

y

S

1

są definiowane jako momenty statyczne figur

składowych względem osi odpowiednio

y i x. Momentami statycznymi względem tych

27

samych osi są także iloczyny

S

x

C

i

S

y

C

;

równość odpowiednich momentów statycznych

umożliwia wyprowadzenie podanych wzorów na położenie środka masy figury złożonej.

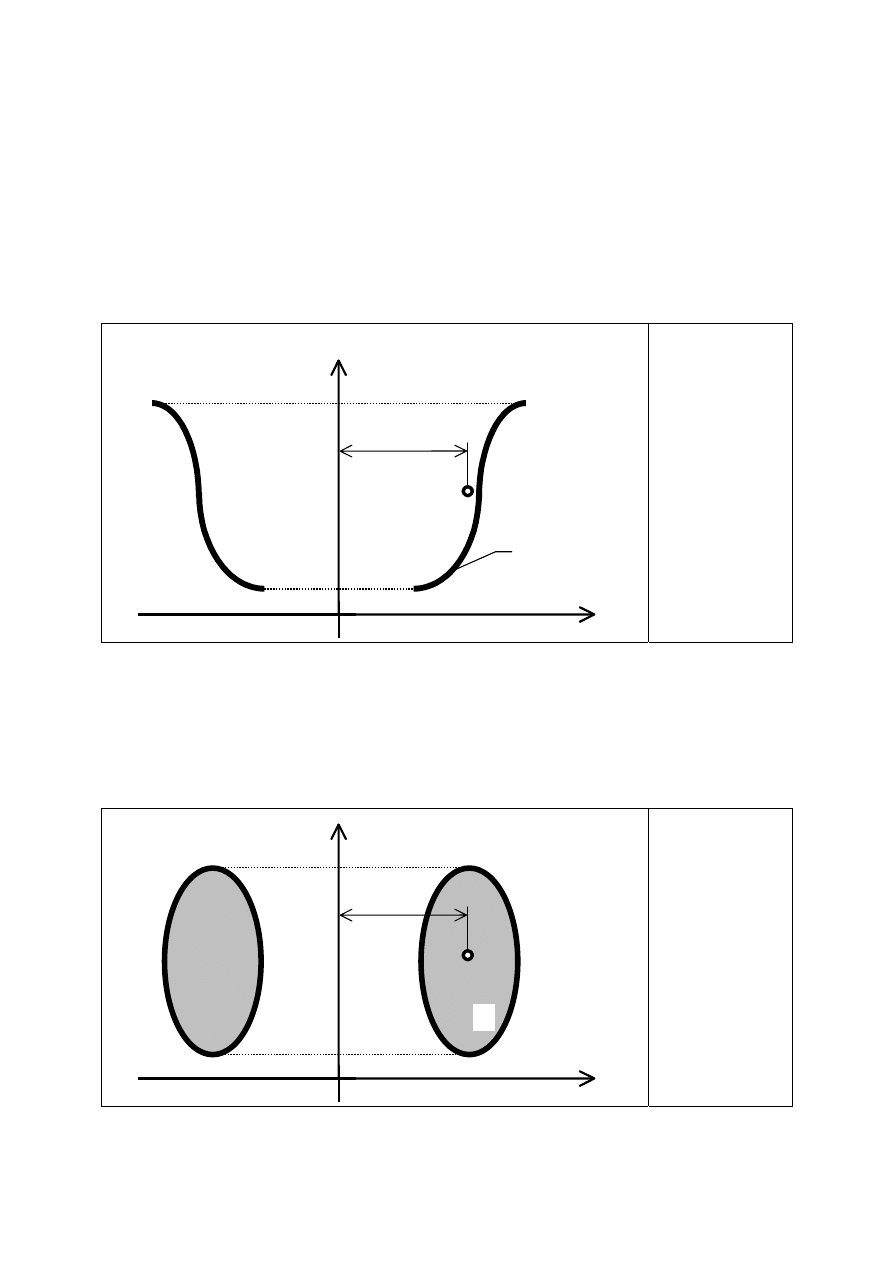
Twierdzenia Guldina-Pappusa

1) Pole powierzchni obrotowej

S, jaka powstaje w wyniku obrotu płaskiej jednorodnej linii o

długości

l dookoła osi znajdującej się w płaszczyźnie linii, jest równe iloczynowi długości

tej linii pomnożonej przez długość obwodu okręgu jaki opisuje środek ciężkości tej linii.

y

x

C

x

C

l

l

x

S

2

C

π

=

,

l – długość linii

2) Objętość bryły obrotowej V, jaka powstaje w wyniku obrotu jednorodnej figury płaskiej o

polu powierzchni

A dookoła osi znajdującej się w płaszczyźnie figury, jest równa

iloczynowi pola powierzchni tej figury pomnożonej przez długość obwodu okręgu jaki
opisuje środek ciężkości tej figury.

y

x

C

x

C

A

A

x

V

2

C

π

=

,

A – pole

powierzchni

figury

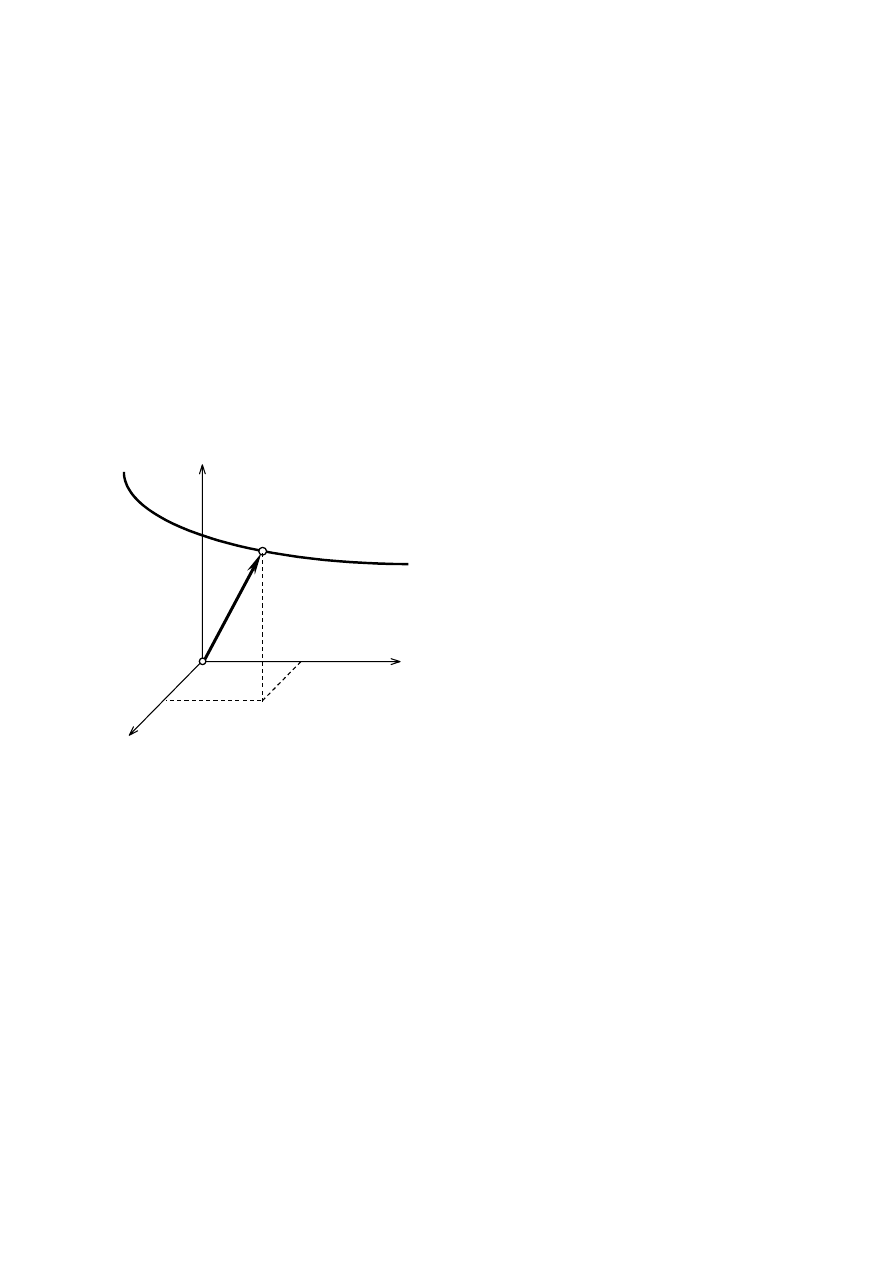
28

KINEMATYKA
Kinematyka punktu

Ruch ciała to zjawisko przebiegające w określonym czasie i polegające na zmianie położenia
tego ciała w przestrzeni względem układu odniesienia. W mechanice przestrzeń i czas to
pojęcia podstawowe, przy czym czas jest niezależny od układu odniesienia i jest taki sam dla
wszystkich punktów przestrzeni.

Ruch ciała materialnego jest uważany za znany jeśli jest możliwy do określenia i opisania
ruch dowolnego punktu należącego do tego ciała.


Opis ruchu we współrzędnych kartezjańskich. Tor punktu

x

y

z

O

A

z

x

y

r

k

Położenie dowolnego punktu w przestrzeni
określają trzy współrzędne układu Oxyz.
W trakcie ruchu punktu współrzędne te
ulegają zmianie w czasie, czyli są funkcjami
czasu t:

x = x(t)
y = y(t)

z = z(t)

Równania te noszą nazwę

równań ruchu

punktu.

Punkt A poruszający się w przestrzeni opisuje krzywą

k, która jest miejscem geometrycznym

jego położeń. Równania ruchu noszą także nazwę

parametrycznych równań toru punktu,

gdzie parametrem jest czas.
Jeśli z równań tych zostanie wyrugowany czas, to otrzymuje się

równanie toru punktu w

postaci

f(x, y, z) = 0

Równanie to obrazuje krzywą

k, po której porusza się punkt.

Wektorowe równanie ruchu punktu materialnego


Położenie punktu w przestrzeni może być określane za pomocą

promienia-wektora

r. Jeśli

punkt porusza się, to wektor

r zmienia w czasie swą wartość, kierunek i zwrot. Stąd

r = r(t)

jest

wektorowym równaniem ruchu punktu.

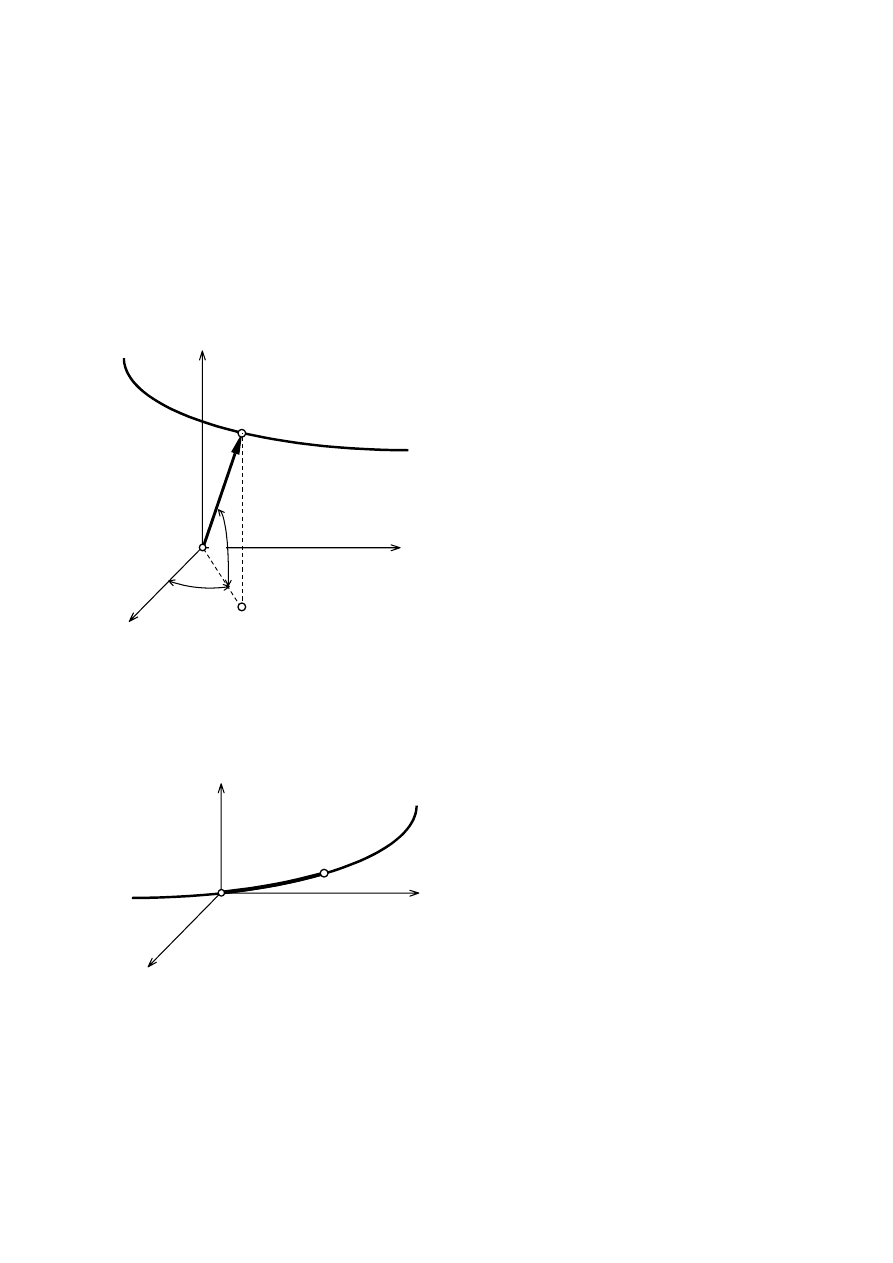
29

Po wprowadzeniu zapisu przy użyciu wersorów poszczególnych osi układu współrzędnych

i,

j, k otrzymuje się

r(t) = i x(t) + j y(t) + k z(t)

Opis ruchu we współrzędnych krzywoliniowych (sferycznych)

x

y

z

O

A

φ

r

k

A’

ψ

Położenie punktu A w układzie sferycznym
jest określane przez podanie długości r
promienia wodzącego

r, kąta dwuściennego

φ

między płaszczyzną O

xz a płaszczyzną OAA’

oraz kąta

ψ

nachylenia promienia

r do

płaszczyzny O

xz. Wszystkie te wielkości są

funkcjami czasu i są powiązane ze
współrzędnymi układu kartezjańskiego w
następujący sposób:

x(t) = r(t) cos

ψ

(

t)

cos

φ

(

t)

y(t) = r(t) cos

ψ

(

t) sin

φ

(

t)

z(t) = r(t) sin

ψ

(

t)

Ruch punktu wyrażony za pomocą współrzędnej łukowej

x

y

z

O

A

k

s

Zakładając, że tor poruszającego się punktu
jest znany i może być zobrazowany jako
krzywa

k, to położenie punktu na torze można

jednoznacznie określić przez podanie
współrzędnej

s mierzonej wzdłuż toru od

danego punktu odniesienia O.
Współrzędna

s o długości równej długości

łuku OA jest drogą punktu A.

W trakcie ruchu punktu współrzędna ta jest funkcją czasu

s = s(t)

Zależność ta jest nazywana

równaniem drogi lub równaniem ruchu punktu na torze.

Prędkość punktu

30

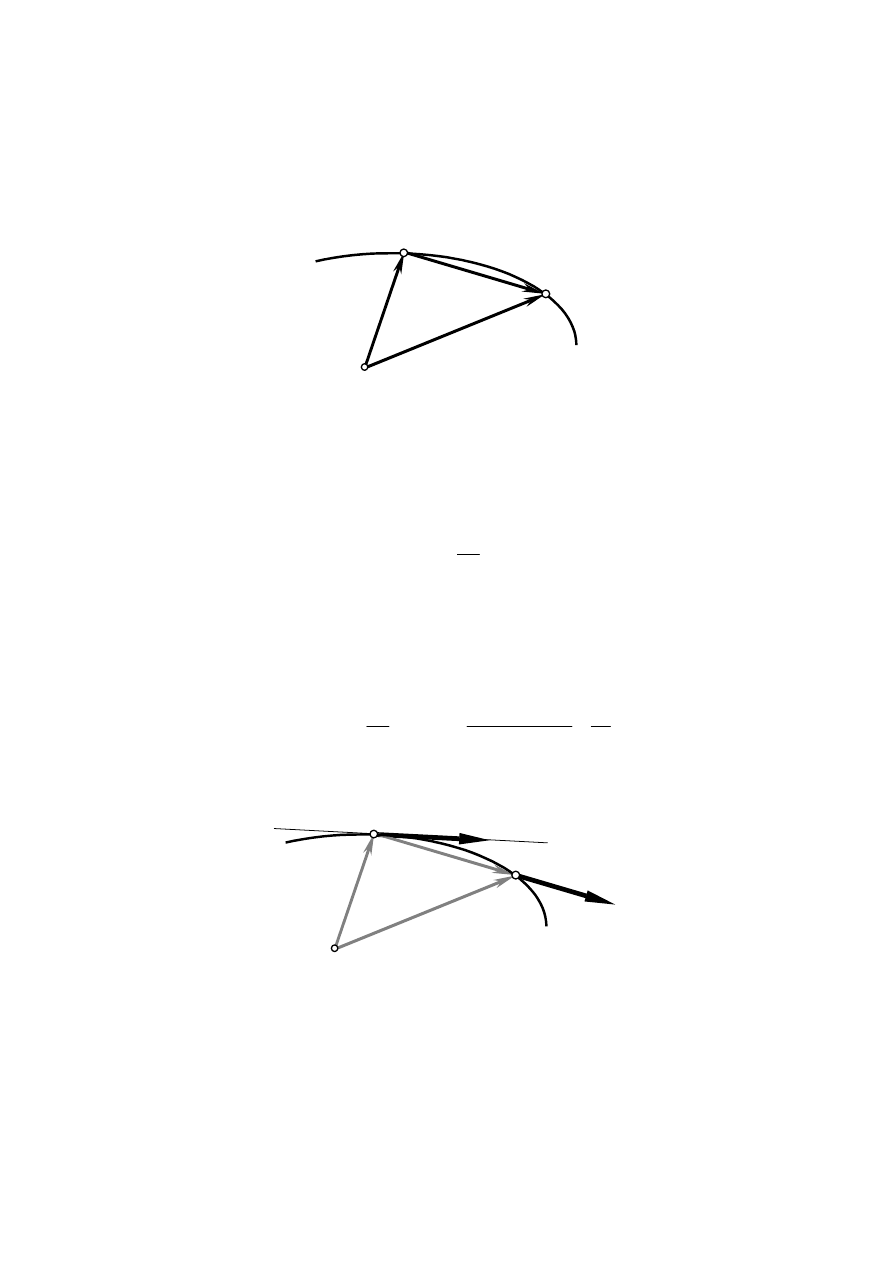
Prędkość jako pochodna promienia wektora

Punkt poruszając się po torze w chwili czasu

t znalazł się w położeniu wyznaczonym przez

promień wektor

r(t), a następnie po czasie

∆

t w położeniu określonym przez wektor

r(t+

∆

t).

O

A

r(t)

A’

r(t+

∆

t)

∆

r

Zmianę położenia punktu można także wyrazić przez wektor

∆

r, który jest równy

∆

r = r(t+

∆

t) -

r(t)

Prędkość średnia punktu jest wektorem definiowanym następująco:

∆t

∆

śr

r

V

=

Kierunek i zwrot wektora prędkości średniej V

śr

jest taki sam jak wektora

∆

r, ponieważ

przyrost czasu jest wielkością skalarną o wartości większej od zera.

Prędkość chwilową (prędkość) punktu definiujemy jako granicę ilorazu różnicowego

dt

d

∆t

t

∆t

t

∆t

∆

∆t

∆t

r

r

r

r

V

=

−

+

=

=

→

→

)

(

)

(

lim

lim

0

0

,

czyli jest to pochodna promienia wektora względem czasu.

V

O

A

r(t)

A’

r(t+

∆

t)

∆

r

V

śr

(

τ

)

Prędkość chwilowa

V ma kierunek stycznej (

τ

) do toru ruchu punktu, ponieważ przy

zmniejszaniu przyrostu czasu

∆

t kierunek wektora

∆

r i wyznaczany przez niego kierunek

wektora

V

śr

zbliża się do kierunku stycznej do toru w punkcie A.

Wyznaczanie prędkości punktu przy opisie ruchu za pomocą współrzędnej łukowej

31

W chwili czasu

t punkt A znalazł się w położeniu określonym współrzędną łukową s(t) równą

przebytej przez niego drodze. Po upływie czasu

∆

t jego droga przyrosła o wartość

∆

s, tak że

w chwili czasu

t +

∆

t całkowita długość przebytej drogi to s +

∆

s.

O

A

s(t)

A’

t+

∆

t

t

∆

s

Wektor

prędkości średniej

V

śr

średniej jest to wektor, który ma kierunek wzdłuż cięciwy

AA’, zwrot zgodny z kierunkiem ruchu, a wartość

∆t

∆s

∆t

V

śr

=

=

AA'

Prędkość średnia jest ilorazem drogi do czasu, w jakim ta droga została przebyta.

s(t)

V

t+

∆

t

V

śr

O

A

t+

∆

t

t

∆

s

A’

(

τ

)

Zmniejszanie przyrostu czasu

∆

t i tym samym drogi

∆

s powoduje, że kierunek wektora

prędkości średniej

V

śr

zbliża się przy

∆

t

→ 0 do kierunku stycznej to toru w punkcie A.

Wektor

V o kierunku stycznej (

τ

) nosi nazwę

prędkości chwilowej (prędkości) punktu.

Wartość wektora

V jest definiowana w następujący sposób:

)

(

)

(

)

(

)

(

lim

lim

0

0

t

s

dt

t

ds

∆t

t

s

∆t

t

s

∆t

∆s

V

∆t

∆t

&

=

=

−

+

=

=

→

→

Wartość bezwzględna (moduł) wektora prędkości jest równy pierwszej pochodnej drogi
względem czasu.
W naukach fizykalnych pochodną względem czasu oznacza się często kropką rysowaną nad
symbolem funkcji, która ma być poddana operacji różniczkowania.

Przyspieszenie punktu materialnego

32

Wektor prędkości punktu materialnego poruszającego się po torze krzywoliniowym zmienia
swój kierunek, a jeżeli ruch punktu jest ruchem zmiennym, to zmianie ulega także moduł
wektora prędkości.
Przyjmuje się, że w chwili czasu

t prędkość punktu wyraża wektor

V

0

, a po upływie czasu

∆

t,

czyli w chwili

t +

∆

t prędkość jest wyrażona przez wektor

V

1

.

V

V

1

A

t+

∆

t

t

A

1

Różnica wektorów

V

1

-

V

0

=

∆

V określa przyrost prędkości w czasie

∆

t. Stosunek przyrostu

wektora prędkości do czasu, w jakim ten przyrost nastąpił nazywamy

przyspieszeniem

średnim punktu

a

śr

:

∆t

∆

śr

V

a

=

V

V

1

A

t+

∆

t

A

1

∆

V

a

śr

V

1

V

a ∆

śr

Wektor przyspieszenia średniego ma kierunek i zwrot wektora

∆

V.

Przyspieszeniem chwilowym (przyspieszeniem) punktu nazywamy wektor określany jako
granicę ilorazu różnicowego

dt

d

∆t

∆

∆t

V

V

a

=

=

→0

lim

Ponieważ wektor prędkości jest definiowany jako

dt

d

r

V

=

,

to wektor przyspieszenia może być także wyrażony jako druga pochodna promienia wektora
względem czasu

2

2

dt

d

dt

d

r

V

a

=

=

33

Wektor przyspieszenia jest więc pierwszą pochodną wektora prędkości lub drugą pochodną
promienia wektora względem czasu.

Wektor przyspieszenia może być wyrażony w postaci sumy jego rzutów na osie
prostokątnego układu współrzędnych:

z

y

x

z

y

x

a

a

a

k

j

i

a

a

a

a

+

+

=

+

+

=

Korzystając z definicji przyspieszenia i rozkładając na składowe wektory prędkości i
położenia można napisać także, że

dt

dV

dt

dV

dt

dV

dt

d

z

y

x

k

j

i

V

a

+

+

=

=

lub

2

2

2

2

2

2

2

2

dt

z

d

dt

y

d

dt

x

d

dt

d

k

j

i

r

a

+

+

=

=

Stąd moduły składowych wektora przyspieszenia można przedstawić następująco:

2

2

dt

x

d

dt

dV

a

x

x

=

=

,

2

2

dt

y

d

dt

dV

a

y

y

=

=

,

2

2

dt

z

d

dt

dV

a

z

z

=

=

Długość wektora przyspieszenia jest równa

2

2

2

z

y

x

a

a

a

a

+

+

=

Przyspieszenie normalne i styczne

W analizie ruchu wektor przyspieszenia jest wyrażany często poprzez składową styczną
i normalną do toru

n

n

t

t

n

t

a

a

dt

d

e

e

a

a

V

a

+

=

+

=

=

gdzie:

a

t

,

a

n

to przyspieszenia odpowiednio styczne i normalne,

e

t

to wersor stycznej (

τ

) do

toru,

e

n

to wersor normalnej (

n) do toru.

34

V

S

A

e

t

(

τ

)

(n)

e

n

ρ

Na rysunku zaznaczono

promień krzywizny toru

ρ

, który jest położony na normalnej (

n),

i którego długość wyznacza położenie

środka krzywizny toru - punktu S.

Płaszczyzna utworzona przez wersory styczny

e

t

i normalny do toru

e

n

to płaszczyzna ściśle

styczna, stąd wektor przyspieszenia leży w płaszczyźnie ściśle stycznej.

V

S

A

a

t

(

τ

)

(n)

a

n

ρ

a

Wartości bezwzględne wektorów przyspieszeń stycznego i normalnego oblicza się na
podstawie wzorów

dt

dV

a

t

=

,

ρ

2

V

a

n

=

Ze wzorów tych wynika, że wartość przyspieszenia normalnego jest zawsze większa od zera,
natomiast wartość przyspieszenia stycznego może być zarówno większa jak i mniejsza od
zera, ponieważ zależy ona od zmiany wartości bezwzględnej prędkości w czasie. Zwrot
wektora przyspieszenia stycznego może być więc zgodny lub przeciwny do zwrotu wektora
prędkości.

Moduł wektora przyspieszenia obliczyć można na podstawie wzoru

2

2

n

t

a

a

a

+

=

35

W przypadku ruchu odbywającego się ze

stałą prędkością przyspieszenie styczne jest równe

zeru, a ruch taki nazywamy

jednostajnym. Przyspieszenie normalne jest równe zeru tylko w

przypadku

ruchu prostoliniowego.

Ruch punktu materialnego po okręgu

Rozpatruje się ruch punktu A po okręgu o promieniu

r odbywający się od położenia

początkowego A

0

.

A

a

t

ϕ

r

a

n

V

A

0

O

s

Współrzędna

s o długości równej długości łuku AA

0

jest drogą punktu A.

Droga kątowa (

ϕ

) czyli kąt jaki zatoczył punkt A jest powiązana z drogą

s (wyrażaną w

mierze łukowej) związkiem

r

t

t

s

)

(

)

(

ϕ

=

[m]

Wartość bezwzględna prędkości liniowej

V jest więc równa

ω

ϕ

r

dt

d

r

dt

ds

V

=

=

=

⎥⎦

⎤

⎢⎣

⎡

s

m

gdzie

dt

d

ϕ

ω

=

⎥⎦

⎤

⎢⎣

⎡

s

rad

to

prędkość kątowa (pochodna drogi kątowej względem czasu).

Przyspieszenie styczne jest pochodną prędkości liniowej (iloczynu prędkości kątowej
i promienia), stąd można zapisać, że

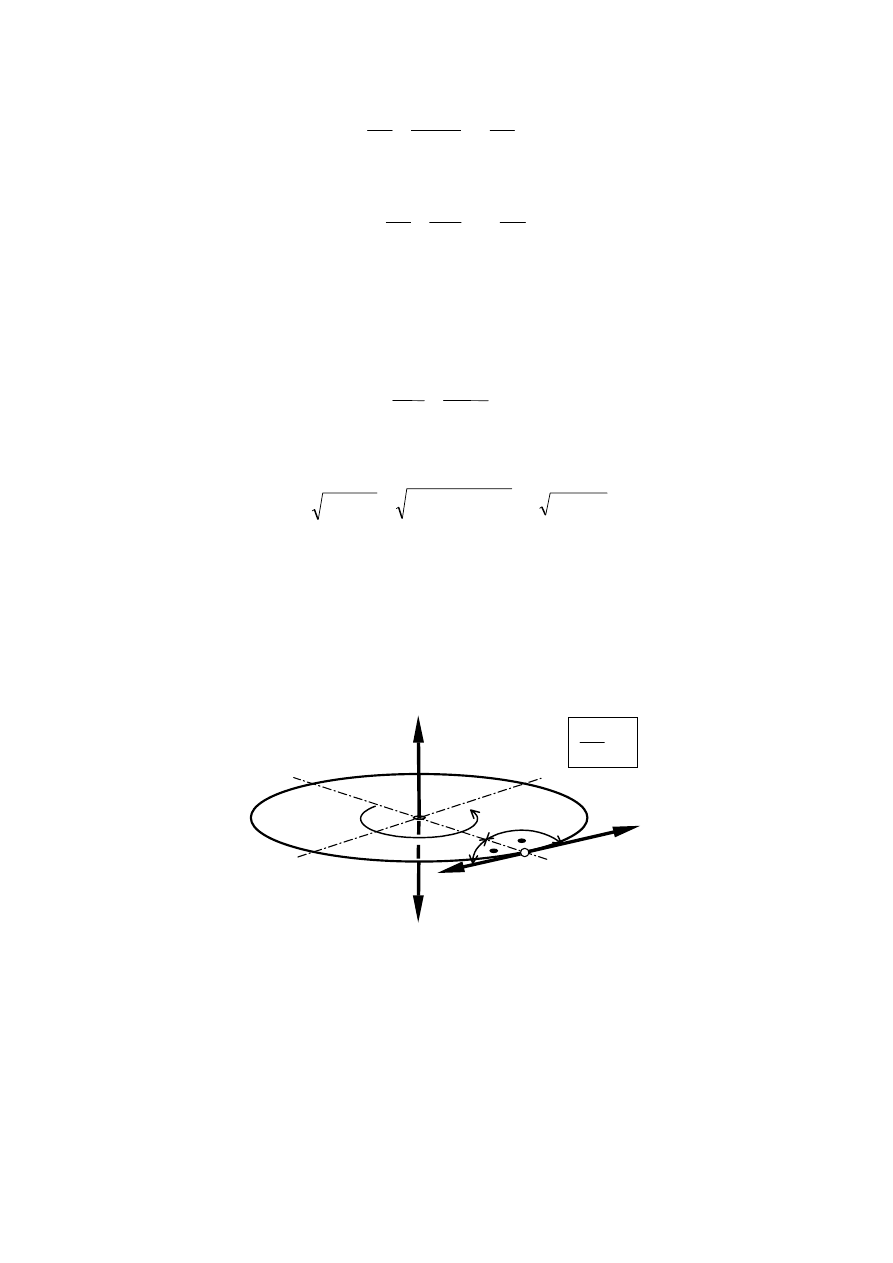
36

ε

ω

ω

)

(

r

dt

d

r

dt

r

d

dt

dV

a

t

=

=

=

=

,

gdzie

⎥⎦

⎤

⎢⎣

⎡

=

=

2

2

2

s

rad

dt

d

dt

d

ϕ

ω

ε

jest

przyspieszeniem kątowym określającym zmianę prędkości kątowej w czasie.

Przyspieszenie normalne w ruchu po okręgu wyraża się w funkcji prędkości kątowej przez
podstawienie:

( )

r

r

r

r

V

a

n

2

2

2

ω

ω

=

=

=

Przyspieszenie całkowite jest wektorem o wartości

( ) ( )

4

2

2

2

2

2

2

ω

ε

ω

ε

+

=

+

=

+

=

r

r

r

a

a

a

n

t

Prędkość kątowa i przyspieszenie kątowe to wielkości wektorowe. Każdy z tych wektorów
ma kierunek prostopadły do płaszczyzny okręgu, po jakim porusza się punkt. Ich zwrot dla
prawoskrętnego układu współrzędnych jest ustalany za pomocą reguły śruby prawoskrętnej.
W przypadku ruchu opóźnionego, gdy wartość prędkości kątowej maleje w funkcji czasu,
zwrot wektora przyspieszenia kątowego

ε

jest przeciwny do zwrotu wektora prędkości

kątowej

ω

(zwrot wektora przyspieszenia stycznego

a

t

będzie przez analogię przeciwny do

zwrotu wektora prędkości liniowej

V).

ω

V

A

ω

0

<

dt

d

ω

ε

a

t

Ruch złożony punktu

Opisywany ruch punktu rozpatrywano względem nieruchomego układu współrzędnych.
Ruchy naturalne ciał to ruchy złożone, ponieważ zachodzą one względem innych ciał, które
także są w ruchu. Np. ruch pasażerów w jadącym pociągu jest ruchem złożonym, ponieważ
pasażerowie przemieszczają się względem wagonu, a ten wchodząc w skład pociągu,
przemieszcza się razem z nim względem mijanego słupa trakcyjnego. Z kolei cały układ,

37

łącznie ze słupem związanym z podłożem, znajduje się w ruchu obrotowym jaki Ziemia
wykonuje względem swej osi obrotu. Ruchy ciał są więc ruchami wielokrotnie złożonymi co
nie jest jednoznaczne z tym, że wszystkie ruchy składowe muszą być brane pod uwagę przy
opisywaniu konkretnego zjawiska.
Ruchy jednych ciał względem innych, które są także w ruchu nazywamy

ruchami

względnymi. Ruch unoszenia to ruch ruchomego układu współrzędnych związanego z danym
ciałem względem układu nieruchomego.

Ruch bezwzględny punktu lub bryły to ruch

względem nieruchomego układu współrzędnych.


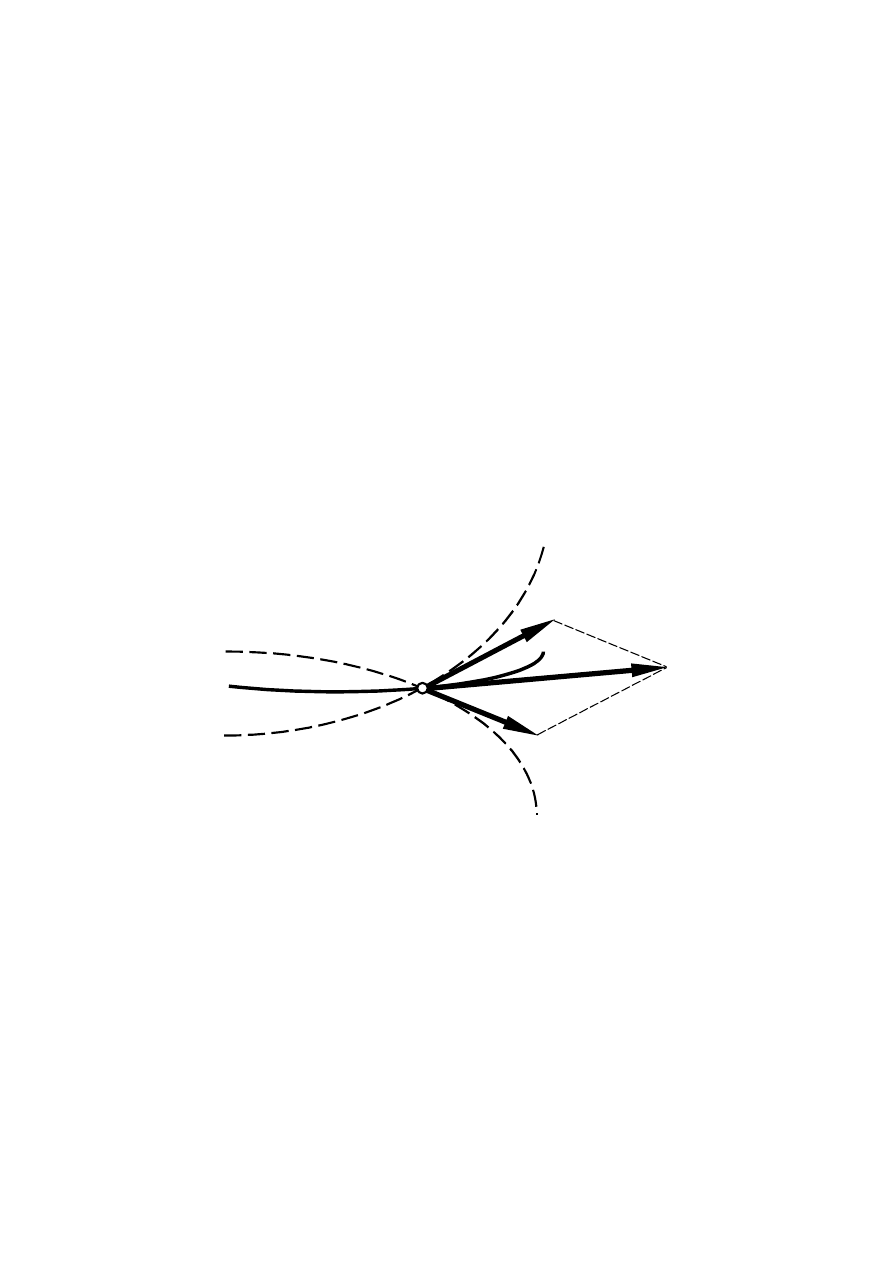
Składanie prędkości w ruchu złożonym

Jeśli punkt A znajduje się w ruchu składającym się z dwóch ruchów, to jego

prędkość

bezwzględna

V o kierunku stycznym do toru bezwzględnego będzie wypadkową prędkości

względnej

V

w

, która jest styczna do toru względnego

k

w

i

prędkości unoszenia

V

u

, która jest

styczna do toru unoszenia

k

u

V = V

w

+ V

u

A

k

u

V

w

V

u

V

k

w

k

Składanie przyspieszeń w ruchu złożonym. Przyspieszenie Coriolisa

Przyspieszenie bezwzględne

a w ruchu złożonym punktu jest równe sumie geometrycznej

przyspieszenia w ruchu względnym

a

w

,

przyspieszenia w ruchu unoszenia

a

u

i

przyspieszenia

Coriolisa

a

C

a = a

w

+ a

u

+ a

C

Jeśli ruchy względny i unoszenia są ruchami zmiennymi krzywoliniowymi, to każde z
przyspieszeń tych ruchów ma składową normalną i styczną i wtedy

a = a

wn

+ a

wt

+ a

un

+ a

ut

+ a

C

38

Przyspieszenie Coriolisa

a

C

,

powodowane ruchem obrotowym układu unoszenia, jest równe

podwojonemu iloczynowi wektorowemu prędkości kątowej w ruchu unoszenia

ω

u

i prędkości

względnej

V

w

w

u

V

ω

a

C

2

×

=

Z definicji iloczynu wektorowego wynika, że:
1) długość wektora przyspieszenia Coriolisa jest równa

α

sin

2

w

u

C

V

ω

a

=

, przy czym

α

jest

kątem między wektorami

ω

u

i

V

w

,

2) przyspieszenie Coriolisa będzie równe zeru jeśli:

−

ω

u

= 0, czyli gdy ruch unoszenia jest ruchem postępowym,

− V

w

= 0, czyli gdy prędkość względna jest w danej chwili równa zeru,

−

w

u

V

||

ω

, tzn. gdy wektory prędkości kątowej w ruchu unoszenia i prędkości

względnej są do siebie równoległe.

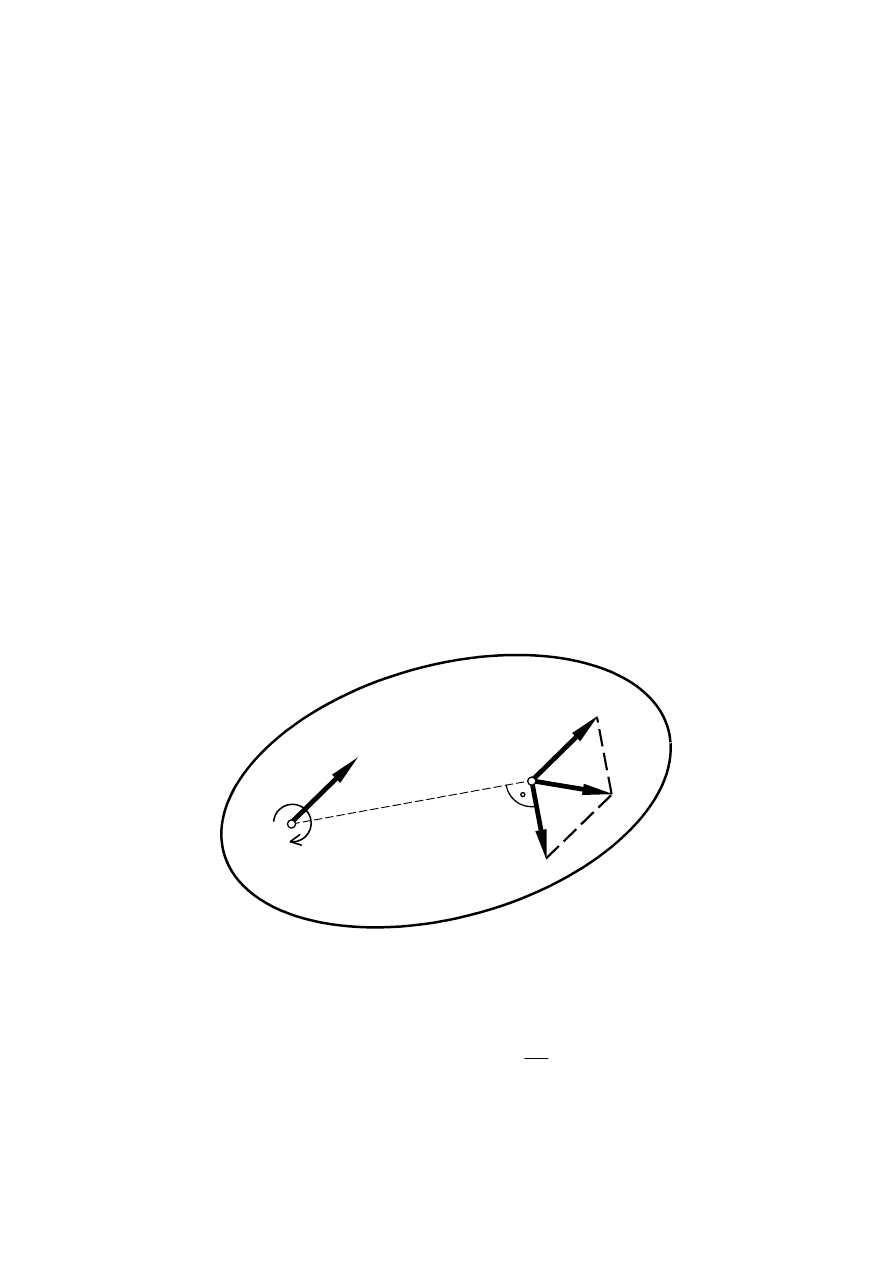
Ruch płaski ciała sztywnego

Ruch płaski ciała sztywnego to ruch, w trakcie którego wszystkie punkty tego ciała poruszają
się w stałej odległości od płaszczyzny kierującej. Ruch płaski można sprowadzić do ruchu
figury będącej rzutem bryły na płaszczyznę kierującą. W związku z tym może być on
traktowany jako złożenie ruchu postępowego w płaszczyźnie kierującej i ruchu obrotowego
względem osi prostopadłej do płaszczyzny kierującej.

ω

V

A

A

B

V

B

V

BA

V

A

Prędkość punktu B bryły sztywnej można interpretować jako sumę geometryczną prędkości
punktu A (

V

A

) i prędkości punktu B względem punktu A (

V

BA

):

AB

×

+

=

+

=

ω

V

V

V

V

A

BA

A

B

gdzie długość wektora

V

BA

jest równa

V

BA

=

ω

AB

39

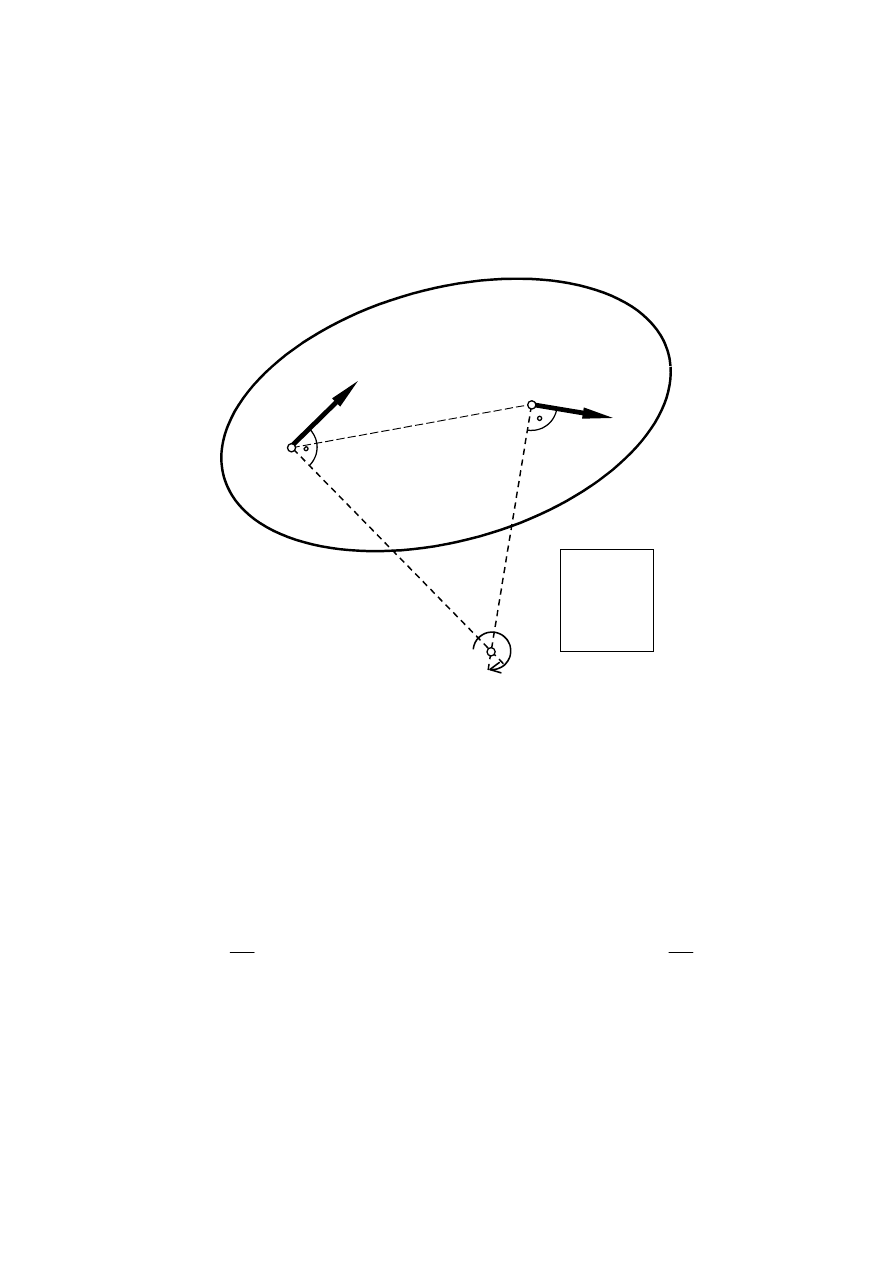
Ruch płaski bryły jako chwilowy ruch obrotowy względem chwilowego środka prędkości

Ruch płaski można także rozważać jako chwilowy ruch obrotowy. Na tej podstawie twierdzi
się, że w każdej chwili czasu prędkości punktów bryły są takie jakby bryła obracała się wokół
pewnej osi prostopadłej do płaszczyzny ruchu (płaszczyzny kierującej). Oś ta jest chwilową
osią obrotu, a punkt jej przecięcia z płaszczyzną kierującą nosi nazwę

chwilowego środka

obrotu.

V

B

A

B

V

A

⊥ AS

V

B

⊥ BS

V

S

= 0

V

A

ω

S

Punkt S to

chwilowy środek obrotu. Punkt ten leży w miejscu przecięcia prostopadłych do

wektorów prędkości wszystkich punktów bryły. W związku z tym może on w danej chwili
należeć do figury będącej rzutem bryły na płaszczyznę kierującą lub też może znajdować się
poza figurą. Jego prędkość liniowa jest równa zeru, a bryła wykonuje wokół niego ruch
obrotowy z

chwilową prędkością

ω

. Położenie chwilowego środka obrotu jest zmienne w

czasie, a miejsce geometryczne jego kolejnych położeń tworzy płaską krzywą –

centroidę.

Znając prędkość punktu A, położenie chwilowego środka obrotu bryły oraz kierunek wektora
prędkości punktu B, wartość

V

B

można obliczyć wg schematu:

AS

BS

BS

AS

A

B

B

A

V

V

V

V

=

=

=

ω

ω

Wyznaczanie prędkości w ruchu płaskim bryły

Wyznaczyć prędkości punktów A, B, C i D jednorodnego krążka staczającego się swobodnie
bez poślizgu po równi pochyłej jeśli prędkość jego środka masy jest równa

V

O

.

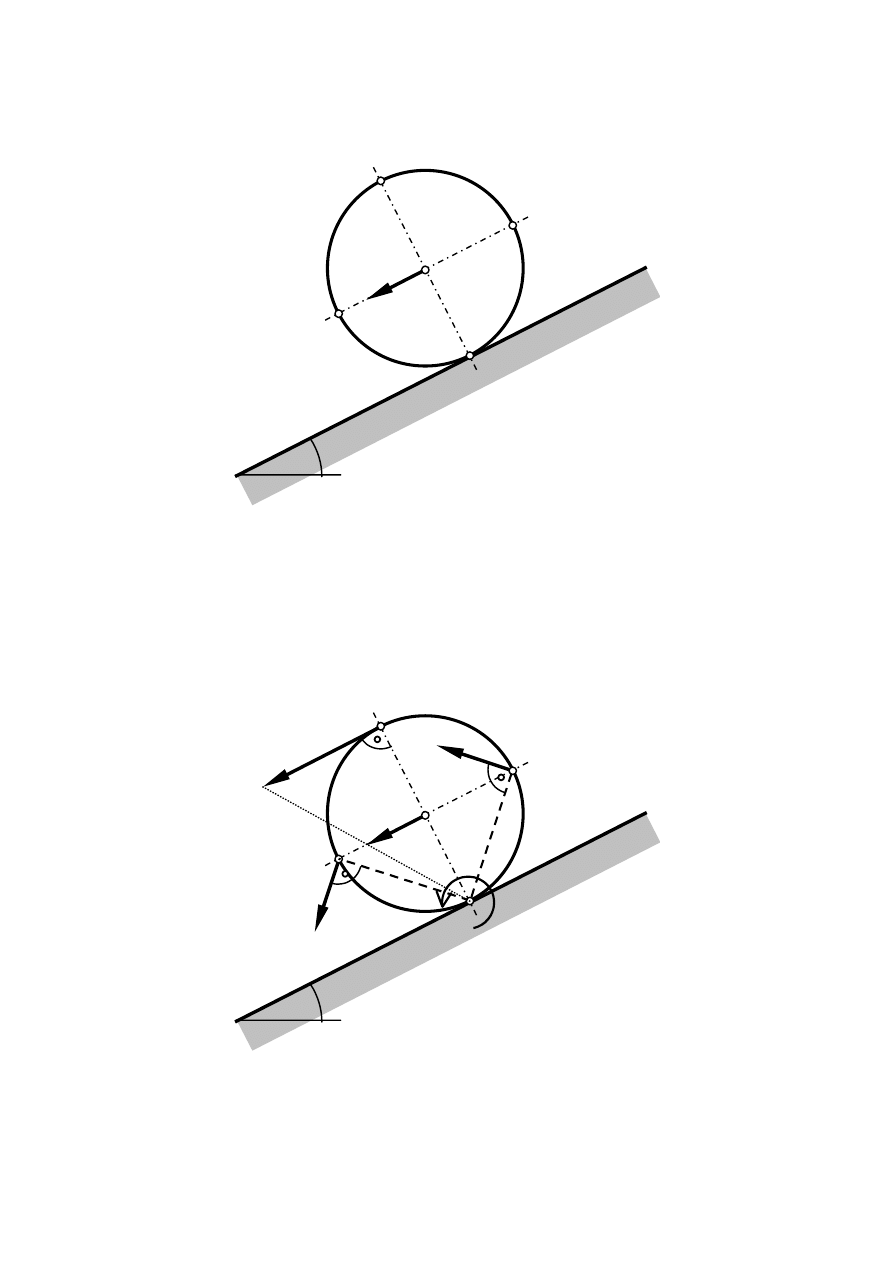
40

α

y

V

O

O

C

B

A

D

W przypadku toczenia bez poślizgu, występującym przy udziale tarcia nierozwiniętego
między bryłą a równią, punkt D jest chwilowym środkiem obrotu. Jego prędkość jest więc
równa zeru, a ruch krążka można traktować jako chwilowy ruch obrotowy wokół tego punktu
z chwilową prędkością obrotową

ω

.

α

y

V

O

ω

O

C

B

A

D

V

A

V

B

V

C

V

D

= 0

Prędkości liniowe punktów A, B i C mają kierunki prostopadłe do odpowiednich odcinków
łączących te punkty z chwilowym środkiem obrotu D. Zwroty wektorów prędkości są
zdeterminowane przez kierunek obrotu krążka.

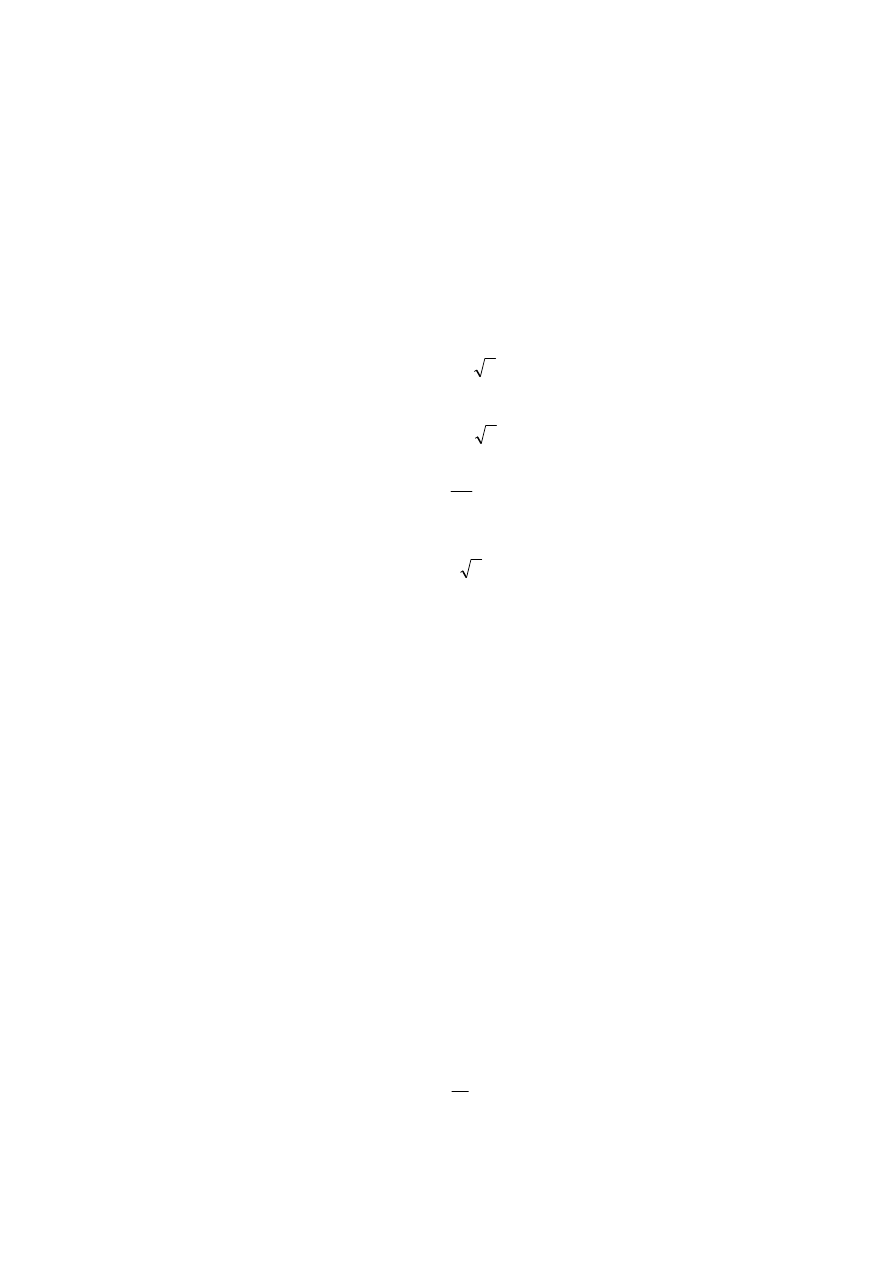
41

Wartość prędkości punktu B, który jest położony na średnicy BOD, jest proporcjonalna do
prędkości punktu O. Interpretacja graficzna tej relacji polegała na wykreśleniu linii
kropkowanej między punktem D a końcem wektora prędkości punktu B.
Ze względu na lokalizację punktów B i O w stosunku do punktu D prędkość punktu B musi
być dwa razy większa od prędkości punktu O, czyli

V

B

= 2

V

O

Ponieważ punkty A i C są położone w tej samej odległości od punktu D (AD = CD), to
wartości ich prędkości muszą być takie same. Oznaczając przez

r promień krążka łatwo

zauważyć, że

AD = CD =

2

r

Stąd

V

A

=

V

C

=

ω

2

r,

gdzie

r

V

O

=

ω

i ostatecznie

V

A

=

V

C

=

2

V

O

DYNAMIKA
Dynamika punktu materialnego

Podstawy mechaniki klasycznej sformułowane przez Newtona w postaci trzech praw
i ogłoszone w 1687 roku w pracy „

Philosophiae naturalis principia mathematica” dotyczą

punktu materialnego. Ze względu na to, że każde ciało można traktować jako zbiór punktów
materialnych, to prawa Newtona mogą być przenoszone na bryły sztywne.


Prawa Newtona

1. Jeżeli siła wypadkowa działająca na punkt materialny jest równa zeru, to punkt ten

pozostaje w spoczynku (jeśli był w spoczynku przed przyłożeniem sił) lub porusza się ze
stałą prędkością wzdłuż linii prostej (jeśli początkowo był w ruchu).

2. Jeżeli siła wypadkowa działająca na punkt materialny o masie

m nie jest równa zeru, to

punkt ten będzie się poruszał z przyspieszeniem proporcjonalnym do wartości tej siły i
zgodnie z jej zwrotem i kierunkiem

m

F

a

=

42

3. Siły wzajemnego oddziaływania między ciałami znajdującymi się w kontakcie mają tę

samą wartość, linię działania i przeciwny zwrot.

Zasada d’Alemberta

Przekształcając równanie opisujące drugie prawo Newtona można zapisać

F = ma

i dalej

F – ma = 0

gdzie

F jest wypadkową układu sił działających na punkt materialny, a jest przyspieszeniem

punktu materialnego.
Po przyjęciu oznaczenia

B = – ma

gdzie

B to siła bezwładności lub siła d’Alemberta, ostatecznie otrzymuje się

F + B = 0

Otrzymane równanie, które ma postać równania równowagi jak w zagadnieniach statyki,
stanowi opis matematyczny

zasady d’Alemberta:

W czasie ruchu punktu materialnego siły rzeczywiste działające na ten punkt równoważą się

w każdej chwili z odpowiednimi siłami bezwładności.

Całkowanie równań różniczkowych ruchu punktu materialnego

x

y

z

O

A

r

F

m

Wektorowe równanie ruchu Newtona

F = ma

po przywołaniu wzoru na przyspieszenie
punktu

2

2

dt

d

r

a

=

przyjmuje postać następującą

2

2

dt

d

m

r

F

=

Równanie to jest równoważne trzem równaniom skalarnym definiującym związki między
składowymi siły wypadkowej działającej na punkt A o masie

m a składowymi przyspieszenia

wzdłuż osi układu odniesienia

43

2

2

dt

x

d

m

F

x

=

,

2

2

dt

y

d

m

F

y

=

,

2

2

dt

z

d

m

F

z

=

gdzie:

F

x

,

F

y

,

F

z

to długości składowych wektora siły

F,

x

a

dt

x

d

=

2

2

,

y

a

dt

y

d

=

2

2

,

z

a

dt

z

d

=

2

2

to długości składowych wektora przyspieszenia

a.

Otrzymane równania są równaniami różniczkowymi zwyczajnymi drugiego rzędu
opisującymi ruch punktu materialnego. Ich rozwiązanie na drodze dwukrotnego całkowania z
odpowiednimi warunkami początkowymi pozwala na wyznaczenie trzech funkcji zależnych
od czasu

x = x(t), y = y(t), z = z(t)

które stanowią kinematyczne równania ruchu punktu

.

Analityczne rozwiązanie różniczkowych równań ruchu jest jednak na ogół trudne, ponieważ
składowe siły

F

x

,

F

y

,

F

z

mogą być zależne od czasu

t, położenia punktu określanego

współrzędnymi

x, y, z oraz prędkości punktu V

x

,

V

y

,

V

z

.

Ruch krzywoliniowy punktu materialnego

Przykład
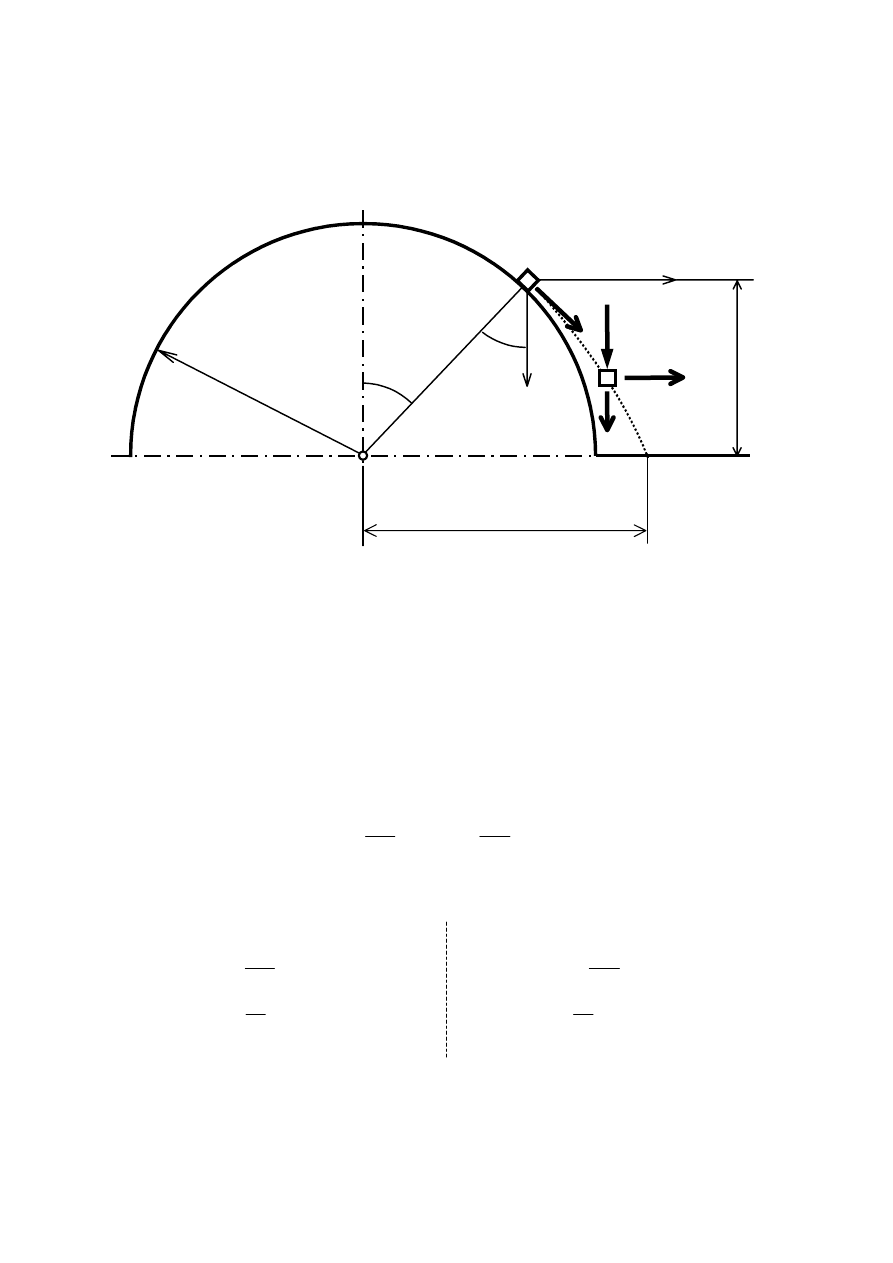
Z wierzchołka półwalca o promieniu

r wzdłuż jego gładkiej pobocznicy zsuwa się punkt

materialny. Wiedząc, że ruch odbywa się bez prędkości początkowej, wyznaczyć kąt

α

, przy

jakim punkt oderwie się od pobocznicy oraz miejsce jego upadku na podłoże.

b

O

r

α

Dane:

r

Szukane:

α

,

b

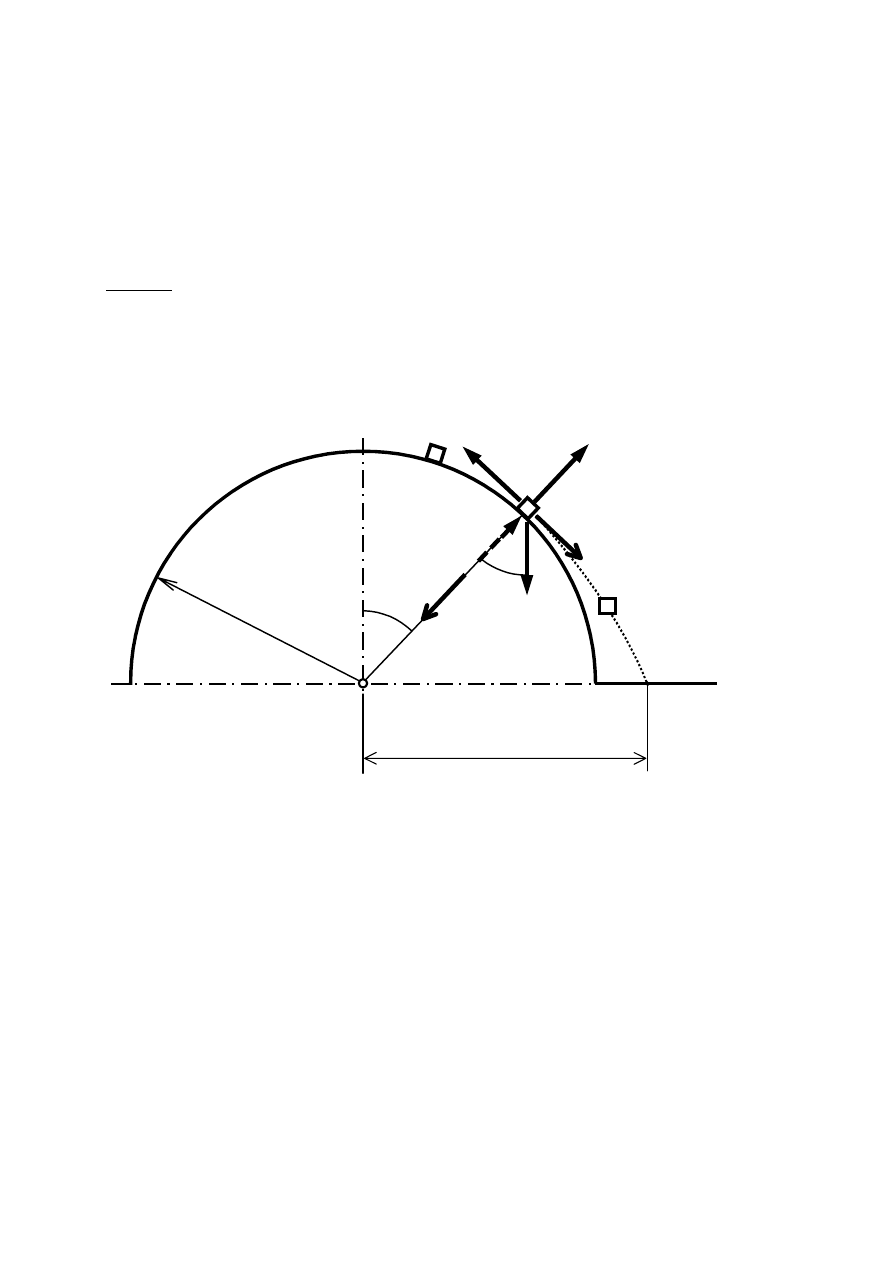
44

Rozwiązanie
Celem opisu ruchu punktu od wierzchołka półwalca do miejsca upadku na podłoże należy
wyróżnić dwie charakterystyczne fazy ruchu: pierwszą CD gdy punkt porusza się wzdłuż
pobocznicy walca i drugą DE gdy jest wyrzucony z prędkością

V

D

i porusza się w przestrzeni.

Te dwie fazy ruchu różnią się torem ruchu oraz układem sił działających na punkt.

Faza CD
Przy opisie ruchu punktu po łuku okręgu najwygodniej jest rozpatrywać ten ruch w rzucie na
kierunki naturalne związane z torem, czyli na kierunek stycznej i kierunek normalnej do toru.
Do sformułowania rozwiązania przy tej fazie ruchu proponuje się zasadę d’Alemberta.
Celem rozwiązania tej fazy ruchu jest wyznaczenie prędkości

V

D

, czyli prędkości

początkowej dla ruchu po krzywej DE.

b

O

r

α

C

E

D

α

B

n

G

N=0

B

t

a

n

a

t

Wzdłuż łuku CD na punkt materialny działają dwie siły czynne:

− siła ciężkości G,

− siła normalna N wyrażająca oddziaływanie półwalca na punkt

oraz dwie siły bezwładności:

− siła bezwładności B

t

= -

m

a

t

o zwrocie przeciwnym do założonego zwrotu wektora

przyspieszenia stycznego),

− siła bezwładności B

n

= -

m

a

n

(o zwrocie przeciwnym do znanego zwrotu wektora

przyspieszenia normalnego).

W położeniu D określonym przez kąt

α

następuje oderwanie punktu od pobocznicy, więc siła

normalna oddziaływania podłoża przyjmuje wartość równą zeru (

N = 0).

Biorąc pod uwagę zwroty wektorów sił czynnych i bezwładności można napisać następujące
równania:

− na kierunku stycznym do toru

45

B

t

–

G sin

α

= 0

− na kierunku normalnym do toru

B

n

–

G cos

α

= 0

Po podstawieniach

B

t

=

m a

t

=

m

dt

dV

D

,

B

n

=

m a

n

= m

r

V

D

2

,

G = mg

równania te rozwiązuje się następująco:

- dla kierunku stycznego

- dla kierunku normalnego

α

sin

g

dt

dV

D

=

α

α

α

sin

g

dt

d

d

dV

D

=

Ponieważ

r

V

dt

d

D

=

=

ω

α

,

to

α

α

d

g

dV

r

V

D

D

sin

=

Po obustronnym scałkowaniu otrzymuje się

C

gr

V

D

+

−

=

cos

2

1

2

α

Stałą całkowania

C wyznacza się z warunku

początkowego:
przy

gr

C

V

D

2

0

,

0

=

→

=

=

α

Stąd ostatecznie otrzymuje się, że:

(

)

cos

1

2

2

α

−

= gr

V

D

α

cos

2

g

r

V

D

=

α

cos

2

gr

V

D

=

Porównując oba otrzymane wzory na prędkość

V

D

wyznacza się wartość kąta

α

, przy jakim

nastąpi oderwanie punktu od pobocznicy:

(

)

α

α

cos

cos

1

2

gr

gr

=

−

cos

α

= 2/3

α

= arc cos(2/3)

Znając wartość kąta

α

, prędkość

gr

V

D

3

2

=

Faza DE
Ruch punktu po krzywej DE odbywa się pod działaniem siły ciężkości. Znając prędkość
początkową tej fazy ruchu przyjmuje się układ współrzędnych D

xy o zwrotach osi zgodnych

46

ze zwrotem rzutów wektora prędkości na te osie. W tej fazie proponuje się sformułowanie
rozwiązanie na podstawie drugiego prawa Newtona.

x

y

b

O

r

α

C

E

D

α

a

y

V

D

a

x

G

h

D

Równania Newtona dla kierunków osi

x i y są można napisać w następującej postaci:

∑

=

=

n

i

ix

x

F

ma

1

,

∑

=

=

n

i

iy

y

F

ma

1

gdzie

F

ix

,

F

iy

to składowe

i-tej siły działającej na punkt materialny.

W rozważanym przypadku na punkt działa tylko jedna siła o kierunku równoległym do
kierunku osi

y, w związku z czym równania Newtona przyjmą postać:

0

2

2

=

dt

x

d

m

,

G

dt

y

d

m

=

2

2

Rozwiązania tych równań celem znalezienia miejsca upadku punktu na podłoże przeprowadza
się równolegle wg schematu:

0

2

2

=

dt

x

d

1

D

dt

dx =

g

dt

y

d

=

2

2

2

D

gt

dt

dy

+

=

47

Stałe wyznacza się z warunków początkowych, które dotyczą chwili czasu

t = 0, kiedy punkt

znajdując się w położeniu D miał prędkość początkową

V

D

.

Przy

t = 0, V

x

=

gr

V

dt

dx

D

3

2

3

2

cos

=

=

α

,

V

y

=

gr

V

dt

dy

D

3

2

3

5

sin

=

=

α

, z czego

wynika, że

gr

D

3

2

3

2

1

=

, natomiast

gr

D

3

2

3

5

2

=

.

Ostatecznie otrzymuje się równania

składowych prędkości w postaci

gr

dt

dx

3

2

3

2

=

gr

gt

dt

dy

3

2

3

5

+

=

Składowa prędkości wzdłuż osi

x jest niezależna od czasu, składowa prędkości wzdłuż osi y

jest wyrażana przez funkcję zależną liniowo od czasu. Po kolejnym całkowaniu otrzymuje się

3

3

2

3

2

D

t

gr

x

+

=

4

2

3

2

3

5

2

1

D

t

gr

gt

y

+

+

=

Przy czasu

t = 0 punkt znajduje się w położeniu D, dla którego x(0) = y(0) = 0, z czego

wynika, że stałe

D

3

=

D

4

= 0 i ostatecznie

t

gr

x

3

2

3

2

=

t

gr

gt

y

3

2

3

5

2

1

2

+

=

Otrzymane

parametryczne równania toru umożliwiają określenie położenia punktu względem

przyjętego układu współrzędnych dla dowolnej chwili czasu

t. Równanie toru punktu otrzyma

się po zdefiniowaniu zmiennej

t na podstawie równania pierwszego i podstawieniu do

równania drugiego:

x

gr

t

2

3

2

3

=

x

x

r

x

gr

gr

x

gr

g

y

2

5

16

27

2

3

2

3

3

2

3

5

2

3

2

3

2

1

2

2

+

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

Równanie toru jest równaniem paraboli.
Z analizy rysunku wynika, że punkt znajdzie się na podłożu jeśli współrzędna y przyjmie

wartość h

D

= r cos

α

= r

3

2

.

By znaleźć współrzędną x odpowiadającą zmiennej zależnej y = h

D

= r

3

2

należy rozwiązać

następujące równanie kwadratowe:

0

3

2

2

5

16

27

2

=

−

+

r

x

x

r

Po obliczeniu wyróżnika wybieramy jeden - dodatni pierwiastek rozwiązania, który jest drugą
współrzędną punktu E - miejsca geometrycznego przecięcia krzywej toru z podłożem.

48

Pierwiastek ten jest równy

(

)

r

x

27

5

23

4

1

−

=

Poszukiwana współrzędna b jest równa

(

)

(

)

r

r

r

r

x

r

b

1.12458

5

5

23

4

27

1

27

5

23

4

3

5

sin

1

≈

+

=

−

+

=

+

=

α

Prawo zachowania i zmienności pędu

Na podstawie drugiego prawa dynamiki Newtona w postaci

F = ma

po uwzględnieniu, że przyspieszenie można wyrazić jako pochodną wektora prędkości
względem czasu

dt

d

V

a

=

otrzymuje się

F

V =

dt

d

m

Masa punktu materialnego jest niezależna od czasu więc może być włączona pod znak
różniczki

( )

F

V =

dt

m

d

Iloczyn masy i wektora prędkości jest nazywany pędem (ilością ruchu) punktu i oznaczany
przez p.
Ostatecznie otrzymuje się

F

p =

dt

d

Z równania tego wynika, że pochodna wektora pędu względem czasu równa jest sile
wypadkowej

F działającej na dany punkt.

Jeżeli siła wypadkowa

F jest równa zeru, to

0

=

dt

dp

i wektor pędu jest stały

p = const.

Stąd prawo zachowania pędu mówi:

Jeżeli na punkt materialny pozostający w ruchu nie działa żadna siła lub działający układ

sił daje wypadkową równą zeru, to pęd takiego układu pozostaje niezmieniony

Jeżeli siła wypadkowa

F nie jest równa zeru, to po obustronnym scałkowaniu równania

( )

dt

m

d

F

V

=

otrzymuje się

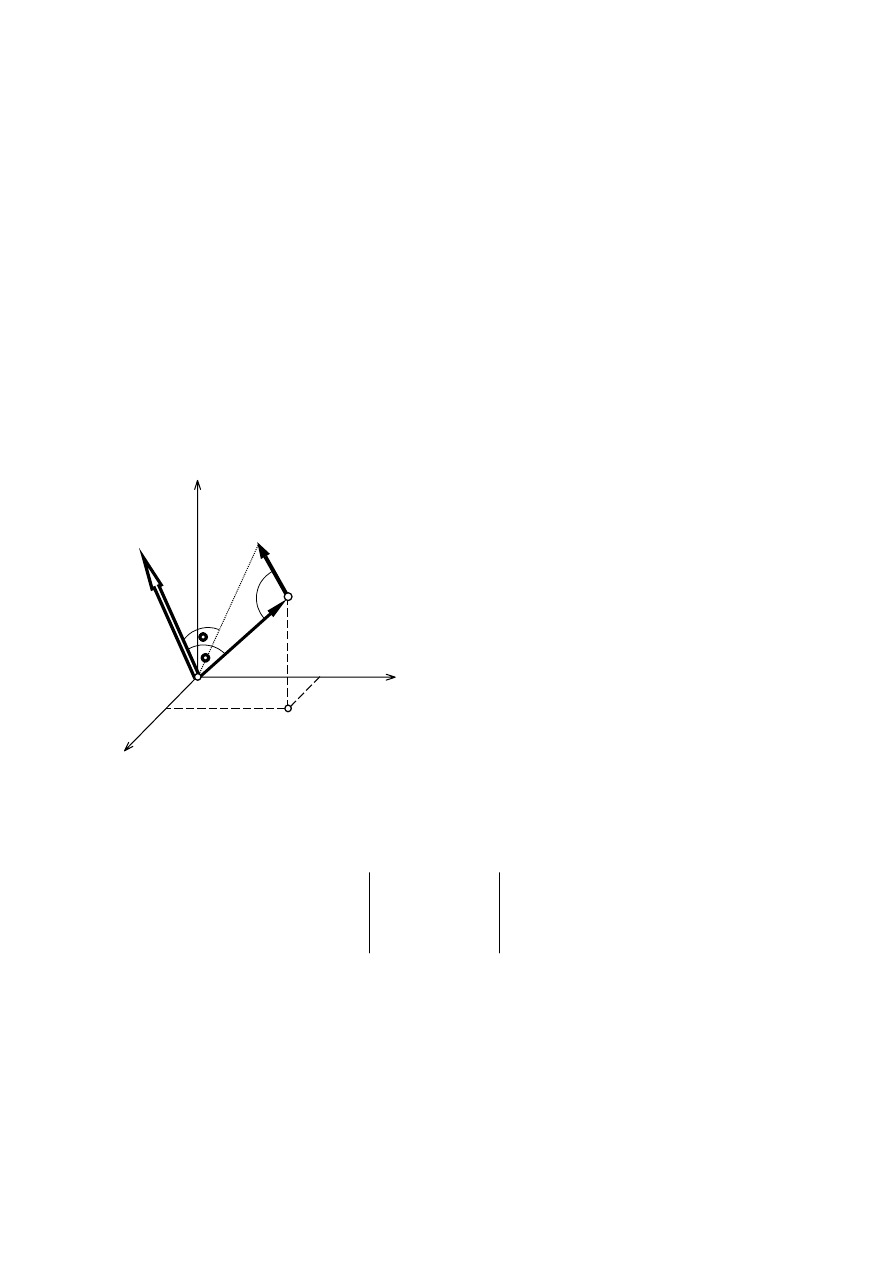
49

( )

∫

∫

=

2

1

2

1

t

t

V

V

dt

m

d

F

V

∫

=

−

2

1

1

2

t

t

dt

m

m

F

V

V

Ostatnie równanie opisuje prawo zmienności pędu o brzmieniu:

Przyrost pędu punktu materialnego w skończonym przedziale czasu jest równy impulsowi

siły (popędowi siły) działającej na ten punkt w tym samym czasie

Kręt punktu materialnego względem bieguna. Prawo zachowania krętu

m

x

y

z

O

r

m

V

α

K

O

y

x

z

Rozważany jest punkt materialny o masie m,
który porusza się z prędkością

V.

Krętem (momentem pędu)

K

O

punktu

materialnego względem bieguna O nazywamy
wektor otrzymywany w wyniku mnożenia
wektorowego wektora położenia punktu

r

przez wektor jego pędu m

V

V

r

K

m

×

=

O

Na podstawie definicji iloczynu wektorowego
długość wektora pędu jest równa

α

sin

O

mVr

K

=

Wyrażając wektory

r i mV poprzez ich składowe i stosując definicję wyznacznikową

iloczynu wektorowego otrzymuje się

z

y

x

z

y

x

K

K

K

mV

mV

mV

z

y

x

m

k

j

i

k

j

i

V

r

K

+

+

=

=

×

=

O

gdzie po rozwinięciu wyznacznika długości składowych wektora krętu są równe

(

)

y

z

x

zV

yV

m

K

−

=

(

)

z

x

y

xV

zV

m

K

−

=

(

)

x

y

z

yV

xV

m

K

−

=

50

W trakcie ruchu swobodnego wektory położenia i prędkości punktu ulegają zmianie w funkcji
czasu. W związku z tym pochodna wektora krętu względem czasu musi być obliczana jako
pochodna iloczynu wektorowego

(

)

( )

O

O

M

F

r

F

r

V

V

V

r

V

r

V

r

K

=

×

=

×

+

×

=

×

+

×

=

×

=

m

dt

m

d

m

dt

d

m

dt

d

dt

d

Ostatecznie pochodna względem czasu wektora krętu

K

O

względem nieruchomego bieguna O

jest równa momentowi siły wypadkowej

F względem tego bieguna

O

O

M

K =

dt

d

Praca i moc

α

A’

x

y

z

O

r

+

dr

F

A

dr

r

Rozważa się punkt, który przemieszcza się z
położenia A określonego przez wektor
położenia

r do sąsiedniego położenia A’

określonego przez wektor

r

+

d

r.

Wektor między położeniami (różniczka d

r)

jest elementarnym przemieszczeniem.
Jeśli na punkt działa siła

F, to praca tej siły

odpowiadająca przemieszczeniu d

r jest

definiowana jako następująca wielkość
skalarna

dL =

F

·

d

r

Praca jest więc iloczynem skalarnym wektora
siły

F i wektora przemieszczenia dr.

Znając kąt

α

między wektorami

F i dr, na podstawie definicji iloczynu wektorowego można

napisać, że

dL = F ds cos

α

lub

dL = F

x

dx + F

y

dy + F

z

dz

gdzie: ds jest różniczką drogi (

⎮

d

r

⎮

= ds) oraz d

r = i dx+j dy +k dz

Praca jako wartość skalarna ma swoją wartość i znak.


Praca siły przy ruchu punktu po torze krzywoliniowym

Punkt poruszający się po torze krzywoliniowym od położenia O przebywa drogę wyrażaną w
mierze łukowej. Pracę wykonywaną przez siłę

F od położenia A

1

do położenia A

2

definiujemy jako

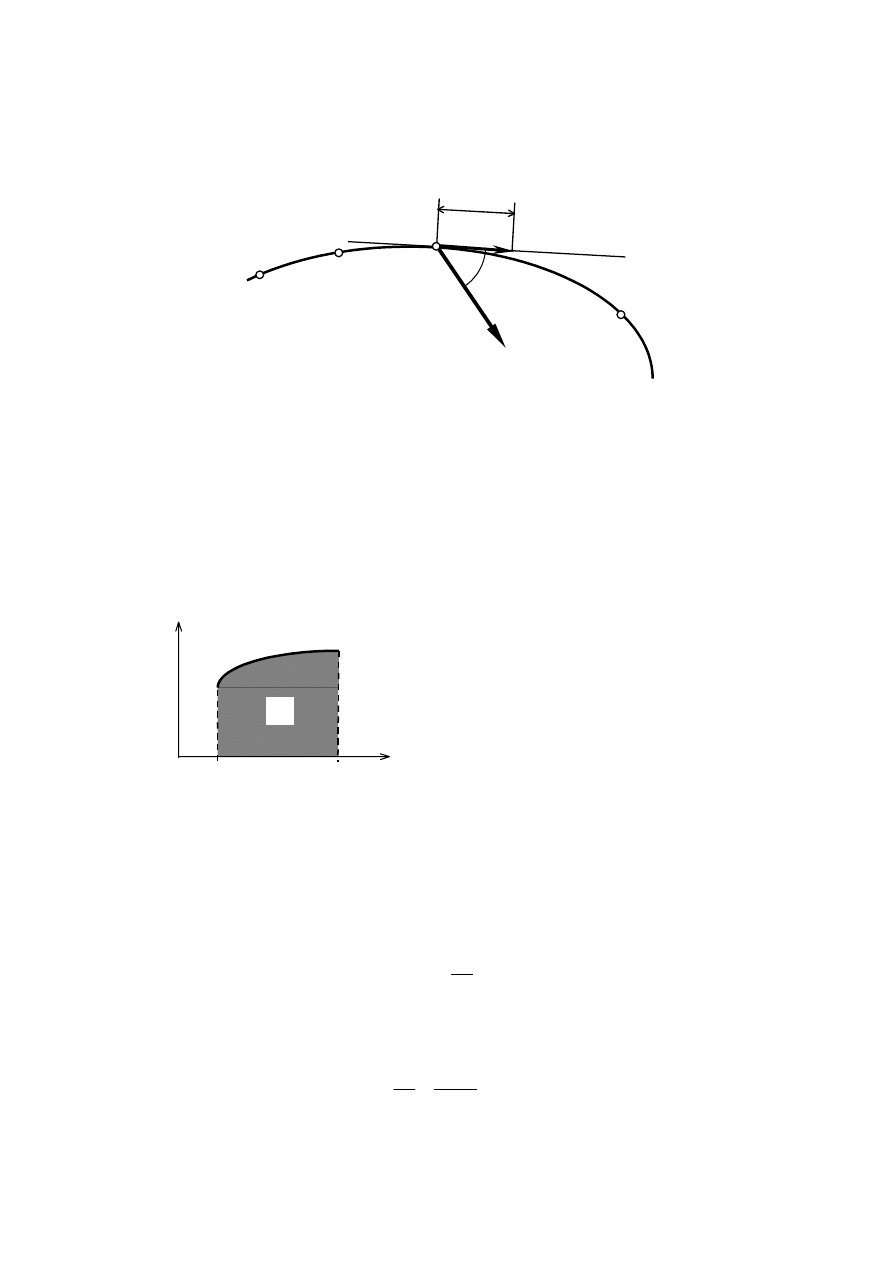
51

∫

⋅

=

2

1

A

A

r

F d

L

A

1

A

t

A

2

F

dr

ds

O

α

Przy założeniu, że OA

1

= s

1

i OA

2

= s

2

, na podstawie definicji iloczynu skalarnego pracę siły

F określamy następująco

∫

∫

=

=

2

1

2

1

cos

s

s

t

s

s

ds

F

ds

F

L

α

gdzie F

t

jest długością składowej wektora

F na kierunku stycznej.

F

t

s

s

2

s

1

L

Pracę

∫

=

2

1

s

s

t

ds

F

L

interpretuje się graficznie

jako pole powierzchni pod krzywą otrzymaną
przez wykreślenie siły F

t

w funkcji drogi s.

Jednostką pracy jest 1 [J] (dżul) czyli praca wykonana przez siłę o wartości 1 [N] na drodze
1 [m].


Moc

Moc definiujemy jako pracę wykonaną w określonej chwili czasu

dt

dL

N

=

Po podstawieniu dL =

F

·

d

r otrzymuje się

V

F

r

F

⋅

=

⋅

=

=

dt

d

dt

dL

N

Jednostką mocy jest 1[W] (wat) czyli 1[J]/[s].

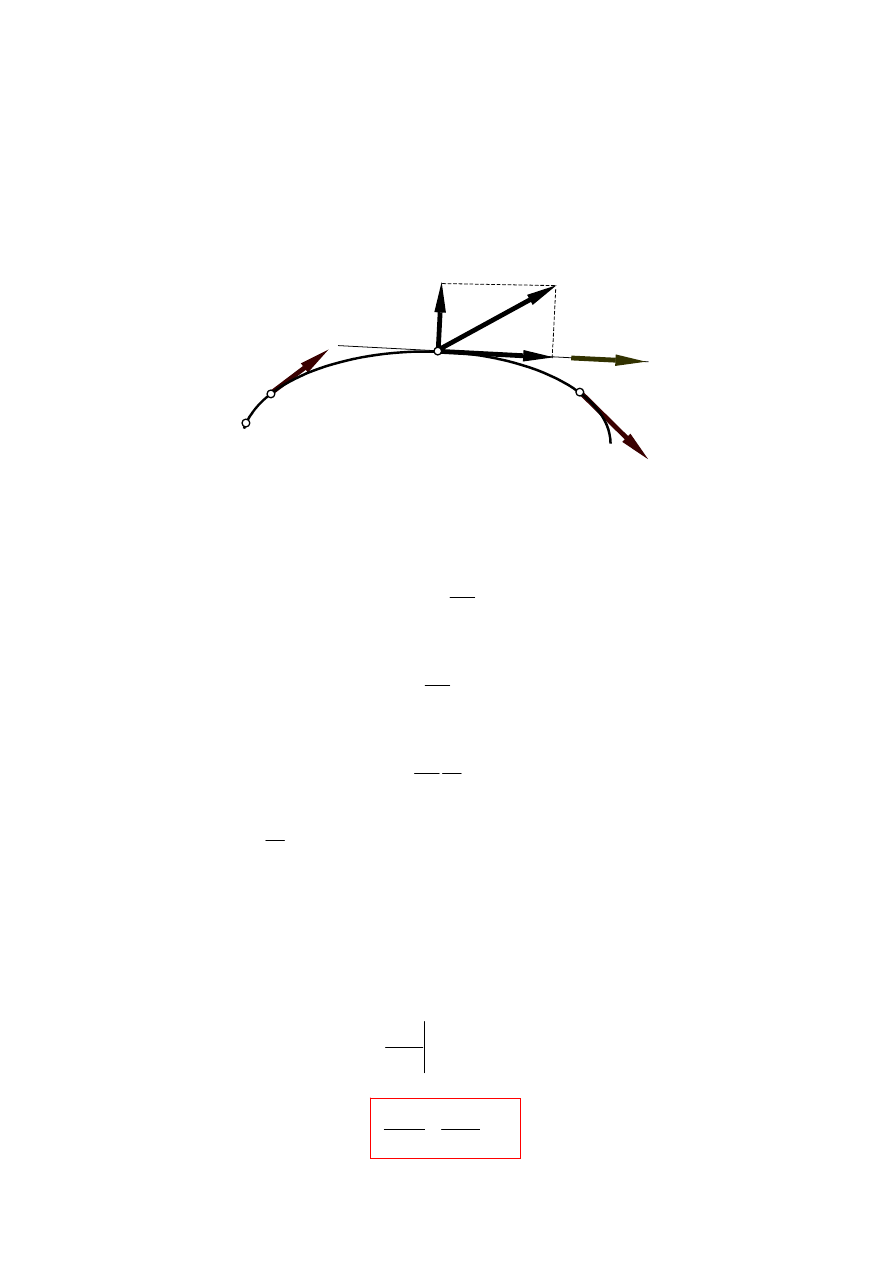
52

Energia kinetyczna punktu materialnego. Prawo równości energii kinetycznej
i pracy

Rozpatruje się ruch punktu materialnego o masie m po torze krzywoliniowym, na który działa
siła

F. Droga punktu mierzona wzdłuż toru od punktu O zmienia się od wartości s

1

w

położeniu A

1

, kiedy punkt osiągnął prędkość V

1

, do wartości s

2

w położeniu A

2

, gdy punkt

porusza się z prędkością V

2

.

F

t

m

A

1

V

2

(t)

V

1

F

n

A

2

F

a

t

O

Z drugiego prawa Newtona zapisanego dla kierunku stycznego (t) wynika, że

t

t

F

ma

=

Ponieważ przyspieszenie styczne jest równe

dt

dV

a

t

=

to możemy zapisać

t

F

dt

dV

m

=

i dalej

t

F

dt

ds

ds

dV

m

=

Po podstawieniu, że

V

dt

ds = i obustronnym pomnożeniu równania przez różniczkę drogi ds

celem rozdzielenia zmiennych otrzymuje się

ds

F

dV

mV

t

=

Obustronne scałkowanie: lewej strony równania w granicach od V

1

do wartości V

2

, natomiast

prawej strony w granicach od s

1

do s

2

prowadzi do

∫

=

2

1

2

1

2

2

s

s

t

V

V

ds

F

mV

i ostatecznie

L

mV

mV

=

−

2

2

2

1

2

2

53

Wielkość skalarną

2

2

mV

E

k

=

nazywamy energią kinetyczną punktu materialnego. Jest to połowa iloczynu masy i kwadratu
prędkości punktu.
Wyprowadzone równanie opisuje matematycznie prawo równości energii kinetycznej i pracy,
które brzmi:

Przyrost energii kinetycznej punktu materialnego w skończonym przedziale czasu jest

równy sumie prac jakie wykonały w tym czasie wszystkie siły działające na ten punkt

Potencjalne pole sił

Potencjalne (zachowawcze) pole sił to takie pole, że w każdym jego punkcie jest określona
funkcja

V

(x, y, z), której pochodne cząstkowe względem x, y i z są równe rzutom siły pola

z przeciwnymi znakami.
Funkcja

V

(x, y, z) to potencjał zachowawczego pola sił lub energia potencjalna tego pola.

x

F

x

z

y

x

V

−

=

∂

∂

)

,

,

(

,

y

F

y

z

y

x

V

−

=

∂

∂

)

,

,

(

,

z

F

z

z

y

x

V

−

=

∂

∂

)

,

,

(

Z zapisu tego wynika, że składowe siły

F są funkcjami współrzędnych x, y i z. Stąd siły

zachowawcze to takie siły, które zależą tylko od lokalizacji ich punktu przyłożenia.
Siłę

F można zapisać jako

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

+

∂

∂

+

∂

∂

−

=

+

+

=

z

V

y

V

x

V

F

F

F

z

y

x

k

j

i

k

j

i

F

lub

V

grad

F

−

=

Energia potencjalna. Prawo zachowania energii mechanicznej

y

x

A

1

y

dy

A

2

y

2

y

1

G

Rozpatruje się ruch punktu materialnego pod
działaniem siły ciężkości

G po torze od

krzywoliniowym od położenia A

1

o

współrzędnej y

1

do położenia A

2

o

współrzędnej y

2

.

Pracę siły ciężkości wyznacza się ze wzoru:

(

)

∫

+

+

=

2

1

A

A

z

y

x

dz

G

dy

G

dx

G

L

54

Siła

G ma składowe o następujących długościach: G

x

= 0, G

y

=-G, G

z

= 0, co po podstawieniu

prowadzi do następującego wyrażenia na pracę:

(

)

y

G

y

y

G

dy

G

L

y

y

∆

−

=

−

−

=

−

=

∫

1

2

2

1

Praca siły ciężkości jest równa iloczynowi tej siły i przemieszczenia pionowego

∆y. Praca ta

jest dodatnia gdy

∆y = y

2

– y

1

< 0, czyli w przypadku gdy ciało zsuwa się w dół.

Pracę siły ciężkości można przedstawić jako różnicę:

L = Gy

1

- Gy

2

= mg y

1

– mg y

2

Praca ta nie zależy od drogi, a jedynie od początkowej i końcowej wartości funkcji mgy.
Funkcję tę nazywamy energią potencjalną:

E

p

= mgh

Praca siły ciężkości może być przedstawiona jako różnica energii potencjalnej określonej w
położeniu początkowym i końcowym

L = E

p

(1)

- E

p

(2)

Prawo zachowania energii mechanicznej

Jeśli punkt materialny porusza się w zachowawczym polu sił, to suma jego energii
kinetycznej i energii potencjalnej zwana energią mechaniczną jest stała

E

k

(1)

+ E

p

(1)

=E

k

(2)

+ E

p

(2)

Literatura

:

1. B.Skalmierski: Mechanika, Wydawnictwo Politechniki Częstochowskiej 2002 (t. 1 i 2)
2. J.Misiak: Mechanika techniczna, PWN Warszawa 1999 (t. I i II)
3. J.Nizioł: Metodyka rozwiązywania zadań z mechaniki, WNT Warszawa 2002
4. J.Leyko: Mechanika ogólna, PWN Warszawa 2006 (t. 1 i 2)
5. J.Leyko; J. Szmelter: Zbiór zadań z mechaniki ogólnej, PWN Warszawa 1976 (t. 1 i 2)
6. I.W.Mieszczerski: Zbiór zadań z mechaniki. PWN Warszawa 1969

7. M.Niezgodziński, T.Niezgodziński: Zbiór zadań z mechaniki ogólnej, PWN Warszawa

2003

8. T.Niezgodziński: Mechanika ogólna, PWN Warszawa 2006
9. Ryszard Buczkowski, Andrzej Banaszek: Mechanika ogólna w ujęciu wektorowym i

tensorowym. Statyka, przykłady i zadania. WNT Warszawa, 2006

10. F.P.Beer, E. Russell Johnston: Vector Mechanics for Engineers. McGraw-Hill Publishing

Company, 2004