Zagadnienia na egzamin

licencjacki z analizy zespolonej

Rozdział 1

Funkcje zmiennnej zespolonej

Definicja: 1.1. Funkcj ˛

a zmiennej zespolonej nazywamy odwzorowanie

f : A → C, gdzie A ⊂ C.
Ka˙zd ˛

a funkcje zmiennej zespolonej mo˙zna przedstawi´c w postaci:

f (z) = u(x, y) + iv(x, y),

gdzie z = x + iy

u - cz˛e´s´c rzeczywista funkcji f, v - cz˛e´s´c urojon ˛

a funkcji f. Oznaczamy odpowied-

nio Ref = u i Imf = v.

1.1

Wielomian

Definicja: 1.2. Wielomianem zmiennej zespolonej o współczynnikach zespolonych
nazywamy odwzorowanie w : A → C, gdzie A ⊂ C okre´slone:

w(z) = a

n

z

n

+ a

n−1

z

n−1

+ . . . + a

1

z + a

0

1.2

Funkcja wykładnicza

Definicja: 1.3. Funkcj ˛

a wykładnicz ˛

a zmiennej zespolonej nazywamy odwzorowanie

f : A → C, gdzie A ⊂ C okre´slone:

f (z) = e

z

gdzie e

z

=

∞

P

n=0

z

n

n!

i szereg ten jest bezwzgl˛ednie zbie˙zny. Własno´sci:

• e

0

= 1

• e

z

1

+z

2

= e

z

1

e

z

2

2

3

Rozdział 1. Funkcje zmiennnej zespolonej

• e

z

= 1

wtedy i tylko wtedy gdy z = 2kπi

• e

z

6= 0 dla dowolnego z ∈ C

1.3

Funkcje trygonometryczne

Szeregi

∞

P

n=0

(−1)

n

z

2n

(2n)!

i

∞

P

n=0

(−1)

n

z

2n+1

(2n+!)!

s ˛

a bezwzgl˛ednie zbie˙zne. Ponadto

cos z =

∞

P

n=0

(−1)

n

z

2n

(2n)!

sin z =

∞

P

n=0

(−1)

n

z

2n+1

(2n+!)!

tan z =

sin z

cos z

ctgz =

cos z

sin z

Własno´sci:

• e

iz

= cos z + i sin z

• sin

2

z + cos

2

z = 1

• Wzory Eulera: cos z =

e

iz

+e

−iz

2

i sin z =

e

iz

−e

−iz

2i

1.4

Funkcja logarytmiczna

Logarytmem zespolonym liczby a nazywamy rozwi ˛

azanie równania e

z

= a

,

które jest postaci:

z = log |a| + i arg a + 2kπi

Logarytmem głównym b ˛

ad´z gał˛ezi ˛

a główn ˛

a nazywamy wielko´s´c

z = log |a| + i arg a

1.5

Pot˛egowanie liczb zespolonych

Dla dowolnych dwóch liczb zespolonych a i b mamy a

b

= e

b log a

3

Rozdział 2

Pochodna funkcji zmiennej
zespolonej

Definicja: 2.1. Funkcja f : A → C, gdzie A ⊂ C jest ró˙zniczkowalna w punkcie
z

0

⇐⇒ istnieje granica lim

z→z

0

f (z)−f (z

0

)

z−z

0

. Je´sli granica ta istnieje, to nazywamy j ˛

a

pochodn ˛

a funkcji f.

Twierdzenie 2.1. Warunek konieczny ró˙zniczkowalno´sci
Je´sli funkcja f jest ró˙zniczkowalna, to jest ci ˛

agła.

Uwaga:

Stwierdzenie odwrotne jest fałszywe.

Jak wiemy, funkcj˛e f mo˙zna przedstawi´c jako:f (z) = u(x, y) + iv(x, y), gdzie
z = x + iy

.

Twierdzenie 2.2. Warunek konieczny ró˙zniczkowalno´sci(Równania Cauchy-
Riemanna)
Je´sli funkcja f jest ró˙zniczkowalna w z

0

, to istniej ˛

a pochodne cz ˛

astkowe u

x

, u

y

, v

x

i v

y

oraz:

u

x

(x

0

, y

0

) = v

y

(x

0

, y

0

)

i u

y

(x

0

, y

0

) = −v

x

(x

0

, y

0

)

Ponadto f

0

(z

0

) = u

x

(x

0

, y

0

) + iv

x

(x

0

, y

0

)

.

Uwaga:

Stwierdzenie odwrotne jest fałszywe.

Niech D b˛edzie obszarem (zbiór otwarty i spójny) w C.

Definicja: 2.2. Funkcja f jest holomorficzna w zbiorze D ⇐⇒ funkcja ta jest
ró˙zniczkowalna w dowolnym punkcie zbioru D.

Definicja: 2.3. Funkcja f jest holomorficzna w punkcie z

0

⇐⇒ jest ró˙zniczkowalna

na pewnym kole otwartym o ´srodku w z

0

.

4

Rozdział 3

Całka

Definicja: 3.1. Funkcja f jest całkowalna w sensie Riemanna ⇐⇒ całkowalne
w sensie Riemanna s ˛

a jej cz˛e´s´c rzeczywista i urojona. Oraz:

b

R

a

f (t)dt =

b

R

a

Ref (t)dt +

b

R

a

Imf (t)dt

Twierdzenie 3.1. Niech C b˛edzie krzyw ˛

a regularna (suma łuków regularnych,

czyli takich, ˙ze równanie opisuj ˛

ace łuk z(t) jest klasy C

1

i z

0

(t) 6= 0

) opisan ˛

a

równaniem z(t), dla t ∈ [a, b]. Wtedy dla funkcji ci ˛

agłej na C mamy, ˙ze f jest

całkowalna oraz

R

C

f (z)dz =

b

R

a

f (z(t))z

0

(t)dt

Funkcja F : D → C jest pierwotna dla f, je´sli jest holomorficzna na D i F’=f.

F pierwotna dla f ⇒

•

R

C

f (z)dz = F (b) − F (a)

, przy zało˙zeniu, ˙ze f jest ci ˛

agła na D i C ł ˛

aczy a i

b

• dla krzywej C zamkni˛etej

R

C

f (z)dz = 0

, je´sli f ci ˛

agła na D

Twierdzenie 3.2. Wzór całkowy Couchy’ego
Je´sli

(a) D jest obszarem ograniczonym krzyw ˛

a regularn ˛

a zamkni˛et ˛

a C dodatnio skierowan ˛

a

(b) funkcja f jest holomorficzna na D i jego brzegu

5

6

Rozdział 3. Całka

to ∀

z∈D

f (z) =

1

2πi

R

C

f (ξ)

ξ−z

dξ

Twierdzenie 3.3. Całkowe Cauchy’ego
Je´sli

(a) D jest obszarem jednospójnym ograniczonym krzyw ˛

a regularn ˛

a zamkni˛et ˛

a C

(b) funkcja f jest holomorficzna na D i jego brzegu

to

R

C

f (z)dz = 0

f jest holomorficzna w pewnym obszarze ⇒ ma w nim wszystkie pochodne i mamy
uogólniony wzór Cauchy’ego:

∀

n∈N

f

(n)

(z) =

n!

2πi

R

C

f (ξ)

(ξ−z)

n+1

dξ

6

Rozdział 4

Rozwijalno´s´c funkcji w szereg

Szeregiem pot˛egowym nazywamy szereg funkcyjny postaci:

+∞

P

n=0

a

n

(z − z

0

)

n

.

4.1

Rozwijalno´s´c w szereg Taylora

Niech D podobnie jak wy˙zej b˛edzie obszarem w C.

Twierdzenie 4.1. Je´sli funkcja f jest holomorficzna w D, to

∀

z

0

∈D

∃

U −otwarty

∀

z∈U

f (z) =

+∞

P

n=0

a

n

(z − z

0

)

n

,

gdzie a

n

=

f

(

n)(z

0

)

n!

.

4.2

Rozwijalno´s´c w szereg Laurenta

Definicja: 4.1. Szereg funkcyjny

+∞

P

n=−∞

a

n

(z − z

0

)

n

=

+∞

P

n=1

a

−n

(z − z

0

)

−n

+

+∞

P

n=0

a

n

(z − z

0

)

n

nazywamy szeregiem Laurenta o ´srodku w z

0

.

Je´słi r = lim sup

n→+∞

n

p|a

n

| i R =

1

lim sup

n→+∞

n

√

|a

n

|

oraz r < R, to szereg Laurenta jest

funkcj ˛

a holomorficzn ˛

a w obszarze pier´scieniowym

D = {z ∈ C : r < |z − z

0

| < R}.

Twierdzenie 4.2. Je´sli funkcja f jest holomorficzna w obszarze pier´scieniowym
D, to

7

8

Rozdział 4. Rozwijalno´s´c funkcji w szereg

∀

z∈D

f (z) =

+∞

P

n=−∞

a

n

(z − z

0

)

n

gdzie a

n

jest okre´slone jak przy rozwini˛eciu Taylora.

Twierdzenie 4.3. Nierówno´s´c Cauchy’ego

Je´sli f jest holomorficzna w kole |z| < R, f (z) =

∞

P

n=0

a

n

z

n

, |f (z)| < M , to

|a

n

| ≤

M

R

n

.

Twierdzenie 4.4. Liouville’a
Ka˙zda funkcja całkowita (okre´slona i holomorficzna na całym C) i ograniczona
jest stała.

Twierdzenie 4.5. Zaasada maksimum
Je´sli

(a) funkcja f jest holomorficzna w D

(b) ∃

z

0

∈D

∃

ρ>0

∀

z∈K(z

0

,ρ)

|f (z)| ≤ |f (z

0

)|

,

to f jest stała.

8

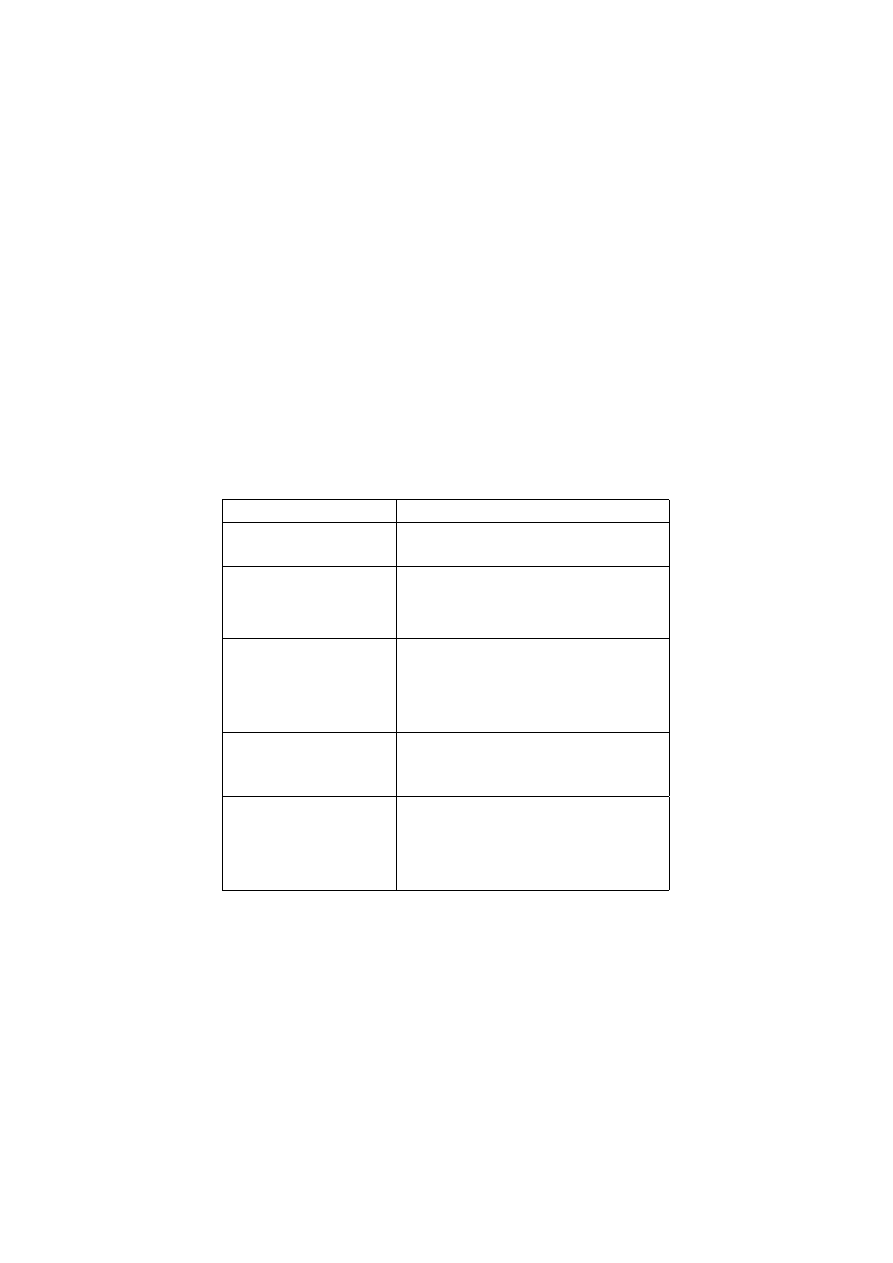
Rozdział 5

Punkty osobliwe i residua

Rodzaj punktu z

0

Definicja

regularny

funkcja f jest holomorficzna na
pewnym kole |z − z

0

| < R

pozornie osobliwy

lim

z→z

0

f (z)

istnieje (a

−n

= 0

dla

n > 1 w rozwini˛eciu w szereg
Laurenta i granica równa si˛e a

0

)

biegun jednokrotny

lim

z→z

0

f (z) = ∞

(dla rozwini˛e-

cia w szereg Laurenta funkcji f
zbiór {n, a

−n

6= 0} jest sko ´nc-

zony)

biegun k-krotny

lim

z→z

0

[(z − z

0

)

k

f (z)]

6=

0

oraz

lim

z→z

0

[(z − z

0

)

k+1

f (z)] = 0

istotnie osobliwy

lim

z→z

0

f (z)

nie

istnieje

(dla

rozwini˛ecia

w

szereg

Lau-

renta funkcji f zbiór {n, a

−n

6= 0}

jest niesko ´nczony)

Definicja: 5.1. Residuum
Liczb˛e a

−1

w rozwini˛eciu funkcji f w szereg Laurenta nazywamy residum funkcji

f w punkcie z

0

i oznaczamy res

z

0

f

Sposoby oblicznania residuum.

9

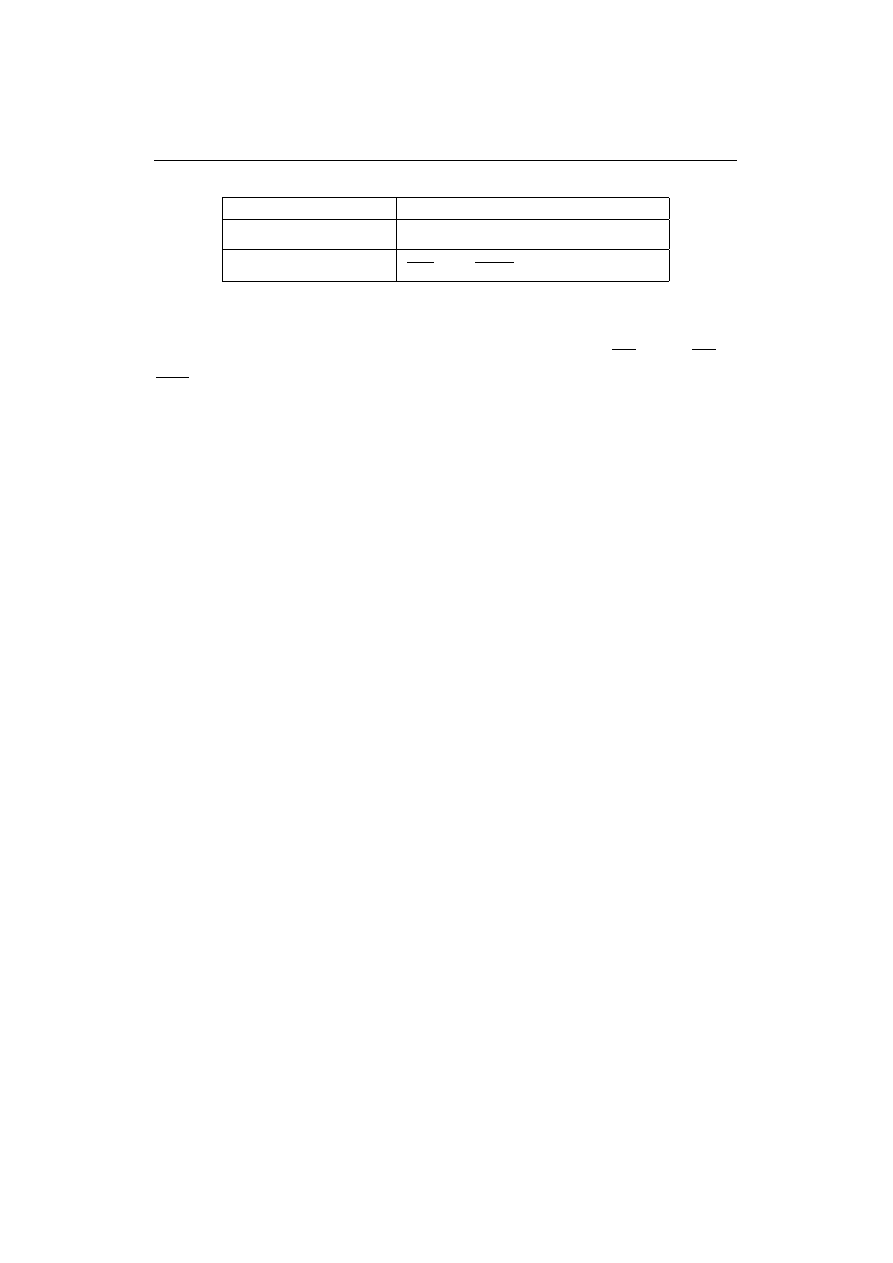
10

Rozdział 5. Punkty osobliwe i residua

Rodzaj punktu z

0

Sposób obliczania

biegun jednokrotny

lim

z→z

0

(z − z

0

)f (z)

biegun m-krotny

1

m−1

lim

z→z

0

∂

m−1

∂

m−1

z

[(z − z

0

)

m

f (z)]

Je´sli funkcje f i g s ˛

a holomorficzne w otoczeniu z

0

oraz z

0

jest zerem k-krotnym f

i zerem n-krotnym g, to z

0

jest biegunem (n-k)-krotym funkcji

f (z)

g(z)

i res

z

0

f (z)

g(z)

=

f (z

0

)

g

0

(z

0

)

Niech D b˛edzie obszarem, którego brzeg jest sko ´nczon ˛

a ilo´sci ˛

a krzywych regu-

larnych zamkni˛etych, zorientowanych dodatnio wzgl˛edem D.

Twierdzenie 5.1. O residuach
Je´sli f jest holomorficzna w C i na jego brzegu poza sko ´nczkon ˛

a ilo´scia punktów

z

1

, ... , z

p

le˙z ˛

acych wewn ˛

atrz D, w których f ma odpowiednio residua A

1

, ... , A

p

,

to

R

C

f (z)dz = 2πi(A

1

+ ... + A

p

)

.

10