
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
S
ZEREG GEOMETRYCZNY
Agitacja
Korzystaj ˛
ac ze wzoru na sum˛e pocz ˛
atkowych wyrazów
łatwo wy-
prowadzi´c wzór
1
2
+
1
4
+
1
8
+
1
16
+ · · · +
1
2
n
=
1
−
1
2
n
.
Oczywi´scie liczba
1
2
n
dla du ˙zych n jest mikroskopijnie mała, wi˛ec mo ˙zna powiedzie´c, ˙ze po-
wy ˙zsza suma „zbli ˙za” si˛e do 1 dowolnie blisko. Mówi ˛
ac dokładniej, je ˙zeli b˛edziemy zwi˛ek-
sza´c n to suma b˛edzie coraz mniej ró ˙zni´c si˛e od 1. Zupełnie formalnie takie rzeczy zapisuje
si˛e za pomoc ˛
a granic, ale na u ˙zytek szkolny u ˙zywa si˛e zapisu
1
2
+
1
4
+
1
8
+
1
16
+ · · · =
1.
Celowo z lewej strony nie napisali´smy ostatniego składnika sumy, bo zapis ten ma sugero-
wa´c, ˙ze dodajemy do siebie wszystkie wyrazy ci ˛
agu (a wi˛ec dodajemy do siebie niesko ´n-
czenie wiele liczb). Sens tego dodawania, jak i wyniku z prawej strony wyja´snili´smy wy ˙zej:
dodaj ˛
ac do siebie liczby z lewej strony zbli ˙zamy si˛e do 1, im wi˛ecej liczb do siebie dodamy,
tym bli ˙zej znajdziemy si˛e 1.
Od razu zauwa ˙zmy, ˙ze dodawanie do siebie niesko ´nczenie wielu liczb nie zawsze ma
sens.
Suma
1
+
1
+
1
+
1
+ · · ·
nie d ˛
a ˙zy do ˙zadnej liczby – dodaj ˛
ac jedynki z lewej strony mo ˙zemy otrzyma´c do-
wolnie du ˙z ˛
a liczb˛e. Symbolicznie zapisujemy to wzorem
1
+
1
+
1
+
1
+ · · · = +
∞.
Jeszcze gorzej jest z sum ˛
a
1
−
1
+
1
−
1
+
1
−
1
+ · · ·
.
Dodaj ˛
ac po kolei składniki z lewej strony na przemian mamy 1 i 0. Trudno w takiej
sytuacji sensownie zdefiniowa´c wynik takiego dodawania.
Definicje
Opisan ˛
a wy ˙zej operacj˛e dodawania do siebie niesko ´nczenie wielu liczb nazywa si˛e w mate-
matyce szeregiem liczbowym. Je ˙zeli dodatkowo liczby, które do siebie dodajemy s ˛
a kolej-
nymi wyrazami ci ˛
agu geometrycznego, to mówimy o szeregu geometrycznym.
Materiał pobrany z serwisu
1

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Ze wzoru na n-ty wyraz ci ˛
agu geometrycznego wiemy, ˙ze ka ˙zdy szereg geome-
tryczny ma posta´c
a
+
aq
+
aq
2
+
aq
3
+ · · · +
aq
n
+ · · ·
Mówimy, ˙ze szereg jest zbie˙zny je ˙zeli jego suma jest liczb ˛
a (w takim samym sensie jak w
pierwszym przykładzie tego poradnika). Je ˙zeli szereg nie jest zbie ˙zny to mówimy, ˙ze jest on
rozbie˙zny
.
Szereg geometryczny
1
2
+
1
4
+
1
8
+
1
16
+ · · ·
jest zbie ˙zny do liczby 1.
Szeregi geometryczne
1
+
1
+
1
+
1
+ · · ·
1
−
1
+
1
−
1
+
1
−
1
+ · · ·
s ˛
a rozbie ˙zne.
Wzór
Widzieli´smy wy ˙zej, ˙ze niektóre szeregi geometryczne s ˛
a zbie ˙zne (czyli ich suma ma sens), a
inne nie. Okazuje si˛e, ˙ze jest bardzo prosta charakteryzacja, kiedy szereg geometryczny jest
zbie ˙zny.
Niezerowy szereg geometryczny
a
1
+
a
1
q
+
a
1
q
2
+
a
1
q
3
+ · · ·
jest zbie ˙zny wtedy i tylko wtedy, gdy
|
q
| <
1.
Co wi˛ecej, mamy bardzo prosty wzór na sum˛e szeregu
S
=
a
1
1
−
q
.
Na mocy powy ˙zszego wzoru mamy
4
3
+
4
9
+
4
27
+ · · · =
4
3
1
−
1
3
=
4
3
2
3
=
2.
Szereg geometryczny
1
−
4
3
+
16
9
−
64
27
+
256
81
+ · · ·
jest rozbie ˙zny, bo
|
q
| =
−
4
3
=
4
3
>
1.
Materiał pobrany z serwisu
2
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
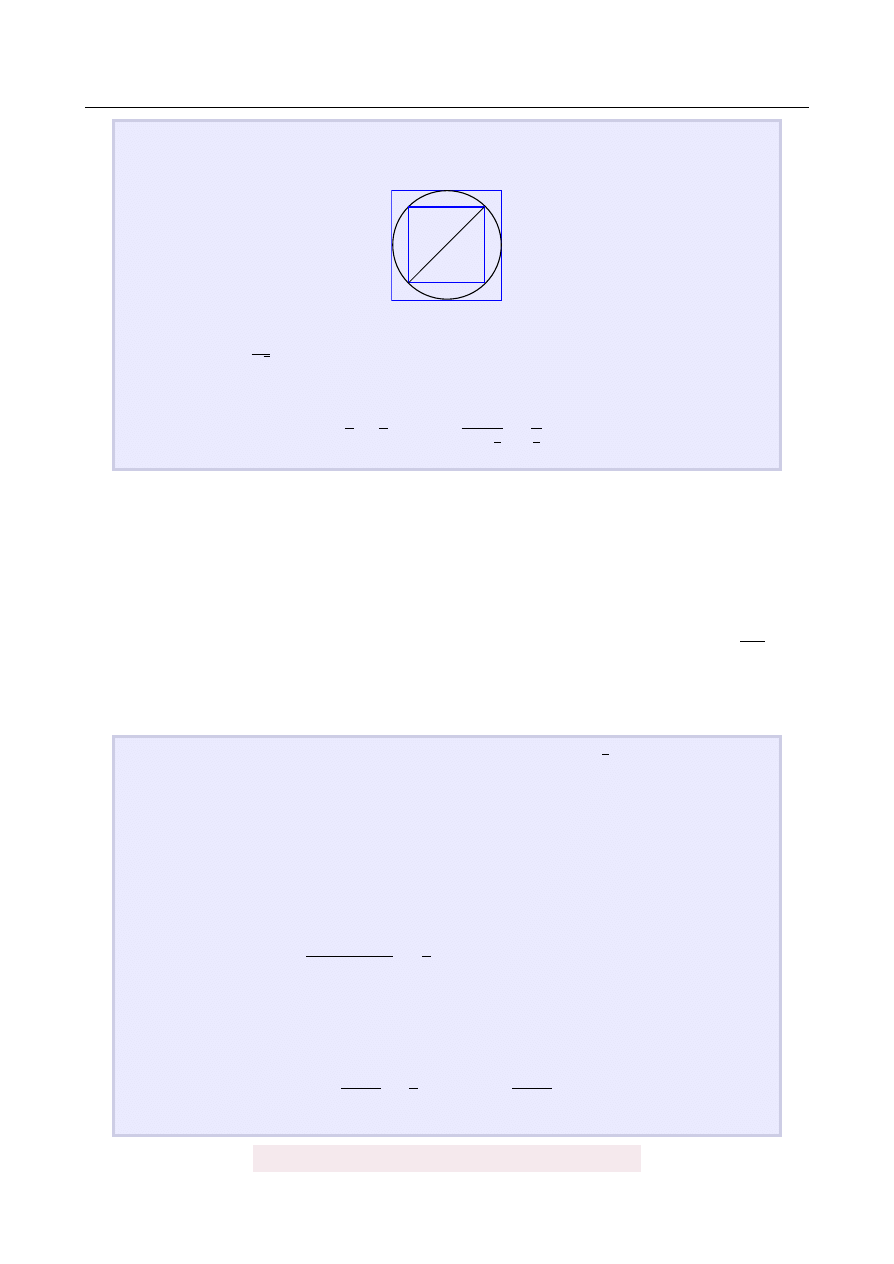
W kwadrat o boku 1 wpisujemy okr ˛
ag. W ten okr ˛
ag wpisujemy kwadrat, w który
wpisujemy okr ˛
ag itd. W ten sposób powstanie niesko ´nczony ci ˛
ag kwadratów. Ob-
liczmy sum˛e pól wszystkich tych kwadratów.
Je ˙zeli oznaczmy bok jednego z kwadratów przez x, to okr ˛
ag wpisany w ten kwa-
drat ma ´srednic˛e x. Jednocze´snie jest to przek ˛
atna kolejnego kwadratu, czyli jego
bok ma długo´s´c
x
√
2
. Zatem pole kolejnego kwadratu jest dwa razy mniejsze od po-
la poprzedniego kwadratu. Pierwszy kwadrat ma pole 1, wi˛ec szukana suma jest
równa
1
+
1
2
+
1
4
+ · · · =
1
1
−
1
2
=
1
1
2
=
2.
Równania i nierówno´sci
Popularny motyw zada ´n szkolnych to równania i nierówno´sci, w których jedna ze stron jest
sum ˛
a szeregu geometrycznego. W tego typu zadaniach mamy do wykonania trzy czynno´sci.
a) Po pierwsze wyznaczamy dziedzin˛e danego równania/nierówno´sci. Oprócz standar-
dowych mianowników, pierwiastków, logarytmów etc., sprawdzamy kiedy dany sze-
reg geometryczny jest zbie ˙zny – sprowadza si˛e to do rozwi ˛
azania nierówno´sci
|
q
| <
1.
b) Zast˛epujemy dany szereg geometryczny jego sum ˛
a, zgodnie ze wzorem S
=
a
1
1
−
q
.
c) Rozwi ˛
azujemy otrzymane równanie/nierówno´s´c (w którym nie ma ju ˙z ˙zadnych kro-
pek) i odrzucamy rozwi ˛
azania, które nie s ˛
a zawarte w wyznaczonej wcze´sniej dziedzi-
nie.
Rozwi ˛
a ˙zmy równanie:
(
1
−
x
) + (
1
−
x
)
2
+ (
1
−
x
)
3
+ · · · =
3
2
−
x.
Z lewej strony równania mamy szereg geometryczny o ilorazie q
=
1
−
x, sprawd´z-
my kiedy jest on zbie ˙zny
|
1
−
x
| <
1
−
1
<
1
−
x
<
1
/
−
1
−
2
< −
x
<
0
/
· (−
1
)
2
>
x
>
0.
Teraz rozwi ˛
azujemy równanie
1
−
x
1
− (
1
−
x
)
=
3
2
−
x
/
·
2x
2
−
2x
=
3x
−
2x
2
2x
2
−
5x
+
2
=
0
∆
=
25
−
16
=
9
x
=
5
−
3
4
=
1
2
∨
x
=
5
+
3
4
=
2.
Drugie rozwi ˛
azanie odrzucamy, bo nie nale ˙zy do dziedziny równania.
Materiał pobrany z serwisu
3
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Zadania
.info
Podoba Ci się ten poradnik?
Pokaż go koleżankom i kolegom ze szkoły!
T
IPS
& T
RICKS
1
Licz ˛
ac sum˛e szeregu geometrycznego warto wył ˛
aczy´c tyle, ile si˛e da przed nawias. Dzi˛eki
temu unikniemy wielokrotnego przepisywania takich samych wyra ˙ze ´n.
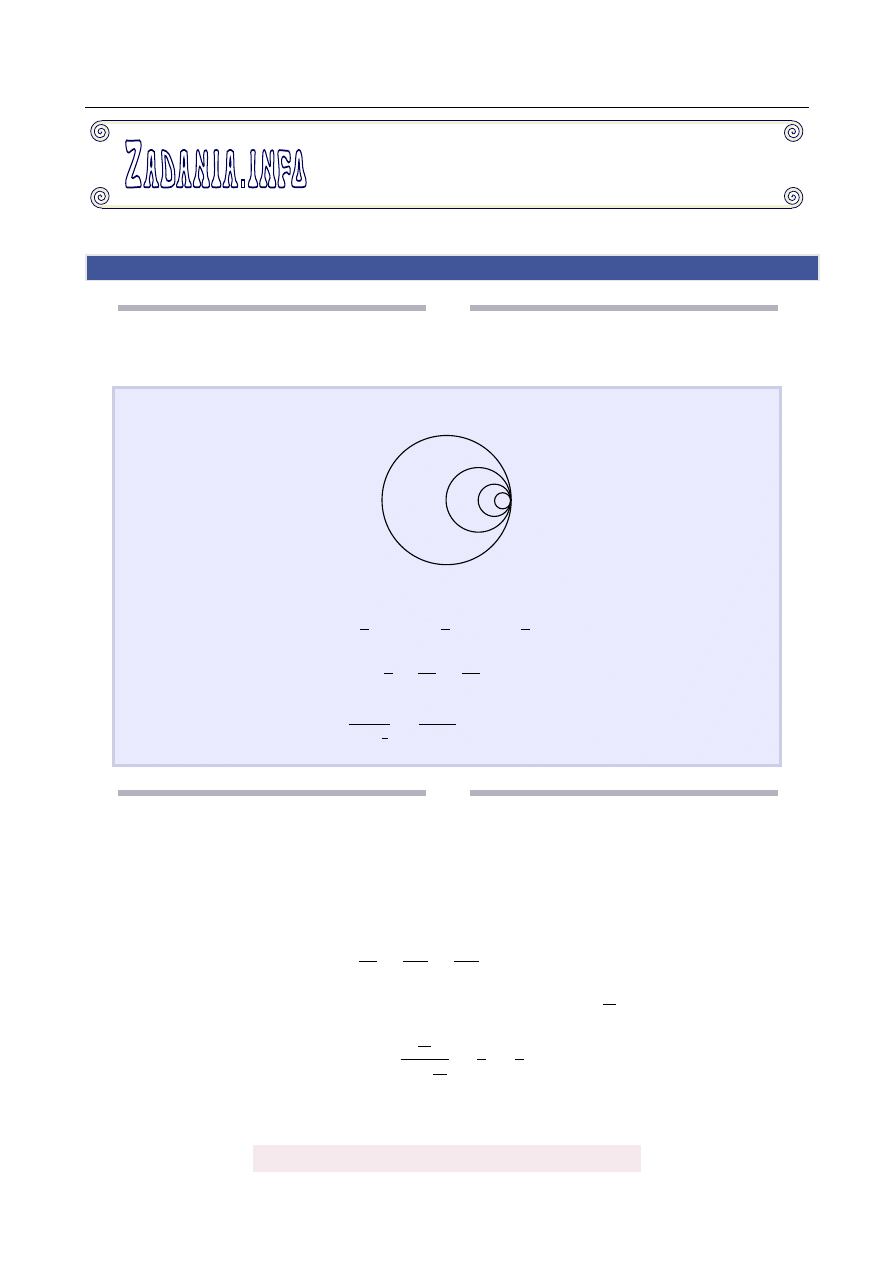
W okr˛egu o promieniu r rysujemy okr ˛
ag o ´srednicy r, nast˛epnie robimy to samo w
nowo narysowanym okr˛egu itd.
Obliczmy sum˛e pól wszystkich narysowanych w ten sposób okr˛egów.
Liczymy
πr
2
+
π
r
2
2
+
π
r
4
2
+
π
r
8
2
+ · · · =
=
πr
2
1
+
1
4
+
1
16
+
1
64
+ · · ·
=
=
πr
2
·
1
1
−
1
4
=
4πr
2
3
.
2
Nie wiem czy si˛e kiedy´s nad tym zastanawiali´scie, ale spróbujmy ustali´c co oznacza zapis
niesko ´nczonego rozwini˛ecia dziesi˛etnego liczby np.
x
=
0, 33333 . . .?
Jest to dokładnie zapis sumy niesko ´nczonego szeregu postaci
3
10
+
3
10
2
+
3
10
3
+ · · ·
.
Akurat w tym przykładzie jest to szereg geometryczny (o ilorazie
1
10
) i umiemy policzy´c jego
sum˛e
x
=
3
10
1
−
1
10
=
3
9
=
1
3
.
Dokładnie tak samo jest z ka ˙zd ˛
a inn ˛
a liczb ˛
a, przy czym na ogół nie mamy do czynienia z
szeregiem geometrycznym i dlatego nie mo ˙zemy skorzysta´c ze wzoru na jego sum˛e.
Materiał pobrany z serwisu
4

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Mamy
π
=
3, 14159 . . .
=
3
+
1
10
+
4
10
2
+
1
10
3
+
5
10
4
+
9
10
5
+ · · ·
Ze wzoru na sum˛e szeregu geometrycznego mamy
0, 99999 . . .
=
9
10
+
9
10
2
+
9
10
3
+ · · · =
9
10
1
−
1
10
=
1.
W pierwszej chwili ta równo´s´c powinna by´c do´s´c zaskakuj ˛
aca, bo przecie ˙z lewa
strona jest mniejsza od 1.
Naprawd˛e jest mniejsza? A o ile? Jak si˛e chwil˛e zastanowicie, to powinno by´c jasne,
˙ze nie uda wam si˛e wcisn ˛
a´c ˙zadnej liczby pomi˛edzy te dwie liczby i wła´snie w tym
sensie s ˛
a one równe.
Je ˙zeli si˛e komu´s wydaje, ˙ze poprzedni przykład jest bardzo osobliwy, to mo ˙ze war-
to podkre´sli´c, ˙ze takich przykładów jest mnóstwo.
Je ˙zeli wystartujemy od jakiejkolwiek liczby ze sko ´nczonym rozwini˛eciem dziesi˛et-
nym, np. od 0,12345, to mo ˙zemy zamieni´c ostatni ˛
a niezerow ˛
a cyfr˛e na cyfr˛e o 1
mniejsz ˛
a i nast˛epnie niesko ´nczenie wiele 9- ˛
atek:
0, 12345
=
0, 1234499999 . . . .
Nie ma na to ˙zadnej rady: po prostu rozwini˛ecia dziesi˛etne nie s ˛
a jednoznaczne (ta
sama liczba mo ˙ze mie´c ró ˙zne rozwini˛ecia dziesi˛etne).
3
Osoby, które pami˛etaj ˛
a jak zamienia si˛e okresowe ułamki dziesi˛etne na zwykłe, mog ˛
a zasto-
sowa´c t˛e sam ˛
a do wyprowadzenia wzoru na sum˛e szeregu geometrycznego. Je ˙zeli oznaczy-
my
x
=
a
+
aq
+
aq
2
+
aq
3
+
aq
4
+ · · ·
to mno ˙z ˛
ac t˛e równo´s´c stronami przez q mamy
xq
=
aq
+
aq
2
+
aq
3
+
aq
4
+ · · · =
x
−
a
a
=
x
−
xq
=
x
(
1
−
q
)
⇒
x
=
a
1
−
q
.
Oczywi´scie powy ˙zszy rachunek nie daje odpowiedzi na pytanie, kiedy szereg geometrycz-
ny jest zbie ˙zny. Jest to tylko sposób na wyprowadzenie wzoru na jego sum˛e.
4
Pami˛etajmy, ˙ze nie ka ˙zde równanie/nierówno´s´c z kropkami musi by´c zadaniem na szereg
geometryczny.
Materiał pobrany z serwisu
5

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Rozwi ˛
a ˙zmy równanie 1
+
4
+
7
+ · · · +
x
=
117.
Lewa strona tego równania jest (sko ´nczon ˛
a!) sum ˛
a pocz ˛
atkowych wyrazów ci ˛
agu
o pierwszym wyrazie a
1
=
1 i ró ˙znicy 3, zatem
2a
1
+
3
(
n
−
1
)
2
·
n
=
177
(−
1
+
3n
)
n
=
234
3n
2
−
n
−
234
=
0
∆
=
2809
=
53
2
⇒
n
=
9.
Zatem x
=
a
9
=
a
1
+
8r
=
25.
5
Jest jeszcze jeden detal, o którym do tej pory nie wspominali´smy, mianowicie szereg geome-
tryczny, którego wszystkie wyrazy s ˛
a zerami. Oczywi´scie jest to szereg zbie ˙zny i jego suma
jest równa 0. Problem polega jednak na tym, ˙ze ten ci ˛
ag nie ma jednoznacznie zdefiniowa-
nego ilorazu i trudno ustali´c, czy spełnia on warunek
|
q
| <
1, czy te ˙z nie. Z tego powodu
zawsze bezpieczniej jest rozwa ˙zy´c ten przypadek osobno.
Rozwi ˛
a ˙zmy nierówno´s´c x
+
x
(
1
−
x
) +
x
(
1
−
x
)
2
+ · · · > −
1.
Lewa strona jest zbie ˙znym szeregiem geometrycznym je ˙zeli
|
1
−
x
| <
1
−
1
<
1
−
x
<
1
/
−
1
−
2
< −
x
<
0
/
· (−
1
)
2
>
x
>
0.
Przy tym zało ˙zeniu mamy
−
1
<
x
1
− (
1
−
x
)
=
x
x
=
1,
czyli nierówno´s´c jest spełniona.
Jest jednak małe „ale”, bo zgubili´smy prawidłowe rozwi ˛
azanie x
=
0 – tak jak
pisali´smy wcze´sniej, przypadek ci ˛
agu zerowego nale ˙zy rozpatrzy´c osobno.
6
Równo´s´c
1
2
+
1
4
+
1
8
+
1
16
+ · · · =
1
ma bardzo prost ˛
a interpretacj˛e geometryczn ˛
a: dzielimy odcinek długo´sci 1 na dwie równe
cz˛e´sci, potem praw ˛
a połow˛e dzielimy ponownie na dwie równe cz˛e´sci itd.
1/2
1/4
1/8
1/16
1/32
Materiał pobrany z serwisu
6

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Je ˙zeli b˛edziemy kontynuowa´c t˛e procedur˛e w niesko ´nczono´s´c, to otrzymamy przedsta-
wienie odcinka długo´sci 1 jako sumy odcinków o długo´sciach kolejno
1
2
,
1
4
,
1
8
,
1
16
, . . ..
7
Niezwykle ciekawe i trudne jest pytanie, czy opisane powy ˙zej dzielenie odcinka na niesko ´n-
czenie wiele cz˛e´sci ma jakikolwiek sens fizyczny. Powiedzmy, ˙ze zaczynamy dzieli´c kawałek
drutu na cz˛e´sci. Dzielimy, dzielimy, po niezbyt długiej chwili dochodzimy do poziomu ato-
mów, dzielimy dalej, mamy kwarki. I co dalej, czy mo ˙zna tak dzieli´c w niesko ´nczono´s´c? Co
ciekawe, współczesne teorie fizyczne skłaniaj ˛
a si˛e ku negatywnej odpowiedzi na to pytanie.
8
Zahaczyli´smy ju ˙z wy ˙zej o fizyk˛e, wi˛ec zahaczmy te ˙z o filozofi˛e. Przypomnijmy klasyczny
paradoks Achillesa i ˙zółwia (jeden z tzw. paradoksów Zenona z Elei).
Achilles i ˙zółw startuj ˛
a w wy´scigu, przy czym ˙zółw zaczyna wy´scig w połowie
trasy wy´scigu, a Achilles biegnie z pr˛edko´sci ˛
a dwa wi˛eksz ˛
a od ˙zółwia.
W momencie gdy Achilles przebiegnie połow˛e dystansu (a wi˛ec znajdzie si˛e w
miejscu, z którego wystartował ˙zółw), ˙zółw przebiegnie
3
4
całej trasy. W momen-
cie, gdy Achilles dobiegnie do tego miejsca ˙zółw ponownie si˛e oddali i przeb˛e-
dzie
7
8
całego dystansu, itd. Za ka ˙zdym razem, gdy Achilles dobiegnie do miejsca,
w którym jeszcze przed chwil ˛
a był ˙zółw, ˙zółw b˛edzie ju ˙z odrobin˛e dalej. W takim
razie Achilles nigdy nie dogoni ˙zółwia.
Sens powy ˙zszego paradoksu oparty jest na naszym intuicyjnym przekonaniu, ˙ze nie da si˛e
w sko ´nczonym czasie wykona´c niesko ´nczenie wielu czynno´sci. Tymczasem wzór
1
2
+
1
4
+
1
8
+
1
16
+ · · · =
1
dowodzi czego´s wr˛ecz przeciwnego: je ˙zeli czynno´sci, które wykonujemy trwaj ˛
a wystarcza-
j ˛
aco krótko, to mog ˛
a zosta´c wykonane w sko ´nczonym czasie. Wracaj ˛
ac do paradoksu Achil-
lesa i ˙zółwia, powy ˙zszy wzór oznacza, ˙ze Achilles i ˙zółw spotkaj ˛
a si˛e dokładnie na mecie
wy´scigu.
9
Wzór na sum˛e szeregu geometrycznego jest prostym wnioskiem ze wzoru na sum˛e pocz ˛
at-
kowych wyrazów
S
n
=
a
1
·
1
−
q
n
1
−
q
.
Je ˙zeli
|
q
| <
1 to q
n
→
0, czyli S
n
→
a
1
1
−
q
(przy n
→ +
∞).
Materiał pobrany z serwisu
7

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
10
Uwa ˙zny czytelnik powinien zauwa ˙zy´c, ˙ze nasza definicja poj˛ecia szeregu jest delikatnie
mówi ˛
ac niejasna. Napisali´smy, ˙ze jest to operacja dodawania do siebie niesko ´nczenie wielu
liczb, ale jest to bardziej filozofia ni ˙z matematyka. Zrobili´smy to celowo, ˙zeby niepotrzebnie
nie komplikowa´c poradnika, ale teraz powiemy krótko jak takie rzeczy zrobi´c porz ˛
adnie.
Zaczynamy od ci ˛
agu liczbowego
(
a
n
)
(w przypadku szeregu geometrycznego zaczyna-
my od ci ˛
agu geometrycznego). Nast˛epnie tworzymy nowy ci ˛
ag, tzw. ci ˛
ag sum cz˛e´sciowych
(
S
n
)
okre´slony (zgodnie z nazw ˛
a) wzorem
S
n
=
a
1
+
a
2
+ · · · +
a
n
.
Przy takich oznaczeniach, przez szereg (odpowiadaj ˛
acy ci ˛
agowi
(
a
n
)
) rozumiemy po prostu
ci ˛
ag sum cz˛e´sciowych
(
S
n
)
. Zauwa ˙zmy, ˙ze na razie nie ma mowy o ˙zadnym dodawaniu
niesko ´nczenie wielu składników, po prostu z jednego ci ˛
agu zrobili´smy drugi ci ˛
ag.
Mówimy, ˙ze szereg
(
S
n
)
jest zbie˙zny je ˙zeli istnieje granica S
=
lim
n
→+
∞
S
n
. W takiej sytuacji
liczb˛e S nazywamy sum ˛
a szeregu S
n
. Zauwa ˙zmy, ˙ze dokładnie teraz pojawiło nam si˛e do-
dawanie niesko ´nczenie wielu składników: przej´scie do granicy w wyra ˙zeniu S
n
odpowiada
dodaniu do siebie wszystkich wyrazów ci ˛
agu
(
a
n
)
.
Prze´sled´zmy powy ˙zsze definicje na przykładzie ci ˛
agu geometrycznego a
n
=
1
2
n
.
Ze wzoru na sum˛e pocz ˛
atkowych wyrazów ci ˛
agu geometrycznego mamy
S
n
=
a
1
+
a
2
+ · · · +
a
n
=
1
2
·
1
−
1
2
n
1
−
1
2
=
1
2
·
2
n
−
1
2
n
−
1
=
1
−
1
2
n
.
W takim razie
lim
n
→+
∞
S
n
=
lim
n
→+
∞
1
−
1
2
n
=
1,
co prowadzi do dobrze ju ˙z nam znanego wzoru
1
2
+
1
4
+
1
8
+
1
16
+ · · · =
1.
11
Skoro ju ˙z zdobyli´smy si˛e na wysiłek porz ˛
adnego zdefiniowania poj˛ecia szeregu, to po-
wiedzmy kilka słów o szeregach, które nie s ˛
a geometryczne. Okazuje si˛e, ˙ze sytuacja bywa
zaskakuj ˛
aca.
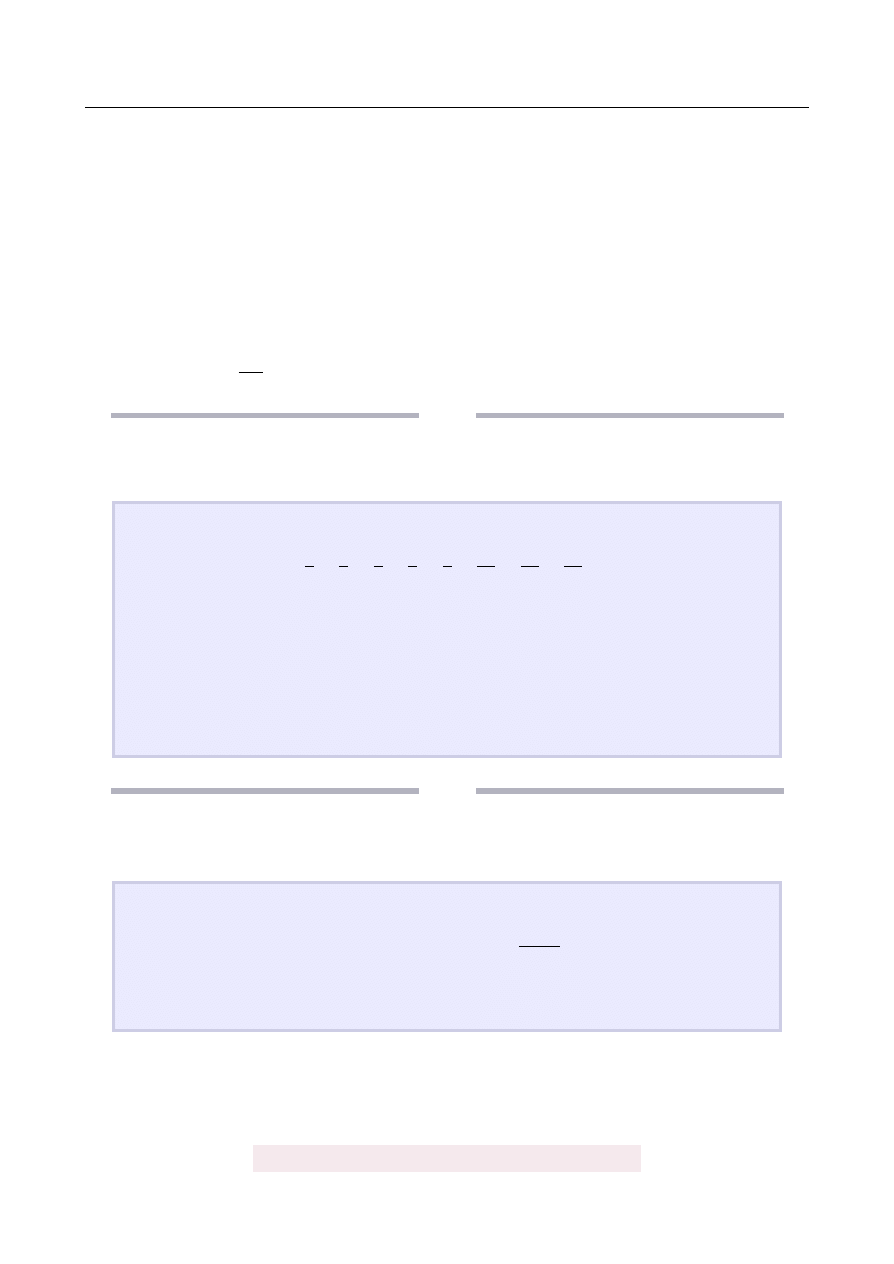
Pierwszy z szeregów
1
+
1
2
+
1
3
+
1
4
+ · · ·
1
+
1
2
2
+
1
3
2
+
1
4
2
+ · · ·
jest rozbie ˙zny (suma ta jest równa
+
∞), a drugi z nich jest zbie˙zny do liczby
π
2
6
!
Materiał pobrany z serwisu
8
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Badanie szeregów zwi ˛
azane jest z dwoma problemami.
a) Po pierwsze, chcemy umie´c sprawdza´c, czy dany szereg jest zbie ˙zny. Jest wiele ro ˙z-
nych kryteriów pozwalaj ˛
acych odpowiada´c na to pytanie i zwykle jest to jeden z te-
matów wykładu z matematyki dla studentów I roku.
b) Je ˙zeli ju ˙z wiemy, ˙ze szereg jest zbie ˙zny, to chcieliby´smy umie´c policzy´c jego sum˛e.
Okazuje si˛e, ˙ze zadanie to jest niezwykle trudne, i nawet w niektórych bardzo prostych
przypadkach nie umiemy tego zrobi´c.
Z punktu widzenia dwóch powy ˙zszych punktów, przypadek szeregu geometrycznego jest
niezwykle elegancki: mamy prosty warunek zbie ˙zno´sci szeregu:
|
q
| <
1, oraz wiemy ile
wynosi jego suma:
a
1
1
−
q
.
12
Mówili´smy o tym jak liczy´c niesko ´nczone sumy, ale okazuje si˛e, ˙ze czasem warto jest umie´c
wykona´c operacj˛e odwrotn ˛
a, tzn. dan ˛
a liczb˛e rozpisa´c jako pewien szereg.
Okazuje si˛e, ˙ze
π
=
4
1
−
4
3
+
4
5
−
4
7
+
4
9
−
4
11
+
4
13
−
4
15
+ · · ·
Fajnie, i co tego? Ano to, ˙ze wyra ˙zenie z prawej strony jest bardzo proste do licze-
nia: mamy tam tylko dodawanie i odejmowanie do´s´c prostych ułamków. Im wi˛ecej
ich we´zmiemy, tym otrzymamy dokładniejsze przybli ˙zenie π.
Nie robi to na was wra ˙zenia? - to spróbujcie wymy´sli´c jakikolwiek sposób na wyli-
czenie π z dokładno´sci ˛
a do pierwszego miejsca po przecinku (czyli 3, 1)? A nawet
jeszcze pro´sciej, spróbujcie uzasadni´c, ˙ze 2
<
π
<
4. Je ˙zeli spróbujecie to zrobi´c, to
powinni´scie doceni´c jak niezwykle wygodny jest powy ˙zszy wzór.
13
Do tej pory mówili´smy tylko o dodawaniu do siebie niesko ´nczenie wielu liczb, ale nie ma
przeszkód, ˙zeby nie post˛epowa´c analogicznie np. w przypadku funkcji.
Ze wzoru na sum˛e szeregu geometrycznego mamy
1
+
x
+
x
2
+
x
3
+ · · · =
1
1
−
x
,
o ile tylko
|
x
| <
1. Lew ˛
a stron˛e powy ˙zszej równo´sci nazywa si˛e szeregiem funk-
cyjnym
i jest to do´s´c naturalne uogólnienie szeregów liczbowych.
Materiał pobrany z serwisu
9
Wyszukiwarka
Podobne podstrony:
Szereg geometryczny
2010 11 05(2),19,26 szeregi, geometria analityczna
ciagi i szeregi, geometryczne, algebraiczne, inne
2010 11 05(2),19,26 szeregi, geometria analityczna
Szeregi Fouriera
WYKŁAD 7 Szeregowy regulacja hamowanie
geometria w płaszczyźnie
GEOMETRIA
GEOMETRIA OBLICZENIOWA I
lec6a Geometric and Brightness Image Interpolation 17
Geometria wykreślna Ćwiczenie 8
Algebra liniowa i geometria kolokwia AGH 2012 13
Analiza matematyczna, lista analiza 2008 6 szeregi
Geometria wykreślna przenikanie brył2
więcej podobnych podstron