
1. WIADOMO´
SCI WSTE,PNE.
1.1. Rachunek zda´
n.
W mowie potocznej formuÃlujemy takie zdania, o kt´orych mo˙zemy powiedzie´c, ˙ze
sa, prawdziwe ba,d´z faÃlszywe bez wzgle,du na to, jaka jest aktualna sytuacja w
otaczaja,cym nas ´swiecie. Na przykÃlad zdanie: ”Je´sli dzi´s jest ´sroda, to jutro
be,dzie czwartek” jest prawdziwe, a zdanie: ”3 jest liczba, parzysta,” jest faÃlszywe.
Natomiast ocena prawdziwo´sci zdania: ”Matematyka jest Ãlatwa” zale˙zy ju˙z od
subiektywnego odczucia osoby je wypowiadaja,cej. W dalszym cia,gu be,da, nas
interesowaÃly zdania pierwszego rodzaju. Przyjmiemy naste,puja,ce oznaczenia i
definicje.
Definicja 1.1.1.
Zdaniem nazywamy w logice wypowied´z orzekaja,ca,, kt´orej
mo˙zna przypisa´c jedna, z dw´och ocen: prawde, lub faÃlsz.
Prawdziwo´s´c i faÃlszywo´s´c nazywamy warto´sciami logicznymi zdania.
Prawde, oznaczamy cyfra, 1, a faÃlsz cyfra, 0.
Zdania be,dziemy oznacza´c symbolami p, q, r, s, a warto´s´c logiczna, zdania w(p).
W´owczas w(p) = 0 oznacza, ˙ze zdanie p jest faÃlszywe, a w(q) = 1 oznacza, ˙ze
zdanie q jest prawdziwe.
Z danych zda´
n mo˙zemy przy pomocy sp´ojnik´ow ”i”, ”lub”, ”je´sli ..., to ...”,
”wtedy i tylko wtedy, gdy ...”, ”nie” tworzy´c nowe zdania. Sp´ojniki te nazywamy
funktorami zdaniotw´orczymi.
Funktory zdaniotw´orcze oznaczamy naste,puja,cymi symbolami i nadajemy im
odpowiednio nazwy
”nie”
∼
negacja
”lub”
∨
alternatywa
”i”
∧
koniunkcja
”je´sli ..., to ...”
⇒
implikacja
”wtedy i tylko wtedy, gdy ...”
⇔
r´ownowa˙zno´s´c
Ze sp´ojnik´ow i zda´
n prostych mo˙zemy tworzy´c zdania zÃlo˙zone. Na mocy
przyje,tych poprzednio oznacze´n definicje, sp´ojnik´ow mo˙zemy zapisa´c przy u˙zyciu
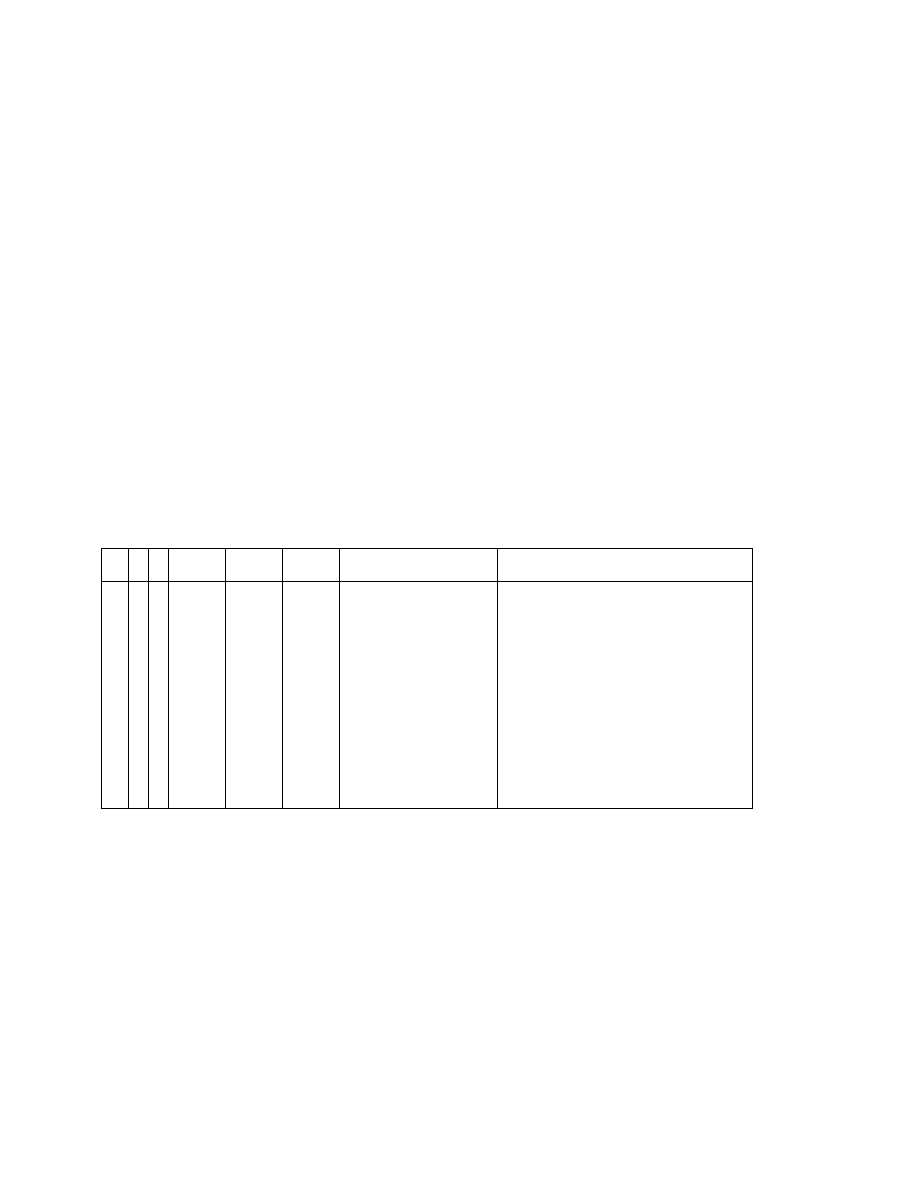
naste,puja,cej tabelki
p
q
∼ p p ∧ q
p ∨ q
p ⇒ q
p ⇔ q
1
1
0
1
1
1
1
0
1
1
0
1
1
0
1
0
0
0
1
0
0
0
0
1
0
0
1
1
1
Zbudowane przy u˙zyciu zmiennych zdaniowych, funktor´ow zdaniotw´orczych
oraz nawias´ow wyra˙zenia rachunku zda´
n nazywamy tak˙ze formuÃlami rachunku
zda´
n albo schematami rachunku zda´
n. Ka˙zda formuÃla staje sie, zdaniem, gdy w
miejsce wyste,puja,cych w niej liter podstawiamy zdania. W´sr´od wszystkich formuÃl
rachunku zda´
n szczeg´olnie wa˙zna, role, peÃlnia, tautologie.
Definicja 1.1.2. Zdanie prawdziwe bez wzgÃledu na warto´sci logiczne zda´
n skÃla-
dowych nazywamy tautologia,.
Wa˙znym zagadnieniem rachunku zda´
n jest sprawdzenie, czy dana formuÃla jest
tautologia,. Najcze,´sciej stosowana, metoda, badania warto´sci logicznej wyra˙ze´n
rachunku zda´
n jest metoda zero-jedynkowa. Polega ona na rozpatrzeniu wszyst-
kich ukÃlad´ow warto´sci logicznych zmiennych zdaniowych wyste,puja,cych w danym
wyra˙zeniu. Metode, ta, zilustrujemy naste,puja,cym przykÃladem.
PrzykÃlad 1.1.1. Sprawdzi´c czy wyra˙zenie
¡
p ⇒ q
¢
⇒
h¡
q ⇒ r
¢
⇒
¡
p ⇒ r
¢i
jest tautologia,.
p q r p ⇒ q q ⇒ r p ⇒ r (q ⇒ r) ⇒ (p ⇒ r) (p ⇒ q) ⇒ [(q ⇒ r) ⇒ (p ⇒ r)]
1 1 1
1
1
1
1
1
1 1 0
1
0
0
1
1
1 0 1
0
1
1
1
1
0 1 1
1
1
1
1
1
1 0 0
0
1
0
0
1
0 1 0
1
0
1
1
1
0 0 1
1
1
1
1
1
0 0 0
1
1
1
1
1
Zadanie 1.1.1. Sprawdzi´c czy podane zdania sa, tautologiami
a) p ⇒
¡
q ⇒ p
¢
,
b)
h
p ⇒
¡
q ⇒ r
¢i
⇒
h¡
p ⇒ q
¢
⇒
¡
p ⇒ r
¢i
,
c) p ⇒
¡
∼ p ⇒ q
¢
,
d)
¡
∼ p ⇒ q
¢
⇒ p,
e)
¡
p ∨ q
¢
⇔
¡
∼ p ⇒ q
¢
,
f )
¡
p ∧ q
¢
⇔
¡
p ⇒∼ q
¢
,
g) ∼
¡
p ∧ q
¢
⇔
¡
∼ p∨ ∼ q
¢
- prawo de Morgana,
2

h) ∼
¡
p ∨ q
¢
⇔
¡
∼ p∧ ∼ q
¢
- prawo de Morgana,
i) ∼
¡
p ⇒ q
¢
⇔
¡
p∧ ∼ q
¢
,
j)
h
p ∧
¡
q ∨ r
¢i
⇔
h¡
p ∧ q
¢
∨
¡
p ∧ r
¢i
-prawo rozdzielno´sci koniunkcji wzgle,dem
alternatywy,
k)
h
p ∨
¡
q ∧ r
¢i
⇔
h¡
p ∨ q
¢
∧
¡
p ∨ r
¢i
-prawo rozdzielno´sci alternatywy wzgle,dem
koniunkcji.
Interptretacja fizyczna koniunkcji i alternatywy.
Niech p, q oznaczja, wyÃla,czniki, z kt´orych ka˙zdy mo˙ze by´c wÃla,czony (stan 1) albo
wyÃla,czony (stan 0). W stanie ”1” wyÃla,cznik przewodzi pra,d, natomiast w stanie
”0” wyÃla,cznik nie przewodzi pra,du. Stan ukÃladu utworzonego przez poÃla,czenie
szeregowe wyÃla,cznik´ow p i q zale˙zy od stanu wyÃla,cznika p i od stanu wyÃla,cznika
q tak, jak warto´s´c logiczna koniunkcji p ∧ q zale˙zy od warto´sci logicznych zda´
n p i
q. W zwia,zku z tym mo˙zna powiedzie´c, ˙ze
koniunkcje, realizuje poÃla,czenie szeregowe.
Podobnie stan ukÃladu utworzonego przez poÃla,czenie r´ownolegÃle wyÃla,cznik´ow p i q
zale˙zy od stanu wyÃla,cznika p lub od stanu wyÃla,cznika q tak, jak warto´s´c logiczna
alternatywy p ∨ q zale˙zy od warto´sci logicznych zda´
n p i q. W zwia,zku z tym
mo˙zna powiedzie´c, ˙ze
alternatywe, realizuje poÃla,czenie r´ownolegÃle.
Warunek konieczny i dostateczny.
Je˙zeli ze zdania p wynika zdanie q (p ⇒ q), to m´owimy, ˙ze
p jest warunkiem dostatecznym (wystarczaja,cym) dla q,
natomiast q jest warunkiem koniecznym dla p.
PrzykÃlad 1.1.2.
Podzielno´s´c liczby n przez 4 jest warunkiem dostatecznym
podzielno´sci liczby n przez 2.
4
±
n ⇒ 2
±
n
Podzielno´s´c liczby n przez 4 nie jest warunkiem koniecznym podzielno´sci
liczby n przez 2, o czym ´swiadczy przykÃlad liczby 6, kt´ora jest podzielna przez 2,
ale nie jest podzielna przez 4.
Mo˙ze sie, zda˙zy´c, ˙ze warunek konieczny jest jednocze´snie warunkiem dostatecznym.
M´owimy w´owczas, ˙ze jest to warunek konieczny i dostateczny.
PrzykÃlad 1.1.3. Podzielno´s´c liczby n przez 2 i przez 5 jest warunkiem koniecznym
i dostatecznym podzielno´sci liczby n przez 10.
¡
2
±
n ∧ 5
±
n
¢
⇒ 10
±
n
3

1.2. Rachunek zbior´
ow.
Poje,cie zbioru i nale˙zenia do zbioru przyjmujemy jako pierwotne i nie wyma-
gaja,ce definiowania.
Je˙zeli element a nale˙zy do zbioru A, to piszemy a ∈ A, w przeciwnym przy-
padku, gdy element a nie nale˙zy do zbioru A piszemy a 6∈ A.
Definicja 1.2.1. Zbi´or, kt´orego wszystkimi elementami sa, a
1
, a
2
, . . . , a
n
nazy-
wamy zbiorem sko´
nczonym.
Zbi´or, kt´ory posiada tylko jeden element nazywamy zbiorem jednoelemen-
towym.
Zbi´or, do kt´orego ˙zaden element nie nale˙zy nazywamy zbiorem pustym.
Zbi´or, kt´ory nie jest ani sko´
nczony, ani pusty nazywamy zbiorem niesko´
nczo-
nym.
Niech A i B be,da, dowolnymi zbiorami.
Definicja 1.2.2. M´owimy, ˙ze zbi´or A jest r´owny zbiorowi B, gdy ka˙zdy element
zbioru A jest elementem zbioru B i ka˙zdy element zbioru B jest elementem zbioru
A. Piszemy wtedy A = B.
Okre´slimy teraz dziaÃlania na zbiorach.
Definicja 1.2.3. Suma, zbior´ow A i B nazywamy zbi´or zÃlo˙zony ze wszystkich
element´ow, kt´ore nale˙za, do zbioru A lub do zbioru B.
a ∈
¡
A ∪ B
¢
⇔
h¡
a ∈ A
¢
∨
¡
a ∈ B
¢i
Definicja 1.2.4. Iloczynem zbior´ow A i B nazywamy zbi´or zÃlo˙zony z element´ow,
kt´ore jednocze´snie nale˙za, do zbioru A i do zbioru B.
a ∈
¡
A ∩ B
¢
⇔
h¡
a ∈ A
¢
∧
¡
a ∈ B
¢i
Definicja 1.2.5. R´o˙znica, zbior´ow A i B nazywamy zbi´or zÃlo˙zony z tych ele-
ment´ow, kt´ore nale˙za, do zbioru A i nie nale˙za, do zbioru B.
a ∈
¡
A \ B
¢
⇔
h¡
a ∈ A
¢
∧ ∼
¡
a ∈ B
¢i
Definicja 1.2.6. Je˙zeli ka˙zdy element zbioru A nale˙zy do zbioru B, to m´owimy,
˙ze zbi´or A zawiera sie, w zbiorze B.
a ∈
¡
A ⊂ B
¢
⇔
h¡
a ∈ A
¢
⇒
¡
a ∈ B
¢i
4

Definicja 1.2.7. Zbiory A i B nazywamy rozÃla,cznymi, je˙zeli nie maja, wsp´olnego
elementu, tzn. A ∩ B = ∅.
Przypu´s´cmy teraz, ˙ze wszystkie rozpatrywane przez nas zbiory, w ustalonym
zagadnieniu sa, podzbiorami jednego zbioru, kt´ory oznaczymy przez X. Wtedy
dla ka˙zdego rozpatrywanego zbioru A mamy: A ⊂ X. Zbi´or X nazywa´c be,dziemy
przestrzenia,.
Definicja 1.2.8. DopeÃlnieniem zbioru A (do przestrzeni X) nazywamy zbi´or
A
0
= X \ A.
x ∈ A
0
⇔
h¡
x ∈ X
¢
∧ ∼
¡
x ∈ A
¢i
PrzykÃlad 1.2.1. DopeÃlnieniem zbioru liczb ujemnych (do zbioru liczb rzeczy-
wistych) jest zbi´or liczb nieujemnych.
Ka˙zde dziaÃlanie w rachunku zbior´ow ma sw´oj odpowiednik w rachunku zda´
n
i na odwr´ot. Mo˙zemy to ustali´c por´ownuja,c okre´slenia odpowiednich dziaÃla´n. Na
przykÃlad iloczynowi zbior´ow odpowiada koniunkcja, gdy˙z a ∈ A ∩ B wtedy i tylko
wtedy, gdy a jest elementem zbioru A i (koniunkcja) jest elementem zbioru B.
Fakt ten prowadzi w konsekwencji do wykorzystania praw rachunku zda´
n przy
dowodzeniu praw rachunku zbior´ow.
Niech dane be,da, dwa dowolne i niepuste zbiory A i B oraz niech a ∈ A i b ∈ B.
Uporza,dkowana, pare, element´ow a i b be,dziemy oznaczali (a, b).
Definicja 1.2.8. Iloczynem kartezja´
nskim zbior´ow A i B nazywamy zbi´or upo-
rza,dkowanych par (a, b) takich, ˙ze a ∈ A i b ∈ B.
A × B = {(a, b) : a ∈ A ∩ b ∈ B}.
Zadanie 1.2.1. Udowodni´c podane r´owno´sci
a) (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C),
b) (A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C),
c) (A ∪ B)
0
= A
0
∩ B
0
,
d) (A ∩ B)
0
= A
0
∪ B
0
,
e) (A \ B) ∩ B = ∅,
f ) A \ B = A ∩ B
0
,
g) A \ B = A \ (A ∩ B),
h) (A \ B) ∩ C = (A ∩ C) \ B,
i) (A ∩ B) ∪ (A
0
∩ B) = B.
Zadanie 1.2.2. Podaj interpretacje, geometryczna, na pÃlaszczy´znie OXY naste,-
puja,cych zbior´ow
a) < 2, 3 > × < 1, 5 >,
b) N × {2},
c) R× < 1, ∞ >,
d) R × {π}.
5

1.3. Funkcje zdaniowe. Kwantyfikatory.
Definicja 1.3.1. Funkcja, zdaniowa, z jedna, zmienna,, okre´slona, w dziedzinie D
nazywamy takie wyra˙zenie zawieraja,ce ta, zmienna,, kt´ore staje sie, zdaniem, gdy
na miejsce zmiennej podstawimy dowolny element zbioru D.
PrzykÃlad 1.3.1.
”x jest liczba, pierwsza,”
Powy˙zsza funkcja zdaniowa ze zmienna, x okre´slona na zbiorze liczb rzeczy-
wistych, na przykÃlad dla x = 2 jest zdaniem prawdziwym, a dla x = 100 jest
zdaniem faÃlszywym.
PrzykÃlad 1.3.2. Ka˙zde r´ownanie oraz ka˙zda nier´owno´s´c sa, funkcjami zdaniowy-
mi.
W´sr´od wszystkich element´ow a z dziedziny D funkcji zdaniowej ϕ wyr´o˙zniamy
te, dla kt´orych zdanie ϕ(a) jest prawdziwe. O takich elementach m´owimy, ˙ze
speÃlniaja, funkcja, zdaniowa,.
Definicja 1.3.2. Funkcje, zdaniowa, nazywamy to˙zsamo´sciowa, , je˙zeli speÃlnia ja,
ka˙zdy element z jej dziedziny, natomiast nazywamy ja, sprzeczna,, je˙zeli nie speÃlnia
jej ˙zaden element z dziedziny.
Dwie funkcje zdaniowe nazywamy r´ownowa˙znymi , gdy maja, wsp´olna, dzie-
dzine, i gdy ka˙zdy element, kt´ory speÃlnia jedna, z nich, speÃlnia tak˙ze druga, i na
odwr´ot.
Je˙zeli dla ka˙zdego x ∈ D funkcja zdaniowa ϕ(x) o dziedzinie D jest zdaniem
prawdziwym, to fakt ten zapisujemy w naste,puja,cy spos´ob
^
x∈D
ϕ(x)
i odczytujemy: ”dla ka˙zdego x jest ϕ(x)”.
Je˙zeli w dziedzinie D istnieje co najmniej jeden element x, dla kt´orego funkcja
zdaniowa ϕ(x) jest zdaniem prawdziwym, to piszemy
_
x∈D
ϕ(x)
i odczytujemy: ”istnieje taki x, ˙ze ϕ(x)”.
Definicja 1.3.3. Funktor
V
nazywamy kwantyfikatorem og´olnym, a funktor
W
-
kwantyfikatorem szczeg´oÃlowym.
6

Zauwa˙zmy, ˙ze kwantyfikator og´olny jest uog´olnieniem koniunkcji
^
x∈X
ϕ(x) ⇔
£
ϕ(x
1
) ∧ ϕ(x
2
) ∧ . . . ∧ ϕ(x
n
)
¤
.
Natomiast kwantyfikator szczeg´oÃlowy jest uog´olnieniem alternatywy
_
x∈X
ϕ(x) ⇔
£
ϕ(x
1
) ∨ ϕ(x
2
) ∨ . . . ∨ ϕ(x
n
)
¤
.
Podamy teraz kilka tautologii rachunku funkcji zdaniowych.
1.
W
x∈X
[ϕ(x) ∨ ψ(x)] ⇔
W
x∈X
ϕ(x) ∨
W
x∈X
ψ(x)
2.
W
x∈X
[ϕ(x) ∧ ψ(x)] ⇒
W
x∈X
ϕ(x) ∧
W
x∈X
ψ(x)
3.
V
x∈X
[ϕ(x) ∧ ψ(x)] ⇔
V
x∈X
ϕ(x) ∧
V
x∈X
ψ(x)
4.
V
x∈X
[ϕ(x) ∨ ψ(x)] ⇐
V
x∈X
ϕ(x) ∨
V
x∈X
ψ(x)
5. Prawa de Morgana dla kwantyfikator´ow
∼
h W
x∈X
ϕ(x)
i
⇔
V
x∈X
∼ ϕ(x)
∼
h V
x∈X
ϕ(x)
i
⇔
W
x∈X
∼ ϕ(x)
PrzykÃlad 1.3.1. Rozwa˙zmy dwa zdania
p =
V
x∈X
£
x ≥ 0 ∨ x < 0
¤
q =
V
x∈X
x ≥ 0 ∨
V
x∈X
x < 0.
Zauwa˙zmy, ˙ze w(p) = 1 oraz w(q) = 0. Zatem jedynie zdanie p mo˙ze wynika´c
ze zdania q (q ⇒ p). Niech teraz
p =
W
x∈X
£
x ≥ 0 ∧ x < 0
¤
q =
W
x∈X
x ≥ 0 ∧
W
x∈X
x < 0.
W tym przypadku w(p) = 0 oraz w(q) = 1. Zatem mo˙ze tylko zachodzi´c
p ⇒ q.
Zadanie 1.3.1. Kt´ore z podanych zda´
n sa, prawdziwe, a kt´ore faÃlszywe.
a)
V
x∈R
sin 2x = 2 sin x cos x,
b)
W
x∈R
sin 2x = 2 sin x,
c)
V
x∈R
√
x
2
= x,
d)
W
x∈R
√
x
2
= −x,
7

e)
V
x∈R
| x |≥ 0,
f )
W
x∈R
V
y∈R
y < x,
g)
V
x∈R
W
y∈R
y < x.
Zadanie 1.3.2. Zbuduj zaprzeczenie podanych zda´
n.
a)
V
x∈R
cos 2x = cos
2
x − sin
2
x,
b)
V
x∈R
W
y∈R
y < x,
c)
W
x∈R
V
y∈R
x < y,
b)
W
x∈R
x
2
− 2 ≤ 0.
1.4. Kres g´
orny i dolny zbioru.
W tym paragrafie be,dziemy rozwa˙za´c podzbiory przestrzeni liczb rzeczywis-
tych R. Niech Z be,dzie dowolnym podzbiorem przestrzeni R.
Definicja 1.4.1. Elementem najwie,kszym zbioru Z nazywamy te, liczbe,, kt´ora
nale˙zy do zbioru Z i jest wie,ksza od ka˙zdego z pozostaÃlych element´ow zbioru Z.
max Z = a ⇔
³
a ∈ Z ∧
^
x∈Z
x ≤ a
´
Elementem najmniejszym zbioru Z nazywamy te, liczbe,, kt´ora nale˙zy do zbioru Z
i jest mniejsza od ka˙zdego z pozostaÃlych element´ow zbioru Z.
min Z = b ⇔
³
b ∈ Z ∧
^
x∈Z
x ≥ b
´
PrzykÃlad 1.4.1. Elementem najmniejszym zbioru liczb naturalnych jest liczba
1.
Zbi´or liczb caÃlkowitych nie ma element´ow najmniejszego i najwie,kszego.
Niech A =< 2; 4 >. Wtedy max A = 4 oraz min A = 2. Je˙zeli A = (2, 4 >, to
min A nie istnieje.
Definicja 1.4.2. Liczbe, a nazywamy ograniczeniem g´ornym zbioru Z, je´sli
^
x∈Z
x ≤ a.
8

Liczbe, a nazywamy ograniczeniem dolnym zbioru Z, je´sli
^
x∈Z
x ≥ a.
PrzykÃlad 1.4.2. Niech dane be,da, zbiory A = {
2n
n+1
: n ∈ N} i B = {
n
2n−1
:
n ∈ N}. Wtedy A = {1,
4
3
,
3
2
,
8
5
,
5
3
, . . .}. Zauwa˙zmy, ˙ze ograniczeniem dolnym
zbioru A moga, by´c mie,dzy innymi naste,puja,ce liczby: -100, -0.5, 0,
1
3
. Ponadto
B = {1,
2
3
,
3
5
,
4
7
, . . .}. W tym przypadku ograniczeniem g´ornym zbioru B sa, mie,dzy
innymi liczby: 1,
3
2
, 2, 101.
Definicja 1.4.3. Zbi´or Z nazywamy ograniczonym od g´ory , je˙zeli istnieje ogra-
niczenie g´orne zbioru Z.
_
M ∈R
^
x∈Z
x ≤ M
Zbi´or Z nazywamy ograniczonym od doÃlu, je˙zeli istnieje ograniczenie dolne zbioru
Z.
_
m∈R
^
x∈Z
x ≥ m
Zbi´or Z nazywamy ograniczonym, je´sli jest ograniczony od g´ory i od doÃlu. W
przeciwnym przypadku zbi´or Z nazywamy nieograniczonym.
PrzykÃlad 1.4.3.
Zbi´or liczb naturalnych jest ograniczony od doÃlu i nie jest
ograniczony od g´ory. Zbi´or odwrotno´sci liczb naturalnych jest ograniczony od
dolu (przez liczbe, 0) i od g´ory (przez liczbe, 1).
Definicja 1.4.4. Kresem g´ornym zbioru nazywamy najmniejsze z ogranicze´
n
g´ornych tego zbioru.
M = sup Z ⇔
^
x∈Z
x ≤ M ∧
^
ε>0
_
x
0
∈Z
x
0
> M − ε
Kresem dolnym zbioru nazywamy najwie,ksze z ogranicze´n dolnych tego zbioru.
m = inf Z ⇔
^
x∈Z
x ≥ m ∧
^
ε>0
_
x
0
∈Z
x
0
< m + ε
Zauwa˙zmy, ˙ze kres g´orny zbioru jest najmniejsza, liczba, ograniczaja,ca, ten zbi´or z
g´ory, za´s kres dolny zbioru jest najwie,ksza, liczba, ograniczaja,ca, ten zbi´or z doÃlu.
Ponadto najmniejszy element zbioru (o ile istnieje) jest jednocze´snie kresem dol-
nym tego zbioru, a najwie,kszy jego element (o ile istnieje) jest kresem g´onym.
9
PrzykÃlad 1.4.4. Rozwa˙zmy zbiory A i B z przykÃladu 1.4.2. Mamy
sup A = 2,
inf A = 1,
sup B = 1,
inf B =
1
2
.
Twierdzenie 1.4.1. (Aksjomat cia,gÃlo´sci Dedekinda) Ka˙zdy niepusty zbi´or ogra-
niczony z g´ory ma kres g´orny. Ka˙zdy niepusty zbi´or ograniczony z doÃlu ma kres
dolny.
Zadanie 1.4.1. Znale´z´c kresy podanych zbior´ow.
A = (−∞, 1 >,
B = (2, ∞),
C = {2
−n
: n ∈ N},
D = {
n
n+1
: n ∈ N},
E = {
n−1
2n
: n ∈ N}.
Definicja 1.4.5. Otoczeniem punktu x
0
o promieniu δ(δ > 0) nazywamy zbi´or
Q(x
0
, δ) = {x : 0 ≤| x − x
0
|< δ}.
Sa,siedztwem punktu x
0
o promieniu δ(δ > 0) nazywamy zbi´or
S(x
0
, δ) = {x : 0 <| x − x
0
|< δ}.
Z powy˙zszej definicji wynika, ˙ze
Q(x
0
, δ) = (x
0
− δ; x
0
+ δ) oraz S(x
0
, δ) = (x
0
− δ; x
0
+ δ) \ {x
0
}.
Zauw˙zmy, ˙ze w definicji 1.4.5. wykorzystano warto´s´c bezwzgle,dna,, kt´ora w
dalszej cze,´sci wykÃladu be,dzie sie, cze,sto pojawia´c. Przypomnimy wie,c definicje, i
pewne wÃlasno´sci warto´sci bezwzgle,dnej.
Definicja 1.4.6.
| x |=
½
x,
x ≥ 0,
−x, x < 0.
WÃla´sciwo´sci warto´sci bezwzgle,dnej:
1. | x |≥ 0,
2. | x |=| −x |,
3. | x |≤ a ⇔ −a ≤ x ≤ a ⇔ x ∈< −a; a >,
4. | x |≥ a ⇔ (x ≥ a ∨ x ≤ −a) ⇔ x ∈ (−∞; −a > ∪ < a; ∞),
5. | x · y |=| x | · | y |,
6. |
x
y
|=
|x|
|y|
, dla y 6= 0,
7. | x + y |≤| x | + | y | (nier´owno´s´c tr´ojka,ta),
10
8. | x − y |≤| x | + | y |,
9.
¯
¯
¯| x | − | y |
¯
¯
¯≤| x + y |,
10.
¯
¯
¯| x | − | y |
¯
¯
¯≤| x − y |.
Ponadto w dalszym cia,gu be,dziemy wykorzystywa´c symbol ”du˙zej sigmy”
Sume, n skÃladnik´ow zapisujemy kr´otko w naste,puja,cy spos´ob
a
1
+ a
2
+ . . . + a
n
=
n
X
k=1
a
k
.
Litere, k nazywamy wska´znikiem sumacyjnym, n za´s - g´orna, granica, sumowania.
Zadanie 1.4.2. Zapisa´c kr´otko przy u˙zyciu symbolu du˙zej sigmy
a) sume, wszystkich liczb naturalnych mniejszych od 80,
b) sume, odwrotno´sci wszystkich liczb naturalnych z przedziaÃlu (π; 14 >,
c) sume, kwadrat´ow wszystkich liczb naturalnych mniejszych od 8,
d) sume, kwadrat´ow odwrotno´sci wszystkich liczb naturalnych z przedziaÃlu (0, 2π).
Zadanie 1.4.3. Oblicz
a)
4
P
k=0
k
2
,
b)
3
P
k=1
k
3
,
c)
3
P
k=0
1
k+1
,
d)
5
P
k=2
k+2
3
,
e)
4
P
k=1
k−1
2k
.
1.5. Zbiory przeliczalne i nieprzeliczalne.
Definicja 1.5.1. M´owimy, ˙ze zbi´or A jest r´ownoliczny ze zbiorem B i piszemy
A ∼ B wtedy i tylko wtedy, gdy istnieje funkcja r´o˙znowarto´sciowa f : A → B,
kt´ora jest odwzorowaniem zbioru A na zbi´or B.
Zauwa˙zmy, ˙ze zbi´or sko´
nczony nie jest r´ownoliczny z ˙zadnym ze swoich pod-
zbior´ow. Istnieja, zbiory , kt´ore sa, r´ownoliczne ze swoimi podzbiorami. Na przy-
kÃlad zbi´or liczb naturalnych jest r´ownoliczny ze zbiorem liczb nieparzystych lub
ze zbiorem liczb podzielnych przez 3. Istotnie w obu tych przypadkach mo˙zemy
znale´z´c r´o˙znowarto´sciwa, funkcje, odwzorowuja,ca, zbi´or liczb naturalnych na jeden
11

z wymienionych zbior´ow. W przypadku zbioru liczb nieparzystych taka, funkcja,
jest f (x) = 2x + 1, x ∈ N, za´s w przypadku zbioru liczb podzielnych przez 3
f (x) = 3x, x ∈ N.
Definicja 1.5.2. Zbi´or Z nazywamy zbiorem niesko´
nczonym wtedy i tylko wtedy,
gdy jest on r´ownoliczny z pewnym swoim podzbiorem.
Na mocy poprzednich rozwa˙za´
n zauwa˙zmy, ˙ze zbi´or liczb naturalnych jest
niesko´
nczony.
Definicja 1.5.3. Zbi´or Z nazywamy zbiorem przeliczalnym wtedy i tylko wtedy,
gdy jest on r´ownoliczny ze zbiorem liczb naturalnych.
Oczywi´scie ka˙zdy zbi´or przeliczalny jest zbiorem niesko´
nczonym.
Cze,sto m´owi sie,, ˙ze zbi´or przeliczalny to zbi´or, kt´orego wszystkie elementy
mo˙zna ustawi´c w cia,g niesko´nczony, przy czym ka˙zdy element zbioru wysta,pi w
tym cia,gu tylko raz.
PrzykÃlad 1.5.1.
Rozwa˙zmy zbi´or liczb caÃlkowitych.
Elementy tego zbioru
ustawmy w naste,puja,cy cia,g
0, 1, −1, 2, −2, 3, −3, . . . .
W cia,gu tym ka˙zda liczba caÃlkowita wysta,pi tylko raz. Oznacza to, ˙ze zbi´or liczb
caÃlkowitych jest przeliczalny.
Definicja 1.5.4. Niepusty zbi´or Z, kt´ory nie jest ani sko´
nczony, ani przeliczalny
nazywamy zbiorem nieprzeliczalnym.
12

2. CIA,GI LICZBOWE.
RozdziaÃl ten rozpoczniemy przypomnieniem podstawowych wiadomo´sci doty-
cza,cych funkcji.
Definicja 2.1. Funkcja f : X → Y odwzorowuja,ca zbi´or X w zbi´or Y jest to
przyporza,dkowanie ka˙zdemu elementowi ze zbioru X dokÃladnie jedenego elementu
ze zbioru Y .
Zbi´or X nazywamy dziedzina, funkcji, a zbi´or Y przeciwdziedzina, lub zbiorem
warto´sci. Elementy zbioru X nazywamy argumentami, a elementy zbioru Y -
warto´sciami funkcji.
Wykresem funkcji y = f (x) nazywamy zbi´or wszystkich punkt´ow (x, f (x)),
x ∈ X.
Czasami be,dziemy stosowa´c naste,puja,ce oznaczenie dziedziny funkcji D
f
.
Interesowa´c nas be,da, przede wszystkim funkcje, kt´orych dziedzina, i prze-
ciwdziedzina, sa, podzbiory zbioru liczb rzeczywistych. Takie funkcje nazywamy
funkcjami liczbowymi. Przy okre´slaniu tych funkcji niekiedy podajemy tylko przy-
porza,dkowanie nie ustalaja,c dziedziny. Obowia,zuje wtedy umowa, ˙ze za dziedzine,
nale˙zy przyja,´c podzbi´or zbioru liczb rzeczywistych, dla kt´orego wz´or ustalaja,cy
przyporza,dkowanie ma sens. Tak rozumiana, dziedzine, nazywamy dziedzina, natu-
ralna,.
Podamy teraz kilka szczeg´olnych wÃlasno´sci funkcji liczbowych.
Definicja 2.2. Funkcje, f nazywamy ograniczona, z doÃlu (z g´ory) na zbiorze A ⊂
D
f
, je˙zeli zbi´or jej warto´sci jest ograniczony z doÃlu (z g´ory), tzn.
_
m∈R
^
x∈A
f (x) ≥ (≤)m
Definicja 2.3. Funkcje, f nazywamy rosna,ca, na zbiorze A ⊂ D
f
, je˙zeli wie,kszej
warto´sci argumentu odpowiada wie,ksza warto´s´c funkcji, tzn.
^
x
1
,x
2
∈A
£
x
1
< x
2
⇒ f (x
1
) < f (x
2
)
¤
(2.1)
Definicja 2.4. Funkcje, f nazywamy maleja,ca, na zbiorze A ⊂ D
f
, je˙zeli wie,kszej
warto´sci argumentu odpowiada mniejsza warto´s´c funkcji, tzn.
^
x
1
,x
2
∈A
£
x
1
< x
2
⇒ f (x
1
) > f (x
2
)
¤
(2.2)
Je˙zeli w warunku (2.1) osÃlabimy druga, nier´owno´s´c, to funkcje, f be,dziemy nazywa´c
niemaleja,ca,. Je´sli za´s osÃlabimy druga, nier´owno´s´c w warunku (2.2), to funkcje,
be,dziemy nazywa´c nierosna,ca,.
13

Powiemy, ˙ze funkcja f jest monotoniczna, gdy jest rosna,ca, maleja,ca, nieros-
na,ca lub niemaleja,ca.
Definicja 2.5. Funkcje, f nazywamy parzysta,, je˙zeli
^
x∈D
f
¡
− x ∈ D
f
∧ f (−x) = f (x)
¢
.
Definicja 2.6. Funkcje, f nazywamy nieparzysta,, je˙zeli
^
x∈D
f
¡
− x ∈ D
f
∧ f (−x) = −f (x)
¢
.
Wykres funkcji parzystej jest symetryczny wzgle,dem osi OY , a wykres funkcji
nieparzystej jest symetryczny wzgle,dem pocza,tku ukÃladu wsp´oÃlrze,dnych.
Definicja 2.7. Funkcje, f nazywamy okresowa,, je˙zeli
_
T >0
^
x∈D
f
£
x + T ∈ D
f
∧ f (x + T ) = f (x)].
Liczbe, T nazywamy wtedy okresem funkcji f.
Zadanie 2.1. Zbada´c monotoniczno´s´c podanych funkcji na wskazanych zbiorach
a) f (x) =
1
x
4
+ 1
, (−∞; 0 >;
b) f (x) =
√
x + 1, < −1; ∞);
c) f (x) =
1
1 + x
2
, < 0, ∞);
d) f (x) = x
2
− 2x, (−∞, 1 >.
Zadanie 2.2. Zbada´c, czy podane funkcje sa, parzyste, czy nieparzyste
a) f (x) = 2
x
+ 2
−x
;
b) f (x) =
sin x
x
3
;
c) f (x) =
2 + x
2
x
5
;
d) f (x) = 3
x
− 3
−x
.
Przypomnimy teraz definicje, cia,gu liczbowego.
Definicja 2.8.
Funkcje, odwzorowuja,ca, zbi´or liczb naturalnych w zbi´or liczb
rzeczywistych nazywamy cia,giem liczbowym.
Warto´sci tej funkcji nazywamy wyrazami cia,gu i oznaczamy f(n) = a
n
.
14

Na mocy tej definicji wÃlasno´sci funkcji, takie jak monotoniczno´s´c i ograniczo-
no´s´c w naturalny spos´ob mo˙zna przenie´s´c na cia,gi liczbowe.
Zadanie 2.3. Zbada´c monotoniczno´s´c podanych cia,g´ow
a) a
n
=
n − 1
n
;
b) a
n
= 5
n
− 3
n
;
c) a
n
=
p
n
2
+ 4 − n;
d) a
n
=
n
2
+ 1
n
2
.
Zadanie 2.4. Podaj przykÃlad cia,gu ograniczonego.
Wa˙zna, role, w zastosowaniach peÃlnia, cia,gi arytmetyczne i geometryczne, znane z
kursu matematyki w szkole ´sredniej. Przypomnijmy w tym miejscu kilka podsta-
wowych wiadomo´sci dotycza,cych tego zagadnienia.
Definicja 2.9. Cia,giem arytmetycznym nazywamy cia,g, w k´orym ka˙zdy wyraz,
z wyja,tkiem pierwszego, r´o˙zni sie, od wyrazu bezpo´srednio go poprzedzaja,cego o
staÃla, liczbe, r´o˙zna, od zera, zwana, r´o˙znica, cia,gu
_
r∈R
^
n∈N\{1}
a
n
− a
n−1
= r
ÃLatwo wykaza´c, ˙ze je˙zeli r > 0, to cia,g jest rosna,cy, a gdy r < 0, to cia,g jest
maleja,cy.
Ponadto dla cia,gu arytmetycznego prawdziwe sa, wzory
^
n∈N\{1}
a
n
= a
1
+ (n − 1)r,
^
n∈N\{1}
a
n
=
a
n−1
+ a
n+1
2
,
^
n∈N\{1}
S
n
= a
1
+ a
2
+ . . . + a
n
=
a
1
+ a
n
2
n,
S
1
= a
1
.
Definicja 2.10.
Cia,giem geometrycznym nazywamy cia,g, w k´orym stosunek
dowolnego wyrazu, z wyja,tkiem pierwszego, do wyrazu bezpo´srednio go poprze-
dzaja,cego jest staÃly.
_
q∈R
^
n∈N\{1}
a
n
a
n−1
= q
15

Liczbe, q nazywamy ilorazem cia,gu.
Dla cia,gu geometrycznego prawdziwe sa, wzory
^
n∈N\{1}
a
n
= a
1
q
n−1
,
^
n∈N\{1}
S
n
= a
1
+ a
2
+ . . . + a
n
= a
1
1 − q
n
1 − q
,
gdy q 6= 1,
^
n∈N\{1}
S
n
= n · a
1
,
gdy q = 1,
oraz
S
1
= a
1
.
Ponadto dla cia,gu o wyrazach dodatnich mamy
^
n∈N\{1}
a
n
=
√
a
n−1
· a
n+1
.
Je˙zeli w cia,gu geometrycznym o wyrazach dodatnich 0 < q < 1, to cia,g ten jest
maleja,cy, je´sli q > 1, to cia,g jest rosna,cy.
ZaÃl´o˙zmy teraz, ˙ze | q |< 1. W´owczas naste,puja,cym wzorem mo˙zemy zsumo-
wa´c wszystkie wyrazy cia,gu geometrycznego {a
n
}
S =
a
1
1 − q
.
Zadanie 2.5. Znale´z´c cia,g arytmetyczny, kt´orego pierwszy wyraz jest r´owny 1, a
suma pocza,tkowych pie,ciu wyraz´ow jest cztery razy mniejsza od sumy naste,pnych
pie,ciu wyraz´ow.
Zadanie 2.6. Sprawdzi´c, ˙ze je˙zeli {a
n
} jest cia,giem geometrycznym, to cia,g
{a
n
+ a
n+1
} jest tak˙ze cia,giem geometrycznym.
Zadanie 2.7. Obliczy´c sume, 1 −
1
√
2
+
1
2
−
1
2
√
2
+ ... .
Zadanie 2.8. Zamieni´c uÃlamek 0, 4(12) na uÃlamek zwykÃly.
Zadanie 2.9. Rozwia,za´c podane r´ownania i nier´owno´sci
a) 2
x
+ 2
2x
+ 2
3x
+ .. = 1,
16

b) (x + 1) + (x + 1)
2
+ (x + 1)
3
+ ... =
q
x +
3
2
,
c) 1 + a + a
2
+ a
3
+ ... + a
x
= (1 + a)(1 + a
2
)(1 + a
4
),
d) (x + 1) + (x + 4) + .. + (x + 28) = 155.
2.1. Granica cia,gu.
Definicja 2.1.1. Liczbe, g nazywamy granica, cia,gu {a
n
}, je˙zeli prawie wszystkie
wyrazy tego cia,gu nale˙za, do otoczenia liczy g o promieniu ε, tj.
lim
n→∞
a
n
= g ⇔
^
ε>0
_
δ
^
n>δ
| a
n
− g |< ε.
Je˙zeli cia,g {a
n
} ma granice, to nazywa´c go be,dziemy cia,giem zbie˙znym.
Definicje, granicy mo˙zna r´ownie˙z sformuÃlowa´c w naste,pujc,y spos´ob: Liczba
g jest granica, cia,gu, gdy wszystkie jego wyrazy r´o˙znia, sie, od g o dowolnie maÃla
liczbe, dodatnia, ε, pocza,wszy od pewnego wska´znika. Wa˙zna jest uwaga, ˙ze na og´oÃl
liczba δ, o kt´orej mowa w definicji, nie mo˙ze by´c ustalona na zawsze, ale zale˙zy od
wyboru ε.
Wa˙zna, role, odgrywa przypadek, gdy cia,g jest zbie˙zny do zera. W´owczas
mamy
lim
n→∞
a
n
= 0 ⇔
^
ε>0
_
δ
^
n>δ
| a
n
|< ε
co oznacza, ˙ze prawie wszystkie wyrazy cia,gu zbie˙znego do zera co do warto´sci
bezwzgle,dnej sa, mniejsze od pewnej maÃlej ustalonej liczby dodatniej ε.
Twierdzenie 2.1.1. Warunkiem koniecznym i dostatecznym zbie˙zno´sci cia,gu
{a
n
} do liczby g jest zbie˙zno´s´c cia,gu {a
n
− g} do zera.
Dow´
od. Konieczno´s´c warunku wynika bezpo´srednio z definicji 2.1.1. granicy
cia,gu.
Aby dowie´s´c dostateczno´sci tego warunku zaÃl´o˙zmy, ˙ze cia,g α
n
= a
n
− g jest
zbie˙zny do zera. Mamy w´owczas
^
ε>0
_
δ
^
n>δ
| α
n
|< ε.
Zatem
^
ε>0
_
δ
^
n>δ
| a
n
− g |< ε.
Co ko´
nczy dow´od.
17
PrzykÃlad 2.1.1. Rozwa˙zmy cia,g {
n
√
n}. Poka˙zemy, ˙ze jest to cia,g zbie˙zny do 1.
Niech wie,c a
n
=
n
√
n − 1. Korzystaja,c ze wzoru Newtona mamy
n = (
n
√
n)
n
= (1 + a
n
)
n
= 1 + na
n
+
µ
n
2
¶
a
2
n
+ . . . + a
n
n
czyli
n − 1 = na
n
+
µ
n
2
¶
a
2
n
+ . . . + a
n
n
.
Niech n ≥ 2. Poniewa˙z a
n
> 0, wie,c
n − 1 >
n(n − 1)
2
a
2
n
czyli
a
2
n
<
2
n
.
Sta,d otrzymujemy
| a
n
|<
r
2
n
.
Zatem
|
n
√
n − 1 |<
r
2
n
.
Oznacza to, ˙ze dla dowolnie wybranego ε > 0 istnieje taka liczba δ =
2
ε
2
, ˙ze
^
n>δ
|
n
√
n − 1 |< ε.
Wobec tego mo˙zemy twierdzi´c, ˙ze
lim
n→∞
n
√
n = 1.
Twierdzenie 2.1.2. Ka˙zdy cia,g zbie˙zny jest ograniczony.
Dow´
od. Niech {a
n
} be,dzie cia,giem zbie˙znym do granicy g. Zatem dla ε = 1
istnieje taka liczba δ, ˙ze dla wszystkich n > δ speÃlniona jest nier´owno´s´c
| a
n
− g |< 1.
Wobec tego, na mocy nier´owno´sci tr´ojka,ta mamy
| a
n
|=| a
n
− g + g |≤| a
n
− g | + | g | .
18

Sta,d wynika, ˙ze dla wszystkich n > δ speÃlniona jest nier´owno´s´c
| a
n
|≤ 1+ | g | .
Dla n ≤ δ niech A oznacza najwie,ksza, z liczb | a
n
|. Niech ponadto M =
max
¡
A, 1+ | g |
¢
. Wtedy dla ka˙zdego n ∈ N mamy | a
n
|≤ M , co oznacza,
˙ze cia,g {a
n
} jest ograniczony.
Z twierdzenia 2.1.2. wynika, ˙ze warunkiem koniecznym zbie˙zno´sci cia,gu licz-
bowego jest jego ograniczono´s´c. Nie jest to jednak warunek dostateczny, o czym
´swiadczy naste,puja,cy przykÃlad.
PrzykÃlad 2.1.2. Niech dany be,dzie cia,g o wyrazie og´olnym a
n
= (−1)
n
. ÃLatwo
wida´c, ˙ze cia,g ten jest ograniczony, gdy˙z
^
n∈N
| (−1)
n
|≤ 1.
Z drugiej strony wyrazami tego cia,gu sa, liczby 1 lub −1. Jednak˙ze ˙zadna z nich
nie jest jego granica,, gdy˙z istnieja, takie otoczenia liczb 1 i −1, w kt´orych nie le˙za,
prawie wszystkie wyrazy cia,gu, np. S(1;
1
2
), S(−1 :
1
2
). Liczba r´o˙zna od 1 i −1
te˙z nie mo˙ze by´c granica, tego cia,gu, bo w jej otoczeniu o dostatecznie maÃlym
promieniu nie znajduje sie, ˙zaden wyraz tego cia,gu. Oznacza to, ˙ze cia,g {(−1)
n
}
nie ma granicy.
Z powy˙zszego przykÃladu wynika te˙z, ˙ze w´sr´od cia,g´ow liczbowych istnieja, takie
cia,gi, kt´ore nie posiadaja, granicy.
Ponadto mo˙zemy r´ownie˙z m´owi´c o cia,gach rozbie˙znych.
Definicja 2.1.2. M´owimy, ˙ze cia,g {a
n
} jest rozbie˙zny do plus niesko´
nczono´sci
wtedy i tylko wtedy, gdy
^
ε
_
δ
^
n>δ
a
n
> ε.
Definicja 2.1.3. M´owimy, ˙ze cia,g {a
n
} jest rozbie˙zny do minus niesko´
nczono´sci
wtedy i tylko wtedy, gdy
^
ε
_
δ
^
n>δ
a
n
< ε.
PrzykÃlad 2.1.3. Ka˙zdy cia,g arytmetyczny o r´o˙znicy dodatniej jest rozbie˙zny do
plus niesko´
nczono´sci. Ka˙zdy cia,g arytmetyczny o r´o˙znicy ujemniej jest rozbie˙zny
do minus niesko´
nczono´sci.
19

Zadanie 2.1.1. Korzystaja,c z definicji granicy cia,gu pokaza´c, ˙ze
a) lim
n→∞
2
n
2
n
−1
= 1,
b) lim
n→∞
3n−1
2n+1
=
3
2
,
lim
n→∞
q
n
=
+∞, q > 1,
1,
q = 1,
0,
| q |< 1.
2.2. DziaÃlania arytmetyczne na granicach cia,g´ow.
Niech dane be,da, cia,gi liczbowe {a
n
} i {b
n
}. Cia,gi
{a
n
+ b
n
},
{a
n
− b
n
},
{a
n
· b
n
}
nazywamy odpowiednio: suma,, r´o˙znica, i iloczynem cia,g´ow {a
n
} i {b
n
}. Je˙zeli
zaÃlo˙zymy dodatkowo, ˙ze
V
n∈N
b
n
6= 0, to cia,g
n a
n
b
n
o
nazywamy ilorazem cia,g´ow {a
n
} i {b
n
}.
Twierdzenie 2.2.1. (o dziaÃlaniach arytmetycznych na granicach cia,g´ow zbie˙z-
nych) Je˙zeli cia,gi {a
n
} i {b
n
} sa, zbie˙zne i
lim
n→∞
a
n
= a
i
lim
n→∞
b
n
= b,
to istnieja, granice cia,g´ow {a
n
+ b
n
}, {a
n
− b
n
}, {a
n
· b
n
} i
1. lim
n→∞
(a
n
+ b
n
) = a + b,
2. lim
n→∞
(a
n
− b
n
) = a − b,
3. lim
n→∞
(a
n
· b
n
) = a · b,
oraz przy zaÃlo˙zeniu, ˙ze
V
n∈N
b
n
6= 0 i b 6= 0 istnieje granica cia,gu
n a
n
b
n
o
i
4. lim
n→∞
a
n
b
n
=
a
b
.
Dow´
od.
Niech ε be,dzie dowolna, liczba, dodatnia,. Poniewa˙z lim
n→∞
a
n
= a i
lim
n→∞
b
n
= b, to istnieja, takie liczby δ
1
i δ
2
, ˙ze speÃlnione sa, naste,puja,ce warunki
^
n>δ
1
| a
n
− a |<
ε
2
^
n>δ
2
| b
n
− b |<
ε
2
.
20

Niech δ = max(δ
1
; δ
2
). Wtedy mamy
1. Dla ka˙zdego n > δ na mocy nier´owno´sci tr´ojka,ta
| (a
n
+ b
n
) − (a + b) |≤| a
n
− a | + | b
n
− b |<
ε
2
+
ε
2
= ε.
Oznacza to, ˙ze lim
n→∞
(a
n
+ b
n
) = a + b.
2. Dla ka˙zdego n > δ na mocy wÃla´sciwo´sci 8 warto´sci bezwzgle,dnej
| (a
n
− b
n
) − (a − b) |≤| a
n
− a | + | b
n
− b |<
ε
2
+
ε
2
= ε.
Oznacza to, ˙ze lim
n→∞
(a
n
− b
n
) = a − b.
Aby dowie´s´c punktu 3 tego twierdzenia zauwa˙zmy, ˙ze z zaÃlo˙zenia lim
n→∞
a
n
= a
na mocy twierdzenia 2.1.2. wynika, ˙ze cia,g {a
n
} jest ograniczony, tzn.
_
M >0
^
n∈N
| a
n
|≤ M.
Ponadto z zaÃlo˙zenia lim
n→∞
a
n
= a i lim
n→∞
b
n
= b wynikaja, odpowiednio naste,puja,ce
warunki
^
n>δ
| a
n
− a |<
ε
2(| b | +1)
^
n>δ
| b
n
− b |<
ε
2M
.
Wobec tego mamy
| a
n
b
n
− ab |=| a
n
b
n
− a
n
b + a
n
b − ab |≤| a
n
| · | b
n
− b | + | b | · | a
n
− a |
≤ M · | b
n
− b | +(| b | +1)· | a
n
− a |
< M
ε
2M
+ (| b | +1) ·
ε
2(| b | +1)
= ε.
Otrzymali´smy zatem
^
ε>0
_
δ
^
n>δ
| a
n
b
n
− ab |< ε.
Dowodza,c punkt 4 twierdzenia zaÃl´o˙zmy, ˙ze
^
n∈N
b
n
6= 0 i
lim
n→∞
b
n
= b 6= 0.
Zatem inf | b · b
n
|= k > 0 oraz
^
ε>0
_
δ
^
n>δ
| b
n
− b |<
kε
2M
.
21

Ponadto z zaÃlo˙zenia lim
n→∞
a
n
= a mamy
_
M >0
^
n∈N
| a
n
|≤ M
oraz
^
ε>0
_
δ
^
n>δ
| a
n
− a |<
| b | ε
2
.
Sta,d dla n > δ otrzymujemy
¯
¯
¯
a
n
b
n
−
a
b
¯
¯
¯ =
¯
¯
¯
a
n
b − b
n
a
b
n
b
¯
¯
¯ =
| a
n
(b − b
n
) + b
n
(a
n
− a) |
| b
n
b |
≤
M
k
| b
n
− b | +
1
| b |
| a
n
− a |
<
M
k
kε
2M
+
1
| b |
| b | ε
2
= ε.
Zatem mamy
^
ε>0
_
δ
^
n>δ
¯
¯
¯
a
n
b
n
−
a
b
¯
¯
¯ < ε,
co ko´
nczy dow´od.
Czasami spotykamy sie, z zagadnieniem obliczenia granicy cia,gu w sytuacji,
gdy nie mo˙zna bezpo´srednio skorzysta´c z twierdzenia o dziaÃlaniach arytmety-
cznych na granicach cia,g´ow zbie˙znych. Taki przypadek ma miejsce, gdy jeden
z rozwa˙zanych cia,g´ow ma granice, niesko´nczona,. W obliczaniu takich granic mo˙ze
nam pom´oc poni˙zsza tabela.
22

Je˙zeli
to
lim
n→∞
a
n
= 0, a
n
> 0
lim
n→∞
1
a
n
= +∞
lim
n→∞
a
n
= 0, a
n
< 0
lim
n→∞
1
a
n
= −∞
lim
n→∞
a
n
= ±∞
lim
n→∞
1
a
n
= 0
lim
n→∞
a
n
= ±∞
lim
n→∞
(a
n
· b
n
) = ±∞
lim
n→∞
b
n
= b > 0
lim
n→∞
a
n
= ±∞
lim
n→∞
(a
n
· b
n
) = ∓∞
lim
n→∞
b
n
= b < 0
lim
n→∞
a
n
= ±∞
lim
n→∞
(a
n
· b
n
) = [0 · ∞] =?
lim
n→∞
b
n
= 0
lim
n→∞
(a
n
· b
n
) = +∞
lim
n→∞
a
n
= lim
n→∞
b
n
= ±∞
lim
n→∞
(a
n
− b
n
) = [∞ − ∞] =?
lim
n→∞
a
n
b
n
=
£
∞
∞
¤
=?
V
n∈N
| a
n
|< M,
lim
n→∞
b
n
= 0
lim
n→∞
(a
n
· b
n
) = 0
V
n∈N
| a
n
|< M,
lim
n→∞
b
n
= ±∞
lim
n→∞
a
n
b
n
= 0
lim
n→∞
a
n
= lim
n→∞
b
n
= 0
lim
n→∞
a
n
b
n
=
£
0
0
i
=?
Znak zapytania oznacza, ˙ze bez bardziej szczeg´oÃlowych informacji o cia,gach
{a
n
} i {b
n
} nic nie mo˙zna powiedzie´c o danych granicach. Symbole z nawias´ow
kwadratowych: 0 · ∞, ∞ − ∞,
∞
∞
,
0
0
nazywamy symbolami nieoznaczonymi.
2.3. Twierdzenia o cia,gach monotonicznych i ograniczonych.
W paragrafie tym podamy pewne twierdzenia, kt´ore uÃlatwia, nam liczenie
granic niekt´orych cia,g´ow liczbowych.
23

Twierdzenie 2.3.1. Je˙zeli cia,g jest monotoniczny i ograniczony, to jest zbie˙zny.
Dow´
od. Niech cia,g {a
n
} be,dzie cia,giem niemaleja,cym i ograniczonym. Na pod-
stawie aksjomatu cia,gÃlo´sci Dedekinda, zbi´or jego wyraz´ow posiada kres g´orny
a = sup{a
n
: n ∈ N}. Wyka˙zemy, ˙ze lim
n→∞
a
n
= a. Niech wie,c ε be,dzie dowolna,
liczba, dodatnia,. Z definicji 1.4.4. kresu g´ornego wynika, ˙ze
^
n≥n
1
a
n
≤ a ∧
_
n
0
a
n
0
> a − ε.
Niech δ = max(n
0
, n
1
). Wtedy z monotoniczno´sci cia,gu {a
n
} mamy
^
n>δ
(a
n
≤ a < a + ε ∧ a − ε < a
n
0
≤ a
n
).
Wobec tego
^
n>δ
a − ε < a
n
< a + ε,
co oznacza, ˙ze
^
ε>0
_
δ
^
n>δ
| a
n
− a |< ε.
W przypadku, gdy cia,g {a
n
} jest nierosna,cy dow´od przebiega w spos´ob analogicz-
ny.
Twierdzenie 2.3.2. Je˙zeli cia,g jest monotoniczny i nieograniczony, to jest roz-
bie˙zny.
Twierdzenie 2.3.3. (o trzech cia,gach) Je˙zeli cia,gi {a
n
} i {c
n
} sa, zbie˙zne do tej
samej granicy oraz
_
n
0
^
n>n
0
a
n
≤ b
n
≤ c
n
,
(2.3.1)
to cia,g {b
n
} jest zbie˙zny do tej samej granicy, co cia,gi {a
n
} i {c
n
}.
Dow´
od. Niech ε be,dzie dowolna, liczba, dodatnia, i niech
lim
n→∞
a
n
= lim
n→∞
c
n
= g.
Wtedy istnieje liczba δ taka, ˙ze
^
n>δ
a
n
∈ O(g, ε) ∧ c
n
∈ O(g, ε).
24
Poniewa˙z cia,g {b
n
} speÃlnia nier´owno´s´c (2.3.1), to
V
n∈N
b
n
∈ O(g, ε).
Twierdzenie 2.3.4. (o dw´och cia,gach) Je˙zeli cia,g {a
n
} jest rozbie˙zny do plus
niesko´
nczono´sci i cia,g {b
n
} speÃlnia warunek
_
n
0
^
n>n
0
a
n
≤ b
n
,
to lim
n→∞
b
n
= +∞.
Twierdzenie 2.3.5. (o dw´och cia,gach) Je˙zeli cia,g {a
n
} jest rozbie˙zny do minus
niesko´
nczono´sci i cia,g {b
n
} speÃlnia warunek
_
n
0
^
n>n
0
a
n
≥ b
n
,
to lim
n→∞
b
n
= −∞.
Zadanie 2.3.1.
Cia,g {a
n
} o wyrazach dodatnich jest maleja,cy. Co mo˙zna
powiedzie´c o zbie˙zno´sci tego cia,gu?
Zadanie 2.3.2. Wykaza´c, ˙ze cia,g
2
n
n!
jest zbie˙zny.
Zadanie 2.3.3. Wykaza´c, ˙ze je˙zeli cia,g {a
n
} jest cia,giem ograniczonym, a cia,g
{b
n
} jest zbie˙zny do zera, to cia,g {a
n
b
n
} ma granice, r´owna, 0.
Zadanie 2.3.4. Oblicz granice cia,g´ow o naste,puja,cych wyrazach og´olnych
a
n
=
n
√
2
n
+ 3
n
+ 5
n
,
b
n
=
n
p
(2 + sin n)
n
+ (2 − cos n)
n
+ 3
n
,
c
n
=
n
r³
3
5
´
n
+
³ 2
7
´
n
,
d
n
=
n +
√
n
√
n
5
+ n
+
n +
√
n + 1
√
n
5
+ n
+ . . . +
n +
√
n + 2n + 1
√
n
5
+ n
.
Zadanie 2.3.5. Oblicz podane granice
a) lim
n→∞
p
2n
2
+
√
n
n
,
i) lim
n→∞
³ 1 + 3 + 5 + ... + 2n − 1
n + 1
− n
´
,
b) lim
n→∞
³p
9n
2
+ 1 − 3n
´
,
j) lim
n→∞
³p
4n
2
+ 3n + 1 − 2n
´
,
c) lim
n→∞
³
n −
√
n
´
,
k) lim
n→∞
1 − 4n
2
2 + 4 + 6 + . . . + 2n
,
d) lim
n→∞
1 +
1
2
+
1
4
+
1
8
+ .. +
¡
1
2
¢
n
1 +
1
3
+
1
9
+
1
27
+ ... +
¡
1
2
¢
n
.
l) lim
n→∞
√
n
q
n +
p
n +
√
n
,
e) lim
n→∞
³ 1
2n
cos n
3
−
3n
6n + 1
´
,
Ãl) lim
n→∞
³ 2n
1 − 3n
− sin n!
n
n
2
+ 1
´
.
25

2.4. Poje,cie podcia,gu. Twierdzenie Bolzano-Weierstrassa.
Definicja 2.4.1. Niech dany be,dzie cia,g liczbowy
{a
n
} = {a
1
, a
2
, a
3
, . . .}
oraz rosna,cy cia,g liczb naturalnych
{n
k
} = {n
1
, n
2
, n
3
, . . .}.
Cia,g
{a
n
k
} = {a
n
1
, a
n
2
, a
n
3
, . . .}
nazywamy podcia,giem cia,gu {a
n
}.
PrzykÃlad 2.4.1. Podcia,gami cia,gu {a
n
} sa, mie,dzy innymi naste,puja,ce cia,gi
{a
2n
} = {a
2
, a
4
, a
6
, . . .};
{a
n+6
} = {a
7
, a
8
, a
9
, . . .};
{a
2n−1
} = {a
1
, a
3
, a
5
, . . .};
{a
3
n
} = {a
3
, a
9
, a
27
, . . .}.
Podamy teraz bez dowodu kilka twierdze´
n dotycza,cych wÃlasno´sci podcia,g´ow.
Twierdzenie 2.4.1. Je˙zeli cia,g {a
n
} jest zbie˙zny do granicy a, to ka˙zdy jego
podcia,g jest zbie˙zny do granicy a.
Twierdzenie 2.4.2. Je˙zeli cia,g {a
n
} jest rozbie˙zny, to ka˙zdy jego podcia,g jest
te˙z rozbie˙zny.
Z twierdze´
n 2.4.1 i 2.4.2 wynika, ˙ze odrzucenie dowolnie wielu wyraz´ow cia,gu
nie zmienia jego granicy. R´ownie˙z doÃla,cznie do cia,gu jednego wyrazu nie zmienia
granicy tego cia,gu. Jednak doÃla,czenie do danego cia,gu niesko´nczenie wielu wyra-
z´ow mo˙ze spowodowa´c zmiane, jego granicy.
Wa˙znym twierdzeniem, kt´ore mo˙zemy wykorzysta´c przy liczeniu granic pew-
nych cia,g´ow jest naste,puja,ce twierdzenie
Twierdzenie 2.4.3. Ka˙zdy cia,g ograniczony zawiera podcia,g zbie˙zny.
Z tego twierdzenia wynika naste,puja,cy wniosek
26

Wniosek 2.4.1. Je´sli wszystkie podcia,gi zbie˙zne danego cia,gu ograniczonego
maja, te, sama, granice,, to dany cia,g jest zbie˙zny do tej granicy.
Zauwa˙zmy, ˙ze wniosek ten mo˙zna wykorzysta´c do pokazania, ˙ze cia,g nie ma
granicy. Wystarczy bowiem wybra´c z tego cia,gu dwa podcia,gi zbie˙zne do dw´och
r´o˙znych granic.
2.5. Liczba e.
Rozwa˙zany cia,g liczbowy o wyrazie og´olnym a
n
=
³
1 +
1
n
´
n
. Zauwa˙zmy, ˙ze gdy
n → ∞, to wyrazy tego cia,gu daja, nam symbol nieoznaczony 1
∞
.
Zauwa˙zmy, ˙ze korzystaja,c z dwumianu Newtona mamy
a
n
= 1 +
µ
n
1
¶
1
n
+
µ
n
2
¶
1
n
2
+ . . . +
µ
n
n
¶
1
n
n
= 1 + 1 +
n(n − 1)
2!
1
n
2
+ . . . +
n(n − 1) . . . [n − (n − 1)]
n!
1
n
n
= 1 + 1 +
1
2!
³
1 −
1
n
´
+ . . . +
1
n!
³
1 −
1
n
´³
1 −
2
n
´
· . . . ·
³
1 −
n − 1
n
´
.
Sta,d otrzymujemy
a
n+1
= 1+1+
1
2!
³
1−
1
n + 1
´
+. . .+
1
(n + 1)!
³
1−
1
n + 1
´³
1−
2
n + 1
´
·. . .·
³
1−
n
n + 1
´
.
Wobec tego mamy a
n
< a
n+1
. Oznacza to, .,ze cia,g
n³
1 +
1
n
´
n
o
jest cia,giem
rosna,cym.
Ponadto zauwa˙zmy, ˙ze
a
n
≤ 2 +
1
2!
+
1
3!
+ . . . +
1
n!
.
Korzystaja,c z faktu, ˙ze
^
k∈N
k! ≥ 2
k−1
otrzymujemy
a
n
≤ 2 +
1
2
+
1
2
2
+ . . . +
1
2
n−1
= 2 +
1
2
1 −
¡
1
2
¢
n−1
1 −
1
2
= 2 +
h
1 −
¡ 1
2
¢
n−1
i
< 3.
27
Oznacza to, ˙ze cia,g
n³
1 +
1
n
´
n
o
jest cia,giem ograniczonym od g´ory.
Zatem na mocy twierdzenia 2.3.1 wnioskujemy, ˙ze cia,g o wyrazie og´olnym
a
n
=
³
1 +
1
n
´
n
ma granice,. Granica, tego cia,gu jest liczba niewymierna, kt´ora,
oznaczamy przez e. Mo˙zna wykaza´c, ˙ze e = 2, 718281828459045 . . . .
Zadanie 2.5.1. Oblicz granice cia,g´ow o wyrazach og´olnych
a) lim
n→∞
³
1 −
2
n
´
n
,
d) lim
n→∞
³ n + 6
n
´
n
,
b) lim
n→∞
³ n
2
+ 5
n
2
´
n
2
,
e) lim
n→∞
³ 2 + n
3 + n
´
n
,
c) lim
n→∞
³ n
3
+ 1
2n
3
´
n
3
,
f ) lim
n→∞
³ n
2
+ 7
n + 1
´
n
.
28

3. FUNKCJA JEDNEJ ZMIENNEJ.
W rozdziale tym om´owimy podstawowe wÃlasno´sci funkcji rzeczywistych jednej
zmiennej rzeczywistej, kt´ore nie byÃly wymienione w rozdziale 2.
W szkole ´sredniej analizowane byÃly takie funkcje elementarne jak funkcja li-
niowa i kwadratowa, wielomiany, funkcje wymierne, pote,gowe, wykÃladnicze, loga-
rytmiczne i trygonometryczne. Oczywi´scie opr´ocz wymienionych funkcji istnieja,
inne funkcje elementarne takie jak funkcje cyklometryczne i hiperboliczne, kt´ore
kr´otko om´owimy w tym rozdziale oraz funkcje nie elementarne. Do najcze,´sciej
spotykanych funkcji nie elementarnych zaliczy´c mo˙zemy mie,dzy innymi
1. funkcje, cze,´s´c caÃlkowita Ent : R → Z dana, wzorem
Ent(x) =
...
,
−2, dla − 2 ≤ x < −1,
−1, dla − 1 ≤ x < 0,
0,
dla 0 ≤ x < 1,
1,
dla 1 ≤ x < 2,
2,
dla 2 ≤ x < 3,
...
;
2. funkcje, signum sgn : R → {−1, 0, 1} dana, wzorem
sgn(x) =
−1, dla x < 0,
0,
dla x = 0,
1,
dla x > 0;
3. funkcje, Dirichleta D : R → {0, 1} dana, wzorem
D(x) =
½
0, dla x 6∈ Q,
1, dla x ∈ Q.
W dalszej cze,´sci wykÃladu be,dziemy cze,sto posÃlugiwa´c sie, takimi poje,ciami jak
superpozycja funkcji i funkcja odwrotna, dlatego te˙z w naste,pnych paragrafach
zdefiniujemy te poje,cia.
3.1. Superpozycja funkcji.
Niech dane be,da, dwie funkcje f : X → Y oraz g : Z → T. Niech ponadto Y ⊂
Z. Je˙zeli ka˙zdemu elementowi x ∈ X przyporza,dkujemy dokÃladnie jeden element
z ∈ T taki, ˙ze z = g(f (x)), to zdefiniujemy w ten spos´ob funkcje, h : X → T
29

okre´slona, r´owno´scia, h(x) = g(f(x)) i zwana, superpozycja, funkcji f i g lub funkcja,
zÃlo˙zona,. Superpozycje, funkcji oznaczamy symbolem g ◦ f. Funkcje, f nazywamy
funkcja, wewne,trzna,, a funkcje, g funkcja, zewne,trzna,.
PrzykÃlad 3.1.1. Niech f (x) = tgx i g(x) = x
2
. W´owczas f : R \ {
π
2
+ kπ; k ∈
Z} → R, g : R → R
+
∪ {0}. Zatem w tym przypadku X = R \ {
π
2
+ kπ; k ∈ Z},
Y = R, Z = R i T = R
+
∪ {0}. Istnieje zatem g ◦ f : R \ {
π
2
+ kπ, k ∈ Z} →
R
+
∪ {0}, przy czym g ◦ f (x) = g(f (x)) = tg
2
x.
Ponadto je´sli zawe,zimy przeciwdziedzine, funkcji g tak aby T ⊂ X, to be,dzie-
my mogli okre´sli´c superpozycje, f ◦ g(x) = f(g(x)) = tg(x
2
).
Oczywi´scie f ◦ g 6= g ◦ f .
3.2. Funkcja odwrotna.
Niech dana be,dzie funkcja f : X → Y i niech A ⊂ X.
Definicja 3.2.1. Funkcje, f nazywamy r´o˙znowarto´sciowa, na zbiorze A wtedy i
tylko wtedy, gdy
^
x
1
,x
2
∈A
³
x
1
6= x
2
⇒ f (x
1
) 6= f (x
2
)
´
.
PrzykÃlad 3.2.1. Funkcja f (x) = x
3
jest r´o˙znowarto´sciowa w caÃlej swojej dzie-
dzinie naturalnej.
Funkcja f (x) = x
2
nie jest r´o˙znowarto´sciowa w swojej dziedzinie natural-
nej, bo na przykÃlad f (−2) = 4 i f (2) = 4. Jednak˙ze funkcja f (x) = x
2
, x ∈
(−∞, 0 > jest r´o˙znowarto´sciowa. Podobnie funkcja f (x) = x
2
, x ∈ (0, ∞) jest
r´o˙znowarto´sciowa.
Definicja 3.2.2. Niech f : X → Y be,dzie funkcja, r´o˙znowarto´sciowa,. Funkcje,
f
−1
: Y → X taka,, ˙ze
f (f
−1
(x)) = f
−1
(f (x)) = x
nazywamy funkcja, odwrotna, do funkcji f.
Zauwa˙zmy, ˙ze tylko funkcje r´o˙znowarto´sciowe posiadaja, funkcje odwrotne.
Funkja odwrotna do danej funkcji ma wykres symetryczny wzgle,dem prostej
y = x.
PrzykÃlad 3.2.2. Niech dana be,dzie funkcja f(x) = x
2
+ 2x − 1. Funkcja ta nie
jest r´o˙znowarto´sciowa w swojej dziedzinie naturalnej, a zatem nie istnieje funkcja
odwrotna do niej.
30
Je´sli zawe,zimy dziedzine, tej funkcji tak, aby byÃla ona r´o˙znowarto´sciowa, to
be,dziemy mogli znale´z´c funkcje, do niej odwrotna,. Zauwa˙zmy, ˙ze
f (x) = (x + 1)
2
− 2, a zatem mo˙zemy dziedzine, zawe,zi´c do jednego ze zbior´ow
(−∞, −1 > lub < −1, ∞).
Rozwa˙zmy, wie,c funkcje, f(x) = x
2
+ 2x − 1, x ∈< −1, ∞). Funkcja ta
jest r´o˙znowarto´sciowa w swojej dziedzinie. Wobec tego istnieje funkcja do niej
odwrotna, kt´ora, mo˙zemy znale´z´c rozwia,zuja,c wzgle,dem x r´ownanie y = x
2
+2x−1.
Korzystaja,c z postaci kanonicznej tr´ojmianu kwadratowego mamy y = (x+1)
2
−2,
a zatem x =
√
y + 2 − 1. Szukana, funkcja, jest wie,c funkcja f
−1
(x) =
√
x + 2 − 1,
kt´orej dziedzina, jest przeciwdziedzina funkcji f, tj < −2, ∞).
Zadanie 3.2.1. Zawe,zi´c dziedzine, podanych funkcji tak, aby byÃly one r´o˙znowar-
to´sciowe, a naste,pnie znale´z´c funkcje odwrotne dla tych funkcji.
a) f (x) = x
2
− 4x + 5,
c) f (x) = 2 −
5
√
x + 1,
b) f (x) = log (x − 4) + 6,
d) f (x) = 3
2x+3
,
3.3. Funkcje cyklometryczne i hiperboliczne.
Wiadomo, ˙ze funkcje trygonometryczne nie sa, r´o˙znowarto´sciowe w swoich dzie-
dzinach naturalnych. Jednak˙ze funkcja sinus na przykÃlad na zbiorze
D
−
π
2
,
π
2
E
jest r´o˙znowarto´sciowa, a zatem na tym zbiorze istnieje funkcja do niej odwrotna.
Podobnie inne funkcje trygonometryczne sa, r´o˙znowarto´sciowe na pewnych prze-
dziaÃlach. Wobec tego istnieja, funkcje odwrotne do funkcji trygonometrycznych.
Funkcje te nazywamy funkcjami cyklometrycznymi lub koÃlowymi, a ich definicje
sa, naste,puja,ce.
Definicja 3.3.1.
Funkcje, odwrotna, do funkcji f(x) = sin x, x ∈
D
−
π
2
,
π
2
E
, nazywamy funkcja, arcus
sinus i piszemy f
−1
(x) = arcsin x, f
−1
:< −1, 1 >→
D
−
π
2
,
π
2
E
.
Funkcje, odwrotna, do funkcji f(x) = cos x, x ∈
D
0, π
E
, nazywamy funkcja, arcus
cosinus i piszemy f
−1
(x) = arccos x, f
−1
:< −1, 1 >→
D
0, π
E
.
Funkcje, odwrotna, do funkcji f(x) = tgx, x ∈
³
−
π
2
,
π
2
´
, nazywamy funkcja, arcus
tangens i piszemy f
−1
(x) = arctgx, f
−1
: R →
³
−
π
2
,
π
2
´
.
Funkcje, odwrotna, do funkcji f(x) = ctgx, x ∈ (0, π), nazywamy funkcja, arcus
cotangens i piszemy f
−1
(x) = arcctgx, f
−1
: R → (0, π).
31

Podamy teraz definicje, funkcji hiperbolicznych.
Definicja 3.3.2.
Funkcje, sinus hiperboliczny okre´slamy wzorem
sinh x =
e
x
− e
−x
2
, x ∈ R.
Funkcje, cosinus hiperboliczny okre´slamy wzorem
cosh x =
e
x
+ e
−x
2
, x ∈ R.
Funkcje, tangens hiperboliczny okre´slamy wzorem
tghx =
sinh x
cosh x
=
e
x
− e
−x
e
x
+ e
−x
, x ∈ R.
Funkcje, cotangens hiperboliczny okre´slamy wzorem
ctghx =
cosh x
sinh x
=
e
x
+ e
−x
e
x
− e
−x
, x ∈ R \ {0}.
32

3.4. Granica i cia,gÃlo´s´c funkcji jednej zmiennej.
W paragrafie tym podamy r´ownowa˙zne definicje Heinego i Cauch’ego granicy
funkcji wÃla´sciwej i niewÃla´sciwej w punkcie wÃla´sciwym oraz niewÃla´sciwym. Be,-
dziemy m´owi´c, ˙ze granica jest wÃla´sciwa, gdy be,dzie ona liczba, sko´nczona,, a nie-
wÃla´sciwa, gdy be,dzie r´owna niesko´nczono´sci.
Niech funkcja rzeczywista f zmiennej rzeczywistej x be,dzie okre´slona w pew-
nym sa,siedztwie S(x
0
, δ) punktu x
0
. ZakÃladamy, ˙ze funkcja f w punkcie x
0
mo˙ze
by´c lub nie by´c okre´slona.
Przypomnimy definicje, Heinego zwana, inaczej definicja, cia,gowa,, granicy wÃla-
´sciwej funkcji f w punkcie wÃla´sciwym x
0
.
Definicja 3.4.1. M´owimy, ˙ze funkcja f ma granice, wÃla´sciwa, g w punkcie wÃla´sci-
wym x
0
, je´sli dla ka˙zdego cia,gu {x
n
} o wyrazach nale˙za,cych do sa,siedztwa S(x
0
, δ)
i zbie˙znego do punktu x
0
cia,g {f(x
n
)} jest zbie˙zny do liczby g.
lim
x→x
0
f (x) = g ⇔
^
{x
n
}
h¡
{x
n
} ⊂ S(x
0
, δ) ∧ lim
n→∞
x
n
= x
0
¢
⇒ lim
n→∞
f (x
n
) = g
i
(3.4.1)
R´ownowa˙zna, definicje, granicy funkcji podaÃl inny matematyk Cauchy. Definicje, ta,
czasami nazywa sie, definicja, epsilonowa,.
Definicja 3.4.2. M´owimy, ˙ze funkcja f ma granice, wÃla´sciwa, g w punkcie wÃla´sci-
wym x
0
, je´sli dla ka˙zdego ε > 0 istnieje takie sa,siedztwo S(x
0
, δ), ˙ze dla ka˙zdego
x ∈ S(x
0
, δ) speÃlniona jest nier´owno´s´c | f (x) − g |< ε.
lim
x→x
0
f (x) = g ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
0 <| x − x
0
|< δ ⇒| f (x) − g |< ε
´
(3.4.2)
Wyka˙zemy teraz, ˙ze istotnie obie definicje sa, r´ownowa˙zne. ZaÃl´o˙zmy na pocza,tku,
˙ze zachodzi warunek (3.4.2) istnienia granicy funkcji. Niech cia,g {x
n
} speÃlnia
warunki (3.4.1). Poniewa˙z lim
n→∞
x
n
= x
0
, wie,c dla dowolnej liczby δ > 0 istnieje
taka liczba k, ˙ze
^
n>k
0 <| x
n
− x
0
|< δ.
Zatem z (3.4.2) otrzymujemy
| f (x
n
) − g |< ε.
33
Oznacza to, ˙ze granica, funkcji f w punkcie x
0
jest liczba g. Zatem pokazali´smy,
˙ze z definicji Cauchy’ego wynika definicja Heinego.
Aby wykaza´c implikacje, odwrotna, udowodnimy, ˙ze negacja warunku (3.4.2) z
definicji Cauchy’ego implikuje negacje, warunku (3.4.1) z definicji Heinego. Negacja
warunku (3.4.2) ma posta´c
_
ε>0
^
δ>0
_
x∈D
f
³
0 <| x − x
0
|< δ∧ | f (x) − g |≥ ε
´
.
Przyjmuja,c zatem δ =
1
n
mo˙zemy okre´sli´c cia,g {x
n
} argument´ow speÃlniaja,cych
nier´owno´sci
0 <| x
n
− x
0
|<
1
n
oraz
| f (x
n
) − g |≥ ε.
Cia,g {x
n
} jest wie,c cia,giem zbie˙znym do x
0
, ale cia,g odpowiadaja,cych mu warto´sci
funkcji {f (x
n
)} nie speÃlnia warunku (3.4.1). Zatem skoro z negacji warunku
(3.4.2) wynika negacja (3.4.1), to znaczy, ˙ze z definicji Heinego wynika definicja
Cauchy’ego.
PrzykÃlad 3.4.1. Udowodnimy, ˙ze je˙zeli x jest miara, Ãlukowa, ka,ta, to lim
x→0
sin x
x
= 1.
Poniewa˙z x → 0, wie,c wystarczy rozwa˙zy´c funkcje, f(x) =
sin x
x
w sa,siedztwie o
promieniu
π
2
punktu 0. Zauwa˙zmy ponadto, ˙ze funkcja f jest parzysta, gdy˙z
f (−x) =
sin(−x)
−x
=
− sin x
−x
=
sin x
x
= f (x). Ograniczymy zatem nasze rozwa˙zania
do prawostronnego sa,siedztwa punktu 0.
34
Na rysunku wida´c, ˙ze pole tr´ojka,ta OAP jest mniejsze od pola wycinka koÃlowego
OAP, a to zn´ow jest mniejsze od pola tr´ojka,ta OAT, czyli
1
2
r
2
sin x <
1
2
r
2
x <
1
2
r
2
tgx.
Wobec tego dla 0 < x <
π
2
mamy
0 < sin x < x < tgx.
Sta,d po podzieleniu wszystkich stron tych nier´owno´sci przez sin x otrzymujemy
1 <
sin x
x
<
1
cos x
,
a przechodza,c do odwrotno´sci mamy
cos x <
sin x
x
< 1.
Mno˙za,c przez −1, a naste,pnie dodaja,c do wszystkich stron 1 dostajemy
0 < 1 −
sin x
x
< 1 − cos x.
Poniewa˙z
1 − cos x = 2 sin
2
x
2
< 2 sin
x
2
< 2
x
2
= x,
wie,c ostatecznie mamy
0 < 1 −
sin x
x
< x.
Aby wykaza´c, ˙ze lim
x→0
sin x
x
= 1 zastosujemy definicje, Cauchy’ego granicy funkcji.
Niech wie,c ε be,dzie dowolna, liczba, dodatnia,. nale˙zy udowodni´c, ˙ze istnieje taka
liczba δ i˙z
^
x
0 <| x |< δ ⇒
¯
¯
¯
sin x
x
− 1
¯
¯
¯ < ε,
co na mocy wcze´sniejszych rozwa˙za´
n, zachodzi wtedy, gdy x < ε. Zatem liczba, δ,
kt´orej istnienie nale˙zaÃlo wykaza´c, jest δ = ε.
Z wylicze´
n zawartych w tym przykÃladzie otrzymujemy bardzo przydatne nie-
r´owno´sci
^
0<x<
π
2
0 < sin x < x < tgx,
35

^
x∈R
| sin x |≤| x | .
Podamy teraz definicje cia,gowe i epsilonowe granic niewÃla´sciwych w punktach
wÃla´sciwych.
Definicja 3.4.3. (Heinego) Powiemy, ˙ze funkcja f ma w punkcie wÃla´sciwym x
0
granice, niewÃla´sciwa, +∞, je´sli ka˙zdemu cia,gowi {x
n
} ⊂ S(x
0
, δ) zbie˙znemu do
punktu x
0
odpowiada cia,g warto´sci funkcji f(x
n
) rozbie˙zny do +∞.
lim
x→x
0
f (x) = +∞ ⇔
^
{x
n
}
h¡
{x
n
} ⊂ S(x
0
, δ) ∧ lim
n→∞
x
n
= x
0
¢
⇒ lim
n→∞
f (x
n
) = +∞
i
Definicja 3.4.4. (Heinego) Powiemy, ˙ze funkcja f ma w punkcie wÃla´sciwym x
0
granice, niewÃla´sciwa, −∞, je´sli ka˙zdemu cia,gowi {x
n
} ⊂ S(x
0
, δ) zbie˙znemu do
punktu x
0
odpowiada cia,g warto´sci funkcji f(x
n
) rozbie˙zny do −∞.
lim
x→x
0
f (x) = −∞ ⇔
^
{x
n
}
h¡
{x
n
} ⊂ S(x
0
, δ) ∧ lim
n→∞
x
n
= x
0
¢
⇒ lim
n→∞
f (x
n
) = −∞
i
Definicja 3.4.5. (Cauchy’ego). Powiemy, ˙ze funkcja f ma w punkcie wÃla´sci-
wym x
0
granice, niewÃla´sciwa, +∞, je´sli dla ka˙zdego ε > 0 istnieje takie sa,siedztwo
S(x
0
, δ), ˙ze dla ka˙zdego x ∈ S(x
0
, δ) speÃlniona jest nier´owno´s´c f (x) > ε.
lim
x→x
0
f (x) = +∞ ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
0 <| x − x
0
|< δ ⇒ f (x) > ε
´
Definicja 3.4.6. (Cauchy’ego). Powiemy, ˙ze funkcja f ma w punkcie wÃla´sci-
wym x
0
granice, niewÃla´sciwa, −∞, je´sli dla ka˙zdego ε > 0 istnieje takie sa,siedztwo
S(x
0
, δ), ˙ze dla ka˙zdego x ∈ S(x
0
, δ) speÃlniona jest nier´owno´s´c f (x) < ε.
lim
x→x
0
f (x) = −∞ ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
0 <| x − x
0
|< δ ⇒ f (x) < ε
´
Naste,pne definicje okre´slaja, poje,cie granicy funkcji w niesko´nczono´sci.
Definicja 3.4.7.
(Heinego) M´owimy, ˙ze funkcja f ma w punkcie niewÃla´sci-
wym +∞ granice, wÃla´sciwa, g, je´sli ka˙zdemu cia,gowi {x
n
} rozbie˙znemu do +∞
odpowiada cia,g warto´sci funkcji f(x
n
) zbie˙zny do g.
lim
x→+∞
f (x) = g ⇔
^
{x
n
}
h
lim
n→∞
x
n
= +∞ ⇒ lim
n→∞
f (x
n
) = g
i
36

Definicja 3.4.8.
(Heinego) M´owimy, ˙ze funkcja f ma w punkcie niewÃla´sci-
wym −∞ granice, wÃla´sciwa, g, je´sli ka˙zdemu cia,gowi {x
n
} rozbie˙znemu do −∞
odpowiada cia,g warto´sci funkcji f(x
n
) zbie˙zny do g.
lim
x→−∞
f (x) = g ⇔
^
{x
n
}
h
lim
n→∞
x
n
= −∞ ⇒ lim
n→∞
f (x
n
) = g
i
Definicja 3.4.9. (Cauchy’ego). M´owimy, ˙ze funkcja f ma w punkcie niewÃla´sci-
wym +∞ granice, wÃla´sciwa, g, je´sli dla ka˙zdego ε > 0 istnieje taka liczba δ, ˙ze dla
ka˙zdego argumentu x > δ speÃlniona jest nier´owno´s´c | f (x) − g |< ε.
lim
x→+∞
f (x) = g ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
x > δ ⇒| f (x) − g |< ε
´
Definicja 3.4.10. (Cauchy’ego). M´owimy, ˙ze funkcja f ma w punkcie niewÃla´sci-
wym −∞ granice, wÃla´sciwa, g, je´sli dla ka˙zdego ε > 0 istnieje taka liczba δ, ˙ze dla
ka˙zdego argumentu x < δ speÃlniona jest nier´owno´s´c | f (x) − g |< ε.
lim
x→−∞
f (x) = g ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
x < δ ⇒| f (x) − g |< ε
´
PrzykÃlad 3.4.2. Wyka˙zemy, ˙ze lim
x→+∞
³
1 +
1
x
´
x
= e. Z uwagi na to, ˙ze x → +∞
mo˙zemy zaÃlo˙zy´c i˙z x > 1. Niech n = Entx, w´owczas n ≤ x < n + 1. Sta,d mamy
1
n + 1
<
1
x
<
1
n
i w konsekwencji
³
1 +
1
n + 1
´
n
<
³
1 +
1
x
)
x
<
³
1 +
1
n
´
n+1
.
Zauwa˙zmy, ˙ze
lim
n→∞
a
n
= lim
n→∞
³
1 +
1
n + 1
´
n
= e
i
lim
n→∞
b
n
= lim
n→∞
³
1 +
1
n
´
n+1
= e.
Wobec tego dla dowolnej lizcby ε > 0 istnieje liczba δ > 0 taka, ˙ze
^
n>δ
| a
n
− e |< ε∧ | b
n
− e |< ε.
37

Zatem dla ka˙zdego x takiego, ˙ze x ≥ Entx = n > δ mamy
¯
¯
¯
³
1 +
1
x
)
x
− e
¯
¯
¯ < ε.
Tym samym wykazali´smy istnienie liczby δ, kt´ora wyste,puje w definicji Cauchy’ego
granicy w punkcie niewÃla´sciwym.
Zdefinujemy teraz granice niewÃla´sciwe funkcji w niesko´
nczono´sciach.
Definicja 3.4.11. (Heinego) Powiemy, ˙ze funkcja f ma w punkcie niewÃla´sciwym
+∞ granice, niewÃla´sciwa, +∞, je´sli ka˙zdemu cia,gowi {x
n
} rozbie˙znemu do +∞
odpowiada cia,g warto´sci funkcji f(x
n
) rozbie˙zny do +∞.
lim
x→+∞
f (x) = +∞ ⇔
^
{x
n
}
h
lim
n→∞
x
n
= +∞ ⇒ lim
n→∞
f (x
n
) = +∞
i
Definicja 3.4.12. (Heinego) Powiemy, ˙ze funkcja f ma w punkcie niewÃla´sciwym
−∞ granice, niewÃla´sciwa, +∞, je´sli ka˙zdemu cia,gowi {x
n
} rozbie˙znemu do −∞
odpowiada cia,g warto´sci funkcji f(x
n
) rozbie˙zny do +∞.
lim
x→−∞
f (x) = +∞ ⇔
^
{x
n
}
h
lim
n→∞
x
n
= −∞ ⇒ lim
n→∞
f (x
n
) = +∞
i
Definicja 3.4.13. (Heinego) Powiemy, ˙ze funkcja f ma w punkcie niewÃla´sciwym
+∞ granice, niewÃla´sciwa, −∞, je´sli ka˙zdemu cia,gowi {x
n
} rozbie˙znemu do +∞
odpowiada cia,g warto´sci funkcji f(x
n
) rozbie˙zny do −∞.
lim
x→+∞
f (x) = −∞ ⇔
^
{x
n
}
h
lim
n→∞
x
n
= +∞ ⇒ lim
n→∞
f (x
n
) = −∞
i
Definicja 3.4.14. (Heinego) Powiemy, ˙ze funkcja f ma w punkcie niewÃla´sciwym
−∞ granice, niewÃla´sciwa, −∞, je´sli ka˙zdemu cia,gowi {x
n
} rozbie˙znemu do −∞
odpowiada cia,g warto´sci funkcji f(x
n
) rozbie˙zny do −∞.
lim
x→−∞
f (x) = −∞ ⇔
^
{x
n
}
h
lim
n→∞
x
n
= −∞ ⇒ lim
n→∞
f (x
n
) = −∞
i
38

Definicja 3.4.15. (Cauchy’ego). Powiemy, ˙ze funkcja f ma w punkcie niewÃla´sci-
wym +∞ granice, niewÃla´sciwa, +∞, je´sli dla ka˙zdego ε > 0 istnieje taka liczba δ,
˙ze dla ka˙zdego argumentu x > δ speÃlniona jest nier´owno´s´c f (x) > ε.
lim
x→+∞
f (x) = +∞ ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
x > δ ⇒ f (x) > ε
´
Definicja 3.4.16. (Cauchy’ego). Powiemy, ˙ze funkcja f ma w punkcie niewÃla´sci-
wym −∞ granice, niewÃla´sciwa, +∞, je´sli dla ka˙zdego ε > 0 istnieje taka liczba δ,
˙ze dla ka˙zdego argumentu x < δ speÃlniona jest nier´owno´s´c f (x) > ε.
lim
x→−∞
f (x) = +∞ ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
x < δ ⇒ f (x) > ε
´
Definicja 3.4.17. (Cauchy’ego). Powiemy, ˙ze funkcja f ma w punkcie niewÃla´sci-
wym +∞ granice, niewÃla´sciwa, −∞, je´sli dla ka˙zdego ε > 0 istnieje taka liczba δ,
˙ze dla ka˙zdego argumentu x > δ speÃlniona jest nier´owno´s´c f (x) < ε.
lim
x→+∞
f (x) = −∞ ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
x > δ ⇒ f (x) < ε
´
Definicja 3.4.18. (Cauchy’ego). Powiemy, ˙ze funkcja f ma w punkcie niewÃla´sci-
wym −∞ granice, niewÃla´sciwa, −∞, je´sli dla ka˙zdego ε > 0 istnieje taka liczba δ,
˙ze dla ka˙zdego argumentu x < δ speÃlniona jest nier´owno´s´c f (x) < ε.
lim
x→−∞
f (x) = −∞ ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
x < δ ⇒ f (x) < ε
´
Niech teraz funkcja f be,dzie okre´slona przynajmniej na lewostronnym sa,siedztwie
punktu x
0
, tj. na zbiorze S
−
(x
0
) = (x
0
− δ, x
0
). Zdefinujemy granice lewostronne
funkcji f .
Definicja 3.4.19. (Heinego) M´owimy, ˙ze funkcja f ma w punkcie wÃla´sciwym x
0
granice, lewostronna, wÃla´sciwa, g, je´sli ka˙zdemu cia,gowi {x
n
} ⊂ S
−
(x
0
) zbie˙znemu
do x
0
odpowiada cia,g warto´sci funkcji f(x
n
) zbie˙zny do g.
lim
x→x
−
0
f (x) = g ⇔
^
{x
n
}
h¡
{x
n
} ⊂ S
−
(x
0
) ∧ lim
n→∞
x
n
= x
0
¢
⇒ lim
n→∞
f (x
n
) = g
i
Definicja 3.4.20. (Heinego) M´owimy, ˙ze funkcja f ma w punkcie wÃla´sciwym
x
0
granice, lewostronna, niewÃla´sciwa, +∞, je´sli ka˙zdemu cia,gowi {x
n
} ⊂ S
−
(x
0
)
zbie˙znemu do x
0
odpowiada cia,g warto´sci funkcji f(x
n
) rozbie˙zny do +∞.
lim
x→x
−
0
f (x) = +∞ ⇔
^
{x
n
}
h¡
{x
n
} ⊂ S
−
(x
0
) ∧ lim
n→∞
x
n
= x
0
¢
⇒ lim
n→∞
f (x
n
) = +∞
i
39

Definicja 3.4.21. (Heinego) M´owimy, ˙ze funkcja f ma w punkcie wÃla´sciwym
x
0
granice, lewostronna, niewÃla´sciwa, −∞, je´sli ka˙zdemu cia,gowi {x
n
} ⊂ S
−
(x
0
)
zbie˙znemu do x
0
odpowiada cia,g warto´sci funkcji f(x
n
) rozbie˙zny do −∞.
lim
x→x
−
0
f (x) = −∞ ⇔
^
{x
n
}
h¡
{x
n
} ⊂ S
−
(x
0
) ∧ lim
n→∞
x
n
= x
0
¢
⇒ lim
n→∞
f (x
n
) = −∞
i
Definicja 3.4.22. (Cauchy’ego). M´owimy, ˙ze funkcja f ma w punkcie wÃla´sciwym
x
0
granice, lewostronna, wÃla´sciwa, g, je´sli dla ka˙zdego ε > 0 istnieje taka liczba δ,
˙ze dla ka˙zdego argumentu x ∈ S
−
(x
0
) speÃlniona jest nier´owno´s´c | f (x) − g |< ε.
lim
x→x
−
0
f (x) = g ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
0 < x
0
− x < δ ⇒| f (x) − g |< ε
´
Definicja 3.4.23. (Cauchy’ego). M´owimy, ˙ze funkcja f ma w punkcie wÃla´sciwym
x
0
granice, lewostronna, niewÃla´sciwa, +∞, je´sli dla ka˙zdego ε > 0 istnieje taka liczba
δ, ˙ze dla ka˙zdego argumentu x ∈ S
−
(x
0
) speÃlniona jest nier´owno´s´c f (x) > ε.
lim
x→x
−
0
f (x) = +∞ ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
0 < x
0
− x < δ ⇒ f (x) > ε
´
Definicja 3.4.24. (Cauchy’ego). M´owimy, ˙ze funkcja f ma w punkcie wÃla´sciwym
x
0
granice, lewostronna, niewÃla´sciwa, −∞, je´sli dla ka˙zdego ε > 0 istnieje taka liczba
δ, ˙ze dla ka˙zdego argumentu x ∈ S
−
(x
0
) speÃlniona jest nier´owno´s´c f (x) < ε.
lim
x→x
−
0
f (x) = −∞ ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
0 < x
0
− x < δ ⇒ f (x) < ε
´
Je´sli funkcja f jest okre´slona przynajmniej na prawostronnym sa,siedztwie punktu
x
0
, tj. na zbiorze S
+
(x
0
) = (x
0
, x
0
+ δ), to granice prawostronne funkcji f defini-
ujemy w naste,puja,cy spos´ob.
Definicja 3.4.25. (Heinego) Powiemy, ˙ze funkcja f ma w punkcie wÃla´sciwym x
0
granice, prawostronna, wÃla´sciwa, g, je´sli ka˙zdemu cia,gowi {x
n
} ⊂ S
+
(x
0
) zbie˙znemu
do x
0
odpowiada cia,g warto´sci funkcji f(x
n
) zbie˙zny do g.
lim
x→x
+
0
f (x) = g ⇔
^
{x
n
}
h¡
{x
n
} ⊂ S
+
(x
0
) ∧ lim
n→∞
x
n
= x
0
¢
⇒ lim
n→∞
f (x
n
) = g
i
40

Definicja 3.4.26. (Heinego) Powiemy, ˙ze funkcja f ma w punkcie wÃla´sciwym
x
0
granice, prawostronna, niewÃla´sciwa, +∞, je´sli ka˙zdemu cia,gowi {x
n
} ⊂ S
+
(x
0
)
zbie˙znemu do x
0
odpowiada cia,g warto´sci funkcji f(x
n
) rozbie˙zny do +∞.
lim
x→x
+
0
f (x) = +∞ ⇔
^
{x
n
}
h¡
{x
n
} ⊂ S
+
(x
0
) ∧ lim
n→∞
x
n
= x
0
¢
⇒ lim
n→∞
f (x
n
) = +∞
i
Definicja 3.4.27. (Heinego) Powiemy, ˙ze funkcja f ma w punkcie wÃla´sciwym
x
0
granice, prawostronna, niewÃla´sciwa, −∞, je´sli ka˙zdemu cia,gowi {x
n
} ⊂ S
+
(x
0
)
zbie˙znemu do x
0
odpowiada cia,g warto´sci funkcji f(x
n
) rozbie˙zny do −∞.
lim
x→x
+
0
f (x) = −∞ ⇔
^
{x
n
}
h¡
{x
n
} ⊂ S
+
(x
0
) ∧ lim
n→∞
x
n
= x
0
¢
⇒ lim
n→∞
f (x
n
) = −∞
i
Definicja 3.4.28. (Cauchy’ego). Powiemy, ˙ze funkcja f ma w punkcie wÃla´sciwym
x
0
granice, prawostronna, wÃla´sciwa, g, je´sli dla ka˙zdego ε > 0 istnieje taka liczba δ,
˙ze dla ka˙zdego argumentu x ∈ S
+
(x
0
) speÃlniona jest nier´owno´s´c | f (x) − g |< ε.
lim
x→x
+
0
f (x) = g ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
0 < x − x
0
< δ ⇒| f (x) − g |< ε
´
Definicja 3.4.29. (Cauchy’ego). Powiemy, ˙ze funkcja f ma w punkcie wÃla´sci-
wym x
0
granice, prawostronna, niewÃla´sciwa, +∞, je´sli dla ka˙zdego ε > 0 istnieje
taka liczba δ, ˙ze dla ka˙zdego argumentu x ∈ S
+
(x
0
) speÃlniona jest nier´owno´s´c
f (x) > ε.
lim
x→x
+
0
f (x) = +∞ ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
0 < x − x
0
< δ ⇒ f (x) > ε
´
Definicja 3.4.30. (Cauchy’ego). Powiemy, ˙ze funkcja f ma w punkcie wÃla´sci-
wym x
0
granice, prawostronna, niewÃla´sciwa, −∞, je´sli dla ka˙zdego ε > 0 istnieje
taka liczba δ, ˙ze dla ka˙zdego argumentu x ∈ S
+
(x
0
) speÃlniona jest nier´owno´s´c
f (x) < ε.
lim
x→x
+
0
f (x) = −∞ ⇔
^
ε>0
_
δ>0
^
x∈D
f
³
0 < x − x
0
< δ ⇒ f (x) < ε
´
W dalszej cze,´sci tego paragrafu okre´slimy dziaÃlania na granicach funkcji. Najpierw
jednak znajdziemy zwia,zek mie,dzy istnieniem granicy, a ograniczono´scia, funkcji.
41
Twierdzenie 3.4.1. Je˙zeli funkcja f ma w punkcie x
0
granice, sko´nczona,, to
istnieje sa,siedztwo punktu x
0
, w kt´orym funkcja f jest ograniczona.
Dow´
od. Niech lim
x→x
0
f (x) = g i niech ε > 0 be,dzie obrane dowolnie. Wtedy z
definicji Cauchego granicy funkcji mamy
_
δ>0
^
x∈S(x
0
,δ)
| f (x) − g |< ε.
Sta,d otrzymujemy
g − ε < f (x) < g + ε.
Oznacza to, ˙ze funkcja f jest ograniczona na sa,siedztwie S(x
0
, δ).
Twierdzenie 3.4.2. Je˙zeli funkcje f i g sa, okre´slone w pewnym sa,siedztwie
punktu x
0
i maja, w punkcie x
0
granice wÃla´sciwe, to suma, r´o˙znica i iloczyn tych
funkcji maja, granice wÃla´sciwe oraz
1. lim
x→x
0
[f (x) + g(x)] = lim
x→x
0
f (x) + lim
x→x
0
g(x),
2. lim
x→x
0
[f (x) − g(x)] = lim
x→x
0
f (x) − lim
x→x
0
g(x),
3. lim
x→x
0
[f (x) · g(x)] = lim
x→x
0
f (x) · lim
x→x
0
g(x).
Je´sli ponadto lim
x→x
0
g(x) 6= 0, to iloraz
f
g
jest okre´slony w pewnym sa,siedztwie
punktu x
0
oraz
4. lim
x→x
0
f (x)
g(x)
=
lim
x→x
0
f (x)
lim
x→x
0
g(x)
.
Dow´
od. Niech lim
x→x
0
f (x) = a i lim
x→x
0
f (x) = b oraz niech ε > 0 be,dzie dowolne.
Istnieje w´owczas taka liczba δ > 0, ˙ze
^
x∈S(x
0
,δ)
| f (x) − a |<
ε
2
oraz
^
x∈S(x
0
,δ)
| g(x) − b |<
ε
2
.
Aby dowie´s´c r´owno´sci 1 korzystamy z nier´owno´sci tr´ojka,ta i otrzymujemy
| [f (x) + g(x)] − [a + b] |≤| f (x) − a | + | g(x) − b |<
ε
2
+
ε
2
< ε.
Oznacza to, ˙ze granica, funkcji f + g jest liczba a + b
Podobnie wykorzystuja,c odpowiednia, wÃla´sciwo´s´c warto´sci bezwzgle,dnej ma-
my
| [f (x) − g(x)] − [a − b] |≤| f (x) − a | + | g(x) − b |<
ε
2
+
ε
2
< ε.
42
Co dowodzi sÃluszno´sci r´owno´sci 2.
Udowodnimy teraz punkt 3. Zauwa˙zmy, ˙ze
| f (x)g(x) − ab |=| f (x)g(x) − ag(x) + ag(x) − ab |
=| g(x)[f (x) − a] + a[g(x) − b] |≤| g(x) || f (x) − a | + | a || g(x) − b | .
Z twierdzenia 3.4.1. mamy
_
M >0
| g(x) |< M
przy czym staÃla, M mo˙zna dobra´c tak aby | a |< M.
Ponadto
lim
x→x
0
f (x) = a ⇔
^
ε>0
_
δ
^
x∈S(x
0
,δ)
| f (x) − a |<
ε
2M
oraz
lim
x→x
0
g(x) = b ⇔
^
ε>0
_
δ
^
x∈S(x
0
,δ)
| g(x) − b |<
ε
2M
.
Zatem otrzymujemy
| f (x)g(x) − ab |< M
ε
2M
+ M
ε
2M
= ε,
co na mocy definicji granicy Cauchy’ego oznacza, ˙ze granica, funkcji f · g jest a · b,
a to nale˙zaÃlo wykaza´c.
Dowodza,c punkt 4, zauwa˙zmy, ˙ze
¯
¯
¯
f (x)
g(x)
−
a
b
¯
¯
¯ =
¯
¯
¯
f (x)b − g(x)a
g(x)b
¯
¯
¯
=
¯
¯
¯
f (x)b − ab + ab − g(x)a
g(x)b
¯
¯
¯ =
¯
¯
¯
b[f (x) − a] + a[b − g(x)]
g(x)b
¯
¯
¯
≤
¯
¯
¯
b[f (x) − a] + a[b − g(x)]
g(x)b
¯
¯
¯.
Poniewa˙z funkcje f i g maja, granice wÃla´sciwe, to zachodza, naste,puja,ce nier´owno´sci
lim
x→x
0
f (x) = a ⇔
^
ε>0
_
δ
^
x∈S(x
0
,δ)
| f (x) − a |<
εk
2
oraz
lim
x→x
0
g(x) = a ⇔
^
ε>0
_
δ
^
x∈S(x
0
,δ)
| g(x) − b |<
εk
2 | a |
.
43
Ponadto niech inf | g(x) · b |= k > 0. Zatem mamy
¯
¯
¯
f (x)
g(x)
−
a
b
¯
¯
¯ <
εk
2
1
k
+
εk
2 | a |
| a |
k
= ε.
Dowodzi to r´owno´sci 4.
Powy˙zsze twierdzenie jest r´ownie˙z prawdziwe dla granic jednostronnych w
punkcie x
0
oraz w przypadku , gdy punkt x
0
jest niewÃla´sciwy.
Twierdzenie 3.4.2 dotyczy dziaÃla´
n arytmetycznych na granicach wÃla´sciwych
funkcji. W przypadku, gdy mamy do czynienia z granicami niewÃla´sciwymi mo˙zemy
posÃlu˙zy´c sie, naste,puja,ca, tabelka,.
Je˙zeli
to
lim
x→x
0
f (x) = 0
+
lim
x→x
0
1
f (x)
= +∞
lim
x→x
0
f (x) = 0
−
lim
x→x
0
1
f (x)
= −∞
lim
x→x
0
f (x) = ±∞
lim
x→x
0
1
f (x)
= 0
lim
x→x
0
f (x) = ±∞
lim
x→x
0
(f (x) · g(x)) = ±∞
lim
x→x
0
g(x) = b > 0
lim
x→x
0
f (x) = ±∞
lim
x→x
0
(f (x) · g(x)) = ∓∞
lim
x→x
0
g(x) = b < 0
lim
x→x
0
f (x) = ±∞
lim
x→x
0
(f (x) · g(x)) = [0 · ∞] =?
lim
x→x
0
g(x) = 0
lim
x→x
0
f (x) = ±∞
lim
x→x
0
(f (x) · g(x)) = [0 · ∞] =?
lim
x→x
0
g(x) = 0
44

lim
x→x
0
(f (x) · g(x)) = +∞
lim
x→x
0
(f (x) + g(x)) = +∞
lim
x→x
0
f (x) = lim
x→x
0
g(x) = +∞
lim
x→x
0
(f (x) − g(x)) = [∞ − ∞] =?
lim
x→x
0
f (x)
g(x)
=
£
∞
∞
¤
=?
lim
x→x
0
(f (x) · g(x)) = +∞
lim
x→x
0
(f (x) + g(x)) = −∞
lim
x→x
0
f (x) = lim
x→x
0
g(x) = −∞
lim
x→x
0
(f (x) − g(x)) = [∞ − ∞] =?
lim
x→x
0
f (x)
g(x)
=
£
∞
∞
¤
=?
V
x
| f (x) |< M,
lim
x→x
0
g(x) = 0
+
lim
x→x
0
f (x)
g(x)
= +∞
V
x
| f (x) |< M,
lim
x→x
0
g(x) = 0
−
lim
x→x
0
f (x)
g(x)
= −∞
V
x
| f (x) |< M,
lim
x→x
0
g(x) = ±∞
lim
x→x
0
f (x)
g(x)
= 0
lim
x→x
0
f (x) = lim
x→x
0
g(x) = 0
lim
x→x
0
f (x)
g(x)
=
£
0
0
i
=?
Analogiczne relacje zachodza, dla granic niewÃla´sciwych w punktach niewÃla´sci-
wych oraz dla granic jednostronnych.
Twierdzenie 3.4.3.
(granica funkcji zÃlo˙zonej) Je˙zeli funkcje f i g speÃlniaja,
warunki
1. lim
x→x
0
f (x) = y
0
,
2.
V
x∈S(x
0
,δ)
f (x) 6= y
0
,
3. lim
y→y
0
g(y) = q,
to lim
x→x
0
g(f (x)) = q.
Dow´
od. W dowodzie tego twierdzenia skorzystamy z definicji Heinego granicy
funkcji. Z zaÃlo˙ze´
n wynika, ˙ze
_
δ>0
^
{x
n
}
h¡
{x
n
} ⊂ S(x
0
, δ) ∧ lim
n→∞
x
n
= x
0
¢
⇒ lim
n→∞
f (x
n
) = y
0
i
(3.4.3)
_
δ>0
^
{y
n
}
h¡
{y
n
} ⊂ S(y
0
, δ) ∧ lim
n→∞
y
n
= y
0
¢
⇒ lim
n→∞
g(y
n
) = q
i
.
(3.4.4)
45
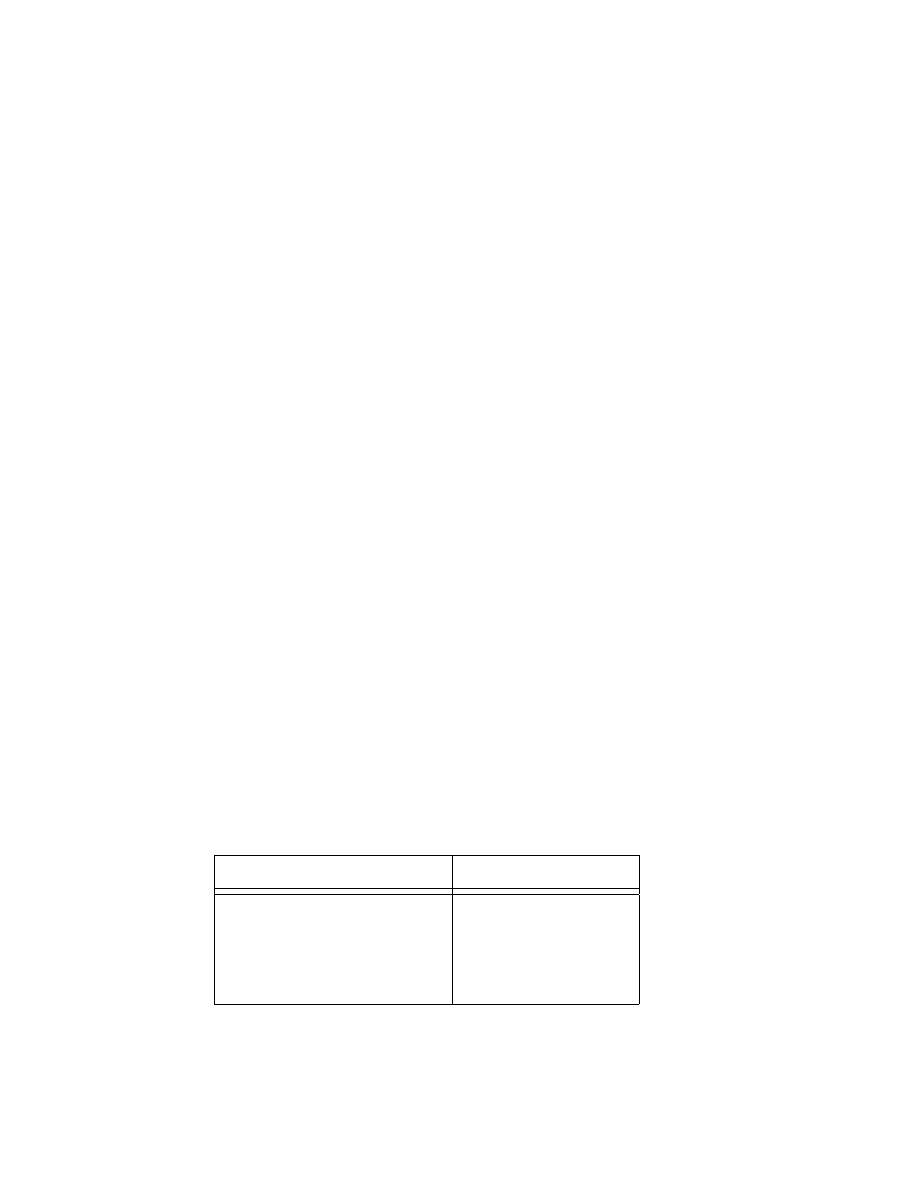
Nale˙zy wykaza´c, ˙ze
_
δ>0
^
{x
n
}
h¡
{x
n
} ⊂ S(x
0
, δ) ∧ lim
n→∞
x
n
= x
0
¢
⇒ lim
n→∞
g(f (x
n
)) = q
i
.
Niech wie,c {x
n
} be,dzie dowolnym cia,giem speÃlniaja,cym warunki
_
δ>0
{x
n
} ⊂ S(x
0
, δ)
lim
n→∞
x
n
= x
0
.
Wtedy korzystaja,c z (3.4.3) i przyjmuja,c w (3.4.4) y
n
= f (x
n
) otrzymamy, ˙ze
lim
n→∞
y
n
= y
0
, przy czym
V
n
y
n
6= y
0
. Zatem
lim
n→∞
g(f (x
n
)) = lim
n→∞
g(y
n
) = q.
Co ko´
nczy dow´od.
Twierdzenie 3.4.4. Je˙zeli funkcje f i g maja, w punkcie x
0
granice wÃla´sciwe, to
lim
x→x
0
h
f (x)
i
g(x)
=
h
lim
x→x
0
f (x)
i lim
x→x0
g(x)
.
Dow´
od. Twierdzenie to wynika z naste,puja,cego faktu
h
f (x)
i
g(x)
= e
g(x) ln f (x)
oraz z tego, ˙ze
lim
x→x
0
e
x
= e
x
0
.
Oczywi´scie powy˙zsze twierdzenia zachodza, r´ownie˙z w przypadku, gdy punkt x
0
jest niewÃla´sciwy oraz dla granic jednostronnych. W przypadku, gdy funkcje f i
g maja, granice niewÃla´sciwe zachodzi´c moga, przypadki om´owione w naste,puja,cej
tabeli.
Je˙zeli
to
lim
x→x
0
f (x) = a, 0 < a < 1
lim
x→x
0
h
f (x)
i
g(x)
= 0
lim
x→x
0
g(x) = +∞
46

lim
x→x
0
f (x) = a, a > 1
lim
x→x
0
h
f (x)
i
g(x)
= +∞
lim
x→x
0
g(x) = +∞
lim
x→x
0
f (x) = a, 0 < a < 1
lim
x→x
0
h
f (x)
i
g(x)
= +∞
lim
x→x
0
g(x) = −∞
lim
x→x
0
f (x) = a, a > 1
lim
x→x
0
h
f (x)
i
g(x)
= 0
lim
x→x
0
g(x) = −∞
lim
x→x
0
f (x) = 1
lim
x→x
0
h
f (x)
i
g(x)
= [1
∞
] =?
lim
x→x
0
g(x) = ±∞
lim
x→x
0
f (x) = ∞
lim
x→x
0
h
f (x)
i
g(x)
= 0
lim
x→x
0
g(x) = a, −∞ ≤ a < 0
lim
x→x
0
f (x) = ∞
lim
x→x
0
h
f (x)
i
g(x)
= ∞
lim
x→x
0
g(x) = a, 0 < a ≤ +∞
lim
x→x
0
f (x) = ∞
lim
x→x
0
h
f (x)
i
g(x)
= [∞
0
] =?
lim
x→x
0
g(x) = 0
lim
x→x
0
f (x) = 0
lim
x→x
0
h
f (x)
i
g(x)
= [0
0
] =?
lim
x→x
0
g(x) = 0
47

Kolejne twierdzenia, kt´ore podamy bez dowodu, dotycza, pewnych u˙zytecz-
nych w praktyce wÃlasno´sci granic funkcji.
Twierdzenie 3.4.5. (warunek konieczny i dostateczny istnienia granicy) Funkcja
f ma w punkcie x
0
granice, wÃla´sciwa, (niewÃla´sciwa,) g wtedy i tylko wtedy, gdy
istnieja, w tym punkcie granice jednostronne wÃla´sciwe (niewÃla´sciwe) i sa, sobie
r´owne, tj.
h
lim
x→x
+
0
f (x) = g ∧ lim
x→x
−
0
f (x) = g
i
⇔ lim
x→x
0
f (x) = g.
Oczywi´scie z tego twierdzenia wynika, ˙ze je´sli granice jednostronne w punkcie x
0
sa, r´o˙zne to w tym punkcie funkcja nie ma granicy.
Twierdzenie 3.4.6. (o trzech funkcjach) Je˙zeli funkcje f , g i h speÃlniaja, naste,-
puja,ce warunki
1.
W
δ>0
V
x∈S(x
0
,δ)
f (x) ≤ g(x) ≤ h(x),
2. lim
x→x
0
f (x) = lim
x→x
0
h(x) = g,
to lim
x→x
0
g(x) = g.
Twierdzenie 3.4.7. (o dw´och funkcjach) Je˙zeli funkcje f i g speÃlniaja, naste,puja,ce
warunki
1.
W
δ>0
V
x∈S(x
0
,δ)
f (x) ≤ g(x),
2. lim
x→x
0
f (x) = ∞,
to lim
x→x
0
g(x) = ∞.
Je˙zeli natomiast funkcje f i g speÃlniaja, warunki
1.
W
δ>0
V
x∈S(x
0
,δ)
f (x) ≤ g(x),
2. lim
x→x
0
g(x) = −∞,
to lim
x→x
0
f (x) = −∞.
Twierdzenia 3.4.6 i 3.4.7 zachodza, r´ownie˙z dla granic jednostronnych i w
przypadku, gdy punkt x
0
jest niewÃla´sciwy.
Zadanie 3.4.1.
Narysowa´c przykÃladowe wykresy funkcji f : R → R, kt´ore
speÃlniaja, jednocze´snie wszystkie podane warunki
a) lim
x→−∞
f (x) = −2, lim
x→1
f (x) = 3, lim
x→+∞
f (x) = 0;
b) lim
x→−∞
f (x) = −∞, lim
x→0
−
f (x) = 0, lim
x→0
+
f (x) = −∞, lim
x→+∞
f (x) = 4;
c) lim
x→−∞
f (x) = 1,
lim
x→(−2)
f (x) = −∞, lim
x→+∞
f (x) = −1;
48
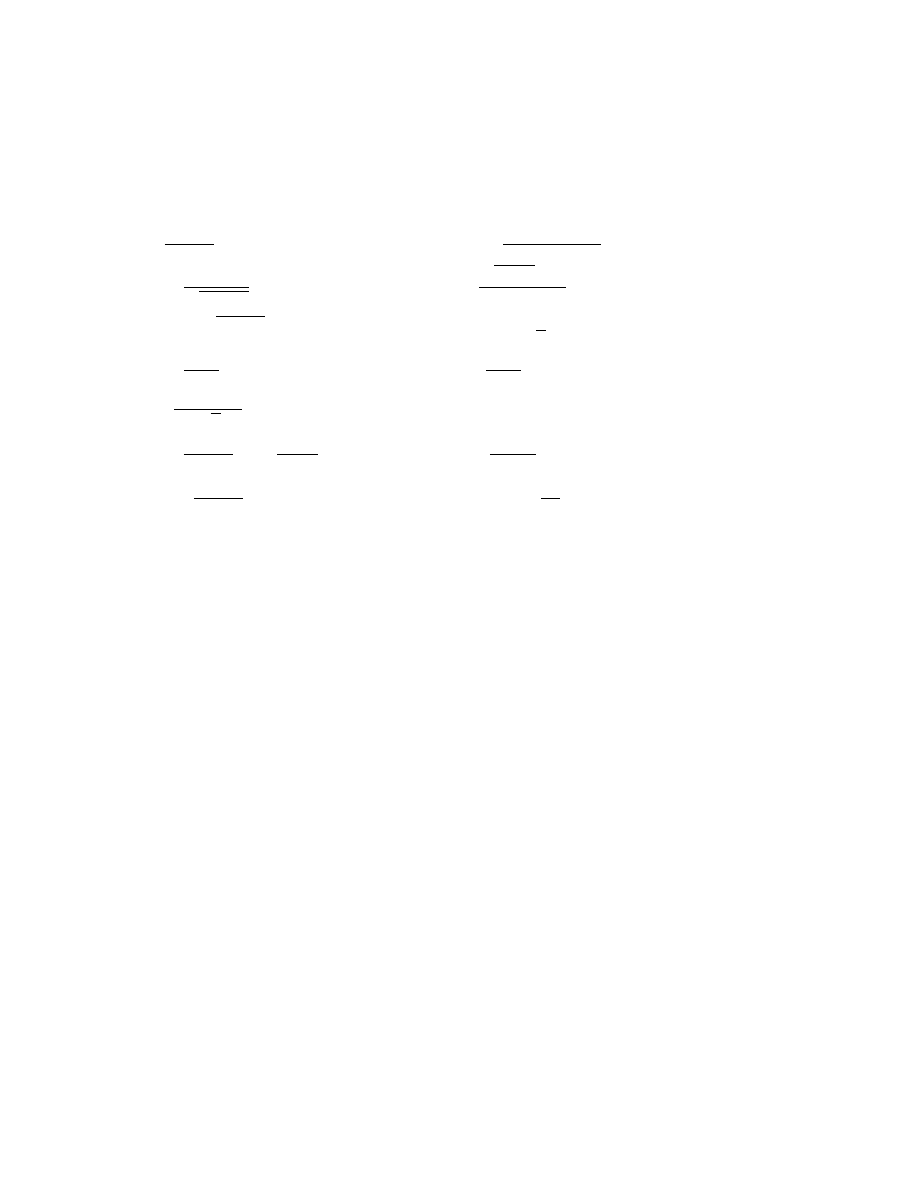
d) lim
x→−∞
f (x) = 0, lim
x→2
−
f (x) = +∞, lim
x→2
+
f (x) = −∞, lim
x→+∞
f (x) = 7.
Zadanie 3.4.2. Oblicz podane granice
a) lim
x→1
x
3
− 1
x
4
− 1
,
h) lim
x→+∞
2 · 5
x
− 2
x
4 · 3
x
+ 5
x+1
,
b) lim
x→−∞
x
√
x
2
+ 1
,
i) lim
x→5
√
x − 1 − 2
x − 5
,
c) lim
x→+∞
x
¡p
x
2
+ 1 − x
¢
,
j) lim
x→+∞
x sin
1
x
,
d) lim
x→+∞
sin x
x
,
k) lim
x→π
sin x
x
,
e) lim
x→0
+
2 + cos x
√
x
,
l) lim
x→+∞
¡
sin 2x − e
x
¢
,
f ) lim
x→1
+
³ x
2
− 1
x − 1
+ ln
1
x − 1
´
,
Ãl) lim
x→0
−
cos 2x
sin
2
x
,
g) lim
x→+∞
³ x
2
+ 5
x
2
− 7
´
x
2
+1
,
m) lim
x→0
−
arctg
1
x
2
.
Przejdziemy teraz do om´owienia poje,cia cia,gÃlo´sci funkcji rzeczywistej jednej
zmiennej rzeczywistej.
ZaÃl´o˙zmy, ˙ze funkcja f jest okre´slona na otoczeniu punktu x
0
.
Definicja 3.4.31. M´owimy, ˙ze funkcja f jest cia,gÃla w punkcie x
0
, je´sli granica
funkcji w punkcie x
0
jest r´owna warto´sci funkcji w tym punkcie, tj. je´sli
lim
x→x
0
f (x) = f (x
0
).
W sensie definicji Heinego cia,gÃlo´s´c funkcji w punkcie x
0
oznacza, ˙ze
^
{x
n
}
h¡
{x
n
} ⊂ S(x
0
, δ) ∧ lim
n→∞
x
n
= x
0
¢
⇒ lim
n→∞
f (x
n
) = f (x
0
)
i
.
Natomiast w sensie definicji Cauchy’ego mamy: funkcja f jest cia,gÃla w punkcie x
0
wtedy i tylko wtedy, gdy
^
ε>0
_
δ>0
^
x∈D
f
³
0 <| x − x
0
|< δ ⇒| f (x) − f (x
0
) |< ε
´
.
W szczeg´olno´sci je´sli granica w powy˙zszej definicji jest jednostronna, to mo˙zemy
m´owi´c o cia,gÃlo´sci jednostronnej.
49

Definicja 3.4.32. Funkcja f jest cia,gÃla lewostronnie w punkcie x
0
wtedy i tylko
wtedy, gdy
lim
x→x
−
0
f (x) = f (x
0
).
Definicja 3.4.33. Funkcja f jest cia,gÃla prawostronnie w punkcie x
0
wtedy i tylko
wtedy, gdy
lim
x→x
+
0
f (x) = f (x
0
).
Twierdzenie 3.4.8. (warunek konieczny i dostateczny cia,gÃlo´sci funkcji w punk-
cie) Niech funkcja f be,dzie okre´slona przynajmniej na otoczeniu punktu x
0
. Funk-
cja f jest cia,gÃla w punkcie x
0
wtedy i tylko wtedy, gdy jest lewostronnie i pra-
wostronnie cia,gÃla w tym punkcie.
Definicja 3.4.34. Powiemy, ˙ze funkcja f jest cia,gÃla na zbiorze A je´sli jest ona
cia,gÃla w ka˙zdym punkcie tego zbioru.
PrzykÃlad 3.4.4. Wszystkie funkcje elementarne sa, cia,gÃle w swoich dziedzinach.
Ponadto funkcja staÃla jest funkcja, cia,gÃla, w caÃlej swojej dziedzinie.
Twierdzenie 3.4.9. Je˙zeli funkcje f i g sa, cia,gÃle w punkcie x
0
, to cia,gÃle sa, w
tym punkcie r´ownie˙z funkcje f + g, f − g, f · g i
f
g
, o ile g(x
0
) 6= 0.
Twierdzenie 3.4.10. Je˙zeli funkcja f jest cia,gÃla w punkcie x
0
i funkcja g jest
cia,gÃla w punkcie y
0
= f (x
0
), to funkcja zÃlo˙zona g ◦ f jest cia,gÃla w punkcie x
0
.
PrzykÃlad 3.4.5. Sko´
nczone sumy, r´o˙znice, iloczyny, jak r´ownie˙z iloraz funkcji
elementarnych sa, funkcjami cia,gÃlymi.
Twierdzenie 3.4.11. Je˙zeli funkcja f jest cia,gÃla i monotoniczna na przedziale
< a, b >, to funkcja odwrotna f
−1
jest cia,gÃla i monotoniczna na przedziale
f (a), f (b)
®
.
Oczywiste jest, ˙ze istnieja, funkcje niecia,gÃle w pewnych punktach lub na
pewnych zbiorach.
PrzykÃlad 3.4.6. Funkcja dana wzorem
f (x) =
½
x, dla x 6= 0,
1,
dla x = 0
(3.4.5)
50

jest niecia,gÃla w punkcie 0.
PrzykÃlad 3.4.7.
Zauwa˙zmy, ˙ze funkcja Dirichleta nie jest cia,gÃla w ˙zadnym
punkcie swojej dziedziny. Jest ona jednak cia,gÃla na zbiorze liczb wymiernych.
Funkcja Ent jest tylko prawostronnie cia,gÃla w ka˙zdym punkcie be,da,cym liczba,
caÃlkowita,. Natomiast funkcja sgn jest funkcja, cia,gÃla, w caÃlej swojej dziedzinie z
wyja,tkiem punktu 0.
Powy˙zsze przykÃlady sugeruja,, ˙ze mo˙zna m´owi´c o wielu rodzajach niecia,gÃlo´sci
funkcji.
Definicja 3.4.35. Funkcja f ma niecia,gÃlo´s´c pierwszego rodzaju, je´sli istnieja,
granice jednostronne w punkcie x
0
r´o˙zne od warto´sci funkcji w tym punkcie, tj.
je´sli
lim
x→x
+
0
f (x) = g
1
6= f (x
0
) ∧
lim
x→x
−
0
f (x) = g
2
6= f (x
0
).
W szczeg´olno´sci, gdy lim
x→x
+
0
f (x) 6= lim
x→x
−
0
f (x), to m´owimy, ˙ze funkcja f ma niecia,g-
Ãlo´s´c pierwszego rodzaju typu ”skok”. Je´sli za´s lim
x→x
+
0
f (x) = lim
x→x
−
0
f (x), to powiemy,
˙ze funkcja f ma niecia,gÃlo´s´c pierwszego rodzaju typu ”luka”.
Definicja 3.4.36. Funkcja f ma niecia,gÃlo´s´c drugiego rodzaju, je´sli co najmniej
jedna z granic jednostronnych w punkcie x
0
nie istnieje lub jest niewÃla´sciwa.
PrzykÃlad 3.4.6. Funkcja sgn w punkcie 0 ma niecia,gÃlo´s´c pierwszgo rodzaju typu
”skok”.
Funkcja dana wzorem (3.4.5) ma w punkcie 0 niecia,gÃlo´s´c pierwszgo rodzaju
typu ”luka”.
Funkcja f (x) =
1
x
w punkcie 0 ma niecia,gÃlo´s´c drugiego rodzaju.
Zadanie 3.4.3. Zbadaj cia,gÃlo´s´c podanych funkcji
a)f (x) =
x
2
− 1
| x − 1 |
, dla x 6= 1,
−2,
dla x = 1,
b)f (x) =
x
2
cos
1
x
, dla x > 0,
0,
dla x = 0,
e
1
x
,
dla x < 0,
c)f (x) =
½
7x − 2, dla x ≤ 1,
x
2
,
dla x > 1,
51

d)f (x) =
1
1 + e
1
x
, dla x 6= 0,
0,
dla x = 0,
e)f (x) =
sin x
x
,
dla x < 0,
0,
dla x = 0,
2
x
− 1
x
, dla x > 0.
Zadanie 3.4.4. Wyznaczy´c parametry a i b tak, aby podane funkcje byÃly cia,gÃle.
a)f (x) =
( sin x
ax
, dla x < 0,
x + b, dla x ≥ 0,
b)f (x) =
½
x,
dla | x |≤ 1,
x
2
+ ax + b, dla | x |> 1.
3.5. WÃlasno´sci funkcji cia,gÃlych w przedziaÃlach domknie,tych.
W paragrafie tym wymienimy kilka u˙zytecznych wÃlasno´sci funkcji cia,gÃlych, na
kt´ore w dalszym cia,gu be,dziemy sie, powoÃlywa´c.
1. Je˙zeli istnieje granica wÃla´sciwa funkcji f w punkcie x
0
i funkcja g jest cia,gÃla w
punkcie y
0
= lim
x→x
0
f (x), to
lim
x→x
0
g[f (x)] = g[ lim
x→x
0
f (x)].
WÃlasno´s´c ta ma r´ownie˙z miejsce w przypadku granic jednostronnych oraz granic
w punktach niewÃla´sciwych.
2. Je˙zeli funkcja f jest cia,gÃla w punkcie x
0
oraz f (x
0
) > 0, to istnieje takie
otoczenie punktu x
0
, ˙ze dla ka˙zdego x ∈ O(x
0
, δ) ∩ D
f
speÃlniona jest nier´owno´s´c
f (x) > 0.
3. Je˙zeli funkcja f jest cia,gÃla w punkcie x
0
oraz f (x
0
) < 0, to istnieje takie
otoczenie punktu x
0
, ˙ze dla ka˙zdego x ∈ O(x
0
, δ) ∩ D
f
speÃlniona jest nier´owno´s´c
f (x) < 0.
4. Je˙zeli funkcja f jest cia,gÃla na przedziale domknie,tym < a, b >, to
a) funkcja f jest ograniczona na przedziale < a, b >,
b)
W
c
1
,c
2
f (c
1
) = inf{f (x) : a ≤ x ≤ b} ∧ f (c
2
) = sup{f (x) : a ≤ x ≤ b}.
Powy˙zsza, wÃlasno´s´c udowodniÃl w XVIII wieku niemiecki matematyk Karl
Weierstrass i dlatego znana jest ona jako twierdzenie Weierstrassa. Maja,c na
52

my´sli te, wÃlasno´s´c mo˙zemy powiedzie´c, ˙ze funkcja cia,gÃla na przedziale domknie,tym
osia,ga swoje kresy, tj. osia,ga kres dolny i kres g´orny zbioru swoich warto´sci.
5. Je˙zeli funkcja f jest cia,gÃla na przedziale < a, b > oraz speÃlnia warunek f(a) <
f (b), to
^
y∈
¡
f (a),f (b)
¢
_
c∈(a,b)
f (c) = y.
WÃlasno´s´c ta znana jest jako twierdzenie Darboux.
Je˙zeli dodatkowo zaÃlo˙zymy, ˙ze funkcja f jest rosna,ca, to punkt c jest wyzna-
czony jednoznacznie.
Analogiczna, wÃlasno´s´c mamy w przypadku, gdy f(a) > f(b). W´owczas punkt
c jest wyznaczony jednoznacznie dla maleja,cej funkcji f.
6.
Je˙zeli funkcja f jest cia,gÃla na przedziale < a, b > oraz speÃlnia warunek
f (a)f (b) < 0, to
_
c∈(a,b)
f (c) = 0.
WÃlasno´s´c ta wynika z twierdzenia Daboux.
Je˙zeli dodatkowo funkcja f jest monotoniczna, to punkt c wyznaczony jest
jednoznacznie.
WÃlasno´s´c ta, mo˙zemy wykorzysta´c do wyznaczenia miejsc zerowych funkcji f.
PrzykÃlad 3.5.1. Rozwa˙zmy funkcje, f(x) = e
2x
2
+x
−
2
x
. Funkcja ta jest funkcja,
cia,gÃla, na przedziale
D
1
2
, 1
E
, poniewa˙z jest r´o˙znica, funkcji cia,gÃlych. Zauwa˙zmy, ˙ze
f
³ 1
2
´
= e − 4 < 0,
f (1) = e
3
− 2 > 0.
Zatem f
³
1
2
´
· f (1) < 0. Z wÃlasno´sci 6 wynika wie,c, ˙ze istnieje w przedziale
³
1
2
, 1
´
taki punkt c, ˙ze
e
2x
2
+x
−
2
x
= 0.
Wobec tego r´ownanie e
2x
2
+x
−
2
x
= 0 w przedziale
³
1
2
, 1
´
ma co najmniej jeden
pierwiastek.
53

4. RACHUNEK R ´
O ˙ZNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ.
W rozdziale tym zdefinujemy pojecie pochodnej funkcji rzeczywistej jednej
zmiennej rzeczywistej. Naste,pnie podamy zwia,zki mie,dzy wÃlasno´sciami pochodnej
funkcji, a zachowaniem sie, samej funkcji, jak r´ownie˙z kilka u˙zytecznych zastosowa´n
rachunku pochodnych.
4.1. Pochodna i r´
o˙zniczka rze,du n ≥ 1.
Niech funkcja f be,dzie okre´slona w pewnym otoczeniu punktu x
0
. Symbolem ∆x
oznacza´c be,dziemy przyrost argumentu x funkcji f, tzn. ∆x = x−x
0
, x ∈ O(x
0
, δ).
Przyrostowi argumentu ∆x odpowiada przyrost warto´sci funkcji, kt´ory oznacza´c
be,dziemy przez ∆f(x), tzn. ∆f(x) = f(x
0
+ ∆x) − f (x
0
).
Definicja 4.1.1. Ilorazem r´o˙znicowym funkcji f w punkcie x
0
odpowiadaja,cym
przyrostowi argumentu ∆x nazywamy liczbe, dana, wzorem
∆f (x
0
)
∆x
=
f (x
0
+ ∆x) − f (x
0
)
∆x
.
Interpretacja geometryczna i fizyczna ilorazu r´
o˙znicowego.
W interpretacji geometrycznej iloraz r´o˙znicowy jest tangensem nachylenia siecznej
przechodza,cej przez punkty
³
x
0
, f (x
0
)
´
,
³
x
0
+ ∆x, f (x
0
+ ∆x)
´
wykresu funkcji
f do dodatniej cze,´sci osi OX.
W interpretacji fizycznej iloraz r´o˙znicowy
∆f
∆x
przedstawia pre,dko´s´c ´srednia,
poruszaja,cego sie, punktu po drodze y = f(x), kt´ora jest funkcja, czasu x. Pre,dko´s´c
ta liczona jest od chwili x
0
do chwili x
0
+ ∆x.
Iloraz r´o˙znicowy
∆f
∆x
mo˙zna zinterpretowa´c r´ownie˙z jako ´srednie nate,˙zenie pra,-
du mie,dzy chwila, x
0
i chwila, x
0
+ ∆x, gdzie f (x) jest funkcja, czasu x opisuja,ca,
Ãladunek jaki przepÃlyna, w dodatnim kierunku przez poprzeczny przekr´oj przewod-
nika.
Definicja 4.1.2. Niech funkcja f be,dzie okre´slona przynajmniej na otoczeniu
punktu x
0
. Pochodna, funkcji f w punkcie x
0
nazywamy granice, wÃla´sciwa, iloraz´ow
r´o˙znicowych funkcji f w punckie x
0
i oznaczamy ja, f
0
(x
0
), tj.
lim
x→x
0
f (x) − f (x
0
)
x − x
0
= f
0
(x
0
).
Zauwa˙zmy, ˙ze powy˙zsza granica mo˙ze nie istnie´c lub by´c granica, niewÃla´sciwa,. W
takim przypadku m´owimy, ˙ze funkcja f w punkcie x
0
nie ma pochodnej.
54
Ponadto je´sli wprowadzimy oznaczenie h = x − x
0
, to pochodna, funkcji mo-
˙zemy zdefiniowa´c wzorem
f
0
(x
0
) = lim
h→0
f (x
0
+ h) − f (x
0
)
h
,
o ile granica taka istnieje. W wielu przypadkach wz´or ten okazuje sie, by´c bardziej
u˙zyteczny.
W interpretacji geometrycznej pochodna funkcji f w punkcie x
0
, o ile ist-
nieje, jest r´owna wsp´oÃlczynnikowi kierunkowemu stycznej do wykresu funkcji f w
punkcie x
0
, tzn. f
0
(x
0
) = tgα, gdzie α jest ka,tem jaki styczna do wykresu funkcji
w punkcie x
0
tworzy z osia, OX.
W interpretacji fizycznej pochodna jest pre,dko´scia, punktu poruszja,cego sie,
po drodze y = f (x) w chwili x
0
.
Pochodna, mo˙zna r´ownie˙z zinterpretowa´c jako nate,˙zenie pra,du w chwili x
0
,
gdzie f (x) jest funkcja, czasu x opisuja,ca, Ãladunek jaki przepÃlywa przez poprzeczny
przekr´oj przewodnika.
O funkcji, kt´ora ma pochodna, w ka˙zdym punkcie swojej dziedziny be,dziemy
m´owi´c, ˙ze jest r´o˙zniczkowalna. Je´sli w punkcie x
0
funkcja f nie be,dzie miaÃla
pochodnej, to powiemy, ˙ze jest ona w tym punkcie nier´o˙zniczkowalna.
PrzykÃlad 4.1.1. Niech f (x) =| x − 2 | i x
0
= 2. Zauwa˙zmy, ˙ze
lim
h→0
+
f (x
0
+ h) − f (x
0
)
h
= lim
h→0
+
| h |
h
= 1
oraz
lim
h→0
−
f (x
0
+ h) − f (x
0
)
h
= lim
h→0
−
| h |
h
= −1.
Wynika sta,d, ˙ze lim
h→0
f (x
0
+ h) − f (x
0
)
h
nie istnieje. Zatem funkcja f (x) =| x − 2 |
w punkcie 2 nie ma pochodnej.
PrzykÃlad 4.1.2. Rozwa˙zmy funkcje, f(x) = sin x. Dla funkcji tej mamy
lim
h→0
f (x
0
+ h) − f (x
0
)
h
= lim
h→0
sin(x
0
+ h) − sin x
0
h
= lim
h→0
2 sin
x
0
+h−x
0
2
cos
x
0
+h+x
0
2
h
55

= lim
h→0
sin
h
2
cos
2x
0
+h
2
h
2
= cos x
0
.
Mo˙zemy zatem napisa´c
[sin x]
0
= cos x.
Zadanie 4.1.1. Korzystaja,c z definicji wyznacz pochodne podanych funkcji w
zadanych punktach
a) f (x) = (x − 4)
3
, x
0
= 1;
c) f (x) =
1
x
,
x
0
= 2;
b) f (x) = cos x,
x
0
∈ R;
d) f (x) =
√
x − 1 , x
0
∈ R.
Zadanie 4.1.2. Zbada´c istnienie pochodnych podanych funkcji we wskazanych
punktach
a) f (x) =| sin x |, x
0
= 0;
b) f (x) = (x − 4)
2
3
, x
0
= 4;
c) f (x) =
½
x sin
1
x
, x 6= 0,
0,
x = 0,
x
0
= 0;
d) f (x) =
½
2x
2
− 1, x ≥ 1,
2 − x,
x < 1,
x
0
= 1.
Podamy teraz warunek konieczny istnienia pochodnej funkcji, kt´ory jedno-
cze´snie podaje nam zwia,zek mie,dzy r´o˙zniczkowalno´scia, funkcji, a jej cia,gÃlo´scia,.
Twierdzenie 4.1.1. Je˙zeli funkcja f ma pochodna, w punkcie x
0
, to jest cia,gÃla
w tym punkcie.
Dow´
od. Niech funkcja f ma pochodna, w punkcie x
0
. Istnieje wtedy granica
lim
x→x
0
f (x) − f (x
0
)
x − x
0
.
Mamy wykaza´c, ˙ze funkcja f jest cia,gÃla w punkcie x
0
, tj.
lim
x→x
0
f (x) = f (x
0
).
R´ownowa˙znie wyka˙zemy, ˙ze lim
x→x
0
£
f (x) − f (x
0
)
¤
= 0. Istotnie mamy
lim
x→x
0
£
f (x) − f (x
0
)
¤
= lim
x→x
0
h f(x) − f(x
0
)
x − x
0
· (x − x
0
)
i
56

= lim
x→x
0
f (x) − f (x
0
)
x − x
0
lim
x→x
0
(x − x
0
) = f
0
(x
0
) · 0 = 0.
Z twierdzenia tego wynika, ˙ze je˙zeli funkcja jest r´o˙zniczkowalna, to jest cia,gÃla.
Oczywi´scie impilkacja odwrotna jest niezawsze prawdziwa o czym ´swiadczy nas-
te,puja,cy przykÃlad.
PrzykÃlad 4.1.3. Zauwa˙zmy, ˙ze funkcja f (x) =| x | jest funkcja, cia,gÃla, w punkcie
x
0
= 0. Istotnie
lim
x→0
f (x) = lim
x→0
| x |= 0 = f (0).
Ale
lim
h→0
+
f (h) − f (0)
h
= lim
h→0
| h |
h
= lim
h→0
h
h
= 1
oraz
lim
h→0
−
f (h) − f (0)
h
= lim
h→0
| h |
h
= lim
h→0
h
h
= −1.
Oznacza to, ˙ze funkcja f (x) =| x | nie ma pochodnej w punkcie x
0
. Zatem w tym
przypadku cia,gÃlo´s´c nie pocia,ga za soba, r´o˙zniczkowalno´sci.
Pochodne wa˙zniejszych funkcji elementarnych
[c]
0
= 0
[x
n
]
0
= nx
n−1
h 1
x
i
0
= −
1
x
2
[a
x
]
0
= a
x
ln a
[log
a
x]
0
=
1
x ln a
[
√
x]
0
=
1
2
√
x
[e
x
]
0
= e
x
[ln x]
0
=
1
x
[sin x]
0
= cos x
[arcsin x]
0
=
1
√
1 − x
2
[sinh x]
0
= cosh x
[cos x]
0
= − sin x
[arccos x]
0
=
−1
√
1 − x
2
[cosh x]
0
= sinh x
[tgx]
0
=
1
cos
2
x
[arctgx]
0
=
1
1 + x
2
[tghx]
0
=
1
cosh
2
x
[ctgx]
0
=
−1
sin
2
x
[arcctgx]
0
=
−1
1 + x
2
[ctghx]
0
= −
1
sinh
2
x
57
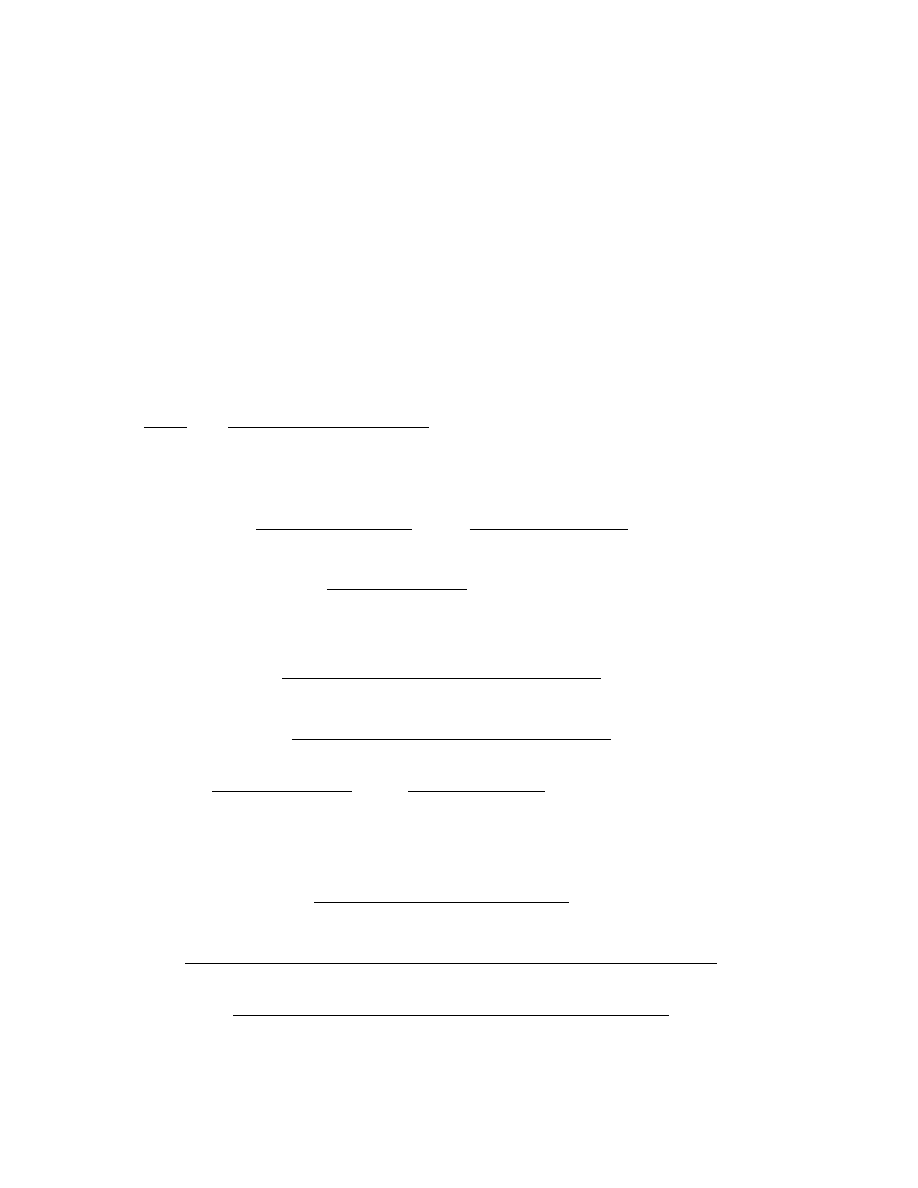
Aby wyznaczy´c pochodne funkcji be,da,cych suma,, r´o˙znica,, iloczynem lub ilo-
razem funkcji elemetarnych korzysta´c be,dziemy z naste,puja,cego twierdzenia.
Twierdzenie 4.1.2. Je˙zeli funkcje f i g maja, pochodne w punkcie x
0
, to
1.
£
c · f (x
0
)
¤
0
= c · f
0
(x
0
),
2.
£
f (x
0
) + g(x
0
)
¤
0
= f
0
(x
0
) + g
0
(x
0
),
3.
£
f (x
0
) − g(x
0
)
¤
0
= f
0
(x
0
) − g
0
(x
0
),
4.
£
f (x
0
) · g(x
0
)
¤
0
= f
0
(x
0
)g(x
0
) + f (x
0
)g
0
(x
0
),
5.
h f(x
0
)
g(x
0
)
i
0
=
f
0
(x
0
)g(x
0
) − f (x
0
)g
0
(x
0
)
[g(x
0
)]
2
(o ile g
0
(x
0
) 6= 0).
Dow´
od. Aby udowodni´c punkt 1 zauwa˙zmy, ˙ze
lim
h→0
cf (x
0
+ h) − cf (x
0
)
h
= lim
h→0
c[f (x
0
+ h) − f (x
0
)]
h
c lim
h→0
f (x
0
+ h) − f (x
0
)
h
= c · f
0
(x
0
).
Udowodnimy teraz punkt 2 naszego twierdzenia.
lim
h→0
[f (x
0
+ h) + g(x
0
+ h)] − [f (x
0
) + g(x
0
)]
h
= lim
h→0
[f (x
0
+ h) − f (x
0
)] + [g(x
0
+ h) − g(x
0
)]
h
= lim
h→0
f (x
0
+ h) − f (x
0
)
h
+ lim
h→0
g(x
0
+ h) − g(x
0
)
h
= f
0
(x
0
) + g
0
(x
0
).
Punkt 3 dowodzi sie, w analogiczny spos´ob.
Wyka˙zemy teraz prawdziwo´s´c wzoru 4.
lim
h→0
f (x
0
+ h)g(x
0
+ h) − f (x
0
)g(x
0
)
h
= lim
h→0
f (x
0
+ h)g(x
0
+ h) − f (x
0
)g(x
0
+ h) + f (x
0
)g(x
0
+ h) − f (x
0
)g(x
0
)
h
= lim
h→0
g(x
0
+ h)[f (x
0
+ h) − f (x
0
)] + f (x
0
)[g(x
0
+ h) − g(x
0
)]
h
58

= lim
h→0
g(x
0
+ h)
f (x
0
+ h) − f (x
0
)
h
+ lim
h→0
f (x
0
)
g(x
0
+ h) − g(x
0
)
h
= g(x
0
)f
0
(x
0
) + f (x
0
)g
0
(x
0
).
Aby wykaza´c prawdziwo´s´c punktu 5 zauwa˙zmy, ˙ze
lim
h→0
f (x
0
+h)
g(x
0
+h)
−
f (x
0
)
g(x
0
)
h
= lim
h→0
1
h
f (x
0
+ h)g(x
0
) − f (x
0
)g(x
0
+ h)
g(x
0
+ h)g(x
0
)
= lim
h→0
1
h
f (x
0
+ h)g(x
0
) − f (x
0
)g(x
0
) + f (x
0
)g(x
0
) − f (x
0
)g(x
0
+ h)
g(x
0
+ h)g(x
0
)
= lim
h→0
1
h
g(x
0
)[f (x
0
+ h) − f (x
0
)] − f (x
0
)[g(x
0
+ h) − g(x
0
)]
g(x
0
+ h)g(x
0
)
= lim
h→0
1
g(x
0
+ h)g(x
0
)
h g(x
0
)[f (x
0
+ h) − f (x
0
)]
h
−
f (x
0
)[g(x
0
+ h) − g(x
0
)]
h
i
=
1
g(x
0
)g(x
0
)
h
g(x
0
)f
0
(x
0
) − f (x
0
)g
0
(x
0
)
i
,
co ko´
nczy dow´od.
Twierdzenie 4.1.3. (o pochodnej funkcji zÃlo˙zonej) Je˙zeli funkcja f ma pochodna,
w punkcie x
0
, a funkcja g ma pochodna, w punkcie f(x
0
), to
[g(f (x))]
0
= g
0
(f (x
0
))f
0
(x
0
).
Twierdzenie 4.1.4. (o pochodnej funkcji odwrotnej) Niech funkcja f speÃlnia
naste,puja,ce warunki
1. f jest cia,gÃla na pewnym otoczeniu punktu x
0
,
2. f jest monotoniczna na otoczeniu punktu x
0
,
3. f ma pochodna, w punkcie x
0
r´o˙zna, od zera.
Wtedy funkcja odwrotna do funkcji f ma pochodna, w punkcie y
0
= f (x
0
) oraz
¡
f
−1
¢
0
(x
0
) =
1
f
0
(x
0
)
.
PrzykÃlad 4.1.4. Zauwa˙zmy, ˙ze funkcja f (x) = sin x, x ∈
³
−
π
2
,
π
2
´
speÃlnia
zaÃlo˙zenia twierdzenia 4.1.4. Zatem korzystaja,c z powy˙zszej r´owno´sci mo˙zemy
wyprowadzi´c wz´or na pochodna, funkcji f(x) = arcsin x.
59
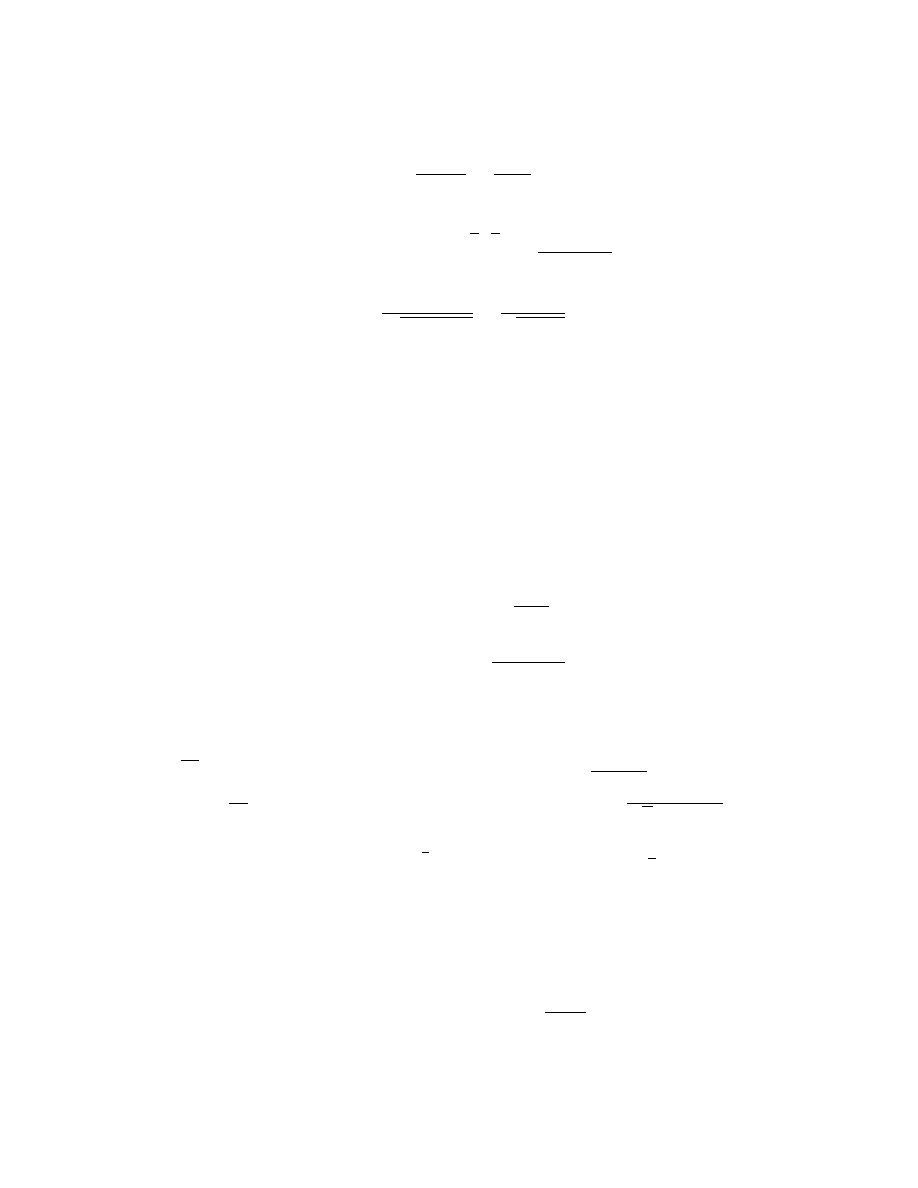
Niech wie,c x = sin y. Mamy w´owczas y = arcsin x oraz
[arcsin x]
0
=
1
[sin y]
0
=
1
cos y
.
Funkcje, sinus rozwa˙zamy na przedziale
³
−
π
2
,
π
2
´
. Na tym przedziale funkcja
cosinus przyjmyje warto´sci dodatnie. Zatem cos y =
p
1 − sin
2
y oraz
[arcsin x]
0
=
1
p
1 − sin
2
y
=
1
√
1 − x
2
.
W analogiczny spos´ob mo˙zemy wyprowadzi´c wzory na pochodne pozostaÃlych fun-
kcji cyklometrycznych.
Korzystaja,c z twierdzenia o pochodnej funkcji zÃlo˙zonej oraz z faktu, ˙ze funkcje
f (x) = e
x
oraz f (x) = ln x sa, wzajemnie odwrotne wyznaczymy teraz pochodna,
funkcji [f (x)]
g(x)
.
h
[f (x)]
g(x)
i
=
h
e
g(x) ln f (x)
i
0
= e
g(x) ln f (x)
h
g(x) ln f (x)
i
0
= e
g(x) ln f (x)
h
g
0
(x) ln f (x) + g(x)
1
f (x)
f
0
(x)
i
= [f (x)]
g(x)
h
g
0
(x) ln f (x) +
g(x)f
0
(x)
f (x)
i
.
Zadanie 4.1.3. Wyznaczy´c pochodne naste,puja,cych funkcji
a(x) =
√
x
3
arccos x
b(x) = log
2
x · sinh x
c(x) =
e
x
+sin x
cos x−e
x
d(x) = arcsin
√
x
7
f (x) = tg e
−3x
g(x) = ln
3
p√
x + x
2
− e
h(x) = x
cosh x
k(x) = 2
arctg
1
x
l(x) = log
x
ctg
x
3
Zadanie 4.1.4. Napisa´c r´ownania stycznych do wykres´ow funkcji we wskazanych
punktach
a) f (x) = e
x
,
x
0
= 0;
c) f (x) = sin x,
x
0
= π;
b) f (x) = arctg(−x
2
), x
0
= 1;
d) f (x) = ln
√
1 + x,
x
0
= 0.
60
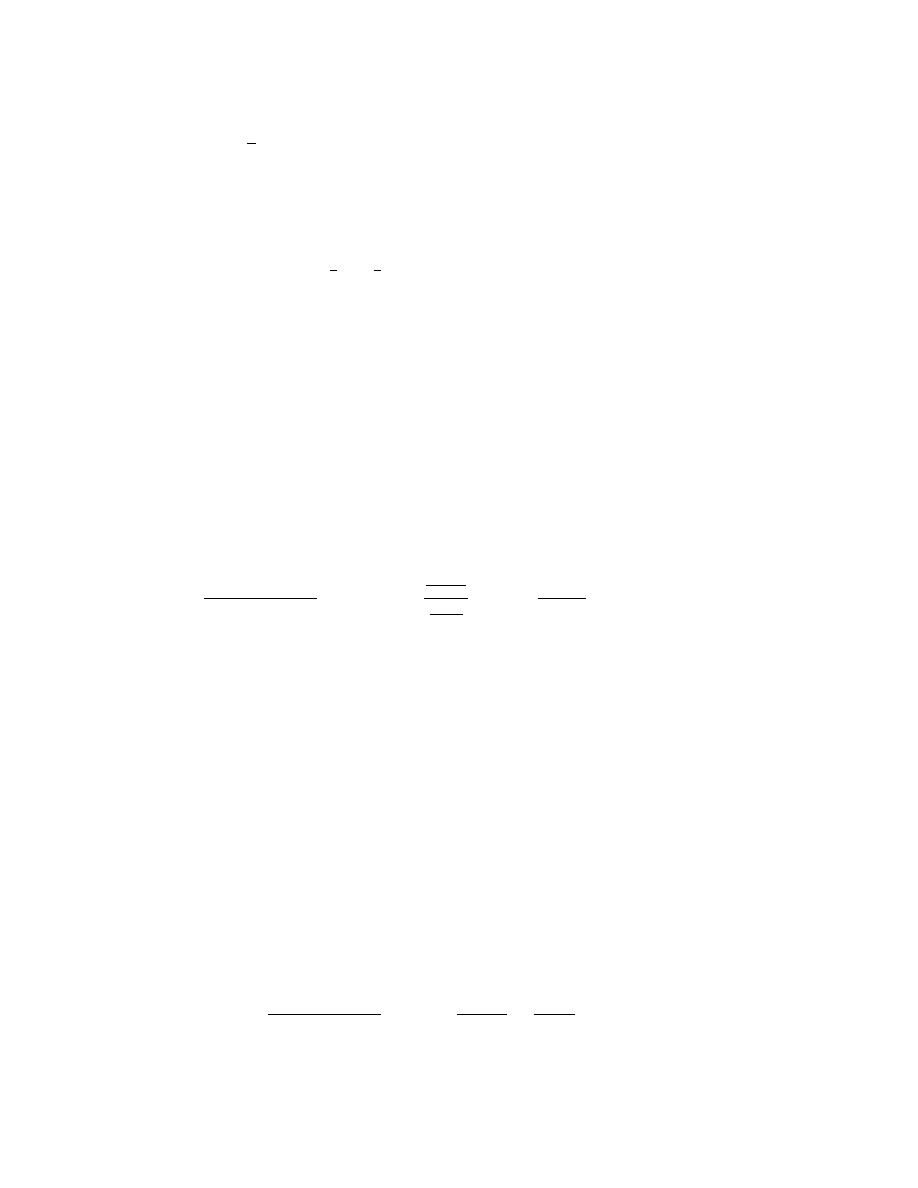
Zadanie 4.1.5. Napisa´c r´ownanie tej stycznej do wykresu funkcji f (x) = 3 − x
2
,
kt´ora tworzy ka,t
π
3
z dodatnia, cze,´scia, osi OX.
Zadanie 4.1.6. Dla jakich warto´sci parametr´ow a i b wykres funkcji f (x) =
−x
2
+ ax + b jest styczny do prostej y = x w punkcie (−1, −1)?
Zadanie 4.1.7.
Dla funkcji f (x) = x
3
+ 3x
2
− 5 napisa´c r´ownanie stycznej
prostopadÃlej do prostej y =
1
3
x +
1
6
.
Pochodna, funkcji bardzo cze,sto wykorzystuje sie, do szacowania bÃle,d´ow po-
miaru. Aby om´owi´c pokr´otce ten problem zdefiniujmy poje,cie r´o˙zniczki funkcji.
Definicja 4.1.3. R´o˙zniczka, funkcji f w punkcie x
0
dla przyrostu ∆x argumentu
x nazywamy iloczyn f
0
(x
0
)∆x.
R´o˙zniczke, oznaczamy symbolem df, tzn.
df (x
0
) = f
0
(x
0
)∆x.
Przyrost ∆x argumentu x nazywamy r´o˙zniczka, zmiennej x i cze,sto oznaczamy
symbolem dx.
Zauwa˙zmy, ˙ze
lim
x→x
0
df (x) − ∆f (x)
df (x)
= lim
x→x
0
³
1 −
∆f (x)
∆x
df (x)
dx
´
= 1 −
f
0
(x
0
)
f
0
(x
0
)
= 1 − 1 = 0.
Zatem mo˙zemy napisa´c
df (x
0
) − ∆f (x
0
) ≈ 0.
Sta,d wynika, ˙ze
∆f (x
0
) ≈ df (x
0
).
Ponadto ∆f (x
0
) = f (x
0
+ ∆x) − f (x
0
), wie,c
f (x
0
+ ∆x) ≈ f (x
0
) + df (x
0
).
Zatem
f (x
0
+ ∆x) ≈ f (x
0
) + f
0
(x
0
)∆x,
o ile istnieje pochodna funkcji f w punkcie x
0
.
Powy˙zszy wz´or stosujemy do obliczania przybli˙zonej warto´sci przyrostu fun-
kcji f w punkcie x
0
. BÃla,d jaki popeÃlniamy zaste,puja,c przyrost funkcji ∆f jej
r´o˙zniczka, df, da,˙zy szybciej do zera ni˙z przyrost argumentu ∆x. Istotnie mamy
lim
x→x
0
∆f (x) − df (x)
∆x
= lim
x→x
0
³ ∆f(x)
∆x
−
df (x)
dx
´
= 0.
61

Rozwa˙zania powy˙zsze prowadza, do naste,puja,cego zastosowania r´o˙zniczki funkcji
do szacowania bÃle,d´ow pomiaru. Niech wielko´sci fizyczne x i y be,da, zwia,zane
zale˙zno´scia, funkcyjna, y = f(x), przy czym zakÃladamy, ˙ze istnieje pochodna f
0
(x
0
).
Niech ponadto ∆x oznacza bÃla,d bezwzgle,dny pomiaru wielko´sci x. Wtedy bÃla,d
bezwzgle,dny ∆y obliczanej wielko´sci y wyra˙za sie, przybli˙zonym wzorem
∆y ≈| f
0
(x
0
) | ∆x.
Zadanie 4.1.8. Korzystaja,c z r´o˙zniczki funkcji obliczy´c przybli˙zone warto´sci
podanych wyra˙ze´
n
a)
4
√
15, 96,
b) arctg1.05,
c) cos 0, 03.
Je´sli w dowolnym punkcie x ∈ A istnieje pochodna f
0
funkcji f , to jest ona
pewna, funkcja, okre´slona, na zbiorze A. Mo˙zemy wie,c wyznaczy´c pochodna, tej
funkcji w ka˙zdym punkcie zbioru A i tym samym otrzyma´c nowa, funkcje,, kt´ora,
mo˙zna zr´o˙zniczkowa´c. Jak wida´c r´o˙zniczkowanie mo˙ze by´c wielokrotnie pow-
tarzane. A zatem mo˙zna zdefiniowa´c poje,cie pochodnej dowolnego rze,du.
Definicja 4.1.4. Pochodna, n-tego rze,du funkcji f w punkcie x
0
definiujemy in-
dukcyjnie
f
(n)
(x
0
) =
h
f
(n−1)
(x
0
)
i
0
,
dla n ≥ 2,
gdzie f
(1)
(x
0
) = f
0
(x
0
). Ponadto przyjmujemy f
(0)
(x
0
) = f (x
0
).
Oczywi´scie mo˙zemy r´ownie˙z m´owi´c o r´o˙zniczce n-tego rze,du.
Definicja 4.1.5. R´o˙zniczke, n-tego rze,du funkcji f w punkcie x
0
definiujemy w
wzorem
d
n
f (x
0
) = f
(n)
(x
0
)(∆x)
n
.
Twierdzenie 4.1.5. (wz´or Leibniza) Niech funkcje f i g maja, pochodne n-tego
rze,du w punkcie x
0
. Wtedy
(f · g)
(n)
(x
0
) =
n
X
k=0
µ
n
k
¶
f
(n−k)
(x
0
) · g
(k)
(x
0
).
Zadanie 4.1.9. Obliczy´c pochodna, n-tego rze,du funkcji
a) f (x) = ln x,
b) f (x) = sin x,
c) f (x) = cos x.
Zadanie 4.1.10. Zastosowa´c wz´or Leibniza do wyznaczenia n-tych pochodnych
funkcji
a) f (x) = xe
x
,
b) f (x) = e
x
sin x,
c) f (x) = x ln x.
62

4.2. Twierdzenia o warto´sci ´sredniej.
W paragrafie tym podamy bez dowod´ow kilka wa˙znych twierdze´
n analizy
matematycznej, z kt´orych mo˙zna otrzyma´c wnioski pozwalaja,ce na badanie pod-
stawowych wÃlasno´sci funkcji rzeczywistej jednej zmiennej rzeczywistej.
Twierdzenie 4.2.1. (Rolle’a) Je˙zeli funkcja f speÃlnia naste,puja,ce warunki:
1. jest cia,gÃla na przedziale < a, b >,
2. jest r´o˙zniczkowalna na przedziale (a, b),
3. f (a) = f (b),
to
_
c∈(a,b)
f
0
(c) = 0.
Interpretacja geomertyczna twierdzenia Rolle’a: Na wykresie funkcji cia,gÃlej na
przedziale domknie,tym, r´o˙zniczkowalnej wewna,trz tego przedziaÃlu i przyjmuja,cej
jednakowa, warto´s´c na jego ko´ncach istnieje punkt, w kt´orym styczna jest r´owno-
legÃla do osi OX.
PrzykÃlad 4.2.1. Rozwa˙zmy funkcje, f(x) = x
4
na przedziale < −2, 2 >. Za-
uwa˙zmy, ˙ze funkcja f (x) = x
4
jest cia,gÃla na przedziale < −2, 2 > i r´o˙zniczkowalna
wewna,trz tego przedziaÃlu, f
0
(x) = 4x
3
. Ponadto f (−2) = 16 i f (2) = 16. Wobec
tego funkcja f (x) = x
4
speÃlnia zaÃlo˙zenia twierdzenia Rolle’a, a zatem w przedziale
< −2, 2 > istnieje taki punkt c, ˙ze f
0
(c) = 0. Oczywi´scie tym punktem jest c = 0.
Rozwa˙zmy teraz na przedziale < −2, 2 > funkcje, f(x) = x
3
. Funkcja ta
jest oczywi´scie cia,gÃla na przedziale < −2, 2 > i r´o˙zniczkowalna wewna,trz tego
przedziaÃlu. Zauwa˙zmy jednak, ˙ze f (−2) = −8 i f (2) = 8. A zatem jedno z
zaÃlo˙ze´
n twierdzenia Rolle’a nie jest speÃlnione. Nieoznacza to w tym przypadku,
˙ze w przedziale < −2, 2 > nie mo˙zna znale´z´c takiego punktu, w kt´orym pochodna
znika. Wystarczy rozwia,za´c r´ownanie 3x
2
= 0, aby stwierdzi´c, ˙ze w punkcie c = 0
pochodna funkcji f (x) = x
3
jest r´owna zero.
Taka sytuacja jak powy˙zej nie zawsze zachodzi. PrzykÃladem jest funkcja
f (x) =| x |. Rozwa˙zmy ta, funkcje, r´ownie˙z na przedziale < −2, 2 >. Jak wiadomo,
funkcja f (x) =| x | jest cia,gÃla na przedziale < −2, 2 >. Niestety nie jest ona
r´o˙zniczkowalna wewna,trz tego przedzialu, gdy˙z nie ma pochodnej w punkcie x
0
=
0. Ale f (−2) = 2 i f (2) = 2. Nie sa, wie,c speÃlnione wszystkie zaÃlo˙zenia twierdzenia
Rolle’a, a zatem w przedziale < −2, 2 > nie znajdziemy takiego punktu c, aby
f
0
(c) = 0. Istotnie tak jest, gdy˙z jedynym takim punktem m´ogÃlby by´c punkt
x
0
= 0, a tam pochodna nie istnieje.
Z twierdzenia Rolle’a wynika istnienie punktu, w kt´orym pochodna znika, co
nie wyklucza faktu, ˙ze takich punkt´ow mo˙ze by´c kilka.
63

PrzykÃlad 4.2.2. Funkcja f (x) = sin x na przedziale < 0, 4π > speÃlnia zaÃlo˙zenia
twierdzenia Rolle’a, jest cia,gÃla w ka˙zdym punkcie tego przedziaÃlu i jest r´o˙znicz-
kowalna wewna,trz niego oraz f(0) = 0 i f(4π) = 0. Poniewa˙z f
0
(x) = cos x,
wie,c Ãlatwo wida´c, ˙ze punkt o kt´orym mowa w tezie twierdzenia Rolle’a to c =
π
2
,
c =
3π
2
, c =
5π
2
, oraz c =
7π
2
.
Twierdzenie 4.2.2. (Lagrange’a) Je˙zeli funkcja f speÃlnia naste,puja,ce warunki:
1. jest cia,gÃla na < a, b >,
2. jest r´o˙zniczkowalna na (a, b),
to
_
c∈(a,b)
f
0
(c) =
f (b) − f (a)
b − a
.
Twierdzenie to wynika z twierdzenia Rolle’a. Wystarczy zauwa˙zy´c, ˙ze funkcja
g(x) = f (x) − f (a) −
f (b) − f (a)
b − a
(x − a)
speÃlnia zaÃlo˙zenia twierdzenia Rolle’a.
Ponadto mamy
g
0
(x) = f
0
(x) −
f (b) − f (a)
b − a
.
Zatem
_
c∈(a,b)
g
0
(c) = 0 ⇔
_
c∈(a,b)
f
0
(c) −
f (b) − f (a)
b − a
= 0.
Interpretacja geomertyczna twierdzenia Lagrange’a: Na wykresie funkcji cia,gÃlej na
przedziale domknie,tym i r´o˙zniczkowalnej wewna,trz tego przedziaÃlu istnieje punkt,
w kt´orym styczna jest r´ownolegÃla do siecznej Ãla,cza,cej punkty
³
a, f (a)
´
,
³
b, f (b)
´
.
Z twierdzenia Lagrange’a otrzymujemy naste,puja,ce zwia,zki monotoniczno´sci
funkcji z jej pochodna,.
Wniosek 4.2.1. Je˙zeli dla ka˙zdego x ∈ (a, b) f
0
(x) = 0, to funkcja f jest staÃla
na (a, b).
Wniosek 4.2.2. Je˙zeli dla ka˙zdego x ∈ (a, b) f
0
(x) > 0 (f
0
(x) ≥ 0), to funkcja f
jest rosna,ca (niemaleja,ca) na (a, b).
Wniosek 4.2.3. Je˙zeli dla ka˙zdego x ∈ (a, b) f
0
(x) < 0 (f
0
(x) ≤ 0), to funkcja f
jest maleja,ca (nierosna,ca) na (a, b).
64

Twierdzenie 4.2.3.
(Cauchy’ego) Je˙zeli funkcje f i g speÃlniaja, naste,puja,ce
warunki:
1. sa, cia,gÃle na < a, b >,
2. sa, r´o˙zniczkowalne na (a, b),
3.
V
x∈(a,b)
g
0
(x) 6= 0, to
_
c∈(a,b)
f
0
(c)
g
0
(c)
=
f (b) − f (a)
g(b) − g(a)
.
Zadanie 4.2.1. Sprawdzi´c, czy podane funkcje speÃlniaja, twierdzenie Rolle’a w
zadanych przedziaÃlach i je´sli to mo˙zliwe wyznaczy´c c wyste,puja,ce w tezie tego
twierdzenia
a) f (x) =
3
√
x
2
+ 1, < −1, 1 >;
b) f (x) = | x − 1 |
3
, < 0, 2 >;
c) f (x) = x(x
2
− 1), < −1, 1 >;
d) f (x) = ln sin x,
D
π
6
,
5π
6
E
.
Zadanie 4.2.2. Korzystaja,c z twierdzenia Lagrange’a udowodni´c nier´owno´sci
a)
x
1 + x
< ln(1 + x) < x, dla x > 0;
b) e
x
≥ 1 + x, dla x ∈ R.
Zadanie 4.2.3. Wyznaczy´c przedziaÃly monotoniczno´sci podanych funkcji
a) f (x) =
x
x
2
+ 1
,
b) f (x) = sin x + cos x,
c) f (x) = arctgx − ln x,
d) f (x) = (1 + x)e
2x
.
65

4.3. ReguÃla de l’Hˆ
ospitala.
Twierdzenie, kt´ore om´owimy w tym paragrafie zostaÃlo odkryte przez matema-
tyka szwajcarskiego Bernoulliego, a ogÃlosiÃl je drukiem poraz pierwszy w podre,czni-
ku analizy matematycznej, jego ucze´
n, matematyk francuski de l’Hˆospital. Dlatego
te˙z twierdzenie to znane jest obecnie jako reguÃla de l’Hˆospitala. Twierdzenie to
jest niezwykle u˙zyteczne przy liczeniu granic funkcji.
Twierdzenie 4.3.1. (de l’Hˆospitala) Je˙zeli
1. dziedziny funkcji
f
g
i
f
0
g
0
zawieraja, pewne sa,siedztwo punktu x
0
,
2. lim
x→x
0
f (x) = 0 = lim
x→x
0
g(x)
³
lim
x→x
0
f (x) = ∞ = lim
x→x
0
g(x)
´
,
3. istnieje granica wÃla´sciwa lub niewÃla´sciwa lim
x→x
0
f
0
(x)
g
0
(x)
,
to istnieje granica lim
x→x
0
f (x)
g(x)
i ponadto lim
x→x
0
f (x)
g(x)
= lim
x→x
0
f
0
(x)
g
0
(x)
.
Twierdzenie 4.3.1 jest r´ownie˙z prawdzie dla granic jednostronnych i granic
liczonych w punktach niewÃla´sciwych.
Z reguÃly de l’Hˆospitala mo˙zemy skorzysta´c w naste,puja,cych przypadkach.
Przypadek 1. Niech lim
x→x
0
f (x) = 0 i lim
x→x
0
g(x) = 0 lub niech lim
x→x
0
f (x) = ∞
i lim
x→x
0
g(x) = ∞. Obliczanie granicy lim
x→x
0
f (x)
g(x)
poprzez formalne podstawienie
warto´sci granicznych daje nam symbol nieoznaczony
h
0
0
i
lub odpowiednio
h
∞
∞
i
.
W tym przypadku bezpo´srednie (by´c mo˙ze wielokrotne) zastosowanie reguÃly de
l’Hˆospitala doprowadzi nas do rozwia,zania.
PrzykÃlad 4.3.1. Obliczy´c granice, lim
x→0
e
x
− e
−x
x
.
Zauwa˙zmy, ˙ze
lim
x→0
e
x
− e
−x
x
=
h 0
0
i
.
Zatem je´sli tylko istnieje granica
lim
x→0
[e
x
− e
−x
]
0
[x]
0
,
to jest ona r´owna poszukiwanej przez nas granicy.
66

Mamy
lim
x→0
[e
x
− e
−x
]
0
[x]
0
= lim
x→0
e
x
+ e
−x
1
= 2.
A zatem poniewa˙z sa, speÃlnione wszystkie zaÃlo˙zenia twierdzenia 4.3.1, to
lim
x→0
e
x
− e
−x
x
= 2.
Przypadek 2.
Niech lim
x→x
0
f (x) = 0 i lim
x→x
0
g(x) = ∞.
Obliczaja,c granice,
lim
x→x
0
[f (x) · g(x)] poprzez formalne postawienie warto´sci granicznych otrzymamy
symbol nieoznaczony [0 · ∞]. Aby wyznaczy´c te, granice, zauwa˙zmy, ˙ze zasta,pienie
mno˙zenia dzieleniem doprowadzi nas do zamiany symbolu nieoznaczonego [0 · ∞]
na jeden z symboli
h
∞
∞
i
lub
h
0
0
i
. Daje nam to mo˙zliwo´s´c zastosowania reguÃly de
l’Hˆospitala, o ile zaÃlo˙zenia twierdzenia 4.3.1 sa, speÃlnione. Mamy bowiem
lim
x→x
0
f (x) · g(x) = lim
x→x
0
f (x)
1
g(x)
=
h 0
0
i
lub
lim
x→x
0
f (x) · g(x) = lim
x→x
0
g(x)
1
f (x)
=
h ∞
∞
i
.
PrzykÃlad 4.3.2. Obliczy´c granice, lim
x→∞
xe
−x
.
W tym przypadku zaÃlo˙zenia twierdzenia 4.3.1 sa, speÃlnione, zatem mamy
lim
x→+∞
xe
−x
=
h
0 · ∞
i
= lim
x→+∞
x
e
x
=
h ∞
∞
i
H
= lim
x→+∞
1
e
x
= 0.
Przypadek 3. Niech lim
x→x
0
f (x) = ∞ i lim
x→x
0
g(x) = ∞. Formalne postawienie
warto´sci granicznych podczas liczenia granicy lim
x→x
0
[f (x) − g(x)] daje nam symbol
nieoznaczony [∞ − ∞]. Zauwa˙zmy, ˙ze w´owczas mamy
lim
x→x
0
[f (x) − g(x)] = lim
x→x
0
1
g(x)
−
1
f (x)
1
f (x)g(x)
=
h 0
0
i
.
A zatem po takim przeksztaÃlceniu mo˙zemy zastosowa´c reguÃle, l’Hˆospitala, o ile
oczywi´scie zaÃlo˙zenia twierdzenia 4.3.1 sa, speÃlnione.
67

PrzykÃlad 4.3.3. Obliczy´c granice, lim
x→0
³ 1
tgx
−
1
x
´
. W tym przypadku mamy
lim
x→0
³ 1
tgx
−
1
x
´
=
h
∞ − ∞
i
= lim
x→0
x − tgx
xtgx
=
h 0
0
i
H
= lim
x→0
1 −
1
cos
2
x
tgx +
x
cos
2
x
= lim
x→0
− sin
2
x
sin x cos x + x
=
h 0
0
i
H
= lim
x→0
−2 sin x cos x
cos
2
x − sin
2
x + 1
= 0.
Przypadek 4. Niech lim
x→x
0
f (x) = 0 i lim
x→x
0
g(x) = 0. W´owczas formalne pod-
stawienie warto´sci granicznych podczas wyznaczania granicy lim
x→x
0
£
f (x)
¤
g(x)
daje
symbol nieoznaczony
h
0
0
i
. Jednak˙ze zapisanie tej granicy w innej postaci
lim
x→x
0
£
f (x)
¤
g(x)
= lim
x→x
0
e
g(x) ln f (x)
sprowadza problem do wyznaczenia granicy lim
x→x
0
g(x) ln f (x), kt´ora przy powy˙z-
szych zaÃlo˙zeniach daje symbol nieoznaczony
£
0 · ∞
¤
. A zatem wystarczy dalej
poste,powa´c jak w przypadku 2.
Podobna, sytuacje, mamy, gdy lim
x→x
0
f (x) = 1 i lim
x→x
0
g(x) = ∞. W´owczas
lim
x→x
0
£
f (x)
¤
g(x)
=
h
1
∞
i
= lim
x→x
0
e
g(x) ln f (x)
= e
[0·∞]
i dalej poste,pujemy jak w przypadku 2.
W analogiczny spos´ob poste,pujemy w sytuacji, gdy lim
x→x
0
f (x) = ∞ oraz
lim
x→x
0
g(x) = 0 i chcemy obliczy´c granice, lim
x→x
0
£
f (x)
¤
g(x)
. Wtedy
lim
x→x
0
£
f (x)
¤
g(x)
=
h
∞
0
i
= lim
x→x
0
e
g(x) ln f (x)
= e
[0·∞]
.
PrzykÃlad 4.3.4. Obliczy´c granice, lim
x→0
x
x
.
Zauwa˙zmy, ˙ze
lim
x→0
x
x
= lim
x→0
e
x ln x
.
Ponadto
lim
x→0
x ln x =
£
0 · ∞
¤
= lim
x→0
ln x
1
x
=
h ∞
∞
i
H
= lim
x→0
1
x
−1
x
2
= − lim
x→0
x = 0.
Wobec tego lim
x→0
x
x
= e
0
= 1.
68

4.4. Wz´
or Taylora i Maclaurina. Zastosowanie rachunku r´
o˙zniczkowego
do aproksymacji funkcji.
Wz´or Taylora oraz wynikaja,cy z niego wz´or Maclaurina, o kt´orych be,dzie
mowa w tym paragrafie wykorzystuje sie, do obliczania przybli˙zonych warto´sci
funkcji. Ze wzor´ow tych mo˙zemy otrzyma´c przybli˙zenia z mniejszym bÃle,dem ni˙z
wykorzystuja,c r´o˙zniczke, pierwszego rze,du.
Twierdzenie 4.4.1. (Wz´or Taylora) Je˙zeli
1. funkcja f ma cia,gÃle pochodne rze,du (n−1) wÃla,cznie na przedziale domknie,tym
[x
0
, x],
2. funkcja f ma pochodna, rze,du n wewna,trz przedziaÃlu (x
0
, x),
to
_
c∈(x
0
,x)
f (x) = f (x
0
) +
n−1
X
k=1
f
(k)
(x
0
)
k!
(x − x
0
)
k
+
f
(n)
(c)
n!
(x − x
0
)
n
.
Zauwa˙zmy, ˙ze dla n = 1 za wzoru Taylora wynika twierdzenie Lagrange’a.
Je˙zeli wprowadzimy oznaczenie h = x − x
0
, to wz´or Taylora mo˙zemy zapisa´c
w wygodniejszej postaci
f (x
0
+h) = f (x
0
)+
f
0
(x
0
)
1!
h+
f
00
(x
0
)
2!
h
2
+
f
(3)
(x
0
)
3!
h
3
+
f
(n−1)
(x
0
)
(n − 1)!
h
n−1
+
f
(n)
(c)
n!
h
n
.
Ostatni skÃladnik w powy˙zszym wzorze nazywamy reszta, Lagrange’a n-tego rze,du
i oznaczamy symbolem R
n
, tzn.
R
n
=
f
(n)
(c)
n!
h
n
.
Reszte, te, mo˙zna r´ownie˙z zapisa´c w naste,puja,cej postaci
R
n
=
f
(n)
(x
0
+ θh)
n!
h
n
,
gdzie θ ∈ (0, 1).
KÃlada,c we wzorze Taylora x
0
= 0 otrzymujemy
f (x) = f (0) +
n−1
X
k=1
f
(k)
(0)
k!
x
k
+
f
(n)
(c)
n!
x
n
.
69

Wz´or ten nazywamy wzorem Maclaurina.
Zauwa˙zmy, ˙ze pomijaja,c reszte, we wzorze Maclaurina, otrzymamy wz´or przy-
bli˙zony
f (x) ≈
n−1
X
k=0
f
(k)
(0)
k!
x
k
,
(4.4.1)
kt´ory mo˙zemy wykorzysta´c do obliczania warto´sci funkcji f . BÃla,d bezwzgle,dny
∆, jaki popeÃlniamy posÃluguja,c sie, tym wzorem, jest r´owny warto´sci bezwzgle,dnej
reszty R
n
, tj.
∆ =
¯
¯
¯
f
(n)
(c)
n!
x
n
¯
¯
¯.
R´owno´s´c ta sÃlu˙zy do oceny bÃle,du jaki popeÃlniamy zaste,puja,c ”prawdziwa,” warto´s´c
funkcji warto´scia, przybli˙zona, wyliczona, z u˙zyciem wielomianu znajduja,cego sie, po
prawej stronie wzoru (4.4.1).
PrzykÃlad 4.4.1. Napiszemy wz´or Maclaurina dla funkcji f (x) = e
x
. Zauwa˙zmy,
˙ze funkcja f ma pochodna, dowolnego rze,du postaci f
(n)
(x) = e
x
, a zatem f
(n)
(0) =
1. Wobec tego mamy
e
x
=
n−1
X
k=0
x
k
k!
+
e
c
n!
x
n
,
gdzie | c |<| x |.
Je´sli wie,c be,dziemy chcieli wykorzysta´c ten wz´or do obliczenia przybli˙zonej
warto´sci funkcji f (x) = e
x
w pewnym punkcie jej dziedziny, to bÃla,d bezwzgle,dny
jaki popeÃlnimy speÃlnia warunek
∆ =
x
n!
e
c
≤
| x |
n!
e
|x|
.
Wyliczmy wie,c, przy u˙zyciu powy˙zszych rozwa˙za´n przybli˙zona, warto´s´c liczby e i
oce´
nmy popeÃlniony bÃla,d bezwzgle,dny. Mamy
e ≈
n−1
X
k=0
1
k!
,
przy czym
∆ ≤
e
n!
<
3
n!
.
Droga, pr´ob ustalamy, ˙ze najmniejsza, liczba, naturalna, n speÃlniaja,ca, pow˙zsza, nie-
r´owno´s´c jest n = 8. Zatem otrzymujemy
e ≈
7
X
k=0
1
k!
=
685
252
70
z bÃledem mniejszym jak
3
8!
< 0, 000075.
Zadanie 4.4.1. Napisa´c wz´or Taylora z reszta, Lagrange’a dla podanych funkcji
f , punkt´ow x
0
oraz dla wskazanego n
a) f (x) =
1
√
x
,
x
0
= 1,
n = 3;
b) f (x) =
√
1 + x,
x
0
= 0,
n = 2;
c) f (x) = arcsin x,
x
0
= 0,
n = 3;
d) f (x) = cosh x,
x
0
= 0,
n = 4;
Zadanie 4.4.2. Napisa´c wz´or Maclaurina dla funkcji
a) f (x) = sin x,
b) f (x) = cos x,
c) f (x) = ln(1 + x),
d) f (x) = e
x+2
,
e) f (x) = sin 2x.
Zadanie 4.4.3.
Wykorzystuja,c wz´or Maclaurina obliczy´c warto´sci podanych
wyra˙ze´
n ze wskazana, dokÃladno´scia,
a) cos 0, 2,
0, 0001;
b) ln 0, 9,
0, 01;
a) sin 1,
0, 0001;
b)
√
1, 2,
0, 001.
4.5. Ekstrema funkcji.
Paragraf ten be,dzie po´swie,cony zastosowaniu rachunku pochodnych do wyz-
naczania ekstremum funkcji rzeczywistej jednej zmiennej rzeczywistej. Na pocza,t-
ku przypomnimy definicje ekstremum lokalnego wÃla´sciwego funkcji.
Niech x
0
∈ R oraz niech funkcja f be,dzie okre´slona przynajmniej na otoczeniu
punktu x
0
.
Definicja 4.5.1. Funkcja f ma w punkcie x
0
maksimum lokalne wÃla´sciwe, je˙zeli
_
δ>0
^
x∈S(x
0
,δ)
f (x) < f (x
0
).
Definicja 4.5.2. Funkcja f ma w punkcie x
0
minimum lokalne wÃla´sciwe, je˙zeli
_
δ>0
^
x∈S(x
0
,δ)
f (x) > f (x
0
).
71
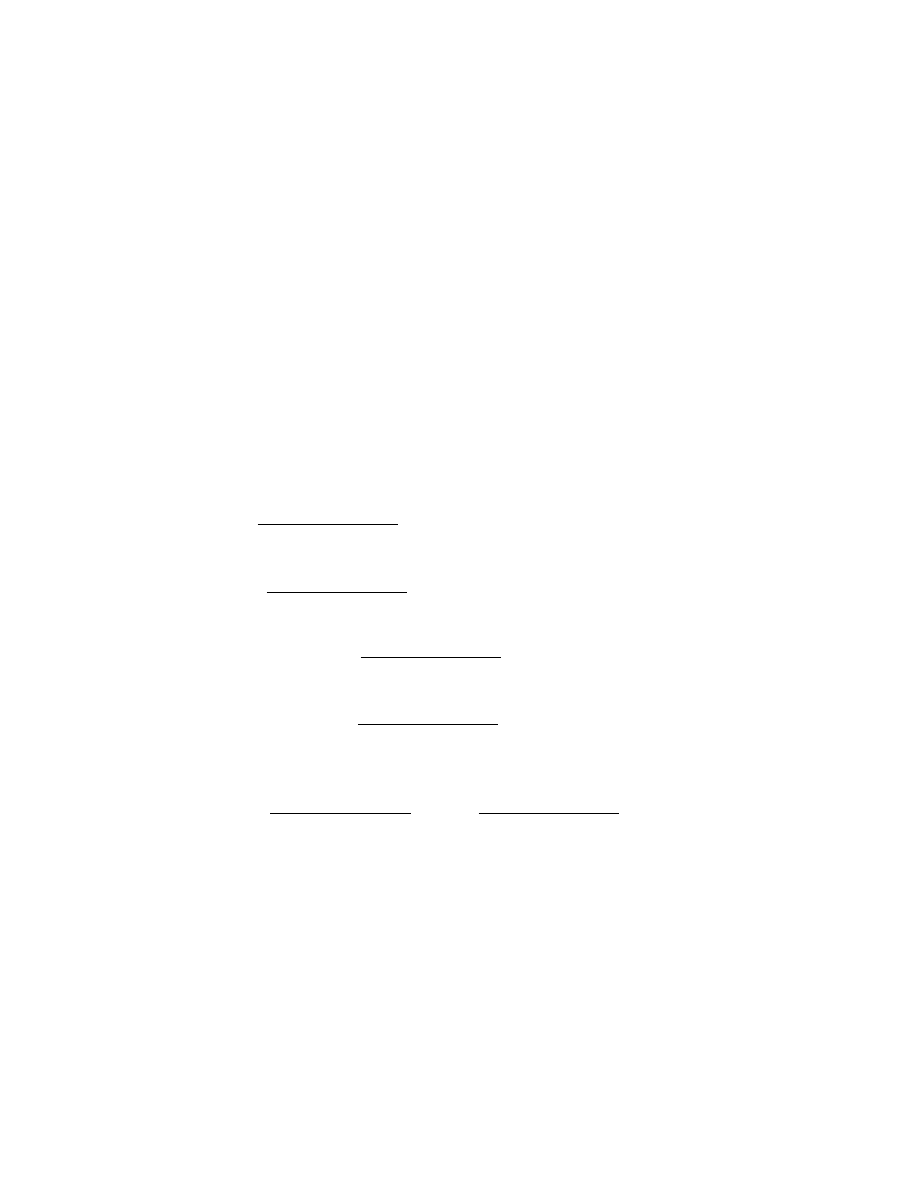
Powy˙zsze definicje okre´slaja, poje,cie ekstremum funkcji w odniesieniu do dostate-
cznie maÃlego otoczenia punktu x
0
. Mo˙zemy r´ownie˙z zdefiniowa´c poje,cie ektremum
absolutnego funkcji, kt´ore odnosi sie, do pewnego zbioru na kt´orym rozwa˙zana
funkcja jest okre´slona lub do jej dziedziny naturalnej i oznacza po prostu warto´s´c
najwie,ksza, i najmniejsza, funkcji.
Podamy teraz warunki konieczne i dostateczne istnienia ekstremum lokalnego
funkcji f w punkcie x
0
.
Warunek konieczny istnienia ekstremum
Twierdzenie 4.5.1. (Fermata) Je´sli funkcja f
1. ma ekstremum lokalne wÃla´sciwe w punkcie x
0
,
2. ma pochodna, w punkcie x
0
,
to
f
0
(x
0
) = 0.
Dow´
od. ZaÃl´o˙zmy, ˙ze funkcja f ma w punkcie x
0
maksimum lokalne wÃla´sciwe i
jest w tym punkcie r´o˙zniczkowalna. W´owczas istnieje taka liczba δ > 0, ˙ze
f (x
0
+ h) − f (x
0
)
h
≥ 0,
dla
− δ < h < 0
oraz
f (x
0
+ h) − f (x
0
)
h
≤ 0,
dla 0 < h < δ.
Zatem
lim
h→0
−
f (x
0
+ h) − f (x
0
)
h
≥ 0
i
lim
h→0
+
f (x
0
+ h) − f (x
0
)
h
≤ 0.
Poniewa˙z funkcja jest r´o˙zniczkowalna w punkcie x
0
, to
lim
h→0
−
f (x
0
+ h) − f (x
0
)
h
= lim
h→0
+
f (x
0
+ h) − f (x
0
)
h
.
Wobec tego mamy
f
0
(x
0
) ≥ 0 i f
0
(x
0
) ≤ 0,
co oznacza, ˙ze f
0
(x
0
) = 0.
W przypadku minimum lokalnego dow´od przebiega w analogiczny spos´ob.
W interpretacji geometrycznej twierdzenie Fermata oznacza, ˙ze w punkcie, w
kt´orym funkcja osia,ga ekstermum, styczna do wykresu funkcji jest r´ownolegÃla
do osi OX.
72

Zauwa˙zmy, ˙ze twierdzenie Fermata podaje tylko warunek konieczny istnienia
ekstremum funkcji. Wobec tego twierdzenie odwrotne nie zawsze zachodzi, o czym
´swiadczy poni˙zszy przykÃlad.
PrzykÃlad 4.5.1. Rozwa˙zmy funkcje, f(x) = x
3
. Jak wiadomo funkcja ta jest
r´o˙zniczkowalna dla ka˙zdego x ∈ R. Zauwa˙zmy, ˙ze f
0
(0) = 0 mimo, i˙z w punkcie
x
0
= 0 funkcja ta nie ma ekstermum.
Z naszych rozwa˙za´
n wynika, ˙ze funkcja f mo˙ze posiada´c ekstremum lokalne
wÃla´sciwe jedynie w tych punktach, w kt´orych pochodna jest r´owna zero. Zauwa˙zmy
ponadto, ˙ze funkcja mo˙ze r´ownie˙z posiada´c eksteremum w punktach, w kt´orych
pochodna w og´ole nie istnieje.
PrzykÃlad 4.5.2. Rozaw˙zmy funkcje, f(x) =| x + 1 |. Zauwa˙zmy, ˙ze funkcja ta w
punkcie x
0
= −1 nie ma pochodnej. Istotnie
lim
h→0
+
f (−1 + h) − f (−1)
h
= lim
h→0
+
| h |
h
= 1
oraz
lim
h→0
−
f (−1 + h) − f (−1)
h
= lim
h→0
−
| h |
h
= −1.
Zauwa˙zmy jednak, ˙ze w punkcie x
0
= −1 nasza funkcja osia,ga minimum r´owne 0,
gdy˙z
^
x∈R
| x + 1 |≥ 0
oraz
| x + 1 |= 0 dla x = −1.
Pierwszy warunek dostateczny istnienia ekstremum
Twierdzenie 4.5.2. Je˙zeli funkcja f jest cia,gÃla i posiada pochodna, na pewnym
sa,siedztwie punktu x
0
oraz
W
δ
V
x
0
−δ<x<x
0
f
0
(x) < 0
W
δ
V
x
0
<x<x
0
+δ
f
0
(x) > 0
(4.5.1)
to funkcja f w punkcie x
0
ma minimum lokalne wÃla´sciwe,
je´sli natomiast zamiast powy˙zszego warunku zachodzi warunek
W
δ
V
x
0
−δ<x<x
0
f
0
(x) > 0
W
δ
V
x
0
<x<x
0
+δ
f
0
(x) < 0
(4.5.2)
73

to funkcja f w punkcie x
0
ma maksimum lokalne wÃla´sciwe.
Dow´
od. Niech x ∈ S(x
0
, δ). Na przedziale domknie,tym o ko´ncach x i x
0
funkcja
f jest cia,gÃla i ponadto jest ona r´o˙zniczkowalna wewna,trz tego przedziaÃlu, a zatem
speÃlnione sa, zaÃlo˙zenia twierdzenia Lagrange’a. Mamy wie,c
_
c∈<x,x
0
>
f (x) − f (x
0
) = f
0
(x
0
)(x − x
0
).
Zauwa˙zmy, ˙ze iloczyn po prawej stronie powy˙zszej r´owno´sci dla x < x
0
na mocy
warunku (4.5.1) jest dodatni. Podobnie dla x > x
0
. Wobec tego mamy
^
x∈S(x
0
,δ)
f (x) − f (x
0
) > 0,
co oznacza, ˙ze
^
x∈S(x
0
,δ)
f (x) > f (x
0
).
Zatem w punkcie x
0
funkcja osia,ga minimum lokalne.
W przypadku maksimum lokalnego dow´od przebiega w analogiczny spos´ob.
Wniosek 4.5.1. (warunek konieczny i dostateczny istnienia ekstremum funkcji)
Je˙zeli f
0
(x
0
) = 0 i ponadto
W
δ
V
x
0
−δ<x<x
0
f
0
(x) < 0
W
δ
V
x
0
<x<x
0
+δ
f
0
(x) > 0
to funkcja f w punkcie x
0
ma minimum lokalne wÃla´sciwe,
je´sli natomiast zamiast powy˙zszego warunku zachodzi warunek
W
δ
V
x
0
−δ<x<x
0
f
0
(x) > 0
W
δ
V
x
0
<x<x
0
+δ
f
0
(x) < 0
to funkcja f w punkcie x
0
ma maksimum lokalne wÃla´sciwe.
Drugi warunek dostateczny istnienia ekstremum
Twierdzenie 4.5.3. Je˙zeli funkcja f na pewnym otoczeniu punktu x
0
ma druga,
pochodna, r´o˙zna, od zera i cia,gÃla, w punkcie x
0
oraz je˙zeli f
0
(x
0
) = 0, to
1. funkcja f w punkcie x
0
ma maksimum lokalne wÃla´sciwe, gdy f
00
(x
0
) < 0,
74

1. funkcja f w punkcie x
0
ma minimum lokalne wÃla´sciwe, gdy f
00
(x
0
) > 0.
Zadanie 4.5.1. Wyznaczy´c ekstrema lokalne podanych funkcji
a(x) = e
x
+ e
−x
,
b(x) =
x
1 + x
2
,
c(x) = x
√
4 − x,
d(x) = 2 sin x + cos
2
x,
f (x) =
ln x
x
,
g(x) = (x − 5)e
x
,
h(x) = x
100
+ 2x
50
,
k(x) = sin
3
x + cos
3
x,
l(x) = x
x
.
Zadanie 4.5.2. Znale´z´c warto´s´c najwie,ksza, i najmniejsza, podanych funkcji na
wskazanych przedziaÃlach
f (x) = 2 sin x + sin 2x,
D
0,
3
2
π
E
;
g(x) = x − 2
√
x,
< 0, 5 >;
h(x) = x
2
ln x,
< 1, e >;
k(x) = arctgx −
x
2
, < 0, 2 >.
4.6. Wkle,sÃlo´s´c i wypukÃlo´s´c.
W paragrafie tym wykorzystamy rachunek r´o˙zniczkowy do okre´slenia poÃlo˙ze-
nia wykresu funkcji wzgle,dem siecznej lub wzgle,dem stycznej.
Niech funkcja f be,dzie okre´slona na pewnym przedziale (a, b).
Definicja 4.6.1. Powiemy, ˙ze funkcja f jest wypukÃla na przedziale (a, b), je´sli
^
a<x
1
<x
2
<b
^
0<λ<1
f (λx
1
+ (1 − λ)x
2
) ≤ λf (x
1
) + (1 − λ)f (x
2
).
W interpretacji geometrycznej oznacza to, ˙ze ka˙zdy odcinek siecznej wykresu le˙zy
wy˙zej lub pokrywa sie, z fragmentem wykresu poÃlo˙zonym mie,dzy punktami, przez
kt´ore przechodzi sieczna.
Je˙zeli w powy˙zszej definicji zachodzi nier´owno´s´c ostra to funkcje, f nazywa´c
be,dziemy ´sci´sle wypukÃla,.
Definicja 4.6.2. Powiemy, ˙ze funkcja f jest wkle,sÃla na przedziale (a, b), je´sli
^
a<x
1
<x
2
<b
^
0<λ<1
f (λx
1
+ (1 − λ)x
2
) ≥ λf (x
1
) + (1 − λ)f (x
2
).
W interpretacji geometrycznej oznacza to, ˙ze ka˙zdy odcinek siecznej wykresu le˙zy
ni˙zej lub pokrywa sie, z fragmentem wykresu poÃlo˙zonym mie,dzy punktami, przez
kt´ore przechodzi sieczna.
75

Je˙zeli w powy˙zszej definicji zachodzi nier´owno´s´c ostra to funkcje, f nazywa´c
be,dziemy ´sci´sle wkle,sÃla,.
Niech A oznacza punkt krzywej y = f (x) o odcie,tej x, a B - punkt o tej samej
odcie,tej, ale le˙za,cy na stycznej do krzywej y = f(x) w punkcie x
0
. W´owczas
rze,dne tych punkt´ow sa, r´owne odpowiednio
y
A
= f (x),
y
B
= f (x
0
) + f
0
(x
0
)(x − x
0
).
Zauwa˙zmy, ˙ze mo˙zemy poda´c r´ownowa˙zne definicje wypukÃlo´sci i wkle,sÃlo´sci funkcji.
Definicja 4.6.3. Powiemy, ˙ze funkcja f jest wypukÃla w punkcie x
0
je´sli
_
r>0
^
x∈S(x
0
,r)
y
A
− y
B
≥ 0,
to znaczy, gdy
_
r>0
^
x∈S(x
0
,r)
f (x) ≥ f (x
0
) + f
0
(x
0
)(x − x
0
).
Geometrycznie w my´sl tej definicji, wypukÃlo´s´c funkcji oznacza, ˙ze pewna cze,´s´c
krzywej y = f (x), odpowiadaja,ca dostatecznie maÃlemu sa,siedztwu punktu x
0
,
znajduje sie, nad styczna, do tej krzywej w punkcie x
0
.
Definicja 4.6.3. Powiemy, ˙ze funkcja f jest wkle,sÃla w punkcie x
0
je´sli
_
r>0
^
x∈S(x
0
,r)
y
A
− y
B
≤ 0,
to znaczy, gdy
_
r>0
^
x∈S(x
0
,r)
f (x) ≤ f (x
0
) + f
0
(x
0
)(x − x
0
).
Geometrycznie w my´sl tej definicji, wkle,sÃlo´s´c funkcji oznacza, ˙ze pewna cze,´s´c
krzywej y = f (x), odpowiadaja,ca dostatecznie maÃlemu sa,siedztwu punktu x
0
,
znajduje sie, pod styczna, do tej krzywej w punkcie x
0
.
Oczywi´scie, je´sli w powy˙zszych definicjach nier´owno´sci sa, ostre to funkcje, f
nazywamy odpowiednio ´sci´sle wypukÃla, lub ´sci´sle wkle,sÃla, w punkcie x
0
.
Je´sli funkcja jest wypukÃla (wkle,sÃla) w ka˙zdym punkcie przedziaÃlu (a, b), to
be,dziemy m´owi´c, ˙ze jest ona wypukÃla (wkle,sÃla) w przedziale (a, b).
Podamy teraz warunki na to by funkcja f byÃla funkcja, wypukÃla, ba,d´z wkle,sÃla,.
76

Warunek dostateczny wypukÃlo´sci
Twierdzenie 4.6.1. Niech funkcja f ma pochodna, pierwszego rze,du na przedziale
(a, b) oraz niech istnieje pochodna drugiego rze,du tej funkcji w ka˙zdym punkcie
tego przedziaÃlu taka, ˙ze
V
x∈(a,b)
f
00
(x
0
) 6= 0. Wtedy
1. je´sli
V
x∈(a,b)
f
00
(x
0
) > 0, to funkcja jest wypukÃla na przedziale (a, b),
2. je´sli
V
x∈(a,b)
f
00
(x
0
) < 0, to funkcja jest wkle,sÃla na przedziale (a, b).
Definicja 4.6.5. Powiemy, ˙ze punkt P (x
0
, f (x
0
)) jest punktem przegie,cia wykresu
funkcji f , wtedy i tylko wtedy, gdy istnieje taka liczba δ, ˙ze funkcja f jest ´sci´sle wy-
pukÃla na lewostronnym sa,siedztwie punktu x
0
i jest ´sci´sle wkle,sÃla na prawostron-
nym sa,siedztwie punktu x
0
lub odwrotnie.
Z definicji tej wynika, ˙ze punkt jest punktem przegie,cia wykresu funkcji, gdy
funkcja zmienia w nim rodzaj wypukÃlo´sci, czyli gdy wykres funkcji przechodzi z
jednej strony stycznej na druga,.
W kolejnym twierdzeniu podamy warunek konieczny istnienia punktu prze-
gie,cia.
Twierdzenie 4.6.2. Je˙zeli punkt (x
0
, f (x
0
)) jest punktem przegie,cia wykresu
funkcji i f
00
(x
0
) istnieje, to
f
00
(x
0
) = 0.
Znaczenie powy˙zszego warunku dla wyznaczania punkt´ow przegie,cia jest analog-
iczne do znaczenia twierdzenia Fermata dla wyznaczania ekstrem´ow funkcji. Je˙zeli
funkcja f ma cia,gÃla, pochodna, drugiego rze,du na pewnym przedziale, to punktem
przegie,cia mo˙ze by´c tylko taki punkt x
0
, kt´ory speÃlnia r´ownanie f
00
(x
0
) = 0.
Punkt ten jest punktem przegie,cia, gdy pochodna drugiego rze,du zmienia znak w
sa,siedztwie punktu x
0
.
Poni˙zszy przykÃlad pokazuje, ˙ze zerowanie sie, drugiej pochodnej jest tylko
warunkiem koniecznym na to by istniaÃl punkt przegie,cia.
PrzykÃlad 4.6.1. Rozwa˙zmy funkcje, f(x) = x
4
. Mamy f
0
(x) = 4x
3
i f
00
(x) =
12x
2
. Zatem f
00
(x) = 0 wtedy i tyklo wtedy, gdy x = 0. Jednak˙ze punkt x
0
= 0
nie jest punktem przegie,cia naszej funkcji, bo
V
x6=0
f
00
(x) > 0, co oznacza, ˙ze druga
pochodna w otoczeniu punktu x
0
= 0 nie zmienia znaku.
Zadanie 4.6.1. Zbadaj wypukÃlo´s´c podanych funkcji i wyznacz punkty przegie,cia
wykresu tych funkcji.
d(x) = e
−x
,
f (x) = arctgx,
g(x) = ln x,
h(x) = 3
x
,
k(x) =
x
1+x
2
,
l(x) = (ln x)
2
− ln x.
77

4.7. Asymptoty.
ZaÃl´o˙zmy, ˙ze funkcja f ma dziedzine, zÃlo˙zona, z sumy pewnych przedziaÃl´ow.
ponadto niech funkcja f be,dzie cia,gÃla i monotoniczna na tych przedziaÃlach. Wyz-
naczaja,c granice funkcji f w punktach ko´ncowych dziedziny uzyskujemy dane
pozwalaja,ce naszkicowa´c wykres funkcji.
Niech funkcja f be,dzie okre´slona i cia,gÃla na pewnym sa,siedztwie punktu
wÃla´sciwego c.
Definicja 4.7.1. Je˙zeli funkcja f jest cia,gÃla w prawostronnym sa,siedztwie punktu
c oraz
lim
x→c
+
f (x) = +∞
lub
lim
x→c
+
f (x) = −∞,
to powiemy, ˙ze prosta x = c jest prawostronna, asymptota, pionowa, wykresu funkcji
f .
Definicja 4.7.2. Je˙zeli funkcja f jest cia,gÃla w lewostronnym sa,siedztwie punktu
c oraz
lim
x→c
−
f (x) = +∞
lub
lim
x→c
−
f (x) = −∞,
to powiemy, ˙ze prosta x = c jest lewostronna, asymptota, pionowa, wykresu funkcji
f .
Je˙zeli prosta x = c jest prawostronna, i lewostronna, asymptota, pionowa, wykresu
funkcji f , to powiemy, ˙ze jest ona obustronna, asymptota, pionowa,.
Z powy˙zszych definicji wynika, ˙ze wykres funkcji mo˙ze posiada´c asymptoty
pionowe jedynie w sko´
nczonych kra´
ncach dziedziny.
Definicja 4.7.3.
Je˙zeli funkcja f jest cia,gÃla w pewnym sa,siedztwie punktu
niewÃla´sciwego +∞ i je˙zeli istnieje prosta y = ax + b taka, ˙ze
lim
x→+∞
[f (x) − (ax + b)] = 0
to gdy a 6= 0, prosta, y = ax + b nazywamy asymptota, uko´sna, prawostronna,
wykresu funkcji f , a gdy a = 0, to wtedy ta, prosta, nazywamy asymptota, pozioma,
prawostronna, wykresu funkcji f.
Definicja 4.7.4.
Je˙zeli funkcja f jest cia,gÃla w pewnym sa,siedztwie punktu
niewÃla´sciwego −∞ i je˙zeli istnieje prosta y = ax + b taka, ˙ze
lim
x→−∞
[f (x) − (ax + b)] = 0
78

to gdy a 6= 0, prosta, y = ax + b nazywamy asymptota, uko´sna, lewostronna,
wykresu funkcji f , a gdy a = 0, to wtedy ta, prosta, naywamy asymptota, pozioma,
lewostronna, wykresu funkcji f.
Zauwa˙zmy, ˙ze asymptota pozioma jest szczeg´olnym przypadkiem asymptoty uko´s-
nej. Zatem istnienie asymptoty poziomej wyklucza istnienie asymptoty uko´snej i
na odwr´ot.
Ponadto, poniewa˙z istnienie asymptot uko´snych, a tym samym i poziomych
zale˙zy od zachowania sie, funkcji w niesko´nczono´sciach, to mo˙ze zdarzy´c sie, tak, ˙ze
wykres funkcji przetnie taka, asymptote,, by´c mo˙ze nawet wielokrotnie, w punktach
dziedziny dostatecznie odlegÃlych od punkt´ow niewÃla´sciwych.
Niemo˙zliwe jest natomiast by wykres funkcji m´ogÃl przecia,´c asymptote, piono-
wa,, gdy˙z jej istnienie wia,˙ze sie, z istnieniem granicy funkcji w punkcie, kt´ory nie
nale˙zy do dziedziny funkcji.
Naste,puja,ce twierdzenie podaje warunek konieczny i dostateczny istnienia
asymptoty uko´snej funkcji f .
Twierdzenie 4.7.1. Prosta y = ax + b jest asymptota, uko´sna, wykresu funkcji f
wtedy i tylko wtedy, gdy
a = lim
x→±∞
f (x)
x
i
b = lim
x→±∞
£
f (x) − ax
¤
.
Dow´
od. ZaÃl´o˙zmy najpierw, ˙ze prosta y = ax + b jest asymptota, uko´sna, prawo-
stronna, wykresu funkcji f. A zatem z definicji 4.7.3. mamy
lim
x→+∞
[f (x) − (ax + b)] = 0.
Korzystaja,c z twierdzenia o dziaÃlaniach arytmerycznych na granicach sko´nczonych
otrzymamy
lim
x→+∞
f (x) − (ax + b)
x
=
h 0
+∞
i
= 0.
Z drugiej strony mamy
lim
x→+∞
f (x) − (ax + b)
x
= lim
x→+∞
³ f(x)
x
− a −
b
x
´
= lim
x→+∞
f (x)
x
− a.
Zatem
lim
x→+∞
f (x)
x
− a = 0.
79

Co oznacza, ˙ze
lim
x→+∞
f (x)
x
= a.
Korzystaja,c ponownie z twierdzenia o dziaÃlaniach arytmerycznych na granicach
sko´
nczonych dostajemy
lim
x→+∞
[f (x) − ax] = lim
x→+∞
[f (x) − (ax + b) + b] = b.
Tym samym warunek konieczny zostaÃl udowodniony.
Aby udowodni´c warunek dostateczny zaÃl´o˙zmy, ˙ze
a = lim
x→+∞
f (x)
x
i
b = lim
x→+∞
£
f (x) − ax
¤
.
Zatem z drugiej r´owno´sci dostajemy
lim
x→+∞
[f (x) − ax − b] = 0,
co daje nam
lim
x→+∞
[f (x) − (ax + b)] = 0.
Zatem prosta y = ax + b jest asymptota, uko´sna, prawostronna, wykresu funkcji f.
W przypadku asymptoty lewostronnej dow´od przebiega analogicznie.
Z twierdzenia 4.7.1 wynika, ˙ze je´sli jedna z wymienionych granic nie istnieje
lub jest niewÃla´sciwa, to wykres funkcji nie posiada asymptoty uko´snej. Ponadto
z twierdzenia 4.7.1. otrzymujemy naste,puja,cy warunek konieczny i dostateczny
istnienia asymptoty poziomej.
Wniosek 4.7.1. Prosta y = b jest asymptota, pozioma, lewostronna, wykresu
funkcji f wtedy i tylko wtedy, gdy
lim
x→−∞
f (x) = b.
Prosta y = b jest asymptota, pozioma, prawostronna, wykresu funkcji f wtedy i
tylko wtedy, gdy
lim
x→+∞
f (x) = b.
Oczywi´scie je´sli powy˙zsze granice nie istnieja, lub sa, niewÃla´sciwe, to wykres funkcji
f nie ma asymptot poziomych.
80

Zadanie 4.7.1. Wyznacz wszystkie asymptoty wykresu podanych funkcji
a(x) =
sin
2
x
x
,
b(x) = e
1
x
,
c(x) = ln(x − 4),
d(x) =
√
x
2
− 1,
f (x) =
sin x
x
2
,
g(x) =
x
arctgx
,
h(x) = x ln
³
e +
1
x
´
,
k(x) = x − arctgx,
l(x) =
1
e
x
− 1
.
4.8. Funkcja okre´slona parametrycznie i jej pochodna.
Niech dane be,da, dwa r´ownania
½
x = ϕ(t),
y = ψ(t),
(4.8.1)
gdzie ϕ i ψ sa, pewnymi funkcjami, a t jest liczba, z pewnego przedziaÃlu < a, b >.
W´owczas ka˙zdej warto´sci t ∈< a, b > odpowiadaja, dwie warto´sci x i y. Je˙zeli x i
y be,dziemy traktowa´c jako wsp´oÃlrze,dne punktu pÃlaszczyzny, to ka˙zdej warto´sci t
odpowiada pewien punkt pÃlaszczyzny OXY . Wobec tego r´ownania (4.8.1) opisuja,
pewna, krzywa, na pÃlaszczy´znie. R´ownania (4.8.1) nazywamy r´ownaniami parame-
trycznymi krzywej, a t nazywamy parametrem.
Zauwa˙zmy, ˙ze je´sli funkcja ϕ jest r´o˙znowarto´sciowa na przedziale < a, b >, to
istnieje do niej funkcja odwrotna, a wie,c z r´ownania x = ϕ(t) mo˙zemy wyznaczy´c
parametr t = ϕ
−1
(x). Wtedy y = ψ(ϕ
−1
(x)). Mo˙zemy wie,c znale´z´c zale˙zno´s´c
funkcyjna, mie,dzy zmiennymi x i y postaci y = f(x). Funkcja f = ψ ◦ ϕ
−1
jest
w´owczas okre´slona parametrycznie r´ownaniami (4.8.1). Podobnie je˙zeli funkcja
ψ jest funkcja, r´o˙znowarto´sciowa, na przedziale < a, b >, to t = ψ
−1
(y) oraz
x = ϕ(ψ
−1
(y)). Wtedy r´ownie˙z istnieje zale˙zno´s´c funkcyjna x = h(y) mie,dzy
zmiennymi x i y. Funkcja h jest funkcja, okre´slona, parametrycznie.
PrzykÃlad 4.8.1. Rozwa˙zmy okra,g o ´srodku w punkcie (0, 0) i promieniu dÃlugo´sci
1. R´ownanie tego okre,gu ma naste,puja,ca, posta´c
x
2
+ y
2
= 1.
Zauwa˙zmy, ˙ze rozwa˙zany okra,g mo˙zemy okre´sli´c naste,puja,cymi r´ownaniami para-
metrycznymi
½
x = cos t,
y = sin t,
(4.8.2)
gdzie t ∈< 0, 2π).
81

Ponadto dla y ≥ 0 mamy y =
√
1 − x
2
, co zachodzi, gdy t ∈< 0, π). A
zatem dla t ∈< 0, π) funkcja f (x) =
√
1 − x
2
jest okre´slona parametrycznie
przez r´ownania (4.8.2). Oczywi´scie na przedziale < 0, π) funkcja ϕ(t) = cos t
jest r´o˙znowarto´sciowa. R´ownie˙z dla t ∈ (π, 2π) funkcja ϕ jest r´o˙znowarto´sciowa, a
zatem i w tym przedziale mo˙zemy wyznaczy´c funkcje, f okre´slona, parametrycznie
przez r´ownania (4.8.2).
ZaÃl´o˙zmy, ˙ze funkcja ϕ wyste,puja,ca w r´ownaniach (4.8.1) ma pochodna, staÃlego
znaku na przedziale < a, b >. Oznacza to, ˙ze na tym przedziale funkcja ϕ jest
monotoniczna, a tym samym jest to funkcja r´o˙znowarto´sciowa. Wobec tego istnieje
funkcja f okre´slona parametrycznie r´ownaniami (4.8.1). W´owczas korzystaja,c z
twierdzenia o pochodnej funkcji zÃlo˙zonej i twierdzenia o pochodnej funkcji odwrot-
nej mamy
f
0
(x) =
h
ψ(ϕ
−1
(x))
i
0
= ψ
0
(t)
h
ϕ
−1
(x)
i
0
=
ψ
0
(t)
ϕ
0
(t)
.
Ponadto otrzymujemy
f
00
(x) =
h ψ
0
(t)
ϕ
0
(t)
i
0
=
ψ
00
(t)ϕ
0
(t) − ψ
0
(t)ϕ
00
(t)
[ϕ
0
(t)]
2
h
ϕ
−1
(x)
i
0
=
ψ
00
(t)ϕ
0
(t) − ψ
0
(t)ϕ
00
(t)
[ϕ
0
(t)]
3
.
Podobnie gdy funkcja ψ na przedziale < a, b > ma pochodna, staÃlego znaku, to
funkcja h = ϕ ◦ ψ
−1
okre´slona r´ownaniami (4.8.1) istnieje, a jej pochodne pier-
wszego i drugiego rze,du okre´slaja, wzory
h
0
(y) =
ϕ
0
(t)
ψ
0
(t)
,
h
00
(y) =
ϕ
00
(t)ψ
0
(t) − ϕ
0
(t)ψ
00
(t)
[ψ
0
(t)]
3
.
Poni˙zej podamy r´ownania parametryczne najcze,´sciej spotykanych krzywych
82

PrzykÃlad 4.8.2.
1. okra,g o´srodku w punkcie (a, b) i promieniu dÃlugo´sci r
½
x = a + r cos t,
y = b + r sin t,
t ∈< 0, 2π),
2. elipsa o osiach a i b
½
x = a cos t,
y = b sin t,
t ∈< 0, 2π),
3. hiperbola o osiach a i b
½
x = a cosh t,
y = b sinh t,
t ∈ R,
4. asteroida
½
x = a cos
3
t,
y = a sin
3
t,
t ∈< 0, 2π),
5. li´s´c Kartezjusza
x =
3at
t
3
+ 1
,
y =
3at
2
t
3
+ 1
,
t ∈ R,
6. cykloida
½
x = a(t − sin t),
y = a(1 − cos t),
t ∈ R,
83

7. kardioida
½
x = a(2 cos t − cos 2t),
y = a(2 sin t − sin 2t),
t ∈< 0, 2π).
4.9. Badanie krzywych danych parametrycznie.
Niech dana be,dzie krzywa okre´slona parametrycznie r´ownaniami (4.8.1).
Chca,c naszkicowa´c ta, krzywa, w ukÃladzie wsp´oÃlrze,dnych prostoka,tnych przedziaÃl
< a, b > dzielimy na podprzedziaÃly na kt´orych jedna z funkcji ϕ lub ψ ma pochodna,
staÃlego znaku. Punkty, w kt´orych obie funkcje maja, zerowe pochodne nazywamy
punktami osobliwymi, gdy˙z w takich punktach nie mo˙zemy wyznaczy´c ani funkcji
f , ani h. Je˙zeli dodatkowo w punkcie osobliwym pochodne drugiego rze,du funkcji
ϕ i ψ sa, r´o˙zne od zera, to taki punkt nazywa´c be,dziemy punktem zwrotu. W
punkcie zwrotu isnieje styczna do krzywej, a jej r´ownanie ma naste,puja,ca, posta´c
ψ
00
(t
0
)[x − ϕ(t
0
)] − ϕ
00
(t
0
)[y − ψ(t
0
)] = 0,
gdzie t
0
jest warto´scia, parametru odpowiadaja,ca, punktowi zwrotu.
Je˙zeli krzywa jest okre´slona r´ownaniami parametrycznymi (4.8.1), to asymp-
toty tej krzywej wyznaczamy w naste,puja,cy spos´ob.
Je˙zeli istnieja, granice
lim
t→t
0
ϕ(t) = c < ∞
lim
t→t
0
ψ(t) = ±∞,
to prosta x = c jest asymptota, pionowa, krzywej (4.8.1).
Je˙zeli natomiast istnieja, granice
lim
t→t
0
ψ(t) = b < ∞
lim
t→t
0
ϕ(t) = ±∞,
to prosta y = b jest asymptota, pozioma, krzywej (4.8.1).
Asymptota uko´sna y = ax + b krzywej (4.8.1) istnieje wtedy, gdy
lim
t→t
0
ϕ(t) = ±∞
lim
t→t
0
ψ(t) = ±∞
i w´owczas
a = lim
t→t
0
ψ(t)
ϕ(t)
i b = lim
t→t
0
[ψ(t) − aϕ(t)].
Aby zbada´c krzywa, dana, r´ownaniami (4.8.1) nale˙zy
84

1
o
. Znale´z´c dziedziny funkcji ϕ i ψ, a tym samym wyznaczy´c zakres zmienno´sci
parametru t.
2
o
. Wyznaczy´c asymptoty krzywej.
3
o
. Wyznaczy´c przedziaÃly staÃlego znaku pochodnych pierwszego rze,du funkcji ϕ
i ψ.
4
o
. Znale´z´c punkty zwrotu i styczne w tych punktach.
5
o
. Wyznaczy´c pochodne pierwszego i drugiego rze,du funkcji f .
6
o
. Zbada´c funkcje, f, korzystaja,c z metod badania funkcji jednej zmiennej.
Zadanie 4.9.1. Zbadaj podane krzywe i naszkicuj je w ukÃladzie wsp´oÃlrze,dnych
prostoka,tnych
a)
½
x = 2t − t
2
,
y = 3t − t
3
;
c)
x =
2 + t
2
1 + t
2
,
y =
t
3
1 + t
2
;
b)
½
x = t + e
−t
,
y = 2t + e
−2t
;
d)
x =
t
2
t − 1
,
y =
t
t
2
− 1
.
85

5. RACHUNEK CAÃLKOWY FUNKCJI JEDNEJ ZMIENNEJ.
W pia,tym rodziale zdefiniujemy poje,cie caÃlki oznaczonej i nieoznaczonej, a
naste,pnie podamy zastosowania caÃlki oznaczonej do obliczania p´ol powierzchni,
dÃlugo´sci krzywej i obje,to´sci bryÃl obrotowych.
5.1. CaÃlka jako funkcja pierwotna nieoznaczona.
W wielu zagadnieniach nauki i techniki mamy doczynienia z wyznaczeniem
funkcji o podanej pochodnej.
Definicja 5.1.1. Funkcje, F nazywamy funkcja, pierwotna, funkcji f w danym
przedziale I, je´sli
^
x∈I
F
0
(x) = f (x).
PrzykÃlad 5.1.1. Zauwa˙zmy, ˙ze
[sin x]
0
= cos x,
[sin x + 2]
0
= cos x,
[sin x − π]
0
= cos x.
Zatem funkcja, pierwotna, funkcji f(x) = cos x jest ka˙zda funkcja postaci F(x) =
sin x + c, gdzie c jest pewna, staÃla, rzeczywista,.
Twierdzenie 5.1.1. Niech F be,dzie funkcja, pierwotna, do funkcji f na danym
przedziale I. Wtedy
1. G(x) = F (x) + c, gdzie c ∈ R jest dowolna, staÃla,, jest funkcja, pierwotna, funkcji
f na I.
2. Ka˙zda, funkcje, pierwotna, do funkcji f na przedziale I mo˙zna przedstawi´c w
postaci F (x) + c, gdzie c jest dowolna, staÃla,.
Dow´
od. ZaÃl´o˙zmy, ˙ze funkcja F jest pierwotna do funkcji f na danym przedziale
I. Wtedy funkcja G(x) = F (x) + c jest r´ownie˙z funkcja, pierwotna, do funkcji f,
gdy˙z
G
0
(x) = [F (x) + c] = F
0
(x) = f (x).
Je˙zeli dwie funkcje F i G sa, funkcjami pierwotnym funkcji f, to r´o˙znia, sie, one
tylko staÃla,, co wynika z definicji 5.1.1.
Z powy˙zszego twierdzenia wynika, ˙ze wystarczy znale´z´c tylko jedna, funkcje,
pierwotna, do danej funkcji f, aby zna´c wszystkie inne funkcje pierwotne, albowiem
r´o˙znia, sie, one mie,dzy soba, tylko staÃlym skÃladnikiem.
Podamy teraz warunek dostateczny istnienia funkcji pierwotnej.
86

Twierdzenie 5.1.2. Je˙zeli funkcja f jest cia,gÃla na przedziale I, to ma na tym
przedziale funkcje, pierwotna,.
Definicja 5.1.2. Niech F be,dzie funkcja, pierwotna, funkcji f na danym przedziale
I. CaÃlka, nieoznaczona, funkcji f nazywamy zbi´or funkcji
{F (x) + c : c ∈ R}
i oznaczamy
Z
f (x)dx.
Iloczyn f (x)dx nazywa sie, wyra˙zeniem podcaÃlkowym, a funkcje, f(x) nazywa sie,
funkcja, podcaÃlkowa,.
WÃlasno´sci caÃlki nieoznaczonej podamy w naste,puja,cych twierdzeniach. Wy-
nikaja, one z definicji funkcji pierwotnej oraz z wÃlasno´sci pochodnej.
Twierdzenie 5.1.3. Niech f ma funkcje, pierwotna, na danym przedziale I. Wte-
dy
1.
V
x∈I
h R
f (x)dx
i
0
= f (x),
2.
V
x∈I
R
f
0
(x)dx = f (x) + c,
c ∈ R.
Twierdzenie 5.1.4. Niech funkcje f i g maja, funkcje pierwotne i niech a, b ∈ R
be,da, pewnymi staÃlymi. Wtedy
Z
af (x) + bg(x)dx = a
Z
f (x)dx + b
Z
g(x)dx.
Zauwa˙zmy, ˙ze ka˙zdy wz´or rachunku r´o˙zniczkowego orzekaja,cy, ˙ze pochodna, pewnej
funkcji F jest funkcja f , prowadzi do odpowiedniego wzoru rachunku caÃlkowego.
Wobec tego mo˙zemy uÃlo˙zy´c naste,puja,ca, tablice, caÃlek.
87
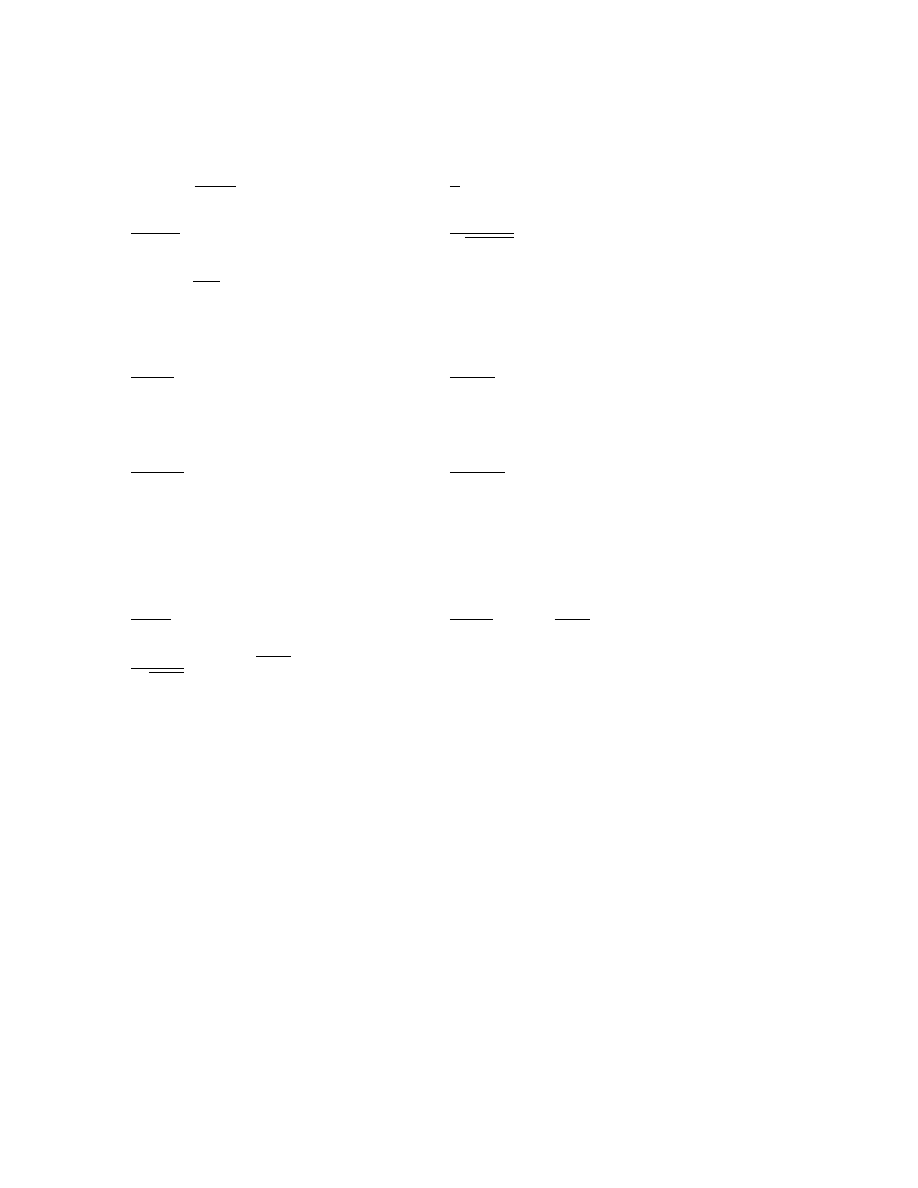
CaÃlki wa˙zniejszych funkcji elementarnych
Z
x
n
dx =
x
n+1
n + 1
+ c, n 6= 1
Z
1
x
dx = ln | x | +c
Z
1
1 + x
2
dx = arctgx + c
Z
1
√
1 − x
2
dx = arcsin x + c
Z
a
x
dx =
a
x
ln a
+ c
Z
e
x
dx = e
x
+ c
Z
sin xdx = − cos x + c
Z
cos xdx = sin x + c
Z
1
sin
2
x
dx = −ctgx + c
Z
1
cos
2
x
dx = tgx + c
Z
sinh xdx = cosh x + c
Z
cosh xdx = sinh x + c
Z
1
sinh
2
x
dx = −ctghx + c
Z
1
cosh
2
x
dx = tghx + c
Ponadto korzystaja,c z reguÃl r´o˙zniczkowania funkcji zÃlo˙zonych mo˙zemy wyprowa-
dzi´c wzory na caÃlkowanie wa˙zniejszych typ´ow funkcji.
Z
f
0
(x)
f (x)
dx = ln | f (x) | +c
Z
f
0
(x)
f
2
(x)
dx = −
1
f (x)
+ c
Z
f
0
(x)
p
f (x)
dx = 2
p
f (x) + c
5.2. CaÃlkowanie przez cze,´sci i przez podstawienie.
Na pocza,tku podamy jeden z najsilniejszych sposob´ow caÃlkowania, tj. metode,
caÃlkowania przez podstawienie zwana, czasami caÃlkowaniem przez zmiane, zmiennej.
Twierdzenie 5.2.1. Niech funkcja f cia,gÃla na danym przedziale I ma funkcje,
pierwotna, F i niech funkcja ϕ ma cia,gÃla, pochodna,. Wtedy
Z
f (ϕ(x))ϕ
0
(x)dx = F (ϕ(x)) + c.
Dow´
od. Niech F
0
(x) = f (x). Zauwa˙zmy, ˙ze z twierdzenia o pochodnej funkcji
zÃlo˙zonej mamy
h
F (ϕ(x)) + c
i
0
= F
0
(ϕ(x))ϕ
0
(x) = f (ϕ(x))ϕ
0
(x).
88

Zatem mamy teze, twierdzenia.
Druga, bardzo u˙zyteczna, metoda, caÃlkowania jest caÃlkowanie przez cze,´sci.
Twierdzenie 5.2.2. Je˙zeli funkcje f i g maja, cia,gÃle pochodne, to
Z
f (x)g
0
(x)dx = f (x)g(x) −
Z
f
0
(x)g(x)dx.
Dow´
od. Niech funkcje f i g maja, cia,gÃle pochodne. Wtedy mamy
[f (x)g(x)]
0
= f
0
(x)g(x) + f (x)g
0
(x).
CaÃlkuja,c obustronnie otrzymujemy
Z
[f (x)g(x)]
0
dx =
Z
[f
0
(x)g(x) + f (x)g
0
(x)]dx.
Korzystaja,c z twierdzenia 5.1.3 oraz 5.1.4 dostajemy
f (x)g(x) + c =
Z
f
0
(x)g(x)dx +
Z
f (x)g
0
(x)dx,
co daje nam teze, twierdzenia, bo staÃla c wyste,puje w obu caÃlkach.
Zadanie 5.2.1. Oblicz podane caÃlki stosuja,c wz´or na caÃlkowanie przez podsta-
wienie
a)
Z
arctg
2
x
1 + x
2
dx,
d)
Z
(2x + 3) cos(x
2
+ 3x)dx,
b)
Z
sin xe
cos x
dx,
e)
Z
1
√
4x − 5
dx,
c)
Z
1
3x + 7
dx,
f )
Z
tgxdx.
Zadanie 5.2.2. Oblicz podane caÃlki stosuja,c wz´or na caÃlkowanie przez cze,´sci
a)
Z
x
2
sin xdx,
d)
Z
x
3
cos xdx,
b)
Z
e
x
cos xdx,
e)
Z
arctgxdx,
c)
Z
ln xdx,
f )
Z
x
3
ln xdx.
89
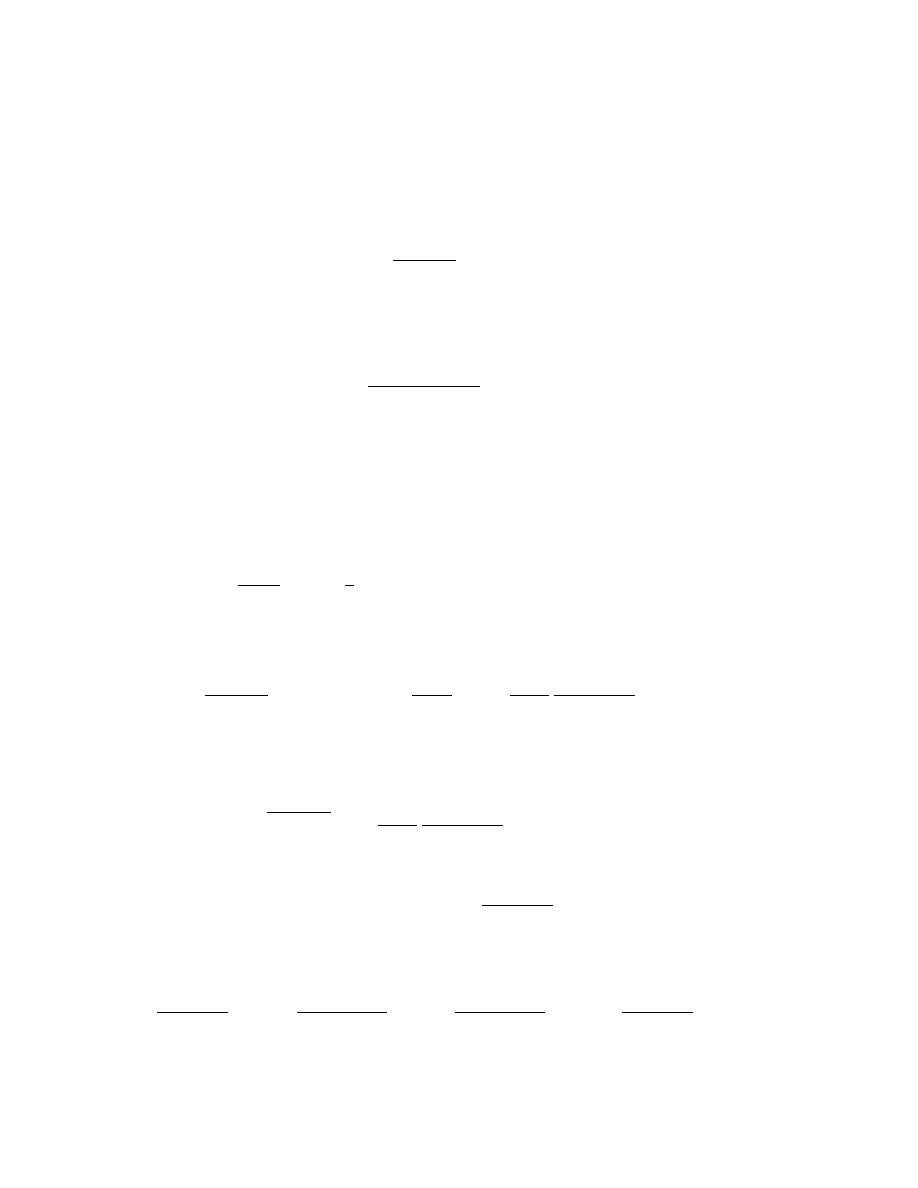
5.3. CaÃlkowanie funkcji wymiernych.
Opiszemy teraz metody caÃlkowania funkcji wymiernych, tj. funkcji kt´ore sa,
ilorazami dw´och wielomian´ow. W´sr´od funkcji wymiernych wyr´o˙zniamy mie,dzy
innymi funkcje zwane uÃlamkami prostymi pierwszego rodzaju postaci
A
(x − a)
r
,
gdzie A i a sa, pewnymi staÃlymi rzeczywistymi, a r jest staÃla, naturalna,
oraz funkcje wymierne zwane uÃlamkami prostymi drugiego rodzaju postaci
Ax + B
(x
2
+ px + q)
r
,
gdzie A i B sa, pewnymi staÃlymi rzeczywistymi, r jest staÃla, naturalna,, a staÃle p i
q speÃlniaja, warunek p
2
− 4q < 0.
Najpierw zajmiemy sie, obliczeniem caÃlki z uÃlamk´ow prostych pierwszego ro-
dzaju. ZaÃl´o˙zmy, ˙ze r = 1. Wtedy korzystaja,c ze wzoru na caÃlkowanie przez
podstawienie kÃlada,c t = x − a otrzymujemy
Z
A
x − a
= A
Z
1
t
dt = A ln | t | +c = A ln | x − a | +c.
Niech teraz r 6= 1. KÃlada,c jak wy˙zej t = x − a dostajemy
Z
A
(x − a)
r
= A
Z
t
−r
dt = A
t
1−r
1 − r
+ c =
A
1 − r
1
(x − a)
r−1
+ c.
Wobec tego mamy
Z
A
(x − a)
r
=
A ln | x − a | +c,
r = 1,
A
1 − r
1
(x − a)
r−1
+ c, r ≥ 2.
Do obliczania caÃlek z uÃlamk´ow prostych drugiego rodzaju potrzebna jest umie-
je,tno´s´c caÃlkowania funkcji wymiernej postaci
1
(1 + x
2
)
r
, r ≥ 2. Funkcje, taka,
caÃlkujemy korzystaja,c ze wzoru rekurencyjnego, kt´ory otrzymujemy w naste,puja,cy
spos´ob
Z
1
(1 + x
2
)
r
dx =
Z
1 + x
2
− x
2
(1 + x
2
)
r
dx =
Z
1
(1 + x
2
)
r−1
dx −
Z
x
x
(1 + x
2
)
r
dx.
90

Druga, z caÃlek obliczamy korzystaja,c ze wzoru na caÃlkowanie przez cze,´sci kÃlada,c
f (x) = x,
g
0
(x) =
x
(1 + x
2
)
r
,
f
0
(x) = 1,
g(x) =
1
2
(1 + x
2
)
1−r
1 − r
.
Mamy w´owczas
Z
x
x
(1 + x
2
)
r
dx =
x
2
(1 + x
2
)
1−r
1 − r
−
1
2
Z
(1 + x
2
)
1−r
1 − r
dx
Zatem dostajemy
Z
1
(1 + x
2
)
r
dx =
x
2
(1 + x
2
)
1−r
r − 1
+
³
1 +
1
2(1 − r)
´ Z
1
(1 + x
2
)
r−1
dx
=
x
2
(1 + x
2
)
1−r
r − 1
+
2r − 3
2r − 2
Z
1
(1 + x
2
)
r−1
dx.
Wobec tego otrzymali´smy naste,puja,cy wz´or rekurencyjny
Z
1
(1 + x
2
)
r
dx =
x
2(r − 1)(1 + x
2
)
r−1
+
2r − 3
2r − 2
Z
1
(1 + x
2
)
r−1
dx.
(5.3.1)
Podamy teraz metody caÃlkowania uÃlamk´ow prostych drugiego rodzaju. Dla r = 1
mamy
Z
Ax + B
x
2
+ px + q
dx =
A
2
Z
2x + p
x
2
+ px + q
dx +
³
B −
Ap
2
´ Z
1
x
2
+ px + q
dx.
Pierwsza, z caÃlek obliczamy przez podatawienie t = x
2
+ px + q otrzymuja,c
Z
2x + p
x
2
+ px + q
dx = ln | x
2
+ px + q | +c.
Aby wyznaczy´c druga, caÃlke, zauwa˙zmy, ˙ze
x
2
+ px + q =
4q − p
2
4
h³ 2x + p
p
4q − p
2
´
2
+ 1
i
.
Zatem kÃlada,c t =
2x+p
√
4q−p
2
dostajemy
Z
1
x
2
+ px + q
dx =
2
p
4q − p
2
4q − p
2
Z
1
1 + t
2
dt
91

=
2
p
4q − p
2
4q − p
2
arctgt + c =
2
p
4q − p
2
4q − p
2
arctg
2x + p
p
4q − p
2
+ c.
Ostatecznie mamy wie,c
Z
Ax + B
x
2
+ px + q
dx =
A
2
ln | x
2
+ px + q | +
³
B −
Ap
2
´ 2
p
4q − p
2
4q − p
2
arctg
2x + p
p
4q − p
2
+ c.
W przypadku, gdy r ≥ 2 poste,pujemy podobnie rozbijaja,c caÃlke, na sume, dw´och
caÃlek
Z
Ax + B
(x
2
+ px + q)
r
dx =
A
2
Z
2x + p
(x
2
+ px + q)
r
dx +
³
B −
Ap
2
´ Z
1
(x
2
+ px + q)
r
dx.
Pierwsza, z nich caÃlkujemy jak wy˙zej przez podstawienie t = x
2
+px+q otrzymuja,c
Z
2x + p
(x
2
+ px + q)
r
dx =
1
1 − r
(x
2
+ px + q)
1−r
+ c.
Druga, r´ownie˙z caÃlkujemy przez podstawienie kÃlada,c t =
2x+p
√
4q−p
2
. Wtedy mamy
Z
1
(x
2
+ px + q)
r
dx =
4
r
p
4q − p
2
2(4q − p
2
)
r
Z
1
(1 + t
2
)
r
dt.
Korzystaja,c dalej ze wzoru rekurencyjnego (5.3.1) ostatecznie otrzymamy
Z
Ax + B
(x
2
+ px + q)
r
dx =
A
2
1
1 − r
(x
2
+ px + q)
1−r
+
³
B −
Ap
2
´
4
4q − p
2
h 2x + p
4(r − 1)
1
(x
2
+ px + q)
r−1
+
2r − 3
2r − 2
Z
1
(x
2
+ px + q)
r−1
dx
i
.
Posiadaja,c umieje,tno´s´c caÃlkowania uÃlamk´ow prostych mo˙zemy wyznaczy´c funkcje,
pierwotna, dowolnej funkcji wymiernej, gdy˙z mo˙zna ja, przedstawi´c jako sume, wielo-
mianu i uÃlamk´ow prostych pierwszego i drugiego rodzaju. Niech dana be,dzie
funkcja wymierna f (x) =
Q
n
(x)
P
m
(x)
. Je˙zeli stopie´
n licznika jest nie mniejszy ni˙z
stopie´
n mianownika (n ≥ m), to dziela,c wielomian Q
n
(x) przez wielomian P
m
(x)
otrzymujemy
Z
f (x)dx =
Z
W
n−m
(x)dx +
Z
V
k
(x)
P
m
(x)
dx,
92

gdzie k < m. Zatem wystarczy dokÃladniej om´owi´c przypadek gdy stopie´
n licznika
jest mniejszy ni˙z stopie´
n mianownika (n < m), tj. przypadek funkcji wymiernej
wÃla´sciwej. W takim przypadku, aby scaÃlkowa´c funkcje, wymierna, nale˙zy rozÃlo˙zy´c
ja, na uÃlamki proste
f (x) =
r
X
i=1
³ A
i1
x − x
i
+
A
i2
(x − x
i
)
2
+ . . . +
A
ik
i
(x − x
i
)
k
i
´
+
s
X
i=1
³ B
i1
x + C
i1
x
2
+ p
i
x + q
i
+
B
i2
x + C
i2
(x
2
+ p
i
x + q
i
)
2
+ . . . +
B
il
i
x + C
il
i
(x
2
+ p
i
x + q
i
)
l
i
´
.
(5.3.2)
Nieznane staÃle A
ij
, B
ij
, C
ij
wyznaczamy tak zwana, metoda, wsp´oÃlczynnik´ow nieoz-
naczonych. Metoda ta polega na pomno˙zeniu r´ownania (5.3.2) przez mianownik
funkcji wymiernej f (x). Otrzymane w ten spos´ob r´ownanie jest r´owno´scia, dw´och
wielomian´ow. Po uporza,dkowaniu tych wielomian´ow budujemy ukÃlad r´owna´n
por´ownuja,c wsp´oÃlczynniki stoja,ce przy tych samych pote,gach x. Rozwia,zanie
otrzymanego rozkÃladu daje nam wsp´oÃlczynniki poszukiwanego rozkÃldu funkcji
wymiernej wÃla´sciwej na uÃlamki proste.
Podsumowuja,c ten paragraf podamy pewien algorytm caÃlkowania funkcji wy-
miernej.
Algorytm caÃlkowania funkcji wymiernej
1
o
. Funkcje, wymierna, zapisujemy w postaci sumy wielomianu (zerowego, gdy
stopie´
n licznika jest mniejszy od stopnia mianownika) i funkcji wymiernej
wÃla´sciwej.
2
o
. Mianownik funkcji wymiernej wÃla´sciwej rozkÃladamy na czynniki nierozkÃladal-
ne.
3
o
. Zapisujemy rozkÃlad teoretyczny funkcji na uÃlamki proste.
4
o
. Znajdujemy nieznane wsp´oÃlczynniki rozkÃladu teoretycznego.
5
o
. Obliczamy caÃlki z wyznaczonych uÃlamk´ow prostych.
6
o
. Porza,dkujemy otrzymane wyniki.
Zadanie 5.3.1. Oblicz podane caÃlki
a)
Z
x
4
+ 6x
3
+ 10x
2
+ x
x
2
+ 6x + 10
dx,
d)
Z
x
4
+ 1
x
4
− 1
dx,
b)
Z
x
5
+ x
4
− 8
x
3
− 4x
dx,
e)
Z
x
2
x
2
− 6x + 10
dx,
c)
Z
x
3
+ x
2
+ x + 2
(x
2
+ 1)(x
2
+ 1)
dx,
f )
Z
x
4
+ 2x
2
+ 4
(x
2
+ 1)
3
dx.
93
5.4. CaÃlkowanie niewymierno´sci stopnia drugiego - podstawienia Eu-
lera.
Om´owili´smy sposoby caÃlkowania wyra˙ze´
n wymiernych. W dalszym cia,gu
zasadniczym sposobem caÃlkowania be,dzie znalezienie takich podstawie´n, kt´ore
sprowadzaja, wyra˙zenie podcaÃlkowe do postaci wymiernej. Jako przykÃlady takiego
poste,powania rozpatrzymy pewne przypadki caÃlkowania wyra˙ze´n zawieraja,cych
pierwiastki.
1
o
. Je˙zeli funkcja podcaÃlkowa jest funkcja, wymierna, pote,g zmiennej x o wykÃladni-
kach uÃlamkowych
m
n
, gdzie n, m ∈ R sa, wzgle,dnie pierwsze, to podstawienie
x = t
N
, gdzie N jest najmniejszym wsp´olnym mianownikiem uÃlamk´ow
m
n
,
sprowadza caÃlke, z funkcji niewymiernej do caÃlki z funkcji wymiernej.
2
o
. Je˙zeli funkcja podcaÃlkowa jest funkcja, wymierna, pote,g wyra˙zenia ax + b o
wykÃladnikach uÃlamkowych
m
n
, gdzie n, m ∈ R sa, wzgle,dnie pierwsze, to pod-
stawienie ax + b = t
N
, gdzie N jest najmniejszym wsp´olnym mianownikiem
uÃlamk´ow
m
n
, sprowadza caÃlke, z funkcji niewymiernej do caÃlki z funkcji wy-
miernej.
3
o
. Je˙zeli funkcja podcaÃlkowa jest funkcja, wymierna, pote,g wyra˙zenia
ax + b
cx + d
o
wykÃladnikach uÃlamkowych
m
n
, gdzie n, m ∈ R sa, wzgle,dnie pierwsze, to pod-
stawienie
ax + b
cx + d
= t
N
, gdzie N jest najmniejszym wsp´olnym mianownikiem
uÃlamk´ow
m
n
, sprowadza caÃlke, z funkcji niewymiernej do caÃlki z funkcji wy-
miernej.
4
o
. Je˙zeli funkcja pocaÃlkowa jest funkcja, wyra˙zenia
√
ax
2
+ bx + c, gdzie b
2
−
4ac 6= 0, to naste,puja,ce podstawienia zwane podstawieniami Eulera sprowadza,
ta, caÃlke, do caÃlki z funkcji wymiernej.
(i) pierwsze podstawienie Eulera stosujemy w przypadku, gdy a > 0
p
ax
2
+ bx + c = t −
√
ax.
Podnosza,c stronami do kwadratu to podstawienie i odpowiednio porza,dkuja,c do-
stajemy
x =
t
2
− c
2
√
at + b
oraz
dx = 2
√
at
2
+ bt + c
√
a
(2
√
at + b)
2
dt.
Ponadto mamy
p
ax
2
+ bx + c =
√
at
2
+ bt +
√
ac
2
√
at + b
.
94
Podstawienie to jak wida´c sprowadzi nam caÃlke, z funkcji niewymiernej do caÃlki z
funkcji wymiernej. Po scaÃlkowaniu nale˙zy jeszcze powr´oci´c do zmiennej x kÃlada,c
t =
p
ax
2
+ bx + c +
√
ax.
Podobnie mo˙zemy dokona´c podstawienia
p
ax
2
+ bx + c = t +
√
ax.
(ii) drugie podstawienie Eulera stosujemy, gdy c > 0
p
ax
2
+ bx + c = tx −
√
c.
W tym przypadku mamy
x =
2
√
ct + b
t
2
− a
, dx = −2
√
t
2
+ bt + a
√
c
(t
2
− a)
2
dt.
p
ax
2
+ bx + c =
√
ct
2
+ bt +
√
ca
t
2
− a
.
Ponadto
t =
1
x
(
p
ax
2
+ bx + c −
√
c).
Mo˙zemy r´ownie˙z w tym przypadku dokona´c podstawienia
p
ax
2
+ bx + c = tx +
√
c.
(iii) trzecie podstawienie Eulera stosujemy, gdy ∆ > 0.
Wtedy ax
2
+ bx + c = a(x − x
1
)(x − x
2
). Zatem podstawiaja,c
p
ax
2
+ bx + c = t(x − x
1
).
otrzymujemy
x =
ax
2
− x
1
t
2
a − t
2
,
dx =
2a(x
2
− x
1
)t
(a − t
2
)
2
dt.
p
ax
2
+ bx + c =
a(x
2
− x
1
)t
a − t
2
.
Ponadto mamy
t =
s
a(x − x
2
)
x − x
1
.
W tym przypadku mo˙zna r´ownie˙z dokona´c podstawienia
p
ax
2
+ bx + c = t(x − x
2
).
95
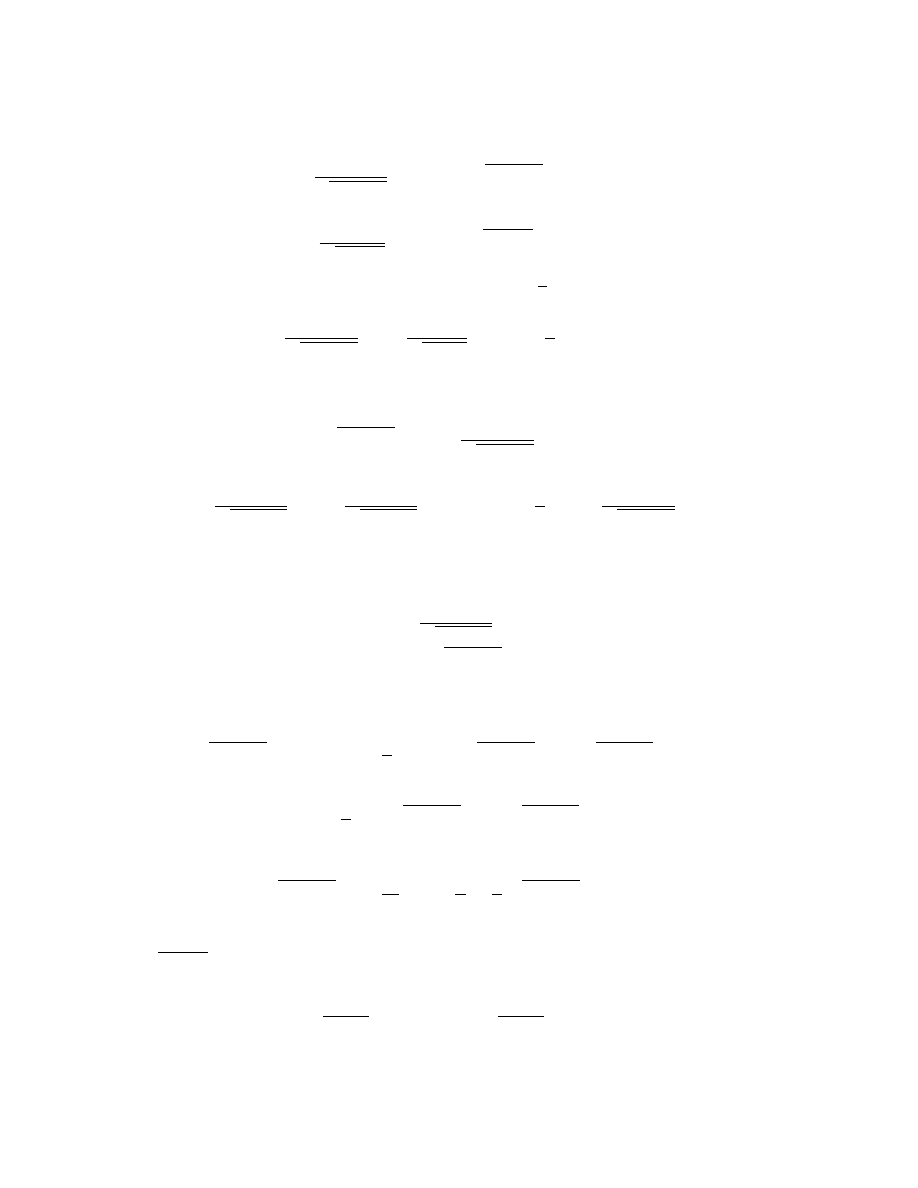
Wa˙znym ze wzgle,du na zastosowania jest przypadek caÃlek stowarzyszonych postaci
Z
dx
√
a
2
− x
2
Z p
a
2
− x
2
dx
Z
dx
√
x
2
+ k
Z p
x
2
+ kdx,
gdzie k > 0. Zauwa˙zmy, ˙ze stosuja,c podstawienie t =
x
a
w pierwszej z tych caÃlek
otrzymujemy
Z
dx
√
a
2
− x
2
=
Z
dt
√
1 − t
2
= arcsin
x
a
+ c.
Druga, caÃlke, obliczamy w naste,puja,cy spos´ob
Z p
a
2
− x
2
dx =
Z
a
2
− x
2
√
a
2
− x
2
dx
= a
2
Z
dx
√
a
2
− x
2
−
Z
x
x
√
a
2
− x
2
dx = a
2
arcsin
x
a
−
Z
x
x
√
a
2
− x
2
dx.
Aby wyznaczy´c powy˙zsza, caÃlke, skorzystamy ze wzoru na caÃlkowanie przez cze,´sci
kÃlada,c
f (x) = x,
g
0
(x) =
x
√
a
2
− x
2
,
f
0
(x) = 1,
g(x) = −
p
a
2
− x
2
.
Zatem mamy
Z p
a
2
− x
2
dx = a
2
arcsin
x
a
−
³
− x
p
a
2
− x
2
+
Z p
a
2
− x
2
dx
´
= a
2
arcsin
x
a
+ x
p
a
2
− x
2
−
Z p
a
2
− x
2
dx.
Wobec tego
Z p
a
2
− x
2
dx =
a
2
2
arcsin
x
a
+
x
2
p
a
2
− x
2
+ c.
Obliczymy teraz kolejna, caÃlfke, stowarzyszona,, stosuja,c pierwsze podstawienie Eu-
lera
√
x
2
+ k = t − x. W´owczas mamy
x =
t
2
− k
2t
oraz
dx =
t
2
+ k
2t
2
dt.
96
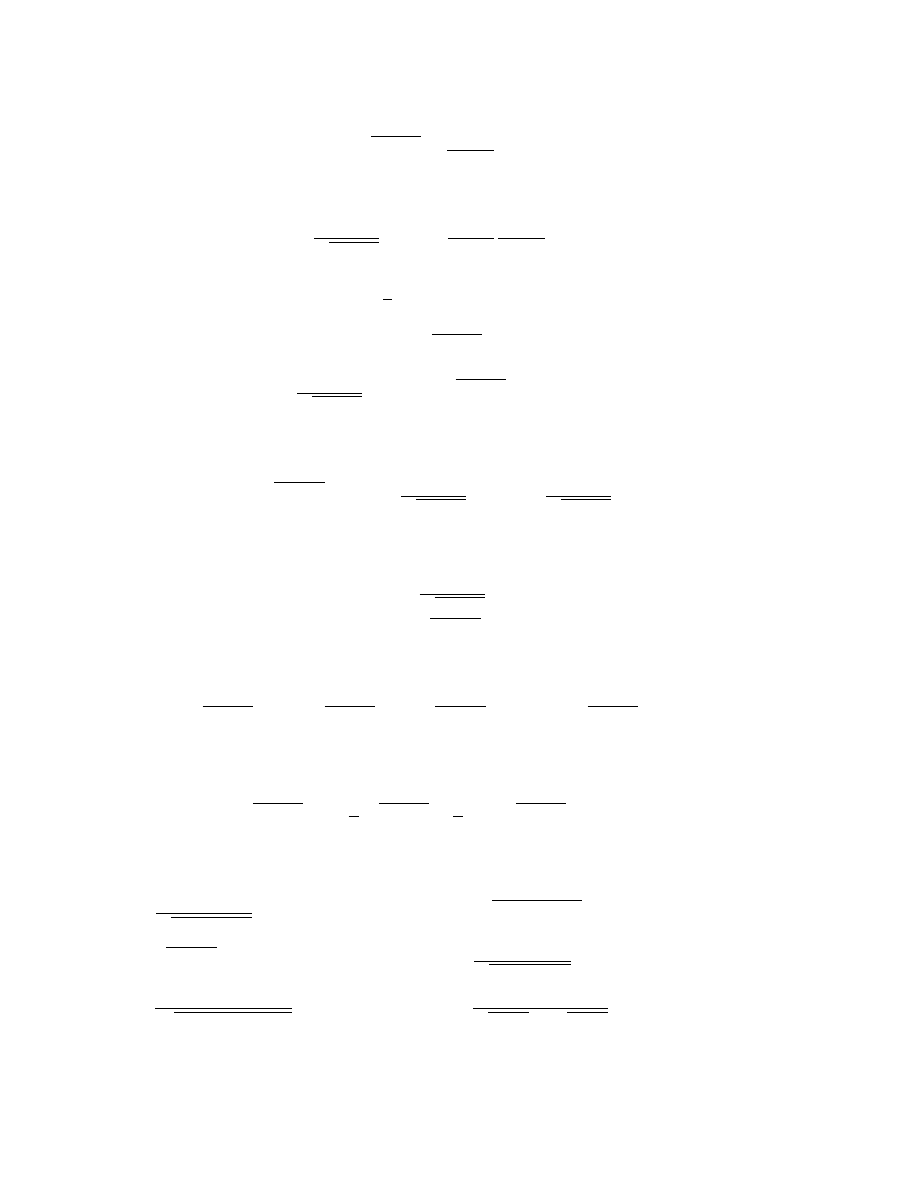
Ponadto
p
x
2
+ k =
t
2
+ k
2t
.
Zatem otrzymujemy
Z
1
√
x
2
+ k
dx =
Z
2t
t
2
+ k
t
2
+ k
2t
2
dt
=
Z
1
t
dt = ln | t | +c.
Z naszego podstawienia wynika, ˙ze t =
√
x
2
+ k + x. Zatem
Z
1
√
x
2
+ k
dx = ln |
p
x
2
+ k + x | +c.
Aby wyznaczy´c caÃlke, stowarzyszona, z powy˙zsza, caÃlka, zauwa˙zmy, ˙ze
Z p
x
2
+ kdx =
Z
x
x
√
x
2
+ k
dx + k
Z
dx
√
x
2
+ k
.
Pierwsza, z powy˙zszych caÃlek caÃlkujemy przez cze,´sci przyjmuja,c
f (x) = x,
g
0
(x) =
x
√
x
2
+ k
,
f
0
(x) = 1,
g(x) =
p
x
2
+ k.
Wobec tego otrzymujemy
Z p
x
2
+ kdx = x
p
x
2
+ k −
Z p
x
2
+ kdx + k ln |
p
x
2
+ k + x | .
Zatem mamy
Z p
x
2
+ kdx =
x
2
p
x
2
+ k +
k
2
ln |
p
x
2
+ k + x | +c.
Zadanie 5.4.1. Oblicz podane caÃlki
a)
Z
1
√
1 − x − x
2
dx,
d)
Z p
x
2
+ 2x + 5dx,
b)
Z p
x − x
2
dx,
e)
Z
1
√
x
2
+ x + 2
dx,
c)
Z
1
3
p
(x − 1)(x + 1)
2
dx,
f )
Z
1
√
x + 1 +
3
√
x + 1
dx.
97
5.5. CaÃlkownie funkcji trygonometrycznych.
W paragrafie tym podamy sposoby caÃlkowania funkcji trygonometrycznych.
Rozwa˙zmy caÃlke,
Z
R(sin x, cos x)dx.
(5.5.1)
Do obliczenia caÃlki (5.5.1) mo˙zemy zawsze zastosowa´c tzw. podstawienie standar-
dowe postaci t = tg
x
2
. W tym przypadku mamy
x = 2arctgx, zatem dx =
2dt
1 + t
2
.
Zauwa˙zmy, ˙ze
cos x = cos
2
x
2
− sin
2
x
2
= cos
2
x
2
³
1 −
sin
2 x
2
cos
2 x
2
´
=
1
cos
2 x
2
+sin
2 x
2
cos
2 x
2
³
1 −
sin
2 x
2
cos
2 x
2
´
=
1 − tg
2 x
2
1 + tg
2 x
2
oraz
sin x = 2 sin
x
2
cos
x
2
= 2
sin
x
2
cos
x
2
cos
2
x
2
=
2tg
x
2
1 + tg
2 x
2
.
Zatem
sin x =
2t
1 + t
2
,
cos x =
1 − t
2
1 + t
2
.
Podstawienie standardowe sprowadzi nam caÃlke, z funkcji trygonomertycznej do
caÃlki z funkcji wymiernej lub niewymiernej w zale˙zno´sci od postaci funkcji R.
Czasami zdarza sie,, ˙ze funkcja podcaÃlkowa jest funkcja, nieparzysta, w´owczas
mo˙zna taka, caÃlke, obliczy´c w prostszy spos´ob. Zachodzi´c mo˙ze jeden z naste,puja,-
cych przypadk´ow.
1
o
. Je˙zeli funkcja podcaÃlkowa jest funkcja, nieparzysta, wzgle,dem funkcji cosinus,
tj.
R(sin x, − cos x) = −R(sin x, cos x)
to postawienie t = sin x sprowadzi, rozwa˙zana, caÃlke, do caÃlki z funkcji wy-
miernej, ba,d´z niewymiernej.
2
o
. Je˙zeli funkcja podcaÃlkowa jest funkcja, nieparzysta, wzgle,dem funkcji sinus, tj.
R(− sin x, cos x) = −R(sin x, cos x)
98
to postawienie t = cos x sprowadzi, rozwa˙zana, caÃlke, do caÃlki z funkcji wy-
miernej, ba,d´z niewymiernej.
3
o
. Niech funkcja podcaÃlkowa be,dzie funkcja, parzysta, wzgle,dem funkcji sinus i
cosinus, tj.
R(− sin x, − cos x) = R(sin x, cos x).
Wtedy rozwa˙zana caÃlka musi by´c caÃlka, postaci
Z
R(sin
2
x, cos
2
x, sin x cos x)dx.
Postawienie t = tgx sprowadzi, te, caÃlke, do caÃlki z funkcji wymiernej, ba,d´z
niewymiernej. Mamy bowiem
cos
2
x =
1
cos
2
x+sin
2
x
cos
2
x
=
1
1 + tg
2
x
oraz
sin
2
x =
sin
2
x
cos
2
x
cos
2
x =
tg
2
x
1 + tg
2
x
.
Ponadto
sin x cos x =
sin x
cos x
cos
2
x =
tgx
1 + tg
2
x
.
Zatem stosuja,c podstawienie t = tgx mamy
sin
2
x =
t
2
1 + t
2
cos
2
x =
1
1 + tgx
sin x cos x =
t
1 + t
2
Z podtawienia wynika ponadto, ˙ze
x = arctgx.
Wobec tego
dx =
dt
1 + t
2
.
Do wyznaczania caÃlki z funkcji trygonometrycznej postaci
Z
R(sin mx, cos nx)dx.
stosujemy jeden z naste,puja,cych wzor´ow
sin mx sin nx =
1
2
[cos(m − n)x − cos(m + n)x]
99

cos mx cos nx =
1
2
[cos(m − n)x + cos(m + n)x]
sin mx cos nx =
1
2
[sin(m − n)x + sin(m + n)x]
Na zako´
nczenie om´owimy spos´ob caÃlkowania funkcji f (x) = sin
n
x i f (x) =
cos
n
x, gdzie n ∈ R. Zauwa˙zmy, ˙ze
Z
sin
n
xdx =
Z
sin
n−1
x sin xdx.
Korzystaja,c ze wzoru na caÃlkowanie przez cze,´sci, gdzie
f (x) = sin
n−1
x,
g
0
(x) = sin x,
f
0
(x) = (n − 1) sin
n−2
x cos x,
g(x) = − cos x.
otrzymujemy
Z
sin
n
xdx = − sin
n−1
x cos x + (n − 1)
Z
cos
2
x sin
n−2
xdx
= − sin
n−1
x cos x + (n − 1)
Z
(1 − sin
2
x) sin
n−2
xdx
= − sin
n−1
x cos x + (n − 1)
Z
sin
n−2
xdx − (n − 1)
Z
sin
n
xdx.
Sta,d mamy naste,puja,cy wz´or rekurencyjny
Z
sin
n
xdx = −
1
n
sin
n−1
x cos x +
n − 1
n
Z
sin
n−2
xdx, n ≥ 2.
Podobnie kÃlada,c we wzorze na caÃlkowanie przez cze,´sci
f (x) = cos
n−1
x,
g
0
(x) = cos x,
f
0
(x) = −(n − 1) cos
n−2
x sin x,
g(x) = sin x.
mamy
Z
cos
n
xdx = cos
n−1
x sin x + (n − 1)
Z
sin
2
x cos
n−2
xdx
= cos
n−1
x sin x + (n − 1)
Z
(1 − cos
2
x) cos
n−2
xdx
= cos
n−1
x sin x + (n − 1)
Z
cos
n−2
xdx − (n − 1)
Z
cos
n
xdx.
100

Wobec tego otrzymujemy naste,puja,cy wz´or rekurencyjny
Z
cos
n
xdx =
1
n
cos
n−1
x sin x +
n − 1
n
Z
cos
n−2
xdx, n ≥ 2.
Zadanie 5.5.1. Oblicz podane caÃlki
a)
Z
1
cos x
dx,
e)
Z
1
sin(3x − 1)
dx,
b)
Z
1
sin x + cos x
dx,
f )
Z
sin
2
xdx,
c)
Z
sin 2x cos 3xdx,
g)
Z
sin
4
x
cos x
dx,
d)
Z
sin
x
2
sin
x
3
dx,
h)
Z
cos
2
x sin
3
xdx,
101

5.6. CaÃlka oznaczona Riemanna i jej wÃlasno´sci.
Niech w przedziale < a, b > be,dzie dana funkcja cia,gÃla y = f(x) przyjmuja,ca
tylko dodatnie warto´sci. Rozpatrzmy figure, ABCD, ograniczona, przez krzywa,
y = f (x), dwa odcinki prostych x = a, x = b oraz odcinek osi OX odpowiadaja,cy
przedziaÃlowi < a, b >. Figure, tego typu nazywamy trapezem krzywoliniowym.
Zajmiemy sie, problemem wyznaczenia pola trapezu krzywoliniowego ABCD.
Podzielmy podstawe, AB naszej figury w dowolny spos´ob na mniejsze odcinki i po-
prowad´zmy przez punkty podziaÃlu odcinki pionowe (prostopadÃle do osi OX). W
ten spos´ob trapez krzywoliniowy rozcinamy na pewna, ilo´s´c pask´ow. Ka˙zdy z tak
otrzymanych pask´ow zasta,pimy pewnym prostoka,tem o tej samej podstawie co
dany pasek i o wysoko´sci r´ownej rze,dnej wykresu w pasku, skrajnej z lewej strony.
W ten spos´ob figure, ABCD zasta,pimy pewna, figura, schodkowa,, skÃladaja,ca, sie, z
prostoka,t´ow.
Niech liczby
a = x
0
< x
1
< x
1
< . . . < x
i
< x
i+1
< . . . < x
n
= b
oznaczaja, odcie,te punkt´ow podziaÃlu. Podstawa i-tego prostoka,ta
(i = 1, 2, ..., n − 1) ma dÃlugo´s´c r´owna, r´o˙znicy x
i+1
− x
i
, kt´ora, oznaczymy ∆x
i
.
Zauwa˙zmy, ˙ze wysoko´s´c i-tego prostoka,ta jest r´owna y
i
= f (x
i
). Zatem pole
rozwa˙zanego prostoka,ta r´owne jest f(x
i
)∆x
i
.
102

Sumuja,c pola wszystkich prostoka,t´ow otrzymamy przybli˙zone pole trapezu
krzywoliniowego
P ≈
n−1
X
i=0
f (x
i
)∆x
i
.
Je´sli dokonamy ge,stszego podziaÃlu odcinka AB, to pole otrzymanej w powy˙zszy
spos´ob figury schodkowej be,dzie bli˙zsze polu trapezu krzywoliniowego. Zatem
przy nieograniczonym zmniejszaniu sie, wszystkich ∆x
i
bÃla,d przybli˙zenia zmierza
do zera. Wobec tego dokÃladne pole trapezu otrzymamy jako granice,
P = lim
∆x
i
→0
n−1
X
i=0
f (x
i
)∆x
i
.
Poniewa˙z pole, otrzymane z powy˙zszego wzoru jako warto´s´c graniczna, okazuje
sie, jednocze´snie funkcja, pierwotna, funkcji f, to zacze,to stosowa´c jako oznaczenie
wy˙zej wypisanej granicy, symbolu caÃlki.
Oznaczmy teraz przez λ najwie,ksza, spo´sr´od r´o˙znic ∆x
i
= x
i+1
− x
i
, i =
1, 2, . . . , n − 1. W ka˙zdym z odcink´ow < x
i
, x
i+1
> wybie˙zmy dowolny punkt δ
i
i
utw´orzmy sume,
σ =
n−1
X
i=0
f (δ
i
)∆x
i
.
Definicja 5.6.1. Sko´
nczona, granice, sum σ przy λ → 0
lim
λ→0
n−1
X
i=0
f (δ
i
)∆x
i
nazywamy caÃlka, oznaczona, Riemanna funkcji f w przedziale < a, b > i oznaczamy
b
Z
a
f (x)dx.
Liczby a i b nosza, odpowiednio nazwy dolnej i g´ornej granicy caÃlki.
Powy˙zsza, definicje, mo˙zemy zapisa´c naste,puja,co
b
Z
a
f (x)dx = lim
λ→0
n−1
X
i=0
f (δ
i
)∆x
i
103

Zauwa˙zmy, ˙ze podana definicja dotyczy tylko funkcji ograniczonej. Gdyby funkcja
f byÃla nieograniczona, to w dowolnym podziale przedziaÃlu < a, b > znale´zliby´smy
taki podprzedziaÃl < x
i
, x
i+1
>, w kt´orym funkcja byÃlaby ograniczona. Wtedy
dobieraja,c odpowiednio δ
i
mo˙zna by sprawi´c, ˙ze warto´s´c f (δ
i
) byÃlaby dowolnie
du˙za. Wtedy r´ownie˙z i suma σ byÃla by odpowiednio du˙za. A zatem nie mogÃlaby
istnie´c sko´
nczona granica sum z definicji 5.6.1.
Wynika sta,d, naste,puja,cy warunek konieczny istnienia caÃlki oznaczonej.
Twierdzenie 5.6.1.
Je˙zeli isnieje caÃlka oznaczona funkcji f na przedziale
< a, b >, to funkcja f jest ograniczona.
Na poparcie tego faktu podamy jeszcze przykÃlad.
PrzykÃlad 5.6.1. Rozwa˙zmy funkcje, Dirichleta dana, wzorem
D(x) =
½
0, dla x 6∈ Q,
1, dla x ∈ Q.
Niech
x
0
< x
1
< x
1
< . . . < x
i
< x
i+1
< . . . < x
n
be,dzie dowolnym podziaÃlem przedziaÃlu < 0, 1 >. Je˙zeli δ
i
jest liczba, wymierna,, to
D(δ
i
) = 1 i
n−1
X
i=0
D(δ
i
)∆x
i
=
n−1
X
i=0
∆x
i
= b − a.
Je˙zeli natomiast δ
i
jest liczba, niewymierna,, to D(δ
i
) = 0 i
n−1
X
i=0
D(δ
i
)∆x
i
= 0
Zatem
lim
λ→0
n−1
X
i=0
f (δ
i
)∆x
i
nie istnieje. Jednak˙ze wiadomo, ˙ze funkcja Dirichleta jest ograniczona.
W dalszym cia,gu je˙zeli istnieje caÃlka oznaczona z funkcji f na przedziale
< a, b >, to be,dziemy m´owi´c, ˙ze funkcja f jest caÃlkowalna na tym przedziale.
Mo˙zna udowodni´c, ˙ze naste,puja,ce funkcje sa, caÃlkowalne:
1. Ka˙zda funkcja cia,gÃla na przedziale < a, b > jest w tym przedziale caÃlkowalna.
104

2. Ka˙zda funkcja ograniczona w przedziale < a, b > i maja,ca w nim sko´nczona,
liczbe, punkt´ow niecia,gÃlo´sci jest caÃlkowalna na < a, b >.
3. Ka˙zda funkcja monotoniczna i ograniczona na przedziale < a, b > jest caÃlko-
walna w tym przedziale.
ZaÃl´o˙zmy teraz, ˙ze funkcje f i g sa, caÃlkowalne na przedziale < a, b >.
WÃlasno´sci caÃlki oznaczonej
1.
a
Z
a
f (x)dx = 0,
2.
b
Z
a
[cf (x) + dg(x)]dx = c
b
Z
a
f (x)dx + d
b
Z
a
g(x)dx, gdzie c i d sa, pewnymi staÃlymi
rzeczywistymi,
3.
b
Z
a
f (x)dx =
c
Z
a
f (x)dx +
b
Z
c
f (x)dx,
4.
b
Z
a
f (x)dx = −
a
Z
b
f (x)dx.
Naste,puja,ce twierdzenie podaje nam spos´ob obliczania caÃlek nieoznaczonych
za pomoca, funkcji pierwotnych.
Twierdzenie 5.6.2. (Newtona-Leibniza, I gÃl´owne twierdzenie rachunku caÃlkowe-
go) Je˙zeli funkcja f jest cia,gÃla na przedziale < a, b >, to
b
Z
a
f (x)dx = F (b) − F (a),
gdzie F jest funkcja, pierwotna, funkcji f.
Cze,sto zamiast F(b) − F(a) be,dziemy pisa´c F(x)
¯
¯
¯
b
a
.
Naste,puja,ce twierdzenia be,dziemy wykorzystywa´c przy wyliczaniu caÃlek oz-
naczonych.
Twierdzenie 5.6.3. (caÃlkowanie przez cze,´sci caÃlki oznaczonej) Je˙zeli funkcje f i
g maja, cia,gÃle pochodne na przedziale < a, b >, to
b
Z
a
f
0
(x)g(x)dx = f (x)g(x)
¯
¯
¯
a
b
−
b
Z
a
f (x)g
0
(x)dx.
105

Twierdzenie 5.6.4. (caÃlkowanie przez podstawienie caÃlki oznaczonej ) Je˙zeli
1. funkcja φ :< α, β >→< a, b > ma cia,gÃla, pochodna, na (α, β),
2. φ(α) = a, φ(β) = b,
3. funkcja f jest cia,gÃla na przedziale < a, b >,
to
b
Z
a
f (x)dx =
β
Z
α
f (φ(t))φ
0
(t)dt.
Twierdzenie 5.6.5. (twierdzenie caÃlkowe o warto´sci ´sredniej) Je˙zeli funkcja f
jest cia,gÃla na < a, b >, to
_
c∈(a,b)
b
Z
a
f (x)dx = (b − a)f (c).
Dow´
od. Twierdzenie to wynika z twierdzenia Lagrange’a. Niech F be,dzie funkcja,
pierwotna, funkcji f. Wtedy F speÃlnia zaÃlo˙zenia twierdzenia Lagrange’a, a wie,c
_
c∈(a,b)
F
0
(c) =
F (b) − F (a)
b − a
.
Zatem korzystaja,c z twierdzenia Newtona-Leibniza mamy
_
c∈(a,b)
f (c) =
b
R
a
f (x)dx
b − a
,
co ko´
nczy dow´od.
Twierdzenie 5.6.6. Je˙zeli funkcja f i g sa, caÃlkowalne na przedziale < a, b >
oraz dla ka˙zdego x ∈< a, b > f (x) ≤ g(x), to
b
Z
a
f (x)dx ≤
b
Z
a
g(x)dx.
Z twierdzenia tego wynika dla nas wa˙zany wniosek, na kt´ory be,dziemy sie, cze,sto
powoÃlywa´c w naste,pnym paragrafie.
106

Wniosek 5.6.6. Je˙zeli funkcja f jest ograniczona, tzn.
_
M,m
^
x∈<a,b>
m ≤ f (x) ≤ M,
to
m(b − a) ≤
b
Z
a
f (x)dx ≤ M (b − a).
Na zako´
nczenie tego paragrafu zauwa˙zmy jeszcze, ˙ze dla funkcji podcaÃlkowej
nieparzystej na przedziale < −a, a >, tj. speÃlniaja,cej warunek
^
x∈<−a,a>
− x ∈< −a, a >⇒ f (−x) = −f (x),
mamy
a
Z
−a
f (x)dx =
0
Z
−a
f (x)dx +
a
Z
0
f (x)dx.
Stosuja,c podstawienie t = −x w pierwszej z caÃlek otrzymujemy
a
Z
−a
f (x)dx = −
0
Z
a
f (−t)dt +
a
Z
0
f (x)dx
=
0
Z
a
f (x)dx +
a
Z
0
f (x)dx =
a
Z
a
f (x)dx = 0.
A zatem je´sli funkcja podcaÃlkowa jest nieparzysta i przedziaÃl caÃlkowania jest sy-
metryczny wzgle,dem zera, to
a
Z
−a
f (x)dx = 0.
Podobnie, gdy funkcja podcaÃlkowa jest parzysta, tj. gdy speÃlnia warunek
^
x∈<−a,a>
− x ∈< −a, a >⇒ f (−x) = f (x),
stosuja,c podstawienie t = −x otrzymujemy
a
Z
−a
f (x)dx = −
0
Z
a
f (−t)dt +
a
Z
0
f (x)dx
107

= −
0
Z
a
f (x)dx +
a
Z
0
f (x)dx = 2
a
Z
0
f (x)dx.
A zatem je´sli funkcja podcaÃlkowa jest parzysta i przedziaÃl caÃlkowania jest syme-
tryczny wzgle,dem zera, to
a
Z
−a
f (x)dx = 2
a
Z
0
f (x)dx.
Zadanie 5.6.1. Oblicz podane caÃlki oznaczone
a)
1
Z
0
√
x −
3
√
x
x
2
dx,
d)
π
2
Z
0
sin x + cos xdx,
b)
π
Z
0
tgxdx,
e)
e
2
Z
e
1
x
dx,
c)
0
Z
−1
e
−x
dx,
f )
1
Z
0
1
1 + x
2
dx,
5.7. Podstawowe twierdzenia rachunku caÃlkowego.
Jedno z podstawowych twierdze´
n rachunku caÃlkowego poznali´smy w poprzed-
nim paragrafie, mowa o twierdzeniu Newtona-Leibniza. W paragrafie 5.7 udowod-
nimy drugie podstawowe twierdzenie rachunku caÃlkowego. W tym celu zdefiniowa´c
musimy poje,cie funkcji g´ornej granicy caÃlkowania.
Definicja 5.7.1. Niech funkcja f be,dzie funkcja, caÃlkowalna, na przedziale
< a, b >. Funkcje, dana, wzorem
F (x) =
x
Z
c
f (t)dt,
x ∈< a, b >
nazywamy funkcja, g´ornej granicy caÃlkowania.
Podamy teraz kilka wÃlasno´sci funkcji F zdefiniowanej powy˙zej.
108

Twierdzenie 5.7.1. Je˙zeli funkcja f jest funkcja, caÃlkowalna, na przedziale
< a, b >, to funkcja g´ornej granicy caÃlkowania jest funkcja, cia,gÃla, na przedziale
< a, b >.
Dow´
od. Niech x i x
0
be,da, dowolne i niech nale˙za, do przedziaÃlu < a, b >. Wtedy
F (x) − F (x
0
) =
x
Z
c
f (t)dt −
x
0
Z
c
f (t)dt
=
x
Z
c
f (t)dt +
c
Z
x
0
f (t)dt =
x
Z
x
0
f (t)dt.
Poniewa˙z funkcja f jest caÃlkowalna na przedziale < a, b >, to jest na tym przedziale
ograniczona, a zatem
_
M >0
^
x∈<a,b>
| f (x) |≤ M.
Na mocy wniosku 5.6.6 mamy
¯
¯
¯
x
Z
x
0
f (t)dt
¯
¯
¯ ≤ M | x − x
0
| .
Zatem
| F (x) − F (x
0
) |≤ M | x − x
0
| .
Sta,d
^
M
_
δ
^
x∈<a,b>
| x − x
0
|< δ ⇒| F (x) − f (x
0
) |< M δ
co oznacza, ˙ze
lim
x→x
0
F (x) = F (x
0
),
x ∈< a, b > .
Wobec tego funkcja g´ornej granicy caÃlkowania jest cia,gÃla na przedziale < a, b >.
Twierdzenie 5.7.2. (II gÃl´owne twierdzenie rachunku caÃlkowego) Je˙zeli funkcja f
jest caÃlkowalna na < a, b > i cia,gÃla w pewnym punkcie x
0
∈< a, b >, to funkcja
g´ornej granicy caÃlkowania ma pochodna, w punkcie x
0
oraz F
0
(x
0
) = f (x
0
).
Dow´
od. Zauwa˙zmy, ˙ze
F (x
0
+ ∆x) − F (x
0
)
∆x
=
x
0
+∆x
R
c
f (t)dt −
x
0
R
c
f (t)dt
∆x
=
x
0
+∆x
R
x
0
f (t)dt
∆x
.
109

Niech ε > 0. Poniewa˙z f jest cia,gÃla na < a, b >, to
_
δ
^
x∈<a,b>
| x − x
0
|< δ ⇒ f (x
0
) − ε < f (x) < f (x
0
) + ε.
Zatem
x
0
+∆x
Z
x
0
(f (x
0
) − ε)dt <
x
0
+∆x
Z
x
0
f (t)dt <
x
0
+∆x
Z
x
0
(f (x
0
) + ε)dt.
Sta,d mamy
(f (x
0
) − ε)∆x <
x
0
+∆x
Z
x
0
f (t)dt < (f (x
0
) + ε)∆x.
Wobec tego
f (x
0
) − ε <
F (x
0
+ ∆x) − F (x
0
)
∆x
< f (x
0
) + ε.
Otrzymali´smy zatem
¯
¯
¯
F (x
0
+ ∆x) − F (x
0
)
∆x
− f (x
0
)
¯
¯
¯ < ε,
co oznacza, ˙ze F
0
(x
0
) = f (x
0
).
5.8. CaÃlka niewÃla´sciwa.
W poprzednich paragrafach zdefiniowali´smy caÃlke, oznaczona, po przedziale
sko´
nczonym. W tym paragrafie zajmiemy sie, problemem caÃlki oznaczonej po
przedziale niesko´
nczonym.
ZaÃl´o˙zmy na pocza,tek, ˙ze funkcja f jest okre´slona w przedziale (a, b > i ˙ze jest
ona caÃlkowalna w ka˙zdym przedziale < h, b >, gdzie a < h < b. Ponadto zaÃl´o˙zmy,
˙ze funkcja f jest nieograniczona w ka˙zdym przedziale (a, h). Powiemy wtedy, ˙ze
funkcja f ma osobliwo´s´c w punkcie a.
Definicja 5.8.1. CaÃlka, niewÃla´sciwa, nazywamy naste,puja,ca, granice,
lim
h→a
+
b
Z
h
f (x)dx.
CaÃlke, niewÃla´sciwa, oznacza´c be,dziemy tak jak caÃlke, oznaczona,. Zatem mo˙zemy
napisa´c
b
Z
a
f (x)dx = lim
h→a
+
b
Z
h
f (x)dx,
110

gdy funkcja f ma w punkcie a osobliwo´s´c.
ZaÃl´o˙zmy teraz, ˙ze funkcja f ma osobliwo´a´c w punkcie b, tzn. jest okre´slona
w przedziale < a, b), caÃlkowalna w ka˙zdym przedziale < a, h >, gdzie a < h < b i
jest nieograniczona w ka˙zdym przedziale (h, b).
Definicja 5.8.2. CaÃlka, niewÃla´sciwa, nazywamy naste,puja,ca, granice,
lim
h→b
−
b
Z
h
f (x)dx.
Z uwagi na wcze´sniejsze oznaczenia mo˙zemy zatem napisa´c
b
Z
a
f (x)dx = lim
h→b
−
h
Z
a
f (x)dx,
gdy funkcja f ma w punkcie b osobliwo´s´c.
Naste,puja,ce twierdzenie uÃlatwi nam obliczanie caÃlek niewÃla´sciwych.
Twierdzenie 5.8.1. Je˙zeli funkcja f ma osobliwo´s´c w punkcie a, to
b
Z
a
f (x)dx = F (b) − lim
h→a
+
F (h).
Je˙zeli natomiast funkcja f ma osobliwo´s´c w pyunkcie b, to
b
Z
a
f (x)dx = lim
h→b
−
F (h) − F (a).
W przypadku, gdy funkcja f ma osobliwo´s´c wewna,trz przedziaÃlu caÃlkowania,
to mo˙zemy posta,pi´c jak naste,puje
b
Z
a
f (x)dx =
c
Z
a
f (x)dx +
b
Z
c
f (x)dx,
gdzie c nie jest osobliwo´scia, funkcji f.
Podobnie poste,pujemy, gdy oba ko´nce przedziaÃlu caÃlkowania sa, punktami
nieosobliwymi funkcji podcaÃlkowej.
Czasami zdarzy´c sie, mo˙ze, ˙ze przedziaÃl caÃlkowania jest nieograniczony.
111

Definicja 5.8.3. Naste,puja,ce granice nazywamy caÃlkami niewÃla´sciwymi
∞
Z
a
f (x)dx = lim
h→∞
h
Z
a
f (x)dx,
b
Z
−∞
f (x)dx = lim
h→−∞
b
Z
h
f (x)dx.
W przypadku, gdy caÃlkujemy funkcje, po caÃlym zbiorze liczb rzeczywistych mo˙zemy
posta,pi´c w naste,puja,cy spos´ob
∞
Z
−∞
f (x)dx =
c
Z
−∞
f (x)dx +
∞
Z
c
f (x)dx.
Zadanie 5.8.1. Oblicz podane caÃlki niewÃla´sciwe
a)
2
Z
1
x
√
x − 1
dx,
d)
2
Z
0
1
x
2
− 4x + 3
dx,
b)
1
Z
0
x ln xdx,
e)
∞
Z
1
ln x
x
dx,
c)
∞
Z
0
dx
1 + x
3
,
f )
∞
Z
e
dx
x ln(ln x)
,
112

5.9. Zastosowania caÃlki oznaczonej.
Podamy teraz pewne zastosowania caÃlki oznaczonej.
Zastosowania w geometrii
1. Niech funkcje f i g be,da, caÃlkowalne na przedziale < a, b > oraz niech d(x) ≤
g(x) dla ka˙zdego x ∈< a, b >. Wtedy pole trapezu krzywolinowego ograniczo-
nego wykresami funkcji d i g oraz prostymi x = a, x = b wyra˙za sie, wzorem:
P =
b
Z
a
[g(x) − d(x)]dx
2. Niech funkcja f ma cia,gÃla, pochodna, na przedziale < a, b >. Wtedy dÃlugo´s´c
Ãluku krzywej Γ = {(x, f (x)) : x ∈< a, b >} wyra˙za sie, wzorem
l =
b
Z
a
p
1 + [f
0
(x)]
2
dx.
113

Je˙zeli krzywa Γ dana jest parametrycznie r´ownaniami
½
x = ϕ(t),
y = ψ(t),
t ∈< α, β >
(5.9.1)
to dÃlugo´s´c Ãluku tej krzywej dana jest wzorem
l =
β
Z
α
p
[ϕ
0
(t)]
2
+ [ψ
0
(t)]
2
dt.
3. Niech f be,dzie funkcja, nieujemna, i caÃlkowalna, na przedziale < a, b >. Pon-
adto niech T oznacza trapez krzywoliniowy ograniczony wykresem funkcji f ,
osia, OX oraz prostymi x = a, x = b. Wtedy obje,to´s´c bryÃly powstaÃlej z obrotu
trapezu T wok´oÃl osi OX wyra˙za sie, wzorem
V = π
b
Z
a
[f (x)]
2
dx.
W przypadku, gdy wykres funkcji f jest krzywa, zadana, parametrycznie r´ow-
naniami 5.9.1, to
V = π
β
Z
α
[ψ(t)]
2
| ϕ
0
(t) | dt.
4. Niech funkcja f ma cia,gÃla, pochodna, na przedziale < a, b >. Wtedy pole
powierzchni powstaÃlej z obrotu wykresu funkcji f wok´oÃl osi OX wyra˙za sie,
wzorem
S = 2π
b
Z
a
| f (x) |
p
1 + [f
0
(x)]
2
dx
114

W przypadku, gdy wykres funkcji f dany jest r´ownaniami 5.9.1, mamy
S = 2π
β
Z
α
| ψ(t) |
p
[ϕ
0
(t)]
2
+ [ψ
0
(t)]
2
dt.
Zastosowania w fizyce
1. Niech punkt materialny porusza sie, po pÃlaszczy´znie lub w przestrzeni ze
zmienna, szybko´scia, v(t). Wtedy droga przebyta przez ten punkt w przedziale
czasowym < t
1
, t
2
> dana jest wzorem
l =
t
2
Z
t
1
v(t)dt.
2. ZaÃl´o˙zmy, ˙ze r´ownolegle do osi OX dziaÃla zmienna siÃla F (x). Praca wykonana
przez te, siÃle, od punktu x = a do punktu x = b wyra˙za sie, wzorem
W =
b
Z
a
F (x)dx.
115

6. LICZBY ZESPOLONE
Rozwa˙zmy zbi´or uporza,dkowanych par liczb rzeczywistych (a, b). Przyjmijmy,
˙ze dwie pary liczbowe (a, b), (c, d) sa, r´owne wtedy i tylko wtedy, gdy a = c i b = d.
Okre´slmy w zbiorze par liczbowych dwa dziaÃlania:
? dodawanie (a, b) + (c, d) = (a + c, b + d),
(6.1)
? mno˙zenie (a, b) · (c, d) = (ac − bd, ad + cb).
(6.2)
Zauwa˙zmy, ˙ze powy˙zsze dziaÃlania maja, naste,puja,ce wÃlasno´sci:
1.
o
Ãla,czno´s´c dodawania, tj.
(a, b) + [(c, d) + (e, f )] = [(a, b) + (c, d)] + (e, f )
2.
o
element neutralny dodawania, tj.
_
(x,y)
^
(a,b)
(a, b) + (x, y) = (a, b), w tym przypadku (x, y) = (0, 0)
3.
o
element przeciwny dodawania, tj.
^
(a,b)
_
(x,y)
(a, b) + (x, y) = (0, 0), w tym przypadku (x, y) = (−a, −b)
4.
o
przemienno´s´c dodawania, tj.
(a, b) + (c, d) = (c, d) + (a, b)
5.
o
Ãla,czno´s´c mno˙zenia, tj.
(a, b) · [(c, d) · (e, f )] = [(a, b) · (c, d)] · (e, f )
6.
o
element neutralny mno˙zenia, tj.
_
(x,y)
^
(a,b)
(a, b) · (x, y) = (a, b), w tym przypadku (x, y) = (1, 0)
7.
o
element odwrotny mno˙zenia, tj.
^
(a,b)6=(0,0)
_
(x,y)
(a, b)·(x, y) = (0, 0), w tym przypadku (x, y) =
³
a
a
2
+ b
2
,
−b
a
2
+ b
2
´
116

8.
o
przemienno´s´c mno˙zenia, tj.
(a, b) · (c, d) = (c, d) · (a, b)
9.
o
rozdzielno´s´c mno˙zenia wzgle,dem dodawania, tj.
(a, b) · [(c, d) + (e, f )] = (a, b)(c, d) + (a, b)(e, f )
Poka˙zemy teraz, ˙ze istotnie dziaÃlania zdefiniowane wzorami (6.1) i (6.2) maja,
wÃlasno´sci 1-9.
Ad. 1.
o
Zauwa˙zmy, ˙ze
(a, b) + [(c, d) + (e, f )] = (a, b) + (c + e, d + f ) = (a + (c + e), b + (d + f ))
= ((a + c) + e, (b + d) + f ) = (a + c, b + d) + (e, f ) = [(a, b) + (c, d)] + (e, f )
Ad. 2.
o
Aby wyznaczy´c element neutralny dodawania nale˙zy rozwia,za´c naste,pu-
ja,cy ukÃlad r´owna´n
½
a + x = a
b + y = b
ÃLatwo zauwa˙zy´c, ˙ze rozwia,zaniem tego ukÃladu jest x = 0 i y = 0.
Ad. 3.
o
W tym przypadku, aby wyznaczy´c element przeciwny musimy znale´z´c
rozwia,zanie ukÃladu
½
a + x = 0
b + y = 0
Rozwia,zaniem powy˙zszego ukÃladu jest x = −a i y = −b.
Ad. 4.
o
WÃlasno´s´c ta wynika z przemienno´sci dodawania liczb rzeczywistych, mamy
bowiem
(a, b) + (c, d) = (a + c, b + d) = (c + a, d + b) = (c, d) + (a, b)
Ad. 5.
o
Korzystajc, ze wzoru (6.2) otrzymujemy
(a, b) · [(c, d) · (e, f )] = (a, b) · (ce − df, cf + de)
= (a(ce − df ) − b(cf + de), a(cf + de) + b(ce − df ))
= (ace − adf − bcf − bde, acf + ade + bce − bdf )
= ((ac − bd)e − (ad + bc)f, (ac − bd)f + (ad + bc)e)
= (ac − bd, ad + bc) · (e, f ) = [(a, b) · (c, d)] · (e, f )
117

Ad. 6.
o
Chca,c znale´z´c element neutralny mno˙zenia rozwia,zujemy ukÃlad r´owna´n
½
ax − by = a
bx + ay = b
Otrzymujemy x = 1 i y = 0
Ad. 7.
o
Zauwa˙zmy, ˙ze element odwrotny mno˙zenia jest rozwia,zaniem ukÃladu
r´owna´
n
½
ax − by = 1
bx + ay = 0
Zatem mamy (x, y) =
³
a
a
2
+ b
2
,
−b
a
2
+ b
2
´
.
Ad. 8.
o
Przemienno´s´c mno˙zenia wynika z przemienno´sci mno˙zenia liczb rzeczy-
wistych, gdy˙z
(a, b) · (c, d) = (ac − bd, ad + bc) = (ca − db, da + cb) = (c, d) · (a, b)
Ad. 9.
o
W tym przypadku korzystaja,c z rozdzielno´sci mno˙zenia wzgle,dem do-
dawania liczb rzeczywistych mamy
(a, b) · [(c, d) + (e, f )] = (a, b) · (c + e, d + f )
= (a(c + e) − b(d + f ), a(d + f ) + b(c + e)) = (ac + ae − bd − bf, ad + af + bc + be)
= ((ac−bd)+(ae−bf ), (ad+bc)+(af +be)) = (ac−bd, ad+bc)+(ae−bf, af +be)
= (a, b) · (c, d) + (a, b) · (e, f )
Definicja 6.1. Zbi´or par liczbowych z dziaÃlaniami dodawania i mno˙zenia zdefi-
niowanymi odpowiednio wzorami (6.1) i (6.2) nazywamy ciaÃlem liczb zespolonych
i oznaczamy (C, +, ·). Elementy zbioru C nazywamy liczbami zespolonymi. Pier-
wszy element pary (a, b) nazywamy cze,´scia, rzeczywista,, a drugi cze,´scia, urojona,.
Pare, (a, 0) nazywa´c be,dziemy liczba, czysto rzeczywista,, a pare, (0, b)-czysto
urojona,.
Pare, (0, 1) nazywamy jednostka, urojona, i oznaczamy j.
Zauwa˙zmy, ˙ze
j
2
= (0, 1)(0, 1) = (0 · 0 − 1 · 1, 1 · 0 + 0 · 1) = (−1, 0) = −1
Najcze,´sciej liczbe, zespolona, oznacza´c be,dziemy litera, z. Zatem przy powy˙zszych
oznaczeniach mo˙zemy napisa´c
z = (a, b) = a + jb, a ∈ R, b ∈ R
118

Taka, posta´c be,dziemy nazywa´c postacia, algebraiczna, liczby zespolonej.
Cze,´s´c rzeczywista, liczby z oznaczamy Rez, za´s cze,´s´c urojona, przez Imz.
Wobec tego be,dziemy r´ownie˙z pisa´c
z = Rez + jImz
Zauwa˙zmy, ˙ze liczbe, zespolona, z mo˙zemy zinterpretowa´c geometrycznie jako wek-
tor o pocza,tku w punkcie (0, 0) i ko´ncu w punkcie (Rez, Imz).
6.1. DziaÃlania arytmetyczne w zakresie liczb zespolonych.
Wzory (6.1) i (6.2) definiuja, nam dwa dziaÃlania arytmetyczne w zakresie
liczb zespolonych, tj. dodawanie i mno˙zenie. Poznamy jeszcze dwa dziaÃlania,
kt´ore zdefiniujemy w oparciu o dziaÃlanie dodawania i mno˙zenia tj. odejmowanie
i dzielenie. Odja,´c liczbe, zespolona, z
2
od liczby zespolonej z
1
to znaczy doda´c do
liczby z
1
element przeciwny wzgle,dem dodawania do liczby z
2
z
1
− z
2
= (a, b) − (c, d) = (a, b) + (−c, −d) = (a − b, c − d)
Podzieli´c liczbe, zespolona, z
1
przez liczbe, zespolona, z
2
to znaczy pomno˙zy´c liczbe,
z
1
przez element odwrotny wzgle,dem mno˙zenia do liczby z
2
z
1
z
2
=
(a, b)
(c, d)
= (a, b) ·
³
c
c
2
+ d
2
,
−d
c
2
+ d
2
´
=
³ ac + bd
c
2
+ d
2
,
bc − ad
c
2
+ d
2
´
.
Definicja 6.1.1. Liczba, sprze,˙zona, do liczby zespolonej z = a + jb nazywamy
liczbe, z o przeciwnej cze,´sci urojonej, tj. liczbe, okre´slona, wzorem
z = a − jb
Zauwa˙zmy, ˙ze na to aby podzieli´c przez siebie dwie liczby zespolone w postaci
algebraicznej wystarczy licznik i mianownik pomno˙zy´c przez liczbe, sprze,˙zona, do
mianownika.
WÃlasno´sci sprze,˙zenia liczb zespolonych:
1. z
1
+ z
2
= z
1
+ z
2
,
2. z
1
− z
2
= z
1
− z
2
,
3. z
1
· z
2
= z
1
· z
2
,
119
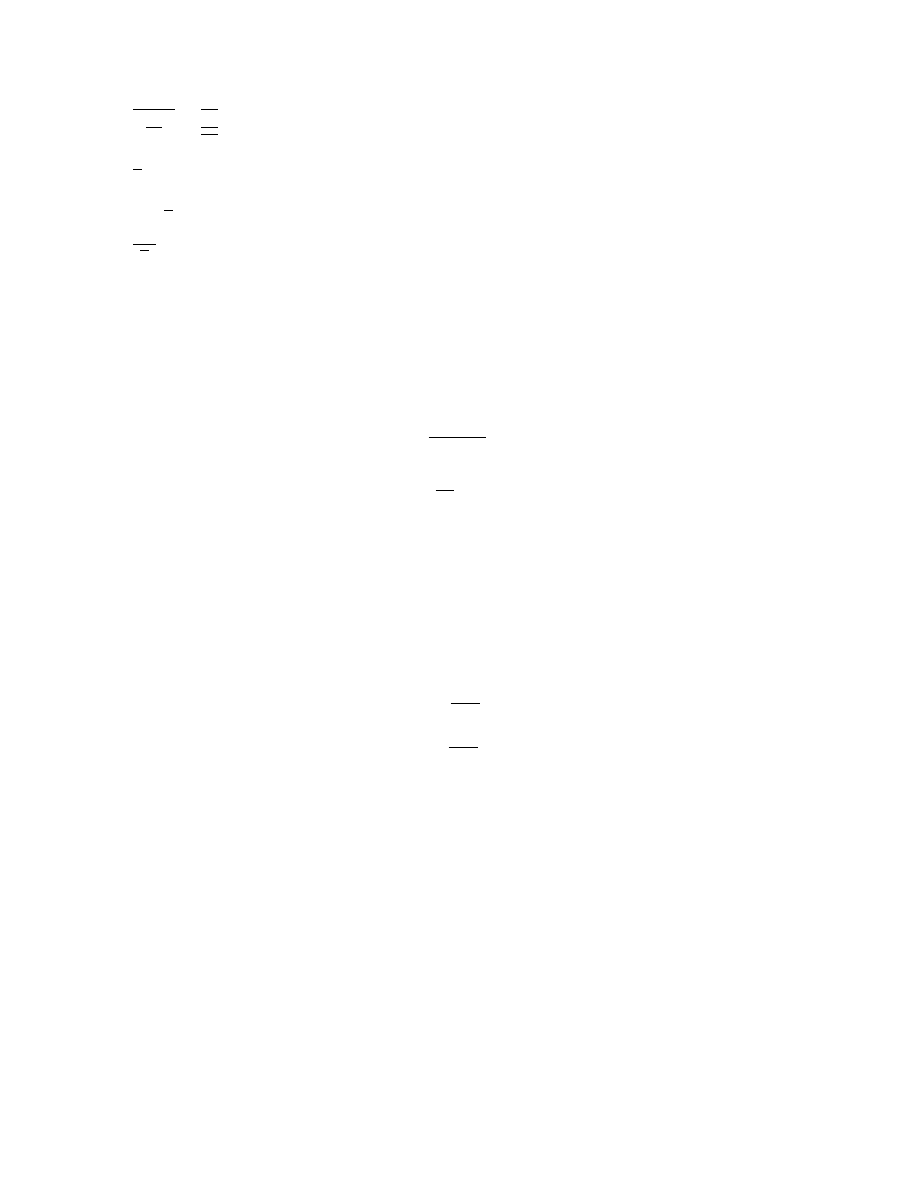
4.
³ z
1
z
2
´
=
z
1
z
2
,
5. z + z = 2Rez,
6. z − z = 2jImz,
7. (z) = z.
6.2. Posta´
c trygonometryczna i wykÃladnicza liczby zespolonej
W poprzednim paragrafie poznali´smy posta´c algebraiczna, liczby zespolonej.
Natomiast w tym paragrafie poznamy inne jej postaci.
Definicja 6.2.1. ModuÃlem liczby zespolonej z = x + jy nazywamy liczbe, rzeczy-
wista, | z | oke´slona, wzorem
| z |=
p
x
2
+ y
2
.
Zauwa˙zmy, ˙ze
| (x, 0) |=
√
x
2
=| x | .
Mo˙zemy zatem powiedzie´c, ˙ze moduÃl liczby zaspolonej jest uog´olnieniem poje,cia
warto´sci bezwzgle,dnej liczby rzeczywistej.
ModuÃl liczby zespolonej mo˙zemy zinterpretowa´c geometrycznie jako dÃlugo´s´c
wektora odpowiadaja,cego danej liczbie zespolonej.
Definicja 6.2.2. Argumentem liczby zespolonej z = x+jy nazywamy ka˙zda, liczbe,
rzeczywista, ϕ speÃlniaja,ca, ukÃlad r´owna´n
cos ϕ =
x
| z |
sin ϕ =
y
| z |
(6.2.1)
Zauwa˙zmy, ˙ze argument liczby zero jest nieokre´slony, poniewa˙z jej moduÃl jest
r´owny zero. Ponadto z wÃlasno´sci funkcji trygonometrycznych wynika, ˙ze ka˙zda
liczba zespolona r´o˙zna od zera ma przeliczalnie wiele argument´ow, kt´ore r´o˙znia,
sie, od siebie o caÃlkowita, wielokrotno´s´c 2π. Spo´sr´od wszystkich argument´ow liczby
zespolonej wyr´o˙zniamy ten, kt´ory nale˙zy do przedziaÃlu < 0, 2π) i nazywamy go
argumentem gÃl´ownym liczby zespolonej przyjmuja,c oznaczenie Argz.
Geomertycznie argument liczby zespolonej jest miara, ka,ta jaki tworzy wektor
odpowiadaja,cy tej liczbie z dodatnia, cze,´scia, osi rzeczywitej.
Zauwa˙zmy, ˙ze ze wzor´ow (6.2.1) wynika, ˙ze
Rez =| z | cos(Argz)
Imz =| z | sin(Argz)
120

Wobec tego ka˙zda, liczbe, zespolona, zapisa´c mo˙zna w naste,puja,cej postaci
z =| z | (cos Argz + j sin Argz).
Powy˙zsza, posta´c nazywamy postacia, trygonometryczna, liczby zespolonej.
Niech teraz dane be,da, dwie dowolne liczby zespolone
z
1
= r
1
(cos ϕ
1
+ j sin ϕ
1
),
z
2
= r
2
(cos ϕ
2
+ j sin ϕ
2
),
gdzie r
i
=| z
i
|, ϕ
i
= Argz
i
dla i = 1, 2. Zauwa˙zmy, ˙ze
z
1
· z
2
= r
1
r
2
£
cos ϕ
1
cos ϕ
2
− sin ϕ
1
sin ϕ
2
+ j(cos ϕ
1
sin ϕ
2
+ sin ϕ
1
cos ϕ
2
)
¤
.
= r
1
r
2
£
cos(ϕ
1
+ ϕ
2
) + j sin(ϕ
1
+ ϕ
2
)
¤
.
Ponadto mamy
z
1
z
2
=
r
1
(cos ϕ
1
+ j sin ϕ
1
)r
2
(cos ϕ
2
− j sin ϕ
2
)
r
2
(cos ϕ
2
+ j sin ϕ
2
)r
2
(cos ϕ
2
− j sin ϕ
2
)
=
r
1
r
2
[cos ϕ
1
cos ϕ
2
+ sin ϕ
1
sin ϕ
2
+ j(sin ϕ
1
cos ϕ
2
− sin ϕ
2
cos ϕ
1
)]
r
2
2
(cos
2
ϕ
2
+ sin
2
ϕ
2
)
=
r
1
r
2
£
cos(ϕ
1
− ϕ
2
) + j sin(ϕ
1
− ϕ
2
)
¤
.
Zatem otrzymujemy naste,puja,ce wÃlasno´sci moduÃlu i argumentu liczby zespolonej
1. moduÃl iloczynu liczb zespolonych jest r´owny iloczynowi moduÃl´ow
| z
1
· z
2
|=| z
1
| · | z
2
|
2. argument iloczynu liczb zespolonych jest r´owny sumie argument´ow
Arg(z
1
· z
2
) = Argz
1
+ Argz
2
3. moduÃl ilorazu liczb zespolonych jest r´owny ilorazowi moduÃl´ow
¯
¯
¯
z
1
z
2
¯
¯
¯ =
| z
1
|
| z
2
|
121
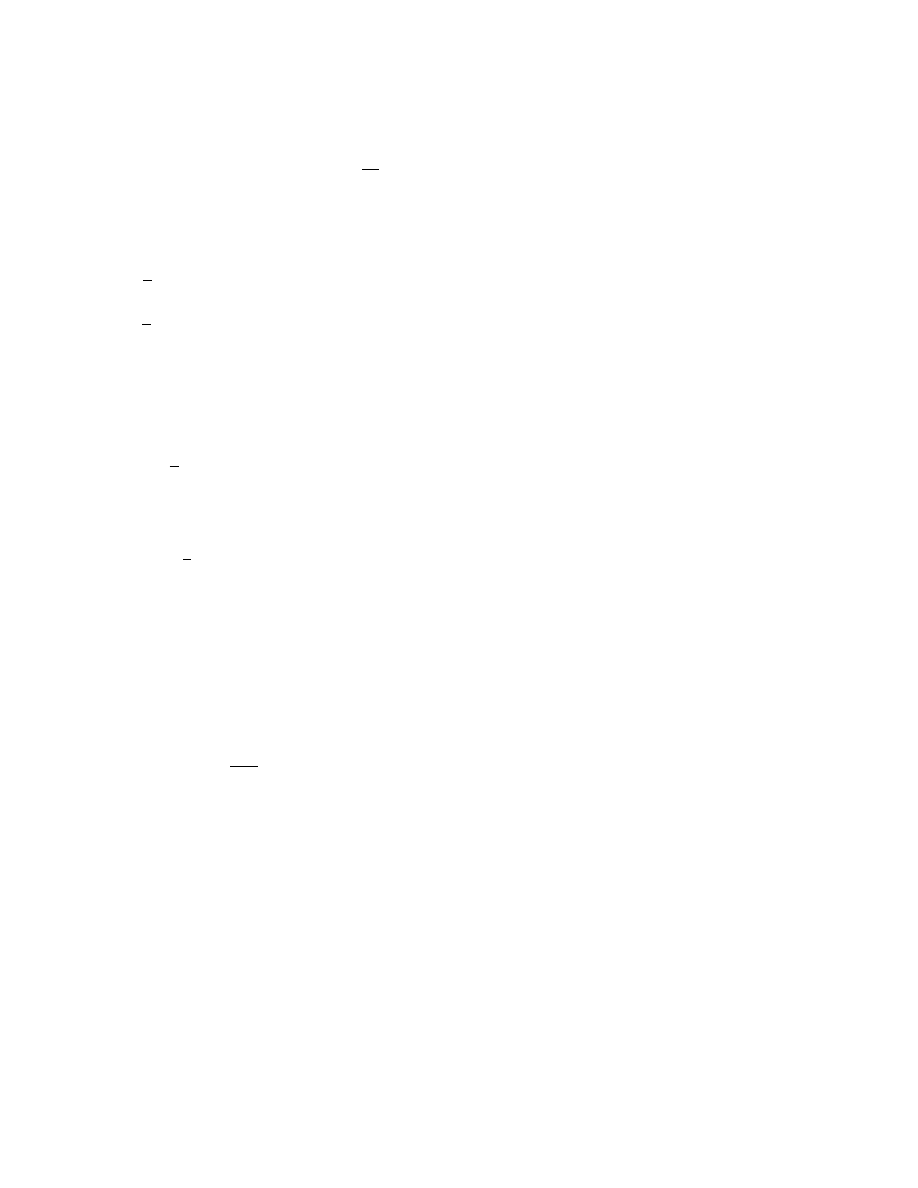
4. argument ilorazu liczb zespolonych jest r´owny r´o˙znicy argument´ow
Arg
³ z
1
z
2
´
= Argz
1
− Argz
2
.
Ponadto mo˙zna udowodni´c naste,puja,ce wÃlasno´sci moduÃlu i argumentu liczby ze-
spolonej
5. | z |=| z |=| −z |,
6. zz =| z |
2
,
7. | z
1
+ z
2
|≤| z
1
| + | z
2
|,
8.
¯
¯
¯ | z
1
| − | z
2
|
¯
¯
¯ ≤| z
1
− z
2
|,
9. Arg(z) = −Argz,
10. Arg(−z) = π + Argz,
11. Arg
¡
1
z
¢
= −Argz.
Definicja 6.2.3. Dla ϕ ∈ R liczbe, zepolona, cos ϕ + j sin ϕ oznaczamy przez e
jϕ
.
Symbol e
jϕ
ma naste,puja,ce wÃlasno´sci
1. e
j(ϕ
1
+ϕ
2
)
= e
jϕ
1
· e
jϕ
2
,
2. e
j(ϕ
1
−ϕ
2
)
=
e
jϕ1
e
jϕ2
,
3.
³
e
jϕ
´
n
= e
jnϕ
,
4. | e
jϕ
|= 1,
5. Arg
¡
e
jϕ
¢
= ϕ.
Symbol podany w definicji 6.2.3 nosi nazwe, symbolu Eulera. Pozwala on
mie,dzy innymi na zapisanie dowolnej liczby zespolonej w tak zwanej postaci wy-
kÃladniczej
z =| z | e
jϕ
,
ϕ = Argz.
122
Zauwa˙zmy, ˙ze dla x ∈ R mamy
e
jx
+ e
−jx
= cos x + j sin x + cos(−x) + j sin(−x)
= cos x + j sin x + cos x − j sin x = 2 cos x.
Ponadto
e
jx
− e
−jx
= cos x + j sin x − [cos(−x) + j sin(−x)
= cos x + j sin x − cos x + j sin x = 2j sin x.
Otrzymujemy sta,d naste,puja,ce wzory zwane wzorami Eulera
cos x =
e
jx
+ e
−jx
2
sin x =
e
jx
− e
−jx
2j
Zadanie 6.2.1. Wykonaj podane dziaÃlania
a) (1 − 3j) + (4 − 5j) · (1 + 2j) + (7 − 3j), b)
2 + 3j
2 + j
,
c)
¯
¯
¯
1 + 3j
3 − 4j
¯
¯
¯,
d) | (2 − j)(2 + j) |.
Zadanie 6.2.2. Naszkicuj zbiory liczb zespolonych speÃlniaja,ce podane warunki
a) | z − 2j |≤ 3 ∨ | z + 2 |≤ 4,
b)
¯
¯
¯
z + j
z
2
+ 1
¯
¯
¯ ≥ 1,
c) Re(z + 1) < 0 ∧ | j − z |< 3,
d) | z + 2 |<| z − j |.
6.3.
Pote,gowanie i pierwiastkowanie liczb zespolonych. Wz´or de
Moivre’a.
Definicja 6.3.1. Pote,ga, stopnia naturalnego z liczby zepolonej z nazywamy n-
krotny iloczyn liczby z przez siebie
z
n
= z · z · . . . · z.
123

Twierdzenie 6.3.1. (wz´or de Moivre’a) Niech z = r(cos ϕ + j sin ϕ), gdzie r > 0
i ϕ ∈ R oraz niech n ∈ N. Wtedy
z
n
= r
n
(cos nϕ + j sin nϕ).
Dow´od tego twierdzenia przeprowadza sie, metoda, indukcji matematycznej.
Definicja 6.3.2. Pierwiastkiem stopnia n ∈ N z liczby zespolonej z nazywamy
ka˙zda, liczbe, zespolona, w speÃlniaja,ca, naste,puja,ca, r´owno´s´c
w
n
= z.
ÃLatwo zauwa˙zy´c, ˙ze liczba zepolona posiada dokÃladnie n piewrwiastk´ow n-tego
stopnia. Posta´c tych pierwiastk´ow podaje naste,puja,ce twierdzenie.
Twierdzenie 6.3.2. Niech z = r(cos ϕ + j sin ϕ), gdzie r > 0 i ϕ ∈ R oraz niech
n ∈ N. Wtedy zbi´or pierwiastk´ow n-tego stopnia z liczby z ma posta´c
z
k
=
n
√
r
³
cos
ϕ + 2kπ
n
+ j sin
ϕ + 2kπ
n
´
, k = 0, 1, . . . , n − 1.
(6.3.1)
Dow´
od. Aby wyznaczy´c pierwiastki n-tego stopnia z liczby z nale˙zy rozwia,za´c
r´ownanie
w
n
= z.
Niech w = q(cos % + j sin %). Wtedy stosuja,c wz´or de Moivre’a otrzymamy
q
n
(cos n% + j sin n%) = r(cos ϕ + j sin ϕ)
Sta,d mamy
q
n
= r
i
n% = ϕ + 2kπ,
gdzie k ∈ Z.
Zatem
q =
n
√
r,
i
% =
ϕ + 2kπ
n
.
Z uwagi na okresowo´s´c funkcji trygonometrycznych pierwiastki z
k
i z
k+n
pokry-
waja, sie,. Wobec tego istnieje tylko n r´o˙znych pierwiastk´ow n-tego stopnia z liczby
zespolonej z.
Pierwiastek, kt´ory otrzymamy ze wzoru (6.3.1) dla k = 0 nazywa´c be,dziemy
gÃl´ownym pierwiastkiem stopnia n z liczby z.
Zauwa˙zmy, ˙ze gÃl´owny pierwiastek z dodatniej liczby rzezcywistej jest r´owny
jej pierwiastkowi arytmetycznemu.
Zbi´or pierwiastk´ow stopnia n ≥ 3 z liczby zespolonej z w interpretacji ge-
omertycznej pokrywa sie, ze zbiorem wierzchoÃlk´ow n-ka,ta foremnego wpisanego
124

w okra,g o promieniu
n
p
| z | i ´sroku w punkcie (0, 0). Pierwszy wierzchoÃlek tego
wieloka,ta znajduje sie, w punkcie z
0
, a ka,ty mie,dzy wektorami odpowiadaja,cymi
pozostaÃlym pierwiastkom sa, r´owne
2π
n
.
Zadanie 6.3.1. Oblicz warto´sci podanych wyra˙ze´
n
a) (1 − j)
12
,
b) (1 +
√
3j)
30
,
c) (
√
3 − j)
8
,
d)
³ 1 − j
−1 +
√
3
´
10
,
e)
³ √3 − j
1 + j
´
6
,
f )
³ √3 − j
−1 −
√
3j
´
12
,
g)
4
√
1 + j,
h)
3
√
−27j,
i)
√
5 − 12j,
j)
p
(5 − 4j)
4
,
k)
3
p
(2 − j)
6
,
l)
4
p
(−2 + 3j)
4
.
Zadanie 6.3.2. Stosuja,c wzory Eulera wyrazi´c podane funkcje w postaci sum
sinus´ow i cosinus´ow wielokrotno´sci ka,ta x
a) sin
3
x,
b) cos
2
x,
c) sin
5
x,
d) cos
4
x + sin
4
x.
6.4. Wielomiany. Zasadnicze twierdzenie algebry.
Poje,cie wielomianu o wsp´oÃlczynnikach rzeczywistych znamy ze szkoÃly ´sredniej.
Teraz rozszerzymy je na wielomiany o wsp´oÃlczynnikach zespolonych.
Definicja 6.4.1. Wielomianem zespolonym stopnia n ∈ N nazywamy funkcje,
f : C → C okre´slona, wzorem
W (z) = c
n
z
n
+ c
n−1
z
n−1
+ . . . + c
1
z + c
0
,
gdzie c
k
∈ C dla 0 ≤ k ≤ n oraz c
n
6= 0.
Wielomiany o wsp´oÃlczynnikach zespolonych podobnie jak wielomiany o wsp´oÃl-
czynnikach rzeczywistych, sa, wtedy r´owne gdy sa, tego samego stopnia i maja,
odpowiednie wsp´oÃlczynniki r´owne. Na wielomianach o wsp´oÃlczynnikach zespo-
lonych mo˙zemy wykonywa´c dziaÃlania w taki sam spos´ob jak na wielomianach o
wsp´oÃlczynnikach rzeczywistych.
Przypomnimy teraz poje,cie pierwiastka wielomianu
Definicja 6.4.2. Liczbe, zepolona, z
0
nazywamy pierwiastkiem wielomianu W (z),
je˙zeli W (z
0
) = 0.
125

Dla wielomian´ow zespolonych prawdziwe jest r´ownie˙z twierdzenie Bezuta.
Twierdzenie 6.4.1. Liczba z
0
jest pierwiastkiem wielomianu W (z) wtedy i tylko
wtedy, gdy istnieje taki wielomian P (z), ˙ze
W (z) = P (z)(z − z
0
).
Podamy teraz kilka wÃlasno´sci wielomian´ow zespolonych.
Twierdzenie 6.4.2. (zasadnicze twierdzenie algebry) Ka˙zdy wielomian zespolony
stopnia naturalnego ma co najmniej jeden pierwiastek zespolony.
Twierdzenie to zostaÃlo sformuÃlowane przez francuskiego matematyka
d’Alemberta. Obecnie znanych jest wiele dowod´ow tego twierdzenia, ale ˙zadnego z
nich nie przytoczymy, poniewa˙z wymagaja, one wprowadzenia wielu dodatkowych
poje,´c matematycznych.
Bezpo´srednia, konsekwencja, tego twierdzenia jest twierdzenie o rozkÃladzie
wielomianu zespolonego.
Twierdzenie 6.4.3. Ka˙zdy wielomian zespolony stopnia naturalnego jest rozkÃla-
dalny na czynniki stopnia pierwszego
W (z) = c
n
(z − x
n
)(z − x
n−1
) . . . (z − x
1
),
gdzie c
n
jest wsp´oÃlczynnikiem przy z
n
, a x
1
, x
2
, . . . , x
n
sa, wszystkimi (niekonie-
cznie r´o˙znymi) pierwiastkami zespolonymi tego wielomianu.
Zadanie 6.4.1. Podane wielomiany rozÃlo˙zy´c na czynniki
W (z) = z
2
+ j,
V (z) = z
3
+ 1,
Q(z) = z
4
− j,
R(z) = z
4
+ jz
2
+ 6,
P (z) = z
4
− (1 + j)
4
.
126

7. MACIERZE I WYZNACZNIKI
W rozdziale 7 zdefiniujemy poje,cie macierzy i wyznacznika. Poznamy r´ownie˙z
pewne wÃlasno´sci macierzy i wyznacznik´ow. WÃlasno´sci te wykorzystywa´c be,dziemy
do rozwia,zywania ukÃlad´ow r´owna´n liniowych, w kt´orych liczba niewiadomych nie
zawsze jest r´owna liczbie r´owna´
n.
7.1. Algebra macierzy.
Paragraf ten po´swie,cony be,dzie og´olnej teorii macierzy.
Definicja 7.1.1. Prostoka,tna, macierza, rzeczywista, (zespolona,) wymiaru m × n
nazywamy prostoka,tna, tablice, zÃlo˙zona, z mn liczb rzeczywistych (zespolonych)
ustawionych w m wierszach i n kolumnach w naste,puja,cy spos´ob
a
11
a
12
. . .
a
1j
. . .
a
1,n−1
a
1,n
a
21
a
22
. . .
a
2j
. . .
a
2,n−1
a
2,n
..
.
..
.
. ..
..
.
. ..
..
.
..
.
a
i1
a
i2
. . .
a
ij
. . .
a
i,n−1
a
i,n
..
.
..
.
. ..
..
.
. ..
..
.
..
.
a
m−1,1
a
m−1,2
. . . a
m−1,j
. . . a
m−1,n−1
a
m−1,n
a
m1
a
m2
. . .
a
mj
. . .
a
m,n−1
a
m,n
← i-ty wiersz
↑
j-ta kolumna
Macierze oznacza´c be,dziemy du˙zymi literami alfabetu, np. A, B, C. Element
stoja,cy w i-tym wierszu i j-tej kolumnie oznacza´c be,dziemy przez a
ij
. Powy˙zsza,
macierz mo˙zemy r´ownie˙z zapisa´c w postaci:
A = [a
ij
]
m×n
Powiemy, ˙ze dwie macierze A = [a
ij
] i B = [b
ij
] sa, r´owne je˙zeli sa, tego samego
wymiaru (maja, ta, sama, liczbe, wierszy i kolumn) oraz
^
1≤i≤m, 1≤j≤n
a
ij
= b
ij
.
Zdefiniujemy teraz kilka wa˙znych rodzaj´ow macierzy.
127

Rodzaje macierzy:
1. Macierz wymiaru m × n, kt´orej wszystkie elementy sa, r´owne 0 nazywamy
macierza, zerowa,.
2. Macierz, w kt´orej liczba wierszy jest r´owna liczbie kolumn nazywamy macierza,
kwadratowa,. Liczbe, wierszy (kolumn) nazywamy wtedy stopniem macierzy.
Elementy macierzy kwadratowej maja,ce ten sam numer wiersza i kolumny
tworza, gÃl´owna, przeka,tna, macierzy.
3. Macierz kwadratowa, stopnia n ≥ 2, w kt´orej wszystkie elementy stoja,ce pod
gÃl´owna, przeka,tna, sa, r´owne 0, nazywamy macierza, tr´ojka,tna, g´orna,. Nato-
miast macierz, w kt´orej wszystkie elementy stoja,ce nad gÃl´owna, przeka,tna, sa,
r´owne 0, be,dziemy nazywa´c macierza, tr´ojka,tna, dolna,.
4. Macierz kwadratowa, stopnia n, w kt´orej wszystkie elementy z wyja,tkiem ele-
ment´ow gÃl´ownej przeka,tnej, sa, r´owne 0 nazywamy, macierza, diagonalna,.
5. Macierz diagonalna, stopnia n, w kt´orej elementy z gÃl´ownej przeka,tnej sa,
r´owne 1 nazywa´c be,dziemy macierza, jednostkowa, stopnia n i oznacza´c I
n
.
6. Macierza, transponowana, do macierzy A = [a
ij
]
m×n
nazywamy macierz B =
[b
ij
] wymiaru n × m, kt´orej elementy sa,, okre´slone wzorem
V
1≤i≤n, 1≤j≤m
b
ij
= a
ji
.
Mo˙zna powiedzie´c, ˙ze macierz transponowana powstaje przez zamiane, wierszy
na kolumny, a kolumn na wiersze. Macierz transponowana, oznacza´c be,dziemy
w naste,puja,cy spos´ob A
T
.
Zauwa˙zmy, ˙ze (A
T
)
T
= A.
7. Macierz A nazywamy macierza, symetryczna, wtedy i tylko wtedy, gdy
A
T
= A
8. Macierz A nazywamy macierza, antysymetryczna, wtedy i tylko wtedy, gdy
A
T
= −A,
gdzie −A = [−a
ij
].
9. Macierza, sprze,˙zona, z macierza, zespolona, A = [a
ij
]
m×n
, nazywamy macierz
A, kt´ora ma elementy sprze,˙zone do element´ow macierzy A
A = [a
ij
], a
ij
∈ C; 1 ≤ i ≤ m, 1 ≤ j ≤ n.
128

Na macierzach mo˙zemy wykonywa´c pewne dziaÃlania. Podamy teraz definicje
tych dziaÃla´
n. Niech dane be,da, dwie macierz prostoka,tne A = [a
ij
]
m×n
i B =
[b
ij
]
m×n
.
Definicja 7.1.2. Suma, macierzy A i B nazywamy macierz C = [c
ij
]
m×n
, kt´orej
elementy okre´slone sa, wzorem
^
1≤i≤m, 1≤j≤n
c
ij
= a
ij
+ b
ij
.
Sume, macierzy oznaczamy w naste,puja,cy spos´ob C = A + B. R´o˙znica, macierzy
A i B nazywamy macierz C = [c
ij
]
m×n
, kt´orej elementy okre´slone sa, wzorem
^
1≤i≤m, 1≤j≤n
c
ij
= a
ij
− b
ij
.
W takim przypadku pisa´c be,dziemy C = A−B. Zauwa˙zmy, ˙ze dziaÃlania dodawania
i odejmowania macierzy okre´slone sa, tylko na macierzach tego samego wymiaru.
Macierz wynikowa ma taki sam wymiar jak macierze A i B.
Definicja 7.1.3. Iloczynem macierzy A przez liczbe, γ nazywamy macierz C =
[c
ij
]
m×n
, kt´orej elementy okre´slone sa, wzorem
^
1≤i≤m, 1≤j≤k
c
ij
= γa
ij
.
W´owczas be,dziemy pisa´c C = γA.
Wy˙zej zdefiniowane dziaÃlania maja, naste,puja,ce wÃlasno´sci:
1. A + B = B + A,
2. A + (B + C) = (A + B) + C,
3. γ(A + B) = γA + γB,
4. (γ + δ)A = γA + δA,
5. (γδ)A = γ(δA),
6. (A + B)
T
= A
T
+ B
T
,
7. (γA)
T
= γA
T
.
129

Definicja 7.1.4. Niech macierz A = [a
ij
] ma wymiar m × n, a macierz B = [b
ij
]
ma wymiar n×k. Iloczynem macierzy A i B nazywamy macierz C = [c
ij
] wymiaru
m × k, kt´orej elementy dane sa, wzorem
^
1≤i≤m, 1≤j≤n
c
ij
=
n
X
l=1
a
il
b
lj
.
Iloczyn macierzy oznaczamy w spos´ob naste,puja,cy C = A · B.
Zauwa˙zmy, ˙ze mno˙zenie macierzy nie zawsze jest wykonalne.
Zgodnie z
definicja, macierze A i B mo˙zemy tylko wtedy przez siebie pomno˙zy´c, gdy liczba kol-
umn macierzy A jest r´owna liczbie wierszy macierzy B. Wynika sta,d, ˙ze mno˙zenie
macierzy prostoka,tnych nie zawsze jest przemienne.
Element c
ij
macierzy C = A · B otrzymujemy sumuja,c iloczyny odpowiada-
ja,cych sobie element´ow i-tego wiersza macierzy A i j-tej kolumny macierzy B.
WÃlasno´sci mno˙zenia macierzy
1. Je˙zeli macierz A jest wymiaru m × n i macierze B i C sa, wymiaru n × k, to
A(B + C) = AB + AC.
2. Je˙zeli macierze A i B sa, wymiaru m × n i macierz C jest wymiaru n × k, to
(A + B)C = AC + BC.
3. Je˙zeli macierz A jest wymiaru m × n i macierz B jest wymiaru n × k oraz γ
jest pewna, liczba, rzeczywista, lub zespolona,, to
A(γB) = (γA)B = γ(AB).
4. Je˙zeli macierz A jest wymiaru m × n, macierz B jest wymiaru n × k, a macierz
C ma wymiar k × l, to
(AB)C = A(BC).
5. Je˙zeli macierz A jest wymiaru m × n, a macierz B jest wymiaru n × k, to
(AB)
T
= B
T
A
T
.
Zamiast A · A · A . . . A be,dziemy pisa´c A
n
. Je˙zeli macierz A jest macierza, kwadra-
towa, to wtedy mamy
(A
n
)
T
= (A
T
)
n
.
130

7.2. Wyznaczniki.
Niech A
ij
oznacza macierz jaka, otrzymamy z macierzy A poprzez skre´slenie
i-tego wiersza i j-tej kolumny.
Definicja 7.2.1. Wyznacznikiem macierzy kwadratowej A = [a
ij
] nazywamy
liczbe, rzeczywista, lub zespolona, detA okre´slona, w naste,puja,cym wzorem rekuren-
cyjnym
1. je˙zeli stopie´
n macierzy A jest r´owny 1, to
detA = a
11
,
2. Je˙zeli stopie´
n n macierzy A jest wie,kszy ni˙z 1, to
detA =
n
X
i=1
(−1)
k+i
a
ki
detA
ki
,
gdzie 1 ≤ k ≤ n jest numerem dowolnie wybranego wiersza z macierzy A.
Definicje, ta, podaÃl matematyk francuski Laplace, dlatego te˙z licza,c wyznacznik
macierzy be,dziemy m´owi´c, ˙ze stosujemy metode, rozwinie,cia Laplace’a wzgle,dem
k-tego wiersza. Oczywi´scie, w my´sl tej definicji warto´s´c wyznacznika nie zale˙zy od
wyboru wiersza wzgle,dem, kt´orego be,dziemy go rozwija´c.
Zauwa˙zmy, ˙ze wyznacznik zdefiniowany jest tylko dla macierzy kwadratowych.
Nie mo˙zna wie,c posÃluguja,c sie, powy˙zsza, definicja,, policzy´c wyznacznika z dowolnej
macierzy prostoka,tnej.
Wyznacznik macierzy mo˙zemy r´ownie˙z obliczy´c dokonuja,c rozwinie,cia wzgle,-
dem dowolnej kolumny danej macierzy. W´owczas je˙zeli stopie´
n macierzy A jest
wie,kszy od 1, to
detA =
n
X
j=1
(−1)
k+j
a
jk
detA
jk
,
gdzie 1 ≤ k ≤ n jest numerem dowolnie wybranej kolumny z macierzy A.
WÃlasno´sci wyznacznik´
ow.
1. Wyznacznik macierzy kwadratowej maja,cej wiersz lub kolumne, zÃlo˙zona, z
samych zer jest r´owny zero.
2. Je˙zeli w macierzy kwadratowej zamienimy miejscami dwa wiersze albo dwie
kolumny, to jej wyznacznik zmieni znak na przeciwny.
131

3. Wyznacznik macierzy kwadratowej , w kt´orej dwa wiersze lub dwie kolumny
maja, proporcjonalne elementy jest r´owny zero.
4. Je˙zeli jedna, z kolumn lub jeden z wierszy pomno˙zymy przez dowolna, liczbe,
c, to wyznacznik macierzy zostanie r´ownie˙z pomno˙zony przez c.
5. Wyznacznik macierzy tr´ojka,tej dolnej i tr´ojka,tnej g´ornej jest r´owny iloczynowi
element´ow stoja,cych na gÃl´ownej przeka,tnej.
6. Wyznacznik macierzy kwadratowej nie zmieni sie, je˙zeli dowolny wiersz po-
mno˙zymy przez liczbe, r´o˙zna, od zera i dodamy go do innego wiersza. Taka
sama wÃlasno´s´c zachodzi r´ownie˙z dla kolumn.
7. Wyznacznik macierzy transponowanej do macierzy kwadratowej A jest r´owny
wyznacznikowi tej macierzy.
8. Wyznacznik macierzy jednostkowej, niezale˙znie od jej stopnia, jest r´owny je-
den.
Powy˙zsze wÃlasno´sci mo˙zemy wykorzysta´c do obliczania wyznacznik´ow. W
szczeg´olno´sci korzystaja,c z wÃlasno´sci 5 i 6 wyznacznik macierzy kwadratowej
mo˙zemy obliczy´c poprzez sprowadzenie jej do macierzy tr´ojka,tnej g´ornej ba,d´z dol-
nej. Dokonujemy tego wykorzystuja,c przede wszystkim wÃlasno´s´c 6. Oczywi´scie
otrzymana macierz tr´ojka,tna nie be,dzie r´owna macierzy wyj´sciowej, ale be,dzie
miaÃla taki sam wyznacznik.
Algorytm obliczania wyznacznika w oparciu o wÃlasno´s´c 5 i 6 nazywamy algo-
rytmem Gaussa i przebiega on wedÃlug naste,puja,cego schematu:
Wiersz 1 mno˙zymy przez −
a
21
a
11
i dodajemy do wiersza drugiego. Mo˙zemy ta,
operacje, zapisa´c symbolicznie w naste,puja,cy spos´ob w
2
−
a
21
a
11
w
1
. W wyniku
takiego poste,powania w miejscu elementu a
12
otrzymamy 0. Podobnie poste,-
pujemy, aby wyzerowa´c pozostaÃle elementy kolumny pierwszej. PosÃlugujemy sie,
tylko wierszem pierwszym. Dokonujemy w tym celu naste,puja,cych operacji
w
3
−
a
31
a
11
w
1
w
4
−
a
41
a
11
w
1
..
.
w
n
−
a
n1
a
11
w
1
Naste,pnie posÃluguja,c sie, wierszem drugim z nowo powstaÃlej macierzy zerujemy
elementy stoja,ce pod gÃl´owna, przeka,tna, z kolumny drugiej dokonuja,c operacji
w
3
−
a
0
31
a
0
22
w
2
132
w
4
−
a
0
41
a
0
22
w
2
..
.
w
n
−
a
0
n1
a
0
22
w
2
,
gdzie a
0
ij
= a
ij
− a
i1
a
1j
a
11
.
Dalej zerujemy elementy le˙za,ce pod gÃl´owna, przeka,tna, w kolumnie trzeciej
wykorzystuja,c wiersz trzeci. DziaÃlania kontynuujemy, a˙z do uzyskania macierzy
tr´ojka,tnej g´ornej. Tak otrzymana macierz ma wyznacznik r´owny iloczynowi ele-
ment´ow z gÃl´ownej przeka,tnej, a ponadto jej wyznacznik jest taki sam jak macierzy
wyj´sciowej.
Podamy jeszcze jedna, wa˙zna, wÃlasno´s´c wyznacznik´ow.
Twierdzenie 7.2.1. (Cauchy’ego) Niech A i B be,da, macierzami kwadratowymi
tego samego stopnia. Wtedy
det(A · B) = detA · detB.
7.3. Macierz odwrotna.
Niech A be,dzie macierza, kwadratowa, stopnia n.
Definicja 7.3.1. Macierza, nieosobliwa, nazywamy macierz kwadratowa,, kt´orej
wyznacznik jest r´o˙zny od zera. Macierz, kt´ora ma wyznacznik r´owny zero nazy-
wamy macierza, osobliwa,.
Definicja 7.3.2. Macierza, odwrotna, do macierzy A nazywamy macierz oznaczona,
przez A
−1
, kt´ora speÃlnia naste,puja,cy warunek
A · A
−1
= A
−1
· A = I,
gdzie I jest macierza, jednostkowa,.
Macierz do kt´orej istnieje macierz odwrotna nazywa´c be,dziemy macierza, od-
wracalna,.
Naste,puja,ce twierdzenie podaja, kilka wÃla´sciwo´sci macierzy odwrotnej.
Twierdzenie 7.3.1. Macierz odwracalna jest nieosobliwa.
Dow´
od. Twierdzenie to wynika z twierdzenia Cauchy’ego, mamy bowiem
det(A · A
−1
) = detA · detA
−1
.
133

Z drugiej strony korzystaja,c z wÃlasno´sci 8 wyznacznika otrzymujemy
det(A · A
−1
) = detI = 1.
Zatem
detA · detA
−1
= 1
oznacza to, ˙ze detA 6= 0.
Twierdzenie 7.3.2. Macierz odwrotna do macierzy nieosobliwej jest nieosobliwa.
Dow´
od.
Fakt ten wynika bezpo´srednio z dowodu twierdzenia poprzedniego.
Skoro
detA · detA
−1
= 1,
to detA
−1
6= 0.
Z dowodu twierdzenia 7.3.1 otrzymujemy r´ownie˙z naste,puja,cy fakt
Twierdzenie 7.3.3. Wyznacznik macierzy odwrotnej do macierzy A r´owny jest
odwrotno´sci wyznacznika macierzy A
detA
−1
=
1
detA
.
W kolejnym twierdzeniu wyka˙zemy, ˙ze ka˙zda macierz nieosobliwa jest od-
wracalna, tzn. udowodnimy twierdzenie odwrotne do twierdzenia 7.3.1. Metoda
dowodu be,dzie konstruktywna. Jednak˙ze wcze´sniej zdefiniujemy kilka pomoc-
niczych poje,´c.
Definicja 7.3.3. Minorem M
ij
odpowiadaja,cym elementowi a
ij
nazywamy wy-
znacznik jaki otrzymamy z wyznacznika macierzy A przez skre´slenie i-tego wiersza
i j-tej kolumny.
Definicja 7.3.4.
DopeÃlnieniem algebraicznym D
ij
elementu a
ij
wyznacznika
macierzy A = [a
ij
] nazywamy iloczyn minora odpowiadaja,cego elementowi a
ij
oraz czynnika (−1)
i+j
D
ij
= (−1)
i+j
M
ij
Twierdzenie 7.3.4. Je˙zeli macierz kwadratowa A stopnia n jest nieosobliwa, to
A
−1
=
1
detA
D
11
D
12
. . . D
1,n
D
21
D
22
. . . D
2,n
..
.
..
.
..
.
..
.
D
n1
D
n2
. . . D
n,n
T
134

gdzie D
ij
oznaczaja, dopeÃlnienia algebraiczne element´ow a
ij
macierzy A.
Dow´
od. Niech C = [c
ij
], gdzie
c
ij
=
D
ji
detA
oraz niech
δ
ij
=
½
1, i = j,
0, i 6= j.
Oczywi´scie I = [δ
ij
]. Wyka˙zemy, ˙ze A · C = I.
Element stoja,cy w i-tym wierszu i j-tej kolumnie macierzy A · C oznaczmy
przez [AC]
ij
. Mamy zatem
[AC]
ij
=
n
X
k=1
a
ik
c
kj
=
1
detA
n
X
k=1
a
ik
D
jk
=
1
detA
n
X
k=1
a
ik
(−1)
j+k
detA
jk
= δ
ij
,
gdy˙z dla i = j
n
X
k=1
a
ik
detA
jk
= detA,
a dla i 6= j powy˙zsza suma jest rozwinie,ciem Laplace’a wyznacznika o dw´och
jednakowych wiersza lub kolumnach.
Podobnie mo˙zemy wykaza´c, ˙ze C · A = I.
Zadanie 7.3.1. Wykonaj podane dziaÃlania
a) A · B − C
2
,
b) 3C − A · B,
b) A · B + 2C,
a) C · A · B,
b) A
T
· C + C · B
T
,
b) A
T
· B
T
− B · A,
gdzie
A =
2
3
1 −2
4 −1
, B =
·
3 −1
3
1 −2
1
¸
, C =
1
−2 −2
1
3
3
−3
2
4
.
Zadanie 7.3.2. Korzystaja,c z wÃlasno´sci wyznacznik´ow wykaza´c, ˙ze
a)
¯
¯
¯
¯
¯
¯
a + b c − a b + c
a + c b − c
a + b
b + c
a − b a + c
¯
¯
¯
¯
¯
¯
= 0,
b)
¯
¯
¯
¯
¯
¯
p
q
r
q + r p + r p + q
−r
−r
−r
¯
¯
¯
¯
¯
¯
= 0,
135

Zadanie 7.3.3. Znale´z´c macierze odwrotne do podanych macierzy
A =
2
−3
3
−1
4
−4
2
−1
0
, C =
1
−2
0
−1
0
3
1
1
−1
2
0
2
−2
3
−1
4
.
7.4. Rza,d macierzy.
Na pocza,tku tego paragrafu rozszerzymy poje,cie minora.
Definicja 7.4.1. Minorem stopnia k macierzy A nazywamy wyznacznik stopnia
k jaki otrzymamy z macierzy A przez skre´slenie pewnej liczby kolumn i wierszy.
PrzykÃlad 7.4.1. Niech dana be,dzie macierz
A =
·
2
3
−1
1 −2
4
¸
.
Macierz ta posiada naste,puja,ce minory drugiego stopnia
M
1
= det
·
3
−1
−2
4
¸
= 10, M
2
= det
·
2 −1
1
4
¸
= 9, M
3
= det
·
2
3
1 −2
¸
= −7,
przy czym minor M
1
powstaÃl przez skre´slenie pierwszej kolumny, M
2
- przez
skre´slenie drugiej kolumny, a M
3
- trzeciej kolumny. Jednym z mior´ow pierwszego
stopnia jest minor jaki otrzymamy przez skre´slenie pierwszej i drugiej kolumny
oraz drugiego wiersza M = det[−1] = −1.
Definicja 7.4.2. Rze,dem macierzy A = [a
ij
]
m×n
nazywamy
1) liczbe, zero, gdy macierz jest zerowa, tj.
V
1≤i≤m, 1≤j≤n
a
ij
= 0,
2) liczbe, r´owna, najwie,kszemu ze stopni jej r´o˙znych od zera minor´ow, gdy macierz
A jest niezerowa.
Rza,d macierzy oznacza´c be,dziemy symbolem rzA.
PrzykÃlad 7.4.2. Rozwa˙zmy macierz
A =
1 2 3
4 5 6
7 8 9
.
136

Z macierzy tej mo˙zna utworzy´c tylko jeden minor trzeciego stopnia. Jest on r´owny
wyznacznikowi macierzy A. Zauwa˙zmy, ˙ze detA = 0 oraz, ˙ze
det
·
1 2
4 5
¸
= −3 6= 0.
Zatem rzA = 2 poniewa˙z z macierzy tej mo˙zemy utworzy´c nieosobliwa, macierz
stopnia 2 (poprzez skre´slenie jednego wiersza i kolumny), a wszystkie jej minory
trzeciego stopnia sa, r´owne zero.
WÃlasno´sci rze,du macierzy.
1. Rza,d macierzy nieosobliwej stopnia n jest r´owny n; rza,d niezerowej macierzy
kwadratowej osobliwej jest mniejszy od jej stopnia.
2. Rza,d macierzy nie ulegnie zmianie je´sli do dowolnego wiersza (kolumny) do-
damy inny wiersz (kolumne,) pomno˙zony przez liczbe, r´o˙zna, od zera.
3. Przestawienie wierszy (kolumn) macierzy nie zmienia jej rze,du.
4. Rza,d macierzy nie zmieni sie, je˙zeli wykre´slimy z niej kolumne, lub wiersz zÃlo˙zony
z samych zer.
Zadanie 7.4.1. Wyznacz rze,dy podanych macierzy
A
2 1 3 6
1 0 1 2
3 1 4 8
, B =
1
2
1
2
1
−1
1
−1 −2
−5 −4
1
.
7.5. Wzory Cramera.
Definicja 7.5.1. UkÃlad r´owna´
n postaci
a
11
x
1
+a
12
x
2
+ · · ·
+a
1n
x
n
= b
1
a
21
x
1
+a
22
x
2
+ · · ·
+a
2n
x
n
= b
2
· · ·
· · ·
· · ·
· · ·
· · ·
a
m1
x
1
+a
m2
x
2
+ · · · +a
mn
x
n
= b
m
(7.5.1)
nazywamy ukÃladem m r´owna´
n liniowych z n niewiadomymi x
1
, x
2
, . . . , x
n
. Macierz
A =
a
11
a
12
· · ·
a
1n
a
21
a
22
· · ·
a
2n
· · ·
· · ·
· · ·
· · ·
a
m1
a
m2
· · · a
mn
137

nazywamy macierza, gÃl´owna, ukÃladu, macierze
B =
b
1
b
2
· · ·
b
m
,
X =
x
1
x
2
· · ·
x
n
nazywamy odpowiednio kolumna, (macierza,) wyraz´ow wolnych i kolumna, (macie-
rza,) niewiadomych.
Powy˙zszy ukÃlad mo˙zemy zapisa´c w naste,puja,cej postaci macierzowej
AX = B.
Definicja 7.5.2. Rozwia,zaniem ukÃladu r´owna´n liniowych (7.5.1) nazywamy ka˙zdy
cia,g (x
1
, x
2
, . . . , x
n
) liczb rzeczywistych speÃlniaja,cych ten ukÃlad.
Je˙zeli istnieje dokÃladnie jeden cia,g (x
1
, x
2
, . . . , x
n
), kt´ory speÃlnia ukÃlad (7.5.1),
to m´owimy, ˙ze ukÃlad r´owna´
n liniowych jest oznaczony. W przypadku, gdy takich
cia,g´ow jest niesko´nczenie wiele ukÃlad be,dziemy nazywa´c nieoznaczonym. Nato-
miast ukÃlad r´owna´
n, kt´ory nie ma rozwia,za´n nazywamy sprzecznym.
Definicja 7.5.3. UkÃlad r´owna´
n liniowych (7.5.1), w kt´orym kolumna wyraz´ow
wolnych jest macierza, zerowa, nazywamy ukÃladem jednorodnym.
Definicja 7.5.4. UkÃladem Cramera nazywamy ukÃlad, w kt´orym macierz gÃl´owna
jest macierza, kwadratowa, nieosobliwa,.
Twierdzenie 7.5.1. (Cramera) UkÃlad Cramera ma dokÃladnie jedno rozwia,zanie
naste,puja,cej postaci
X =
1
detA
detA
1
detA
2
..
.
detA
n
,
gdzie A
j
dla 1 ≤ j ≤ n oznacza macierz A, w kt´orej j-ta, kolumne, zasta,piono
kolumna, wyraz´ow wolnych.
Poniewa˙z macierz A jest macierza, nieosobliwa,, to ukÃlad Cramera mo˙zna
r´ownie˙z rozwia,za´c wykorzystuja,c macierz odwrotna,. Mianowicie
X = A
−1
· B.
Z twierdzenia Cramera wynika, ˙ze ukÃlad r´owna´
n liniowych, w kt´orym liczba r´ow-
na´
n jest taka sama jak liczba niewiadomych jest
138

1. oznaczony, je´sli detA 6= 0,
2. nieoznaczony, je´sli detA = 0 i
V
1≤j≤n
detA
j
= 0,
3. sprzeczny, je´sli detA = 0 i
W
1≤j≤n
detA
j
6= 0.
Zauwa˙zmy, ˙ze jedynym rozwia,zaniem jednorodnego ukÃladu Cramera jest roz-
wia,zanie zerowe
x
1
= 0, x
2
= 0, . . . , x
n
= 0.
Zadanie 7.5.1. Rozwia,˙z podane ukÃlady r´owna´n
a)
x
1
+6x
2
−x
3
= 8
−x
1
−4x
2
+5x
3
= 0
2x
1
+13x
2
+5x
3
= 10
b)
x
1
+2x
2
+3x
3
−x
4
= 3
3x
1
+6x
2
+3x
3
+x
4
= 1
2x
1
+4x
2
+7x
3
−4x
4
= 14
−x
1
+2x
2
− x
3
+ x
4
= −3
c)
x
1
+x
2
−x
3
= 1
2x
1
+3x
2
+x
3
= 0
2x
1
+2x
2
−2x
3
= −2
d)
2x
1
+2x
2
+2x
3
= 4
3x
1
+6x
2
+3x
3
= 1
x
1
+x
2
+x
3
= −2
c)
½
x
1
+x
2
= 0
2x
1
+3x
2
= 0
d)
2x
1
+x
2
−2x
3
= 0
−x
1
+5x
2
+3x
3
= 0
x
1
+x
2
+x
3
= 0
Zadanie 7.5.2.
Przedyskutowa´c rozwia,zalno´s´c podanych ukÃlad´ow r´owna´n w
zale˙zno´sci od warto´sci parametru p.
a)
x
1
+px
2
−x
3
= 1
x
1
−10x
2
−6x
3
= 3
2x
1
−x
2
+px
3
= 0
b)
ax
1
+x
2
+x
3
= 1
x
1
+ax
2
+x
3
= a
x
1
+x
2
+ax
3
= a
2
139

7.6. UkÃlady r´
owna´
n liniowych. Twierdzenia Kroneckera-Capelliego.
Niech dany be,dzie ukÃlad r´owna´n
a
11
x
1
+a
12
x
2
+ · · ·
+a
1n
x
n
= b
1
a
21
x
1
+a
22
x
2
+ · · ·
+a
2n
x
n
= b
2
· · ·
· · ·
· · ·
· · ·
· · ·
a
m1
x
1
+a
m2
x
2
+ · · · +a
mn
x
n
= b
m
(7.6.1)
Macierz
A =
a
11
a
12
· · ·
a
1n
a
21
a
22
· · ·
a
2n
· · ·
· · ·
· · ·
· · ·
a
m1
a
m2
· · · a
mn
(7.6.2)
nazywamy macierza, gÃl´owna, ukÃladu, natomiast macierze
B =
b
1
b
2
· · ·
b
m
,
X =
x
1
x
2
· · ·
x
n
nazywamy odpowiednio kolumna, (macierza,) wyraz´ow wolnych i kolumna, (macie-
rza,) niewiadomych. Ponadto macierz
U =
a
11
a
12
· · ·
a
1n
b
1
a
21
a
22
· · ·
a
2n
b
2
· · ·
· · ·
· · ·
· · ·
· · ·
a
m1
a
m2
· · · a
mn
b
m
(7.6.3)
powstaÃla, z macierzy A przez doÃlaa,czenie kolumny wyraz´ow wolnych nazywamy
macierza, uzupeÃlniona,.
Twierdzenie 7.6.1. (Kroneckera-Capelliego) UkÃlad r´owna´
n liniowych (7.6.1) ma
rozwia,zanie wtedy i tylko wtedy, gdy rzA = rzU, przy czym gdy rzA = rzU = n,
to ukÃlad ma dokÃladnie jedno rozwia,zanie, gdy rzA = rzU < n, to ukÃlad ma
niesko´
nczenie wiele rozwia,za´n zale˙znych od n − r parametr´ow.
Zauwa˙zmy, ˙ze je˙zeli ukÃlad (7.6.1) jest ukÃladem jednorodnym, to macierz
uzupeÃlniona U powstaje przez dopisanie do macierzy gÃl´ownej A kolumny zÃlo˙zonej z
samych zer. Zatem rze,dy tych macierzy sa, takie same, co oznacza, ˙ze ka˙zdy ukÃlad
jednorodny ma zawsze rozwia,zanie. Na mocy twierdzenia Kroneckera-Capelliego
ma on rozwia,zanie niezerowe tylko wtedy, gdy rza,d macierzy gÃl´ownej jest mniejszy
od liczby niewiadomych.
140

Do rozwia,zywania ukÃlad´ow r´owna´n liniowych mo˙zemy zastosowa´c metode, elimi-
nacji Gaussa. Ka˙zedmu ukÃladowi r´owna´
n odpowiada pewna macierz uzupeÃlniona
i na odwr´ot maja,c dana, macierz mo˙zemy ja, potraktowa´c jako macierz uzupeÃlniona,
pewnego ukÃladu r´owna´
n liniowych. Stosuja,c metode, eliminacji Gaussa do rozwia,-
zania ukÃladu r´owna´
n sprowadzamy jego macierz uzupeÃlniona, do macierzy naste,-
puja,cej postaci
1
0
. . .
0
| p
1,r+1
p
1,r+2
. . .
p
1n
| z
1
0
1
. . .
0
| p
2,r+1
p
2,r+2
. . .
p
2n
| z
2
..
.
..
.
. ..
..
.
|
..
.
..
.
. ..
..
.
|
..
.
0
0
. . .
1
| p
r,r+1
p
r,r+2
. . .
p
rn
| z
r
−− −− −− −−
−−
−−
−− −−
−−
0
0
. . .
0
|
0
0
. . .
0
| z
r+1
,
gdzie rzA = r. W´owczas,
1) je˙zeli z
r+1
6= 0, ukÃlad jest sprzeczny,
2) je˙zeli ostani wiersz nie pojawi sie, i n = r, to ukÃlad jest oznaczony i ma
rozwia,zanie postaci
x
1
= z
1
,
x
2
= z
2
, . . . , x
n
= z
n
.
3) je˙zeli ostani wiersz nie pojawi sie, i n > r, to ukÃlad jest nieoznaczony, a jego
rozwia,zania zale˙za, od parametr´ow (x
r+1
, x
r+2
, . . . , x
n
) w naste,puja,cy spos´ob
x
1
x
2
..
.
x
r
=
z
1
z
2
..
.
z
r
−
p
1,r+1
p
1,r+2
. . . p
1n
p
2,r+1
p
2,r+2
. . . p
2n
..
.
..
.
. .. ...
p
r,r+1
p
r,r+2
. . . p
rn
x
r+1
x
r+2
..
.
x
n
Zadanie 7.6.1. Rozwia,˙z podane ukÃlady r´owna´n
a)
x
1
+6x
2
−x
3
= 0
−x
1
−4x
2
+5x
3
= 6
3x
1
+17x
2
= 0
2x
1
+13x
2
+5x
3
= 8
b)
x
1
+2x
2
+3x
3
−x
4
= 0
3x
1
+6x
2
+3x
3
+x
4
= 5
2x
1
+4x
2
+7x
3
−4x
4
= −6
Zadanie 7.6.2.
Przedyskutowa´c rozwia,zalno´s´c podanych ukÃlad´ow r´owna´n w
zale˙zno´sci od warto´sci parametru p.
a)
x
1
+px
2
−x
3
= 1
x
1
−10x
2
−6x
3
= 3
2x
1
−x
2
+px
3
= 0
b)
2x
1
+3x
2
−x
3
= 0
px
2
+(p + 1)x
3
= −1
x
1
+5x
2
= 1
2x
1
+x
2
+3x
3
= −1
141

7.7. Warto´sci wÃlasne wektory wÃlasne i wielomian charakterystyczny
macierzy kwadratowej.
Niech dana be,dzie macierz kwadratowa A = [a
ij
]
n×n
, n ≥ 2 o elementach
rzeczywistych lub zespolonych. Zdefinujemy pewne charakterystyki tej macierzy.
Definicja 7.7.1. Niech V = [v
j
]
n×1
be,dzie macierza, kolumnowa, o n wierszach.
Ka˙zda, liczbe, λ speÃlniaja,ca, r´ownanie
A · V = λV
nazywamy warto´scia, wÃlasna, macierzy A, a macierz V nazywamy wektorem wÃla-
snym macierzy A odpowiadaja,cym warto´sci wÃlasnej λ.
Warunek z definicji 7.7.1 mo˙zemy zapisa´c w naste,puja,cej postaci
(A − λI) · V = 0,
(7.7.1)
gdzie I jest macierza, jednostkowa, tego samego stopnia co macierz A.
R´ownaniu macierzowemu (7.7.1) odpowiada naste,puja,cy ukÃlad r´owna´n
(a
11
− λ)v
1
+a
12
v
2
+ . . .
+a
1,n
v
n
= 0
a
21
v
1
+(a
22
− λ)v
2
+ . . .
+a
2,n
v
n
= 0
· · ·
· · ·
· · ·
· · ·
a
n,1
v
1
+a
n,2
v
2
+ . . . +(a
n,n
− λ)v
n
= 0
UkÃlad ten jest ukÃladem jednorodnym, zatem ma rozwia,zania niezerowe wtedy, gdy
wyznacznik macierzy gÃl´ownej jest r´owny zero, tj.
det(A − λI) = 0.
(7.7.2)
Macierz A − λI nazywa´c be,dziemy macierza, charakterystyczna, , za´s wyz-
nacznik tej macierzy rozpatrywany be,dzie jako funkcja zmiennej λ, kt´ora, nazwiemy
wielomianem charakterystycznym macierzy A. R´ownanie (7.7.2) nazywa´c be,dzie-
my r´ownaniem charakterystycznym. Rozwia,zania tego r´ownania sa, oczywi´scie
pierwiastkami wielomianu charakterystycznego. Jak Ãlatwo zauwa˙zy´c sa, to warto´sci
wÃlasne macierzy A.
Wielomian chakterystyczny ma ciekawa, wÃlasno´s´c, kt´ora, podamy w twierdze-
niu udowodnionym przez Cayleya i Hamiltona.
Twierdzenie 7.7.1. Ka˙zda macierz kwadratowa speÃlnia swoje r´ownanie charak-
terystyczne.
142

Innymi sÃlowy ka˙zda macierz kwadratowa jest pierwiastkiem swojego wielomi-
anu charakterystycznego.
GÃl´ownym zastosowaniem twierdzenia Cayleya-Hamiltona jest wyznaczanie
macierzy odwrotnej do danej macierzy nieosobliwej. Aby wyznaczy´c macierz
odwrotna, do macierzy nieosobliwej A nale˙zy wstawi´c ja, do jej r´ownania charak-
terystycznego, a naste,pnie pomno˙zy´c go stronami przez A
−1
.
PrzykÃlad 7.7.1. Rozwia,˙zmy r´ownanie 7.7.2 kÃlada,c
A =
1
2
0
0
1
0
−1 −2 1
.
Otrzymamy w´owczas naste,puja,ce r´ownanie charakterystyczne
−λ
3
+ 3λ
2
− 3λ + 1 = 0.
Jedynym rozwia,zaniem tego r´ownania jest λ = 1. Zatem macierz A ma tylko jedna,
warto´s´c wÃlasna,. Aby wyznaczy´c wektor wÃlasny odpowiadaja,cy tej warto´sci nale˙zy
rozwia,za´c r´ownanie
0
2 0
0
0 0
−1 2 0
·
x
y
z
=
0
0
0
lub r´ownowa˙znie ukÃlad r´owna´
n
½
2y
= 0
−x +2y = 0
ÃLatwo zauwa˙zy´c, ˙ze ten jednorodny ukÃlad r´owna´
n ma niesko´
nczenie wiele rozwia,z´n
postaci x = 0, y = 0, z = p, gdzie p ∈ R. Zatem wektorem odpowiadaja,-
cym warto´sci wÃlasnej ka˙zdy wektor postaci
0
0
p
. W szczeg´olno´sci za wektor
odpowiadaja,cy warto´sci wÃlasnej λ = 1 mo˙zna przyja,´c wektor
0
0
1
.
Wyznaczmy teraz macierz odwrotna, do macierzy A. Zgodnie z twierdzeniem
Cayleya-Hamiltona macierz A speÃlnia swoje r´ownanie charakterystyczne −λ
3
+
3λ
2
− 3λ + 1 = 0. Mamy wobec tego
A
3
− 3A
2
+ 3A = 1.
143

Mno˙za,c powy˙zsze r´ownanie przez A
−1
i korzystaja,c z tego, ˙ze A
−1
· A = I otrzy-
mujemy
A
−1
= A
2
− 3A + 3I.
Wobec tego
A
−1
=
1
4
0
0
1
0
−2 −6 1
+
−3 −6
0
0
−3
0
3
6
−3
+
3 0 0
0 3 0
0 0 3
=
1 −2 0
0
1
0
1
0
1
.
Zadanie 7.7.1. Znale´z´c warto´sci wÃlasne i wektory wÃlasne naste,puja,cych macierzy
A =
1
3
0
3 −2 −1
0 −1
1
, B =
1 2 3 4
1 2 3 4
1 2 3 4
1 2 3 4
, C =
1 −1
2
0
3
−1
0
0
4
.
Zadanie 7.7.2. Korzystaja,c z twierdzenia Cayleya-Hamiltona znale´z´c macierze
odwrotne (o ile istnieja,) do macierzy z zadania poprzedniego.
7.8. Diagonalizacja macierzy.
W paragrafie tym zostanie podana pewna metoda pote,gowania macierzy kwa-
dratowej.
Niech A i B be,da, macierzami kwadratowymi tego samego stopnia n. Powiemy,
˙ze macierze A i B sa, macierzami podobnymi, je˙zeli istnieje nieosobliwa macierz P
stopnia n taka, ˙ze
B = P · A · P
−1
.
Macierze podobne charakteryzuja, sie, tym, ˙ze maja, te same warto´sci wÃlasne. Za-
chodzi naste,puja,ce twierdzenie
Twierdzenie 7.8.1. Je˙zeli macierz kwadratowa A stopnia n ma n liniowo nie-
zale˙znych wektor´ow wÃlasnych, to istnieja, macierze A
0
i T takie, ˙ze macierz T jest
nieosobliwa, macierz A
0
jest diagonalna oraz
A = T
−1
· A
0
· T.
(7.8.1)
R´ownanie (7.8.1) nazywa´c be,dziemy postacia, diagonalna, macierzy A. Mo˙zna
udowodni´c, ˙ze macierz A
0
jest macierza, diagonalna,, kt´orej elementami sa, warto´sci
144

wÃlasne macierzy A, natomiast kolumny macierzy T
−1
tworza, wektory wÃlasne
macierzy A.
Ponadto zauwa˙zmy, ˙ze dla m ∈ N
A
m
= [T
−1
· A
0
· T ]
m
= T
−1
· A
0
· T · T
−1
· A
0
· T . . . · T
−1
· A
0
· T.
Poniewa˙z T
−1
· T = I i A · I = A, wie,c mamy
A
m
= T
−1
· (A
0
)
m
· T,
gdzie kolumny macierzy T
−1
tworza, wektory wÃlasne macierzy A, a macierz A
0
jest
macierza, diagonalna,, kt´orej elementy na gÃl´ownej przeka,tnej sa, r´owne warto´sciom
wÃlasnym odpowiadaja,cym poszczeg´olnym wektorom wÃlasnym.
ÃLatwo wykaza´c, ˙ze m-ta, pote,ga, macierzy diagonalnej A
0
jest macierz diago-
nalna, kt´orej elememtami sa, m-te pote,gi macierzy element´ow A
0
.
PrzykÃlad 7.8.1. Niech dana be,dzie macierz
A =
1
2
0
0
2
0
−2 −2 −1
.
Rozwia,zuja,c r´ownanie
det
1 − λ
2
0
0
2 − λ
0
−2
−2
−1 − λ
= 0
wyznaczymy warto´sci wÃlasne macierzy A, kt´orymi sa,
λ
1
= 1,
λ
2
= 2,
λ
3
= −1.
Wyznaczymy teraz wektor wÃlasny odpowiadaja,cy warto´sci λ
1
. W tym celu roz-
wia,zujemy r´ownanie
(A − λ
1
I) · V = 0,
gdzie V jest macierza, kolumnowa,, o trzech wierszach. Rozwia,zanie tego r´ownania
otrzymamy poprzez rozwia,zanie jednorodnego ukÃladu r´owna´n postaci
2y
= 0
y
= 0
−2x −2y −2z = 0
145

Rozwia,zanie powy˙zszego ukÃladu mo˙zemy zapisa´c w postaci
x
0
−x
. Zatem jako
wektor wÃlasny mo˙zemy przyja,´c wektor
1
0
−1
. Podobnie wyznaczamy pozostaÃle
wektory wÃlasne. I tak wektorem wÃlasnym odpowiadaja,cym warto´sci λ
1
jest wektor
2
1
−2
, a warto´sci λ
3
odpowiada wektor
0
0
1
. ÃLatwo wykaza´c, ˙ze wektory te sa
,
liniowo niezale˙zne. Wobec tego mo˙zna wyznaczy´c posta´c diagonalna, macierzy A.
Jako macierz T
−1
mo˙zemy przyja,´c macierz
T
−1
=
1
2
0
0
1
0
−1 −2 1
.
Macierz A
0
tworza, warto´sci wÃlasne macierzy A. W pierwszym wierszu tej macierzy
umieszczamy warto´s´c wÃlasna,, kt´ora odpowiada wektorowi wÃlasnemu z pierwszej
kolumny macierzy T
−1
, w drugim wierszu umieszczamy warto´s´c wÃlasna, odpowia-
daja,ca, wektorowi wÃlasnemu z drugiej kolumny macierzy T
−1
i.t.d. Zatem
A
0
=
1 0
0
0 2
0
0 0 −1
.
Teraz nale˙zy znale´z´c macierz odwrotna, do macierzy T
−1
. Macierz ta, wyznaczyli-
´smy w przykÃladzie 7.7.1. Wobec tego otrzymujemy naste,puja,ca, posta´c diagonalna
macierzy A
A =
1
2
0
0
1
0
−1 −2 1
·
1 0
0
0 2
0
0 0 −1
·
1 −2 0
0
1
0
1
0
1
.
Uwaga. Kolejno´s´c wpisywania wektor´ow wÃlasnych do macierzy T
−1
jest dowolna
nale˙zy jedynie w tej samej kolejno´sci wpisywa´c odpowiednie warto´sci wÃlasne do
macierzy A
0
. Oczywi´scie posta´c diagonalna macierzy A nie jest jednoznaczna i
zale˙zy od kolejno´sci umieszczenia wektor´ow wÃlasnych w macierzy T
−1
.
146

Zadanie 7.8.1. Oblicz
a)
1
2
0
0
2
0
−2 −2 −1
4
,
b)
4 3 −3
2 3 −2
4 4 −3
6
.
Zadanie 7.8.2. Dla jakich warto´sci m macierz
·
2 −1
3 −2
¸
m
jest macierza, jedno-
stkowa, stopnia 2.
147

9. GEOMETRIA ANALITYCZNA.
W rozdziale 9 rozwa˙za´c be,dziemy przede wszystkim geometrie, przestrzeni, w
kt´orej zostaÃl wprowadzony ukÃlad wsp´oÃlrze,dnych karezja´nskich, tj. ukÃlad trzech
wzajemnie prostopadÃlych osi liczbowych. RozdziaÃl rozpoczniemy od om´owienia
pewnych wÃlasno´sci najcze,´sciej spotykanych krzywych stopnia drugiego.
9.1. Krzywe stopnia drugiego na pÃlaszczy´
znie.
W paragrafie 4.8 podane byÃly r´ownania parametryczne pewnych krzywych,
kt´ore traktowane byÃly jako wykresy funkcji danych parametrycznie. Mie,dzy in-
nymi podano r´ownania parametryczne okre,gu, elipsy i hiperboli. W tym para-
grafie podamy inne r´ownania opisuja,ce te krzywe, kt´ore wraz z parabola, sa, cze,sto
nazywane krzywymi stopnia drugiego lub krzywymi sto˙zkowymi.
Nasze rozwa˙zania prowadzi´c be,dziemy na pÃlaszczy´znie z prostoka,tnym ukÃla-
dem wsp´oÃlrze,dnych. Na pocza,tek przypomnijmy, ˙ze przeksztaÃlcenie pÃlaszczyzny,
kt´ore nie zmienia odlegÃlo´sci nazywamy przeksztaÃlceniem izometrycznym. Jako
przykÃlad przeksztaÃlcenia izometrycznego mo˙zemy wymieni´c symetrie, punktowa,,
symetrie, osiowa,, translacje, (przesunie,cie) oraz obr´ot.
Om´owimy teraz podstawowe wÃlasno´sci pewnych krzywych stopnia drugiego.
Definicja 9.1.1. Elipsa, nazywamy krzywa, be,da,ca, zbiorem punkt´ow pÃlaszczyny,
kt´orych wsp´oÃlrze,dne speÃlniaja, r´ownanie
x
2
a
2
+
y
2
b
2
= 1
(9.1.1)
oraz ka˙zda, krzywa,, kt´ora z niej powstanie poprzez przeksztaÃlcenie izometryczne
pÃlaszczyzny.
148

Licze, 2a nazywamy osia, wielka, elipsy, a liczbe, 2b-osia, maÃla. Punkty (a, 0), (−a, 0),
(0, b), (0, −b) nazywamy wierzchoÃlkami elipsy. Oznaczmy c =
p
| a
2
− b
2
|. Punkty
(c, 0), (−c, 0) nazywamy ogniskami elipsy, za´s proste o r´ownaniach x =
a
2
c
i
x = −
a
2
c
nazywamy kierownicami elipsy.
Elipsa dana r´ownaniem (9.1.1) ma naste,puja,ce wÃlasno´sci:
1
o
. Suma odlegÃlo´sci dowolnego punktu elipsy od jej ognisk jest r´owna dÃlugo´sci osi
wielkiej.
2
o
. Stosunek odlegÃlo´sci dowolnego punktu elipsy od ogniska do jego odlegÃlo´sci od
kierownicy jest mniejszy od 1.
3
o
. ´
Srodkiem symetrii elipsy jest punkt (0, 0).
4
o
. Proste x = 0 i y = 0 sa, osiami symetrii elipsy.
Elpise, mo˙zemy otrzyma´c poprzez przekr´oj powierzchni sto˙zka pÃlaszczyzna,, kt´ora
przecina jego tworza,ca, pod ka,tem ostrym.
Definicja 9.1.2. Hiperbola, nazywamy krzywa, be,da,ca, zbiorem punkt´ow pÃlaszczy-
ny, kt´orych wsp´oÃlrze,dne speÃlniaja, r´ownanie
x
2
a
2
−
y
2
b
2
= 1
(9.1.2)
oraz ka˙zda, krzywa,, kt´ora z niej powstanie poprzez przeksztaÃlcenie izometryczne
pÃlaszczyzny.
149

Licze, 2a nazywamy osia, rzeczywista, hiperboli , a liczbe, 2b-osia, urojona,. Punkty
(a, 0) i (−a, 0) nazywamy wierzchoÃlkami hiperboli. Niech c =
√
a
2
+ b
2
. Punkty
(c, 0), (−c, 0) nazywamy ogniskami hiperboli, za´s proste x =
a
2
c
i x = −
a
2
c
-jej
kierownicami.
Hiperbola dana r´ownaniem (9.1.2) ma naste,puja,ce wÃlasno´sci:
1
o
. Warto´s´c bezwzgle,dna r´o˙znicy odlegÃlo´sci dowolnego punktu hiperboli od jej
ognisk jest r´owna dÃlugo´sci osi rzeczywistej.
2
o
. Stosunek odlegÃlo´sci dowolnego punktu hiperboli od ogniska do jego odlegÃlo´sci
od kierownicy jest wie,kszy od 1.
3
o
. ´
Srodkiem symetrii hiperboli jest punkt (0, 0).
4
o
. Proste x = 0 i y = 0 sa, osiami symetrii hiperboli.
5
o
. Proste y =
b
a
x i y = −
b
a
x sa, asymtotami hiperboli.
Hiperbole, mo˙zemy otrzyma´c poprzez przekr´oj powierzchni sto˙zka pÃlaszczyzna,,
kt´ora przecina jego tworza,ca, pod ka,tem rozwartym.
Definicja 9.1.3. Parabola, nazywamy krzywa, be,da,ca, zbiorem punkt´ow pÃlaszczy-
ny, kt´orych wsp´oÃlrze,dne speÃlniaja, r´ownanie
y
2
= 2px, p > 0
(9.1.3)
oraz ka˙zda, krzywa,, kt´ora z niej powstanie poprzez przeksztaÃlcenie izometryczne
pÃlaszczyzny.
150

Punkt (0, 0) nazywamy wierzchoÃlkiem paraboli. Ogniskiem paraboli nazywamy
punkt (
p
2
, 0), a prosta, o r´ownaniu x = −
p
2
-kierownica, paraboli .
Parabola dana r´ownaniem (9.1.3) ma naste,puja,ce wÃlasno´sci:
1
o
. Dowolny punkt paraboli jest jednakowo odlegÃly od jej ogniska i kierownicy.
2
o
. Parabola nie ma ´srodka symetrii.
3
o
. Osia, symetrii paraboli jest prosta y = 0.
Parabole, mo˙zemy otrzyma´c poprzez przekr´oj powierzchni sto˙zka pÃlaszczyzna, r´ow-
nolegÃla, do jego tworza,cej.
9.2. Iloczyn skalarny, wektorowy i mieszany.
Niech V be,dzie zbiorem wektor´ow przestrzeni, tzn. odcink´ow, kt´orym nadano
kierunek i zwrot, a K zbiorem liczb rzeczywistych. Suma, wektor´ow
→
a i
→
b nazy-
wamy wektor, kt´ory jest przeka,tna, r´ownolegÃloboku rozpie,tego na wektorach
→
a
i
→
b . Iloczynem wektora
→
v przez liczbe, rzeczywista, α ∈ K w nazywamy wektor
α ·
→
v , kt´ory ma taki sam kierunek i zwrot jak wektor
→
v , a jego dÃlugo´s´c jest α-razy
wie,ksza od dÃlugo´sci wektora
→
v , je˙zeli α ≥ 1; je˙zeli 0 < α < 1, to wektor α ·
→
v ma
taki sam kierunek i zwrot jak wektor
→
v , a jego dÃlugo´s´c jest α-razy mniejsza od
dÃlugo´sci wektora
→
v ; je˙zeli α < 0, to wektor α ·
→
v ma przeciwny zwrot do wektora
→
v , a jego dÃlugo´s´c jest α-razy wie,ksza, gdy | α |≥ 1 i α-razy mniejsza, gdy | α |< 1;
je˙zeli α = 0, to α ·
→
v =
→
0 , gdzie
→
0 jest wektorem zerowym.
Na elementach zbioru V zdefiniujemy jeszcze inne dziaÃlania. R´o˙znica, wek-
tor´ow
→
a i
→
b nazywamy wektor be,da,cy suma, wektora
→
a i wektora −
→
b , gdzie
wektor −
→
b jest wektorem powstaÃlym poprzez pomno˙zenie wektora
→
b przez liczbe,
−1.
Wa˙znymi ze wzgle,du na zastosowania, dziaÃlaniami na wektorach sa, iloczyn
skalarny, wektorowy i mieszany.
Definicja 9.2.1. Iloczynem skalarnym wektor´ow
→
v i
→
w nazywamy licze, dana,
wzorem
→
v ◦
→
w =|
→
v ||
→
w | cos(
→
v ,
→
w),
gdzie |
→
v | oznacza dÃlugo´s´c wektora
→
v , a (
→
v ,
→
w) miare, ka,ta mie,dzy wektorami
→
v
i
→
w.
Iloczyn skalarny ma naste,puja,ce wÃlasno´sci
151

1.
→
v ◦
→
w =
→
w ◦
→
v ,
2. (
→
v ◦
→
w) ◦
→
u =
→
v ◦ (
→
w ◦
→
u ),
3.
→
v ◦ (
→
w +
→
u ) =
→
v ◦
→
w +
→
v ◦
→
u ,
4. (α ·
→
v ) ◦
→
w = α · (
→
v ◦
→
w),
5.
→
v ◦
→
v =|
→
v |
2
.
Wektor, kt´orgo dÃlugo´s´c jest r´o˙zna od zera nazywa´c be,dziemy wektorem nieze-
rowym. Wektor zerowy oznacza´c be,dziemy przez
→
0 , wektor ten ma dÃlugo´s´c r´owna,
zero i zakÃladamy, ˙ze nie ma on ani kierunku, ani zwrotu.
Powiemy, ˙ze wektory sa, prostopadÃle, gdy miara ka,ta mie,dzy nimi jest r´owna
π
2
. Je˙zeli miara ka,ta mie,dzy wektorami jest r´owna 0 lub π, to wektory nazywa´c
be,dziemy r´ownolegÃlymi.
Twierdzenie 9.2.1. Niezerowe wektory
→
v i
→
w sa, prostopadÃle wtedy i tylko wtedy,
gdy
→
v ◦
→
w = 0.
Dow´
od. ZaÃl´o˙zmy najpierw, ˙ze wektory
→
v i
→
w sa, prostopadÃle. Wtedy cos(
→
v ,
→
w) =
0. Z definicji 9.2.1 wynika wie,c, ˙ze
→
v ◦
→
w = 0. Je˙zeli zaÃlo˙zymy, ˙ze
→
v ◦
→
w = 0 oraz
˙ze wektory
→
v i
→
w sa, niezerowe, to wtedy z definicji 9.2.1 wynika, ˙ze cos(
→
v ,
→
w) = 0.
Zatem (
→
v ,
→
w) =
π
2
, co oznacza, ˙ze wektory
→
v i
→
w sa, prostopadÃle.
Z definicji iloczynu skalarnego oraz z powy˙zszego twierdzenia wynikaja, naste,-
puja,ce wa˙zne zastosowania iloczynu skalarnego
Iloczyn skalarny mo˙zemy wykorzysta´c do
1. obliczenia dÃlugo´sci wektora korzystaja,c ze wzoru
|
→
v |=
p
→
v ◦
→
v ,
2. wyznaczenia cosinusa ka,ta mie,dzy wektorami ze wzoru
cos(
→
v ,
→
w) =
→
v ◦
→
w
|
→
v ||
→
w |
,
3. sprawdzenia, czy wektory sa, prostopadÃle w oparciu o warunek
→
v ◦
→
w = 0.
Definicja 9.2.2. Iloczynem wektorowym wektor´ow
→
v i
→
w nazywamy wektor
→
u =
→
v ×
→
w speÃlniaja,cy warunki
152

1. kierunek wektora
→
u jest taki, ˙ze wektor ten jest prostopadÃly do wektora
→
v oraz
do wektora
→
w,
2. zwrot wektora
→
u wyznaczony jest przez reguÃle, ´sruby prawoskre,tnej,
3. dÃlugo´s´c wektora
→
u dana jest wzorem
|
→
u |=|
→
v ||
→
w | sin(
→
v ,
→
w).
Iloczyn wektorowy ma naste,puja,ce wÃlasno´sci
1.
→
v ×
→
w = −
→
w ×
→
v ,
2.
→
v × (
→
w +
→
u ) =
→
v ×
→
w +
→
v ×
→
u ,
3. α · (
→
v ×
→
w) = (α ·
→
v ) ×
→
w,
Twierdzenie 9.2.2. Niezerowe wektory
→
v i
→
w sa, r´ownolegÃle wtedy i tylko wtedy,
gdy
→
v ×
→
w =
→
0 .
Dow´
od. Je˙zeli zaÃlo˙zymy, ˙ze wektory
→
v i
→
w sa, r´ownolegÃle, to z definicji 9.2.2
mamy
|
→
v ×
→
w |=|
→
v ||
→
w | sin 0 = 0.
Je˙zeli natomiast zaÃlo˙zymy, ˙ze
→
v ×
→
w =
→
0 , to z definicji 9.2.2 mamy sin(
→
v ,
→
w) = 0.
Zatem (
→
v ,
→
w) = 0 lub (
→
v ,
→
w) = π, co ko´
nczy dow´od.
Zauwa˙zmy, ˙ze dÃlugo´s´c iloczynu wektorowego
→
v ×
→
w dana jest wzorem znanym
jako pole r´ownolegÃloboku rozpie,tego na wektorach
→
v i
→
w.
Z powy˙zszych rozwa˙za´
n mo˙zemy wywnioskowa´c naste,puja,ce zastosowania
iloczynu wektorowego.
Iloczyn wektorowy mo˙zemy wykorzysta´c do
1. obliczenia pola r´ownolegÃloboku rozpie,tego na wektorach
→
v i
→
w wzorem
P =|
→
v ×
→
w |,
2. obliczenia pola tr´ojka,ta rozpie,tego na wektorach
→
v i
→
w wzorem
P =
1
2
|
→
v ×
→
w |,
3. sprawdzenia czy wektory sa, r´ownolegÃle w oparciu o warunek
→
v ×
→
w =
→
0 .
153

Definicja 9.2.3. Iloczynem mieszanym wektor´ow
→
v ,
→
w i
→
u nazywamy liczbe,
r´owna, iloczynowi skalarnemu wektora
→
v i wektora be,da,cego iloczynem wektoro-
wym wektora
→
w przez wektor u, tzn.
→
v ◦ (
→
w ×
→
u ).
Z powy˙zszej definicji wynika, ˙ze zamiana miejscami dw´och wektor´ow w ilo-
czynie mieszanym zmienia jego znak na przeciwny.
Zauwa˙zmy, ˙ze
→
v ◦ (
→
w ×
→
u ) =|
→
v ||
→
w ×
→
u | cos(
→
v ,
→
w ×
→
u ),
gdzie |
→
w ×
→
u | r´owna sie, polu r´ownolegÃloboku rozpie,tego na wektorach
→
w i
→
u ,
a |
→
v | cos(
→
v ,
→
w ×
→
u ) r´owna sie, dÃlugo´sci wektora r´ownolegÃlego do wektora
→
w ×
→
u .
Sta,d oraz z poni˙zszego rysunku wynika, ˙ze iloczyn mieszany mo˙zna geometrycznie
zinterpretowa´c jako obje,to´s´c r´ownolegÃlo´scianu rozpie,tego na wektorach
→
v ,
→
w i
→
u .
Twierdzenie 9.2.4. Niezerowe wektory
→
v ,
→
w i
→
u le˙za, na jednej pÃlaszczy´znie
wtedy i tylko wtedy, gdy ich iloczyn mieszany jest r´owny zero.
Dow´
od. Je˙zeli wektory
→
v ,
→
w i
→
u le˙za, na tej samej pÃlaszczy´znie, to albo
→
w ×
→
u = 0
albo wektor
→
w ×
→
u jest prostopadÃly do wektora
→
v . Zatem
→
v ◦ (
→
w ×
→
u ) = 0.
154

Je˙zeli
→
v ◦ (
→
w ×
→
u ) = 0, to znaczy, ˙ze wektory
→
v i
→
w ×
→
u sa, prostopadÃle lub
→
w ×
→
u =
→
0 . Wobec tego istnieje pÃlaszczyzna, na kt´orej le˙za, te wektory.
Z powy˙zszych rozwa˙za´
n wynika, ˙ze iloczyn mieszany mo˙zemy wykorzysta´c do
1. obliczenia obje,to´sci r´ownolegÃloboku rozpie,tego na wektorach
→
v ,
→
w i
→
u korzy-
staja,c ze wzoru
V =|
→
v ◦ (
→
w ×
→
u ) |,
gdzie | · | w powy˙zszym wzorze oznacza warto´s´c bezwzgle,dna,.
2. obliczenia obje,to´sci czworo´scianu rozpie,tego na wektorach
→
v ,
→
w i
→
u ze wzoru
V =
1
6
|
→
v ◦ (
→
w ×
→
u ) |,
3. sprawdzenia, czy wektory le˙za, na jednej pÃlaszczy´znie w oparciu o warunek
→
v ◦ (
→
w ×
→
u ) = 0.
Je˙zeli w dowolnym punkcie przestrzeni wprowadzimy ukÃlad wsp´oÃlrze,dnych prosto-
ka,tnych, tj. tr´ojke, osi liczbowych wzajemnie prostopadÃlych, to ka˙zdemu punk-
towi przestrzeni mo˙zemy przyporza,dkowa´c dokÃladnie jedna, uporza,dkowana, tr´ojke,
liczbowa, zwana, wsp´oÃlrze,dnymi punktu, i na odwr´ot, ka˙zdej uporza,dkowanej tr´ojce
liczb rzeczywistych odpowiada dokÃladnie jeden punkt przestrzeni. Ponadto ka˙zde-
mu wektorowi
→
AB mo˙zemy przyporza,dkowa´c tr´ojke, liczb rzeczywistych zwanych
wsp´oÃlrze,dnymi wektora, w naste,puja,cy spos´ob: je˙zeli A(a
1
, a
2
, a
3
) i B(b
1
, b
2
, b
3
),
to
→
AB = [b
1
− a
1
, b
2
− a
2
, b
3
− a
3
]. W ten spos´ob elementy zbioru V mo˙zemy
traktowa´c jako uporza,dkowane tr´ojki liczb rzeczywistych. Niech
→
v = [v
1
, v
2
, v
3
] i
niech
→
w = [w
1
, w
2
, w
3
]. Wtedy dodawanie wektor´ow zdefiniowane be,dzie wzorem
→
v +
→
w = [v
1
+ w
1
, v
2
+ w
2
, v
3
+ w
3
],
natomiast mno˙zenie wektora przez liczbe, definiuje wz´or
α ·
→
v = [αv
1
, αv
2
, αv
3
].
Wektory
→
i = [1, 0, 0],
→
j = [0, 1, 0],
→
k = [0, 0, 1],
nazywa sie, wersorami ukÃladu wsp´oÃlrze,dnych. Wektor
→
i jest wersorem osi OX,
wektor
→
j -osi OY , a
→
k jest wersorem osi OZ.
155
DziaÃlania okre´slone w definicjach 9.2.1, 9.2.2 i 9.2.4 wyra˙zaja, sie, naste,puja,-
cymi wzorami
iloczyn skalarny:
→
v ◦
→
w = v
1
w
1
+ v
2
w
2
+ v
3
w
3
,
iloczyn wektorowy:
→
v ×
→
w = [v
2
w
3
− v
3
w
2
, v
3
w
1
− v
1
w
3
, v
1
w
2
− v
2
w
1
],
co mo˙zna zapisa´c w naste,puja,cy spos´ob
→
v ×
→
w =
¯
¯
¯
¯
¯
¯
→
i
→
j
→
k
v
1
v
2
v
3
w
1
w
2
w
3
¯
¯
¯
¯
¯
¯
,
iloczyn mieszany:
→
v ◦ (
→
w ×
→
u ) =
¯
¯
¯
¯
¯
¯
v
1
v
2
v
3
w
1
w
2
w
3
u
1
u
2
u
3
¯
¯
¯
¯
¯
¯
.
Zadanie 9.2.1. Obliczy´c dÃlugo´s´c wektora
→
v = 4
→
a + 2
→
b , je˙zeli wiadomo, ˙ze
|
→
a |= 2, |
→
b |= 3 i (
→
a ,
→
b ) =
π
6
.
Zadanie 9.2.2. Obliczy´c ka,t mie,dzy wektorami
→
v i
→
w, je˙zeli wiadomo, ˙ze
→
v =
3
→
a +
→
b ,
→
w =
→
b − 2
→
a oraz |
→
a |= 1, |
→
b |= 2 i (
→
a ,
→
b ) =
π
2
.
Zadanie 9.2.2. Obliczy´c ka,t mie,dzy wektorami
→
v = 3
→
a + 2
→
b i
→
w =
→
a + 5
→
b ,
je˙zeli wektory
→
a i
→
b sa, wzajemnie prostopadÃlymi wektorami jednostkowymi.
Zadanie 9.2.3.
Wykaza´c, ˙ze je˙zeli dwa niezerowe wektory
→
v i
→
w speÃlniaja,
warunek |
→
v +
→
w |=|
→
v −
→
w |, to sa, one prostopadÃle.
Zadanie 9.2.4. Wyznaczy´c miare, ka,ta jaki tworza, niezerowe wektory
→
v i
→
w,
je˙zeli wektor
→
v jest dwa razy dÃlu˙zszy ni˙z wektor
→
w oraz |
→
v −
→
w |=
√
3 |
→
w |.
Zadanie 9.2.5. Okre´sli´c wzajemne poÃlo˙zenie wektor´ow
→
u =
→
a + 2
→
b ,
→
v = 2
→
a −
→
b
i
→
w = 2
→
b − 4
→
a , je˙zeli wektory
→
a i
→
b sa, wzajemnie prostopadÃle i jednostkowe.
Zadanie 9.2.6. Dane sa, wektory
→
a = [2, 3, 4],
→
b = [1, 0, 1] i
→
c = [1, 2, −1].
Znale´z´c dÃlugo´s´c wektora
→
v = 2(
→
a ◦
→
b ) ·
→
c +
1
25
(
→
b ◦
→
b ) ·
→
a + (
→
a ◦
→
c ) ·
→
b .
156

Zadanie 9.2.7. Dane sa, wektory
→
a = [3, −1, −2],
→
b = [1, 2, −1]. Znale´z´c dÃlugo´s´c
wektora
→
w = (2
→
a +
→
b ) ×
→
b .
Zadanie 9.2.8. Obliczy´c tangens ka,ta zawartego mie,dzy wektorami
→
a = [0, 1, 2]
i
→
b = [2, −1, 0].
Zadanie 9.2.9. Obliczy´c pole r´ownolegÃloboku rozpie,tego na wektorach
→
a =
[1, 1, 1] i
→
b = [0, 2, 3].
Zadanie 9.2.10. Obliczy´c obje,to´s´c czworo´scianu rozpie,tego na wektorach
→
a =
[0, 1, 1],
→
b = [2, 0, −2] i
→
c = [1, −1, 3].
9.3. R´
ownania pÃlaszczyzny i prostej w przestrzeni.
PÃlaszczyzne, w przestrzeni euklidesowej mo˙zemy wyznaczy´c w jeden z naste,-
puja,cych sposob´ow.
I. Niech dany be,dzie punkt P
0
(x
0
, y
0
, z
0
) le˙za,cy na pÃlaszczy´znie π oraz niezerowy
wektor
→
n = [A, B, C] prostopadÃly do tej pÃlaszczyzny. Wtedy dowolny punkt
P (x, y, z) pÃlaszczyzny π speÃlnia r´ownanie
→
n ◦
→
P
0
P = 0.
Sta,d otrzymujemy r´ownanie pÃlaszczyzny przechodza,cej przez dany punkt i prosto-
padÃlej do danego wektora
A(x − x
0
) + B(y − y
0
) + C(z − z
0
) = 0.
(9.3.1)
Opuszczaja,c nawiasy i kÃlada,c D = −Ax
0
−By
0
−Cz
0
otrzymamy r´ownanie og´olne
pÃlaszczyzny postaci
Ax + By + Cz + D = 0.
Je˙zeli D 6= 0, to dziela,c stronami przez −D powy˙zsze r´ownanie mo˙zemy pÃlaszczyzne,
przedstawi´c w tzw. postaci odcinkowej
x
a
+
y
b
+
z
c
= 1,
gdzie a = −
D
A
, b = −
D
B
, c = −
D
C
. PÃlaszczyzna ta odcina na osi OX odcinek
dÃlugo´sci | a |, na osi OY odcinek dÃlugo´sci | b |, a na osi OZ-| c | (mierza,c od
pocza,tku ukÃladu wsp´oÃlrze,dnych).
157

Wektor
→
n prostopadÃly do pÃlaszczyzny nazywamy wektorem normalnym pÃla-
szczyzny.
II. Niech opr´ocz punktu P
0
dane be,da, dwa nier´ownolegÃle wektory
→
v = [v
x
, v
y
, v
z
] i
→
w = [w
x
, w
y
, w
z
] do kt´orych pÃlaszczyzna π jest r´ownolegÃla. Wtedy dowolny punkt
P pÃlaszczyzny tworzy z punktem P
0
wektor be,da,cy kombinacja, liniowa, wektor´ow
→
v i
→
w, tj.
→
P
0
P = t
→
v + s
→
w, t, s ∈ R.
Mamy zatem
x − x
0
= tv
x
+ sw
x
y − y
0
= tv
y
+ sw
y
z − z
0
= tv
z
+ sw
z
Sta,d otrzymujemy naste,puja,ce r´ownania parametryczne pÃlaszczyzny
x = x
0
+ tv
x
+ sw
x
y = y
0
+ tv
y
+ sw
y
z = z
0
+ tv
z
+ sw
z
t, s ∈ R.
W tym przypadku wektor normalny pÃlaszczyzny jest iloczynem wektorowym wek-
tor´ow
→
v i
→
w.
III. Niech teraz dane be,da, trzy punkty P
0
(x
0
, y
0
, z
0
), P
1
(x
1
, y
1
, z
1
), P
2
(x
2
, y
2
, z
2
).
Trzy punkty w przestrzeni wyznaczaja, dokÃladnie jedna, pÃlaszczyzne,, zatem dowo-
lny punkt P tej pÃlaszczyzny z punktem P
0
utworzy wektor, kt´ory jest kombinacja,
liniowa, wektor´ow
→
P
0
P
1
i
→
P
0
P
2
. Wektory
→
P
0
P ,
→
P
0
P
1
i
→
P
0
P
2
le˙za, wie,c na jednej
pÃlaszczy´znie, a zatem speÃlniona jest r´owno´s´c
¯
¯
¯
¯
¯
¯
x − x
0
x
1
− x
0
x
2
− x
0
y − y
0
y
1
− y
0
y
2
− y
0
z − z
0
z
1
− z
0
z
2
− z
0
¯
¯
¯
¯
¯
¯
= 0.
Powy˙zsze r´ownanie nazywa sie, r´ownaniem pÃlaszczyzny przechodza,cej przez trzy
punkty.
Niech dane be,da, dwie pÃlaszczyzny, jedna z wektorem normalnym
→
w, a druga z
wektorem normalnym
→
v . PÃlaszczyzny te moga, by´c
1. r´ownolegÃle, je´sli ich wektory normalne sa, r´ownolegÃle, tj. gdy
→
v ×
→
w =
→
0 ,
2. prostopadÃle, je´sli ich wektory normalne sa, prostopadÃle, tj. gdy
→
v ◦
→
w = 0,
3. przecina´c sie, pod dowolnym ka,tem, wtedy
→
v ×
→
w 6=
→
0 ∧
→
v ◦
→
w 6= 0.
158

Podane teraz be,da, sposoby wyznaczania prostej w przestrzeni euklidesowej.
I. Niech prosta l przechodzi przez punkt P
0
(x
0
, y
0
, z
0
) i niech be,dzie r´ownolegÃla
do niezerowego wektora
→
v = [v
x
, v
y
, v
z
]. W´owczas ka˙zdy punkt P (x, y, z) le˙za,cy
na tej prostej speÃlnia warunek
→
P
0
P = t
→
v , t ∈ R.
Sta,d mamy
x − x
0
= tv
x
y − y
0
= tv
y
z − z
0
= tv
z
A zatem otrzymujemy naste,puja,ce r´ownania parametryczne prostej
x = x
0
+ tv
x
y = y
0
+ tv
y
z = z
0
+ tv
z
t, s ∈ R.
Zauwa˙zmy, ˙ze wyznaczaja,c z ka˙zdego z tych r´owna´n parametr t mo˙zemy napisa´c
naste,puja,cy cia,g r´owno´sci
x − x
0
v
x
=
y − y
0
v
y
=
z − z
0
v
z
,
kt´ore sa, nazywane r´ownaniami kierunkowymi prostej.
Wektor
→
v r´ownolegÃly do prostej nazywa´c be,dziemy wektorem kierunkowym
prostej.
II. Prosta, mo˙zemy r´ownie˙z zada´c jako cze,´s´c wsp´olna, dw´och nier´ownolegÃlych
pÃlaszczyzn, tj.
½
A
1
x + B
1
y + C
1
z + D
1
= 0
A
2
x + B
2
y + C
2
z + D
2
= 0
M´owimy wtedy, ˙ze prosta dana jest r´ownaniami krawe,dziowymi.
Oczywi´scie powy˙zsze r´ownania opisuja, prosta, tylko wtedy, gdy macierz gÃl´ow-
na i uzupeÃlniona tego ukÃladu sa, tego samego rze,du.
W tym przypadku wektor kierunkowy prostej jest iloczynem wektorowym
wektor´ow normalnych powy˙zszych pÃlaszczyzn, tj.
→
v = [A
1
, B
1
, C
1
] × [A
2
, B
2
, C
2
].
Niech dane be,da, dwie proste w przestrzeni
l :
x − x
1
a
x
=
y − y
1
a
y
=
z − z
1
a
z
,
k :
x − x
2
b
x
=
y − y
2
b
y
=
z − z
2
b
z
.
159

Jak Ãlatwo zauwa˙zy´c wektorem kierunkowym prostej l jest wektor
→
a = [a
x
, a
y
, a
z
],
a wektorem kierunkowym prostej k jest wektor
→
b = [b
x
, b
y
, b
z
]. Niech
W =
¯
¯
¯
¯
¯
¯
x
1
− x
2
y
1
− y
2
z
1
− z
2
a
x
a
y
a
z
b
x
b
y
b
z
¯
¯
¯
¯
¯
¯
.
Okre´slimy teraz wzajemne poÃlo˙zenie prostych.
1.
proste sa, sko´sne, tzn. nie maja, punkt´ow wsp´olnych i nie le˙za, w jednej
pÃlaszczy´znie, je˙zeli
W 6= 0.
2.
proste sa, r´ownolegÃle, tzn. nie maja, punkt´ow wsp´olnych i le˙za, w jednej
pÃlaszczy´znie, je˙zeli
W = 0 i
→
a ×
→
b = 0.
3. proste sa, prostopadÃle, je´sli
W = 0 i
→
a ◦
→
b = 0
4. proste przecinaja, sie,, je´sli
W = 0 i
→
a ×
→
b 6= 0.
Powr´o´cmy jeszcze do sposob´ow wyznaczania pÃlaszczyzny. Z wcze´sniejszych roz-
wa˙za´
n wynika, ˙ze aby okre´sli´c r´ownanie pÃlaszczyzny nale˙zy przede wszystkim
zna´c wsp´oÃlrze,dne jej wektora normalnego oraz dowolnego punktu le˙za,cego na tej
pÃlaszczy´znie.
Podamy teraz jeszcze dwa sposoby wyznaczania pÃlaszczyzny.
IV. Je˙zeli pÃlaszczyzna jest r´ownolegÃla do dw´och prostych wzajemnie r´ownolegÃlych,
to jej wektor normalny jest iloczynem wektorowym wektora kierunkowego prostych
oraz wektora, kt´orego pocza,tek le˙zy na jednej prostej, a koniec na drugiej. Maja,c
wektor normalny i wybieraja,c dowolny punkt z jednej prostej mo˙zemy napisa´c
r´ownanie og´olne pÃlaszczyzny.
V. Je˙zeli pÃlaszczyzna jest r´ownolegÃla do dw´och przecinaja,cych sie, prostych to
jej wektor normalny jest iloczynem wektorowym wektor´ow kierunkowych tych
prostych. Maja,c wektor normalny i wybieraja,c dowolny punkt z jednej prostej
mo˙zemy napisa´c r´ownanie og´olne pÃlaszczyzny.
W dalszej cze,´sci tego paragrafu om´owione be,da, sposoby obliczania odlegÃlo´sci
mie,dzy punktami, prostymi i pÃlaszczyznami w przestrzeni euklidesowej.
160

A.
odleg losc mie
,
dzy dwoma punktami
OdlegÃlo´s´c punktu A(a
1
, a
2
, a
3
) od punktu B(b
1
, b
2
, b
3
) wyznacza sie, jako dÃlu-
go´s´c wektora wektora
→
AB. Mamy zatem
AB =
p
(b
1
− a
1
)
2
+ (b
2
− a
2
)
2
+ (b
3
− a
3
)
2
.
B.
odleg losc punktu od prostej
Niech dana be,dzie prosta l :
x − x
0
v
x
=
y − y
0
v
y
=
z − z
0
v
z
. OdlegÃlo´s´c punktu A
od prostej l mo˙zemy obliczy´c jako wysoko´s´c r´ownolegÃloboku rozpie,tego na wek-
torach
→
v = [v
x
, v
y
, v
z
] i
→
M A, gdzie M (x
0
, y
0
, z
0
). W tym celu wykorzystamy dwa
r´ownowa˙zne wzory na pole P tego r´ownolegÃloboku.
161

Mamy zatem
P =|
→
v ×
→
M A |
P =|
→
v | ·h,
gdzie h jest szukana, wysoko´scia,. Sta,d otrzymujemy naste,puja,cy wz´or na odlegÃlo´s´c
punktu A od prostej l
d(A, l) =
|
→
v ×
→
M A |
|
→
v |
.
C.
odleg losc punktu od p laszczyzny
Rozwa˙zmy pÃlaszczyzne, π dana, r´ownaniem Ax + By + Cz + D = 0. OdlegÃlo´s´c
punktu P (x
0
, y
0
, z
0
) od tej pÃlaszczyzny jest r´owna dÃlugo´sci rzutu wektora
→
M P ,
gdzie M (x
1
, y
1
, z
1
) jest dowolnym punktem pÃlaszczyzny, na kierunek wektora
→
n =
[A, B, C], kt´ory jest wektorem normalnym pÃlaszczyzny π.
162

Mamy wie,c
cos α =
d
|
→
M P |
.
Sta,d oraz ze wzoru na cosinus ka,ta mie,dzy wektorami otrzymujemy
d =|
→
M P |
→
P M ◦
→
n
|
→
M P | · |
→
v |
=
A(x
0
− x
1
) + B(y
0
− y
1
) + C(z
0
− z
1
)
√
A
2
+ B
2
+ C
2
.
Poniewa˙z punkt M le˙zy na pÃlaszczy´znie π, to jego wsp´oÃlrze,dne speÃlniaja, r´ownanie
tej pÃlaszczyzny, zatem mamy
−Ax
1
− By
1
− Cx
1
= D.
Sta,d otrzymujemy naste,puja,cy wz´or na odlegÃlo´s´c punktu P od pÃlaszczyzny π
d(P, π) =
| Ax
0
+ By
0
+ Cz
0
+ D |
√
A
2
+ B
2
+ C
2
.
Warto´s´c bezwzgle,dna w liczniku znalazÃla sie, z tego powodu, ˙ze odlegÃlo´s´c nie mo˙ze
by´c liczba, ujemna,.
D.
odleg losc mie
,
dzy prostymi rownoleg lymi
Niech dane be,da, dwie proste r´ownolegÃle k i l o wektorze kierunkowym
→
v .
Prosta k niech przechodzi przez punkt A, a prosta l-przez punkt B. OdlegÃlo´s´c
mie,dzy tymi prostymi mo˙zemy obliczy´c jako odlegÃlo´s´c punktu A od prostej l
korzystaja,c ze wzoru podanego w punkcie (B). Mamy wie,c
d(l, k) =
|
→
v ×
→
AB |
|
→
v |
.
163

E.
odleg losc mie
,
dzy prostymi skosnymi
Rozwa˙zmy dwie proste sko´sne
l :
x − x
1
a
x
=
y − y
1
a
y
=
z − z
1
a
z
,
k :
x − x
2
b
x
=
y − y
2
b
y
=
z − z
2
b
z
.
Jak Ãlatwo zauwa˙zy´c odlegÃlo´s´c mie,dzy tymi prostymi r´owna jest wysoko´sci
r´ownolegÃlo´scianu rozpie,tego na wektorach
→
a ,
→
b i
→
KL, gdzie
→
KL = [x
1
− x
2
, y
1
−
y
2
, z
1
− z
2
]. Korzystaja,c z dw´och r´ownowa˙znych wzor´ow na obje,to´s´c V tego
r´ownolegÃlo´scianu otrzymujemy
V =|
→
KL ◦ (
→
a ×
→
b ) |
V =|
→
a ×
→
b | ·h,
gdzie h jest szukana, wysoko´scia, r´ownolegÃlo´scianu. Sta,d otrzymujemy naste,puja,cy
wz´or na odlegÃlo´s´c mie,dzy prostymi sko´snymi
d(l, k) =
|
→
KL ◦ (
→
a ×
→
b ) |
|
→
a ×
→
b |
.
164
F.
odleg losc mie
,
dzy p laszczyznami rownoleg lymi
Niech dane be,da, dwie pÃlaszczyzny α i β o wektorze normalnym
→
n. Niech
pÃlaszczyzna α przechodzi przez punkt A, a pÃlaszczyzna β-przez B. OdlegÃlo´s´c
mie,dzy tymi pÃlaszczyznami obliczymy jako odlegÃlo´s´c punktu A od pÃlaszczyzny β.
Korzystaja,c ze wzoru danego w punkcie (C) otrzymujemy
d(α, β) =
| Ax
0
+ By
0
+ Cz
0
+ d |
√
A
2
+ B
2
+ C
2
,
gdzie (x
0
, y
0
, z
0
) sa, wsp´oÃlrze,dnymi punktu A.
Zadanie 9.3.1. Dany jest czworo´scian o wierzchoÃlkach A(1, 0, −2), B(2, 1, −1),
C(2, −2, 0) oraz D. Wyznaczy´c dÃlugo´s´c wysoko´sci poprowadzonej z wierzchoÃlka
A wiedza,c, ˙ze punkt D le˙zy na prostej l :
x + 2
3
=
y + 4
2
=
z − 2
−3
, za´s obje,to´s´c
czworo´scianu wynosi
1
6
.
Zadanie 9.3.2. Napisa´c r´ownanie prostej przechodza,cej przez punkt A(1, 2, 0),
przecinaja,cej prosta, k :
x − 2
3
=
y + 1
−1
=
z + 3
2
oraz r´ownolegÃlej do pÃlaszczyzny
π : 2x − 3y − z + 5 = 0.
Zadanie 9.3.3. Znale´z´c r´ownanie pÃlaszczyzny π przechodza,cej przez prosta, l i
pocza,tek ukÃladu wsp´oÃlrze,dnych, je˙zeli prosta l przechodzi przez punkt P(1, −1, 0)
i przecina prostopadle prosta, k :
½
x − z − 3 = 0
y + 2z + 3 = 0
.
165

Zadanie 9.3.4. Wyznaczy´c rzut prostej
½
2x − y + z − 1 = 0
x + y − z + 1 = 0
na pÃlaszczyzne,
π : x + 2y − z = 0.
Zadanie 9.3.5. Przez punkt A(0, 1, 1) poprowadzi´c prosta, przecinaja,ca, prosta,
l :
½
x − 1 = 0
z + 1 = 0
i prostopadÃla, do prostej l :
½
y + 1 = 0
x + 2y − 7z = 0.
Zadanie 9.3.6. Napisa´c r´ownanie pÃlaszczyzny przechodza,cej przez punkt B i
prosta, l, je˙zeli punkt B jest punktem przebicia pÃlaszczyzny α : x+2y +2z +3 = 0
prosta, k :
x + 2
−1
=
y + 1
2
=
z
−1
, za´s prosta l jest cze,´scia, wsp´olna, pÃlaszczyzn
β : 2x − 2y − z = 0
i γ : −x + 2y + 3z − 1 = 0.
Zadanie 9.3.7. Znale´z´c r´ownanie pÃlaszczyzny przecinaja,cej prostopadle proste
l :
x = 1 + t
y = −1 − 2t
z = 3 − t
t ∈ R
k :
x = 2 + 4t
y = −t
z = −1 + 2t
t ∈ R
9.4. Powierzchnie stopnia drugiego.
W przestrzeni euklidesowej r´ownanie pierwszego stopnia (ze wzgle,du na zmi-
enne x, y i z) opisuje pÃlaszczyzne,. R´ownania, w kt´orych wsp´oÃlrze,dne dowol-
nego punktu przestrzeni P (x, y, z) wyste,puja, w drugiej pote,dze opisuja, pewne
powierzchnie zwane powierzchniami stopnia drugiego. Podamy tak zwane r´owna-
nia kanoniczne najcze,´sciej spotykanych powierzchni stopnia drugiego oraz r´ownania
krzywych jakie otrzymamy w przecie,ciu tych powierzchni z pÃlaszczyznami ukÃladu
wsp´oÃlrze,dnych.
Zauwa˙zmy, ˙ze wektorem normalny do pÃlaszczyzny XY jest wersor osi OZ.
Ponadto pÃlaszczyzna XY przechodzi przez punkt O(0, 0, 0). Korzystaja,c z r´ow-
nania (9.2.1) otrzymujemy r´ownanie pÃlaszczyzny XY , tj. z = 0. Podobnie otrzy-
mamy, ˙ze r´ownanie x = 0 jest r´ownaniem pÃlaszczyzny Y Z, a r´ownanie y = 0
opisuje pÃlaszczyzne, XZ.
166

Do powierzchni stopnia drugiego zaliczamy mie,dzy innymi naste,puja,ce powierzch-
nie
1.
elipsoida
Elipsoida, nazywamy powierzchnie, dana, r´ownaniem
x
2
a
2
+
y
2
b
2
+
z
2
c
2
= 1.
W przecie,ciu elipsoidy pÃlaszczyznami ukÃladu wsp´oÃlrze,dnych otrzymujemy naste,-
puja,ce krzywe:
• z pÃlaszczyzna, XY -elipse,
(
z = 0
x
2
a
2
+
y
2
b
2
= 1
• z pÃlaszczyzna, Y Z-elipse,
(
x = 0
y
2
b
2
+
z
2
c
2
= 1
• z pÃlaszczyzna, XZ-elipse,
y = 0
x
2
a
2
+
z
2
c
2
= 1
Zauw˙zmy, ˙ze dla a = b = c = r > 0 otrzymamy powierzchnie, zwana, sfera, o ´srodku
w punkcie (0, 0, 0) i promieniu r. Og´olne r´ownanie sfery o ´srodku (x
0
, y
0
, z
0
) i
promieniu r ma posta´c (x − x
0
)
2
+ (y − y
0
)
2
+ (z − z
0
)
2
= r
2
.
167

2.
hiperboloida jednopow lokowa
Hiperboloida, jednopowÃlokowa, nazywamy powierzchnie, dana, r´ownaniem
x
2
a
2
+
y
2
b
2
−
z
2
c
2
= 1.
W przecie,ciu hiperboloidy jednopowÃlokowej pÃlaszczyznami ukÃladu wsp´oÃlrze,dnych
otrzymujemy naste,puja,ce krzywe
• z pÃlaszczyzna, XY -elipse,
(
z = 0
x
2
a
2
+
y
2
b
2
= 1
• z pÃlaszczyzna, Y Z-hiperbole,
(
x = 0
y
2
b
2
−
z
2
c
2
= 1
• z pÃlaszczyzna, XZ-hiperbole,
y = 0
x
2
a
2
−
z
2
c
2
= 1
168

3.
hiperboloida dwupow lokowa
Hiperboloida, dwupowÃlokowa, nazywamy powierzchnie, dana, r´ownaniem
x
2
a
2
+
y
2
b
2
−
z
2
c
2
= −1.
W przecie,ciu hiperboloidy dwupowÃlokowej pÃlaszczyznami ukÃladu wsp´oÃlrze,dnych
otrzymujemy naste,puja,ce krzywe
• z pÃlaszczyzna, XY -zbi´or pusty
• z pÃlaszczyzna, Y Z-hiperbole,
(
x = 0
z
2
c
2
−
y
2
b
2
= 1
• z pÃlaszczyzna, XZ-hiperbole,
y = 0
z
2
c
2
−
x
2
a
2
= 1
169

4.
sto˙zek
Sto˙zkiem nazywamy powierzchnie, dana, r´ownaniem
x
2
a
2
+
y
2
b
2
−
z
2
c
2
= 0.
W przecie,ciu sto˙zka pÃlaszczyznami ukÃladu wsp´oÃlrze,dnych otrzymujemy naste,pu-
ja,ce krzywe
• z pÃlaszczyzna, XY -punkt (0, 0, 0)
• z pÃlaszczyzna, Y Z-pare, prostych
(
x = 0
z =
c
b
y
∨
(
x = 0
z = −
c
b
y
• z pÃlaszczyzna, XZ-pare, prostych
(
x = 0
z =
c
a
x
∨
(
x = 0
z = −
c
a
x
170

5.
paraboloida eliptyczna
Parabolioda, eliptyczna, nazywamy powierzchnie, dana, r´ownaniem
z =
x
2
a
2
+
y
2
b
2
.
W przecie,ciu paraboloidy eliptycznej pÃlaszczyznami ukÃladu wsp´oÃlrze,dnych otrzy-
mujemy naste,puja,ce krzywe
• z pÃlaszczyzna, XY -punkt (0, 0, 0)
• z pÃlaszczyzna, Y Z-prabole,
(
x = 0
z =
1
b
2
y
2
• z pÃlaszczyzna, XZ-parabole,
(
y = 0
z =
1
a
2
x
2
171

6.
paraboloida hiperboliczna
Parabolioda, hiperboliczna, nazywamy powierzchnie, dana, r´ownaniem
z =
x
2
a
2
−
y
2
b
2
.
W przecie,ciu paraboloidy hiperbolicznej pÃlaszczyznami ukÃladu wsp´oÃlrze,dnych otrzy-
mujemy naste,puja,ce krzywe
• z pÃlaszczyzna, XY -pare, prostych
(
z = 0
y =
b
a
x
∨
(
x = 0
y = −
b
a
x
• z pÃlaszczyzna, Y Z-prabole,
(
x = 0
z = −
1
b
2
y
2
• z pÃlaszczyzna, XZ-parabole,
(
y = 0
z =
1
a
2
x
2
172

7.
walec eliptyczny
Walcem eliptycznym nazywamy powierzchnie, dana, r´ownaniem
x
2
a
2
+
y
2
b
2
= 1.
W przecie,ciu walca eliptycznego pÃlaszczyznami ukÃladu wsp´oÃlrze,dnych otrzymu-
jemy naste,puja,ce krzywe
• z pÃlaszczyzna, XY -elipse,
(
z = 0
x
2
a
2
+
y
2
b
2
= 1
• z pÃlaszczyzna, Y Z-pare, prostych
½
x = 0
y = b
∨
½
x = 0
y = −b
• z pÃlaszczyzna, XZ-prae, prostych
½
y = 0
x = a
∨
½
y = 0
x = −a
173

8.
walec hiperboliczny
Walcem hiperbolicznym nazywamy powierzchnie, dana, r´ownaniem
x
2
a
2
−
y
2
b
2
= 1.
W przecie,ciu walca hiperbolicznego pÃlaszczyznami ukÃladu wsp´oÃlrze,dnych otrzy-
mujemy naste,puja,ce krzywe
• z pÃlaszczyzna, XY -hiperbole,
(
z = 0
x
2
a
2
−
y
2
b
2
= 1
• z pÃlaszczyzna, Y Z-zbi´or pusty
• z pÃlaszczyzna, XZ-pare, prostych
½
y = 0
x = a
∨
½
y = 0
x = −a
174

9.
walec paraboliczny
Walcem parabolicznym nazywamy powierzchnie, dana, r´ownaniem y
2
= 2px.
W przecie,ciu walca parabolicznego pÃlaszczyznami ukÃladu wsp´oÃlrze,dnych otrzymu-
jemy naste,puja,ce krzywe
• z pÃlaszczyzna, XY -parabole,
½
z = 0
y
2
= 2px
• z pÃlaszczyzna, Y Z-o´s OZ
y = 0
x = 0
z = t,
t ∈ R
• z pÃlaszczyzna, XZ-o´s OZ
y = 0
x = 0
z = t,
t ∈ R
Zadanie 9.4.1. Znale´z´c ´srodek i promie´
n sfery o r´ownaniu x
2
+ y
2
+ z
2
+ 2x −
4y + 6z − 2 = 0.
Zadanie 9.4.2. Jakie powierzchnie okre´slaja, r´ownania
a) −
x
2
5
+
y
2
+ z
2
2
= 0,
b) x
2
− y
2
− z
2
= 1,
c)
y
2
9
+
z
2
16
= 1,
d) x
2
+ y
2
− z = 0,
Zadanie 9.4.3. Zbada´c jaka, powierzchnie, opisuje r´ownanie z =
y
2
9
−
x
2
4
, a
naste,pnie wyznaczy´c krzywe jakie otrzymamy przecinaja,c ta, powierzchnie, pÃla-
szczyznami: z = 1, x = 3 i y = −2.
175
Wyszukiwarka
Podobne podstrony:
podrecznik całki itd QVSIL63WWVVVLGNRNUXM7QOBUO2Y2NAU53R5U3A
CALKI ITD
całki pochodne itd
podrecznik 2 18 03 05
Amadeus Basic Podręcznik szkoleniowy
Excel Nieoficjalny podrecznik excnop
5 Czujniki Podrecznik PL
Podrecznik uzytkownika
Odpowiedzi calki biegunowe id Nieznany
Podręczny zestaw znaków umownych instrukcjiK 1
LISTA 14 Całki krzywoliniowe
więcej podobnych podstron