Prace Naukowe Instytutu Maszyn i Napędów Elektrycznych

Nr 44 Politechniki Wrocławskiej Nr 44

————————————————————————————————————————————

Studia i Materiały Nr 19 1996

______________

*Instytut Maszyn i Napędów Elektrycznych Politechniki Wrocławskiej, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław

elektrotechnika, silniki indukcyjne,

charakterystyki statyczne, obliczenia

Krzysztof MAKOWSKI*

METODA OBWODOWO-POLOWA WYZNACZANIA

CHARAKTERYSTYK STATYCZNYCH JEDNOFAZOWEGO

SILNIKA INDUKCYJNEGO Z POMOCNICZYM

UZWOJENIEM ZWARTYM

Przedstawiono sposób wyznaczania charakterystyk statycznych jednofazowych silników indukcyjnych
z pomocniczym uzwojeniem zwartym metodą obwodowo-polową. Uwzględnia ona w pełni nasycenie
obwodu żelaza, złożoną geometrię przekroju poprzecznego, różnorodność materiałową i niesymetrię uzwojeń.
Określono równania obwodowo-polowe, parametry elektromagnetyczne oraz sposób rozwiązywania równań
przy założeniu sinusoidalnej zmienności przebiegów. Uzyskane z obliczeń charakterystyki momentu
elektromagnetycznego i prądu pobieranego przez silnik porównano z wynikami pomiarów.

1. WPROWADZENIE

W projektowaniu jednofazowych silników indukcyjnych z pomocniczym uzwojeniem

zwartym dokładne określenie charakterystyk pracy uzależnione jest od dokładności
określenia parametrów elektromagnetycznych obwodu zastępczego. W klasycznych
metodach obwodowych parametry te są określane na podstawie przybliżonych rozkładów
pola elektromagnetycznego po przyjęciu często daleko idących uproszczeń. Dzięki
rozwojowi metod numerycznych powstały możliwości bardziej dokładnej analizy pola
elektromagnetycznego oraz dokładniejszego określania parametrów elektromagnetycznych
silnika.

Proponowana metoda obwodowo-polowa stanowi połączenie rozwiązywania równań

obwodowych silnika z wyznaczaniem rozkładu pola w przekroju poprzecznym silnika
z zastosowaniem metody elementów skończonych. Uzyskany dla określonych prądów
uzwojeń rozkład pola elektromagnetycznego jest podstawą do określenia sem
indukowanych w uzwojeniach silnika, wchodzących jako zmienne parametry do równań
obwodowych napięć.

30

Zastosowana dwuwymiarowa analiza rozkładu pola elektromagnetycznego w obszarze

przekroju poprzecznego umożliwia uwzględnienie niesymetrii rozłożenia i zasilania
uzwojeń oraz niesymetrii budowy i silnie zróżnicowanego nasycenia obwodu
magnetycznego silnika. Dwuwymiarowa analiza pola nie daje możliwości uwzględnienia
zmiany rozkładu pola elektromagnetycznego wzdłuż osi wału silnika oraz nie obejmuje pól
strumieni rozproszenia połączeń czołowych uzwojeń. Możliwe jest jednak uwzględnienie
tych strumieni rozproszenia za pomocą indukcyjności połączeń czołowych określonych w
klasyczny sposób [7, 9, 11], traktując je jako stałe parametry w równaniach napięć, jak
również uwzględnienie skosu żłobków za pomocą współczynnika skosu korygującego
indukowane sem w uzwojeniach, dzięki czemu metoda ta może być traktowana jako
pseudoprzestrzenna. W prezentowanej pracy przedstawiono równania obwodowe i
związane z nimi równanie quasi-stacjonarnego pola elektromagnetycznego w przekroju
silnika wraz ze sposobem rozwiązywania tych równań przy założeniu sinusoidalnej
zmienności przebiegów. Zamieszczono również obliczone charakterystyki statyczne
momentu elektromagnetycznego i prądu w funkcji prędkości obrotowej, które porównano z
wynikami pomiarów badanego silnika.

2. RÓWNANIA OBWODOWO-POLOWE

2.1. Założenia metody

Prezentowana metoda oparta jest na modelu obwodowo-polowym jednofazowego

silnika indukcyjnego z pomocniczym uzwojeniem zwartym przedstawionym na rys.1.

Rys.1. Schemat zastępczy obwodowo-polowy jednofazowego silnika indukcyjnego

z pomocniczym uzwojeniem zwartym

Fig. 1. Circuit-field equivalent diagram of single-phase shaded pole induction motor

Zgodnie z rzeczywistymi warunkami zasilania silnika tylko jedno uzwojenie stojana

jest zasilane, a pozostałe uzwojenia (pomocnicze uzwojenia stojana, klatkowe uzwojenie

31

wirnika) są zwarte, przy czym uzwojenie wirnika zastąpiono szeregiem uzwojeń
harmonicznych. Parametry rezystancyjne na schemacie reprezentują całkowite rezystancje
uzwojeń, natomiast parametry indukcyjne

− reaktancje strumieni rozproszenia połączeń

czołowych uzwojeń. Obszar sprzężenia elektromechanicznego silnika został zredukowany
do dwuwymiarowego pola elektromagnetycznego w przekroju poprzecznym, w środku
długości silnika. Pominięto przy tym blachowanie rdzenia stojana i wirnika, zjawisko
histerezy magnetycznej i straty w żelazie.

2.2. Równania napięć

Przy formułowaniu równań napięć dla uzwojeń stojana i klatkowego uzwojenia wirnika

założono, że rzeczywisty rozkład prądu w prętach wzdłuż obwodu wirnika można zastapić
skończoną liczbą harmonicznych rozkładów wzbudzonych przez odpowiednie harmoniczne
pola wytworzonego prądem uzwojeń stojana, przyjmując jednocześnie brak wzajemnego
oddziaływania między nimi. Równania napięć odpowiadające obwodom elektrycznym
przedstawionym na rys.1 dla sinusoidalnych warunków zasilania, można zapisać w postaci
zespolonej następująco:

U

R I

j L I

R I

j L I

E

R I

j s L I

E

R I

j s L I

E

s

s

s

c

s

s

s

m

s

m

s

cm

s

m

s

m

s

r

r

c

r

r

r

n

r

n

r

n

cn

r

n

r

n

r

1

1 1

1 1

1 1

1

1 1

1

0

0

0

=

+

+

=

+

+

=

+

+

=

+

+

ω

ω

ω

ω

M

M

M

M

E

1

M

M

(1)

W równaniach tych (

) reprezentują całkowite rezystancje, a (

)

−

indukcyjności połączeń czołowych uzwojeń stojana, natomiast (

) i (

)

−

odpowiednio, całkowite rezystancje i indukcyjności połączeń czołowych n harmonicznych
obwodów wirnika, przy czym n = (h+1)/2, gdzie h

− najwyższy rząd rozpatrywanej

harmonicznej wirnika. Poślizg h – harmonicznej wirnika wywołanej h – harmoniczną
stojana s

R ,...,R

s

m

s

1

L ,...,L

s

m

s

1

R ,...,R

r

n

r

1

L ,...,L

r

n

r

1

h

=1

± h(1

−

s), przy czym znak (

−) odnosi się do składowej współbieżnej, znak (+)

do składowej przeciwbieżnej pola, a s oznacza poślizg wirnika. Człony leżące najbardziej
na prawo w równaniu (1) reprezentują sem indukowane w obwodach stojana i wirnika

(

,...

,

,...

)

E

E

E

E

s

m

s

r

n

r

1

1

od wypadkowego strumienia w płaszczyźnie przekroju

poprzecznego silnika.

Po wprowadzeniu zapisu macierzowego, układ równań (1) przyjmuje postać:

[

]

[

] [ ]

UE

RX

I

=

⋅

,

(2)

32

w której macierze napięć, impedancji i prądu zawierają następujące elementy:

[

]

[

]

[ ]

UE

U

E

E

E

E

RX

R

jwL

R

jwL

R

jws L

R

jws L

I

I

I

I

I

s

m

s

r

m

r

s

s

m

s

m

s

r

c

r

n

r

n

cn

r

s

m

s

r

n

r

=

⎡

⎣

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎤

⎦

⎥

⎥

⎥

⎥

⎥

⎥

⎥

⎥

⎥

=

+

+

+

+

⎡

⎣

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎤

⎦

⎥

⎥

⎥

⎥

⎥

⎥

⎥

⎥

⎥

=

⎡

⎣

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎢

⎤

⎦

⎥

⎥

⎥

⎥

⎥

⎥

⎥

⎥

⎥

1

1

1

1

1

1

1

1

1

1

0

0

0

-

-

-

-

M

M

O

O

M

M

2.3. Równania potencjałów

Pole elektromagnetyczne w przekroju poprzecznym silnika indukcyjnego, przy

założeniu sinusoidalnej zmienności oraz pominięciu prądów polaryzacji i przesunięcia,
opisuje równanie Poissona dla zmiennych zespolonych [4, 10]:

∂

∂

υ

∂

∂

∂

∂

υ

∂

∂

x

A

x

y

A

y

J

⎛
⎝

⎜

⎞
⎠

⎟ +

⎛
⎝

⎜

⎞
⎠

⎟ = −

(3)

w którym

A

A

e

J

J

e

z

j t

z

j t

=

=

(x, y)

i

(x, y)

ω

ω

oznaczają składowe potencjału

wektorowego pola i całkowitej powierzchniowej gęstości prądu skierowane wzdłuż osi
wału silnika,

υ

− reluktywność materiałów, a

ω

− pulsację pola elektromagnetycznego.

Założono przy tym, że reluktywność żelaza zależy jedynie od amplitudy natężenia pola
elektromagnetycznego. Ze względu na nieliniowość zależności reluktywności żelaza i
gęstości prądu od potencjału pola równanie (3) jest nieliniowym równaniem różniczkowym
cząstkowym pola elektromagnetycznego.

Po rozwiązaniu równania obwodowego (2) otrzymuje się prądy uzwojeń, które służą do

określenia całkowitej gęstości prądu występującej po prawej stronie równania (3).

Do rozwiązania równania pola (3) zastosowano metodę wariacyjną polegającą na

minimalizacji funkcjonału energetycznego [1, 5, 10], dla którego równanie (3) jest
równaniem Eulera. Minimalizacji funkcjonału dokonano za pomocą metody elementów
skończonych, dyskretyzując obszar przekroju silnika za pomocą elementów trójkątnych
pierwszego rzędu i założeniu liniowej zmiany potencjału wektorowego wewnątrz elementu.
W wyniku dyskretyzacji równania pola (3), opisanej szczegółowo w pracach [8, 12],
otrzymano algebraiczny układ równań dla zespolonych potencjałów węzłowych zapisany
następująco:

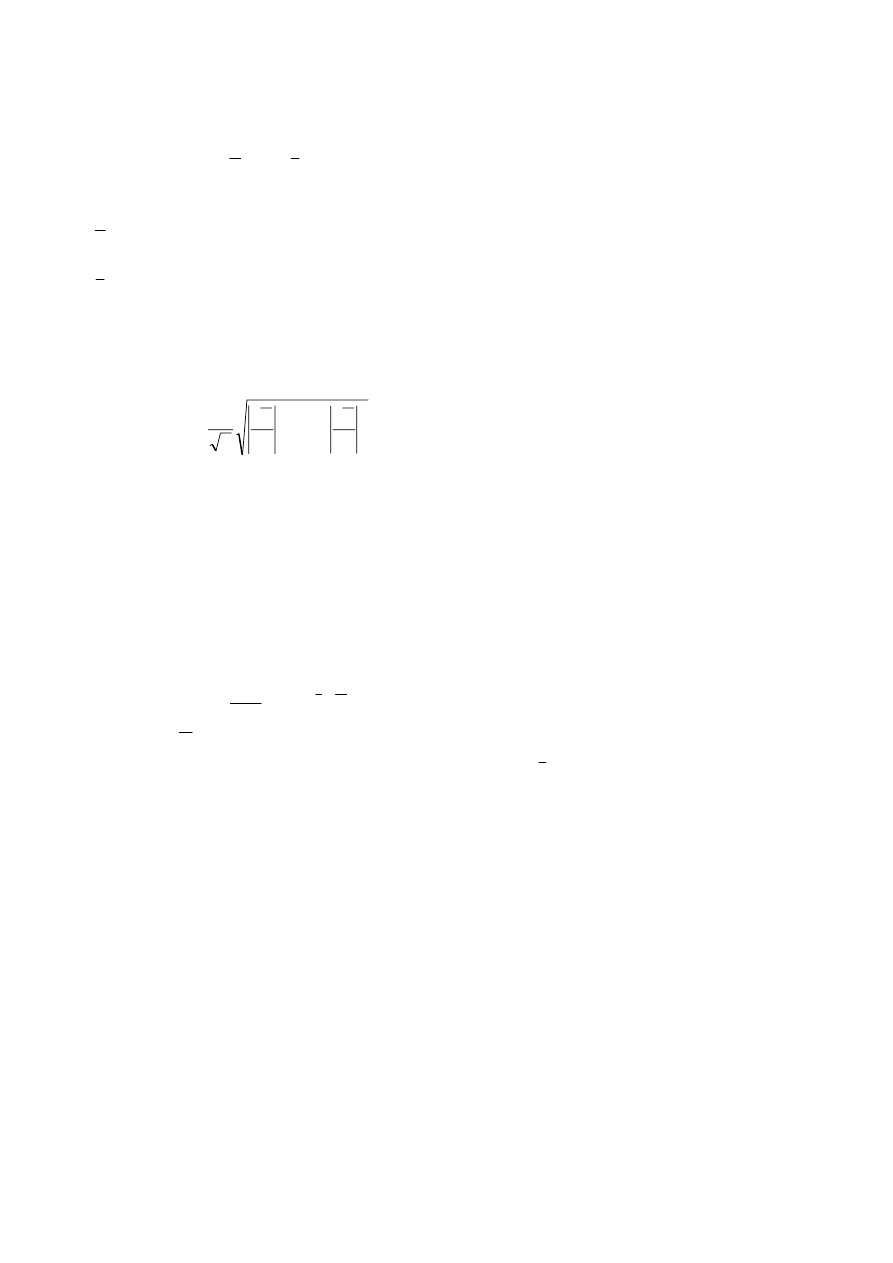
33

[ ] [ ]

[ ]

K

A

J

⋅

=

,

(4)

przy czym poszczególne macierze oznaczają:

[ ]

A

– kolumnowa macierz zespolonych amplitud magnetycznego potencjału wektorowego

w węzłach sieci,

[ ]

J

– kolumnowa macierz zespolonych amplitud gęstości prądów węzłowych,

[ ]

K

– kwadratowa macierz reluktywności elementów.

Wartości zespolonych amplitud potencjałów węzłowych otrzymane z rozwiązania

równania (4) pozwalają wyznaczyć skuteczną wartość indukcji wewnątrz pojedynczego
elementu korzystając z zależności:

B

A

y

A

x

=

+

1

2

2

2

∂

∂

∂

∂

(5)

2.4. MOMENT ELEKTROMAGNETYCZNY

Dla sinusoidalnej zmienności przebiegów elektromagnetycznych, średnią wartość

momentu elektromagnetycznego wytworzonego przez silnik można określić posługując się
średnią wartością skuteczną zespoloną indukcji k–tego pręta wirnika oraz wartością
skuteczną zespoloną sprzężoną prądu k–tego pręta wirnika następująco:

M

d l

I B

esr

p

k

k

k

=

∑

2

Re(

)

*

(6)

przy czym

B

k

− średnia wartość indukcji elementów trójkątnych dyskretyzujących obszar

szczeliny powietrznej na długości podziałki żłobkowej,

I

k

∗

− wartość skuteczna zespolona

sprzężona prądu w k–tym pręcie wirnika otrzymaną w wyniku zsumowania sprowadzonych
prądów harmonicznych, d

p

− średnia średnica klatki wirnika odpowiadająca średnicy

okręgu przechodzącego przez środki ciężkości prętów wirnika, l

−

długość czynna pręta

wirnika.

34

3. PARAMETRY ELEKTROMAGNETYCZNE

Całkowite rezystancje i indukcyjności połączeń czołowych uzwojeń występujące w

macierzy impedancji równania napięć (2) zostały określone w klasyczny sposób na
podstawie prac [7,9,11]. Natomiast indukowane w uzwojeniach sem, występujące w
kolumnowej macierzy napięć, należy wyznaczyć po uwzględnieniu pulsacji pola stojana i
wirnika dla poszczególnych harmonicznych przy zmianach prędkości obrotowej. W tym
celu określono wszystkie indukowane na zasadzie transformacji siły elektromotoryczne dla
pulsacji sieci

ω według zależności:

− dla uzwojeń stojana:

E

j lz A

A

i

s

i

p

n

=

−

ω

(

) ; i = 1,..., m

(7)

− dla pozytywnie zorientowanego pręta wirnika:

E

jw

l

A

A

kp

r

k

k

=

−

−

2

1

(

)

(8a)

− dla negatywnie zorientowanego pręta wirnika:

E

j

l

A

A

kn

r

k

k

=

−

+

ω

2

1

(

)

(8b)

przy czym, jeżeli prąd w pręcie ma zwrot zgodny z dodatnim zwrotem osi z przyjętego
układu kartezjańskiego, to taki pręt nazwany jest pozytywnie zorientowany

− w

przeciwnym przypadku jest negatywnie zorientowany, z

i

−liczba zwojów i–tego uzwojenia

stojana, A A

p

,

n

− zespolone wartości magnetycznego potencjału wektorowego dla

pozytywnie i negatywnie zorientowanego boku uzwojenia stojana, A A

A

k

k

k

,

,

−1

+1

−

wartości magnetycznego potencjału wektorowego dla prawej strony k–tego pręta, pręta
poprzedniego (k–1) i następnego (k+1).

Sem rotacji, indukowane w prętach wirnika, wyznaczono posługując się zależnością:

E

B

krot

r

k

p

o

r

=

d l

ω

2

,

(9)

w której

B

k

p

,

,

d l

określono w równaniu (6), natomiast

ω

o

r

oznacza synchroniczną

prędkość kątową wirnika. Przez zsumowanie sem transformacji i rotacji w prętach wirnika
otrzymuje się schodkowy rozkład indukowanych sem na obwodzie wirnika, którego
rozwinięcie w szereg harmoniczny Fouriera daje harmoniczne przestrzenne sem wirnika dla
pulsacji pola

ω. Po wymnożeniu harmonicznych przez odpowiedni poślizg i współczynnik

skosu, h-harmoniczna sem k–tego pręta wirnika dla prędkości

ω

r <

ω

r

o

przybierze postać:

E

E k s e

kh

r

h

r

skh h

j Ekh

=

ψ

(10)

przy czym k

skh

i s

h

oznaczają kolejno współczynnik skosu i poślizg dla h-harmonicznej

wirnika, a

jest kątem położenia h–harmonicznej sem względem k–tego pręta wirnika.

Ψ

Ekh

4. ROZWIĄZANIE RÓWNAŃ OBWODOWO-POLOWYCH

35

Równania napięć uzwojeń stojana i harmonicznych obwodów wirnika (2) zawierające

sem wyznaczane z rozkładu pola elektromagnetycznego są rozwiązywane dla danego
poślizgu w procesie podwójnej iteracji, przy czym wewnętrzną pętlę iteracyjną tworzy
rozwiązywanie nieliniowego układu równań potencjałów zespolonych (4), a zewnętrzną
pętlę tworzy rozwiązywanie układu liniowych równań obwodowych zespolonych (2) dla
wyznaczonych z rozkładu potencjału wartości indukowanych sem uzwojeń. Uproszczony
schemat blokowy tej procedury przedstawiono na rys.2, przy czym nieliniowe równanie
potencjałów rozwiązywane jest z zastosowaniem metody Newtona

−Raphsona [2] dla

zespolonych potencjałów węzłowych, a zespolony liniowy układ równań obwodowych

− z

użyciem metody eliminacji Gaussa.

Rys. 2. Schemat blokowy obliczeń

Fig. 2. Block diagram of calculation

W wyniku pozytywnie zakończonego procesu rozwiązywania nieliniowych równań

potencjałów przechodzi się do rozwiązywania układu równań napięć, wyznaczając wartości
skuteczne prądów uzwojeń stojana i prądów harmonicznych wirnika. Jeśli uzyskany
przyrost wartości prądu głównego uzwojenia stojana jest dostatecznie mały, przechodzi się
do obliczania momentu elektromagnetycznego, w przeciwnym razie powraca się do
rozwiązywania równań potencjałów. Prąd płynący w k–tym pręcie wirnika otrzymuje się
przez zsumowanie prądów harmonicznych z uwzględnieniem ich położenia na obwodzie
wirnika, a mianowicie:

I

k

h

=

∑

I

kh

,

(11)

36

przy czym:

I

I e

kh

h

j

h k

Ih

=

+

−

(

(

)

ψ

1

)

α

(12)

gdzie

− kąt h–harmonicznej prądu wirnika względem pręta odniesienia,

α

− kąt między

sąsiednimi prętami wirnika.

Ψ

Ih

5. OBLICZENIA CHARAKTERYSTYK

Podstawowym wskaźnikiem służącym do oceny przydatności metody do analizy

silnika indukcyjnego jest możliwość dokładnego wyznaczenia statycznej charakterystyki
mechanicznej i elektromechanicznej. Przykładowych obliczeń tych charakterystyk, z
zastosowaniem procedury opisanej w rozdz. 4, dokonano dla silnika o dwóch zwojach
zwartych na biegunie i nierównomiernej szczelinie powietrznej typu Sz-30.25a o danych
znamionowych: P

n

= 3 W, U

n

= 220 V, n

n

= 2400 obr/min, f = 50 Hz [6], przy czym wzięto

pod uwagę 6 kolejnych nieparzystych harmonicznych przestrzennych prądów wirnika [3].

Rys. 3. Charakterystyka mechaniczna: ---------- obliczenia, x x x pomiar
Fig. 3. Torque/speed characteristics: ---------- computed, x x x measured

37

Rys. 4. Charakterystyka elektromechaniczna: -------- obliczenia, x x x pomiar

Fig. 4. Current/speed characteristics: --------- computed, x x x measured

Obliczone metodą obwodowo-polową charakterystyki momentu i prądu pobieranego

przez silnik przedstawiono na rysunkach 3 i 4 wraz z charakterystykami otrzymanymi
metodą obwodową, opartą na harmonicznym modelu dq silnika, oraz charakterystykami
zmierzonymi zamieszczonymi w pracach [6,7]. Uzyskana dokładność obliczeń
charakterystyk w porównaniu do tych samych charakterystyk otrzymanych z pomiarów jest
wyraźnie większa niż w przypadku metody obwodowej zarówno dla stanu zwarcia, jak i
pracy znamionowej silnika.

6. WNIOSKI

Przedstawiona metoda obwodowo-polowa opisuje w sposób kompletny jednofazowy

silnik indukcyjny z pomocniczym uzwojeniem zwartym w stanach pracy ustalonej. Pozwala
ona na wyznaczenie charakterystyk statycznych i rozkładu pola elektromagnetycznego w
całym przekroju poprzecznym silnika z uwzględnieniem nasycenia żelaza, niesymetrii
uzwojenia i skosu żłobków wirnika. Zastosowana z powodzeniem do analizy
jednofazowego silnika indukcyjnego z pomocniczym uzwojeniem zwartym o pełnej
niesymetrii i silnie zróżnicowanym nasyceniu, metoda ta może być również stosowana do
analizy innych rodzajów silników indukcyjnych, które mają pewne cechy niesymetrii i
nasycony obwód magnetyczny.

38

LITERATURA

[1] Chari M.V.K., Silvester P.P., Finite elements in electric and magnetic field problems, John Wiley&Sons, 1980.
[2] Chua Leon O., Pen-Min Lin., Computer aided analysis of electronic circuits, Prentice Hall Inc., N.J.,USA,1975.
[3] Heller B., Hamata V., Harmonic field effects in induction machines, Elsevier Scientific Publishing Company, N.Y.,

1977.

[4] Litwin R.,Teoria pola elektromagnetycznego, WNT, 1969.
[5] Lowther D.A., Silvester P.P., Computer aided design in magnetics, Spring-Verlag, N.Y. 1986.
[6] Makowski K., Analiza wpływu niesymetrycznej szczeliny na charakterystykę mechaniczną silnika indukcyjnego z

ekranowanymi biegunami, Raport PRE 24, IUE PWr, 1979 (praca doktorska).

[7] Makowski K., Schoepp K., An analysis of shaded pole induction motors with increased starting torque, Electric

Machines and Power Systems, 1983, Vol.8, no.6, s.419–432.

[8] Makowski K., Approximate linearization method of magnetic field computation in single-phase shaded pole

induction motors, XII Symposium on Electromagnetic phenomena in nonlinear circuits, Oct.16-18, 1991, Poznań,
s.291–297.

[9] Ivanov-Smolensky A., Electrical machines, Vol.1, Mir Publishers, Moscov, 1982.
[10] Silvester P.P., Chari M.V.K., Finite element solution of saturable magnetic field problems, IEEE Trans. PAS-89,

1970, no.7, s.1642–1651.

[11] Śliwiński T., Głowacki A., Parametry rozruchowe silników indukcyjnych, Warszawa, PWN, 1982.
[12] Zienkiewicz O.C., Finite element method, McGraw-Hill, 1977.

A CIRCUIT-FIELD METHOD FOR EVALUATION OF STEADY-STATE

CHARACTERISTICS OF A SINGLE-PHASE SHADED POLE INDUCTION MOTOR

A circuit-field combined method of steady-state characteristics evaluation of a single-

phase shaded pole induction motor is presented. Saturation of iron core, complex geometry
of cross-section, asymmetry of windings and heterogeneity of materials are taken into
account. Circuit-field equations, electromagnetic parameters and the way of solution of the
equations for sinusoidal approximation are determined. Calculated mechanical and
electromechanical characteristics of a tested motor were compared with measurements.