Mikroekonomiczna zawodność rynku i regulacja

Zad.1
P=100-2Q

MC=20

a) MR=MC
TR=Q*(100-2Q)

=> MR=-4Q

2

+100

-4Q

2

+100=20 => Q=20

b) P=100-2*20=60
c) w doskonałej konkurencji P=MC => P=20
d)P=MC
100-2Q=20

=> Q=40

e) DWL= 0,5*(40-20)*(60-20)=400

f) DWL=0, bowiem wtedy linia MR pokrywałaby się z D I nie byłoby już trójkąta DWL

Zad2.
a) Potrzeba na budowę obwodnicy 8 tys. m3 betonu. Robimy to przy jak najmniejszym koszcie
krańcowym dlatego dobieramy najmniejsze wartości kosztu krańcowego z tabelki
Betonfix: Q=3 Zager: Q=2 Budmax: Q=3
Π

=3*250000-(100+150+200)*1000+2*250000-(200+200)*1000+3*250000-(200+150+100)*1000=

700000
b) MC=P w doskonałej konkurencji, maksymalny MC to 200 zł/m3 i tyle wynosiłaby cena
c) miasto zaoszczędziłoby 8*250 tys – 8*200 tys = 400000
Zysk Betonfixu: (200-200)+(200-150)+(200-100)=150 tys. zł
Zysk Zager: 0 zł
Zysk Budmax: (200-100)+(200-150)+(200-200)=150 tys. zł

Zad.3
P=100-0,5Q
TC=1000+5Q
a) TR=P*Q=100Q-0,5Q

2

MR=MC
100-Q=5 => Q=95 P=100-0,5*95=52,5
b) Π=TR-TC=0
100Q-0,5Q

2

-1000-5Q=0 -0,5Q

2

+95Q-1000=0

∆

=95

2

-4*(-0,5*-1000)=9025-2000=7025 pierw(∆)=83,81

Q

1

=(-95+83,81)/(2*-0,5)=11,19

Q

2

=(-95-83,81)/(2*-0,5)=178,82

Pierwsze Q odrzucamy, bowiem przy takiej licznie osiągnęlibyśmy startę. Przy drugim Q zysk
ekonomiczny jest 0
P(178,82)=100-0,5*178,82=10,59

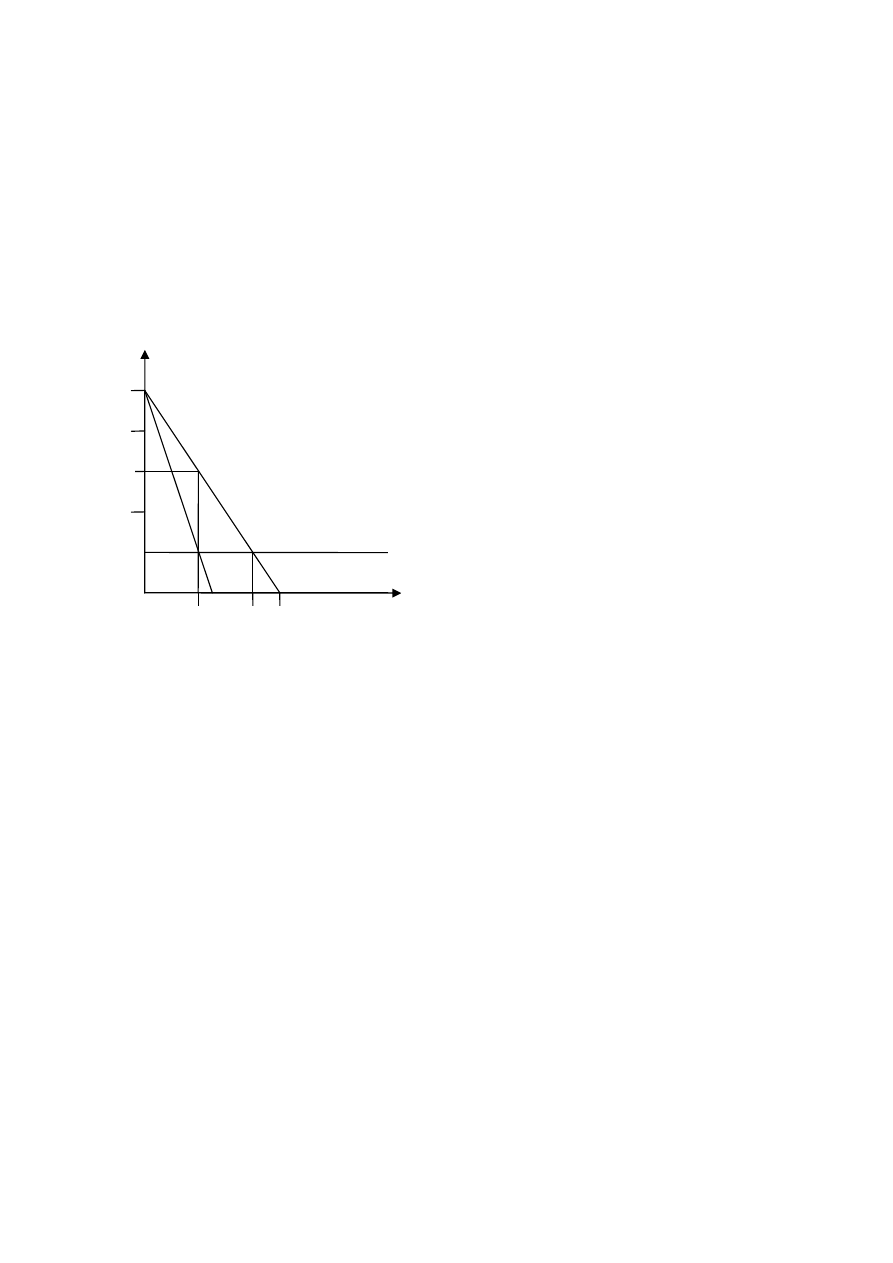
P

DWL

D

MR

20

25

50

40

20

60

100

MC

Q

Zad.4
TC=8000+58Q
P=100-0,01Q

TR=100Q-0,01Q

2

a) MR=MC
-0,02Q+100=58 => Q=2100 => P=79
b) Π=TR-TC=36 100
c) P=MR=MC=58
58=100-0,01Q => Q=4200
d) Π=TR-TC=-0,01*(4200)

2

+42*4200-8000=-8000

dotacja*4200=8000

dotacja=1,91

Zatem żądanie 4 $ za każdą tonę żelatyny jest nieuzasadnione.


Zad5.
P=20-2Q
MC=1000
Qmax=10

a) TR=Q*P=20Q-2Q

2

MR=-4Q+20
MR=MC

-4Q+20=1 Q=4,75

P=20-2*4,75=10,5
b) P=MC

P=1

1=20-2Q

Q=9,5

c) P=20-0,1Q MC=1
-0,1Q+20=1

Q=190

Jedna elektrownia może maksymalnie wytworzyć 10 MWh dlatego potrzeba 19 elektrowni


Zad6.
P=22,5-0,00004Q
TC=3750000+70Q+0,00002Q

2

A) TR=Q*12*(22,5-0,00004Q)= -0,00048Q

2

+270Q

MR=-0,00096Q+270
MC=0,00004Q+70
MR=MC
-0,00096Q+270=0,00004Q+70

Q=200000

P=22,5 – 0,00004*200000=14,5
Π

=TR-TC=-0,005Q

2

+200Q-3750000=16250000

B) r= Π/125=16,25/125=13%

C) 0,12= Π/125

Π=15000000

-0,0005Q

2

+200Q-3750000=15000000

-0,0005Q

2

+200Q-18750000=0

∆

=200

2

-4*(-0,0005*-18750000)=2500 pierw(∆)=50

Q1=(-200-50)/-0,001=250000

Q2=(-200+50)/-0,001=150000

Mamy zapewnić dostęp jak największej liczbie odbiorców dlatego wybieramy Q1
P=22,5-0,00004*250000=12,5

Zad7.
P=3 zł/kg

a) MC=0,6+0,04Q
P=MC w doskonałej konkurencji
3=0,6+0,04Q

Q=60

b) Qm=15000000-1000000P popyt rynkowy
P=0,6+0,04Q

Q=25P-15 podaż indywidualna

N=200000

Qm=5000000P-3000000 podaż rynkowa

5000000P-3000000=15000000-1000000P

P=3

c) MC

2

=1,25MC

1

P=MC

2

=1,25*(0,6+0,04Q)

P=0,75+0,05Q Q=20P-15

Qm=4000000P-3000000
d) Qm=15000000-1000000P=4000000P-3000000

P=3,6

Qm=15000000-1000000*3,6=11400000

Qm/200000=57

Q=57


Zad8.
N=120 Π=1200X – 100X

2

U=C+9Y-Y

2

-XY

a) Π’=0 maksymalizacja zysku
-200X+1200=0

X=6 wtedy Π=3600

b) U’=0
9-2Y-X=0
Y=1,5
c) wyniki nie są optymalne ze społecznego punktu widzenia. Użyteczność każdego z mieszkańców
zmniejsza się w skutek takich zanieczyszczeń o XY czyli 6*1,5=9
Na skutek porozumienia i obniżeniu zanieczyszczeń można by zwiększyć użyteczność mieszkańców.
Przy obniżeniu zanieczyszczeń o 1 m3, firma straci z zysku 100, bo Π(5)=3500, a społeczeństwo zyska
wtedy 120*1,5=180, dlatego jest tutaj możliwe porozumienie. Przy zmniejszeniu zanieczyszczeń o 2 m3,
firma straci z zysku 400, bo Π(4)=3200, a społeczeństwo zyska w sumie 120*2*1,5=360. Dlatego w tej
sytuacji nie dojdzie do porozumienia.


Zad.10
P=40
MIC=10+Q
MCz=4

a) MC=MIC =10+Q
MR=40
MR=MC

40=10+Q Q=30

b) MC=MIC+MCz=14+Q
MR=40
MR=MC

40=14+Q Q=26

Wysokość podatku powinna wynosić 4 zł za każdy m3 zanieczyszczenia


Zad.11
P=700-5Q
MIC=400+Q
EC=60Q+Q

2

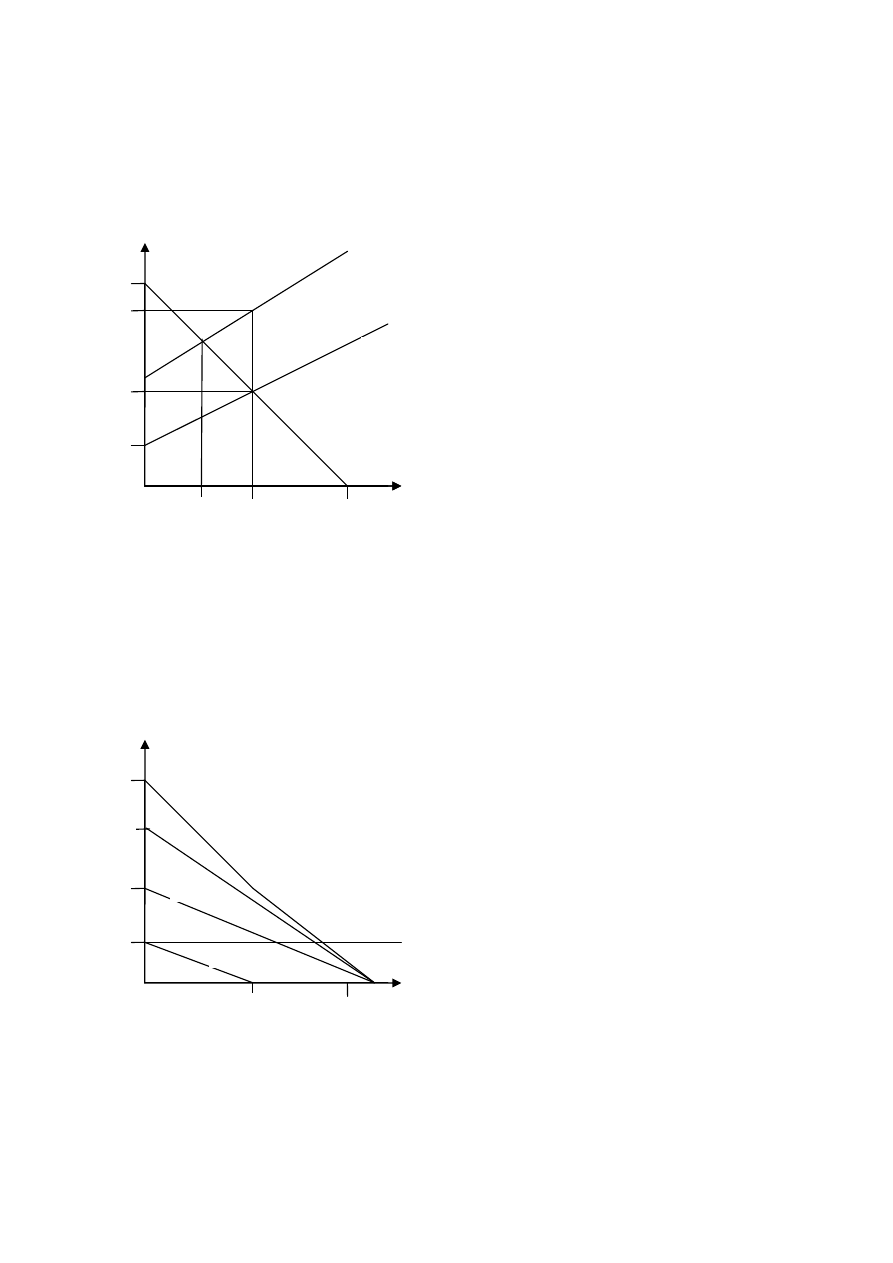
a) P=MIC

700-5Q=400+Q Q=50 P=450

b) MEC=EC’=2Q+60
MTC=MIC+MEC=3Q+460
c) P=MTC
-5Q+700=3Q+460

Q=30 P=3*30+460=550

d) MTC(50)=3*50+460=610
DWL=1/2*160*20=1600

Zad.12
a) MB=10-Q
MC=1
MB=MC
10-Q=1

Q=9

b) MBkw= 4 – 0,4Q
MBks= 1 – 0,2Q
MBc= 15 – 1,6Q dla Q ε <0;5) 14-1,4Q dla Q ε <5;10)

c) MBc=MC tylko MBks się nie zalicza bo jest do maks 1
14-1,4*Q=1

Q = 9,29

Opracował: Kuki © 2012

MB

9,4

10

4

1

P

MBc

5

15

Q

10

MBks

MBkw

MC

MTC

450

400

P

DWL

D

30

140

50

700

MIC

Q

610