Statyczna próba rozciągania

Marcin Graba

POLITECHNIKA ŚWIĘTOKRZYSKA W KIELCACH

WYDZIAŁ

MECHATRONIKI I BUDOWY MASZYN

KATEDRA PODSTAW KONSTRUKCJI MASZYN

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

Cel ćwiczenia

•

Rodzaje wykresów rozciągania

•

Wykres rozciągania z umowną

granicą

plastyczności

•

Wykres rozciągania z wyraźną

granicą

plastyczności

•

Inżynierska i rzeczywista krzywa rozciągania

•

Związki konstytutywne wykorzystywane w opisie krzywej
rozciągania

•

Prawo Ramberga

–

Osgood’a

•

Hipotezy wytrzymałościowe oparte na danych z SPR

•

SPR w procedurach FITNET

•

Energia odkształcenia w SPR

•

Wykonanie ćwiczenia

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

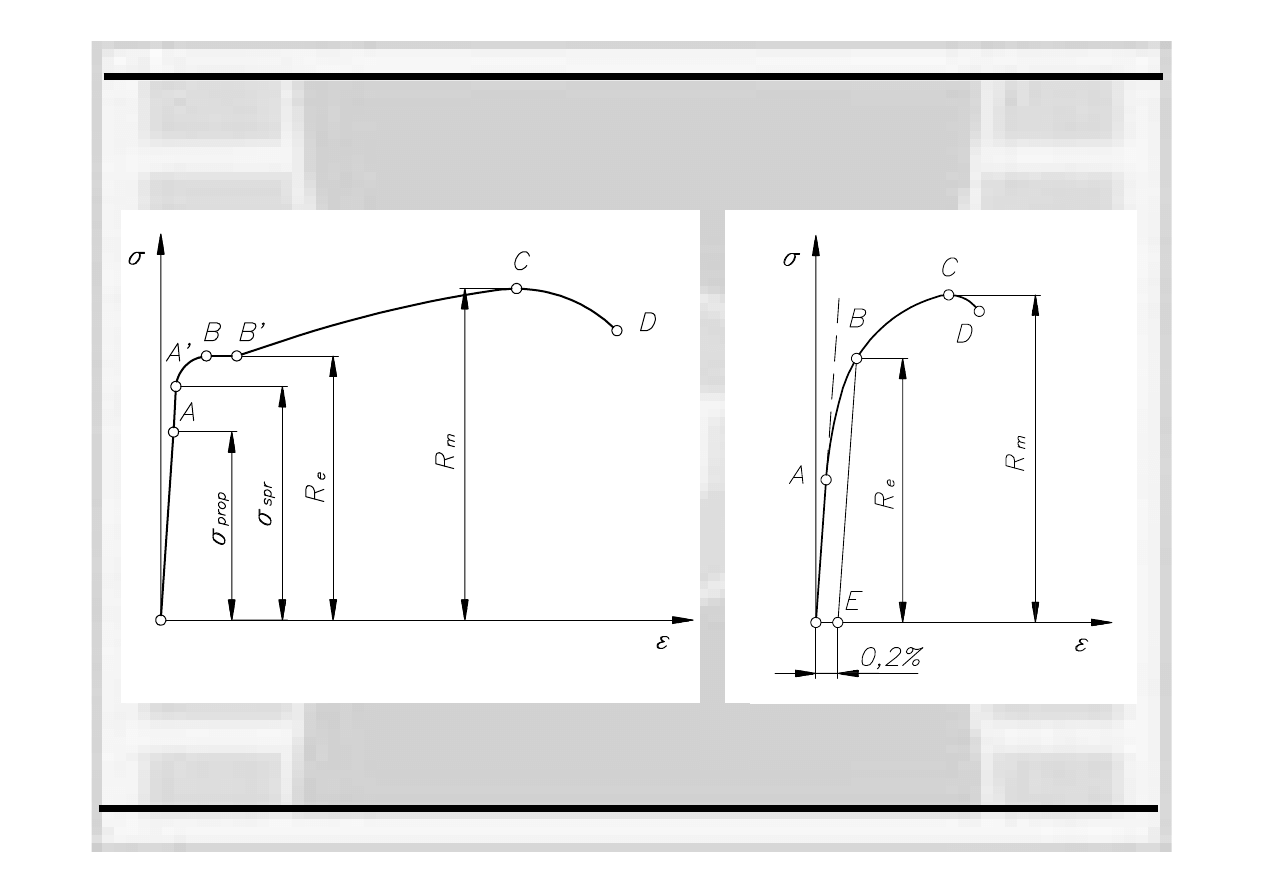
Rodzaje wykresów rozciągania

z wyraźna granicą

plastyczności

z umowną

granicą

plastyczności

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

Wykres rozciągania

z umowną

granicą

plastyczności

•

Umowna granica sprężystości (R

0,05

)

to naprężenia, które

wywołują

w materiale odkształcenia trwałe wynoszące 0,05%

długości pomiarowej L

e

.

•

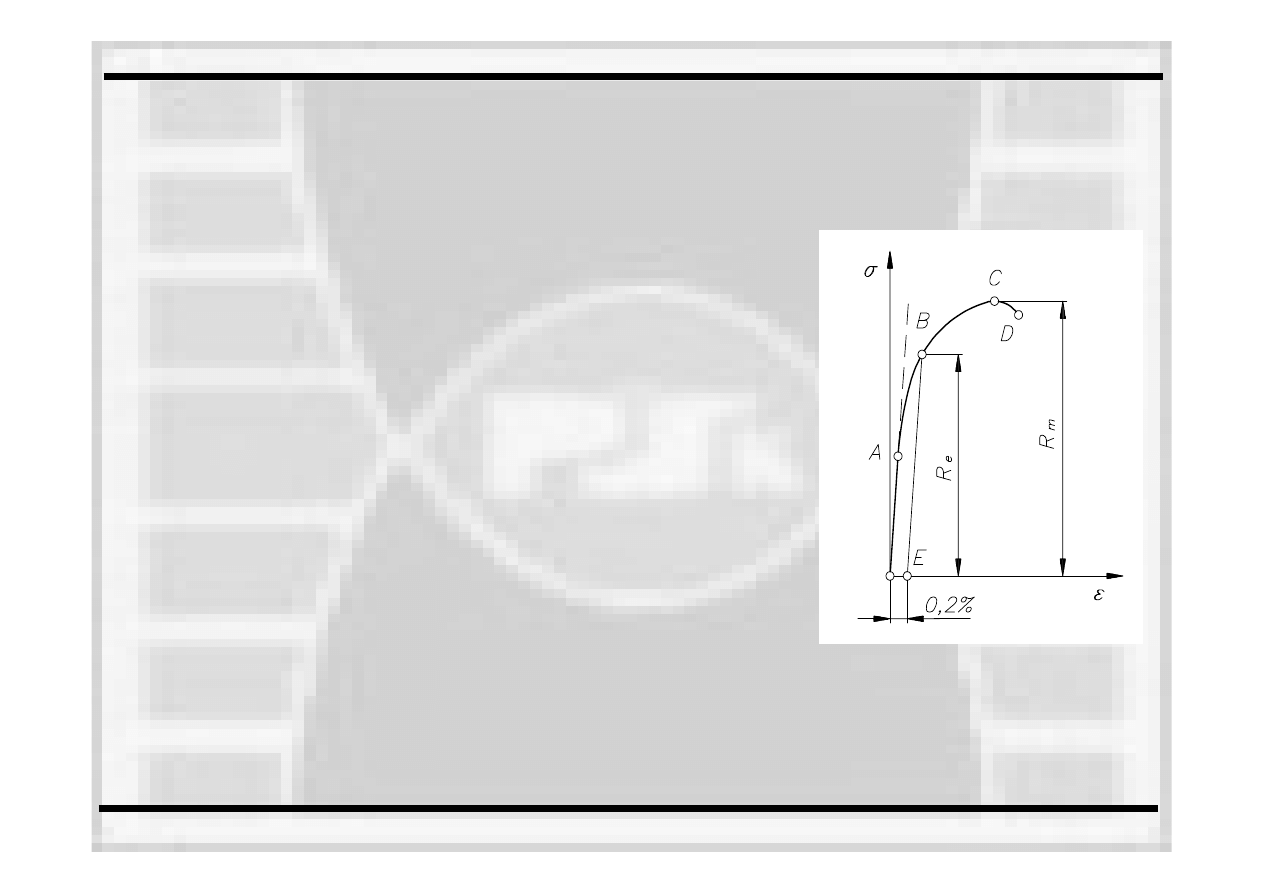
Umowna granica plastyczności (R

0,2

)

to naprężenia, które

wywołują

w materiale odkształcenia trwałe wynoszące 0,2%

długości pomiarowej L

e

. Sposób ich wyznaczenia pokazuje w

uproszczony sposób rysunek obok. Z punktu E na osi
odciętych odpowiadającego odkształceniom 0,2% prowadzi
się

linię

EB równoległą

do początkowego, prostoliniowego

odcinka 0A wykresu rozciągania.

•

Wytrzymałość

na rozciąganie

to naprężenia odpowiadające punktowi C liczone na

podstawie maksymalnej wartości zarejestrowanej siły i początkowego pola przekroju

•

Naprężenia rozrywające

to naprężenia liczone na podstawie wartości siły zarejestrowanej w

punkcie D i pola przekroju próbki w miejscu pęknięcia.

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

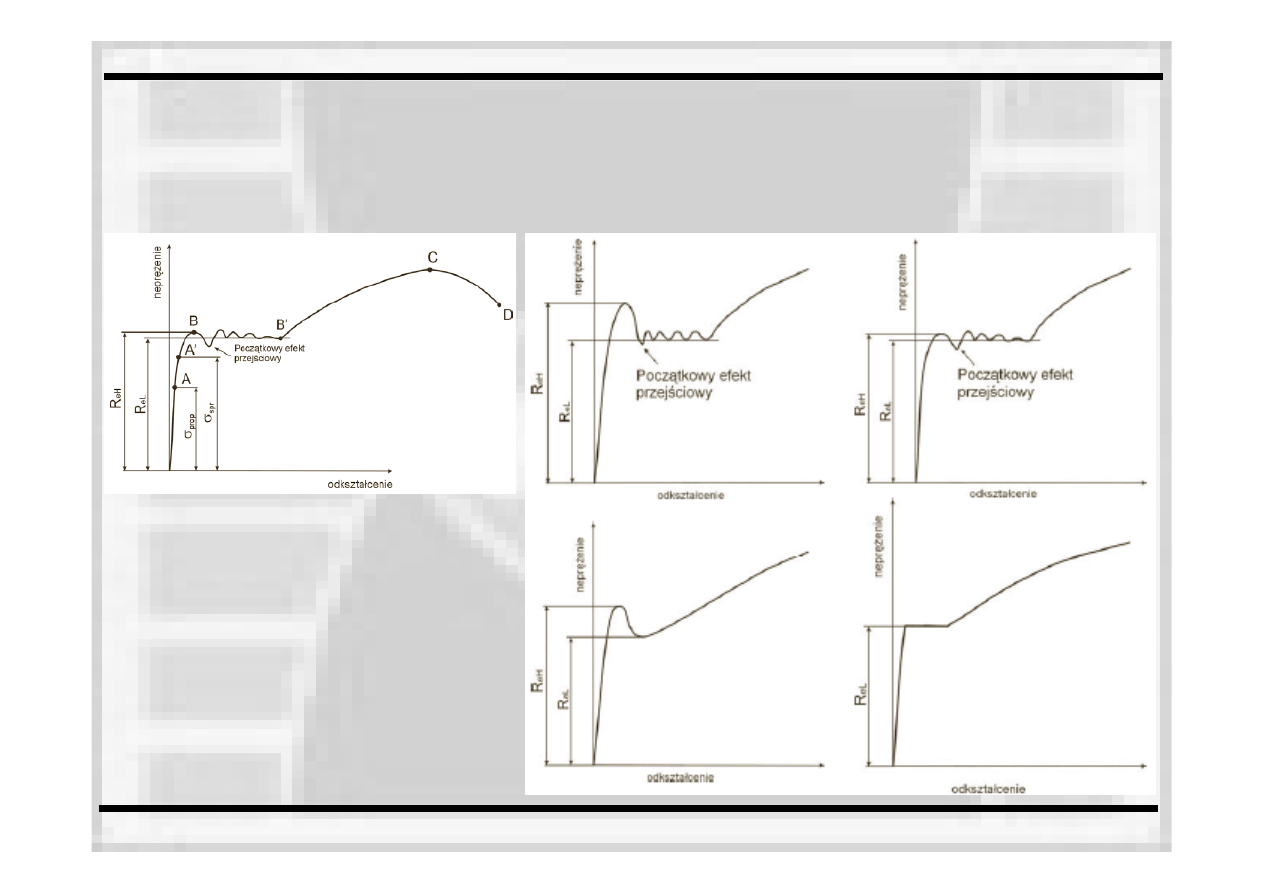
Wykres rozciągania

z wyraźną

granicą

plastyczności

•

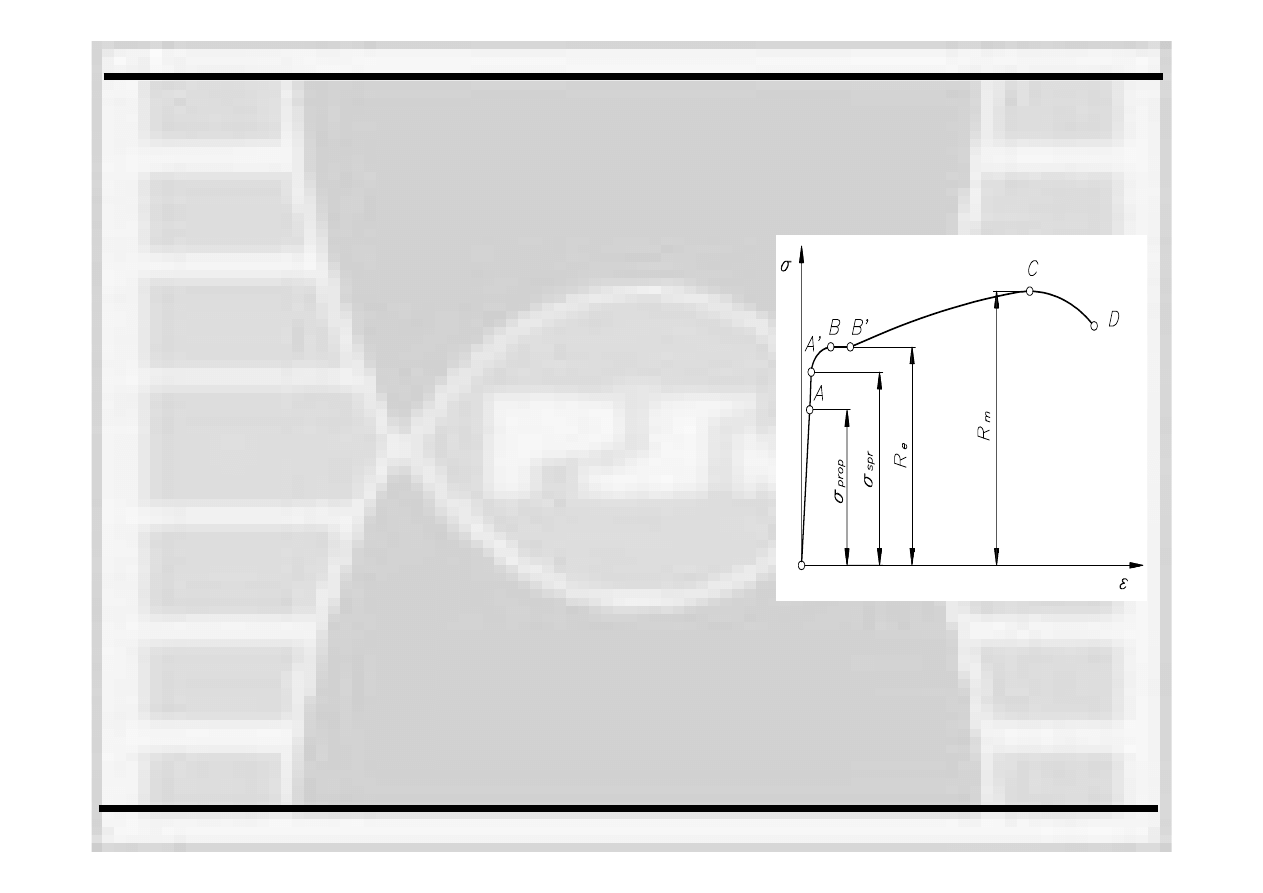
Od 0 do punktu A naprężenia rosną

proporcjonalnie do odkształceń

(obowiązuje prawo Hooka). Na odcinku AA’

przestaje obowiązywać

prawo

Hooka, ale w próbce nie pojawiają

się

jeszcze trwałe odkształcenia.

•

Na odcinku A’B

zależność

ta jest wyraźnie nieliniowa, ale mimo to po

odciążeniu materiał

pozornie wróci do stanu przed obciążeniem (uznaje

się, że trwałe odkształcenia, które powstały są

pomijalnie małe z

praktycznego punktu widzenia). Jeżeli przekroczymy punkt B w materiale
pojawią

się

znaczące odkształcenia plastyczne, które pozostaną

na stałe

po odciążeniu.

•

Na odcinku BB’

materiał

odkształca się

nawet przy zmniejszającym się

obciążeniu zewnętrznym. Proces ten nazywa się

płynięciem materiału

zachodzi dzięki uruchomieniu defektów (dyslokacji), które początkowo nie
mając jeszcze wielu przeszkód poruszają

się łatwo. W wyniku

powstawania coraz to nowych dyslokacji, ich wzajemnego oddziaływania
przy rosnącej ich liczbie pojawia się

proces umacniania materiału (B’C).

•

W punkcie C rejestrowane jest maksimum obciążenia. Od tego punktu naprężenia odnoszone do początkowego
przekroju próbki maleją, aż

do jej zerwania w punkcie D.

•

Odcinek B’D

nie jest rzeczywistym obrazem naprężeń

w przekroju poprzecznym próbki, ponieważ

są

to naprężenia

jakie wynikają

z wartości aktualnej siły siłownika i pola przekroju początkowego. W rzeczywistości pole przekroju na

tym odcinku jest dużo mniejsze dzięki odkształceniom sprężystym, plastycznym i powstawaniu szyjki.

•

Od chwili zainicjowania szyjki naprężenia w przekroju poprzecznym do osi próbki są

w tym obszarze niejednorodne ze

względu na powstające pustki i mikropęknięcia. Naprężenie odcinku B’D

w rzeczywistości jest wyższe i po

przekroczeniu punktu C rośnie.

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

Wykres rozciągania

z wyraźną

granicą

plastyczności

Pojawiające się

na odcinku BB’

nieregularności można
sklasyfikować

na kilka

podstawowych typów i opisać

za

pomocą: górnej (R

eH

) granicy

plastyczności oraz dolnej (R

eL

)

granicy plastyczności.

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

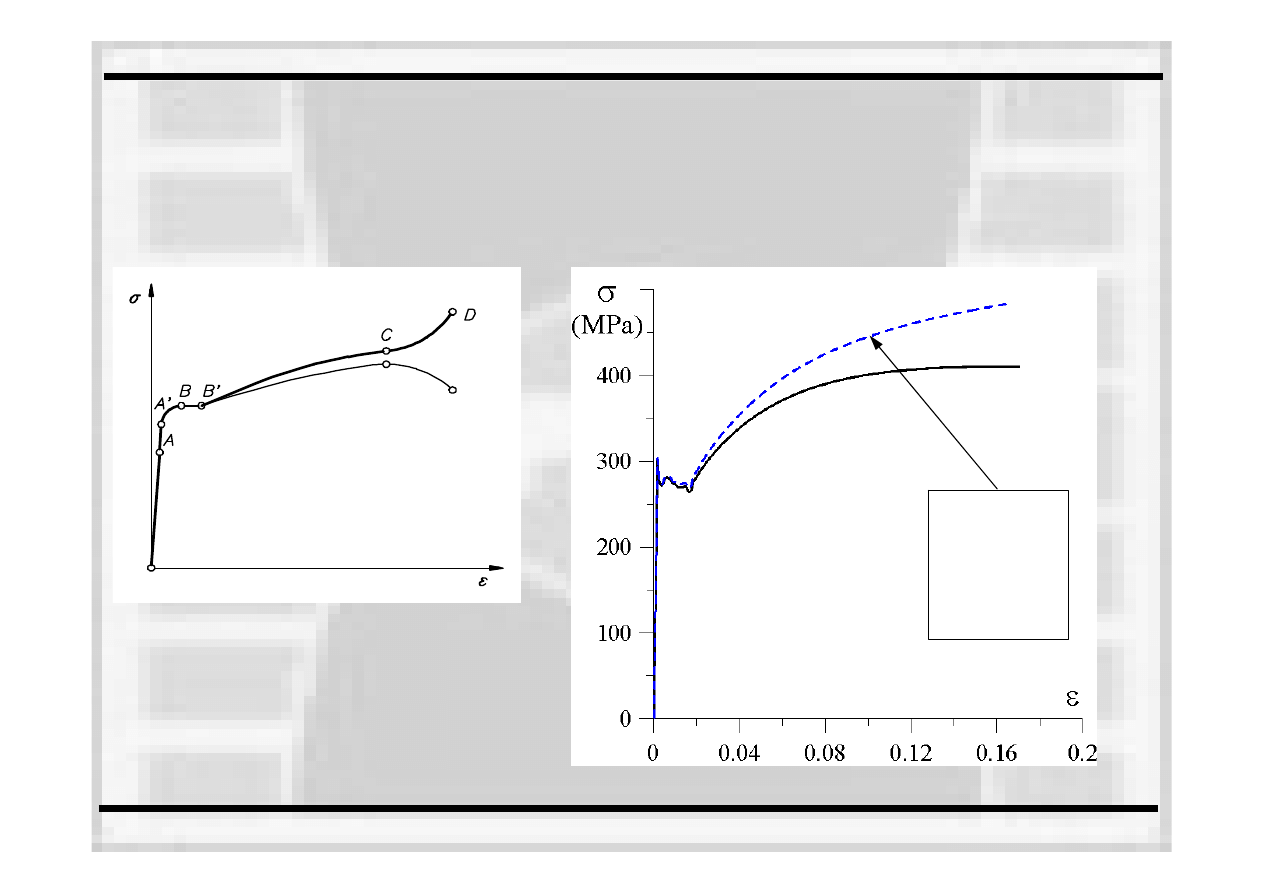
Inżynierska i rzeczywista

krzywa rozciągania

Krzywa rozciągania wyrażona
poprzez

średnie naprężenie

„rzeczywiste”

(

=P/A) oraz średnie

naprężenia umowne (

=P/A

0

)

Zmianę średnicy próbki w miejscu powstania szyjki można uwzględnić

przy

obliczaniu
naprężeń

przy wyznaczaniu wykresu SPR w układzie σ–ε. Wiadomo, że naprężenia

wyznacza się

dzieląc wartość

siły przez pole przekroju, na który ta siła działa:

W najprostszym podejściu w mianowniku wstawiamy zawsze początkowe pole części
pomiarowej. Wiadomo jednak, że podczas próby objętość

części kontrolnej nie

zmienia się. Jeśli jej długość

wzrasta to dla zachowania stałej objętości średnica

musi odpowiednio maleć. Przed rozpoczęciem próby objętość

części kontrolnej

wynosi:

W każdej chwili próby możemy napisać, że:

stąd aktualna średnica wynosi:

Naprężenia wyznaczane na podstawie początkowej średnicy próbki nazywa się

naprężeniami inżynierskimi, zaś

naprężenia wyznaczane na podstawie rzeczywistej

średnicy nazywa się

naprężeniami prawdziwymi lub Cauchy’ego.

4

2

d

A

gdzie

A

F









0

2

0

0

4

l

d

V







aktual

aktual

l

V

d









0

4

aktual

aktual

l

d

V





4

2

0



www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

Inżynierska i rzeczywista

krzywa rozciągania

Krzywa rozciągania wyrażona
poprzez średnie naprężenie
„rzeczywiste”

(

=P/A)

oraz średnie naprężenia umowne
(

=P/A

0

)

)

1

ln(

)

1

(

:

dla

m



























t

t

R

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

Związki konstytutywne

W jednoosiowej próbie rozciągania możemy wyznaczyć

moduł

Young’a

i współczynnik

Poisson’a:





11

11

 E







22

33

11



 

Wielkości te są

całkowicie wystarczającymi własnościami sprężystymi materiału,

pozwalającymi zapisać

uogólnione prawo Hooka:











 

 

ij

ij

ij

kk

E







1

1

Prawo potęgowe Ramberga-Osgooda

opisujące krzywą

rozciągania w jednoosiowej

próbie w zakresie plastycznym można zapisać

za pomocą

równania

N

11

11







gdzie N=1/n

Dwie stałe materiałowe



i n, mają

swe zastosowanie w uogólnionym prawie Ramberga-

Osgooda

na przypadki trójosiowe











ij

e

y

n

ij

y

S















3

2

1

S

ij

ij

kk

ij







 

1

3



e

ij

ij

S S



3

2

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

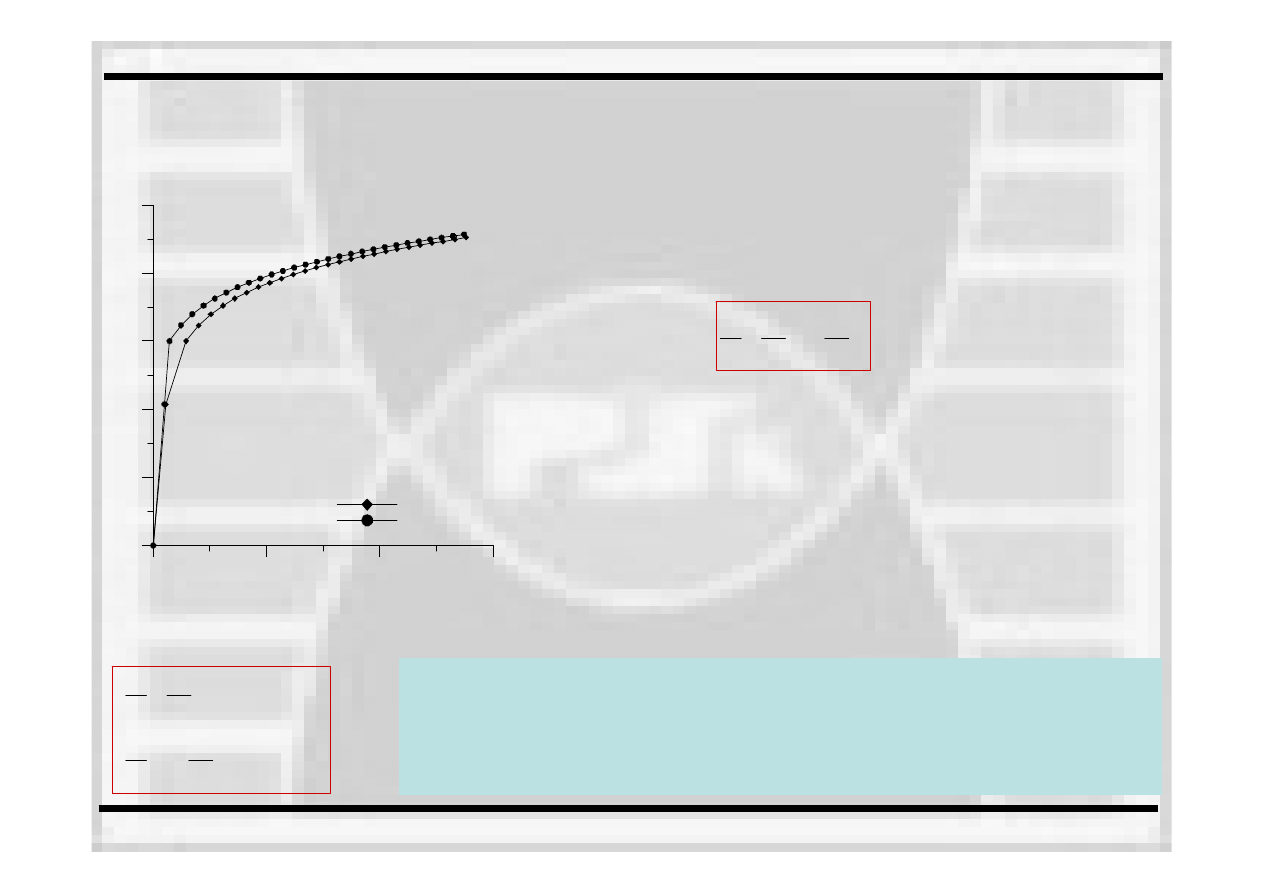
Prawo Ramberga

–

Osgood’a

































0

0

0

0

0

0

dla

dla



























n

0

0.01

0.02

0.03



0

100

200

300

400

500

 [M

P

a

]



0

= 300 MPa

E = 2,075e11 MPa
n = 7;

 = 1

prawo R - O
prawo potęgowe

Krzywą

rozciągania dla materiałów sprężysto–plastycznych,

można opisywać

prawem Ramberga-Osgood’a

(R-O), które dla

przypadku jednoosiowego obciążenia zapisuje się

w następującej

formie

gdzie:



0

jest granicą

plastyczności (R

e

lub R

0,2

);



0

jest

odkształceniem odpowiadającym granicy plastyczności (



0

=



0

/E);

E jest modułem Young’a;



jest stałą, określaną

mianem stałej

umocnienia, n – wykładnikiem potęgowym, określanym mianem
współczynnika umocnienia lub wykładnika umocnienia.

n

















0

0

0















(1)

W szeregu prac dotyczących mechaniki pękania i analizy pól naprężeń

i odkształceń

przed wierzchołkiem

pęknięcia, materiał

sprężysto–plastyczny

opisywany jest inną

wersją

równania (1):

(2)

W podanych powyżej prawach potęgowych (1) i (2) często w obliczeniach
inżynierskich stała umocnienia –



przyjmowana jest jako równa jedności.

Stopień

umocnienia materiału jest wtedy określany jedynie na podstawie

współczynnika umocnienia n. Na rysunku pokazano różnice w
modelowych krzywych opisanych równaniami (1) i (2).

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

Prawo Ramberga

–

Osgood’a

Jeżeli do opisu krzywej rozciągania stosuje się

prawo R-O

opisane wzorem (1) lub prawo

potęgowe (2), to posługując się

dowolnym programem komputerowym, można przy

wykorzystaniu metody najmniejszych kwadratów dopasować

parametry



i n, uzyskując

możliwie najlepszą

zbieżność

otrzymanego równania i wyników doświadczalnych według

odpowiedniego kryterium.
Dopasowanie to można zrobić

dla punktów „rozsądnie wybranych”

z zakresu od

początku zarejestrowanej krzywej doświadczalnej do momentu osiągnięcia maksimum na
krzywej doświadczalnej. Możliwe są

też

proste metody analitycznego wyznaczenia

parametrów



i n.

Okazuje się, że sprawą

kluczową

staje się

ten „rozsądny wybór”

punktów

wykorzystanych do aproksymacji. Zależeć

on może od kilku czynników, między którymi

do najważniejszych należą:
-

cel i zakres analizy (małe czy duże odkształcenia, przewaga odkształceń

sprężystych czy plastycznych),

-

charakter krzywej rozciągania (wyraźna czy umowna granica plastyczności).

Okazuje się, że sposób wyboru punktów wykorzystanych do aproksymacji istotnie
zmienia uzyskane wartości



i n. Istotne staje się

więc ustalenie kryterium wyboru tej

„właściwej”

pary



i n.

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

Prawo Ramberga

–

Osgood’a

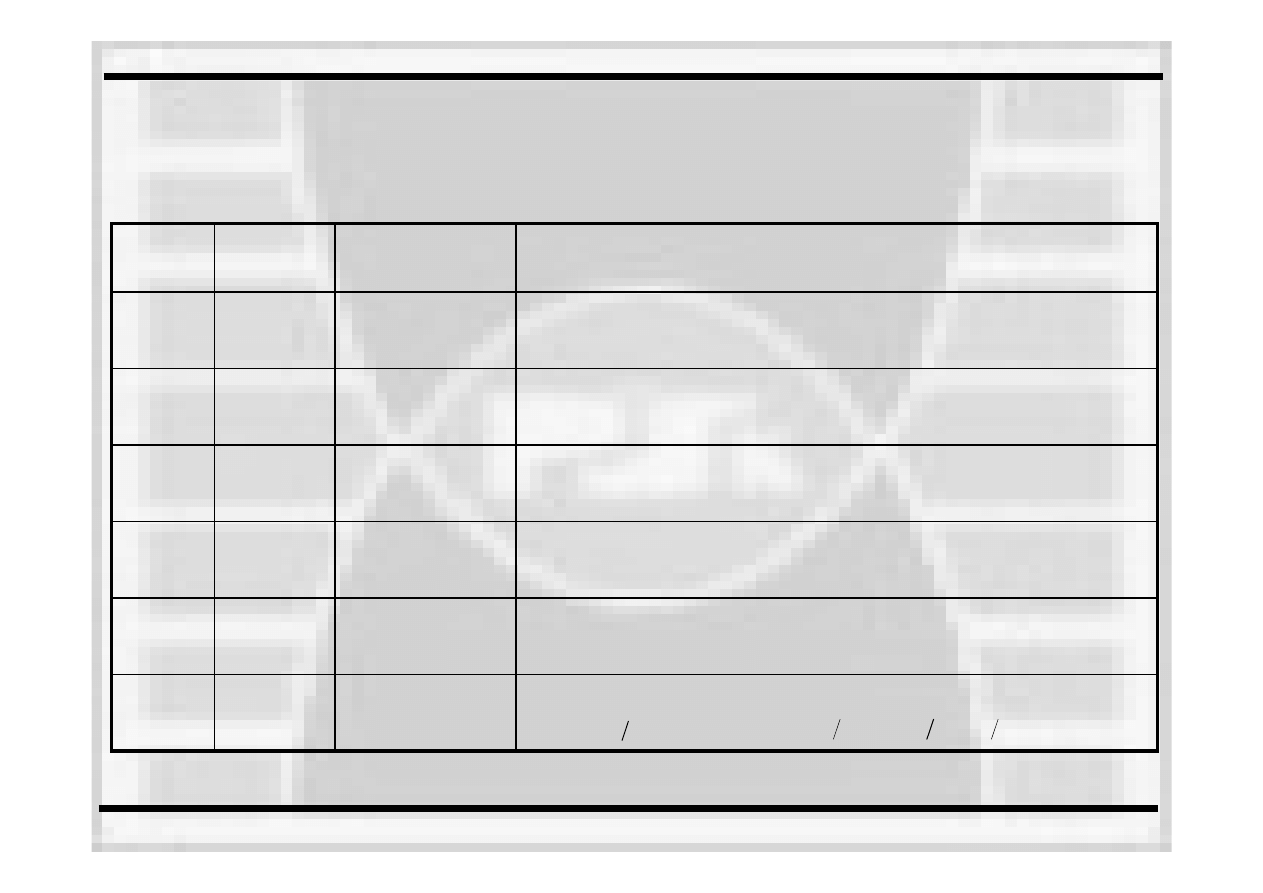
NR

OPCJI

MODEL

DANE

WEJŚCIOWE

SPOSÓB POSZUKIWANIA PARAMETRÓW

KRZYWEJ POTĘGOWEJ



i n

I

Wzór (2)

cała krzywa



0

, R

m

, E

Zakres punktów pomiędzy



0

a R

m

aproksymowano wzorem (2)

II

Wzór (2)

cała krzywa



0

, R

m

, E

Ustalając



= 1, zakres punktów pomiędzy



0

a R

m

aproksymowano wzorem (2)

III

Wzór (2)



0

, R

m

, E

Ustalając



= 1, poszukiwano wykładnika n na podstawie

punktu odpowiadającego wytrzymałości na rozciąganie R

m

IV

Wzór (2)



0

, R

m

, E

Ustalając



= 1, poszukiwano wykładnika n na podstawie

punktu odpowiadającego naprężeniom równym (



0

+R

m

)/2

V

Wzór (2)



0

, R

m

, E

Wykorzystując dwa punkty:



0

oraz R

m

poszukiwano wartości



i n

VI

Wzór (1)



0

, R

m

, E

Wartości



i n wyznaczono zgodnie ze wzorami:

,

0

002

,

0





E





 









 







0

ln

002

,

0

ln





m

m

m

R

E

R

E

n





www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin

Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

Prawo Ramberga

–

Osgood’a

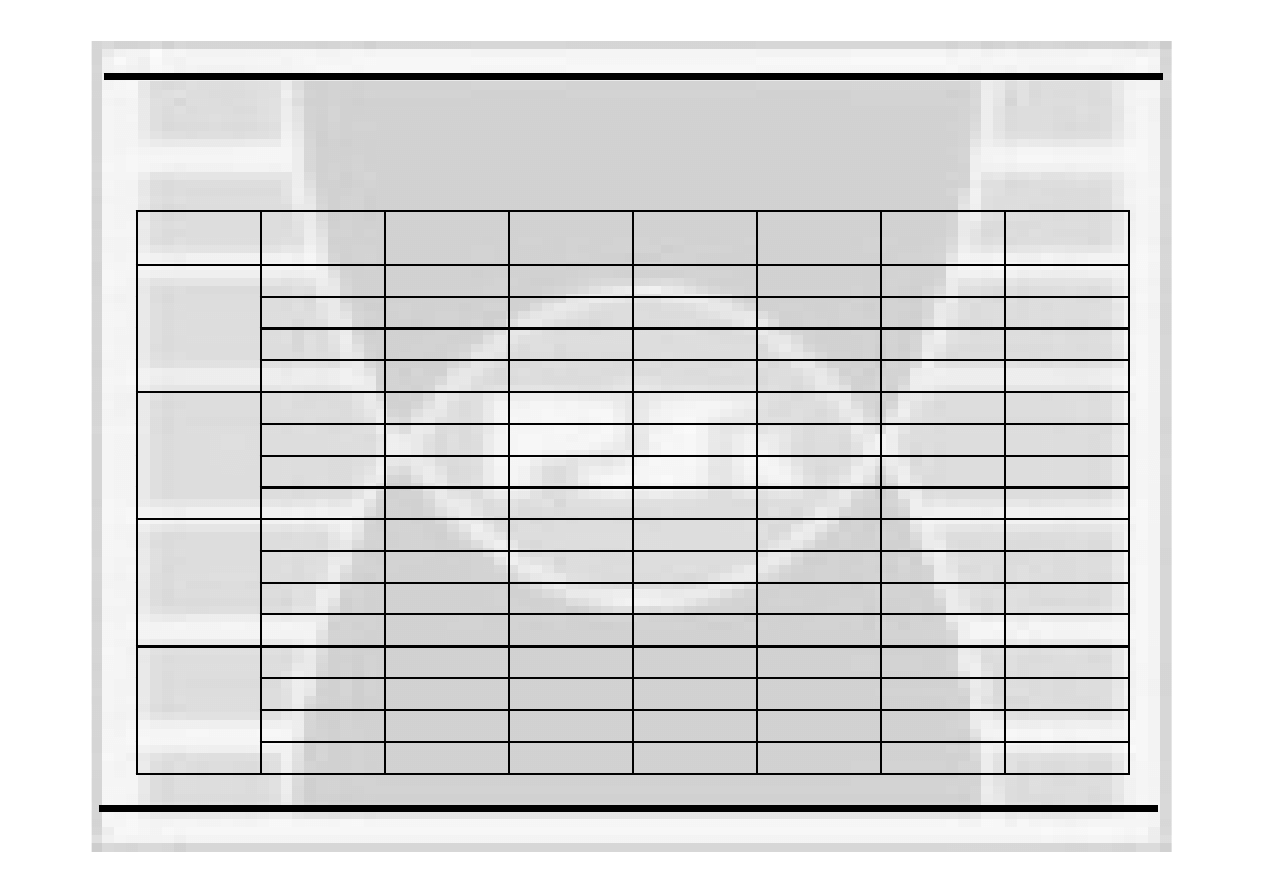
Rodzaj stali

Cecha

materiału

Model I

Model II

Model III

Model IV

Model V

Model VI

E [MPa]

205141,25

205141,25

205141,25 205141,25 205141,25 205141,25



0

[MPa] 1291,91 1291,91 1291,91 1291,91 1291,91 1291,91



0,966651 1

1

1 1,320128

0,317578

stal 40H

,

tem

p. +

16

C

n

17,5134 17,0499 19,7251 15,0951 14,4535 30,5492

E [MPa]

203341,54

203341,54

203341,54 203341,54 203341,54 203341,54



0

[MPa] 1138,75 1138,75 1138,75 1138,75 1138,75 1138,75



0,989054 1

1

1 1,357527

0,357131

stal 3H

13

n

4,2565 4,2327 4,669 10,7656 4,1067 6,2939

E [MPa]

201269,21

201269,21

201269,21 201269,21 201269,21 201269,21



0

[MPa] 1400,77 1400,77 1400,77 1400,77 1400,77 1400,77



1,102211 1

1

1 1,288105

0,287369

stal 40H

n

8,275 9,1848 10,1001 26,6971 8,1749 16,8465

E [MPa]

207564,98

207564,98

207564,98 207564,98 207564,98 207564,98



0

[MPa] 937,22 937,22 937,22 937,22 937,22 937,22



2,725089 1

1

1 1,404644

0,442938

st

al

N

C

6

n

17,3221 29,5763 28,359 38,2945 24,9885 35,7868

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin

Graba –

Politechnika Świętokrzyska w Kielcach

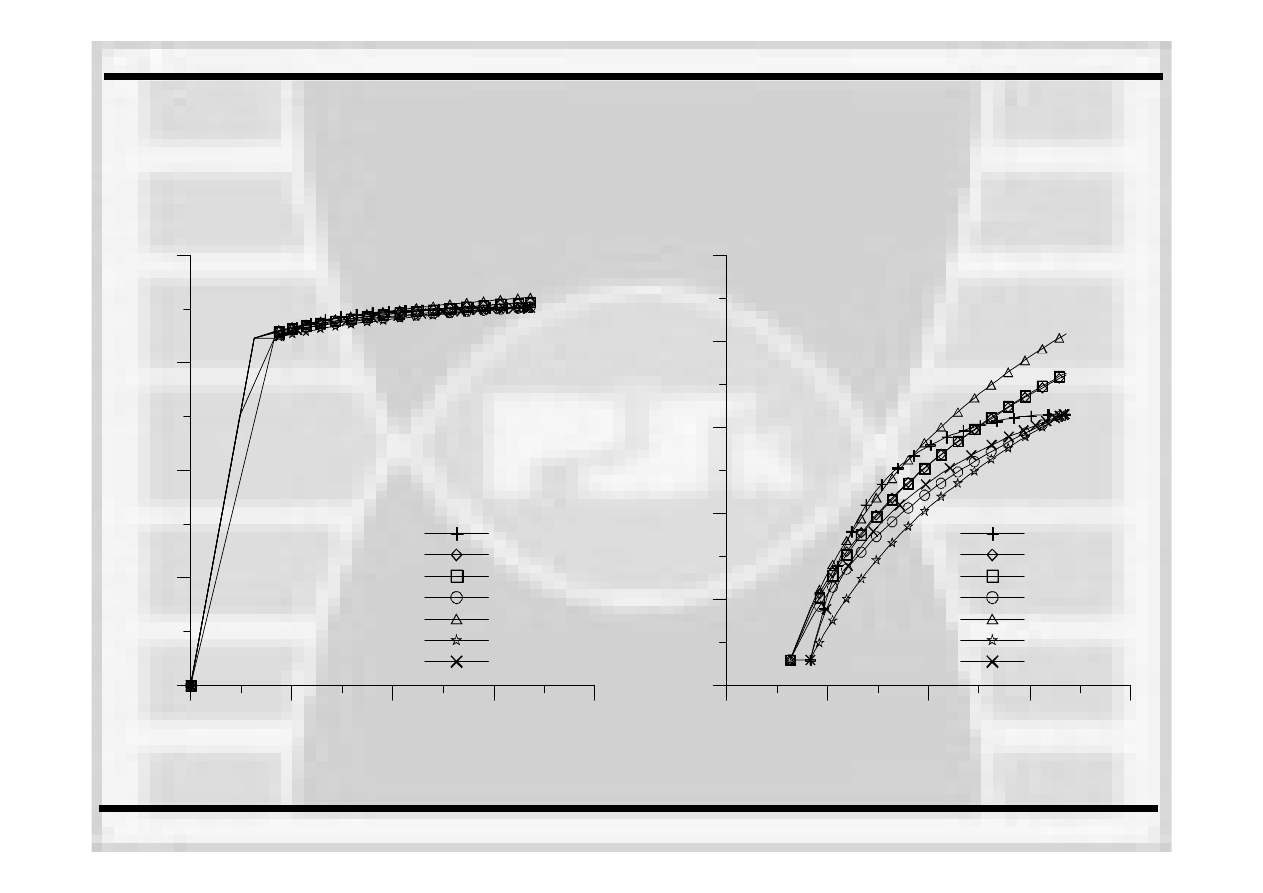
STATYCZNA PRÓBA ROZCIĄGANIA

Prawo Ramberga

–

Osgood’a

0

0.01

0.02

0.03

0.04



0

400

800

1200

1600



[M

P

a

]



Stal 40H
temp. +16



C

model rzeczyw.
model I
model II
model III
model IV
model V
model VI

0

0.01

0.02

0.03

0.04



1280

1320

1360

1400

1440

1480



[M

P

a

]



Stal 40H
temp. +16



C

model rzeczyw.
model I
model II
model III
model IV
model V
model VI

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin

Graba –

Politechnika Świętokrzyska w Kielcach

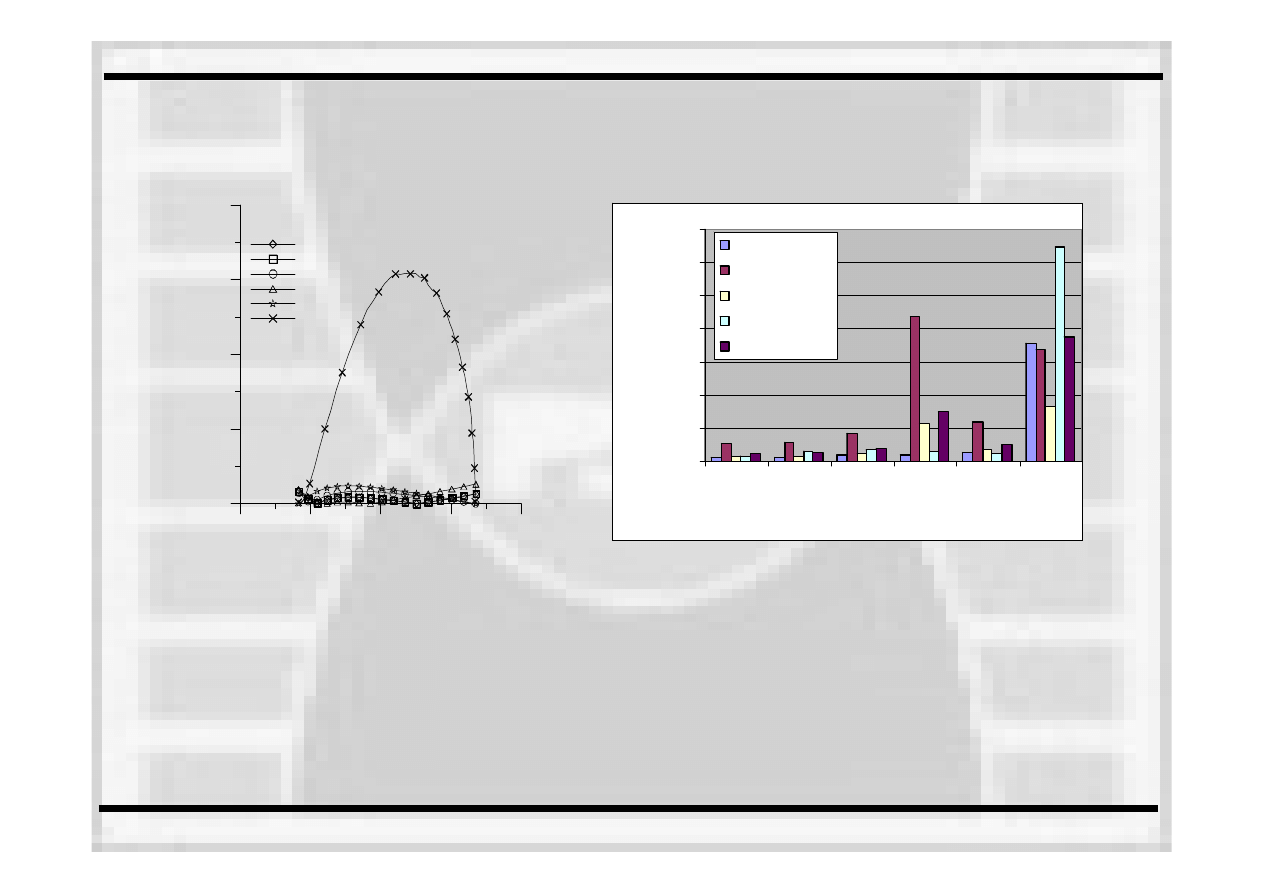
STATYCZNA PRÓBA ROZCIĄGANIA

Prawo Ramberga

–

Osgood’a

0

0.01

0.02

0.03

0.04



0

10

20

30

40

|



rz

e

cz

-



m

odel

|/



rz

e

cz



10

0

%



Stal 40H
temp. +16



C

model I
model II
model III
model IV
model V
model VI

0

5

10

15

20

25

30

35

I

II

III

IV

V

VI

model dopasowania

b

łą

d do

pa

s

o

wa

ni

a m

o

d

e

lo

we

j k

rz

ywe

j

ro

zc

ią

ga

n

ia

do

k

rz

ywej

d

o

ś

w

ia

d

. [%

]

stal 40H +16C
stal 3H13
stal 40H
stal NC6
średnia

Okazuje się

zatem, że wybór punktów wykorzystanych do aproksymacji wpływa na podobieństwo modelowej do

doświadczalnej krzywej rozciągania. Prowadzone obliczenia numeryczne dowodzą, że najmniejszy błąd dopasowania
jest popełniany w przypadku materiałów, dla których uzyskuje się

większe wartości wykładnika umocnienia w prawie

R–O. Popełniany błąd dla stali słabo się

umacniających (n>7), bez względu na model dopasowania jest mniejszy od 2%.

Większe błędy dopasowania uzyskiwane są

dla stali silnie się

umacniających (około 4

5%). Przez błąd rozumiemy

średnią

wartość

różnic pomiędzy wykresem rzeczywistym a modelowym w całym przedziale dopasowania.

Dla wszystkich badanych stali najbardziej zbliżonym do rzeczywistego okazuje się

być

model I lub II dopasowania.

Oparty na wyrażeniu (1) model VI dopasowania obarczony jest największymi błędami. Dla przypadku III modelu

dopasowania, często wykorzystywanego w opisie materiału sprężysto–plastycznego

w rozwiązywaniu zagadnień

z

zakresu nieliniowej mechaniki pękania, można mówić

o błędzie mniejszym od 2,5%.

•

W hipotezie Hubera-Missesa-Henckyego

zakłada się, że materiał

osiąga

stan plastyczny, gdy drugi niezmiennik dewiatora naprężenia osiąga
wartość

krytyczną

k

2

:

•

Wielkość

k

jest traktowana jak granica plastyczności przy czystym

ścinaniu. W przypadku prostej próby rozciągania mamy



22

=



33

=0,



11

=R

e

więc:

•

W hipotezie Treski założono z kolei, że materiał

zaczyna płynąć

kiedy

maksymalne naprężenia styczne osiągną

wartość

krytyczną

k. W

przypadku jednoosiowej próby rozciągania mamy



22

=



33

=0,



11

=R

e

. Na

podstawie analizy koła Mohra otrzymujemy zależność:

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin

Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

Hipotezy wytrzymałościowe

1

2

2

S S

k

ij

ij



2

6

3

2

2

R

k

k

R

e

e











max

;

;



 

 



11

22

11

33

22

33

2

2













k

k

R

e

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin

Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

Własności wytrzymałościowe w SPR

E

- moduł

Young’a

R

p

,

R

0.2

-

umowna granica plastyczności

R

eH

-

górna wartość

wyraźnej granicy plastyczności

R

eL

-

dolna wartość

wyraźnej granicy plastyczności

R

e

- jedna z wartości: R

p

lub 0.95R

eH

lub R

eL

R

m

- wytrzymałość

doraźna

σ

f

- naprężenie płynięcia, σ

f

= 0.5(R

e

+R

m

)

Δε

-

długość

przystanku płynięcia

N - współczynnik umocnienia materiału (N = 1/n)

σ, ε

-

naprężenie i odkształcenie z próby jednoos. rozciągania

σ

t

, ε

t

-

rzeczywiste naprężenie i odkształcenie (dla σ

< R

m

)

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin

Graba –

Politechnika Świętokrzyska w Kielcach

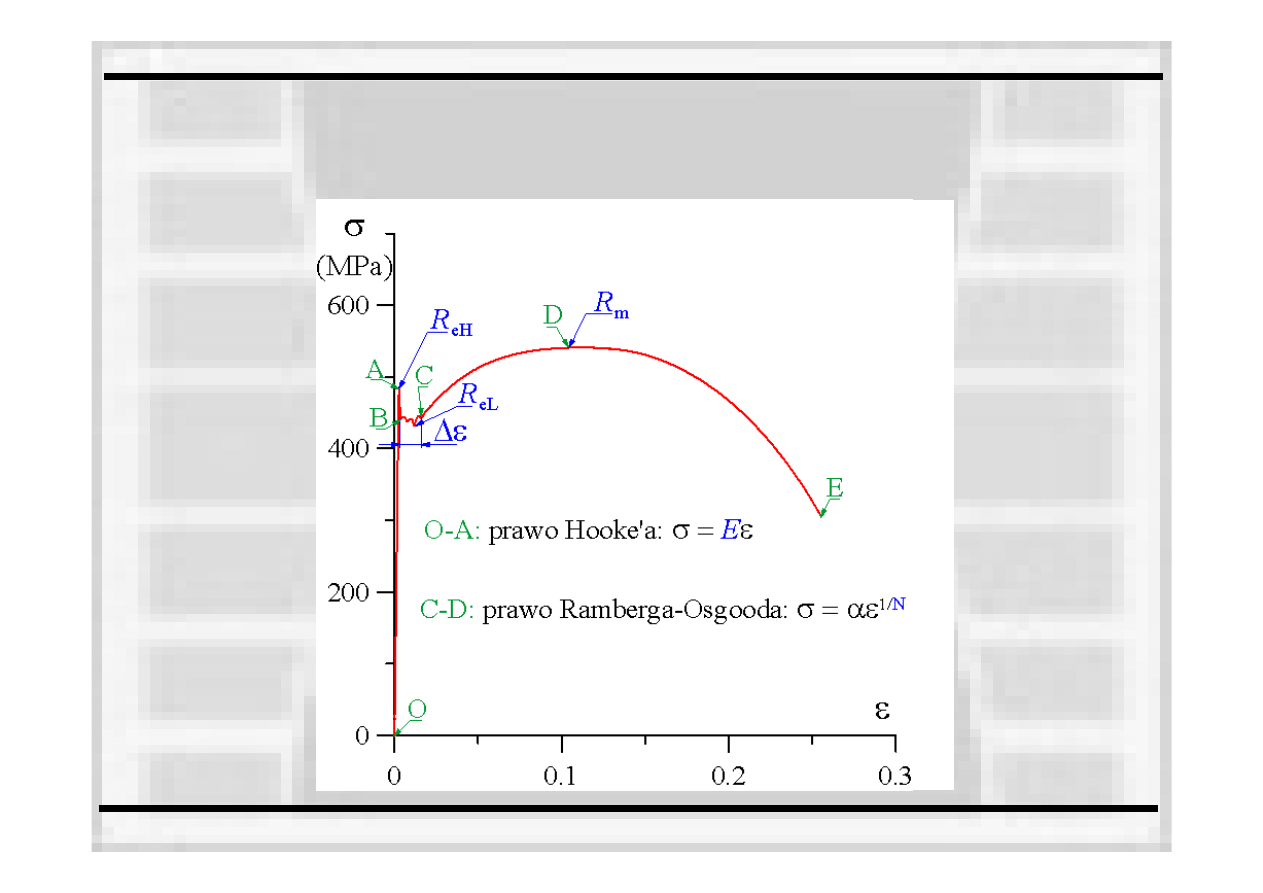
STATYCZNA PRÓBA ROZCIĄGANIA

Własności wytrzymałościowe w SPR

wykres rozciągania dla
materiału z wyraźną

granicą

plastyczności

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin

Graba –

Politechnika Świętokrzyska w Kielcach

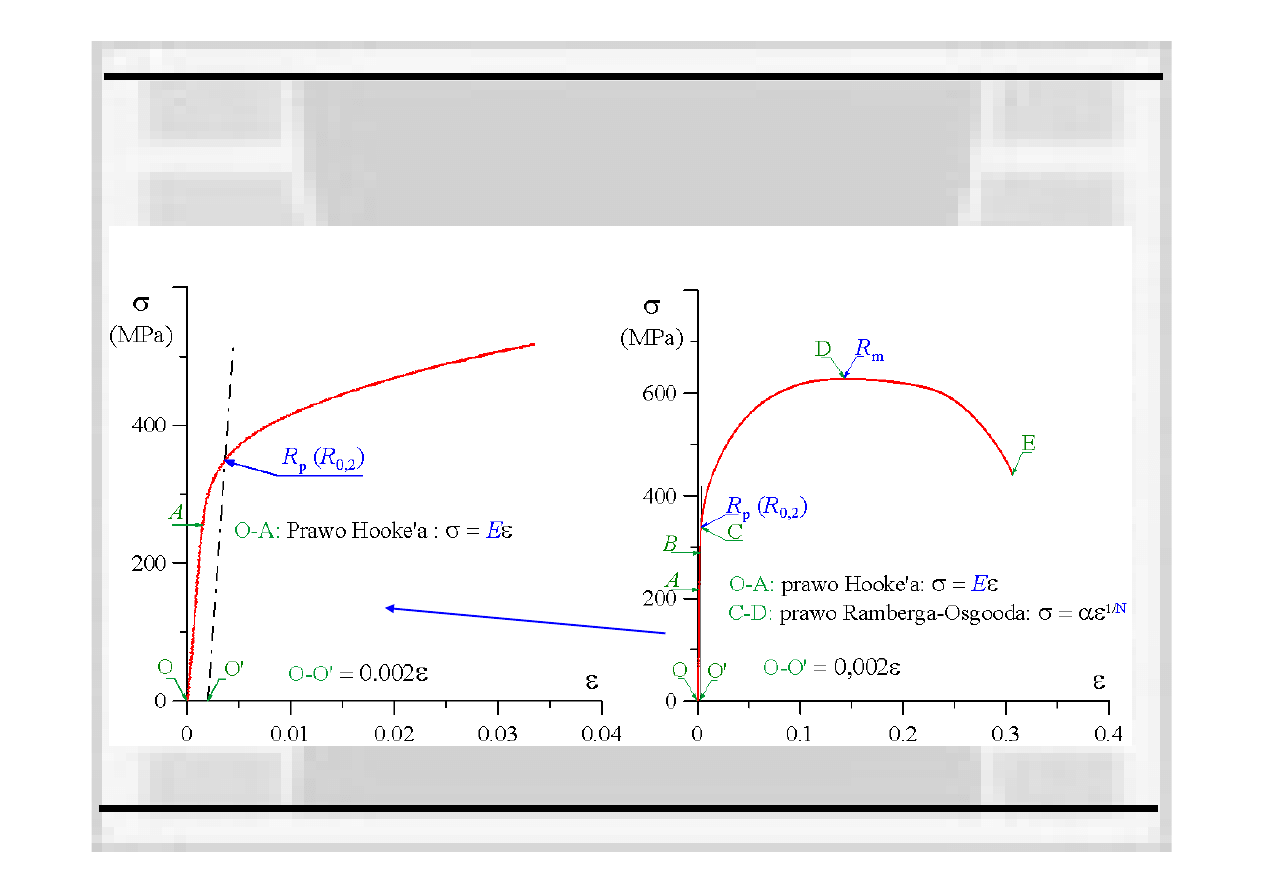
STATYCZNA PRÓBA ROZCIĄGANIA

Własności wytrzymałościowe w SPR

wykres rozciągania dla materiału z umowną

granicą

plastyczności

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin

Graba –

Politechnika Świętokrzyska w Kielcach

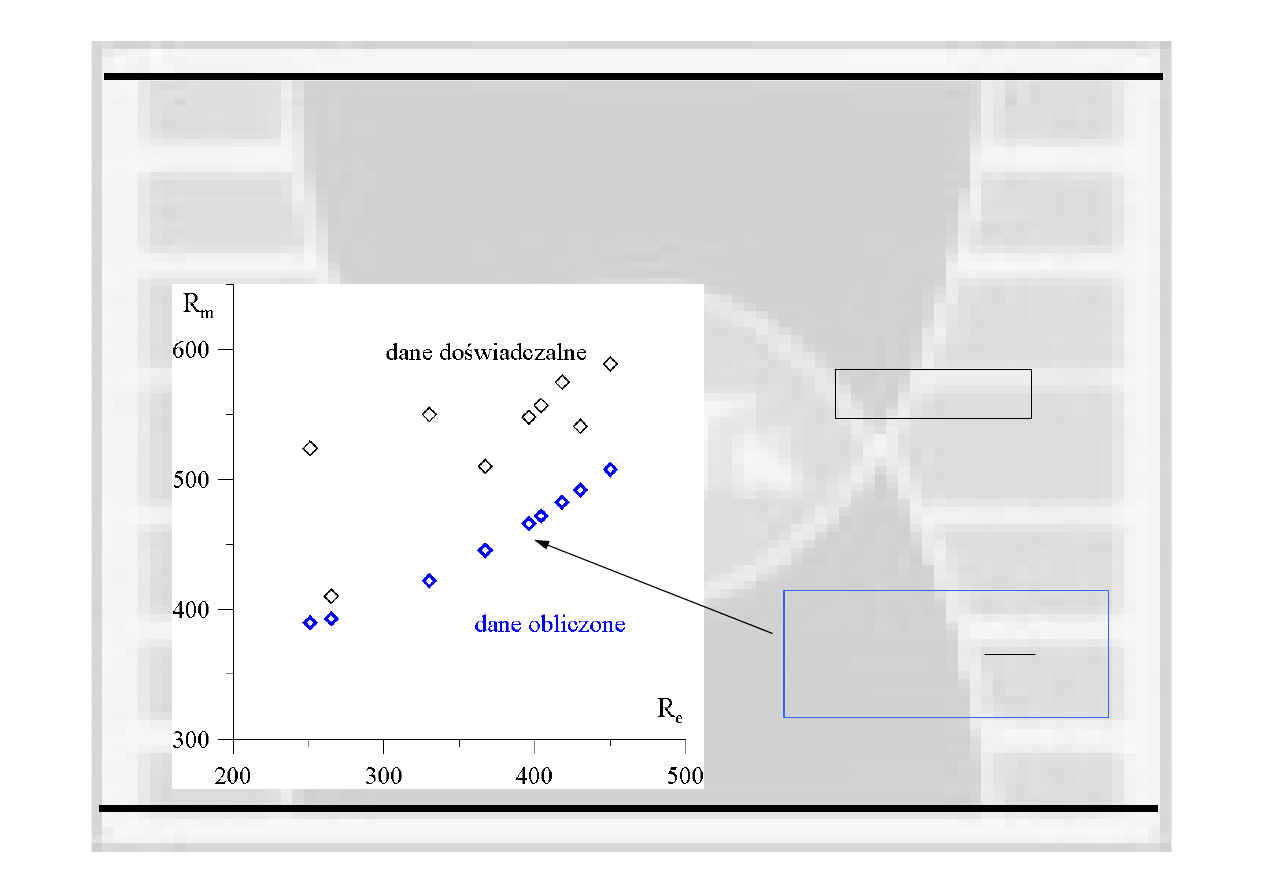
STATYCZNA PRÓBA ROZCIĄGANIA

SPR w procedurach FITNET

eH

eL

95

.

0

R

R



Konserwatywne oszacowanie granicy plastyczności i wytrzymałości doraźnej

materiału































5

.

2

e

e

m

150

2

1

R

R

R

wytrzymałość

doraźna

dolna granica plastyczności

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

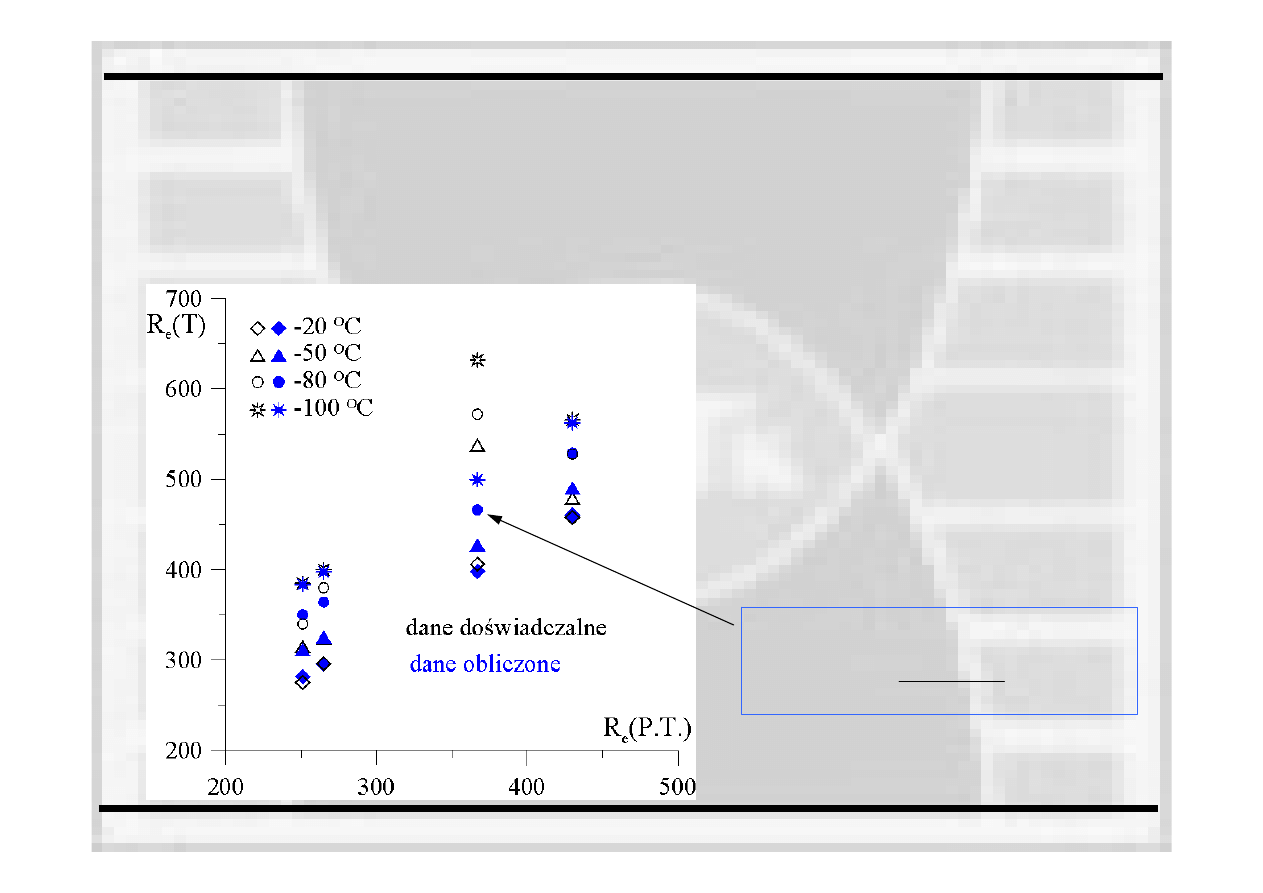
STATYCZNA PRÓBA ROZCIĄGANIA

SPR w procedurach FITNET

Konserwatywne oszacowanie granicy plastyczności R

e

, dla temperatur

obniżonych

)

MPa

(

189

8

.

1

491

10

T.P.

T

dla

5

)

(

)

(











T

R

R

RT

e

T

e

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

SPR w procedurach FITNET

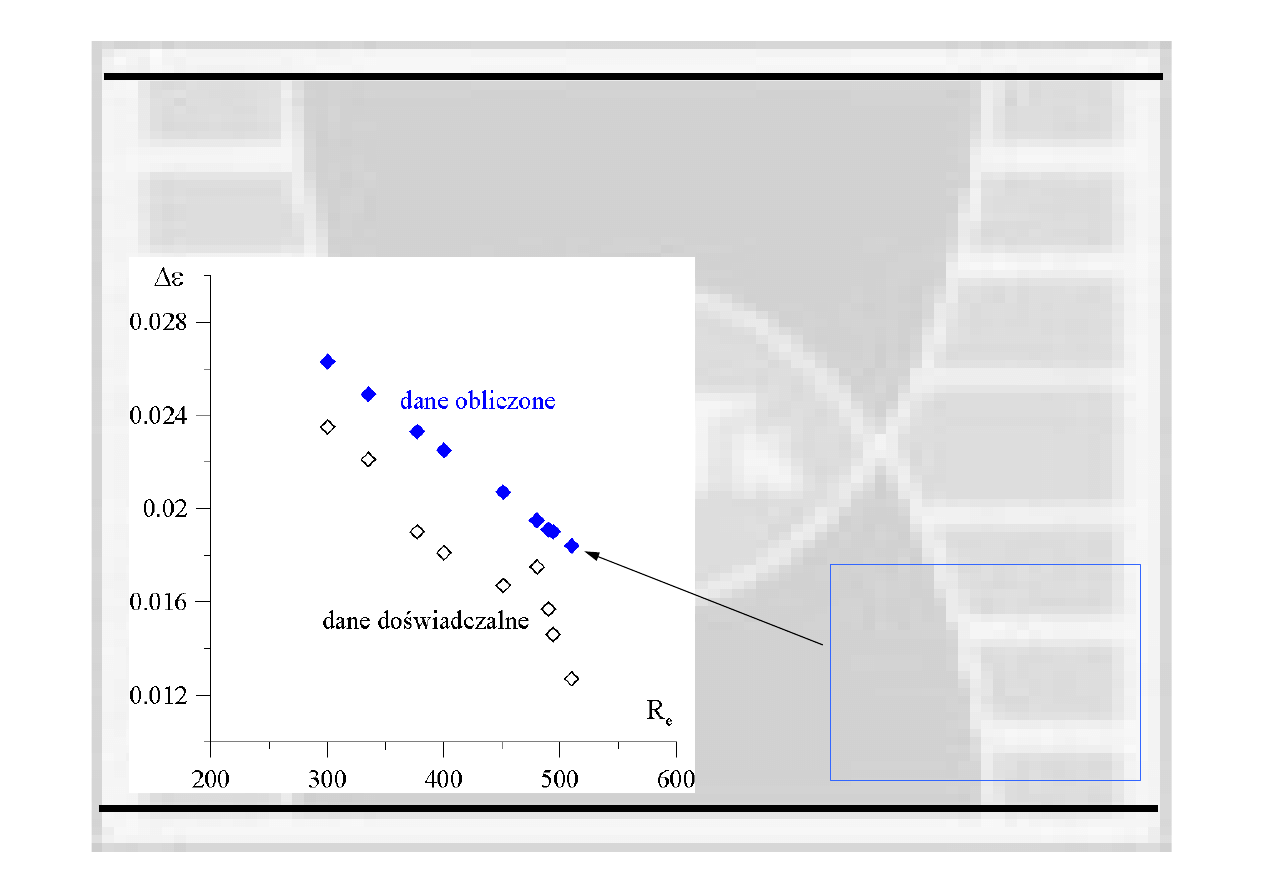
Konserwatywne oszacowanie przystanku plastyczności



0

1000

dla

)

001

.

0

1

(

0375

.

0

1000

dla

e

e

e



















MPa

MPa

R

R

R

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

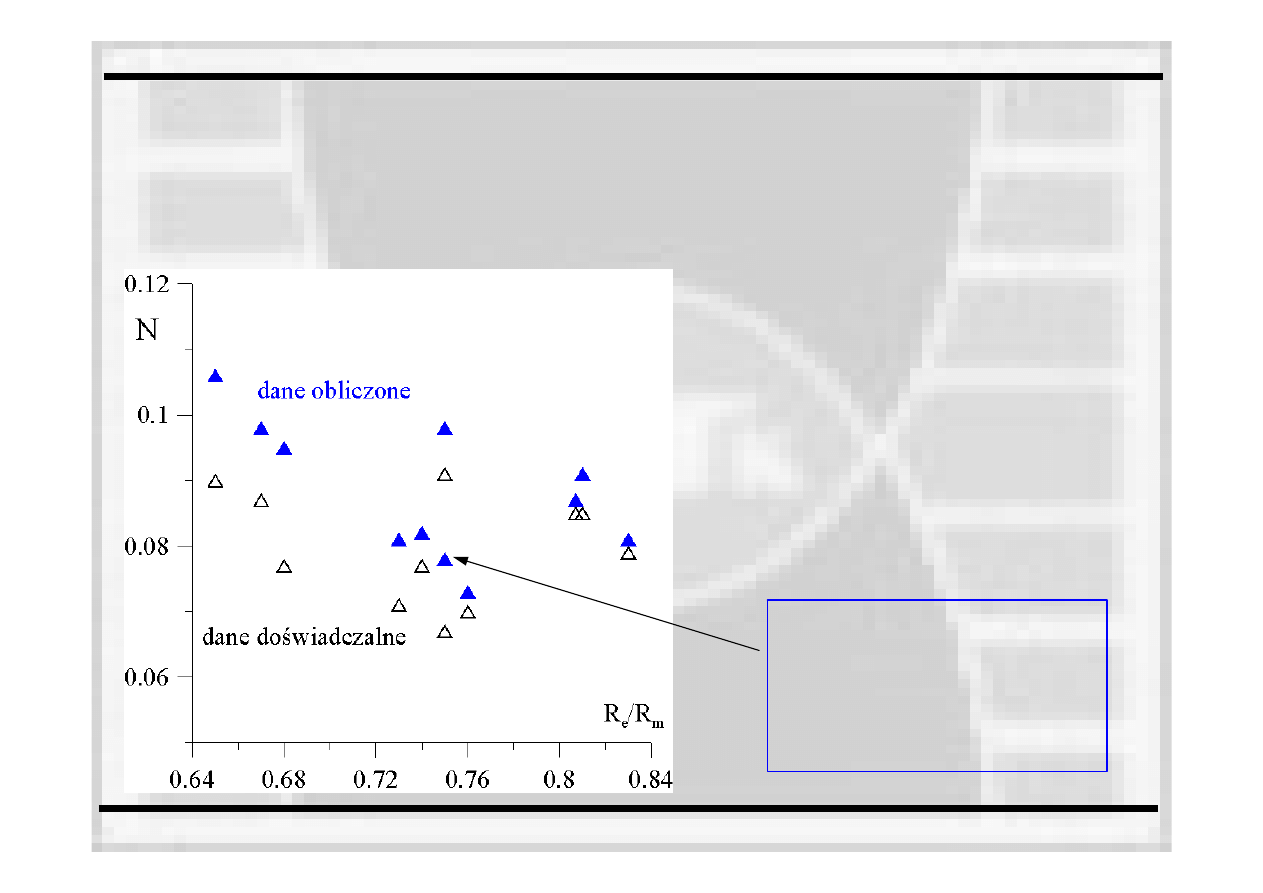
SPR w procedurach FITNET

Konserwatywne oszacowanie współczynnika umocnienia materiału N

)

/

1

(

3

.

0

95

.

0

/

65

.

0

MPa)

(

1000

300

m

e

m

e

e

R

R

N

R

R

R

dla













www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

SPR w procedurach FITNET

•

dla materiału z wyraźną

granicą

plastyczności w analizie wykorzystuje się

minimalna wartość

dolnej granicy plastyczności, R

eL

;

•

jeśli w posiadanych wynikach jest podana wartość

wyraźnej granicy plastyczności, a

nie ma pewności, że jest to dolna granica, to przyjmuje się

ją

jako górna wartość

granicy plastyczności i należy ją

zredukować

o 5% (R

e

=0.95R

eH

gdzie R

eH

jest

minimalną

wartością

ze zbioru wszystkich wyników doświadczenia);

•

jeśli materiał

nie posiada wyraźnej granicy plastyczności, to do obliczenia L

r

stosuje

się

umowna granica plastyczności z tym, że ze zbioru wszystkich wyników {R

0.2

}

wybiera się

najmniejszą

wartość;

Dla uzyskania konserwatywnego wyniku w analizie FITNET do obliczenia
znormalizowanego obciążenia zewnętrznego L

r

należy stosować

minimalną

wartość

granicy plastyczności

ze zbioru danych {R

e

} wg następnych zasad:

Dla sporządzania krzywej zniszczenia FAD -

f(Lr) należy posłużyć

się

średnią

wartością

ze zbioru danych {ReL}.

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

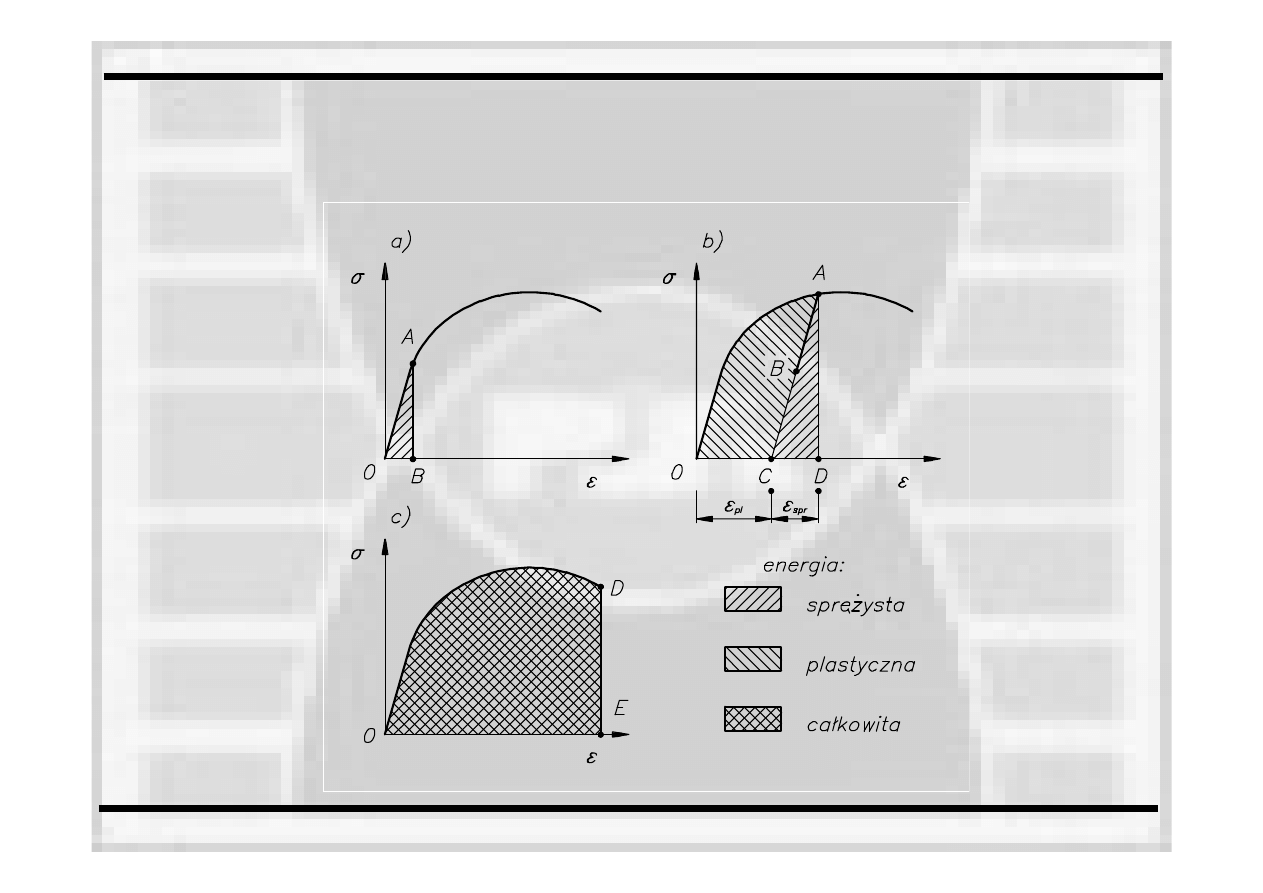
STATYCZNA PRÓBA ROZCIĄGANIA

Energia odkształcenia w SPR

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

Wykonanie ćwiczenia -

sporządzenie

sprawozdania -

część

I

•

Zerwanie próbki wykonanej z materiału z wyraźną

granicą

plastyczności

•

Sporządzenie wykresu

=f() dla bazy ekstensometru

l

0

=50mm (wykres

inżynierski i wykres rzeczywisty)

•

Wyznaczenie wszelkich własności wytrzymałościowych

•

Wyznaczenie parametrów w prawie Ramberg’a-Osgood’a

•

Wyznaczenie energii niezbędnej na zerwanie próbki w oparciu o

wykres P=f(u

eks

)

•

Wyznaczenie własności wytrzymałościowych zgodnie z procedurami

FITNET i porównanie ich z wyznaczonymi wcześniej

•

Wyznaczyć

aktualną średnicę

próbki

•

Wnioski

www.tu.kielce.pl/~mgraba

Copyright

2008 Marcin Graba –

Politechnika Świętokrzyska w Kielcach

STATYCZNA PRÓBA ROZCIĄGANIA

Wykonanie ćwiczenia -

sporządzenie

sprawozdania -

część

II

•

Zerwanie próbki wykonanej z materiału z umowną

granicą

plastyczności wraz z

odciążeniami

(7 odciążeń)

•

Sporządzenie wykresu

=f() dla bazy ekstensometru

l

0

=50mm (wykres

inżynierski i wykres rzeczywisty)

•

Wyznaczenie wszelkich własności wytrzymałościowych

•

Wyznaczenie parametrów w prawie Ramberg’a-Osgood’a

po uprzednim

usunięciu odciążeń

•

Wyznaczenie energii sprężystej, plastycznej i całkowitej dla każdego

odciążenia w oparciu o wykres P=f(u

eks

)

•

Wyznaczenie energii niezbędnej na zerwanie próbki w oparciu o wykres

P=f(ueks)

•

Wyznaczenie własności wytrzymałościowych zgodnie z procedurami FITNET i

porównanie ich z wyznaczonymi wcześniej

•

Wyznaczyć

aktualną średnicę

próbki

•

Wnioski