Ćwiczenia nr 3
Finanse II
Robert Ślepaczuk
1
Teoria portfela papierów wartościowych
Teoria portfela papierów wartościowych jest jednym z najważniejszych działów
nowoczesnych finansów. Dotyczy ona inwestycji finansowych, a przede wszystkim
inwestycji dokonywanych na rynku kapitałowym, tzn. zakupu papierów wartościowych.
I.
Podstawowe charakterystyki papieru wartościowego.
1. Oczekiwana stopa zwrotu jest to średnia ważona możliwych do osiągnięcia stóp przy
czym wagami są prawdopodobieństwa ich osiągnięcia.
∑
=
=
n
i
i
i
R
p
R
1
*
gdzie:
R – oczekiwana stopa zwrotu,
n – liczba możliwych do osiągnięcia wartości stopy zwrotu,
R
i
– i-ta możliwa do osiągnięcia wartość stopy zwrotu,
p
i
– prawdopodobieństwo osiągnięcia i-tej możliwej wartości stopy zwrotu.
W
związku z tym, że zazwyczaj nie jest możliwe określenie rozkładu stóp zwrotu w
przyszłości (tzn. możliwych do osiągnięcia stóp zwrotu i prawdopodobieństw ich
osiągnięcia) to zamiast tego wykorzystuje się stopy zwrotu zrealizowane w przeszłości,
stosując następujący wzór:
n
R
R
n
i
i
∑
=
=
1
W
powyższym wzorze oczekiwana stopa zwrotu oszacowana jest jako średnia
arytmetyczna stóp zwrotu osiągniętych w poprzednich n okresach.
2. Wariancja jest miarą ryzyka papieru wartościowego. Określa zróżnicowanie
możliwych dochodów z tytułu posiadania papieru wartościowego. Im większe jest to
zróżnicowanie, tym większe jest ryzyko związane z papierem wartościowym.
Wariancja papieru wartościowego mierzona jest w procentach podniesionych do
kwadratu według wzoru:
∑
=
−
=
n
i
i
i
R
R
p
V
1
2
)
(
*
gdzie: V – wariancja stopy zwrotu.
Jeśli mamy do dyspozycji tylko zrealizowane stopy zwrotu to wzór przyjmuje
postać:
1
)
(
1
2
−
−
=
∑
=
n
R
R
V
n
i
i
Ćwiczenia nr 3
Finanse II
Robert Ślepaczuk
2
3. Odchylenie standardowe stopy zwrotu jest także miarą ryzyka papieru wartościowego.
Mierzone jest w procentach. Wskazuje ono na przeciętne odchylenie możliwych stóp
zwrotu od oczekiwanej stopy zwrotu. Przyjmuje wartości nieujemne. Podobnie jak
przy wariancji im większe jest odchylenie standardowe, tym większe jest ryzyko
związane z papierem wartościowym.
5
.
0
V
s
=
gdzie: s- odchylenie standardowe.
4. Kowariancja stóp zwrotu mierzy powiązanie stóp zwrotu dwóch akcji. Wskazuje ona
siłę powiązania i jego kierunek. Liczona jest według wzoru:
∑
=
−
−
=
n
i
i
i
i
ij
R
R
R
R
p
1
2
2
1
1
)
(
*
)
(
*
cov
gdzie: cov
ij
– kowariancja pomiędzy akcją pierwszą i drugą,
R
1
– oczekiwana stopa zwrotu akcji pierwszej,
R
2
- oczekiwana stopa zwrotu akcji drugiej,
R
1i
– możliwe stopy zwrotu akcji pierwszej,
R
2i
– możliwe stopy zwrotu akcji drugiej.
Wzór na kowariancję, przy zrealizowanych stopach zwrotu przyjmuje postać:
1
)
(
*
)
(
cov
1
2
2
1
1
−
−
−
=
∑
=
n
R
R
R
R
n
i
i
i
ij
5. Korelacja stóp zwrotu jest także miarą powiązania stóp zwrotu dwóch aktywów.
Obliczana jest na podstawie następującego wzoru:
2
1
1
2
2
1
1
*
)
(
*
)
(
*
s
s
R
R
R
R
p
n
i
i
i
i
ij
∑
=
−
−
=
ρ
natomiast przy zrealizowanych stopach zwrotu:
)
*
(
*
)
1
(
)
(
*
)
(
2
1
1
2
2
1
1
s
s
n
R
R
R
R
n
i
i
i
ij
−
−
−
=
∑
=
ρ
gdzie:
ρ
ij
– współczynnik korelacji dla stopy zwrotu akcji pierwszej i drugiej,
s
1
- odchylenie standardowe stopy zwrotu akcji pierwszej,
s
2
- odchylenie standardowe stopy zwrotu akcji drugiej.
Ćwiczenia nr 3
Finanse II
Robert Ślepaczuk
3
Współczynnik korelacji dwóch akcji określa siłę i kierunek powiązania stóp
zwrotu tych akcji. Właściwości tego współczynnika są następujące:
• Przyjmuje wartości z przedziału [-1,1].
• Wartość bezwzględna współczynnika korelacji wskazuje na siłę powiązania
stóp zwrotu akcji. Im wyższa jest wartość bezwzględna tego współczynnika,
tym powiązanie jest silniejsze. Wynika z tego, że najsilniej powiązane są
akcje, których współczynnik korelacji jest bliski 1 lub –1, a najsłabiej te,
których współczynnik korelacji jest bliski 0.
• Znak współczynnika wskazuje na kierunek powiązania stóp zwrotu akcji. Gdy
jest on dodatni, występuje tzw. korelacja dodatnia akcji. Oznacza to, że
wzrostowi (spadkowi) stopy zwrotu jednej akcji towarzyszy wzrost (spadek)
stopy zwrotu drugiej akcji. Gdy jest on ujemny, występuje tzw. ujemna
korelacja akcji i zachodzi sytuacja odwrotna.
Korelacja i kowariancja powiązane są następującą zależnością:
2
1
*
cov
s
s
ij
ij
=
ρ
II.
Portfel dwuskładnikowy.
Załóżmy, że portfel składa się z dwóch różnych akcji o następujących
charakterystykach:
R
1
, R
2
– oczekiwane stopy zwrotu,
V
1,
V
2
– wariancje,
s
1,
s
2
– odchylenia standardowe,
w
1
,w
2
– udziały wartościowe obu akcji w portfelu, pomiędzy którymi zachodzi
zależność: w
1
+ w
2
=1.
Poszczególne charakterystyki portfela możemy wyliczyć w następujący sposób:
R
p
= w
1
R
1
+ w
2
R
2
,
V
p
= w
1
2
s
1
2
+ w
2
2
s
2
2
+2 w
1
w
2
s
1
s
2
ρ
12
,
s
p
= V
p
0.5
gdzie: R
p
– stopa zwrotu z portfela,
V
p
– wariancja portfela,
s
p
– odchylenie standardowe portfela.
Z powyższych wzorów wynika, że ryzyko portfela dwóch akcji zależy od ryzyka
pojedynczych akcji wchodzących w skład portfela oraz od współczynnika korelacji
tych akcji. Ujemny współczynnik korelacji może nawet powodować zmniejszanie się
ryzyka portfela. Spójrzmy jak wygląda ryzyko portfela przy czterech różnych
wariantach współczynnika korelacji:
• ρ
12
= 1.
V
p
= w
1
2
s
1
2
+ w
2
2
s
2
2
+2 w
1
w
2
s
1
s
2
= (w
1
s
1
+ w
2
s
2
)
2
s
p
= w
1
s
1
+ w
2
s
2.
Ćwiczenia nr 3
Finanse II
Robert Ślepaczuk
4
W przypadku doskonałej korelacji dodatniej akcji ryzyko portfela jest ważoną
średnią ryzyka pojedynczych akcji wchodzących w skład portfela, przy czym
wagami są udziały w portfelu.
Spójrzmy jak wygląda graficzna prezentacja tego przykładu na wykresie.
Rozpatrujemy dwie akcje A i B, o oczekiwanych stopach zwrotu R
A
i R
B
oraz
ryzyku równym s
A
i s
B
.
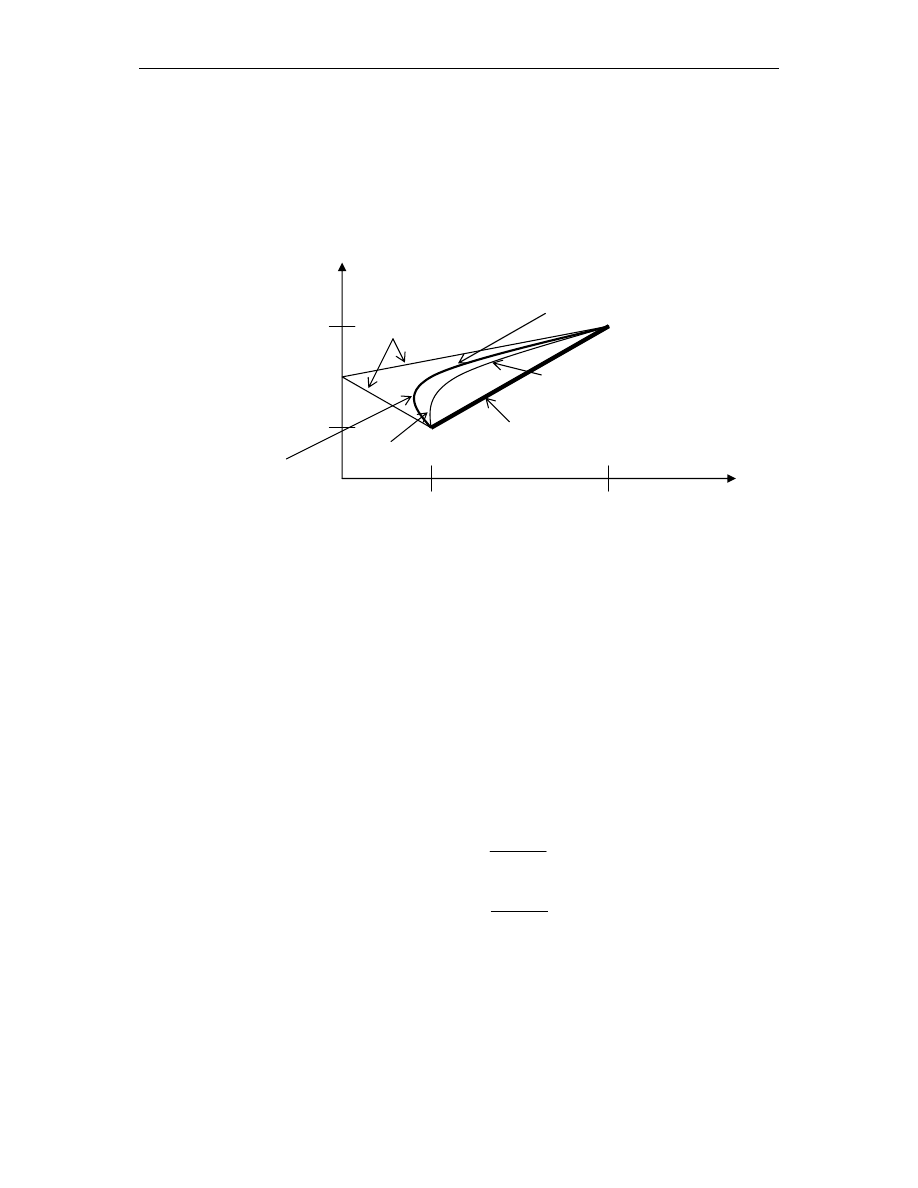
Rysunek nr 1.
Stopa zwrotu i odchylenie standardowe portfela
dwuskładnikowego w zależności od różnych współczynników korelacji.
Możliwe stopy zwrotu i odchylenia standardowe portfela reprezentowane są
przez odcinek AB. Widzimy, że wraz ze wzrostem stopy zwrotu rośnie ryzyko
reprezentowane przez odchylenie standardowe, w miarę jak zwiększamy w
portfelu udział akcji B i zmniejszamy A.
• ρ
12
= -1
V
p
= w
1
2
s
1
2
+ w
2
2
s
2
2
-2 w
1
w
2
s
1
s
2
= (w
1
s
1
- w
2
s
2
)
2
s
p
=
w
1
s
1
- w
2
s
2
Z
powyższych przekształceń wynika, że można znaleźć portfel o zerowym
ryzyku. Po odpowiednich przekształceniach otrzymujemy udziały akcji w portfelu
o zerowym ryzyku:
2
1
2
1
s
s
s
w
+
=
2
1
1
2
s
s
s
w
+
=
Powyższa sytuacja jest reprezentowana na rysunku przez odcinki AC i CB.
Widzimy, że wzdłuż odcinka AC rośnie stopa zwrotu portfela i maleje odchylenie
standardowe. W punkcie C portfel ma zerowe ryzyko i stopę zwrotu równą R
C
.
Następnie wzdłuż odcinka CB rośnie stopa zwrotu i rośnie odchylenie
standardowe, wraz ze wzrostem udziału akcji B w portfelu. Z rysunku nr 1 widać
ponadto, że inwestor nie powinien wybrać portfela, który znajduje się na odcinku
R
R
B
R
A
s
A
s
B
C
ρ
12
= 1
ρ
12
= 0.5
ρ
12
= 0
ρ
12
= -1
A
B
E
F
s
Ćwiczenia nr 3
Finanse II
Robert Ślepaczuk
5
AC. Dla każdego takiego portfela istnieje lepszy, znajdujący się na odcinku CB, tj.
dający wyższą stopę zwrotu przy tym samym odchyleniu standardowym.
• ρ
12
= 0.
W tym przypadku akcje nie są powiązane ze sobą, a ryzyko portfela kształtuje
się następująco:
V
p
= w
1
2
s
1
2
+ w
2
2
s
2
2
s
p
= (w
1
2
s
1
2
+ w
2
2
s
2
2
)
0.5
Minimalna
wartość ryzyka w tym przypadku wynosi:
5
.
0
2
2
2
1
2
1
)
(
*
s
s
s
s
+
i występuje dla portfela o udziałach:
2
2
2
1
2
2
1
s
s
s
w
+
=
2
2
2
1
2
1
2
s
s
s
w
+
=
Sytuacja powyższa jest reprezentowana przez krzywą AFB. Portfelem o
minimalnym ryzyku jest portfel F. Ponownie widzimy, że inwestor nie powinien
wybrać portfela, który znajduje się na krzywej AF. Dla każdego takiego portfela
istnieje lepszy, znajdujący się na łuku FB tj. dający wyższą stopę zwrotu przy tym
samym odchyleniu standardowym.
• ρ
12
= 0,5.
Jest to przypadek o wiele częściej spotykany w praktyce, niż poprzednie.
Miary ryzyka w tym przypadku są równe:
V
p
= w
1
2
s
1
2
+ w
2
2
s
2
2
+ w
1
w
2
s
1
s
2
S
p
= (w
1
2
s
1
2
+ w
2
2
s
2
2
+ w
1
w
2
s
1
s
2
)
0.5
W tym przypadku portfelem o minimalnym ryzyku jest portfel E.
• Przypadek ogólny określający skład portfela o minimalnym ryzyku. Zobaczmy
jakie muszą być udziały portfela o minimalnej wariancji. W tym celu do wzoru
na wariancję portfela wstawiamy w
2
= 1- w
1
, następnie obliczamy pochodną
powyższego wyrażenia po w
1
, przyrównujemy ją do zera i rozwiązujemy
otrzymując następujące udziały:
Ćwiczenia nr 3
Finanse II
Robert Ślepaczuk
6
12
2
1
2
2
2
1
12
2
1
2
2
1
*
*
*
2
*
*
ρ
ρ
s
s
s
s
s
s
s
w
−
+
−
=
12
2
1
2
2
2
1
12
2
1
2
1
2
*
*
*
2
*
*
ρ
ρ
s
s
s
s
s
s
s
w
−
+
−
=
III.
Portfel wieloskładnikowy.
Podobne charakterystyki jak dla portfela dwuskładnikowego możemy także wyznaczyć
dla portfela wieloskładnikowego:
∑
=
=
n
i
i
i
p
R
w
R
1
*
∑
∑ ∑
=
−
=
+
=
+
=
n
i
n
i
n
i
j
ij
j
i
j
i
i
i
p
s
s
w
w
s
w
V
1
1
1
1
2
2
*
*
*
*
2
*
ρ
5
.
0
p
p
V
s
=
oznaczenia takie same jak poprzednio.
W przypadku portfela wieloskładnikowego możemy także dywersyfikować ryzyko
poprzez dobór odpowiednich akcji do portfela. Spójrzmy jak wyglądają wszystkie możliwe
stopy zwrotu i odchylenia standardowe z portfela złożonego z czterech akcji (A, B, C, D).
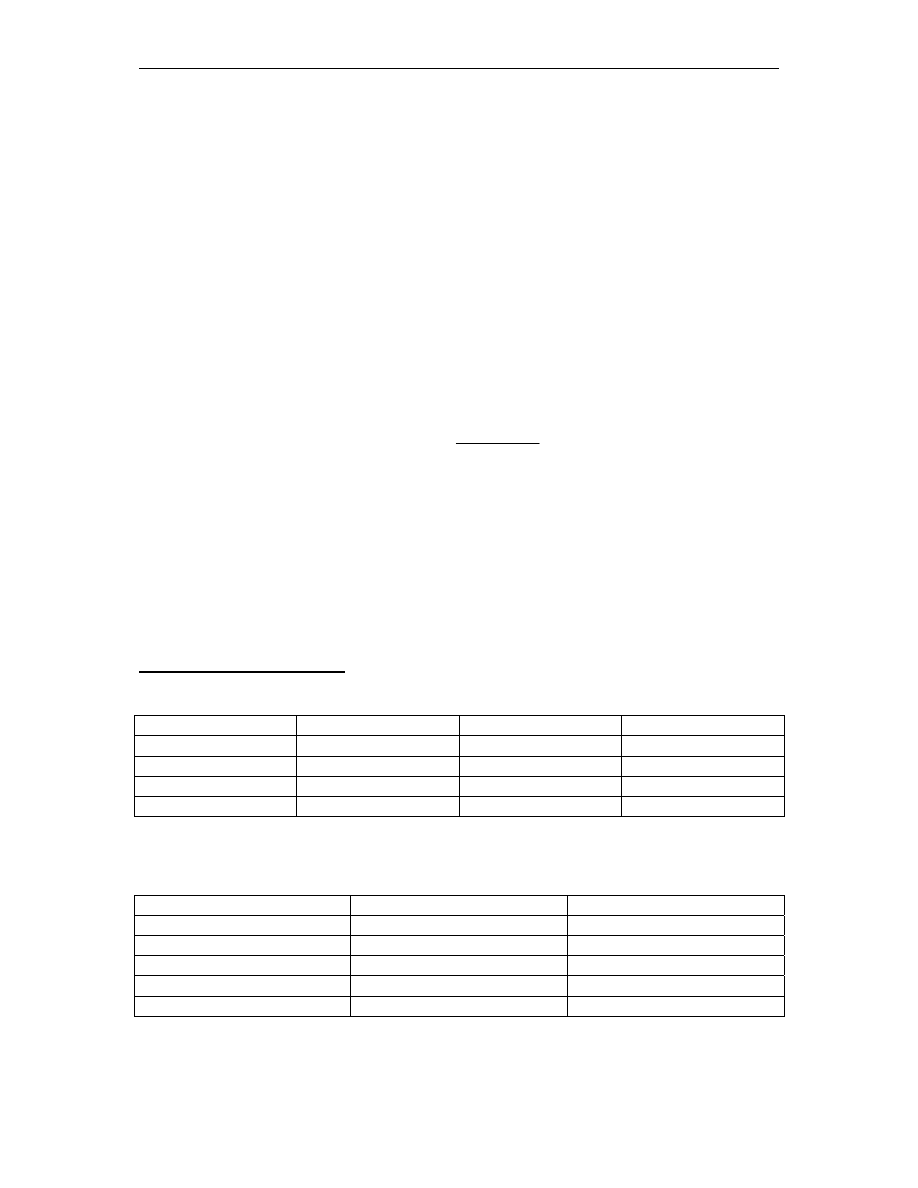
Rysunek nr 2.
Zbiór możliwości dla portfela złożonego z akcji A, B, C i D.
Figura ta nazywa się zbiorem możliwości. Najważniejszą część na tym rysunku
stanowi krzywa ED, która reprezentuje najlepsze portfele ponieważ zachodzi jedna z dwóch
sytuacji:
R
C
B
A
S
E
D
Ćwiczenia nr 3
Finanse II
Robert Ślepaczuk
7
• nie istnieje portfel, który przy tym samym poziomie ryzyka ma wyższą stopę
zwrotu,
• nie istnieje portfel, który przy tej samej wartości stopy zwrotu ma mniejsze
ryzyko.
Podzbiór zbioru możliwości określający te portfele, dla których nie można wskazać
portfeli lepszych, nazywa się granicą efektywną lub zbiorem efektywnym, natomiast portfele
leżące na tej granicy nazywają się portfelami efektywnymi.
Analiza portfelowa Markowitza przyjmuje następujące założenia:
• inwestorzy dążą do maksymalizacji użyteczności swojego bogactwa,
• wszyscy inwestorzy mają ten sam horyzont inwestycyjny,
• inwestorzy mają awersję do ryzyka,
• inwestorzy podejmują swoje decyzje na podstawie stopy zwrotu i odchylenia
standardowego dostępnych alternatyw inwestycyjnych,
• zakładamy brak podatków i kosztów transakcyjnych.
IV.
Portfel zawierający papiery wartościowe wolne od ryzyka.
Do analizy portfelowej możemy także włączyć papiery wartościowe wolne od ryzyka
w celu jeszcze większej redukcji ryzyka poprzez jego właściwą dywersyfikację.
Uwzględnienie papierów wartościowych wolnych od ryzyka w portfelu możemy
potraktować jako utworzenie portfela dwuskładnikowego, przy czym pierwszy składnik to
właśnie papiery wolne od ryzyka, a drugi to portfel efektywny zawierający ryzykowne akcje.
Stopa zwrotu takiego dwuskładnikowego portfela jest równa:
e
f
f
f
p
R
w
R
w
R
*
)
1
(
*
−
+
=
gdzie: R
e
– stopa zwrotu portfela efektywnego,
R
f
– stopa zwrotu papieru wartościowego wolnego od ryzyka,
w
f
– udział papieru wolnego od ryzyka.
Odchylenie standardowe nowo utworzonego portfela jest równe:
e
f
p
s
w
s
*
)
1
(
−
=
Zobaczmy jak wygląda stopa zwrotu i odchylenie standardowe portfela złożonego z
obligacji (papiery wolne od ryzyka F) i akcji (portfel efektywny E).
R
C
B
A
S
E
D
M
F
Ćwiczenia nr 3
Finanse II
Robert Ślepaczuk
8
Nasz portfel zawiera zarówno akcje (zawarte w portfelu efektywnym E), jak i papiery
wartościowe wolne od ryzyka, oznaczone punktem F. Wszystkie możliwe kombinacje
tego portfela reprezentuje prosta FE. Im większy udział lokat wolnych od ryzyka w
portfelu, tym bliżej punktu F znajduje się ten portfel. Widzimy jednak, że portfel
zawierający papiery wolne od ryzyka i portfel M pozwoli stworzyć najlepszą kombinację.
W celu znalezienia portfela M kreślimy półprostą wychodzącą z punktu F i styczną do
zbioru możliwości w najwyższym punkcie. Portfel M nazywa się portfelem rynkowym.
W efekcie otrzymujemy zestaw portfeli leżących na odcinku FM. Teraz odcinek ten
jest zbiorem efektywnym. Zauważmy, że zbiór efektywny wyznaczony dla portfela
zawierającego tylko akcje przestaje nim być po włączeniu do portfela papierów wolnych
od ryzyka. Dla każdego portfela należącego do starego zbioru efektywnego można
znaleźć lepszy portfel w nowym zbiorze efektywnym.
Po
włączeniu do portfela papierów wolnych od ryzyka, zbiór efektywny jest
odcinkiem leżącym na prostej o następującym równaniu:
S
S
R
R
R
R
M
f
M
f
*
)
)
(
−
+
=
gdzie: R – stopa zwrotu,
S – odchylenie standardowe,
R
M
– stopa zwrotu portfela rynkowego,
S
M
- odchylenie standardowe portfela rynkowego.
Prosta ta nazywa się linią rynku kapitałowego (Capital Market Line) i zawiera
portfele efektywne powstałe po uwzględnieniu papierów ryzykownych i wolnych od
ryzyka.
Zadania do ćwiczeń nr 4
Zadanie nr 1.
Oblicz kowariancję stóp zwrotu dla akcji L i M dla poniższych danych:
stan natury
prawdopodobieństwo
stopa zwrotu akcji L stopa zwrotu akcji M
1 0.2
-5%
6%
2 0.4 10 -2
3 0.3 -4 8
4 0.1 7 -9
Następnie proszę obliczyć korelację stóp zwrotu.
Zadanie nr 2.
Akcje A i B miały następujące stopy zwrotu przez ostatnie 5 lat.
Wyznacz współczynnik korelacji i kowariancję dla tych dwóch akcji.
Rok
Stopa zwrotu A %
Stopa zwrotu B %
1991 8 10
1992 -9 -12
1993 14 18
1994 16 20
1995 20 14
Zadanie nr 3.
Mary Clifford posiada portfel złożony z czterech akcji o następującej
wartości rynkowej i stopach zwrotu równych:
Ćwiczenia nr 3
Finanse II
Robert Ślepaczuk
9
Akcja Wartość rynkowa $
Stopa zwrotu %
X 10
000 10
Y 20
000 14
Z 30
000 16
M 40
000 15
Suma = 100 000
Proszę obliczyć stopę zwrotu z portfela.
Zadanie nr 4.
(a) Oblicz stopę zwrotu i odchylenie standardowe dla portfela
złożonego z 20% akcji A i 80% akcji B o następujących charakterystykach:
R
A
=10%, R
B
= 20%, s
A
= 15%, s
B
= 30%,
ρ
AB
= 0,5.
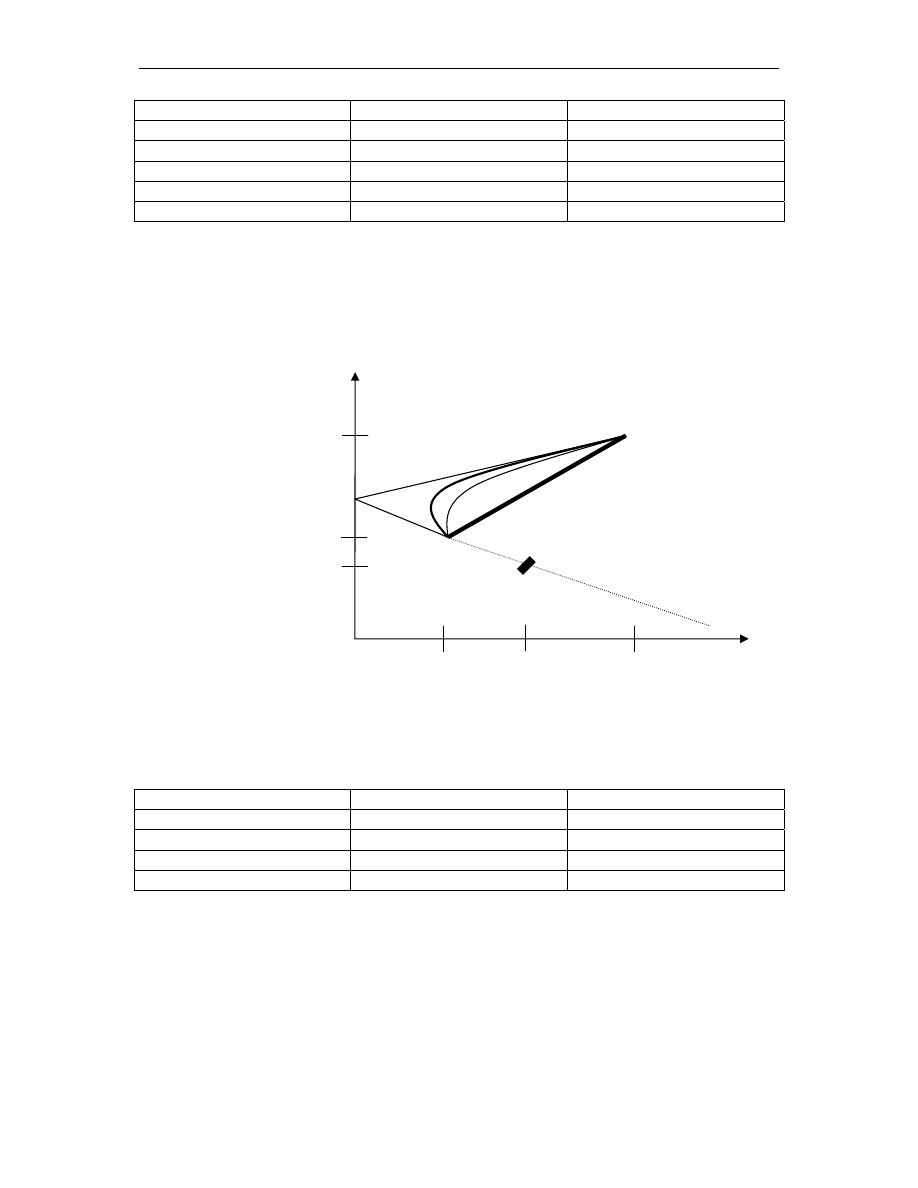
(b) Zakładając, że możliwa jest krótka sprzedaż znajdź udział akcji A i B w portfelu D
przedstawionym na rysunku:
(c) Wyznacz ryzyko portfela złożonego z akcji A i B dla którego współczynnik korelacji jest
równy 0.5, a stopa zwrotu 5%.
Zadanie nr 5.
Dwa aktywa J i K mają następujące charakterystyki:
s
J
=25%, s
K
= 20%, R
J
= 18%, R
K
=14%,
ρ
JK
= -0.2. Wyznacz odchylenie i stopę zwrotu dla
następujących portfeli:
portfel Udział J %
Udział K %
(a) 90 10
(b) 50 50
(c) 40 60
(d) 20 80
Zadanie nr 6.
Oblicz ryzyko i stopę zwrotu dla portfela złożonego z akcji X, Y i Z o
równych udziałach ( 1/3, 1/3 i 1/3) jeśli: R
X
=15%,
R
Y
= 17%,
R
Z
= 20%, s
X
=18%, s
Y
= 20%,
s
Z
=25%,
ρ
XY
= 0.5,
ρ
YZ
= 0.2,
ρ
XZ
= -0.5
.
Zadanie nr 7.
Burr i Poe Corporation mają następujące stopy zwrotu i odchylenia
standardowe: R
B
= 18%, s
B
= 22%, R
P
= 22%, s
P
= 30%,
ρ
BP
= 0.4.Ryzyko portfela złożonego
w 50% z akcji każdej spółki jest równe 21,86%. Wyznacz współczynnik korelacji dla którego
ryzyko portfela spadnie o 25%. Jaka będzie stopa zwrotu takiego portfela?
R
R
B
R
A
s
A
s
B
C
A
B
s
D
5%
Ćwiczenia nr 3
Finanse II
Robert Ślepaczuk
10
Zadanie nr 8.
Firmy W i D mają następujące charakterystyki:
S
W
=30%, s
D
= 40%, R
W
= 20%, R
D
=25%,
ρ
WD
= -1. Wyznacz odchylenie standardowe
portfela o minimalnym ryzyku. Wyznacz odchylenie standardowe portfela o minimalnym
ryzyku jeśli
ρ
WD
= 0.5.
Zadanie nr 9. Załóżmy, że odchylenie standardowe portfela rynkowego jest równe 20%, jego
stopa zwrotu 14%, a aktywów wolnych od ryzyka 9%. Jaką stopę zwrotu otrzyma inwestor z
portfela złożonego w 50% z obu aktywów? Jakie będzie ryzyko takiego portfela?