MODELE RYNKU KAPITAŁOWEGO

 

FINANSE II

 

 

 

1

Model jednowskaźnikowy Sharpe’a. 

Model rynku kapitałowego - CAPM (Capital Asset Pricing Model – Model 

wyceny aktywów kapitałowych). 

Model APT (Arbitrage Pricing Theory – Teoria aritrażu cenowego). 

  

Model jednowskaźnikowy Sharpe’a. 

 
 
Model jednowskaźnkowy stanowi uproszczenie klasycznej teorii portfela 

przedstawionej na poprzednich zajęciach. Opiera się on na założeniu,  że kształtowanie się 
stóp zwrotu akcji jest zdeterminowane czynnikiem, który odzwierciedla zmiany na rynku 
kapitałowym. Na wielu giełdach zaobserwowano, że stopy zwrotu z konkretnej akcji są 
powiązane ze stopą zwrotu indeksu giełdy, zwanego wskaźnikiem rynku i 
odzwierciedlającego ogólną sytuację na giełdzie. 

 
I. 

Linia charakterystyczna papieru wartościowego (Security Characteristic Line). 

 
Zależność stopy zwrotu akcji od stopy zwrotu indeksu giełdy (będącej tu 

odpowiednikiem portfela rynkowego) określa następujące równanie regresji liniowej: 

 

i

M

i

i

i

e

R

R

+

+

=

*

β

α

    (1) 

 

gdzie: R

i

 – stopa zwrotu i-tej akcji; R

M

 – stopa zwrotu indeksu rynku; 

α

i

,

β

i

 – 

współczynniki równania; e

i

 – składnik losowy równania. 

W powyższym równaniu regresji zmienną objaśnianą jest stopa zwrotu akcji, a 

zmienną objaśniającą stopa zwrotu wskaźnika rynku. Równanie regresji po jego oszacowaniu 
jest nazywane linią charakterystyczną papieru wartościowego (security characteristic line). 
Najważniejszy w nim jest współczynnik 

β

i

 zwany współczynnikiem beta. Wskazuje on, o ile 

procent w przybliżeniu wzrośnie stopa zwrotu akcji, gdy stopa zwrotu indeksu giełdy 
wzrośnie o 1 procent. 

Zaznaczając na wykresie punkty oznaczające stopę zwrotu z danej akcji w danym 

okresie i stopę zwrotu z indeksu rynku w tym samym okresie możemy wyznaczyć 
hipotetyczną prostą, będącą linią regresji, która będzie linią charakterystyczną akcji (rys. 1). 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
Rys. nr 1. 

Linia charakterystyczna akcji. 

R

i

 

R

M

 

                                                        * 
                                              *      * 
                                    *         * 
                     *              * 
           *                * 
*               * 
             * 
    * 

MODELE RYNKU KAPITAŁOWEGO

 

FINANSE II

 

 

 

2

Do oszacowania linii charakterystycznej akcji stosuje się metodę najmniejszych 

kwadratów (MNK), która polega na minimalizacji następującego wyrażenia: 

 

2

1

)

*

(

Mt

i

i

it

n

t

R

R

β

α

−

−

∑

=

 

   (2) 

 

gdzie: R

it

 – stopa zwrotu i-tej akcji w t-tym okresie; R

Mt

 – stopa zwrotu wskaźnika 

rynku w t-tym okresie. 

Wyrażenie powyższe oznacza sumę kwadratów różnic między wartościami stóp 

zwrotu akcji, a hipotetycznymi wartościami obliczonymi na podstawie linii regresji. Po 
rozwiązaniu powyższego zadania minimalizacji otrzymujemy następujące wzory: 

 

∑

∑

=

=

−

−

−

=

n

t

M

Mt

n

t

M

Mt

i

it

i

R

R

R

R

R

R

1

2

1

)

(

)

(

*

)

(

β

 

   (3) 

 
 

M

i

i

i

R

R

*

β

α

−

=

 

    (4) 

 
 

gdzie: n- liczba okresów z których pochodzą informacje;  

i

R

 - średnia arytmetyczna 

stóp zwrotu z i-tej akcji; 

M

R  - średnia arytmetyczna stóp zwrotu wskaźnika rynku; 

Na podstawie oszacowanej linii  charakterystycznej akcji można wyznaczyć również 

wariancję wskaźnika rynku i składnika losowego: 

 

1

)

(

2

1

2

−

−

=

∑

=

n

R

R

s

M

Mt

n

t

M

     (5) 

 
 

1

)

*

(

2

1

2

−

−

−

=

∑

=

n

R

R

se

M

i

i

it

n

t

i

β

α

 

   (6) 

 
 

gdzie: 

2

M

s

- wariancja stopy zwrotu indeksu rynku; 

2

i

se

- wariancja składnika 

losowego. 

Model jednowskaźnikowy jest uproszczeniem klasycznej teorii portfela . Uproszczenie 

to spowodowane jest faktem, że do zastosowania teorii portfela niezbędna jest znajomość 
współczynników korelacji stóp zwrotu wszystkich par akcji, co może być pracochłonne. W 
modelu jednowskaźnikowym zachodzą następujące zależności: 

 

M

i

i

i

R

R

*

β

α

+

=

 

    (7) 

 
 

MODELE RYNKU KAPITAŁOWEGO

 

FINANSE II

 

 

 

3

2

2

2

2

*

i

M

i

i

se

s

s

+

=

β

 

    (8) 

 
 

j

i

M

j

i

ij

s

s

s

*

*

*

2

β

β

ρ

=

 

    (9) 

 

Musimy jednak pamiętać, że wzór wyznaczający s

i

2

 jest tylko wzorem przybliżonym 

wyznaczającym ryzyko całkowite akcji, które dokładnie zostanie omówione na kolejnych 
stronach. 

Zaznaczmy jeszcze, że współczynnik beta wiąże ryzyko całkowite akcji z ryzykiem 

portfela rynkowego w następujący sposób: 

 

M

iM

i

i

s

s

ρ

β

*

=

  

 

 

 

 

(10) 

 
 

gdzie: 

ρ

im

 – współczynnik korelacji stopy zwrotu akcji i stopy zwrotu portfela 

rynkowego. 
 
 

II. 

Współczynnik beta (beta coefficient). 

 

Współczynnik beta akcji wskazuje, w jakim stopniu stopa zwrotu akcji reaguje na 

zmiany stopy zwrotu wskaźnika rynku, czyli na zmiany zachodzące na rynku. Może on 
przyjmować różne wartości: 

•  β

i

 = 0 – stopa zwrotu i-tej akcji nie reaguje na zmiany na rynku; wobec tego papier 

wartościowy wolny jest od ryzyka rynku. 

•  0 < β

i

 < 1 – stopa zwrotu i-tej akcji w małym stopniu reaguje na zmiany 

zachodzące na rynku; akcja taka jest nazywana defensywną. 

•  β

i

 = 1 – stopa zwrotu i-tego papieru wartościowego zmienia się w takim samym 

stopniu jak stopa zwrotu rynku; w szczególności, portfel rynkowy ma 
współczynnik beta równy 1. 

•  β

i

 > 1 – stopa zwrotu i-tej akcji w większym stopniu reaguje na zmiany 

zachodzące na rynku; taka akcja jest nazywana agresywną. 

•  β

i

 < 0 – oznacza, że stopa zwrotu reaguje na zmiany odwrotnie niż rynek; jest to 

stosunkowo rzadki przypadek, choć bardzo pożądany, jeśli spodziewany jest 
spadek stóp zwrotu większości akcji na rynku. 

  

III. 

Ryzyko rynkowe, a ryzyko specyficzne akcji. 

 
Ryzyko całkowite akcji (s

i

2

)

 jest sumą dwóch składników. Pierwszy składnik jest to 

ryzyko systematyczne

, inaczej zwane rynkowym. Zależy od ryzyka wskaźnika rynku oraz od 

współczynnika beta, który również świadczy o ryzyku rynku, gdyż odzwierciedla powiązanie 
stopy zwrotu akcji ze stopą zwrotu portfela rynkowego. Z kolei drugi składnik, będący 
wariancją składnika losowego, odzwierciedla ryzyko specyficzne związane z daną akcją. 
Duży udział ryzyka systematycznego w ogólnym ryzyku akcji wskazuje, że ogólne ryzyko 
związane z sytuacją na rynku ma duży wpływ na ryzyko akcji.  

MODELE RYNKU KAPITAŁOWEGO

 

FINANSE II

 

 

 

4

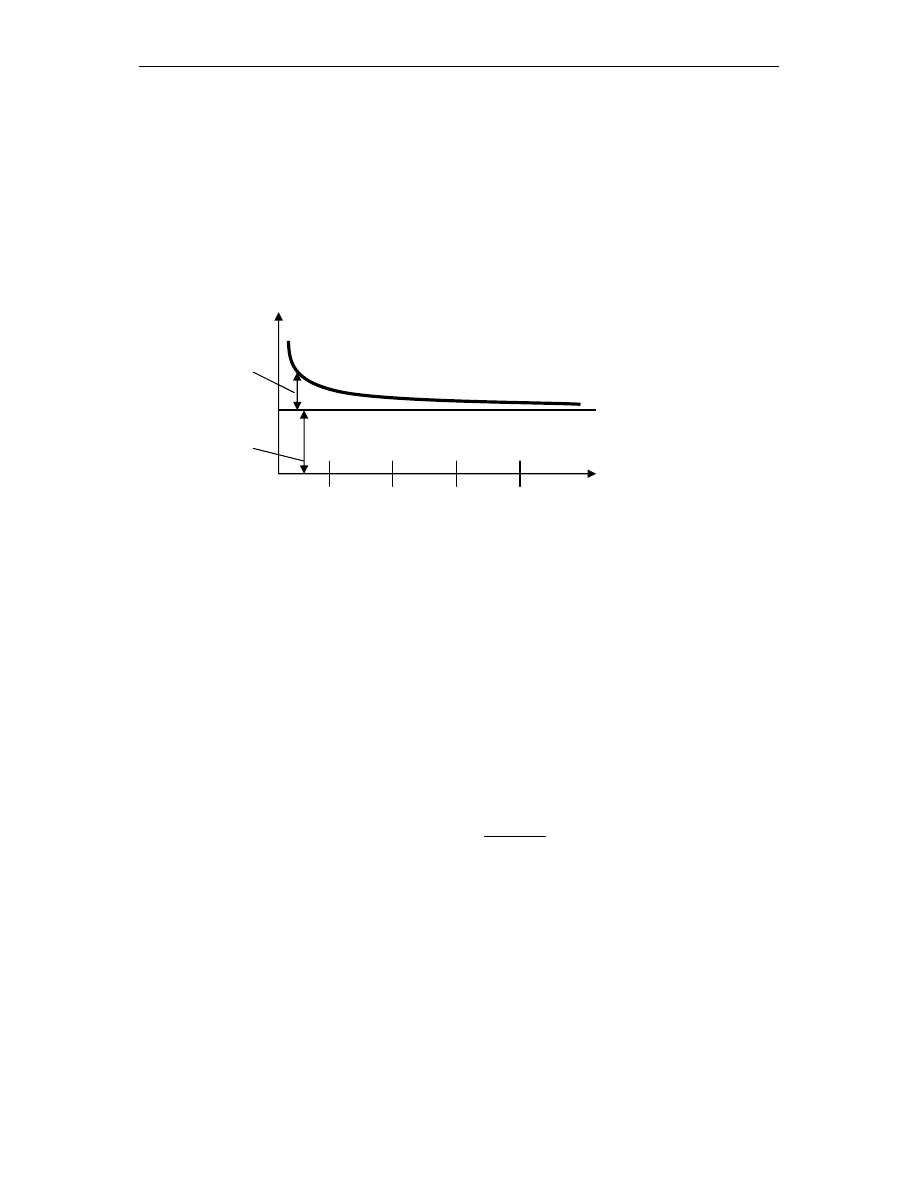
Pojęcie ryzyka systematycznego i ryzyka specyficznego ma bezpośredni związek z 

dywersyfikacją portfela. Jak wiadomo, dywersyfikacja portfela może prowadzić do znacznej 
redukcji ryzyka tego portfela. Jednak ryzyko to nie może być w całości wyeliminowane. 
Umiejętna dywersyfikacja portfela prowadzi do wyeliminowania ryzyka specyficznego akcji 
wchodzących w skład portfela. Jednak pozostaje jeszcze ryzyko rynku, które występuje w 
mniejszym lub większym stopniu we wszystkich akcjach i którego nie można wyeliminować. 
Wraz ze zwiększaniem liczby akcji w portfelu zmniejszamy udział ryzyka specyficznego w 
ryzyku całkowitym, co ilustruje rysunek 2. 

 
 
 
 
 
 
 
 
 
 
 
 
 
Rys. nr 2. 

Ryzyko całkowite, a rozmiar portfela. 

 
Współczynnik beta może być odniesiony nie tylko do pojedynczej akcji, ale również 

do portfela akcji, gdzie stosuje się następujący wzór: 

 

∑

=

=

n

i

i

i

p

w

1

*

β

β

 

 

 

 

 

(11) 

 

Model rynku kapitałowego- CAPM (Capital Asset Pricing Model). 

 
Najpopularniejszym modelem rynku kapitałowego jest CAPM. Twórcami tego 

modelu byli: William Sharpe, John Lintner i Jan Mossin. Podstawą tego modelu są dwie 
zależności:  

•  linia rynku kapitałowego (Capital Market Line) 
 

p

M

f

M

f

p

s

s

R

R

R

R

*

)

(

−

+

=

 

   (12) 

 

•   linia rynku papierów wartościowych (Security Market Line) 

 

)

(

*

f

M

i

f

i

R

R

R

R

−

+

=

β

 

   (13) 

 

gdzie: 

f

M

R

R

−

- premia za ryzyko. 

 Podstawową różnicą pomiędzy obu liniami jest to, że CML dotyczy tylko portfeli 
efektywnych, a SML dotyczy wszystkich portfeli, w tym również pojedynczych papierów 
wartościowych, na rynku będącym w równowadze. 
 

σ

i 

n -liczba losowo wybranych 
akcji w portfelu

 

Ryzyko specyficzne 
(niesystematyczne)

 

Ryzyko systematyczne 
(rynkowe)

 

MODELE RYNKU KAPITAŁOWEGO

 

FINANSE II

 

 

 

5

I. 

Założenia modelu CAPM. 

 
Model CAPM oparty jest na następujących założeniach: 
 

•  decyzje zakupu portfela podejmowane przez inwestorów dotyczą jednego okresu. 

•  użyteczność inwestora jest całkowicie zdeterminowana oczekiwaną stopą zwrotu i 

ryzykiem posiadanego portfela. 

•  istnieje papier wartościowy wolny od ryzyka, który może być nabywany przez 

inwestorów. Jego stopa zwrotu jest to stopa zwrotu wolna od ryzyka. Istnieje 
nieograniczona możliwość udzielania bądź zaciągania kredytu przy stopie wolnej 
od ryzyka 

•  ceny równowagi istnieją tylko wtedy, gdy nie ma transakcji spekulacyjnych. Jest  

to możliwe wtedy, gdy wszyscy uczestnicy rynku dysponują tymi samymi 
informacjami – mają oni te same oczekiwania co do przyszłych wartości stóp 
zwrotu i ryzyka papierów wartościowych. 

•  występuje krótka sprzedaż akcji 

•  koszty transakcji są zerowe. 
•  nie są płacone podatki z tytułu posiadania papierów wartościowych. 

•  papiery wartościowe mogą być dzielone w dowolny sposób. 

•  transakcje pojedynczego inwestora nie mają wpływu na cenę papieru 

wartościowego. 

 

II. 

Charakterystyka modelu. 

 
W modelu CAPM kluczowe znaczenie posiada portfel rynkowy. Jest to portfel, który 

składa się z wszystkich akcji i innych papierów wartościowych o dodatnim ryzyku 
występujących na rynku, przy czym udziały poszczególnych akcji w tym portfelu są równe 
udziałom tych akcji w rynku.  

Pierwszą zależnością w CAPM jest CML, dotycząca wyłącznie portfeli efektywnych. 

Z wzoru na CML wynika, że stopa zwrotu portfela efektywnego jest sumą dwóch składników: 

•  Stopy zwrotu wolnej od ryzyka, którą można interpretować jako „cenę czasu”, 

gdyż jest to wymagana przez inwestora stopa zwrotu rekompensująca rezygnację z 
bieżącej konsumpcji. 

•  Iloczynu 

p

M

f

M

s

s

R

R

*

)

(

−

, gdzie 

)

(

M

f

M

s

R

R

−

 jest to premia za ryzyko, czyli 

dodatkowy procent stopy zwrotu, jaki można uzyskać za zwiększenie ryzyka o 
jednostkę. Jest to zatem cena jednostki ryzyka. Z kolei 

S

p

 jest to ryzyko portfela 

efektywnego. Wynika z tego, że linia rynku kapitałowego może być 
zinterpretowana następująco: 

 

Stopa zwrotu portfela efektywnego = cena czasu + cena jednostki ryzyka * wielkość 

ryzyka portfela efektywnego 

 

Z kolei linia rynku papierów wartościowych (SML) dotyczy dowolnych portfeli, a 

zatem również pojedynczych papierów wartościowych. Oczekiwana stopa zwrotu takiego 
portfela jest także sumą dwóch składników: 

•  Stopy zwrotu wolnej od ryzyka, a więc „ceny czasu”, 

•  Drugi składnik jest to cena ryzyka. Jest to bowiem iloczyn wielkości ryzyka 

systematycznego danego portfela, mierzonego współczynnikiem beta, oraz premii 

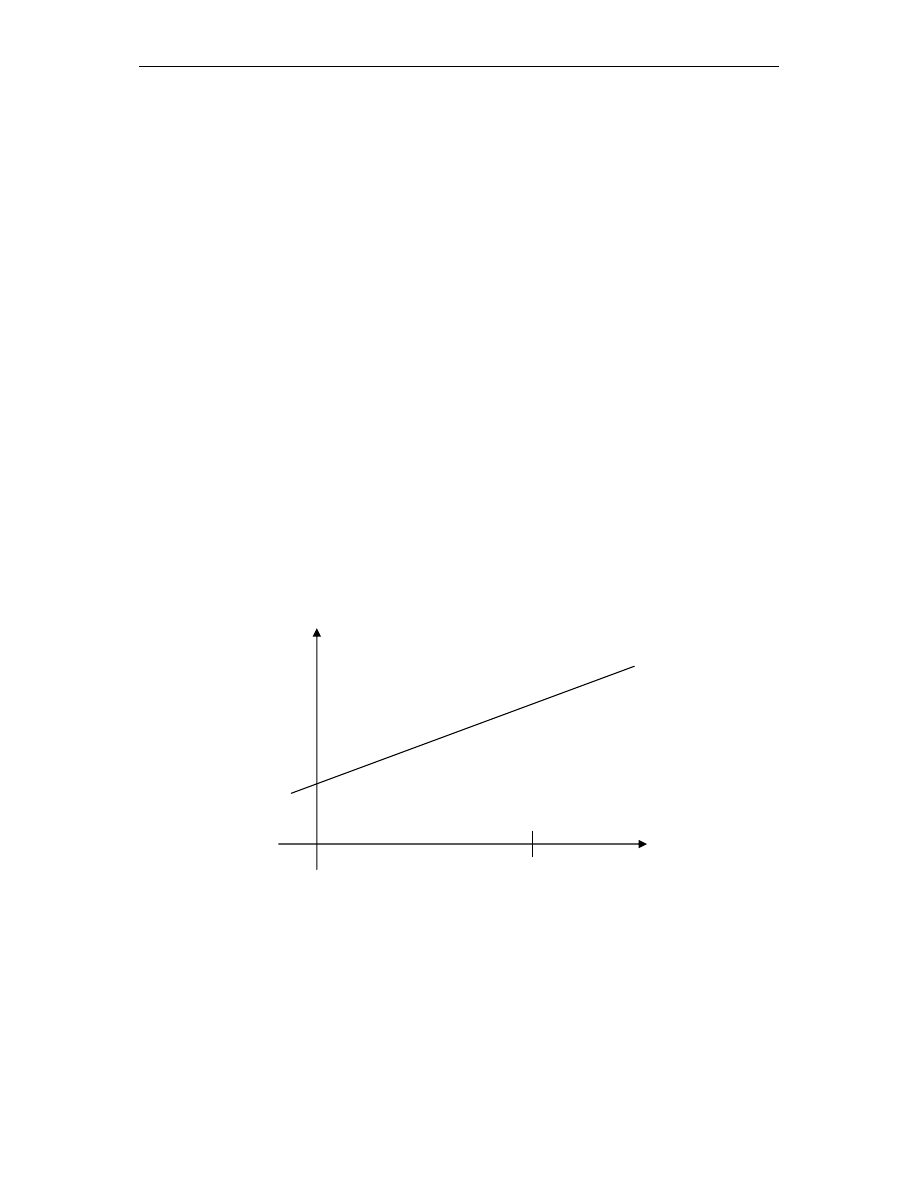
MODELE RYNKU KAPITAŁOWEGO

 

FINANSE II

 

 

 

6

za ryzyko, będącej różnicą między stopą zwrotu portfela rynkowego i stopą zwrotu 
wolną od ryzyka. 

Spójrzmy na kilka wersji SML w zależności od danej wartości współczynnika beta: 
•  β =1, wówczas R=R

M

 (czyli na SML leży również portfel rynkowy); 

•  β=0, wówczas R = R

f

 (czyli na SML leży portfel zawierający instrumenty wolne 

od ryzyka); 

•  β > 1 (portfel agresywny), wówczas R > R

M

; 

•  0 < β < 1 (portfel defensywny), wówczas R

f

 < R < R

M

; 

•  β < 0 , wówczas R < R

f

; 

 
Na podstawie SML można wyznaczyć współczynnik alfa (nie należy go mylić z 

współczynnikiem alfa linii charakterystycznej akcji). Jest on określony następująco: 

 

))

(

*

(

f

M

f

R

R

R

R

−

+

−

=

β

α

    (14) 

 

gdzie: R – oczekiwana stopa zwrotu portfela ( np. oszacowana za pomocą analizy 

fundamentalnej). 

Współczynnik alfa jest nadwyżką oczekiwanej stopy zwrotu nad oczekiwaną stopa 

zwrotu na rynku znajdującym się w równowadze. Jeśli akcja leży na SML to współczynnik 
alfa równy jest zero. Możemy go także wyznaczyć dla portfeli akcji: 

 

∑

=

=

n

i

i

i

p

w

1

*

α

α

 

 

 

 

 

(15) 

 

Interpretację graficzną SML przedstawiam na poniższym rysunku (rys. 3). 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
Rysunek nr 3.  

Linia rynku papierów wartościowych. 

 
Na rysunku na osi odciętych zaznaczone są współczynniki beta portfeli, a na osi 

rzędnych oczekiwane stopy zwrotu portfeli. Zaznaczone tam są różne portfele i linia SML. Na 
SML znajduje się sześć portfeli. Portfel F zawiera tylko instrumenty wolne od ryzyka. Portfel 
M jest to portfel rynkowy. Portfel A jest to portfel defensywny, a portfel D jest to portfel 
agresywny. Oba portfele leżą na SML, z czego wynika że rynki dla tych portfeli są w 
równowadze, a same portfele są dobrze wycenione. Pojęcie „dobrze wyceniony” odnosi się 

R 

* 
M

F 

0 

1

β 

* 
A 

* 
D 

* 
C 

* 
C’

* 
B 

* 
B’

MODELE RYNKU KAPITAŁOWEGO

 

FINANSE II

 

 

 

7

do SML (czyli do CAPM) i oznacza, że oczekiwana stopa zwrotu tych portfeli jest taka sama 
jak większości portfeli o tym samym współczynniku beta.  

Na rysunku zaznaczone są również dwa portfele, które nie leżą na SML. Portfel B leży 

powyżej SML. Współczynnik alfa tego portfela jest dodatni. Oznacza to, że odpowiada mu 
wyższa oczekiwana stopa zwrotu niż portfelowi B’, który ma ten sam współczynnik beta, ale 
leży na SML (czyli jest dobrze wyceniony). Portfel B jest niedoszacowany, lub inaczej 
niedowartościowany. Staje się on dla inwestorów atrakcyjny, co powoduje wzrost popytu na 
portfel B i wzrost jego ceny, a w związku z tym spadek jego oczekiwanej stopy zwrotu. Te 
działania doprowadzą do równowagi i portfel B stanie się portfelem B’, czyli znajdzie się na 
linii SML. 

Z kolei portfel C leży poniżej SML. Współczynnik alfa tego portfela jest ujemny. 

Oznacza to, że odpowiada mu niższa oczekiwana stopa zwrotu niż portfelowi C’, który ma 
ten sam współczynnik beta, ale leży na SML (czyli jest dobrze wyceniony). Portfel C jest 
przeszacowany, lub inaczej przewartościowany. Staje się on dla inwestora nieatrakcyjny, więc 
będzie on się starał dokonać jego sprzedaży (również krótkiej). Spowoduje to zwiększoną 
podaż portfela C, spadek jego ceny, a w związku z tym wzrost jego oczekiwanej stopy 
zwrotu. Te działania doprowadzą do równowagi i portfel C stanie się portfelem C’, czyli 
znajdzie się na linii SML. 

W rzeczywistości oczywiście nigdy nie jest tak, że wszystkie portfele leżą na SML. 

Równowaga jest procesem dynamicznym i większość portfeli jest niedoszacowana lub 
przeszacowana.  

Zobaczmy na koniec następującą zależność. Po podstawieniu do linii SML wzoru 

M

iM

i

i

s

s

ρ

β

*

=

, otrzymujemy w odniesieniu do portfela leżącego na SML:  

 

iM

i

M

f

M

f

i

s

s

R

R

R

R

ρ

*

*

−

+

=

    (16) 

 

Widzimy, że jeśli 

ρ

im

 = 1, to powyższe równanie staje się równaniem  CML. Oznacza 

to, że portfel efektywny w równowadze i portfel rynkowy mają współczynnik korelacji stóp 
zwrotu równy 1. Dla tych dwóch portfeli zmiany stóp zwrotu są proporcjonalne. 
 

Model APT (Arbitrage Pricing Theory – Teoria aritrażu cenowego). 
 
I. 

Prawo jednej ceny. 

 
Teoria arbitrażu cenowego opiera się na prawie jednej ceny, które mówi, że dwa 

identyczne dobra są wyceniane po tej samej cenie. Jeżeli są sprzedawane po różnych cenach, 
wtedy ktokolwiek możemy dokonać arbitrażu, kupując jedno dobro po cenie niższej i 
sprzedając to dobro po cenie wyższej i osiągając w ten sposób dochód bez ryzyka. Arbitraż 
dotyczy głównie rynków finansowych i jest tam dokonywany niemal nieustannie. 

Wniosek z funkcjonowania prawa jednej ceny jest następujący: dwa instrumenty 

finansowe o równym ryzyku muszą mieć te same stopy zwrotu. 

 
II. 

Model APT 

 

Oprócz założenia prawa jednej ceny APT zakłada również jednorodność oczekiwań. 

Zaliczany jest do tzw. modeli czynnikowych, w których zakłada się,  że stopy zwrotu akcji 
generowane są według wzoru: 

MODELE RYNKU KAPITAŁOWEGO

 

FINANSE II

 

 

 

8

 

R

i

 = a

i

 + b

i1

F

1

 + b

i2

F

2

 + ... + b

im

F

m

 + e

i, 

  (17) 

 

gdzie: F

j

 – j-ty czynnik; a

i

 – wyraz wolny; b

ij

 – współczynnik wrażliwości i-tej akcji 

względem j-tego czynnika; e

i

 – składnik losowy równania. 

Z powyższego równania wynika, że stopa zwrotu akcji zależy od m różnego rodzaju 

czynników. W równaniu tym ważną rolę odgrywają współczynniki wrażliwości. Ich 
interpretacja jest podobna do interpretacji współczynnika beta. Otóż współczynnik 
wrażliwości wskazuje, jak zareaguje stopa zwrotu akcji na jednostkową zmianę czynnika, gdy 
pozostałe czynniki nie zmienią się. Współczynniki wrażliwości wyznacza się również dla 
portfela: 

∑

=

=

n

i

ij

i

pj

b

w

b

1

*

 

 

 

 

 

(18) 

 

 gdzie 

: 

b

pj

 – współczynnik wrażliwości portfela względem j-tego czynnika. 

 Na 

rynku 

kapitałowym jest wiele akcji i portfeli. Istnieje  możliwość utworzenia 

portfeli o dowolnej wrażliwości na poszczególne rodzaje czynników. Jest wiele możliwych 
sposobów skonstruowania portfela o jednostkowej wrażliwości na dany czynnik, jak również 
portfela niewrażliwego na żaden z czynników. Portfel, którego wrażliwość na j-ty czynnik 
jest jednostkowa i który jest niewrażliwy na pozostałe czynniki, wyznacza się rozwiązując 
równania: 

∑

=

=

n

i

ij

i

b

w

1

1

*

  

 

 

 

 

(19) 

∑

=

=

n

i

ik

i

b

w

1

0

*

, 

k = 1,...,m 

k ≠ 

j 

   (20) 

 

 

Natomiast portfel, który jest niewrażliwy na wszystkie czynniki wyznacza się 

rozwiązując równanie: 

 

∑

=

=

n

i

ij

i

b

w

1

0

*

, 

j = 1,...,m 

 

 

 

(21) 

 
 

Portfele, które są wrażliwe na jeden czynnik, przy czym współczynnik wrażliwości 

jest jednostkowy, mają  tę samą oczekiwaną stopę zwrotu (prawo jednej ceny i istnienie 
arbitrażu cenowego). Podobnie portfele, które są niewrażliwe na żaden czynnik, powinny 
mieć oczekiwaną stopę zwrotu równą stopie wolnej od ryzyka. 
 Model 

APT 

zakłada,  że na rynku jest wiele akcji i innych papierów wartościowych. 

Podstawą tego modelu jest tzw. portfel arbitrażowy, który spełnia następujące równania: 
 

∑

=

=

n

i

i

x

1

0  

 

 

 

 

 

(22) 

∑

=

=

n

i

ij

i

b

x

1

0

*

, 

 j 

= 

1,...,m 

   (23) 

∑

=

=

n

i

i

i

e

x

1

0

*

   

 

 

 

 

(24) 

 

Równanie pierwsze oznacza, że przy tworzeniu portfela arbitrażowego nie ponosi się 

żadnych nakładów. Równanie środkowe oznacza, że portfel jest niewrażliwy na czynniki 

MODELE RYNKU KAPITAŁOWEGO

 

FINANSE II

 

 

 

9

ryzyka (wyrażenie x

i

b

ij

 jest to zmiana dochodu części portfela zainwestowanej w i-tą akcję, 

która to zmiana jest wywołana zmianą j-tego czynnika). Równanie ostatnie jest to zależność 
przybliżona, która oznacza, że portfel nie ma ryzyka specyficznego (odzwierciedlanego przez 
składnik losowy). 

Na podstawie powyższych równań dochodzimy do właściwego modelu APT, 

określającego stopę zwrotu portfela: 

 

m

m

b

b

b

R

λ

λ

λ

λ

+

+

+

+

=

...

2

2

1

1

0

 

   (25) 

 
gdzie: b

1

,...,b

m

 -  współczynniki wrażliwości portfela względem czynników ryzyka, 

λ

1

,..., 

λ

m

 

– współczynniki równania.  
 Można również dowieść, że współczynniki 

λ

i

 modelu są równe: 

 

λ

0

= R

f

, 

λ

j

 = R

pj

 - R

f

     (j=1,...,m)  

 

 

 

(25) 

 
 gdzie: 

R

f

 – stopa zwrotu wolna od ryzyka; R

pj

 – oczekiwana stopa zwrotu portfela, 

który jest niewrażliwy na wszystkie czynniki oprócz j-tego, a którego wrażliwość na j-ty 
czynnik jest jednostkowa. 
 Zobaczmy 

jeszcze 

interpretację graficzną (rys. 4) modelu jednoczynikowego APT, 

danego wzorem: 

 

 

 

R = R

f

 + b

λ   

 

 

 

 

(26) 

 
 
 
 
 
 
 
 
 
 
 
 
 
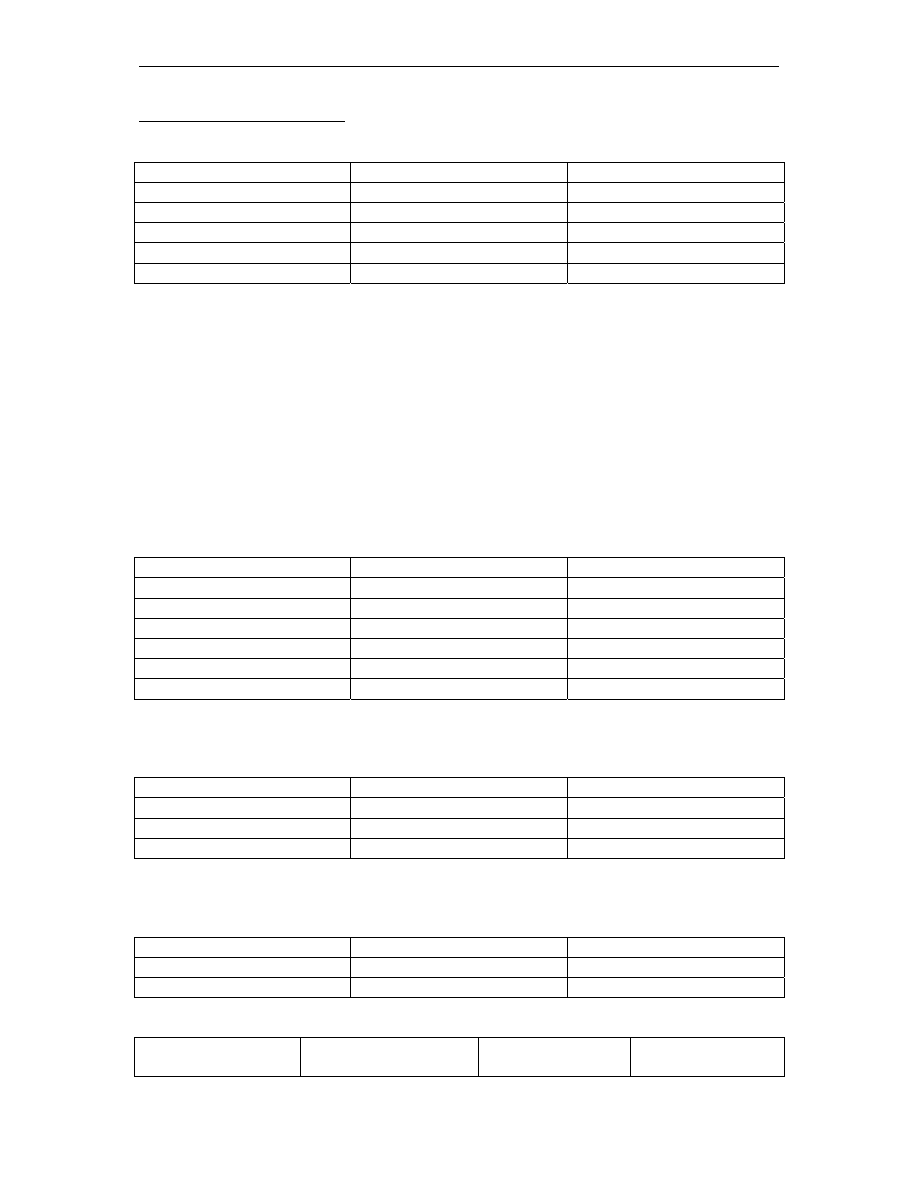
Rysunek nr 4.  

Linia arbitrażu cenowego. 

 
 

Na rys. tym przedstawiona jest tzw. linia arbitrażu cenowego. Jest to zależność 

oczekiwanej stopy zwrotu portfela od współczynnika wrażliwości na czynnik ryzyka. Wyraz 
wolny tej linii odpowiada stopie wolnej od ryzyka.. Z kolei współczynnik kierunkowy, czyli 
wartość 

λ, jest to premia za ryzyko, Inaczej jest to nadwyżka oczekiwanej stopy zwrotu 

portfela nad stopą wolną od ryzyka, przy czym portfel ten ma jednostkową wrażliwość na 
czynnik ryzyka. Jeśli rynek jest w równowadze, portfele są dobrze wycenione i znajdują się 
na linii arbitrażu cenowego. Na rys. 4 przedstawione są również przykłady portfeli 
niedoszacowanych (O) i przeszacowanych (P). Ich interpretacja i proces dochodzenia do 
równowagi jest identyczny jak w modelu CAPM. 
 Ostatnią kwestią przy modelu APT jest odpowiedź na pytanie jakie mogą być czynniki 
ryzyka w nim występujące. Mogą to być np.: zmiany PKB, zmiany stopy bezrobocia, zmiany 
w różnicy stóp procentowych pomiędzy krajami, zmiany stopy inflacji, zmiany indeksu 
produkcji przemysłowej itp. 
 

R 

* 
P 

* 
O 

R

f 

b 

MODELE RYNKU KAPITAŁOWEGO

 

FINANSE II

 

 

 

10

Zadania do ćwiczeń nr 5 

 
Zadanie nr 1.

  

Stopy zwrotu Jarvis Corporation i rynkowe są następujące: 

Rok 

Stopa zwrotu Jarvis 

Stopa zwrotu rynkowa 

1991 -5%  -6% 
1992 14  16 
1993 10  12 
1994 12  14 
1995 17  20 

Oblicz współczynnik beta dla firmy Jarvis. Jaki procent ryzyka całkowitego stanowi ryzyko 
systematyczne? 
 
Zadanie nr 2.  

Załóżmy,  że R

f

 = 8%, R

M

 = 14% i beta = 1.25 dla i-tego papieru 

wartościowego. Oblicz oczekiwaną stopę zwrotu dla papieru wartościowego i. Jak zmieni się 
oczekiwana stopa zwrotu, jeśli R

M

 wzrośnie do 16%? Jak zmieni się ta stopa jeśli 

współczynnik beta zmniejszy się do 0.75? 
 
Zadanie nr 3.  

Dywidenda na akcję dla BMC Corporation wzrastała 6% w ciągu roku 

przez ostatnie 6 lat. Wyznacz wartość akcji BMC, jeśli sytuacja ta będzie trwała w 
przyszłości. Zakładamy, że D

0

 = 3.5, R

f

 =9%, R

M

 = 16% i 

β

BMC

 = 1.3. 

 
Zadanie nr 4.  

Jefferson Investment Company zarządza funduszem złożonym z pięciu 

akcji o następującej wartości rynkowej i współczynnikach beta równych. 

Akcje Wartość rynkowa 

Współczynnik beta 

Zell $100 

000  1.1 

Car 50 

000 1.2 

Arms 75 

000  0.75 

Dole 125 

000  0.8 

Ord 150 

000  1.4 

 Suma: 

500 

000  

Oblicz współczynnik beta portfela. 
 
Zadanie nr 5.  

Zakładamy,  że R

f

 = 9%, R

M

 = 15%. Oczekiwane stopy zwrotu i 

współczynniki beta są dane poniżej: 

Akcje Oczekiwana 

stopa 

zwrotu 

Współczynnik beta 

Hall 14%  1.2 
Izzo 15% 0.75 

Jenn 20%  1.5 

Które akcje są przewartościowane, a które niedowartościowane? 
 
Zadanie nr 6.  

Proszę wyznaczyć linię APT dla dwóch poniższych portfeli 

znajdujących się w równowadze: 

Portfel Oczekiwana 

stopa 

zwrotu 

Współczynnik wrażliwości b 

A 15% 1.5 

B 10% 0.5 

 
Zadanie nr 7.  

Istnieją trzy portfele będące w równowadze: 

Portfel Oczekiwana 

stopa 

zwrotu 

b

1

 

b

2

 

MODELE RYNKU KAPITAŁOWEGO

 

FINANSE II

 

 

 

11

X 16 1 

0.8 

Y 12 

0.6 

0.5 

Z 18 

0.9 

1.1 

Wyznaczyć linię APT. Na rynku dostępny jest papier U nie będący w równowadze, którego 
R=17%, b

U1

 = 0.8, b

U2

 = 0.65. Jaki zysk możemy osiągnąć przez stworzenie strategii 

arbitrażowej z akcji X i Y? Proszę opisać poszczególne transakcje.