1

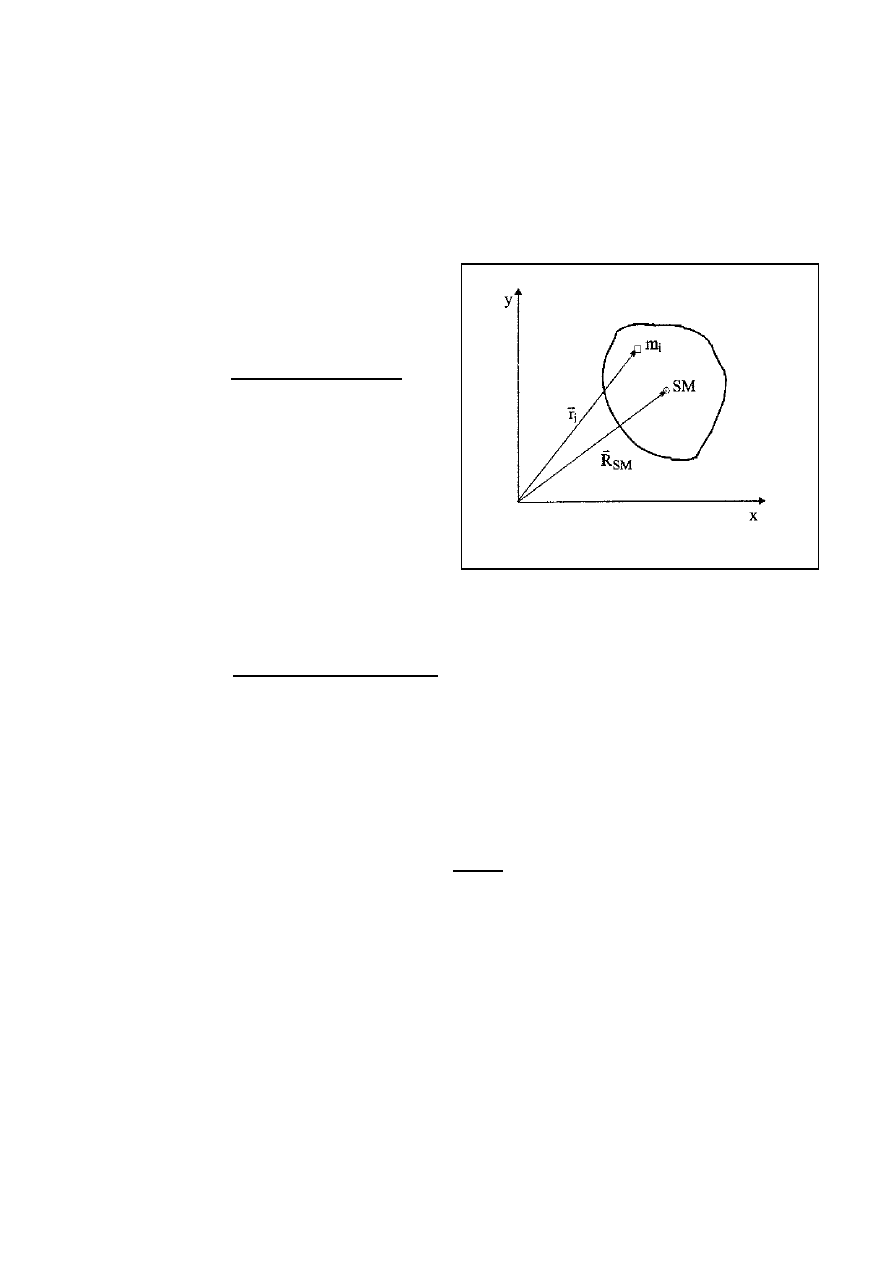
ŚRODEK MASY

•

Położenie środka masy

∑

∑

=

=

=

n

i

i

n

i

i

i

m

r

m

R

1

1

dla dwóch mas

2

1

2

2

1

1

m

m

m

r

r

m

R

+

+

=

•

Prędkość środka masy

dt

R

d

V

=

•

Pęd środka masy

∑

=

=

=

n

i

i

p

V

M

P

1

:

2

RUCH ŚRODKA MASY

∑

=

i

z

i

F

dt

P

d

)

(

Środek masy porusza się w taki sposób, jak

gdyby w nim była skupiona masa całego układu i
do niego była przyłożona suma wszystkich sił
działających na układ.

0

)

(

=

∑

z

i

F

⇒

.

st

n

co

P

=

ZASADA ZACHOWANIA PĘDU

Jeżeli suma sił zewnętrznych działających na układ
jest równa zeru to pęd układu nie ulega zmianie.

Ś

rodek masy porusza się wówczas ruchem

jednostajnym prostoliniowym.

3

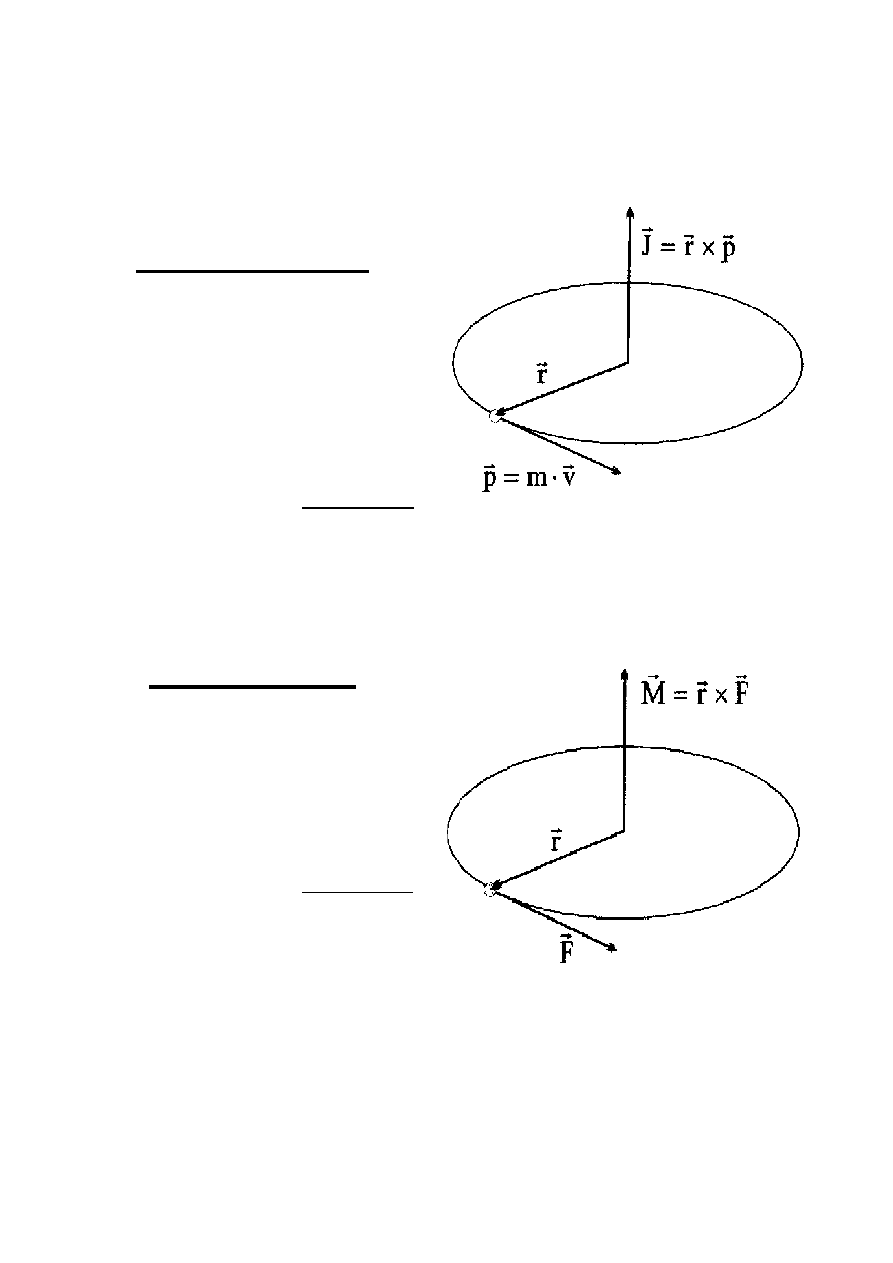
MOMENT PĘDU i MOMENT SIŁY

Moment pędu

J

r

p

= ×

[ ]

J

kg m

s

=

⋅

2

Moment siły

F

r

M

×

=

2

2

s

m

kg

]

M

[

⋅

=

Względem punktu

O

O

O

4

ZMIANA MOMENTU PĘDU UKŁADU

∑

=

=

n

i

z

i

M

dt

J

d

1

)

(

Wszystkie momenty sił muszą być liczone
względem tego samego punktu !

ZASADA ZACHOWANIA

MOMENTU PĘDU

Jeżeli całkowity moment sił zewnętrznych
działających na układ jest równy zeru to moment
pędu układu nie ulega zmianie.

Dotyczy to układów, w których spełniona jest III zasada
dynamiki Newtona

5

ZASADA ZACHOWANIA ENERGII

Istnieje pewna wielkość, zwana energią, nie
ulegająca

zmianie

podczas

różnorodnych

przemian, które zachodzą w przyrodzie.

Energia może występować w różnych postaciach. Mamy
energie grawitacyjną, kinetyczną, sprężystą, cieplną,
elektryczną, chemiczną, promienistą, jądrową i energię
masy.

POLE SIŁ

Polem nazywa się obszar przestrzeni, w którym
każdemu

punktowi

P

jest

jednoznacznie

przyporządkowana pewna wielkość A(P).

Pole sił - obszar przestrzeni, w którym każdemu
punktowi przyporządkowany jest pewien wektor
określający, jaka siła działałaby na dane ciało gdyby
umieszczono je w tym punkcie.

Stacjonarne pole sił nie zmienia się w czasie

6

PRACA

Praca elementarna dW wykonana przez siłę

F

przy przesunięciu ciała o element przyrostu drogi

s

d

na tyle mały, że

F

= const.

( )

dW

F r

dr

=

⋅

[1J =1Nm]

Całkowita praca

i

n

i

i

i

n

r

AB

r

r

F

W

i

∆

⋅

=

∑

=

∞

→

→

∆

1

0

)

(

lim

∫

=

B

A

AB

r

d

r

F

W

)

(

Praca w ruchu jednowymiarowym (1D)

dW = F(x) dx

∫

=

B

A

AB

dx

x

F

W

)

(

7

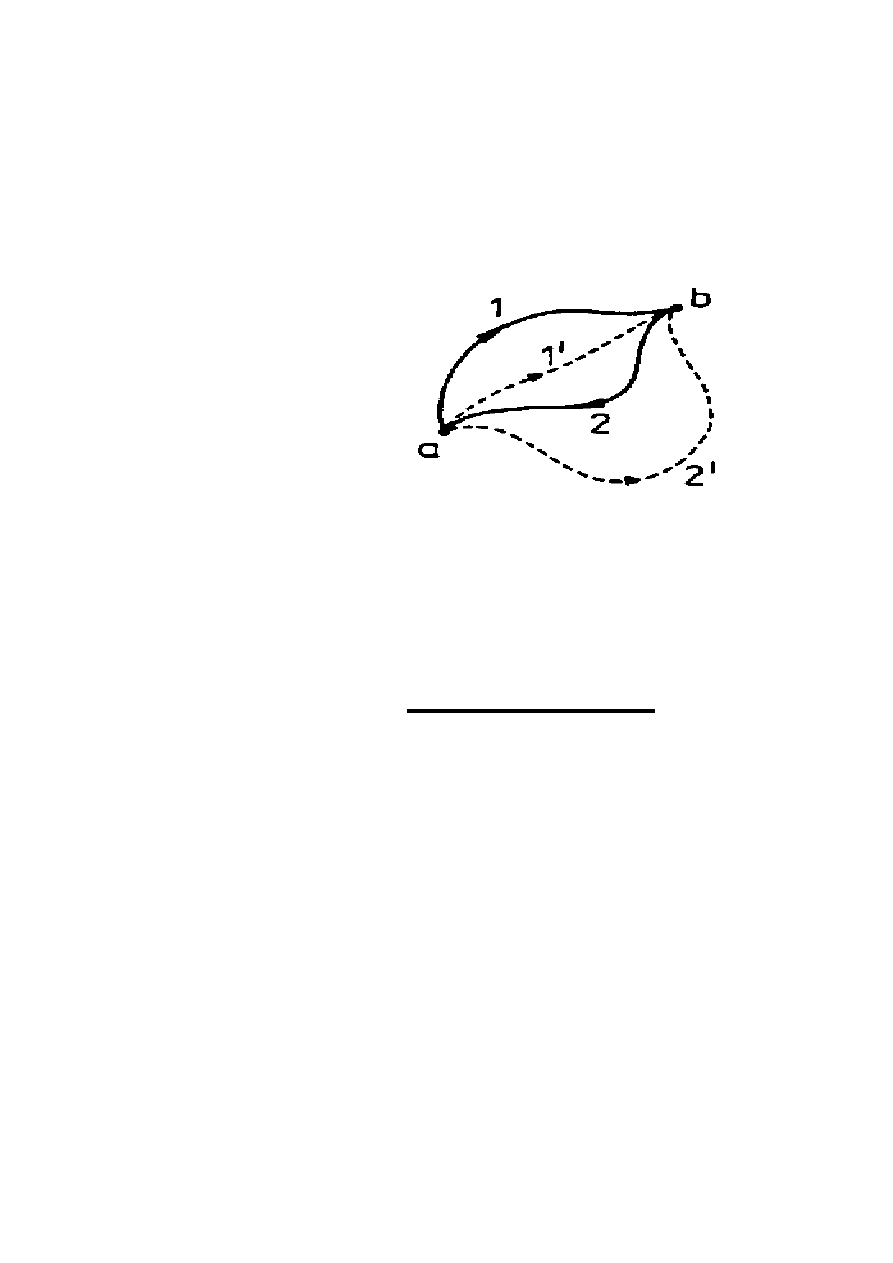
POLE ZACHOWAWCZE

W ogólnym przypadku praca wykonana przy
przesunięciu z punktu A do B zależy od drogi

W

s1

≠

W

s2

≠

W

s3

Siły, albo pola sił mające tę własność, że praca
zależy tylko od położenia punktu początkowego i
końcowego, a nie zależy od drogi po jakiej została
wykonana nazywamy zachowawczymi.

W zachowawczym polu sił praca po drodze
zamkniętej jest równa zeru.

Przykładem sił zachowawczych są siły grawitacyjne
lub elektrostatyczne.

( )

0

F r ds

=

∫

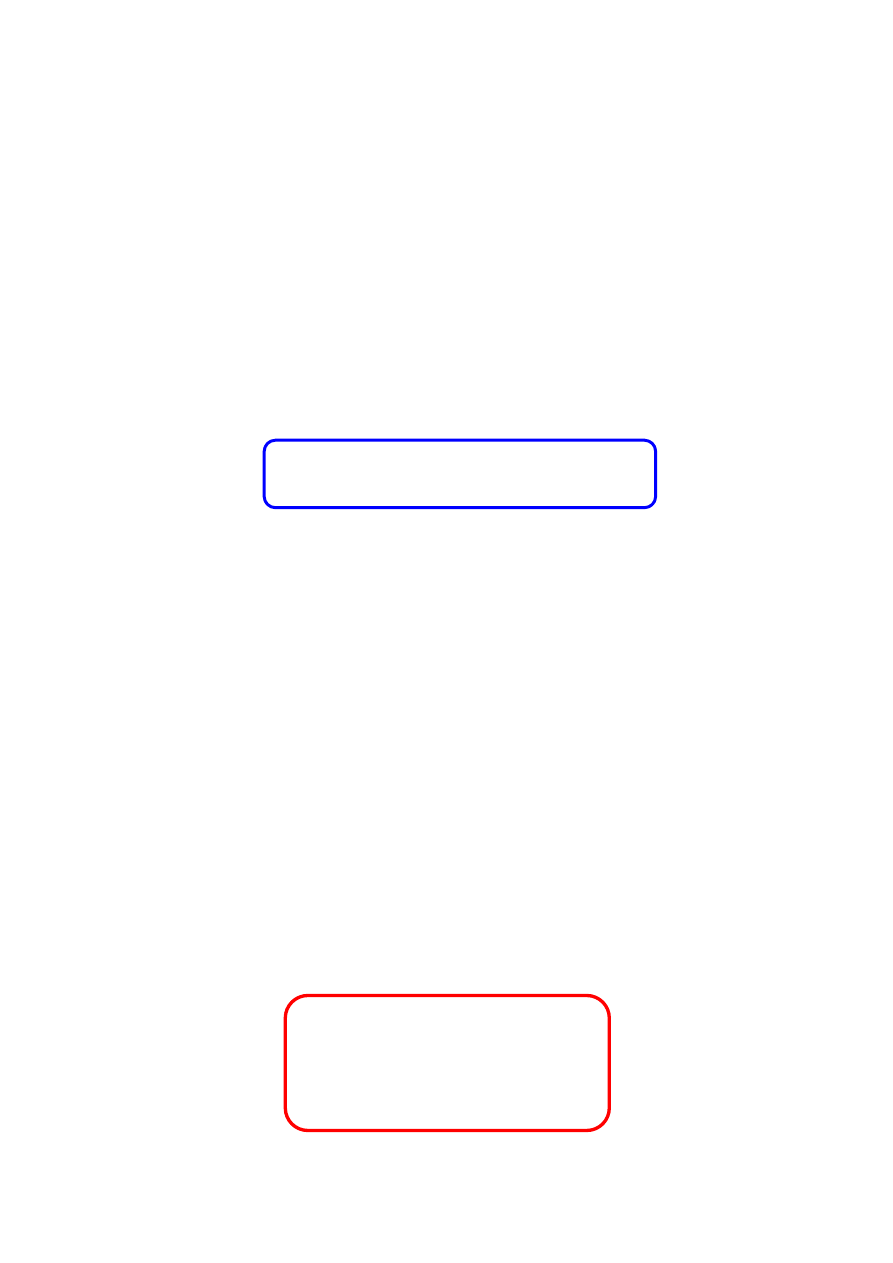
8

ENERGIA POTENCJALNA

Ponieważ praca jest wielkością skalarną, zależną tylko
od wartości całki w punktach A i B

( )

B

AB

A

W

F r ds

=

∫

to możemy określić funkcję skalarną V taką, że

( )

( )

AB

A

B

W

V r

V r

=

−

( )

B

A

B

A

V

V

F r ds

−

=

∫

gdzie

)

(

,

)

(

B

B

A

A

r

V

V

r

V

V

≡

≡

( )

V r

jest określone z dokładnością do stałej:

V’ = V + A

spełnia równanie

'( )

'( )

A

B

AB

V r

V r

W

−

=

Ż

eby V było określone jednoznacznie trzeba ustalić

jego wartość w którymś punkcie, np. V(

∞

) = 0

∫

∞

=

A

A

s

d

r

F

V

)

(

9

GRADIENT *

Dla punktów bardzo blisko położonych

W

AB

= dW

czyli

dW =

−

dV

dV

Fds

= −

podstawiając

z

y

x

F

z

F

y

F

x

F

ˆ

ˆ

ˆ

+

+

=

dz

z

dy

y

dx

x

s

d

ˆ

ˆ

ˆ

+

+

=

otrzymuje się

dV = - ( F

x

dx + F

y

dy + F

z

dz )

równanie to dzielimy stronami przez

dx

x

z

y

x

F

dx

dz

F

dx

dy

F

dx

dx

F

dx

dV

−

=













+

+

−

=

ponieważ

dy/dx = 0

oraz

dz/dx = 0

x

dV

F

dx

= −

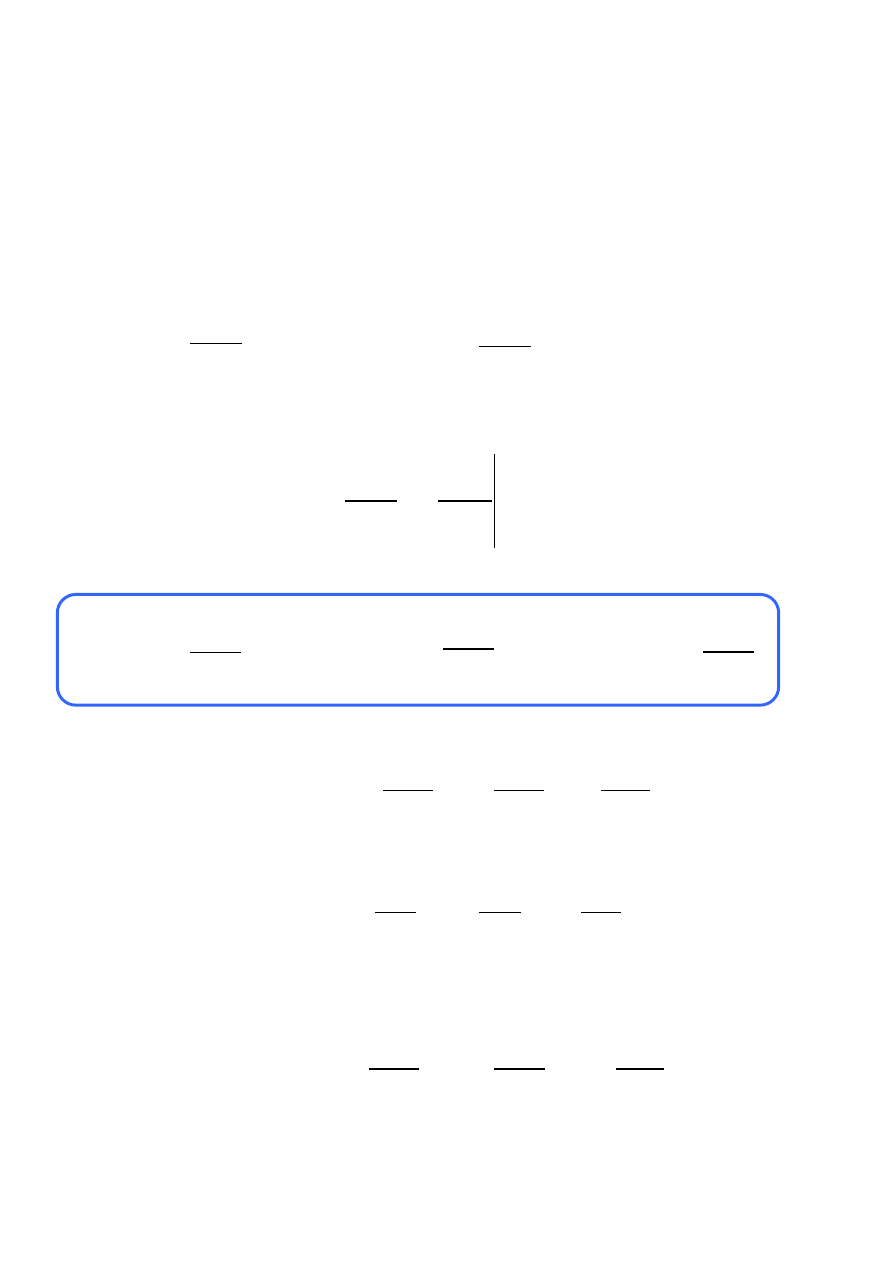
10

GRADIENT *

dzieląc równanie

dV = - ( F

x

dx + F

y

dy + F

z

dz )

przez dy i przez dz otrzymuje się

y

dV

F

dy

= −

z

dV

F

dz

= −

a wprowadzając pochodne cząstkowe

.

.

const

z

const

y

dx

dV

x

V

=

=

≡

∂

∂

x

V

F

x

∂

= −

∂

,

y

V

F

y

∂

= −

∂

,

z

V

F

z

∂

= −

∂













∂

∂

+

∂

∂

+

∂

∂

−

=

→

z

V

z

y

V

y

x

V

x

F

ˆ

ˆ

ˆ

V

z

z

y

y

x

x

F













∂

∂

+

∂

∂

+

∂

∂

−

=

→

ˆ

ˆ

ˆ

operator gradient

ˆ

ˆ

ˆ

x

y

z

x

y

z





∂

∂

∂

∇ ≡

+

+





∂

∂

∂





11

SIŁA POTENCJALNA

Znając rozkład energii potencjalnej można znaleźć
siłę działającą na ciało umieszczone w danym
punkcie

( )

( )

F r

V r

= −∇

)

(r

V

energia potencjalna

( )

F r

siła potencjalna

- operator gradient

∇

ˆ

ˆ

ˆ

grad

x

y

z

x

y

z





∂

∂

∂

∇ ≡

=

+

+





∂

∂

∂





,

,

pochodne cząstkowe

V

V

V

x

y

z

∂

∂

∂

∂

∂

∂

.

.

const

z

const

y

dx

dV

x

V

=

=

≡

∂

∂

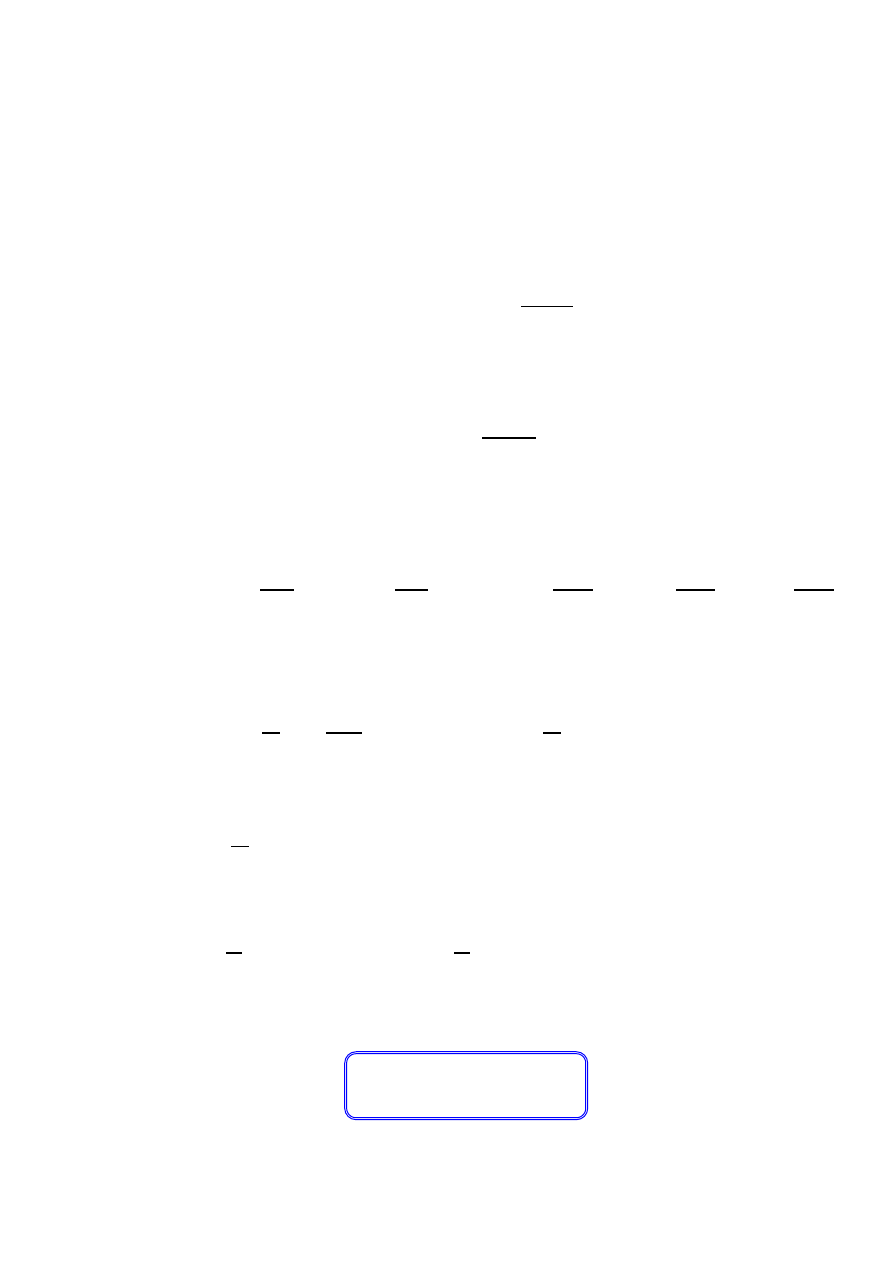
12

ENERGIA KINETYCZNA *

Praca wykonana nad układem ciał przy przejściu od stanu A
do stanu B

B

i

AB

i

i

i

A

dv

W

m

v dt

dt

=

∑ ∫

dla

const.

i

i

i

i

dv

m

F

m

dt

=

=

i

i

ds

v dt

=

dt

x

d

x

dt

x

d

x

x

dt

x

d

x

x

dt

d

x

dt

d

2

)

(

)

(

2

=

+

=

⋅

=

2

2

1

1

2

2

(

)

(

)

B

B

AB

i

i

i

i

i

i

A

A

d

W

m

v

dt

m d v

dt

=

=

∑

∑

∫

∫

(

)

2

2

1

2

( )

( )

AB

i

i

i

i

W

m v B

v A

=

−

∑

∑

∑

−

=

i

i

i

i

i

i

AB

A

v

m

B

v

m

W

2

2

1

2

2

1

)

(

)

(

W

AB

= T

B

- T

A

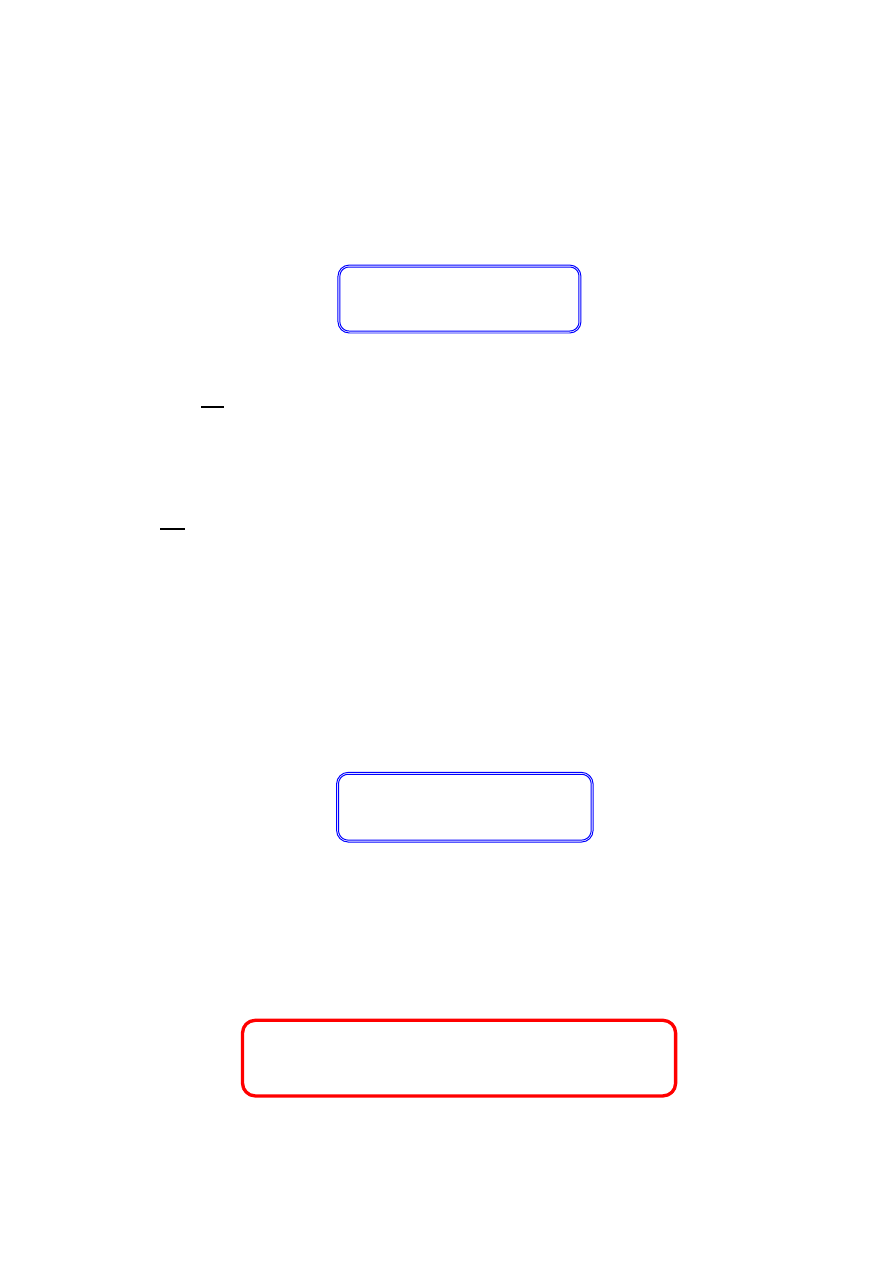
13

ENERGIA KINETYCZNA

1. Praca wykonana nad układem ciał przy przejściu od stanu
A do stanu B

W

AB

= T

B

- T

A

∑

=

i

i

i

A

A

v

m

T

)

(

2

1

2

energia kinetyczna układu w stanie A

2

2

1

i

i

i

v

m

T

=

energia kinetyczna i-tego punktu

2.

Praca wykonana nad układem ciał przy przejściu od stanu
A do stanu B równa się różnicy energii potencjalnych

W

AB

= V

A

- V

B

T

B

- T

A

= V

A

- V

B

T

A

+ V

A

= T

B

+ V

B

= E

14

ZACHOWANIE ENERGII MECHANICZNEJ

Dla dwóch dowolnych stanów układu, A i B,

T

A

+ V

A

= T

B

+ V

B

= E

T

A

i T

B

energia kinetyczna układu w stanie A

i w stanie B

∑

=

i

i

i

A

A

v

m

T

)

(

2

1

2

V

A

i V

B

energia potencjalna układu w stanie A

i

w stanie B

( )

A

A

V

F r ds

∞

=

∫

Jeżeli siły działające na

każdy

z

punktów

materialnych układu odizolowanego są siłami
zachowawczymi, to całkowita energia mechaniczna
układu nie ulega zmianie.

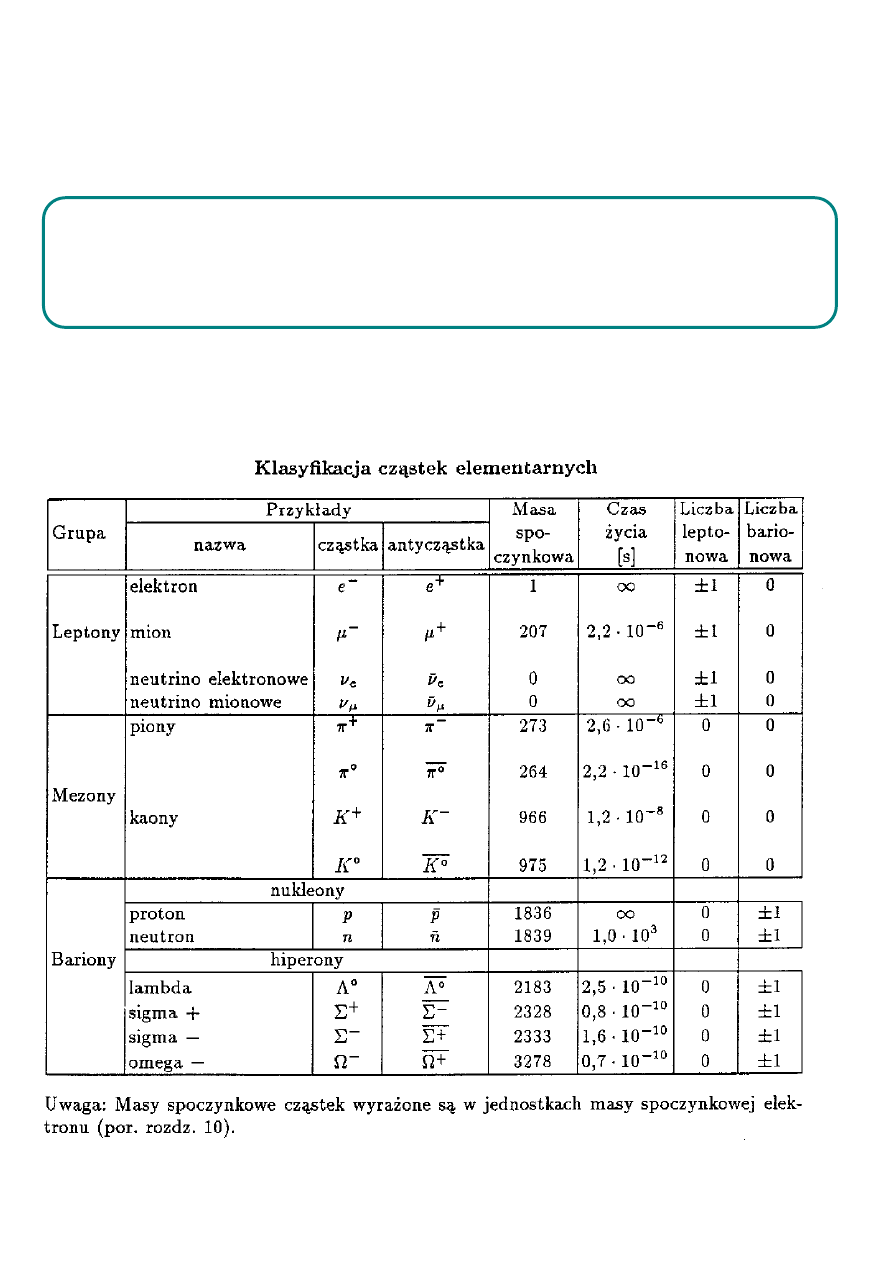
ZASADA ZACHOWANIA ŁADUNKU

W układzie zamkniętym całkowity ładunek pozostaje

stały niezależnie od przebiegających procesów

15

ZASADA ZACHOWANIA

LICZBY LEPTONOWEJ I LICZBY BARIONOWEJ

W układzie zamkniętym suma liczb leptonowych i liczb

barionowych pozostaje stała niezależnie od przebiegających
procesów

Λ

0

→

p

+

+

π

−

µ

−

→

e

−

+

ν

µ

+ ν

e

16

ZASADY ZACHOWANIA A SYMETRIA

W PRZYRODZIE

•

Zasada zachowania pędu wynika z niezmienniczości
względem przesunięcia przestrzennego będącej
konsekwencją jednorodności przestrzeni

•

Zasada zachowania momentu pędu z niezmienniczości
względem obrotu przestrzennego – izotropowości
przestrzeni

•

Zasada zachowania energii z niezmienniczości względem
przesunięcia w czasie – jednorodności czasu.

Twierdzenie Noether

Każdemu rodzajowi symetrii w przyrodzie

odpowiada określona zasada zachowania.

Jest to jedno z najważniejszych twierdzeń fizyki współczesnej.
(Emma Noether 1918 r. )

Najgłębszym poziomem poznania fizycznego są ogólne
zasady wyjawiające związki między prawami fizyki.