29. Skończonej wysokości studnia potencjału, prostokątna 1D.

Porównanie studni skończonej z nieskończoną:

•

Każdy poziom energetyczny w studni skończonej jest niższy niż w nieskończonej.

•

Studnia skończona ma tylko skończoną liczbę stanów związanych i odpowiadających poziomów
energetycznych

•

Zawsze musi istnieć co najmniej jeden poziom (zawsze istnieje jeden stan związany).

•

W żadnej ze studni nie ma stanu o E = 0

•

W stanach o E > U

0

, cząstka nie jest związana (= jest swobodna) i wszystkie wartości jej energii E są

dozwolone (continuum stanów). Funkcje falowe cząstki swobodnej są sinusoidalne dla każdego x.

•

W skończonej studni funkcja falowa wnika w barierą, ale ‘zanika’ w niej ekspotencjalnie, w studni
nieskończonej nie wnika w barierę.

•

Istnieje niezerowe prawdopodobieństwo, że cząstka znajdzie się na zewnątrz studni

Wyprowadzenie:

U=0 dla x należącego (0,L)
U=U

0

dla x>L,x<0

0

)

(

2

0

)

(

2

0

)

(

2

0

)

(

2

2

2

''

2

2

2

"

2

2

2

2

=

+

−

=

=

−

+

=

−

+

∇

−

=

−

+

=

+

ψ

ψ

ψ

ψ

ψ

ψ

ψ

ψ

ψ

ψ

ψ

q

U

E

m

q

U

E

m

E

U

m

E

U

m

p

E

U

m

p

h

h

h

Jedno z rozwiązań:

0

0

<

=

>

=

−

x

Ae

x

Ae

x

L

x

R

γ

γ

ψ

ψ

Na zewnątrz (w części gdzie stały potencjał równy U

0

):

)

Im(

)

(

2

)

(

2

1

)

(

2

0

0

0

2

2

q

E

U

m

i

q

U

E

m

q

U

E

m

q

=

−

−

=

−

=

−

=

γ

h

h

h

Wewnątrz:

mE

k

mE

k

E

m

E

m

p

2

1

2

1

0

2

2

2

2

2

''

2

h

h

h

=

=

=

+

=

ψ

ψ

ψ

ψ

Rozwiązaniem równania jest funkcja

)

sin(

)

cos(

)

(

)

sin(

)

(

2

1

2

1

2

1

δ

δ

δ

ψ

+

=

+

−

+

+

+

=

+

=

−

kx

C

kx

i

A

A

kx

A

A

e

A

e

A

ikx

ikx

m

Rozwiązanie można znormalizować tylko kiedy w odpowiednich warunkach stałe się zerują tak, żeby
zanikała.

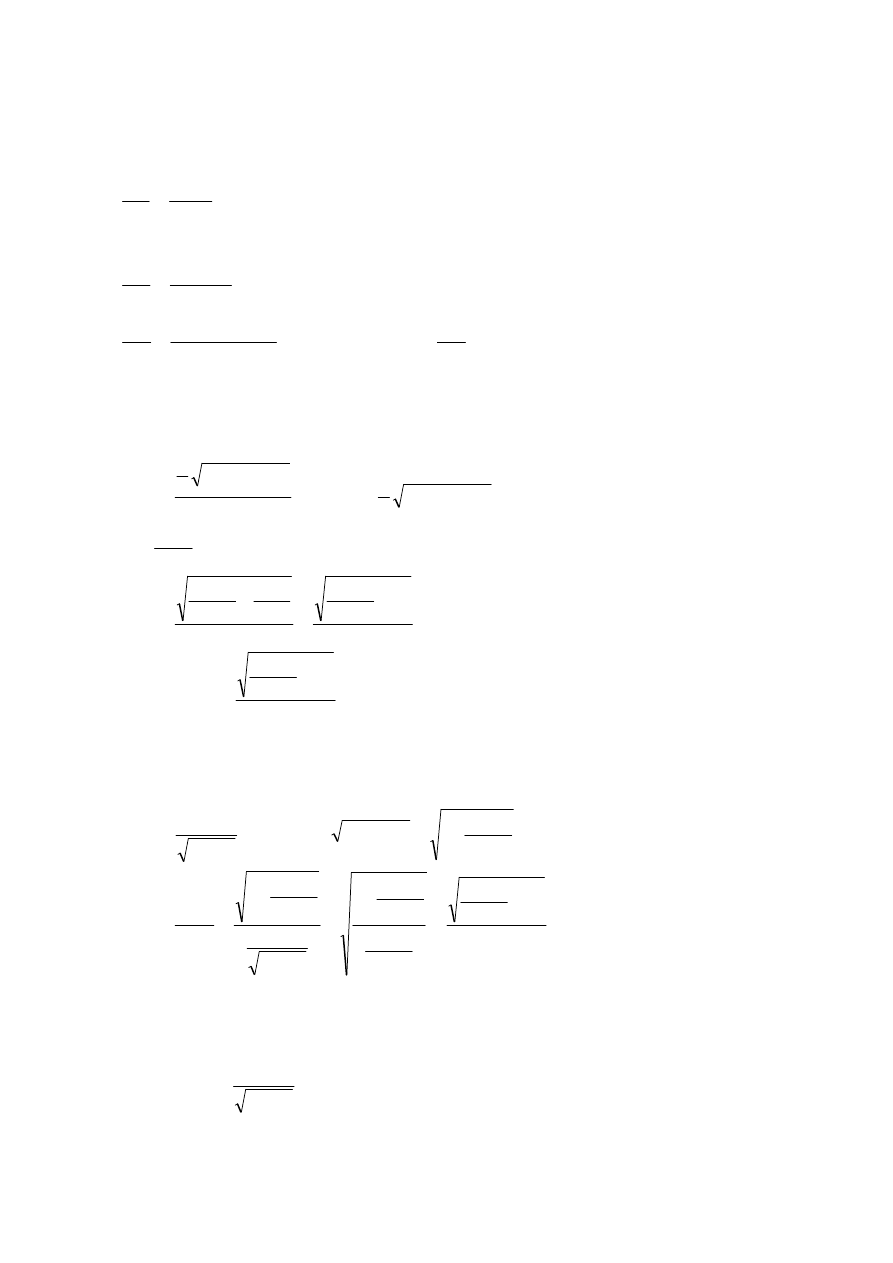
Funkcja obejmuje wartości własne operatora parzystości, poza tym dla stanów stacjonarnych
możemy zawsze wybrać funkcje rzeczywiste.

0

2

2

0

0

2

2

0

2

2

0

0

2

2

0

2

2

2

0

2

2

0

2

2

0

2

2

0

2

2

0

0

'

'

'

'

2

)

sin(

0

2

2

2

1

2

2

1

sin

cos

2

1

sin

1

cos

,

2

sin

0

2

)

(

0

2

2

2

2

)

(

2

1

)

(

2

1

)

(

)

(

0

)

sin(

)

cos(

0

mU

k

kL

L

x

k

k

mU

mU

k

mU

k

mU

k

mU

k

ctg

mU

k

mU

k

L

x

k

k

mU

kL

ctg

x

k

k

mU

k

mE

mU

ctg

m

k

E

E

U

m

bo

k

E

U

m

ctg

kL

kctg

kctg

L

x

dla

kL

kctg

x

dla

kctg

kx

C

kx

Ck

L

x

dla

Be

e

B

x

dla

Ae

e

A

m

m

m

m

x

x

R

R

x

x

L

L

h

h

h

h

h

h

h

h

h

h

h

h

h

h

h

−

=

+

>

>

−

=

−

=

−

=

=

−

=

−

=

=

>

>

−

−

=

+

≤

−

=

−

=

=

−

=

−

=

−

=

+

=

=

+

=

=

=

+

+

=

=

−

=

−

=

=

=

=

−

δ

γ

δ

δ

δ

δ

δ

δ

γ

δ

δ

γ

δ

γ

δ

γ

δ

δ

ψ

ψ

δ

δ

δ

ψ

ψ

γ

γ

ψ

ψ

γ

γ

ψ

ψ

γ

γ

γ

γ

Postępując tak jak powyżej dojdziemy do tego samego.

)

2

arcsin(

)

2

arcsin(

0

0

mU

k

n

kL

mU

k

h

h

−

=

+

=

π

δ

δ

Dodajemy stronami.

2

2

kL

n

n

kL

−

=

⇒

=

+

π

δ

π

δ

Teraz odejmiemy dwa wcześniejsze równania.

)

2

arcsin(

2

)

2

arcsin(

2

0

0

mU

k

kL

n

mU

k

n

kL

h

h

=

−

−

=

π

π

Pierwiastki tego równania wyznaczają poziomy energetyczne

m

k

E

2

2

2

h

=

przy czym dla

skończonej wartości U

0

ilość ich jest skończona.

Wiemy, że

2

kL

n

−

=

π

δ

, oraz oznaczmy

0

2

2

mU

L

kL

h

=

=

ξ

β

.Wstawiamy wszystko do

wzoru powyżej.

β

π

βξ

−

=

2

arcsin

n

Po nałożeniu na wzór sinusa lub cosinusa otrzymujemy:

βξ

β

βξ

β

±

=

±

=

sin

cos

Pierwszy z nich jest dla parzystych n, przy czym interesują nas tylko te rozwiązania, dla
których

0

>

β

tg

. Dla nieparzystych n otrzymaliśmy drugie równanie.

W szczególności dla jamy niezbyt głębokiej, dla której

2

2

0

mL

U

h

<<

, mamy

1

>>

ξ

, i równanie

βξ

β

±

=

sin

nie ma w ogóle pierwiastków. Równanie

βξ

β

±

=

cos

m jeden pierwiastek (dla

znaku + w prawej części równania), równy

)

2

1

1

(

1

2

ξ

ξ

β

−

≈

, zatem w tym przypadku istnieje

tylko jeden poziom energetyczny,

2

0

2

2

0

2

2

2

0

2

2

U

mL

U

mL

E

h

h

−

≈

=

β

położony w pobliżu

wierzchołka jamy.

Najniższy poziom energetyczny w studni potencjału leży w pewnej odległości od dna studni.
Oznacza to ,że nie można położyć cząstki kwantowej na dnie studni. Jest to związane z
zasadą nieoznaczoności. Jeżeli cząstka znajduje się w studni prostokątnej to jest

zlokalizowana w obszarze Δx=L zatem rozmycie jej pędu musi być

L

p

h

~

∆

.

30. Pokazać, że gdy dwa niekomutujące ze sobą operatory komutują z
operatorem

Hˆ

to widmo tego operatora jest zdegenerowane.

Operatory

B

i

A

ˆ

ˆ

ze sobą nie komutują, nie możemy ich więc wyznaczyć jednocześnie.

Funkcją własną operatora Hˆ jest

ψ

A

ˆ

.

ψ

ψ

ψ

B

E

E

B

B

H

ˆ

ˆ

ˆ

ˆ

=

=

W tym wypadku funkcją własną operatora Hˆ jest

ψ

Bˆ

.

Otrzymujemy dwie różne funkcję własne dla tej samej wartości własnej jednego operatora,

co świadczy o tym , że jego widmo jest zdegenerowane. Operatory

B

i

A

ˆ

ˆ

ze sobą nie

komutują, nie możemy ich więc wyznaczyć jednocześnie.

Karola

(wraz ze skryptem profesora, i z notatkami z ćwiczeń z cudownym Januszem :D )

ψ

ψ

ψ

ψ

αψ

ψ

ψ

ψ

A

E

E

A

H

A

A

H

A

E

H

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

ˆ

=

=

=

=

=