Rok I

ARYTMETYKA KOMPUTERÓW

Lista nr

0

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

0

1. Znajd

ź podstawę x systemu naturalnego, w którym: a)

5

41

=

x

, b)

4

22

=

x

c) a

2

=301

x

, d) b

2

=562

x

2. Znajd

ź podstawę

β

systemu naturalnego, w którym liczby naturalne x

1

oraz x

2

s

ą rozwiązaniami

równania ax

2

+ bx+c = 0. Wykonaj obliczenia dla x

1

= 5

β

, x

2

= 8

β

i równania 5

β

x

2

– 50

β

x+125

β

= 0

3* Znajd

ź podstawę systemu naturalnego, w którym x

1

, x

2

∈

s

ą rozwiązaniami równania ax

2

+ bx+c = 0

gdzie a,b,c

∈

(całkowite).**Rozwi

ąż zadanie jeśli wiadomo, że w tym systemie a,x

1

,x

2

s

ą liczbami

jednocyfrowymi, b jest liczb

ą dwucyfrową b = b

1

β

+b

0

, za

ś c jest liczbą o postaci c = c

2

β

2

+ c

1

β

+c

0

,

c

2

= 0 lub 1. Wykonaj obliczenia dla x

1

= 5

β

, x

2

= 8

β

oraz a = 1 lub 3.

4. Wyka

ż, że w standardowym systemie naturalnym o podstawie

β

suma warto

ści cyfr iloczynu liczby

jednocyfrowej przez

β

− 1

jest stała. Ułó

ż tabliczki mnożenia w systemach o bazie

β

= 5, 7, 9, 11, 13.

5* Wyka

ż, że w dowolnym systemie naturalnym suma cyfr iloczynu dowolnej liczby jednocyfrowej przez

najwi

ększą liczbę dwucyfrową {

β

–1,

β

–1}

β

jest stała. Spróbuj uogólni

ć uzyskany wynik.

6. Oblicz metod

ą pisemną iloczyn 0,324

β

×

2,41

β

i iloraz 43,4

β

: 3,2

β

dla

β

= 5, 7, 9, 11, 13 oraz dla

β

=

α

2

,

korzystaj

ąc z tabliczki mnożenia w systemie o podstawie

α

= 3, 4.

7. Przeprowad

ź konwersje podstawy (bazy), z dokładnością do 4 cyfr części ułamkowej wyniku:

a) 674,581

10

= (…)

16

= (…)

4

b) 0CD,12

16

= (…)

2

= (…)

10

c) 3,012

8

= … (…)

2

…= (…)

16

d) 34,56

10

×

2

–5

= (…)

2

= (…)

16

e) 102,21

3

×

5

–2

= (…)

5

f) 0BACA

16

×

5

–3

= (…)

10

g) 6745,81

9

= (…)

7

= (…)

10

h) 0AA,12

11

= (…)

10

= (…)

9

i) 102,21

3

×

15

–2

= (…)

5

j) 34

7

/56

7

= (…)

2

k) 234,(56)

9

= (…)

7

l) 12,3(45)

7

= (…)

10

= (…)

11

8* Wyka

ż, że wynikiem konwersji ułamka nieskracalnego w systemie o danej podstawie, na reprezentację

w innym systemie naturalnym, mo

że być ułamek nieskończony (**okresowy), jeśli istnieje nierozkła-

dalny podzielnik podstawy

źródłowej, który nie jest podzielnikiem podstawy docelowej.

9. Przeprowad

ź konwersję ułamka okresowego na system, w którym jego reprezentacja jest skończona:

a) 0,(27)

10

=

b) 0,(101)

2

=

c) 1 – 0,(56)

9

=

d) 0,(35)

11

– 0,(2)

11

=

e) 0,1(23)

7

=

* Wyka

ż, że taka konwersja ułamka okresowego jest wykonalna w każdym systemie naturalnym.

A. Wyka

ż, że w systemie naturalnym przeniesienie otrzymane w wyniku dodawania lub pożyczka

podczas odejmowania na ka

żdej pozycji są zawsze równe 0 lub 1.

B. Opracuj algorytm dodawania lub odejmowania liczb znakowanych zapisanych w systemie znak-moduł

(SM). Przyjmij,

że znak liczby jest kodowany standardowo (0 – plus, 1 –minus).

C. Opracuj algorytmy działa

ń w systemie naturalnym o dowolnej podstawie:

a) dodawania i odejmowania,

b) mno

żenia,

c) dzielenia

D. Oblicz odpowiednio warto

ści największej i najmniejszej liczby całkowitej, reprezentowanych przez

ła

ńcuch k cyfr w systemie a) naturalnym o podstawie

β

b) negabazowym, c) z cyframi znakowanymi,

d)* uzupełnieniowym pełnym i niepełnym, e)* spolaryzowanym „+

1

/

2

β

k–1

” oraz „+

1

/

2

β

k–1

–1”.

Rok I

ARYTMETYKA KOMPUTERÓW

Lista nr

1

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

1

1. Zapisz w systemie uzupełnieniowym do 2 (U2) z czterema bitami cz

ęści ułamkowej liczby:

a) – 674,581

10

b) – 0A,12

16

c) – 3,012

8

d) + 34,56

10

e) 4,56

10

– 4,5(6)

10

Porównaj otrzymane kody z notacj

ą w systemie uzupełnieniowym do 1 (U1) i systemie znak-moduł.

2. Dodaj i odejmij liczby 4-cyfrowe podane w dziesi

ętnym uzupełnieniowym systemie pełnym (U10):

a) 6745

±

8123

b) 9,745

±

0,8(23)

c) 31,56

±

84,23

d) 9,994

±

9,916

U

żywając lewostronnego rozszerzenia zweryfikuj poprawność wyników otrzymanych na 4 pozycjach.

3* Wyka

ż, że w systemie stałobazowym i uzupełnieniowym, w dodawaniu lub odejmowaniu o ustalonej

liczbie pozycji argumentów i wyniku, u

życie dodatkowej pozycji lewostronnego rozszerzenia wyniku

i argumentów wystarczy do wykrycia nadmiaru (przekroczenia zakresu).

4* Wyka

ż, że w systemach uzupełnieniowych pełnych o bazach skojarzonych konwersję podstawy można

wykona

ć przez grupowanie (

β

→

β

S

) lub dekompozycj

ę cyfr (

β

S

→

β

).

5. Oblicz sum

ę i różnicę liczb danych jako 10011101 i 01111001, 11011101 i 10111101, zakładając, że

podane ła

ńcuchy k = 8 bitów (ciągi zero-jedynkowe) reprezentują liczby w kodzie

a) naturalnym (NB)

b) uzupełnieniowym pełnym (U2)

c) uzupełnieniowym niepełnym (U1)

d) znak-moduł (SM)

e) spolaryzowanym „+2

k–1

–1”

f) spolaryzowanym „+2

k–1

”.

Zweryfikuj poprawno

ść otrzymanych wyników: A) wykonując działanie odwrotne (suma – argument,

ró

żnica + odjemnik) B) używając lewostronnego rozszerzenia (oprócz e) i f)).

6. Znanych jest kilka najbardziej znacz

ących bitów liczb 48-bitowych w kodzie uzupełnieniowym U2.

11101010..?? oraz 10011110..?? Sprawd

ź, czy w ich dodawaniu i odejmowaniu wystąpi nadmiar.

7. Korzystaj

ąc z zależności

Y

X

Y

X

+

=

−

i zakładaj

ąc, że liczby są dane w systemie naturalnym, oblicz:

a) 6745 – 8123

b) 9,745 – 0 , 823

c) 34,56– 81,23

d) 10011101

2

– 01111001

2

Sprawd

ź otrzymane wyniki wykonując działania odwrotne (różnica + odjemnik).

8. Wyka

ż, że w systemie naturalnym lub uzupełnieniowym pełnym mnożenie liczb

m

–pozycyjnych nie

powoduje nadmiaru, je

śli wynik jest kodowany na co najmniej 2

m

pozycjach.

9. Wynik mno

żenia

m

–bitowych liczb w kodzie U2 jest kodowany na 2

m

–1 bitach. Czy jest mo

żliwe

wyst

ąpienie nadmiaru, a jeśli tak to przy jakich wartościach mnożnej i mnożnika?

A. Przyjmuj

ąc, że 6-bitowe operandy są dane w dwójkowym kodzie uzupełnieniowym a) pełnym (U2),

b) niepełnym (U1) wykonaj mno

żenia: i) 110101

×

011011 ii) 011101

×

110111 iii) 101001

×

111111.

Wykonaj mno

żenie (U2) stosując przekodowanie iloczynów częściowych eliminujące rozszerzenia.

B. Poka

ż, że w systemie naturalnym dwójkowym i systemie uzupełnieniowym do 2 mnożenie przez stałą,

która jest sum

ą lub różnicą potęg dwójki można wykonać jako dodawanie skalowanej mnożnej.

C. Oblicz iloczyn liczb 4-cyfrowych podanych w dziesi

ętnym uzupełnieniowym systemie pełnym (U10):

a) 6745

U10

×

8123

U10

b) 9745

U10

×

0823

U10

c) 3156

U10

×

8423

U10

d) 9994

U10

×

9916

U10

Rok I

ARYTMETYKA KOMPUTERÓW

Lista nr

2

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

2

1. Oblicz iloczyn liczb 4-cyfrowych podanych w ósemkowym uzupełnieniowym systemie pełnym (U8):

a) 5745

U8

×

7123

U8

b) 7745

U8

×

0723

U8

c) 3156

U8

×

6423

U8

d) 7774

U8

×

7716

U8

2. Oblicz bezpo

średnio metodą sekwencyjną („kolejnych reszt”) z dokładnością do 4 pozycji znaczących

iloraz liczb reprezentowanych w systemie uzupełnieniowym pełnym

a) 01010011

U2

: 1011

U2

b) 1010011

U2

: 01011

U2

c) 876

U10

: 176

U10

d) 876

U10

: 761

U10

.

3. Wykonaj bezpo

średnio w systemie U10 dzielenia z dokładnością do 4 cyfr znaczących ilorazu:

a) 110101 : 011011

b) 011101 : 110111 c) 101001 : 11111

d) 101001 : 10011

e) 1,10101 : 01101,1

f) 0,11101 : 110,111 g) 1010,01 : 111,11

h) 101001 : 100,11

Sprawd

ź, wykonując mnożenie, poprawność otrzymanych wyników.

4. Wykonaj bezpo

średnio w kodzie U2 dzielenia z dokładnością do 4 cyfr znaczących ilorazu:

a) 110101 : 011011

b) 011101 : 110111 c) 101001 : 11111

d) 101001 : 10011

e) 1,10101 : 01101,1

f) 0,11101 : 110,111 g) 1010,01 : 111,11

h) 101001 : 100,11

Sprawd

ź, wykonując mnożenie, poprawność otrzymanych wyników.

5. Wykonaj bezpo

średnio w kodzie U2 z dokładnością do 4 cyfr znaczących ilorazu dzielenie

nieodtwarzaj

ące liczb:

a) 110101 : 011011

b) 011101 : 110111 c) 101001 : 11111

d) 101001 : 10011

e) 1,10101 : 01101,1

f) 0,11101 : 110,111 g) 1010,01 : 111,11

h) 101001 : 100,11

6. Oblicz metod

ą sekwencyjną („kolejnych reszt”) pierwiastek kwadratowy z liczb

a) 123456

7

, b) 1010 0010 0111 1100

2

, c) 987654321

10

d) 123,456

7

, e) 10100 0100,1111 100

2

z dokładno

ścią do jednej, dwóch i siedmiu cyfr znaczących oraz podaj trzecią i czwartą resztę.

7. Dane jest przybli

żenie pierwiastka kwadratowego z dokładnością do 3 cyfr znaczących i trzecia reszta.

Podaj dwie kolejne cyfry przybli

żenia pierwiastka, jeśli:

a)

Q

3

=123

7

,

r

3

=3456

7

, b)

Q

3

=123

10

,

r

3

= 3456

10

, c)

Q

3

=101

2

,

r

3

=11101

2

,

8. Dane jest przybli

żenie pierwiastka kwadratowego z dokładnością do 4 cyfr znaczących i czwarta reszta

równa 0. Oszacuj warto

ść liczby pierwiastkowanej, jeśli: a)

Q

4

=12,34

7

, b)

Q

4

=1,234

10

, c)

Q

4

=1101

2

.

9. Oblicz metod

ą nieodtwarzającą pierwiastek kwadratowy z liczb:

a) 1010 0010 0111 1100

2

, b) 123,456

8

, c) 10100 0100,1111 100

2

z dokładno

ścią do dwóch i pięciu cyfr znaczących oraz podaj trzecią i czwartą resztę.

A* Poka

ż, że w naturalnym systemie dwójkowym dzielenie przez stałą, która jest sumą lub różnicą

dwóch pot

ęg dwójki, można wykonać przez odejmowanie, jeśli dzielenie nie wytwarza reszty.

Rok I

ARYTMETYKA KOMPUTERÓW

Lista nr

3

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

3

1. Twierdzenie Euklidesa o podzielno

ści liczb orzeka, że największy wspólny podzielnik dwóch liczb

naturalnych jest podzielnikiem reszty z dzielenia wi

ększej przez mniejszą. Wykaż, równoważność tej tezy

z tez

ą, że największy wspólny podzielnik dwóch liczb jest podzielnikiem ich różnicy.

2. Korzystaj

ąc z twierdzenia Euklidesa znajdź największy wspólny podzielnik liczb:

a) 6745 i 8123

b) 9994, 92 i 9916

c) 375, 243, 345 i 126

d) 2

20

–1 oraz 2

5

+1

3. Poka

ż, że liczby 2

k

+ 1 i 2

k + 1

+ 1 s

ą względnie pierwsze (

k

∈

N – jest liczb

ą naturalną)

*Czy prawdziwe jest twierdzenie,

że liczby 2

k

+ 1 i 2

r

+ 1 (

k

,

r

∈

N ) s

ą względnie pierwsze?

4* Wyka

ż, że liczby

)

1

2

(

2

+

n

oraz

)

1

2

(

+

n

i

)

2

2

(

1

2

+

+

n

i

)

1

2

(

−

n

(

n

∈

N ) s

ą względnie pierwsze.

5. Nie wykonuj

ąc dzielenia wyznacz resztę z dzielenia liczby 1011 0011 0111 1101

2

przez

a) 1111

2

b) 10001

2

c) 11111

2

d) 10000001

2

.

6. Stosuj

ąc reguły arytmetyki resztowej oblicz reszty całkowite (dodatnie lub ujemne) wobec modułów:

257

10

, 7

8

, 65

10

, 3F

16

, 11

16

, 0FF

16

dla liczb 4652

8

i 0ABCD

16

, oraz ich sumy, ró

żnicy i iloczynu.

7. Podaj reprezentacj

ę resztową liczby 23456

10

w bazie: a) (29, 30, 31), b) (99, 100, 101), a) (63, 64, 65).

8* Znajd

ź odwrotności multyplikatywne iloczynów par modułów bazy systemu resztowego (

a

–1,

a

,

a

+1)

wzgl

ędem trzeciego z nich, zakładając, że

a

jest liczb

ą parzystą.

9* Wektor (1, 2, 3) jest reprezentacja resztow

ą liczby

x

w bazie (29, 30, 31). Znajd

ź tę liczbę w zbiorze

kongruencji naturalnych (

x

∈

[0, M=29

⋅

30

⋅

31)) i całkowitych (

x

∈

–(M–1) /2, M–1 /2)).

A. Zapisz w 32-bitowym formacie zmiennoprzecinkowym standardu IEEE 754 liczby o warto

ściach:

a) 674,531

8

b) 0,12

8

⋅

8

-51

c) – 0ABC,DE

16

d) 10,1010101010

U2

⋅

4

-61

B. Zapisz w 32-bitowym formacie zmiennoprzecinkowym IEEE 754 pierwiastki kwadratowe z liczb:

a) 1010 0010, 0111 1100

2

, b) 123,456

8

, c) 10100 0100, 1111 100

2

C. Oblicz i zapisz w 32-bitowym formacie zmiennoprzecinkowym standardu IEEE 754 z dokładno

ścią do

5 cyfr znacz

ących pierwiastki kwadratowe z liczb danych w tym formacie:

a) 0 0100 0100 111 1100 1010 0010 0111 1100, b) 0 1010 0101 1111 1010 0100 1111 1111 100

2

c) 0 0100 0101 111 1100 1010 0010 0111 1100, d) 0 1010 0100 1111 1010 0100 1111 1111 100

2

D* Wyka

ż, że w odejmowaniu (dodawaniu) zmiennoprzecinkowym operandów dokładnych, bit

S

dla

znormalizowanej ró

żnicy (sumy) może być wyznaczony przed wykonaniem działania.

E. Wyznacz z dokładno

ścią do 4 bitów znacznika zaokrąglenia argumentów 1,101111011 i 1,101111001

uzupełnione bitami G, R, S. Wykonaj ich mno

żenie i porównaj z wynikiem pełnego mnożenia.

F* Wyka

ż, że w mnożeniu znormalizowanych operandów, bit

S

znormalizowanego iloczynu mo

że być

wyznaczony przed mno

żeniem. Pokaż, że jeden z czynników może być zdenormalizowany.

G* Oszacuj maksymalny bł

ąd przybliżenia różnicy podczas odejmowania znormalizowanych operandów

obliczonych z tak

ą samą dokładnością bezwzględną znacznika (mantysy).

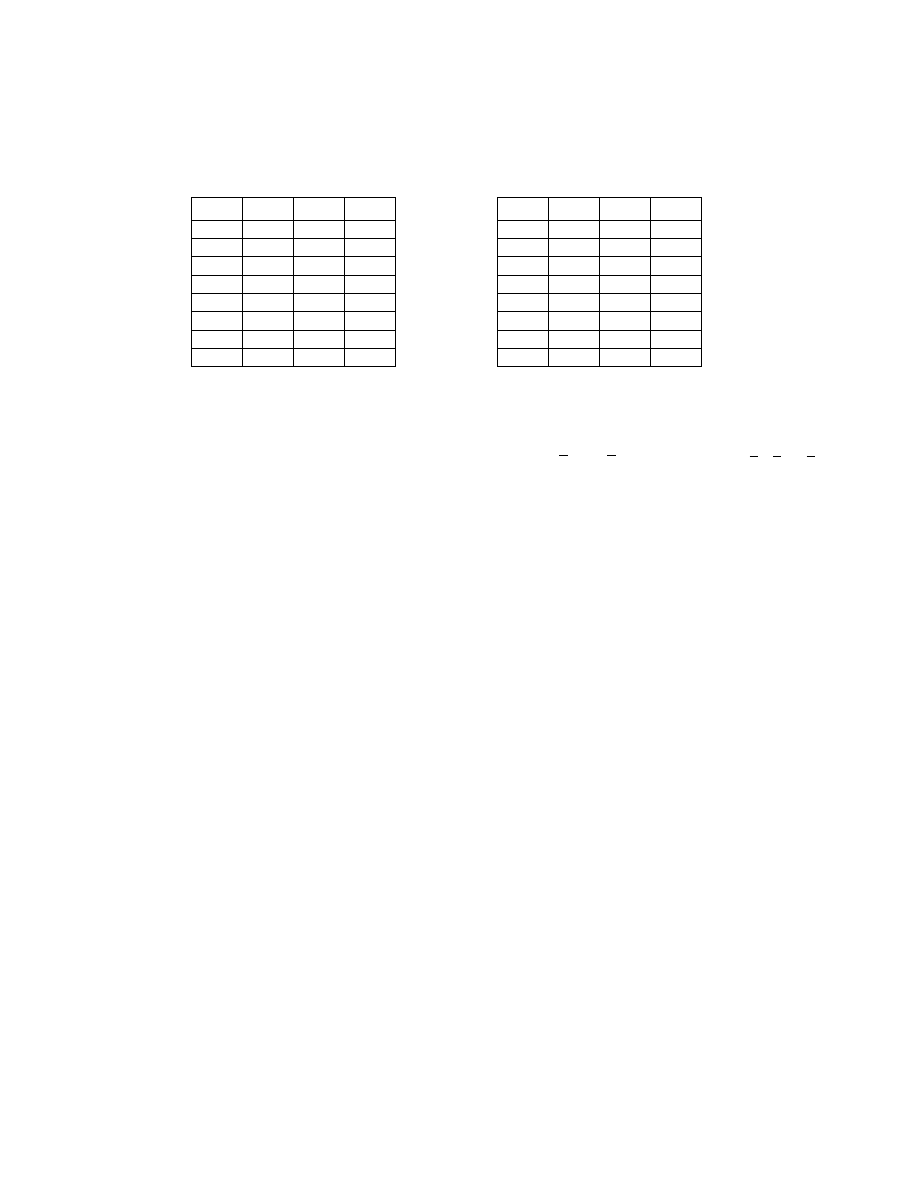
Rok I

ARYTMETYKA KOMPUTERÓW

Lista nr

4

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

4

1. Stosuj

ąc reguły działań w algebrze Boole’a uprość poniższe wyrażenia

a)

x

+(

x

⊕

y

)

b)

xyz

+(

x

⊕

y

) +(

z

⊕

y

)

c)

x

+

xy

+

xyz

d)

zy

+(

x

⊕

y

)

e) z

x

+

z

(

x

⊕

1)

f)

x

+

xy

+(

x

⊕

yz

)

2. Na podstawie tabel warto

ści funkcji logicznych

f

1

i

f

2

(tzw. tabel prawdy) podaj ich wszystkie mintermy

(konstytuenty iloczynu) i maxtermy (konstytuenty sumy) oraz postaci formalne

x

3

x

2

x

1

f

1

(x)

x

3

x

2

x

1

f

2

(x)

0

0

0

0

0

0

0

1

0

0

1

0

0

0

1

1

0

1

0

1

0

1

0

1

0

1

1

0

0

1

1

0

1

0

0

1

1

0

0

0

1

0

1

1

1

0

1

1

1

1

0

1

1

1

0

0

1

1

1

0

1

1

1

1

2a. Ułó

ż

tabele prawdy dla funkcji nadmiaru w dodawaniu / odejmowaniu w kodzie U2 i podaj wyra

ż

enie

logiczne definiuj

ą

ce t

ę

funkcj

ę

3. Wyznacz funkcje dualne i komplementarne do funkcji

2

3

1

2

1

)

(

x

x

x

x

f

+

=

x

i

)

(

)

(

1

2

3

1

3

2

x

x

x

x

x

f

+

+

=

x

oraz ich sumy logicznej i iloczynu logicznego. Narysuj sieci logiczne realizuj

ące te funkcje.

4. Korzystaj

ąc z twierdzenia Shannona rozwiń wszystkie funkcje z zadania 3 względem zmiennej

x

3

.

5. Wyka

ż, że wartość funkcji logicznej [

z

⋅

f

(

x

)+(

z

⊕

f

(

x

))]

f

(

x

) nie zale

ży od zmiennej

z

.

6* Poka

ż, że każdą funkcję logiczną można wyrazić za pomocą tylko funkcji NOR (suma negacji) lub

tylko funkcji NAND (iloczyn negacji).

7. Wyznacz charakterystyki AT sieci logicznych realizujacych funkcje dane przez wyra

żenia w zadaniu 1

8. Subtraktor 1-bitowy realizuje funkcje logiczne ró

żnicy

d

=

f

(

x, y, z

) i po

życzki

b

=

h

(

x, y, z

) równowa

żne

arytmetycznemu równaniu odejmowania 1-bitowego

x

–

y

–

z

= – 2

d

+

b

(

x

,

y

,

z

,

d

,

b

∈

{0, 1}) . Podaj

tabel

ę prawdy subtraktora i wyznacz charakterystyki AT subtraktora 8-bitowego.

9. Sumator 1-bitowy realizuje funkcje logiczne sumy

s

=

f

(

x, y, z

) i przeniesienia

c

=

h

(

x, y, z

) równowa

żne

arytmetycznemu równaniu dodawania 1-bitowego

x

+

y

+

z

= 2

c

+

s

(

x

,

y

,

z

,

s

,

c

∈

{0, 1}) . Zaprojektuj

ogniwo inkrementera realizuj

ącego funkcje

s

=

f

(

x,

1

, z

) oraz

c

=

h

(

x,

1

, z

) i oblicz charakterystyki AT.

A. Sumator warunkowy 1-bitowy realizuje funkcje logiczne warunkowej sumy

s

0

=

f

(

x, y,

0),

s

1

=

f

(

x, y,

1)

i przeniesienia

c

0

=

h

(

x, y,

0),

c

1

=

h

(

x, y,

1) równowa

żne równaniu dodawania 1-bitowego przy

zało

żeniu, że przeniesienie wejściowe jest odpowiednio równe 0 albo 1. Wyznacz te funkcje.

B* Narysuj schemat logiczny sumatora 1-bitowego, którego wyj

ścia sumy i przeniesienia są wytwarzane

z u

życiem multiplekserów sterowanych przeniesieniem wejściowym na podstawie funkcji sumy

i przeniesienia zerowego i jedynkowego

s

0

,

s

1

,

c

0

,

c

1

. Wyznacz charakterystyki AT tego układu.

C* Poka

ż, że charakterystyki AT sieci realizujących funkcję dualną i komplementarną są jednakowe.

Rok I

ARYTMETYKA KOMPUTERÓW

Lista nr

5

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

5

1. Oblicz charakterystyki AT sumatorów uniwersalnych RCA dla kodów

k

-bitowych:

a) uzupełnieniowego pełnego (U2)

b) uzupełnieniowego niepełnego (U1)

c) znak-moduł,

d) spolaryzowanego ujemnie „+2

k–1

”

e) spolaryzowanego dodatnio „+2

k–1

–1”

2. Zaproponuj sposób kodowania cyfr i zaprojektuj sumator jedno- i cztero-pozycyjny dla systemu

a) U10 z kodowaniem cyfr w kodzie „+3” i kodzie BCD

b) dwójkowego negabazowego (

β

= –2),

c)* naturalnego trójkowego (

β

= 3) i dwójkowego z cyfr

ą znakowaną SD (D={–1,0,+1})

3. Oblicz charakterystyki AT sumatora 24-bitowego z przeniesieniami przeskakuj

ącymi (

carry-skip

) je

śli

ma on struktur

ę a) 3-4-4-3-4-4-2, b) 3-3-4-4-4-3-3, c) 4-4-4-4-4-4, d) 6-6-6-6, e) optymalną.

4. Zaprojektuj 8-bitowe układy inkrementacji i dekrementacji i wyznacz ich charakterystyki AT.

5. Zaprojektuj 4- i 8-bitowy sumator sum warunkowych i wyznacz ich charakterystyki AT.

6. Zaprojektuj 4- i 8-bitowy sumator prefiksowy PPA i wyznacz ich charakterystyki AT.

7. W celu dodania

n

operandów

k

-bitowych u

żyto sumatora CSA (

carry-save

). Ile bitów zawiera suma?

Jakie jest opó

źnienie (T) podczas obliczania sumy, jeśli sumę końcową wytwarza

a) sumator ze skro

śną propagacją przeniesień RCA, b) sumator sum warunkowych COSA.

Obliczenia wykonaj dla

n

= 7, 15, 31 oraz

k

= 8, 16, 32.

8. Ile poziomów musi zawiera

ć sumator CSA użyty do redukcji iloczynów częściowych tworzonych

w mno

żeniu liczb 32-bitowych w kodzie naturalnym (NB)? Ile sumatorów elementarnych (3,2)

zawiera najbardziej skomplikowana gał

ąź CSA odpowiadająca bitom o tej samej wadze.

9. Zaprojektuj sumator CSA dodaj

ący odpowiednio 3, 4 i 8 operandów 4-bitowych w kodzie U2.

A. Wyznacz, uwzgl

ędniając czas końcowego dodawania, najkrótszy czas dodawania 32 operandów 64-

bitowych w sumatorze CSA je

śli dysponujesz:

a) reduktorami (3,2) generuj

ącymi przeniesienia 1-bitowe, wnoszące opóźnienia T = 4

ka

żdy

b) *reduktorami (4,2) generuj

ącymi przeniesienia 2-bitowe, wnoszące opóźnienia T = 6

ka

żdy

B* Opracuj i uzasadnij algorytmy konwersji dwójkowo–dziesi

ętnej liczb całkowitych dodatnich, bez

wykonywania dzielenia, je

śli cyfry dziesiętne są kodowane: a) w kodzie BCD, b) w kodzie BCD+3.

C* Zaprojektuj generator reprezentacji resztowej liczby całkowitej 8- i 16-bitowej w kodzie NB

a) mod 1111

2

b) mod 10001

2

c) mod 111

2

d) mod 1001

2

D* Zaprojektuj generator reprezentacji resztowej liczby całkowitej 8- i 16-bitowej w kodzie U2

a) mod 1111

2

b) mod 10001

2

c) mod 111

2

d) mod 1001

2

E. Zaprojektuj sumator mod (2

8

–1) dwóch liczb całkowitych 8-bitowych w kodzie U2.

F* Zaprojektuj sumatory mod (2

4

–1) i mod (2

4

+1) 4 liczb całkowitych 4-bitowych w kodzie U2.

Rok I

ARYTMETYKA KOMPUTERÓW

Lista nr

6

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

6

1. Zakoduj na 8 bitach według prostej i odwrotnej reguły Booth’a w bazie 2 oraz w bazie 4 liczby:

a) –87

10

b) +121

10

c) 101101

2

c) 1011101

U2

2. Przyjmuj

ąc, że 6-bitowe operandy są dane w dwójkowym kodzie uzupełnieniowym a) pełnym (U2),

b) niepełnym (U1) i u

żywając mnożnika przekodowanego wg reguły Booth’a w bazie 2 i 4 wykonaj

mno

żenia: i) 110101

×

011011 ii) 011101

×

110111 iii) 101001

×

111111

3. Oblicz charakterystyki AT matrycy mno

żącej dwa operandy: a) 4-bitowe, b) 8-bitowe c)*

n

-bitowe

4* Zaprojektuj matryc

ę mnożącą operandy 4-bitowe w kodzie U2 z wykorzystaniem przekodowania

mno

żnika wg reguły Bootha w bazie 4. Porównaj z innymi układami matrycowymi.

5. Oblicz charakterystyki AT sumatora CSA u

żytego do redukcji iloczynów częściowych w mnożeniu

operandów 4-, 8- bitowych danych: a) w kodzie NB, b) w kodzie U2 z eliminacj

ą bitów rozszerzenia.

*Podaj oszacowanie charakterystyk AT dla mno

żenia operandów

n

-bitowych.

6. W dzieleniu w systemie naturalnym w bazie 4 skalowana reszta cz

ęściowa ma wartość 2,2

D.

Wyznacz:

analitycznie i na podstawie parametrycznego wykresu dzielenia, kolejne dwie cyfry ilorazu.

7. W dzieleniu w systemie U2 przeskalowana reszta cz

ęściowa ma wartość: i) –0,2

D

, ii) +0,7

D.

Wyznacz:

analitycznie i na podstawie parametrycznego wykresu dzielenia kolejne dwie cyfry ilorazu, zakładaj

ąc,

że dzielnik

D

jest: a) ujemny, b) dodatni.

8. Wykonaj bezpo

średnio w kodzie U2 dzielenia z dokładnością do 4 cyfr znaczących ilorazu:

a) 110101 : 011011

b) 011101 : 110111 c) 101001 : 11111

d) 101001 : 10011

e) 1,10101 : 01101,1

f) 0,11101 : 110,111 g) 1010,01 : 111,11

h) 101001 : 100,11

Sprawd

ź, wykonując mnożenie, poprawność otrzymanych wyników.

9. Wykonaj wykres P-D dla dzielenia w bazie 4 i dzielnika z zakresu [1,2). Podaj ile bitów musi by

ć

porównywanych w celu wyznaczenia cyfr ilorazu.

A. Oblicz charakterystyki AT matryc dziel

ących operandy 8-bitowe w kodzie NB i U2

B. Oblicz metod

ą Newtona iloraz 3,1416 :2,7183.

C. Oce

ń czas obliczania pierwiastka kwadratowego z liczby całkowitej metodą sekwencyjną („kolejnych

reszt”) oraz na podstawie to

żsamości: „suma

n kolejnych nieparzystych liczb naturalnych jest równa

kwadratowi z ich liczby

” (np. 1+3+5=3

2

1+3+5+7=4

2

, 1+3+5+7+9=5

2

itd.)

*Okre

śl minimalny czas obliczeń, jeśli liczba jest zakodowana odpowiednio na 8, 16, 32 bitach.

D* Oszacuj liczb

ę kroków algorytmu CORDIC potrzebnych do obliczenia wartości funkcji exp, ln, sin,

cos, arctg dla argumentu z przedziału [–1,1] z dokładno

ścią do 32 bitów części ułamkowej.

E* Oce

ń czas obliczania pierwiastka trzeciego stopnia na podstawie algorytmu opartego na zależności:

∑∑

∑∑

∑

∑

−

=

=

=

−

=

=

=

=

=

−

⋅

=

⋅

−

⋅

=

−

1

1

1

1

1

0

1

1

2

3

6

2

3

))

1

(

(

3

)

3

3

(

n

j

j

i

n

j

j

i

n

i

n

i

i

i

i

i

i

i

n

n

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

7

Lista nr 0

1. Znajd

ź

podstaw

ę

x systemu naturalnego, w którym: a)

5

41

=

x

, b)

4

22

=

x

c) a

2

=301

x

, d) b

2

=562

x

Wskazówka: a) i b): Nale

ż

y podnie

ść

obie strony równo

ś

ci do kwadratu i rozwi

ą

za

ć

stosowne równanie ze

wzgl

ę

du na nieznan

ą

podstaw

ę

. Trzeba te

ż

zauwa

ż

y

ć

,

ż

e szukana podstawa musi by

ć

wi

ę

ksza od

najwi

ę

kszej z cyfr wyst

ę

puj

ą

cych w równaniu (st

ą

d wynika,

ż

e warto

ś

ci cyfr <10 mo

ż

na uwa

ż

a

ć

za

warto

ś

ci w systemie dziesi

ę

tnym). Na przykład 5

x

×

5

x

=41

x

sk

ą

d wynika,

ż

e 25=4x+1, zatem x=6. Je

ś

li

liczba pierwiastkowana ma k cyfr, to trzeba rozwi

ą

za

ć

równanie stopnia k–1 wzgl

ę

dem x. Na przykład

c) i d): Poniewa

ż

kwadrat jest liczb

ą

trzycyfrow

ą

, to x musi by

ć

liczb

ą

dwucyfrow

ą

, co wi

ę

cej

starsz

ą

cyfr

ą

musi by

ć

1 (bo (

β

)

2

<

301

β

=

3

β

2

+1 <(2

β

)

2

). Mamy st

ą

d równanie (

β

+z

)

2

=

3

β

2

+1, czyli

2

β

2

–2z

β

+

(1–z

2

)

=

0. Zatem (wzory Viete’y), poniewa

ż

z nie mo

ż

e by

ć

równe 1 (bo wtedy wyst

ą

pi

sprzeczno

ść

β

= 1

), jedno z rozwi

ą

za

ń

musi by

ć

ujemne (ujemny jest iloczyn pierwiastków (1–z

2

)).

Poniewa

ż

oba rozwi

ą

zania musz

ą

by

ć

te

ż

całkowite (ich suma wynosi z), to wystarczy bada

ć

warto

ś

ci

nieparzyste z (3,5,7,...). I tak przy z=3 otrzymamy

β

= 4

(lub –1), gdy z=11 to

β

=

15 (lub –4).

Podobnie, dla przykładu d) mamy (2

β

)

2

<

562

β

=

5

β

2

+6

β

+2 <(3

β

)

2

), sk

ą

d wynika,

ż

e starsz

ą

cyfr

ą

liczby b jest 2. Mamy st

ą

d równanie (2

β

+z

)

2

=

5

β

2

+6

β

+2, czyli

β

2

+(6–4z)

β

+(2–z

2

)

=

0 z warunkiem

β

> 6 , a poniewa

ż

z nie mo

ż

e by

ć

równe 1 (bo wtedy

β

=

–1), iloczyn pierwiastków (2–z

2

) jest ujemny

za

ś

suma (4z–6) dodatnia. Otrzymamy odpowiednio dla kolejnych z zestawy (z: suma, iloczyn) takie

jak: (2:+2, –2), (3,+6,–7) –

β

= 7 , (4,+10,–14), (5,+14,–23), (6,+18,–34), ... Je

ś

li kwadrat jest liczb

ą

k-

cyfrow

ą

, to trzeba analizowa

ć

równanie stopnia k–1 wzgl

ę

dem nieznanej podstawy

β

.

2. Znajd

ź

podstaw

ę

β

systemu naturalnego, w którym liczby naturalne x

1

oraz x

2

s

ą

rozwi

ą

zaniami

równania ax

2

+ bx+c = 0. Wykonaj obliczenia dla x

1

= 5

β

, x

2

= 8

β

i równania 5

β

x

2

– 50

β

x+125

β

= 0

Wskazówka: Poniewa

ż

znamy pierwiastki, wi

ę

c na podstawie wzorów Viete’y nale

ż

y uło

ż

y

ć

równania ze

wzgl

ę

du na

β

. W tym zadaniu mamy 5

β

(

x

1

+x

2

) =

50

β

, sk

ą

d natychmiast wynika (5

β

×

10

β

=50

β

)

ż

e x

1

+x

2

= 10

β

=

β

. Trzeba jeszcze sprawdzi

ć

, czy 5

13

×

(5

13

×

8

13

) = 125

13

(OK., bo 13

2

+2

×

13+1 = 200).

*Je

ś

li rozwi

ą

zania równania x

2

– 15

β

x+53

β

= 0 s

ą

naturalne, to x

1

+ x

2

=

β

+ 5 oraz

=

x

1

x

2

=

5

β

+ 3.

Musi wi

ę

c by

ć

x

1

> 5 oraz x

2

<

β

(w przeciwnym razie jeden musi by

ć

ujemny) Je

ś

li x

1

= 6 , x

2

=

β

− 1

,

to

β

=

9

.

(powinny by

ć

dwa symetryczne rozwi

ą

zania dla x

1

oraz x

2

– jedno rozwi

ą

zanie dla

β

).

3* Znajd

ź

podstaw

ę

systemu naturalnego, w którym x

1

, x

2

∈

s

ą

rozwi

ą

zaniami równania ax

2

+ bx+c = 0

gdzie a,b,c

∈

(całkowite).**Rozwi

ąż

zadanie je

ś

li wiadomo,

ż

e w tym systemie a,x

1

,x

2

s

ą

liczbami

jednocyfrowymi, b jest liczb

ą

dwucyfrow

ą

b = b

1

β

+b

0

, za

ś

c jest liczb

ą

o postaci c = c

2

β

2

+ c

1

β

+c

0

,

c

2

= 0 lub 1. Wykonaj obliczenia dla x

1

= 5

β

, x

2

= 8

β

oraz a = 1 lub 3.

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

8

Wskazówka: *Na podstawie wzorów Viete’y uło

ż

y

ć

układ równa

ń

wzgl

ę

dem nieznanej podstawy

β

i nieznanego drugiego pierwiastka x

2

: – a

(

x

1

+ x

2

) =

b oraz a x

1

x

2

=

c. **Pierwiastki całkowite musz

ą

by

ć

podzielnikami c – zale

ż

nie od warto

ś

ci c mo

ż

na okre

ś

li

ć

dozwolony zakres ich warto

ś

ci. Powstałe

przypadki przeanalizowa

ć

(łatwo to zrobi

ć

gdy pierwiastki s

ą

jednocyfrowe), zbada

ć

te

ż

wyró

ż

nik

∆

.

4. Wyka

ż

,

ż

e w standardowym systemie naturalnym o podstawie

β

suma warto

ś

ci cyfr iloczynu liczby

jednocyfrowej przez

β

− 1

jest stała. Ułó

ż

tabliczki mno

ż

enia w systemach o bazie

β

= 5, 7, 9, 11, 13.

Wskazówka: x

×

(

β

– 1 ) = ( x – 1 )

β

+ (

β

– x ), za

ś

( x – 1 ) +

(

β

– x ) =

β

– 1. S

ą

siednie wielokrotno

ś

ci m

najłatwiej obliczy

ć

wykonuj

ą

c dodawanie lub odejmowanie: m

⋅

(a

±

1) = m

⋅

a

±

m.

5* Wyka

ż

,

ż

e w dowolnym systemie naturalnym suma cyfr iloczynu dowolnej liczby jednocyfrowej przez

najwi

ę

ksz

ą

liczb

ę

dwucyfrow

ą

{

β

–1,

β

–1}

β

jest stała. Spróbuj uogólni

ć

uzyskany wynik.

Wskazówka: x

×

|{(

β

–1),(

β

–1)}| = x

×

(

β

2

–1)=(x–1)

β

2

+

β

(

β

–1)+

(

β

–x). Podobnie x

×

|{(

β

–1),…(

β

–1),(

β

–1)}|=

= x

×

(

β

k

–1) = (x–1)

β

k

+(

β

–1)

β

k–1

+…+

β

(

β

–1)+

(

β

–x) , zatem suma cyfr wynosi k(

β

–1).

6. Oblicz metod

ą

pisemn

ą

iloczyn 0,324

β

×

2,41

β

i iloraz 43,4

β

: 3,2

β

dla

β

= 5, 7, 9, 11, 13 oraz dla

β

=

α

2

,

korzystaj

ą

c z tabliczki mno

ż

enia w systemie o podstawie

α

= 3, 4.

Wskazówka: Je

ś

li

α

=

β

2

, to {z,…,x}

α

=

{(z div

β

),(

z mod

β

),…,(x div

β

),(

x mod

β

)}

β

, np. 0,53

9

= 0,1210

3

7. Przeprowad

ź

konwersje podstawy (bazy), z dokładno

ś

ci

ą

do 4 cyfr cz

ęś

ci ułamkowej wyniku:

a) 674,581

10

= (…)

16

= (…)

4

b) 0CD,12

16

= (…)

2

= (…)

10

c) 3,012

8

= … (…)

2

…= (…)

16

d) 34,56

10

×

2

–5

= (…)

2

= (…)

16

e) 102,21

3

×

5

–2

= (…)

5

f) 0BACA

16

×

5

–3

= (…)

10

g) 6745,81

9

= (…)

7

= (…)

10

h) 0AA,12

11

= (…)

10

= (…)

9

i) 102,21

3

×

15

–2

= (…)

5

j) 34

7

/56

7

= (…)

2

k) 234,(56)

9

= (…)

7

l) 12,3(45)

7

= (…)

10

= (…)

11

Wskazówka: Konwersja przez podstaw

ę

skojarzon

ą

(

α

=

β

k

) przy

ś

piesza obliczenia – wyznaczamy k cyfr

w ka

ż

dym kroku (np. konwersj

ę

na system dwójkowy łatwo wykona

ć

przez system ósemkowy). Je

ś

li

mno

ż

nik jest pot

ę

g

ą

podstawy

ź

ródłowej, to skalowanie nale

ż

y wykona

ć

przed konwersj

ą

, a je

ś

li jest

pot

ę

g

ą

bazy docelowej, skalowanie przeprowadzi

ć

po konwersji. Konwersj

ę

ułamka wymiernego (po

skróceniu) wykona

ć

jako konwersj

ę

licznika i mianownika (zawsze dokładna) a nast

ę

pnie dzielenie

z

żą

dan

ą

dokładno

ś

ci

ą

. Ułamek okresowy nale

ż

y zamieni

ć

na ułamek wymierny, albo u

ż

ywaj

ą

c kilku

(>2) cykli okresu zaobserwowa

ć

regularno

ść

zapisu wielokrotno

ś

ci ułamka.

8* Wyka

ż

,

ż

e wynikiem konwersji ułamka nieskracalnego w systemie o danej podstawie, na reprezentacj

ę

w innym systemie naturalnym, mo

ż

e by

ć

ułamek niesko

ń

czony (**okresowy), je

ś

li istnieje nierozkła-

dalny podzielnik podstawy

ź

ródłowej, który nie jest podzielnikiem podstawy docelowej.

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

9

Wskazówka: Znajd

ź

licznik ułamka danego w bazie

β

w bazie p

β

gdy (p,

β

)=1. (dowód podobnej tezy jest

w ksi

ąż

ce „Metody i układy arytmetyki komputerowej”). Twierdzenie kategoryczne („jest” zamiast

„mo

ż

e”) jest fałszywe, bo s

ą

przypadki gdy tak nie jest np. 0,5

10

= 0,1

2

, ale np. 0,1

10

= 0,(00011)

2

.

9. Przeprowad

ź

konwersj

ę

ułamka okresowego na system, w którym jego reprezentacja jest sko

ń

czona:

a) 0,(27)

10

=

b) 0,(101)

2

=

c) 1 – 0,(56)

9

=

d) 0,(35)

11

– 0,(2)

11

=

e) 0,1(23)

7

=

* Wyka

ż

,

ż

e taka konwersja ułamka okresowego jest wykonalna w ka

ż

dym systemie naturalnym.

Wskazówka: Warto

ść

ułamka okresowego jest równa granicy szeregu niesko

ń

czonego. Nale

ż

y obliczy

ć

t

ę

granic

ę

w postaci ułamka wymiernego, skróci

ć

go i wtedy mianownik jest szukan

ą

podstaw

ą

systemu

a licznik wyznacza warto

ść

ułamka w systemie o tej podstawie. Na przykład 0,(3)

10

= 0,3 + 0,03 + … =

= 0,3 / ( 1 – 0,1 ) =

1

/

3

= 0,1

3

, c) 1 – 0,(56)

9

= 0,(32)

9 ,

d) 0,(35)

11

– 0,(2)

11

= 0,(35)

11

– 0,(22)

11

= 0,(13)

11

A. Wyka

ż

,

ż

e w systemie naturalnym przeniesienie otrzymane w wyniku dodawania lub po

ż

yczka

podczas odejmowania na ka

ż

dej pozycji s

ą

zawsze równe 0 lub 1.

Dowód: Poniewa

ż

najwi

ę

ksz

ą

liczb

ą

jest

β

–1, wi

ę

c ich najwi

ę

ksz

ą

sum

ą

jest

β

+(

β

–2), co oznacza

wyst

ą

pienie przeniesienia =1. Je

ś

li t

ę

liczb

ę

powi

ę

kszymy o 1 przeniesienie b

ę

dzie bez zmian.

Poniewa

ż

na pozycji najni

ż

szej przeniesienie jest równe 0, wi

ę

c nigdy nie mo

ż

e wyst

ą

pi

ć

przeniesienie inne ni

ż

0 lub 1.

B. Opracuj algorytm dodawania lub odejmowania liczb znakowanych zapisanych w systemie znak-moduł

(SM). Przyjmij,

ż

e znak liczby jest kodowany standardowo (0 – plus, 1 –minus).

Wskazówka: Sprawd

ź

, jakie działanie nale

ż

y faktycznie wykona

ć

w zale

ż

no

ś

ci od znaków argumentów.

C. Opracuj algorytmy działa

ń

w systemie naturalnym o dowolnej podstawie:

a) dodawania i odejmowania,

b) mno

ż

enia,

c) dzielenia

Wskazówka: Zapisz algorytm dodawania / odejmowania jednopozycyjnego. Utwórz tabliczki mno

ż

enia.

D. Oblicz odpowiednio warto

ś

ci najwi

ę

kszej i najmniejszej liczby całkowitej, reprezentowanych przez

ła

ń

cuch k cyfr w systemie a) naturalnym o podstawie

β

b) negabazowym, c) z cyframi znakowanymi,

d)* uzupełnieniowym pełnym i niepełnym, e)* spolaryzowanym „+

1

/

2

β

k–1

” oraz „+

1

/

2

β

k–1

–1”.

Odpowied

ź

: Nale

ż

y podstawi

ć

do ogólnego wzoru warto

ś

ci odpowiadaj

ą

ce skrajnym liczbom –

w systemie naturalnym i spolaryzowanym odpowiednio zero lub najwi

ę

ksz

ą

cyfr

ę

na ka

ż

dej pozycji,

w systemach uzupełnieniowych odpowiednio {

β/2

–1,

β

–1,…,

β

–1} dla podstaw parzystych oraz

{

β

/2,0,…,0} dla nieparzystych, tak aby zakres był symetryczny.

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

10

Lista nr 1

1. Zapisz w systemie uzupełnieniowym do 2 (U2) z czterema bitami cz

ęś

ci ułamkowej liczby:

a) – 674,581

10

b) – 0A,12

16

c) – 3,012

8

d) + 34,56

10

e) 4,56

10

– 4,5(6)

10

Porównaj otrzymane kody z notacj

ą

w systemie uzupełnieniowym do 1 (U1) i systemie znak-moduł.

Wskazówka: Najpierw kodujemy warto

ść

bezwzgl

ę

dn

ą

, roszerzaj

ą

c j

ą

lewostronnie zerem (w systemie

znak-moduł rozszerzenie jest zb

ę

dne), potem wykonujemy „wchłoni

ę

cie” znaku.

2. Dodaj i odejmij liczby 4-cyfrowe podane w dziesi

ę

tnym uzupełnieniowym systemie pełnym (U10):

a) 6745

±

8123

b) 9,745

±

0,8(23)

c) 31,56

±

84,23

d) 9,994

±

9,916

U

ż

ywaj

ą

c lewostronnego rozszerzenia zweryfikuj poprawno

ść

wyników otrzymanych na 4 pozycjach.

Uwaga: Dodawanie jak w systemie dziesi

ę

tnym, rozszerzeniem dodatniej jest „0”, ujemnej „9”. Je

ś

li

wynik bez cyfry rozszerzenia oznacza t

ę

sam

ą

liczb

ę

co z cyfr

ą

rozszerzenia nie wyst

ą

pił nadmiar. Na

przykład (9)6745 + (9)8123= (9)4858 jest ujemne ale 4858 jest dodatnie, zatem wyst

ą

pił nadmiar.

Poprawne zaokr

ą

glenie w b) wymaga u

ż

ycia 2 cykli okresu.

3* Wyka

ż

,

ż

e w systemie stałobazowym i uzupełnieniowym, w dodawaniu lub odejmowaniu o ustalonej

liczbie pozycji argumentów i wyniku, u

ż

ycie dodatkowej pozycji lewostronnego rozszerzenia wyniku

i argumentów wystarczy do wykrycia nadmiaru (przekroczenia zakresu).

Wskazówka: Zakres argumentów z u

ż

yciem pozycji rozszerzenia jest wi

ę

kszy od oryginalnego, tyle razy,

jaka jest podstawa. Zatem wynik z rozszerzeniami jest zawsze poprawny. Rozszerzenie wyniku jest

zb

ę

dne, je

ś

li nie zostanie przekroczony oryginalny zakres, wi

ę

c wystarczy to sprawdzi

ć

.

4* Wyka

ż

,

ż

e w systemach uzupełnieniowych pełnych o bazach skojarzonych konwersj

ę

podstawy mo

ż

na

wykona

ć

przez grupowanie (

β

→

β

S

) lub dekompozycj

ę

cyfr (

β

S

→

β

).

Wskazówka: Liczby ujemne zapisz w konwencji znak-moduł.

5. Oblicz sum

ę

i ró

ż

nic

ę

liczb danych jako 10011101 i 01111001, 11011101 i 10111101, zakładaj

ą

c,

ż

e

podane ła

ń

cuchy k = 8 bitów (ci

ą

gi zero-jedynkowe) reprezentuj

ą

liczby w kodzie

a) naturalnym (NB)

b) uzupełnieniowym pełnym (U2)

c) uzupełnieniowym niepełnym (U1)

d) znak-moduł (SM)

e) spolaryzowanym „+2

k–1

–1”

f) spolaryzowanym „+2

k–1

”.

Zweryfikuj poprawno

ść

otrzymanych wyników: A) wykonuj

ą

c działanie odwrotne (suma – argument,

ró

ż

nica + odjemnik) B) u

ż

ywaj

ą

c lewostronnego rozszerzenia (oprócz e) i f)).

Wskazówka: W systemach spolaryzowanych wygodnie jest wykona

ć

konwersj

ę

na system U2.

6. Znanych jest kilka najbardziej znacz

ą

cych bitów liczb 48-bitowych w kodzie uzupełnieniowym U2.

11101010..?? oraz

10011110..?? Sprawd

ź

, czy w ich dodawaniu i odejmowaniu wyst

ą

pi nadmiar.

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

11

Wskazówka: Nale

ż

y znale

źć

najwy

ż

sz

ą

pozycj

ę

na której jest zawsze wytwarzane przeniesienie

w dodawaniu (1+1) albo po

ż

yczka w odejmowaniu (0–1), a nast

ę

pnie (wynik na pozycjach wy

ż

szych

od tak znalezionej nie zale

ż

y od warto

ś

ci na pozycjach ni

ż

szych) zbada

ć

2 najwy

ż

sze przeniesienia

lub celowo

ść

u

ż

ycia bitów rozszerzenia lewostronnego.

7. Korzystaj

ą

c z zale

ż

no

ś

ci

Y

X

Y

X

+

=

−

i zakładaj

ą

c,

ż

e liczby s

ą

dane w systemie naturalnym, oblicz:

a) 6745 – 8123

b) 9,745 – 0 , 823

c) 34,56– 81,23

d) 10011101

2

– 01111001

2

Sprawd

ź

otrzymane wyniki wykonuj

ą

c działania odwrotne (ró

ż

nica + odjemnik).

Uwaga: Nale

ż

y sprawdzi

ć

, czy nie powstaje nadmiar (w systemie naturalnym wynik musi by

ć

dodatni!).

8. Wyka

ż

,

ż

e w systemie naturalnym lub uzupełnieniowym pełnym mno

ż

enie liczb m–pozycyjnych nie

powoduje nadmiaru, je

ś

li wynik jest kodowany na co najmniej 2m pozycjach.

Wskazówka: Zakresem iloczynu jest [0, (

β

m

–1

)

2

]= [0,

β

2

m

–2

β

m

+1<

β

2

m

–1]

9. Wynik mno

ż

enia m–bitowych liczb w kodzie U2 jest kodowany na 2m–1 bitach. Czy jest mo

ż

liwe

wyst

ą

pienie nadmiaru, a je

ś

li tak to przy jakich warto

ś

ciach mno

ż

nej i mno

ż

nika?

Wskazówka: Zakresem iloczynu jest [–2

m–1

×

(2

m–1

–1), (–2

m–1

)

2

]= [–2

2m–2

+2

m–1

, 2

2m–2

]. Liczba 2

2m–2

musi

by

ć

zakodowana na 2m bitach, dla pozostałych wystarczy 2m–1 bitów.

A. Przyjmuj

ą

c,

ż

e 6-bitowe operandy s

ą

dane w dwójkowym kodzie uzupełnieniowym a) pełnym (U2),

b) niepełnym (U1) wykonaj mno

ż

enia: i) 110101

×

011011 ii) 011101

×

110111 iii) 101001

×

111111.

*Wykonaj mno

ż

enie (U2) stosuj

ą

c przekodowanie iloczynów cz

ęś

ciowych eliminuj

ą

ce rozszerzenia.

Uwaga: Iloczyn cz

ęś

ciowy odpowiadaj

ą

cy najwy

ż

szemu bitowi mno

ż

nika ma wag

ę

ujemn

ą

. Pami

ę

taj

o bitach

rozszerzenia,

za

ś

w

kodzie

U1

uwzgl

ę

dnij

przeniesienie

okr

ęż

ne

(e-a-c).

* Pami

ę

taj o poprawnym kodowaniu zera, przekodowaniu iloczynu cz

ęś

ciowego odpowiadaj

ą

cego

najwy

ż

szemu bitowi mno

ż

nika oraz korekcji wyniku.

B. Poka

ż

,

ż

e w systemie naturalnym dwójkowym i systemie uzupełnieniowym do 2 mno

ż

enie przez stał

ą

,

która jest sum

ą

lub ró

ż

nic

ą

pot

ę

g dwójki mo

ż

na wykona

ć

jako dodawanie skalowanej mno

ż

nej.

Rozwi

ą

zanie: Oczywiste, to jest po prostu zwykły sekwencyjny algorytm mno

ż

enia.

C. Oblicz iloczyn liczb 4-cyfrowych podanych w dziesi

ę

tnym uzupełnieniowym systemie pełnym (U10):

a) 6745

U10

×

8123

U10

b) 9745

U10

×

0823

U10

c) 3156

U10

×

8423

U10

d) 9994

U10

×

9916

U10

Wskazówka: Warto

ść

przypisana najbardziej znacz

ą

cej cyfrze liczby ujemnej jest ujemna i wynosi d

−

β

,

gdzie d jest standardow

ą

warto

ś

ci

ą

cyfry (|”

β

−1

”| =

β

−1−

β

= −1

) (w systemie U10 |”9”| =

−1

).

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

12

Lista nr 2

1. Oblicz iloczyn liczb 4-cyfrowych podanych w ósemkowym uzupełnieniowym systemie pełnym (U8):

a) 5745

U8

×

7123

U8

b) 7745

U8

×

0723

U8

c) 3156

U8

×

6423

U8

d) 7774

U8

×

7716

U8

Wskazówka: Zauwa

ż

,

ż

e warto

ść

przypisana najbardziej znacz

ą

cej cyfrze liczby ujemnej jest ujemna

i w systemie U8 wynosi d

− 8

, gdzie d jest standardow

ą

warto

ś

ci

ą

cyfry, zatem |”7”|=

−1

.

2. Oblicz bezpo

ś

rednio metod

ą

sekwencyjn

ą

(„kolejnych reszt”) z dokładno

ś

ci

ą

do 4 pozycji znacz

ą

cych

iloraz liczb reprezentowanych w systemie uzupełnieniowym pełnym

a) 01010011

U2

: 1011

U2

b) 1010011

U2

: 01011

U2

c) 876

U10

: 176

U10

d) 876

U10

: 761

U10

.

Wskazówka: Nie zapomnij o skalowaniu, tak aby |X|<|D| oraz odwrotnym przeskalowaniu ilorazu. Aby

unikn

ąć

generowania nieznacz

ą

cych bitów, zadbaj aby |D/2|<|X|<|D|.

3. Wykonaj bezpo

ś

rednio w systemie U10 dzielenia z dokładno

ś

ci

ą

do 4 cyfr znacz

ą

cych ilorazu:

a) 110101 : 011011

b) 011101 : 110111 c) 101001 : 11111

d) 101001 : 10011

e) 1,10101 : 01101,1

f) 0,11101 : 110,111 g) 1010,01 : 111,11

h) 101001 : 100,11

Sprawd

ź

, wykonuj

ą

c mno

ż

enie, poprawno

ść

otrzymanych wyników.

Wskazówka: Zauwa

ż

,

ż

e mo

ż

na tak przeskalowa

ć

dzielnik (dzieln

ą

), aby iloraz był ułamkiem wła

ś

ciwym

4. Wykonaj bezpo

ś

rednio w kodzie U2 dzielenia z dokładno

ś

ci

ą

do 4 cyfr znacz

ą

cych ilorazu:

a) 110101 : 011011

b) 011101 : 110111 c) 101001 : 11111

d) 101001 : 10011

e) 1,10101 : 01101,1

f) 0,11101 : 110,111 g) 1010,01 : 111,11

h) 101001 : 100,11

Sprawd

ź

, wykonuj

ą

c mno

ż

enie, poprawno

ść

otrzymanych wyników.

Wskazówka: Przeskaluj dzielnik (dzieln

ą

) tak, aby iloraz był ułamkiem.

5. Wykonaj w kodzie U2 z dokładno

ś

ci

ą

do 4 cyfr znacz

ą

cych ilorazu dzielenie nieodtwarzaj

ą

ce liczb:

a) 110101 : 011011

b) 011101 : 110111 c) 101001 : 11111

d) 101001 : 10011

e) 1,10101 : 01101,1

f) 0,11101 : 110,111 g) 1010,01 : 111,11

h) 101001 : 100,11

Wskazówka: Przeskaluj dzielnik (dzieln

ą

) tak, aby iloraz był ułamkiem. Wykonaj pierwsze działanie

stosownie do znaków dzielnej i dzielnika (dodaj dzielnik gdy znaki s

ą

przeciwne).

6. Oblicz metod

ą

sekwencyjn

ą

(„kolejnych reszt”) pierwiastek kwadratowy z liczb

a) 123456

7

, b) 1010 0010 0111 1100

2

, c) 987654321

10

d) 123,456

7

, e) 10100 0100,1111 100

2

z dokładno

ś

ci

ą

do jednej, dwóch i siedmiu cyfr znacz

ą

cych oraz podaj trzeci

ą

i czwart

ą

reszt

ę

.

Uwaga: Zwró

ć

uwag

ę

na poprawne wst

ę

pne skalowanie.

7. Dane jest przybli

ż

enie pierwiastka kwadratowego z dokładno

ś

ci

ą

do 3 cyfr znacz

ą

cych i trzecia reszta.

Podaj dwie kolejne cyfry przybli

ż

enia pierwiastka, je

ś

li:

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

13

a) Q

3

=123

7

, r

3

=3456

7

, b) Q

3

=123

10

, r

3

= 3456

10

, c) Q

3

=101

2

, r

3

=11101

2

,

Wskazówka: Przeanalizuj nierówno

ść

, która jest podstaw

ą

obliczenia czwartej cyfry ilorazu – wyst

ę

puje

w niej podwojone skalowane trzecie przybli

ż

enie Q

3

oraz reszta r

3

:

8. Dane jest przybli

ż

enie pierwiastka kwadratowego z dokładno

ś

ci

ą

do 4 cyfr znacz

ą

cych i czwarta reszta

równa 0. Oszacuj warto

ść

liczby pierwiastkowanej, je

ś

li: a) Q

4

=12,34

7

, b) Q

4

=1,234

10

, c) Q

4

=1101

2

.

Wskazówka: Przeanalizuj nierówno

ść

, która jest podstaw

ą

obliczenia pi

ą

tej cyfry ilorazu – wyst

ę

puje

w niej podwojone skalowane czwarte przybli

ż

enie Q

4

oraz reszta r

4

. Zastanów si

ę

jaka musiała by

ć

czwarta reszta, je

ś

li pi

ą

ta jest zerem. Zauwa

ż

,

ż

e mo

ż

e istnie

ć

wiele rozwi

ą

za

ń

.

9. Oblicz metod

ą

nieodtwarzaj

ą

c

ą

pierwiastek kwadratowy z liczb:

a) 1010 0010 0111 1100

2

, b) 123,456

8

, c) 10100 0100,1111 100

2

z dokładno

ś

ci

ą

do dwóch i pi

ę

ciu cyfr znacz

ą

cych oraz podaj trzeci

ą

i czwart

ą

reszt

ę

.

A* Poka

ż

,

ż

e w naturalnym systemie dwójkowym dzielenie przez stał

ą

, która jest sum

ą

lub ró

ż

nic

ą

dwóch pot

ę

g dwójki, mo

ż

na wykona

ć

przez odejmowanie, je

ś

li dzielenie nie wytwarza reszty.

Wskazówka: Przyjmij dla uproszczenia,

ż

e stał

ą

jest 2

m–1

±

1. Zauwa

ż

,

ż

e wtedy X = (2

m–1

±

1)Q, sk

ą

d

wynika,

ż

e Q =

±

(X–2

m–1

Q), zatem warto

ś

ci (k–1) najni

ż

szych bitów ilorazu s

ą

takie jak najni

ż

sze

bity dzielnej, a drugi argument odejmowania lub dodawania na wy

ż

szych pozycjach jest sekwencyjnie

wyznaczany jako warto

ść

o (k–1) pozycji ni

ż

szego bitu obliczonych ju

ż

pozycji ilorazu.

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

14

Lista nr 3

1. Twierdzenie Euklidesa o podzielno

ś

ci liczb orzeka,

ż

e najwi

ę

kszy wspólny podzielnik dwóch liczb

naturalnych jest podzielnikiem reszty z dzielenia wi

ę

kszej przez mniejsz

ą

. Wyka

ż

, równowa

ż

no

ść

tej

tezy z tez

ą

,

ż

e najwi

ę

kszy wspólny podzielnik dwóch liczb jest podzielnikiem ich ró

ż

nicy.

Wskazówka: Reszta jest wynikiem wielokrotnego odejmowania mniejszej od wi

ę

kszej – tyle razy ile

wynosi iloraz. Ró

ż

nica jest wi

ę

c równa wielokrotno

ś

ci mniejszej liczby + reszta...(XmodY=X– kY<Y)

2. Korzystaj

ą

c z twierdzenia Euklidesa znajd

ź

najwi

ę

kszy wspólny podzielnik liczb:

a) 6745 i 8123

b) 9994, 92 i 9916

c) 375, 243, 345 i 126

d) 2

20

–1 oraz 2

5

+1

Wskazówka: Zastosuj twierdzenie Euklidesa b) NWD(a,b,c)= NWD(NWD(a,b), NWD(b,c))

3. Poka

ż

,

ż

e liczby 2

k

+ 1 i 2

k + 1

+ 1 s

ą

wzgl

ę

dnie pierwsze (k

∈

N

– jest liczb

ą

naturaln

ą

)

*Czy prawdziwe jest twierdzenie,

ż

e liczby 2

k

+ 1 i 2

r

+ 1 (k , r

∈

N

) s

ą

wzgl

ę

dnie pierwsze?

Wskazówka: Zastosuj twierdzenie Euklidesa. Zauwa

ż

,

ż

e 2

k + 1

= 2

×

2

k

= 2

k

+ 2

k

*Poka

ż

kontrprzykład – (2

1

+1,2

3

+1) = 3. Udowodnij,

ż

e gdy k jest nieparzyste, to (2

k

+ 1 , 2

k + 2

) = 3 .

4* Wyka

ż

,

ż

e liczby

)

1

2

(

2

+

n

oraz

)

1

2

(

+

n

i

)

2

2

(

1

2

+

+

n

i

)

1

2

(

−

n

(n

∈

N

) s

ą

wzgl

ę

dnie pierwsze.

Wskazówka: Zastosuj twierdzenie Euklidesa i zwi

ą

zki pot

ę

g oraz wzory skróconego mno

ż

enia.

5. Nie wykonuj

ą

c dzielenia wyznacz reszt

ę

z dzielenia liczby 1011 0011 0111 1101

2

przez

a) 1111

2

b) 10001

2

c) 11111

2

d) 10000001

2

.

Wskazówka: Zastosuj wła

ś

ciwo

ś

ci kongruencji i zale

ż

no

ść

(m

±

1) mod m =

±

1 .

6. Stosuj

ą

c reguły arytmetyki resztowej oblicz reszty całkowite (dodatnie lub ujemne) wobec modułów:

257

10

, 7

8

, 65

10

, 3F

16

, 11

16

, 0FF

16

dla liczb 4652

8

i 0ABCD

16

, oraz ich sumy, ró

ż

nicy i iloczynu.

Wskazówka: Zastosuj wła

ś

ciwo

ś

ci kongruencji i zale

ż

no

ść

(m

±

1) mod m =

±

1 .

7. Podaj reprezentacj

ę

resztow

ą

liczby 23456

10

w bazie: a) (29, 30, 31), b) (99, 100, 101), a) (63, 64, 65).

Wskazówka: Wyznacz reprezentacj

ę

liczby w systemie o podstawie a) 30, b) 100, c) 64 oraz zastosuj

wła

ś

ciwo

ś

ci kongruencji i zale

ż

no

ść

(m

±

1) mod m =

±

1 .

8* Znajd

ź

odwrotno

ś

ci multyplikatywne iloczynów par modułów bazy systemu resztowego (a–1, a, a+1)

wzgl

ę

dem trzeciego z nich, zakładaj

ą

c,

ż

e a jest liczb

ą

parzyst

ą

.

Wskazówka: Wykorzystaj zale

ż

no

ść

(m

±

1) mod m =

±

1

9* Wektor (1, 2, 3) jest reprezentacja resztow

ą

liczby x w bazie (29, 30, 31). Znajd

ź

t

ę

liczb

ę

w zbiorze

kongruencji naturalnych (x

∈

[0, M=29

⋅

30

⋅

31)) i całkowitych (x

∈



–(M–1)



/2,



M–1



/2)).

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

15

Wskazówka: Wykorzystuj

ą

c zale

ż

no

ść

(m

±

1) mod m =

±

1 znajd

ź

odwrotno

ś

ci multyplikatywne

niepełnych iloczynów modułów bazy i zastosuj chi

ń

skie twierdzenie o resztach. Zauwa

ż

,

ż

e je

ś

li m

0

jest najmniejszym modułem bazy, to (x, x, x, … , x) = x oraz (–x, –x, –x, … , – x) = –x = M–x, na

przykład zawsze jest (1, 1, 1, … , 1) = 1 oraz (–1, – 1, – 1, … , – 1) = –1 = M –1, a tak

ż

e (m

1

–1, m

2

– 1,

m

3

– 1, … , m

k

– 1) = M –1 = –1.

A. Zapisz w 32-bitowym formacie zmiennoprzecinkowym standardu IEEE 754 liczby o warto

ś

ciach:

a) 674,531

8

b) 0,12

8

⋅

8

-51

c) – 0ABC,DE

16

d) 10,1010101010

U2

⋅

4

-61

Wskazówka: Zapisz liczb

ę

w systemie znak-moduł i tak przeskaluj, aby moduł był standardowy.

B. Zapisz w 32-bitowym formacie zmiennoprzecinkowym IEEE 754 pierwiastki kwadratowe z liczb:

a) 1010 0010, 0111 1100

2

, b) 123,456

8

, c) 10100 0100, 1111 100

2

Wskazówka: Pami

ę

taj o skalowaniu i bicie ukrytym.

C. Oblicz i zapisz w 32-bitowym formacie zmiennoprzecinkowym standardu IEEE 754 z dokładno

ś

ci

ą

do

5 cyfr znacz

ą

cych pierwiastki kwadratowe z liczb danych w tym formacie:

a) 0 0100 0100 111 1100 1010 0010 0111 1100, b) 0 1010 0101 1111 1010 0100 1111 1111 100

2

c) 0 0100 0101 111 1100 1010 0010 0111 1100, d) 0 1010 0100 1111 1010 0100 1111 1111 100

2

Wskazówka: Zwró

ć

uwag

ę

na nieparzyste wykładniki. Pami

ę

taj o skalowaniu i bicie ukrytym.

D* Wyka

ż

,

ż

e w odejmowaniu (dodawaniu) zmiennoprzecinkowym operandów dokładnych, bit S dla

znormalizowanej ró

ż

nicy (sumy) mo

ż

e by

ć

wyznaczony przed wykonaniem działania.

Wskazówka: Rozpatrz przypadki składników o identycznych i ró

ż

nych wykładnikach.

E. Wyznacz z dokładno

ś

ci

ą

do 4 bitów znacznika zaokr

ą

glenia argumentów 1,101111011 i 1,101111001

uzupełnione bitami G, R, S. Wykonaj ich mno

ż

enie i porównaj z wynikiem pełnego mno

ż

enia.

Wskazówka: Bit G to bit pi

ą

ty, bit R wynika z przybli

ż

enia do najbli

ż

szej (tu oboj

ę

tne czy parzystej czy

nieparzystej, bit S wskazuje, czy na odcinanych pozycjach była cho

ć

jedna „1”.

F* Wyka

ż

,

ż

e w mno

ż

eniu znormalizowanych operandów, bit S znormalizowanego iloczynu mo

ż

e by

ć

wyznaczony przed mno

ż

eniem. Poka

ż

,

ż

e jeden z czynników mo

ż

e by

ć

zdenormalizowany.

Wskazówka: Zauwa

ż

,

ż

e iloczyn ma tyle samo pozycji znacz

ą

cych, co ka

ż

dy z czynników, a co najmniej

jeden z czynników ma okre

ś

lony zakres (jest znormalizowany).

G* Oszacuj maksymalny bł

ą

d przybli

ż

enia ró

ż

nicy podczas odejmowania znormalizowanych operandów

obliczonych z tak

ą

sam

ą

dokładno

ś

ci

ą

bezwzgl

ę

dn

ą

znacznika (mantysy).

Wskazówka: Zbadaj najgorszy przypadek. Wykorzystaj analiz

ę

z zad. D

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

16

Lista nr 4

1. Stosuj

ą

c reguły działa

ń

w algebrze Boole’a upro

ść

poni

ż

sze wyra

ż

enia

a) x+(x

⊕

y)

b) xyz+(x

⊕

y) +(z

⊕

y)

c) x+xy+xyz

d) zy+(x

⊕

y)

e) zx+z(x

⊕

1)

f) x+xy+(x

⊕

yz)

Wskazówka: Zamie

ń

wyra

ż

enia zawieraj

ą

ce

⊕

na sumy iloczynów i zminimalizuj.

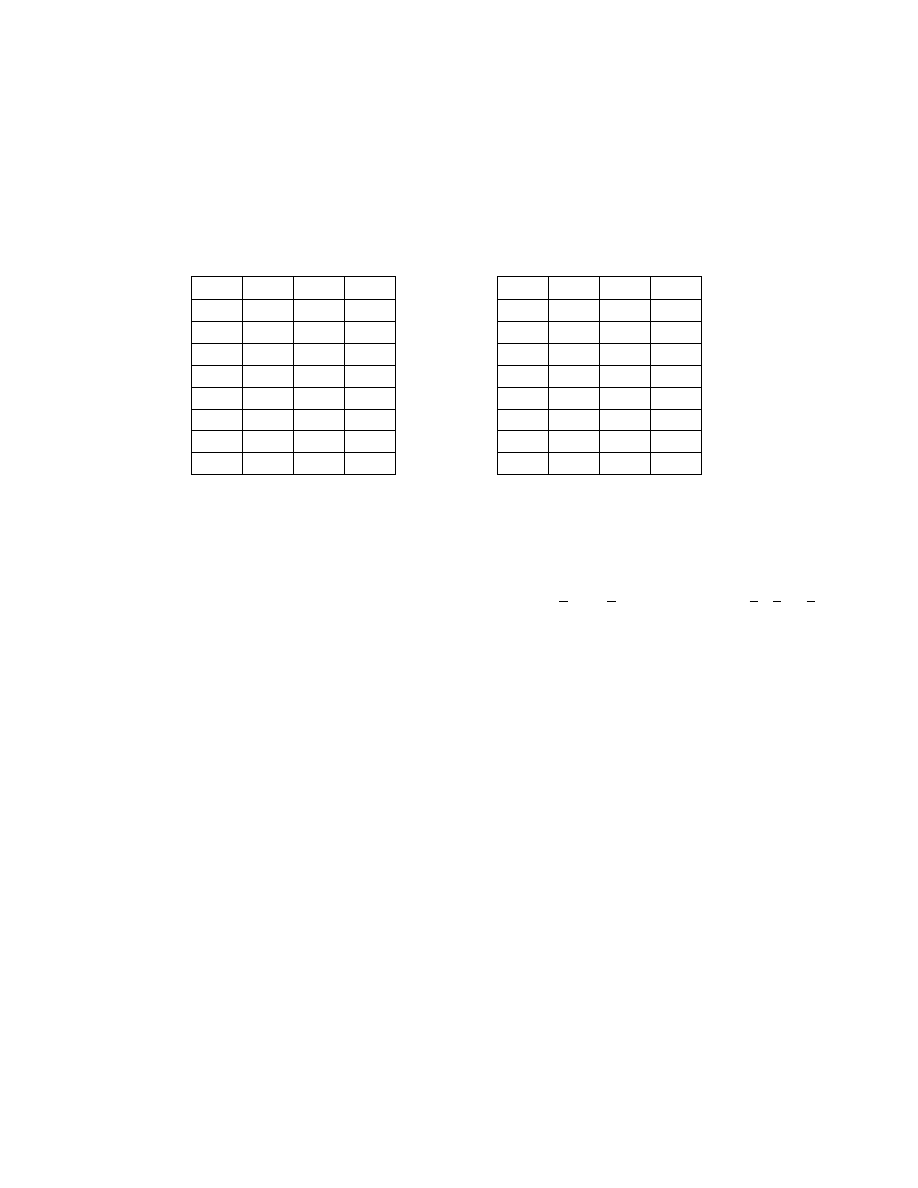
2. Na podstawie tabeli prawdy (tabeli warto

ś

ci) funkcji logicznych f

1

i f

2

podaj ich wszystkie mintermy

(konstytuenty iloczynu) i maxtermy (konstytuenty sumy) oraz postaci formalne

x

3

x

2

x

1

f

1

(

x

)

x

3

x

2

x

1

f

2

(

x

)

0

0

0

0

0

0

0

1

0

0

1

0

0

0

1

1

0

1

0

1

0

1

0

1

0

1

1

0

0

1

1

0

1

0

0

1

1

0

0

0

1

0

1

1

1

0

1

1

1

1

0

1

1

1

0

0

1

1

1

0

1

1

1

1

Wskazówka: Zapisz funkcje jako sumy iloczynów lub iloczyny sum. Upraszczaj wyra

ż

enia bezpo

ś

rednio

na podstawie podobie

ń

stw ci

ą

gów warto

ś

ci zmiennych odpowiadaj

ą

cych tej samej warto

ś

ci funkcji,

np. f(x

1

, … , x

i–1

,

φ

, x

i+1

, … , x

n

) = f(x

1

, … , x

i–1

,

0

, x

i+1

, … , x

n

) + f(x

1

, … , x

i–1

,

1

, x

i+1

, … , x

n

) .

3. Wyznacz funkcje dualne i komplementarne do funkcji

2

3

1

2

1

)

(

x

x

x

x

f

+

=

x

i

)

(

)

(

1

2

3

1

3

2

x

x

x

x

x

f

+

+

=

x

oraz ich sumy logicznej i iloczynu logicznego. Narysuj sieci logiczne realizuj

ą

ce te funkcje.

Wskazówka: Zastosuj prawa de’Morgana.

4. Korzystaj

ą

c z twierdzenia Shannona rozwi

ń

wszystkie funkcje z zadania 3 wzgl

ę

dem zmiennej x

3

.

Wskazówka: Oblicz f(x

3

= 0) oraz f(x

3

= 1) i wyniki podstaw do wzoru Shannona.

5. Wyka

ż

,

ż

e warto

ść

funkcji logicznej [z

⋅

f(x)+(z

⊕

f(x))] f(x) nie zale

ż

y od zmiennej z.

Wskazówka: Zamie

ń

wyra

ż

enie zawieraj

ą

ce

⊕

na sum

ę

iloczynów i zminimalizuj lub poka

ż

,

ż

e ró

ż

nica

boole’owska wzgl

ę

dem z wynosi 0.

6* Poka

ż

,

ż

e ka

ż

d

ą

funkcj

ę

logiczn

ą

mo

ż

na wyrazi

ć

za pomoc

ą

tylko funkcji NOR (suma negacji) lub

tylko funkcji NAND (iloczyn negacji).

Wskazówka: Przedstaw funkcje sumy, iloczynu i negacji za pomoc

ą

funkcji NOR lub NAND

7. Wyznacz charakterystyki AT sieci logicznych realizujacych funkcje dane przez wyra

ż

enia w zadaniu 1

Odpowied

ź

: Wyznacz najdłu

ż

sz

ą

ś

cie

ż

k

ę

, policz bramki przeliczeniowe na tej

ś

cie

ż

ce (T) i wszystkie (A).

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

17

8. Subtraktor 1-bitowy realizuje funkcje logiczne ró

ż

nicy d = f (x, y, z) i po

ż

yczki b = h (x, y, z) równowa

ż

ne

arytmetycznemu równaniu odejmowania 1-bitowego x – y – z = – 2d + b (x , y , z , d , b

∈

{0, 1}) . Podaj

tabel

ę

prawdy subtraktora i wyznacz charakterystyki AT subtraktora 8-bitowego.

Odpowied

ź

: Opó

ź

nienie (T) oblicz osobno dla obu funkcji.

9. Sumator 1-bitowy realizuje funkcje logiczne sumy s = f (x, y, z) i przeniesienia c = h (x, y, z) równowa

ż

ne

arytmetycznemu równaniu dodawania 1-bitowego x + y + z = 2c + s (x , y , z , s , c

∈

{0, 1}) . Zaprojektuj

ogniwo inkrementera realizuj

ą

cego funkcje s = f (x, 1, z) oraz c = h (x, 1, z) i oblicz charakterystyki AT.

Wskazówka: Wyznacz i zminimalizuj funkcje sumy i przeniesienia.

A. Sumator warunkowy 1-bitowy realizuje alternatywne funkcje logiczne warunkowej sumy s

0

= f (x, y, 0),

s

1

= f (x, y, 1) i przeniesienia c

0

= h (x, y, 0), c

1

= h (x, y, 1) równowa

ż

ne arytmetycznemu równaniu

dodawania 1-bitowego przy zało

ż

eniu,

ż

e przeniesienie wej

ś

ciowe jest odpowiednio równe 0 albo 1.

Podaj tabel

ę

prawdy sumatora i wyznacz te funkcje.

Wskazówka: Wyznacz i zminimalizuj funkcje sumy i przeniesienia.

B* Narysuj schemat logiczny sumatora 1-bitowego, którego wyj

ś

cia sumy i przeniesienia s

ą

wytwarzane

z u

ż

yciem multiplekserów sterowanych przeniesieniem wej

ś

ciowym na podstawie funkcji sumy i

przeniesienia zerowego i jedynkowego s

0

, s

1

, c

0

, c

1

. Wyznacz charakterystyki AT tego układu.

Wskazówka: Wyznacz i zminimalizuj funkcje sumy i przeniesienia.

C* Poka

ż

,

ż

e charakterystyki AT sieci realizuj

ą

cych funkcj

ę

dualn

ą

i komplementarn

ą

s

ą

jednakowe.

Wskazówka: Wykorzystaj prawa de’Morgana i równowa

ż

no

ść

charakterystyk AT dla sumy logicznej

i iloczynu logicznego.

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

18

Lista nr 5

1. Oblicz charakterystyki AT sumatorów uniwersalnych RCA dla kodów k-bitowych:

a) uzupełnieniowego pełnego (U2)

b) uzupełnieniowego niepełnego (U1)

c) znak-moduł,

d) spolaryzowanego ujemnie „+2

k–1

”

e) spolaryzowanego dodatnio „+2

k–1

–1”

Wskazówka: Wykorzystaj charakterystyki AT sumatora 1-bitowego.

2. Zaproponuj sposób kodowania cyfr i zaprojektuj sumator jedno- i cztero-pozycyjny dla systemu

a) U10 z kodowaniem cyfr w kodzie „+3” i kodzie BCD

b) dwójkowego negabazowego (

β

= –2),

c)* naturalnego trójkowego (

β

= 3) i dwójkowego z cyfr

ą

znakowan

ą

SD, (D={–1,0,+1})

Wskazówka: a), b) wykorzystaj zwi

ą

zki z sumatorem dwójkowym; c) wyznacz tabele prawdy.

3. Oblicz charakterystyki AT sumatora 24-bitowego z przeniesieniami przeskakuj

ą

cymi (carry-skip) je

ś

li

ma on struktur

ę

a)

3-4-4-3-4-4-2, b) 3-3-4-4-4-3-3,

c) 4-4-4-4-4-4,

d) 6-6-6-6, e)

optymaln

ą

.

Wskazówka:

A

rea: Oblicz liczb

ę

ogniw sumatora i liczb

ę

ogniw ła

ń

cucha przeskoku przeniesienia,

T

ime:Wyznacz

ś

cie

ż

ki krytyczne i oblicz opó

ź

nienie.

4. Zaprojektuj 8-bitowe układy inkrementacji i dekrementacji i wyznacz ich charakterystyki AT.

Wskazówka: Wykorzystaj charakterystyki 1-bitowego ogniwa inkrementera/dekrementera, wyznacz

najdłu

ż

sza scie

ż

k

ę

propagacji przeniesienia.

5. Zaprojektuj 4- i 8-bitowy sumator sum warunkowych i wyznacz ich charakterystyki AT.

Wskazówka: Zauwa

ż

,

ż

e sumatory wej

ś

ciowe s

ą

uproszczone, oblicz liczb

ę

multiplekserów.

6. Zaprojektuj 4- i 8-bitowy sumator prefiksowy PPA i wyznacz ich charakterystyki AT.

Wskazówka: Oce

ń

charakterystyki AT stopnia wej

ś

ciowego, poziomu sieci PPA i stopnia wyj

ś

ciowego.

7. W celu dodania n operandów k-bitowych u

ż

yto sumatora CSA (carry-save). Ile bitów zawiera suma?

Jakie jest opó

ź

nienie (T) podczas obliczania sumy, je

ś

li sum

ę

ko

ń

cow

ą

wytwarza

a) sumator ze skro

ś

n

ą

propagacj

ą

przeniesie

ń

RCA, b) sumator sum warunkowych COSA.

Obliczenia wykonaj dla n = 7, 15, 31 oraz k = 8, 16, 32.

Wskazówka: Liczb

ę

bitów sumy wyznacza jej zakres [0, n (2

k

–1)]. Liczba poziomów s

≤

(lg n/2) / lg 3/2.

Opó

ź

nienie jednego poziomu T=4 (do obu wyj

ść

)

8. Ile poziomów musi zawiera

ć

sumator CSA u

ż

yty do redukcji iloczynów cz

ęś

ciowych tworzonych

w mno

ż

eniu liczb 32-bitowych w kodzie naturalnym (NB)? Ile sumatorów elementarnych (3,2)

zawiera najbardziej skomplikowana gał

ąź

CSA odpowiadaj

ą

ca bitom o tej samej wadze.

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

19

Wskazówka: Patrz poprzednie zadanie.

9. Zaprojektuj sumator CSA dodaj

ą

cy odpowiednio 3, 4 i 8 operandów 4-bitowych w kodzie U2.

Wskazówka: Nie zapomnij o bitach rozszerzenia. Sprawd

ź

skutki, je

ś

li bity te zostan

ą

pomini

ę

te.

A. Wyznacz, uwzgl

ę

dniaj

ą

c czas ko

ń

cowego dodawania, najkrótszy czas dodawania 32 operandów 64-

bitowych w sumatorze CSA je

ś

li dysponujesz:

c) reduktorami (3,2) generuj

ą

cymi przeniesienia 1-bitowe, wnosz

ą

ce opó

ź

nienia T = 4

ka

ż

dy

d) *reduktorami (4,2) generuj

ą

cymi przeniesienia 2-bitowe, wnosz

ą

ce opó

ź

nienia T = 6

ka

ż

dy

Wskazówka: *Oblicz liczb

ę

poziomów i liczb

ę

bitów ko

ń

cowego dodawania.

D* Opracuj i uzasadnij algorytmy konwersji dwójkowo–dziesi

ę

tnej liczb całkowitych dodatnich, bez

wykonywania dzielenia, je

ś

li cyfry dziesi

ę

tne s

ą

kodowane: a) w kodzie BCD, b) w kodzie BCD+3.

Wskazówka: Konwersja BCD na dwójkowy: Zbadaj skutki przesuni

ę

cia o jeden bit w prawo liczby k

≥

2-

pozycyjnej w kodzie BCD. Konwersja dwójkowy na BCD/BCD+3: Wykorzystaj dodawanie.

E* Zaprojektuj generator reprezentacji resztowej liczby całkowitej 8- i 16-bitowej w kodzie NB

a) mod 1111

2

b) mod 10001

2

c) mod 111

2

d) mod 1001

2

Uwaga: *Jest wiele argumentów wej

ś

ciowych, które maj

ą

(b) i d)) ró

ż

ne znaki. Konieczne mo

ż

e by

ć

u

ż

ycie bitów rozszerzenia.

F* Zaprojektuj generator reprezentacji resztowej liczby całkowitej 8- i 16-bitowej w kodzie U2

a) mod 1111

2

b) mod 10001

2

c) mod 111

2

d) mod 1001

2

Wskazówka: Rozwa

ż

kongruencje w zbiorze liczb całkowitych. Zauwa

ż

,

ż

e najwy

ż

sz grupa bitów ma

znak

∑

∑

∑

−

=

−

=

−

−

−

−

−

=

−

−

+

+

−

=

+

−

1

0

2

1

1

2

0

1

1

2

)

2

2

(

2

2

2

s

i

i

i

k

s

i

s

i

i

s

k

k

s

k

i

i

i

k

k

x

x

x

x

x

H. Zaprojektuj sumator mod (2

8

–1) dwóch liczb całkowitych 8-bitowych w kodzie U2.

Wskazówka: Rozwa

ż

kongruencje w zbiorze liczb całkowitych.

G* Zaprojektuj sumatory mod (2

4

–1) i mod (2

4

+1) 4 liczb całkowitych 4-bitowych w kodzie U2.

Wskazówka: Rozwa

ż

kongruencje w zbiorze liczb całkowitych. Przeanalizuj struktury PPA.

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

20

Lista nr 6

1. Zakoduj na 8 bitach według prostej i odwrotnej reguły Booth’a w bazie 2 oraz w bazie 4 liczby:

a) –87

10

b) +121

10

c) 101101

2

c) 1011101

U2

Wskazówka: Zapisz liczby w systemie U2.

2. Przyjmuj

ą

c,

ż

e 6-bitowe operandy s

ą

dane w dwójkowym kodzie uzupełnieniowym a) pełnym (U2),

b) niepełnym (U1) i u

ż

ywaj

ą

c mno

ż

nika przekodowanego wg reguły Booth’a w bazie 2 i 4 wykonaj

mno

ż

enia: i) 110101

×

011011 ii) 011101

×

110111 iii) 101001

×

111111

Wskazówka: Nie zapomnij o bitach rozszerzenia iloczynów cz

ęś

ciowych.

3. Oblicz charakterystyki AT matrycy mno

żą

cej dwa operandy: a) 4-bitowe, b) 8-bitowe c)* n-bitowe

Wskazówka: Policz liczb

ę

elementarnych sumatorów oraz liczb

ę

poziomów akumulacji.

4* Zaprojektuj matryc

ę

mno

żą

c

ą

operandy 4-bitowe w kodzie U2 z wykorzystaniem przekodowania

mno

ż

nika wg reguły Bootha w bazie 4. Porównaj z innymi układami matrycowymi.

Wskazówka: Zaprojektuj element podstawowy matrycy.

5. Oblicz charakterystyki AT sumatora CSA u

ż

ytego do redukcji iloczynów cz

ęś

ciowych w mno

ż

eniu

operandów 4-, 8- bitowych danych: a) w kodzie NB, b) w kodzie U2 z eliminacj

ą

bitów rozszerzenia.

*Podaj oszacowanie charakterystyk AT dla mno

ż

enia operandów n-bitowych.

Wskazówka: Ad b) zauwa

ż

,

ż

e ka

ż

dy operand ma inn

ą

wag

ę

.

6. W dzieleniu w systemie naturalnym w bazie 4 skalowana reszta cz

ęś

ciowa ma warto

ść

2,2D. Wyznacz:

analitycznie i na podstawie parametrycznego wykresu dzielenia, kolejne dwie cyfry ilorazu.

Wskazówka: a) rozwi

ąż

dwa kolejne równania dzielenia; b) zaznacz reszt

ę

na osi odci

ę

tych i graficznie

znajd

ź

kolejn

ą

reszt

ę

(pierwsze odwzorowanie wg odcinka „q=2”), przeskaluj j

ą

i powtórz czynno

ś

ci.

7. W dzieleniu w systemie U2 przeskalowana reszta cz

ęś

ciowa ma warto

ść

: i) –0,2D, ii) +0,7D. Wyznacz:

analitycznie i na podstawie parametrycznego wykresu dzielenia kolejne dwie cyfry ilorazu, zakładaj

ą

c,

ż

e dzielnik D jest: a) ujemny, b) dodatni.

Wskazówka: Patrz poprzednie zadanie.

8. Wykonaj bezpo

ś

rednio w kodzie U2 dzielenia z dokładno

ś

ci

ą

do 4 cyfr znacz

ą

cych ilorazu:

a) 110101 : 011011

b) 011101 : 110111 c) 101001 : 11111

d) 101001 : 10011

e) 1,10101 : 01101,1

f) 0,11101 : 110,111 g) 1010,01 : 111,11

h) 101001 : 100,11

Sprawd

ź

, wykonuj

ą

c mno

ż

enie, poprawno

ść

otrzymanych wyników.

Wskazówka: Nie zapomnij przeskalowa

ć

dzielnej (i/lub dzielnika)

Rok I

ARYTMETYKA KOMPUTERÓW

rozwi

ązania

©Janusz Biernat, ARYT-ZADANIA-schematy’02

25 pa

ździernika 2004

21

9. Wykonaj wykres P-D dla dzielenia w bazie 4 i dzielnika z zakresu [1,2). Podaj ile bitów musi by

ć

porównywanych w celu wyznaczenia cyfr ilorazu.

Wskazówka:

A. Oblicz charakterystyki AT matryc dziel

ą

cych operandy 8-bitowe w kodzie NB i U2

Wskazówka: Przeanalizuj pełn

ą

ś

cie

ż

k

ę

propagacji przeniesienia.

B. Oblicz metod

ą

Newtona iloraz 3,1416 :2,7183.

Wskazówka: Wybierz pierwsze przybli

ż

enie

C. Oce

ń

czas obliczania pierwiastka kwadratowego z liczby całkowitej metod

ą

sekwencyjn

ą

(„kolejnych

reszt”) oraz na podstawie to

ż

samo

ś

ci: „suma n kolejnych nieparzystych liczb naturalnych jest równa

kwadratowi z ich liczby” (np. 1+3+5=3

2

1+3+5+7=4

2

, 1+3+5+7+9=5

2

itd.)

*Okre

ś

l minimalny czas oblicze

ń

, je

ś

li liczba jest zakodowana odpowiednio na 8, 16, 32 bitach.

Wskazówka: Zauwa

ż

,

ż

e

)

1

2

(

)

1

2

(

]

)

1

2

(

[

)

1

2

(

1

1

0

0

+

−

∆

=

+

−

+

−

=

+

−

=

∆

−

−

=
=

=
=

∑

∑

k

k

i

X

i

X

k

k

i

i

k

i

i

k

, wi

ę

c

oszacowaniem pierwiastka jest takie k, przy którym odst

ę

p sumy od X zmienia znak.

D* Oszacuj liczb

ę

kroków algorytmu CORDIC potrzebnych do obliczenia warto

ś

ci funkcji exp, ln, sin,

cos, arctg dla argumentu z przedziału [–1,1] z dokładno

ś

ci

ą

do 32 bitów cz

ęś

ci ułamkowej.

Wskazówka: Zastosuj odpowiednio wzory.

E* Oce

ń

czas obliczania pierwiastka trzeciego stopnia na podstawie algorytmu opartego na zale

ż

no

ś

ci:

∑∑

∑∑

∑

∑

−

=

=

=

−

=

=

=

=

=

−

⋅

=

⋅

−

⋅

=

−

1

1

1

1

1

0

1

1

2

3

6

2

3

))

1

(

(

3

)

3

3

(

n

j

j

i

n

j

j

i

n

i

n

i

i

i

i

i

i

i

n

n

Wskazówka: Zauwa

ż

zwi

ą

zek sumy zewn

ę

trznej z wewn

ę

trzn

ą

.