Wyznaczanie odporności na pękanie
materiałów kruchych –
metoda MML
Marcin Graba
POLITECHNIKA ŚWIĘTOKRZYSKA W KIELCACH
WYDZIAŁ
MECHATRONIKI I BUDOWY MASZYN
KATEDRA PODSTAW KONSTRUKCJI MASZYN
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Cel ćwiczenia
•
Rozrzut wyników doświadczalnych dla wyznaczania K
IC
•
Jak ze zbioru danych K
IC
wybrać
właściwą
wartość?
•
Procedury SINTAP i FITNET
•
Rodzaje pękania i krzywa przejścia krucho plastycznego
•
Omówienie zakresów na krzywej przejścia krucho-plastycznego
•
Metoda MML dla próbek badanych w tej samej temperaturze
•
Metoda MML dla próbek badanych w różnych temperaturach
•
Metoda MML dla zbioru próbek badanych w różnej temperaturze
•
Wpływ liczby wyników na temperaturę
T
0
•
Wykonanie ćwiczenia
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
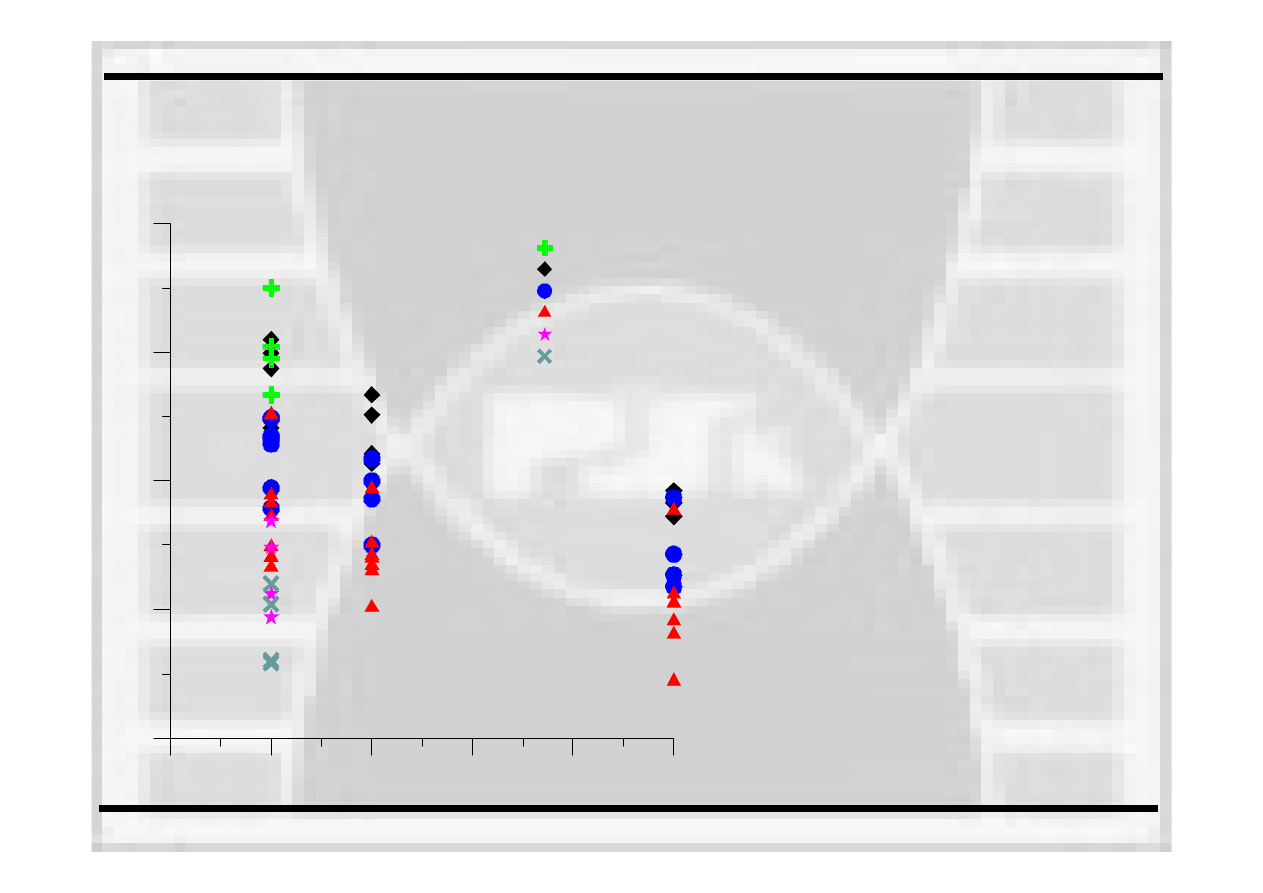
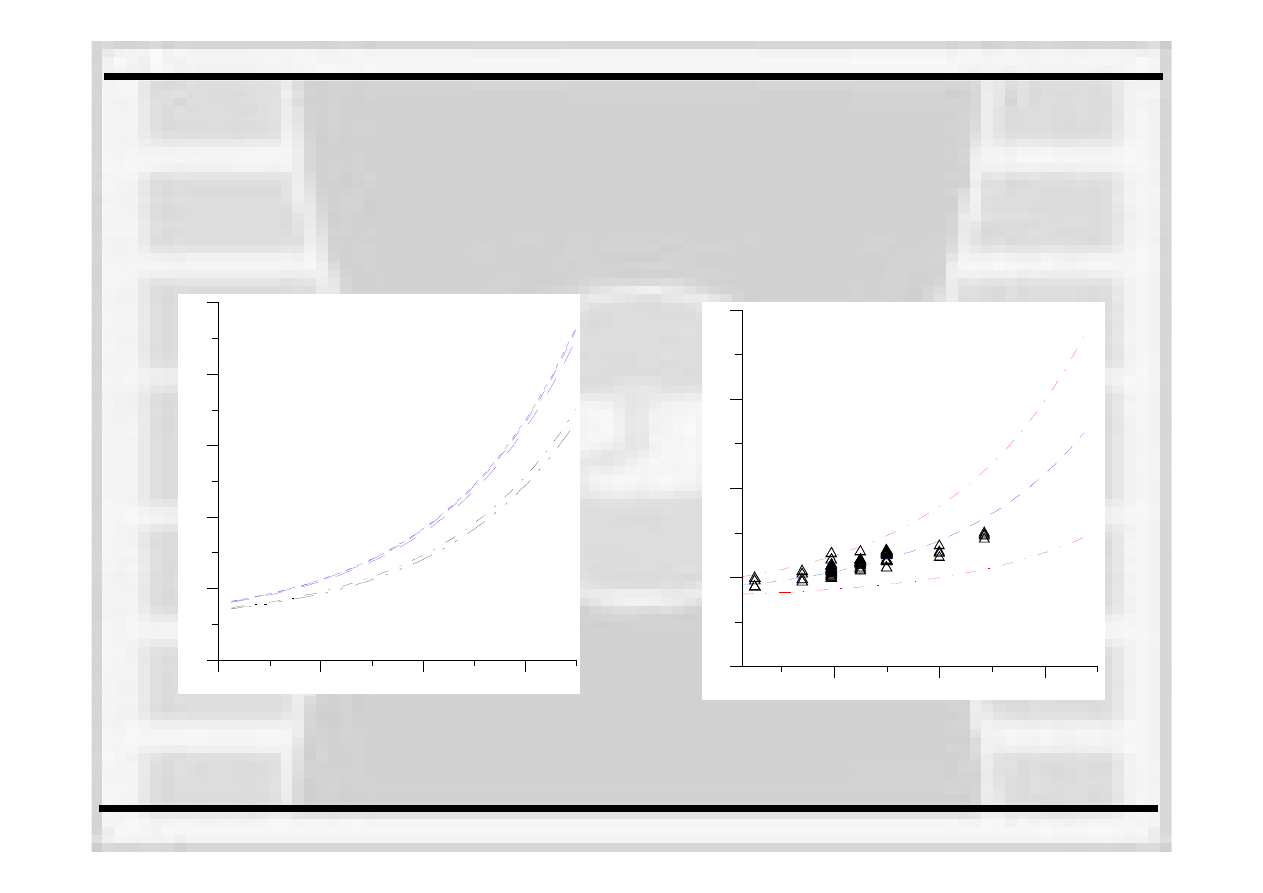
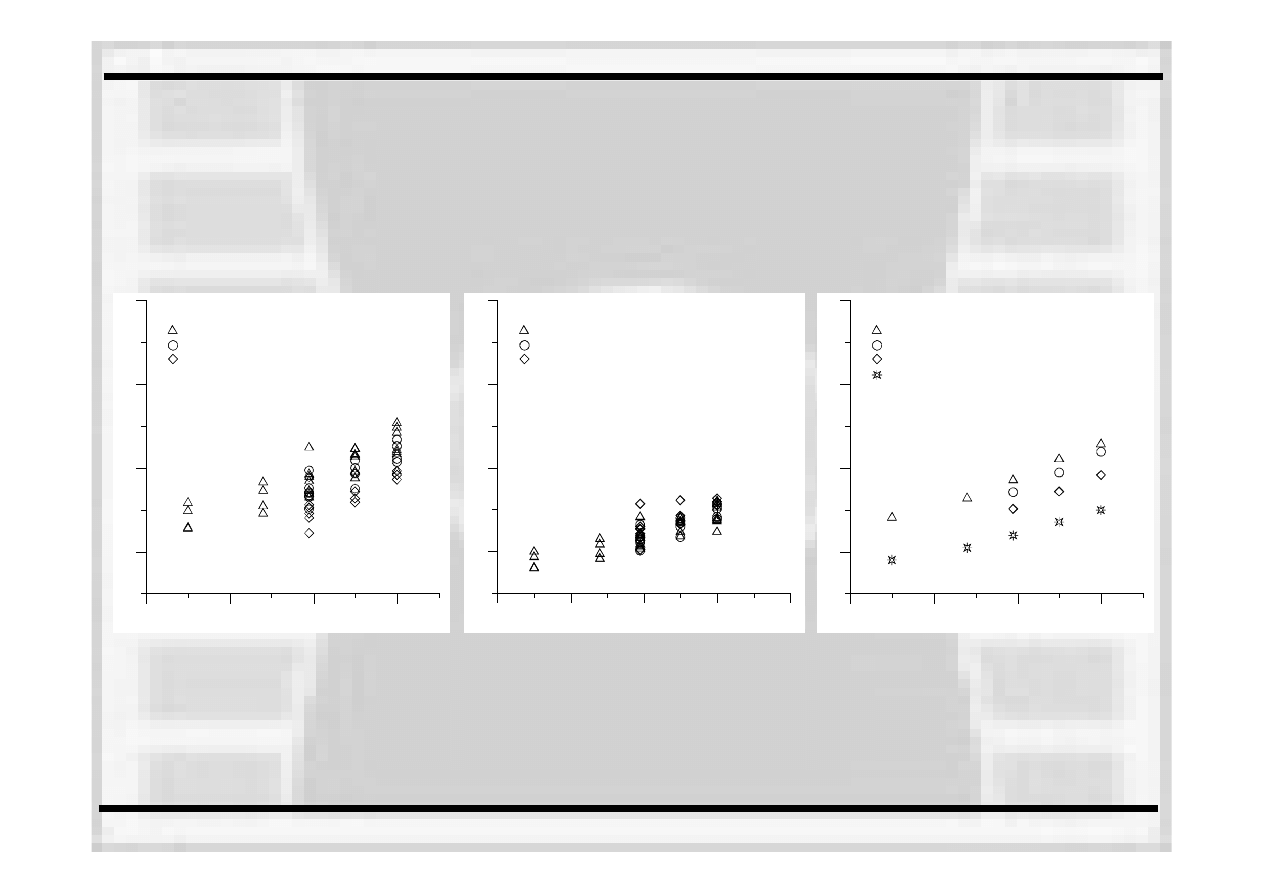
Rozrzut wyników doświadczalnych
dla wyznaczonych wartości K
IC
Rozrzut wyników okazje się
być
dość
duży i może sięgać
nawet 50% lub więcej.
Problemem jest więc wybranie
właściwej wartości będącej
odpornością
na pękanie,
oznaczaną
jako K
mat.
2
4
6
8
10
12
grubość próbki, B [mm]
40
50
60
70
80
ws
p
ó
łcz
yn
ni
k i
n
te
ns
yw
no
ści
n
a
p
ręż
e
ń
, K
[M
Pa
(m
)
0,
5
]
T = 0
°
C
T = -20
°
C
T = -30
°
C
T = -40
°
C
T = -50
°
C
T = -70
°
C
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Rozrzut wyników doświadczalnych
dla wyznaczonych wartości K
IC
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Rozrzut wyników doświadczalnych
dla wyznaczonych wartości K
IC
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Jak ze zbioru danych K
IC
wybrać
właściwą
wartość?
•
policzyć
wartość
średnią
ze zbioru wszystkich wyników–
wszystkie dane
muszą
być
dla tej samej temp., grubości i długości pęknięcia;
•
uszeregować
je w kolejności od najmniejszego do największego
i wyznaczyć
medianę
ze zbioru danych –
wszystkie dane muszą
być
dla tej
samej temp., grubości i długości pęknięcia;
•
uszeregować
je w kolejności od najmniejszego do największego
i wyznaczyć
minimalną
wartość
ze zbioru danych –
wszystkie dane muszą
być
dla tej samej temp., grubości i długości pęknięcia; otrzymany wynik
będzie bardzo konserwatywny i bezpieczny ale nie ekonomiczny;
•
uszeregować
je w kolejności od najmniejszego do największego
i wyznaczyć
maksymalną
wartość
ze zbioru danych –
wszystkie dane muszą
być
dla tej samej temp., grubości i długości pęknięcia; otrzymany wynik nie
będzie konserwatywny, będzie ekonomiczny, ale czy bezpieczny;
•
zastosować
procedury SINTAP i FITNET oraz krzywą
MASTER CURVE;
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
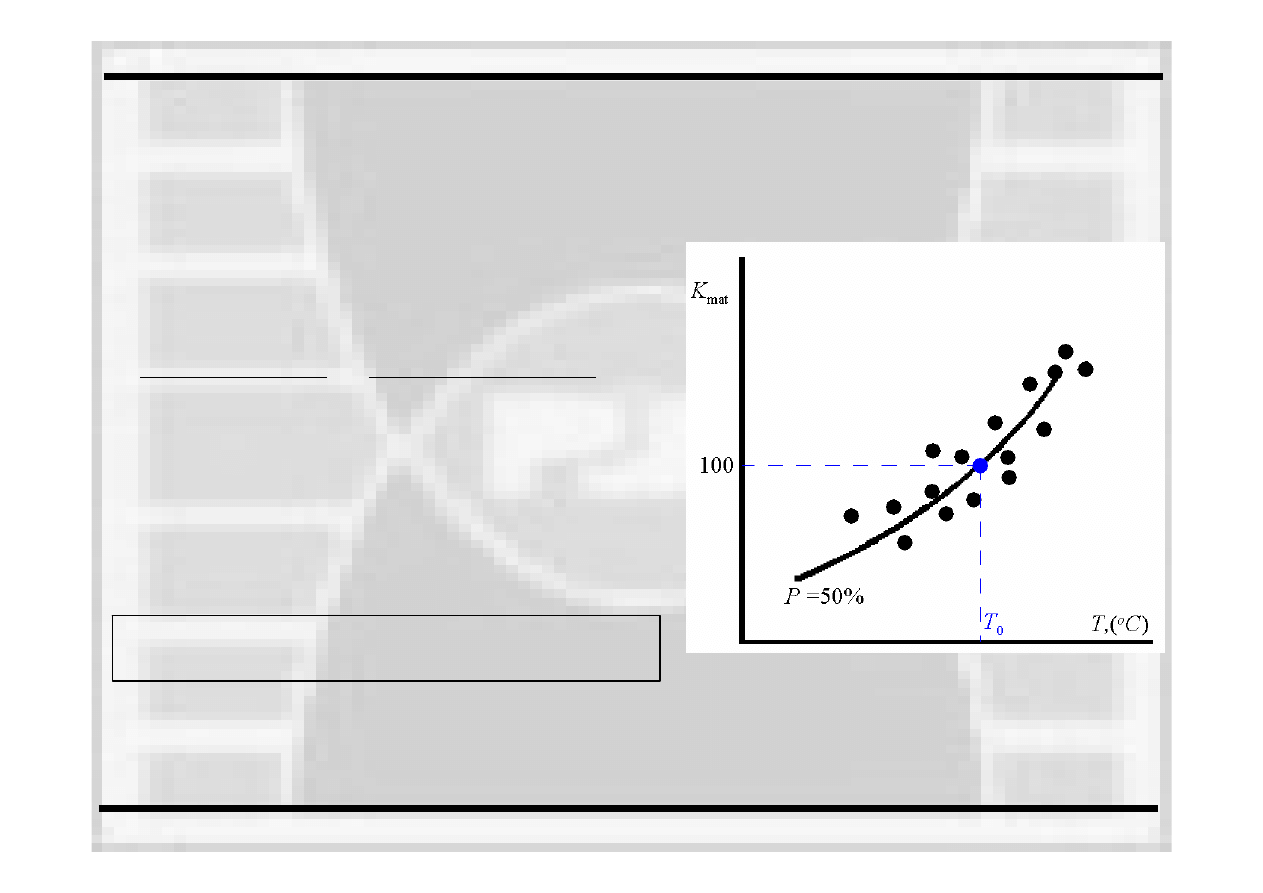
Procedury SINTAP i FITNET
•
zunifikowane podejście do oceny wytrzymałości i niezawodności
elementów konstrukcyjnych zawierających pęknięcia;
•
podstawowym parametrem w procedurze SINTAP/FITNET jest
charakterystyka odporności na pękanie materiału K
mat
;
•
w przypadku pękania kruchego dla wyznaczenia K
mat
zaleca się
wykorzystanie statystycznej procedury maksymalnego
prawdopodobieństwa (Maximum
Likelihood
Method
–
MML) lub
koncepcji krzywej wzorcowej –
„Master Curve”;
•
określając odporność
na pękanie stali ferrytycznych, SINTAP/FITNET
pozwala także wyznaczyć
charakterystyczną
temperaturę
T
0
, będącą
umowną
miarą
temperatury przejścia krucho–plastycznego,
odpowiadającą
K
mat
=100 MPa
⋅m
0,5
;
•
wykreślenie krzywej wzorcowej „Master Curve”, z której wyzna się
K
mat
dla dowolnej temperatury z obszaru krucho–plastycznego
przejścia.
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Rodzaje pękania i krzywa przejścia
krucho -
plastycznego
-200
-160
-120
-80
-40
0
40
0
50
100
150
200
K
mat
T,
O
C
T
0
100
Górne plateu:
pękanie ciągliwe
Dolne plateu:
pękanie kruche
Obszar przejściowy
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Pękanie kruche –
dolne plateu
na
krzywej przejścia krucho -
plastycznego
0
0.05
0.1
0.15
0.2
0.25
0
2
4
6
T= -180
O
C
P
(kN)
u, (mm)
K
JC
= 49.92 MPa(m)
1/2
Na krzywej siła –
przemieszczenie
ekstensometru
obserwuje się
niemal liniowy
przebieg, element konstrukcyjny pęka krucho,
przełom z widocznymi obszarami pękania
transkrystalicznego. Materiał
charakteryzuje
się
niską
odpornością
na pękanie.
Charakterystyka taka widoczna jest dla
zniszczenia w temperaturach bliskich temp.
ciekłego azotu, tj. -196
°C.
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Pękanie kruche –
dolne plateu
na
krzywej przejścia krucho -
plastycznego
Wzrost temperatury o około 50% nie zmienia
przedstawionej poprzednio charakterystyki.
Na krzywej siła –
przemieszczenie
ekstensometru
obserwuje się
również
prawie
liniowy przebieg, element konstrukcyjny pęka
krucho, przełom z widocznymi obszarami
pękania transkrystalicznego. Odporność
na
pękanie nieznacznie wzrasta.
0
0.1
0.2
0.3
0
2
4
6
8
T= -100
O
C
P
(kN)
u, (mm)
K
JC
= 62.02 MPa(m)
1/2
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Pękanie kruche –
dolne plateu
na
krzywej przejścia krucho -
plastycznego
Nieznacznemu wzrostowi temp., towarzyszy wzrost
odporności na pękanie w bardzo niewielkim stopniu. Na
krzywej siła –
przemieszczenie ekstensometru
obserwuje
się
również
prawie liniowy przebieg, ale w końcowym
etapie krzywa ta się
już
zakrzywia, możliwe że przy
wierzchołku pęknięcia pojawiła się
minimalna strefa
plastyczna, określana mianem SYZ, STRENGTH YIELD
ZONE –
strefa zniszczenia plastycznego. Przełom wciąż
jest kruchy. Jest to charakterystyka na granicy pękania
kruchego i krucho –
plastycznego, bądź
dolny zakres
pękania krucho-plastycznego.
0
0.1
0.2
0.3
0
2
4
6
8
T= -80
O
C
P
(kN)
u, (mm)
K
JC
= 67,16 MPa(m)
1/2
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Pękanie kruche –
obszar przejściowy na
krzywej przejścia krucho -
plastycznego
Nieznacznemu wzrostowi temp., towarzyszy wzrost
odporności na pękanie o około 100%, Na krzywej siła –
przemieszczenie ekstensometru
obserwuje się
przebieg
liniowy, z wyraźnym zakrzywieniem po przekroczeniu
punktu odpowiadającego wyznaczaniu KIC. W okolicach
wierzchołka występuje strefa zniszczenia plastycznego -
SYZ, STRENGTH YIELD ZONE. Przełom elementu jest
kruchy z wyraźnymi mostkami plastycznymi. Można
wnioskować że materiał
może pękać
w sposób skokowy.
Jest to charakterystyczne dla środka obszaru
przejściowego.
0
0.2
0.4
0.6
0
2
4
6
8
T= -50
O
C
P
(kN)
u, (mm)
K
JC
= 115,61 MPa(m)
1/2
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Pękanie kruche –
obszar przejściowy na
krzywej przejścia krucho -
plastycznego
Nieznacznemu wzrostowi temp., towarzyszy wzrost
odporności na pękanie o około 100%, Na krzywej siła –
przemieszczenie ekstensometru
obserwuje się
przebieg
liniowy, z wyraźnym zakrzywieniem po przekroczeniu
punktu odpowiadającego wyznaczaniu K
IC
. W okolicach
wierzchołka występuje strefa zniszczenia plastycznego -
SYZ, STRENGTH YIELD ZONE. Przełom elementu jest
kruchy z wyraźnymi mostkami plastycznymi. Można
wnioskować że materiał
może pękać
w sposób skokowy.
Jest to charakterystyczne dla środka obszaru
przejściowego.
0
0.2
0.4
0.6
0
2
4
6
8
T= -50
O
C
P
(kN)
u, (mm)
K
JC
= 115,61 MPa(m)
1/2
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Pękanie kruche –
obszar przejściowy na
krzywej przejścia krucho -
plastycznego
Wzrostowi temp., o około 50% towarzyszy wzrost odporności na
pękanie o około 70%. Na krzywej siła –
przemieszczenie
ekstensometru
obserwuje się
przebieg liniowy, z wyraźnym
zakrzywieniem po przekroczeniu punktu odpowiadającego
wyznaczaniu K
IC
. W okolicach wierzchołka występuje strefa
zniszczenia plastycznego -
SYZ, STRENGTH YIELD ZONE.
Przełom elementu jest kruchy z wyraźnymi mostkami
plastycznymi. Można wnioskować że materiał
może pękać
w
sposób skokowy. Powstałą
strukturę
przełomu po procesie
pękania można określać
mianem „plastra miodu”
–
obszary
pękania kruchego wyraźnie oddzielone są
obszarami pękania
plastycznego. Jest to charakterystyczne dla górnego zakresu
obszaru przejściowego.
0
0.4
0.8
1.2
0
2
4
6
8
10
T= -20
O
C
P
(kN)
u, (mm)
K
JC
= 179,17 MPa(m)
1/2
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Pękanie kruche –
obszar przejściowy na
krzywej przejścia krucho -
plastycznego
Wzrostowi temp., o około 50% towarzyszy wzrost odporności na
pękanie o około 70%. Na krzywej siła –
przemieszczenie
ekstensometru
obserwuje się
przebieg liniowy, z wyraźnym
zakrzywieniem po przekroczeniu punktu odpowiadającego
wyznaczaniu KIC. W okolicach wierzchołka występuje strefa
zniszczenia plastycznego -
SYZ, STRENGTH YIELD ZONE.
Przełom elementu jest kruchy z wyraźnymi mostkami
plastycznymi. Można wnioskować że materiał
może pękać
w
sposób skokowy. Powstałą
strukturę
przełomu po procesie
pękania można określać
mianem „plastra miodu”
–
obszary
pękania kruchego wyraźnie oddzielone są
obszarami pękania
plastycznego. Jest to charakterystyczne dla górnego zakresu
obszaru przejściowego.
0
0.4
0.8
1.2
0
2
4
6
8
10
T= -20
O
C
P
(kN)
u, (mm)
K
JC
= 179,17 MPa(m)
1/2
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Pękanie kruche –
górne plateu
na
krzywej przejścia krucho -
plastycznego
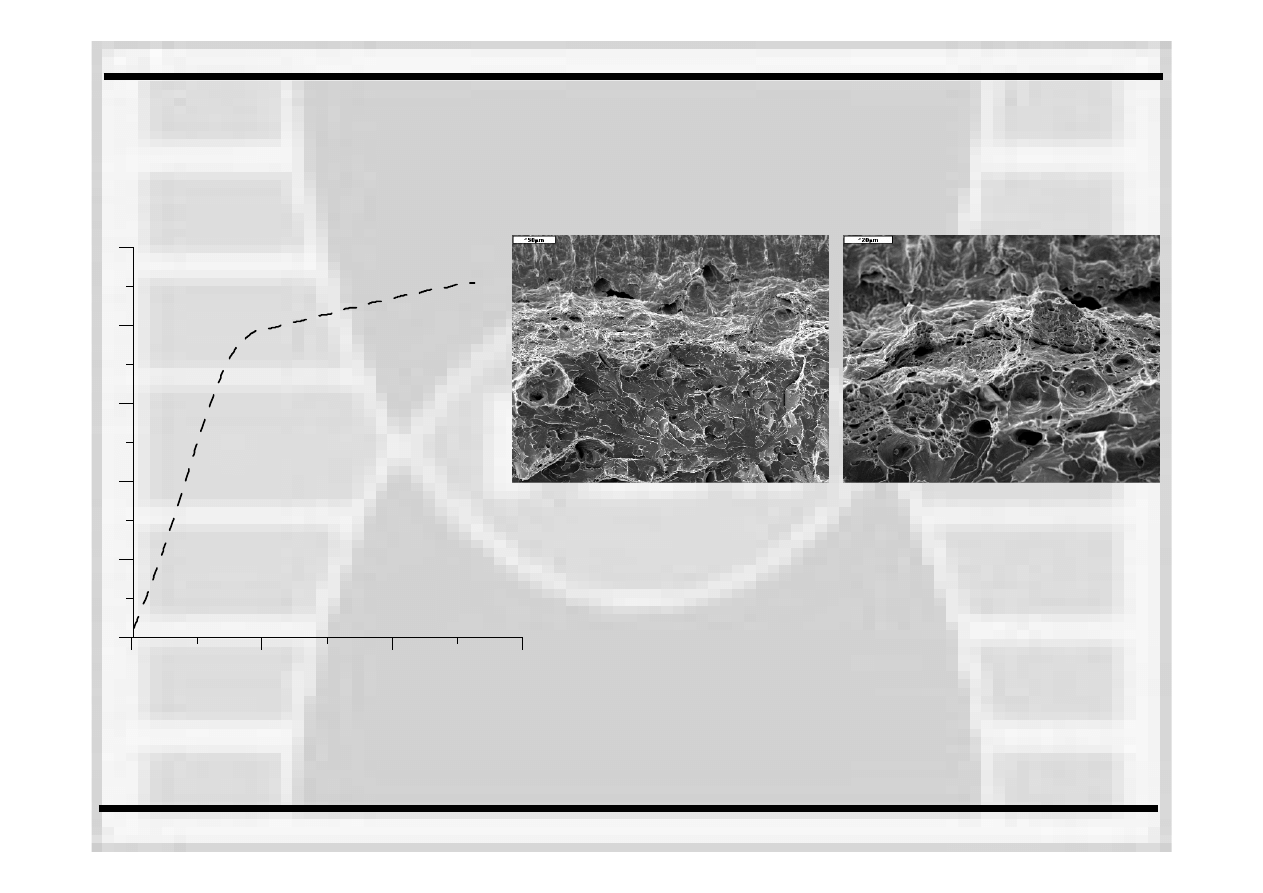
Z reguły jest to zakres dodatnich temperatur. Duża
odporność
na pękanie, Należy stosować
sprężysto-plastyczną
mechanikę
pękania, z
koncepcją
całki J, uzyskiwane są
duże przyrosty
pęknięcia. Przełom elementu konstrukcyjnego ma
charakter ciągliwy. Widoczne są
rozległe obszary
odkształceń
plastycznych, liczne mostki
plastyczne, w większej liczbie występujące w
okolicach wtrąceń
i wad materiału.
0
0.4
0.8
1.2
1.6
0
4
8
12
P
(kN)
Δ
u
ekst.
(mm)
K
JC
= 189,1 MPa(m)
1/2
+ 20
°C
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Procedury FITNET –
metoda MML -
stosowalność
•
zwykle dla materiałów krucho pękających, lub krucho-
plastycznie o ile posiadają
kruchy przełom;
•
przede wszystkim stale ferrytyczne, można je stosować
do
innego typu stali o kruchym przełomie;
•
dla danych w dowolnej liczbie; jeżeli liczba próbek jest
większa od 9 stosuje się
dwa etapy; jeżeli liczba próbek
jest mniejsza bądź
równa 9 stosuje się
trzy etapy analizy;
•
dla danych badanych w tej samej bądź
różnej
temperaturze;
•
dla danych o różnej grubości i długości pęknięcia;
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w tej samej temperaturze
•
cenzurowanie wyników badań;
•
analiza Maximum
Likelihood
Method
–
MML:
-
dwa etapy w przypadku zbioru próbek > 9,
-
trzy etapy w przypadku zbioru próbek
≤
9;
•
koncepcja krzywej wzorcowej (wykreślenie krzywej
wzorcowej Master Curve
oraz określenie temperatury
charakterystycznej T
0
, odpowiadającej odporności na
pękanie równej K
c
=100 MPa
⋅m
0.5
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w tej samej temperaturze
•
Przedstawienie charakterystyk
odporności na pękanie w
jednostkach WIN:
)
1
/(
2
ν
δ
−
=
E
mR
K
C
e
JC
•
Dopasowanie odporności na
pękanie do próbki o
grubości 25 mm:
(
)
ych
ferrytyczn
stali
dla
),
m
MPa
(
20
25
/
)
(
min
25
.
0
min
min
25
=
−
+
=
K
B
K
K
K
K
B
)
1
/(
2
ν
−
=
E
J
K
IC
JC
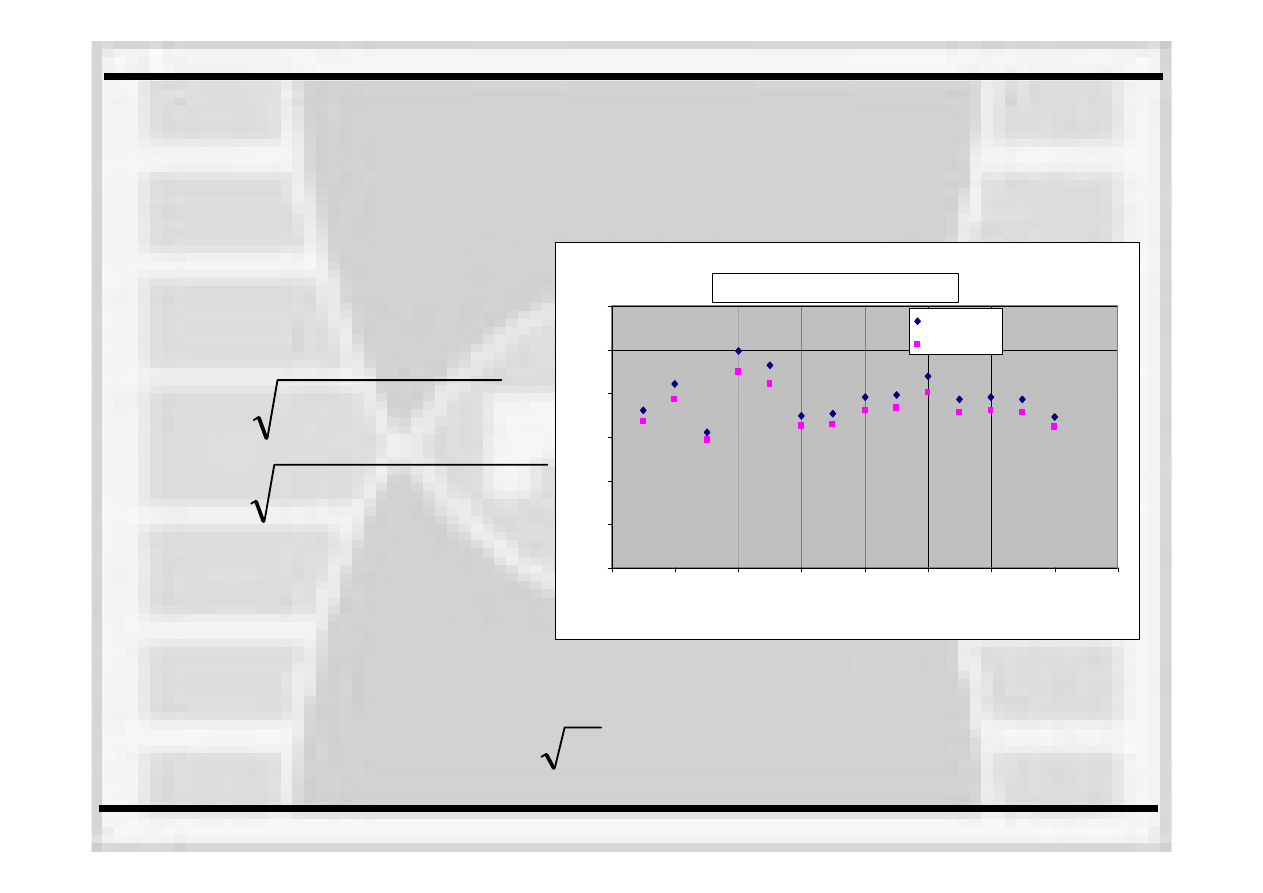
WYKRES I: Populacja danych doświadczalnych Kc oraz Kc(B=25mm)
0
10
20
30
40
50
60
0
2
4
6
8
10
12
14
16
numer próbki
Kc
, Kc
(B
=
25
m
m
)
[M
P
a*
m
^
0,5
]
Kc
Kc(B=25mm)
25
.
0
25
)
25
/
)(
20
(
20
B
K
K
K
B
i
−
+
=
=
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w tej samej temperaturze
•
Wstępna analiza uzyskanych rezultatów
–
wyznaczenie zależności
prawdopodobieństwo zniszczenia w
funkcji odporności na pękanie
25
.
0
1
1
4
min
min
0
)
(
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
=
∑
∑
=
=
n
i
i
n
i
JCi
K
K
K
K
δ
)
(
91
.
0
min
0
min
K
K
K
K
K
med
mat
−
+
=
=
20
;
4
exp
1
}
{
min
min
0
min
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
−
=
K
k
K
K
K
K
K
P
k
mat
mat
•
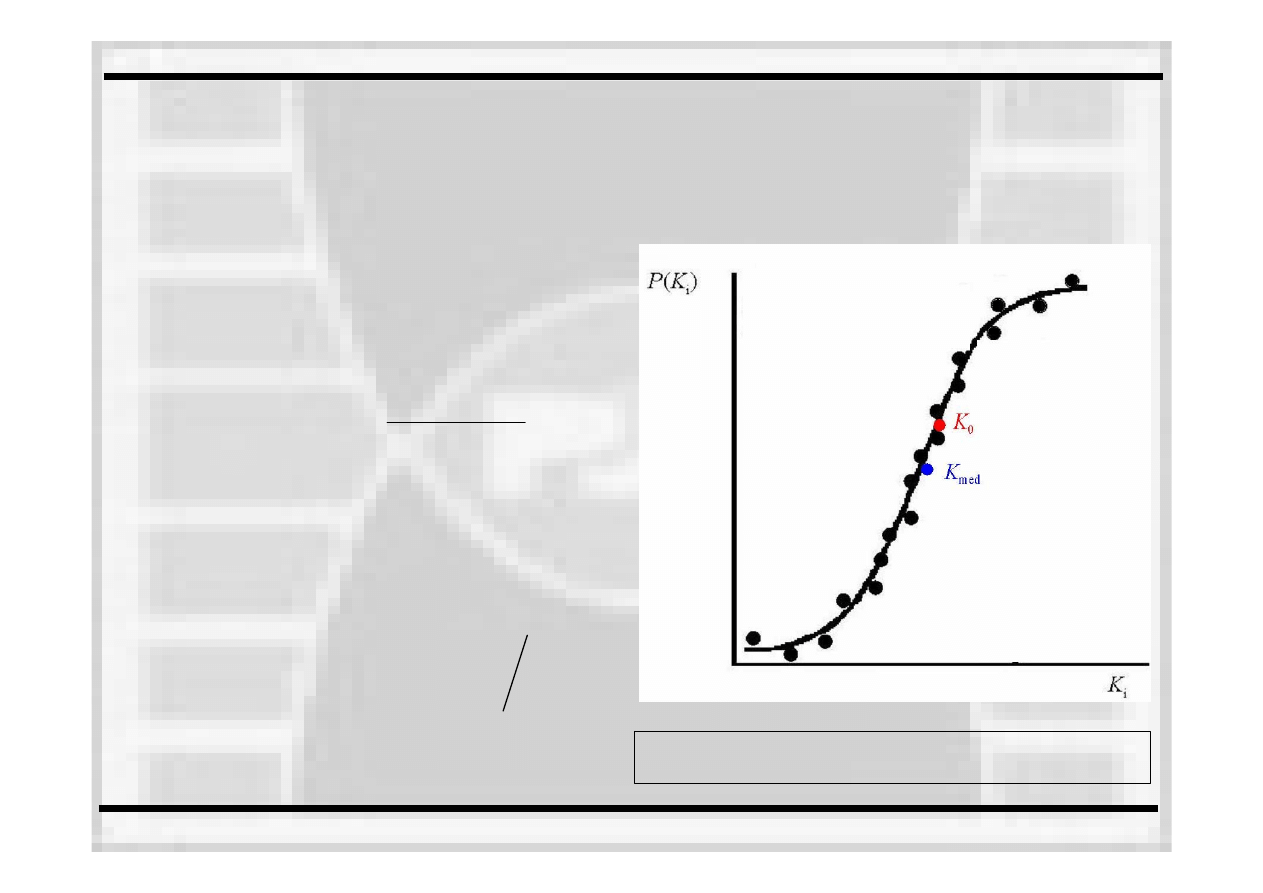
Wstępna analiza uzyskanych rezultatów
–
wyznaczenie odporności na pękanie
jako mediany ze zbioru danych
delta Kroneckera
-
δ
ma wartość
1 dla danej próbki
jeżeli przełom był
kruchy i ma 0 jeżeli przełom miał
inny charakter niż
kruchy
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w tej samej temperaturze
•
Etap 1. Standardowe oszacowanie
wartości medialnej
25
.
0
1
1
4
min
min
)
1
(
0
)
(
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
=
∑
∑
=
=
n
i
i
n
i
JCi
etap
K
K
K
K
δ
)
(
91
.
0
min
)
1
(
0
min
K
K
K
K
K
etap
med
mat
−
+
=
=
1
;
:
dla
)
(
=
<
i
JC
cen
JC
JC
i
i
K
K
K
δ
0
;
:
dla
)
(
)
(
=
=
≥
i
cen
JC
JC
cen
JC
JC
K
K
K
K
i
i
δ
(
)
5
.
0
)
(
30
/
e
o
cen
JC
R
Eb
K
=
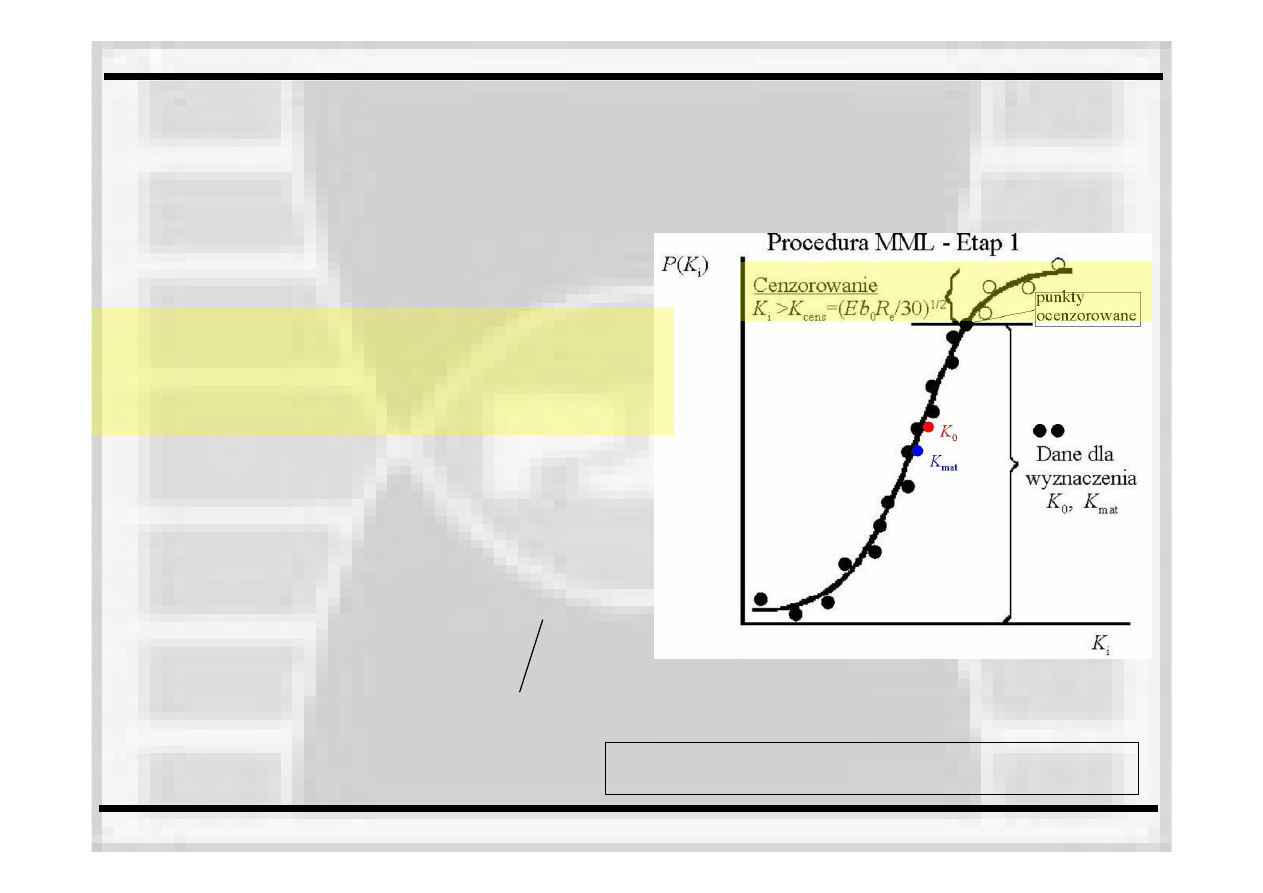
Wstępna analiza uzyskanych rezultatów –
wyznaczenie odporności na pękanie jako
mediany ze zbioru danych
tutaj delta Kronecker’a
ma już
nową
wartość,
zmienioną
na etapie cenzurowania danych w
pierwszym etapie
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w tej samej temperaturze
•
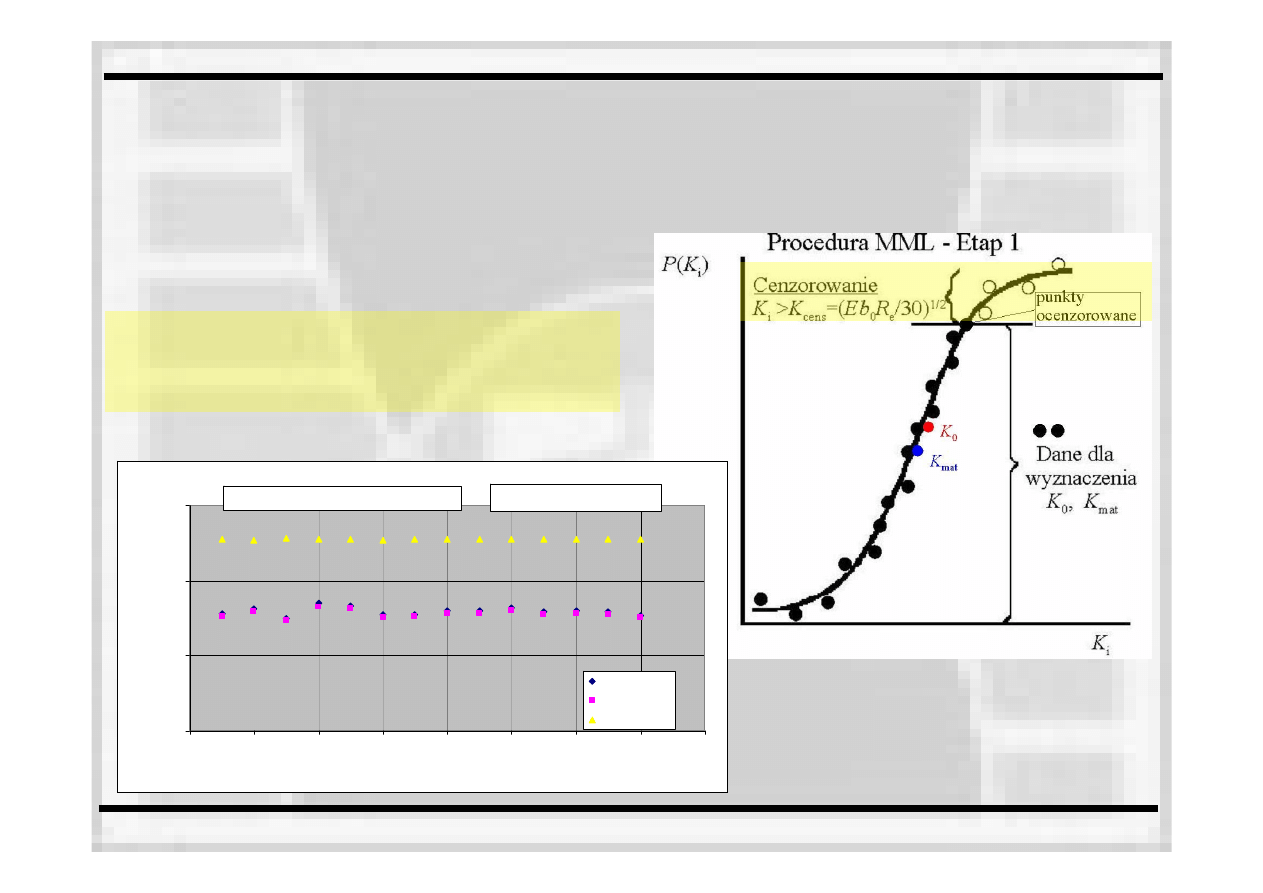
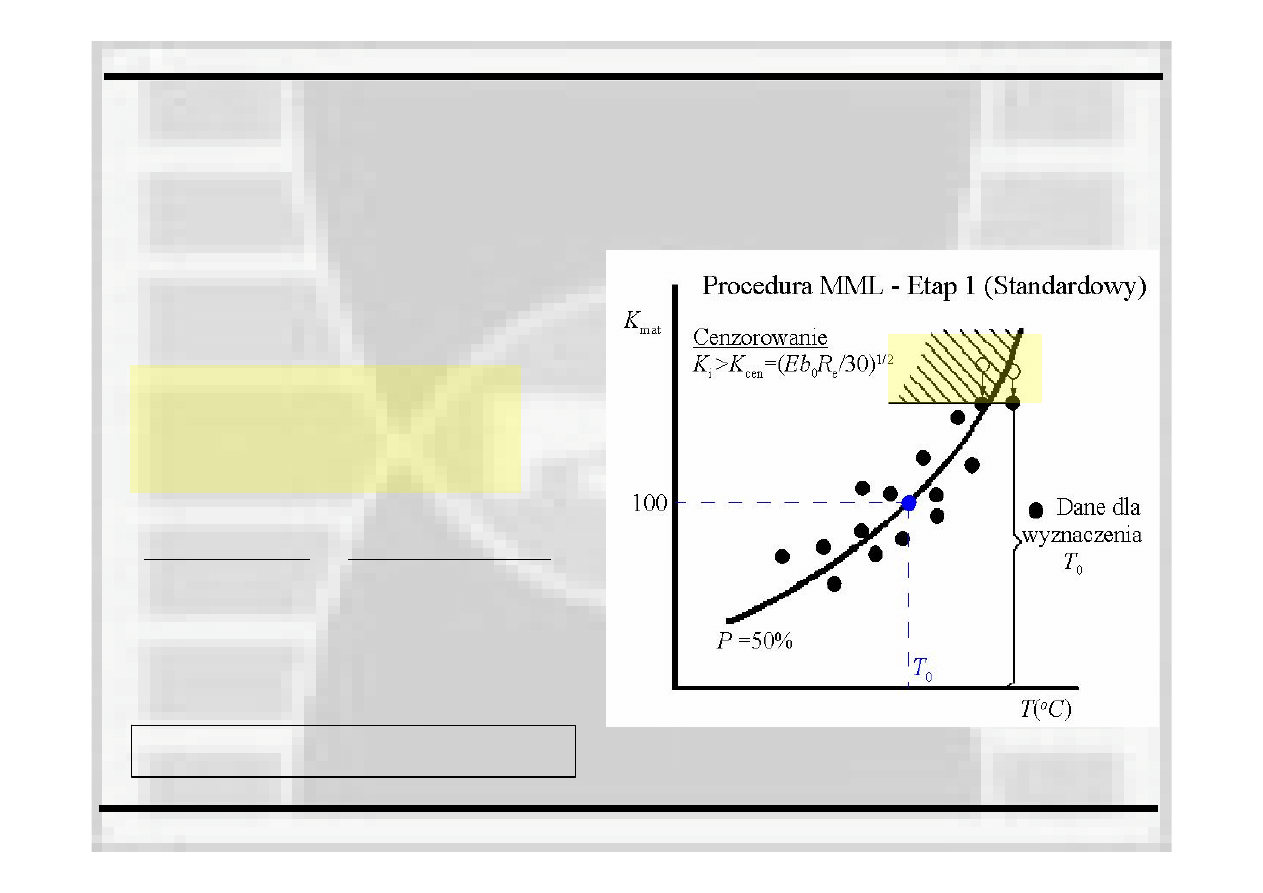
Etap 1. Cenzurowanie danych –
przykład
graficznej interpretacji wyników
1
;
:
dla
)
(
=
<
i
JC
cen
JC
JC
i
i
K
K
K
δ
0
;
:
dla
)
(
)
(
=
=
≥
i
cen
JC
JC
cen
JC
JC
K
K
K
K
i
i
δ
(
)
5
.
0
)
(
30
/
e
o
cen
JC
R
Eb
K
=
WYKRES II: Populacja danych doświadczalnych Kc, Kc(B=25mm) oraz K_cen
1
10
100
1000
0
2
4
6
8
10
12
14
16
numer próbki
Kc,
Kc(
B
=
25m
m)
[
M
P
a
*m
^
0
,5
]
Kc
Kc(B=25mm)
K_cen
25
.
0
25
)
25
/
)(
20
(
20
B
K
K
K
B
i
−
+
=
=
(
)
5
.
0
)
(
30
/
e
o
cen
JC
R
Eb
K
=
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w tej samej temperaturze
•
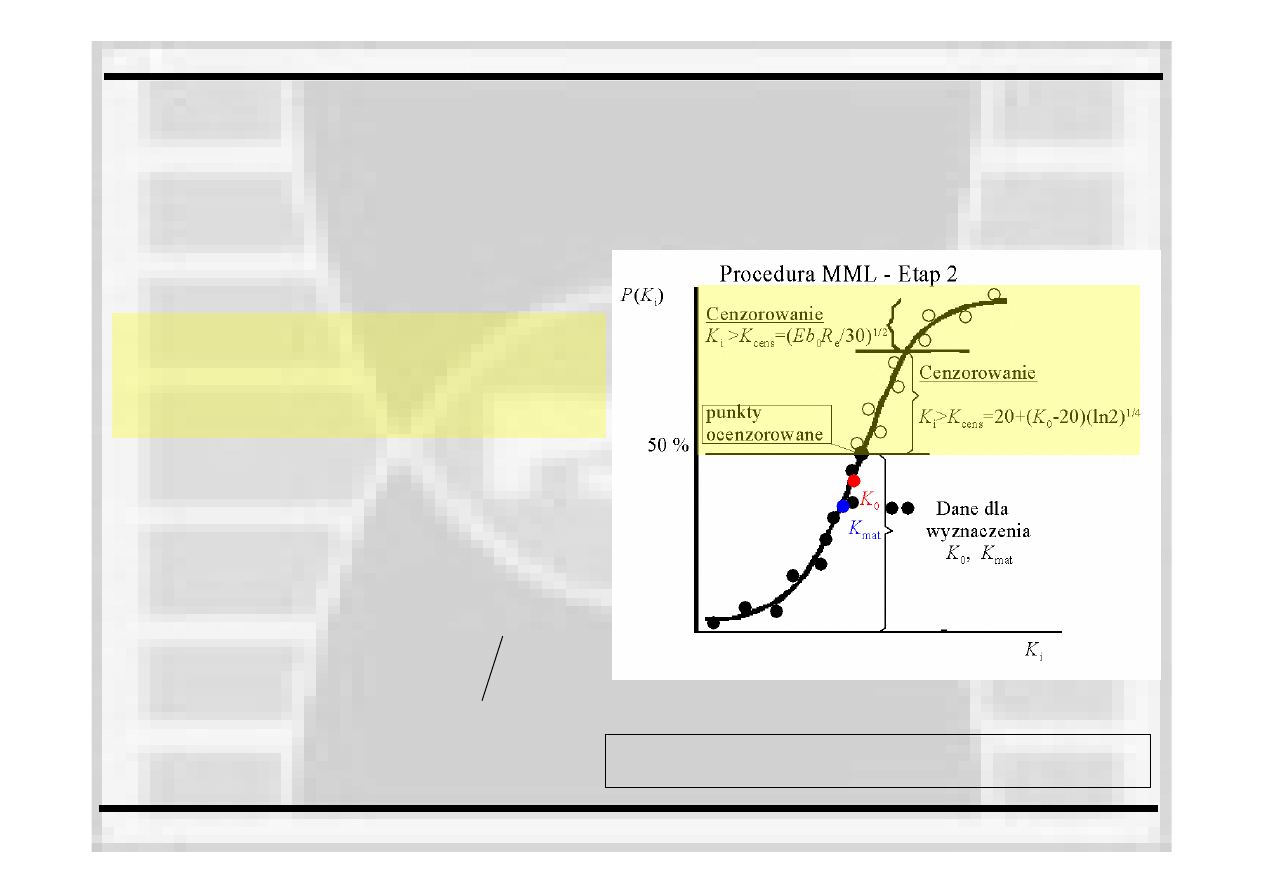
Etap 2. Oszacowanie wartości medialnej
z dolnej części rozkładu P(K
i
)
(
)
min
)
2
(
0
min
91
.
0
K
K
K
K
K
etap
mat
med
−
+
=
=
25
.
0
1
1
4
min
min
)
2
(
0
)
(
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−
+
=
∑
∑
=
=
n
i
i
n
i
JCi
etap
K
K
K
K
δ
1
;
:
dla
=
<
i
JC
CEN
JC
i
i
K
K
K
δ
25
.
0
min
0
min
)
2
(ln
)
(
⋅
−
+
=
K
K
K
K
CENZ
0
;
:
dla
i
=
=
≥
i
CEN
JC
CEN
JC
K
K
K
K
i
δ
Wstępna analiza uzyskanych rezultatów –
wyznaczenie odporności na pękanie jako
mediany ze zbioru danych
tutaj delta Kronecker’a
ma już
nową
wartość,
zmienioną
na etapie cenzurowania danych w drugim
etapie
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w tej samej temperaturze
•
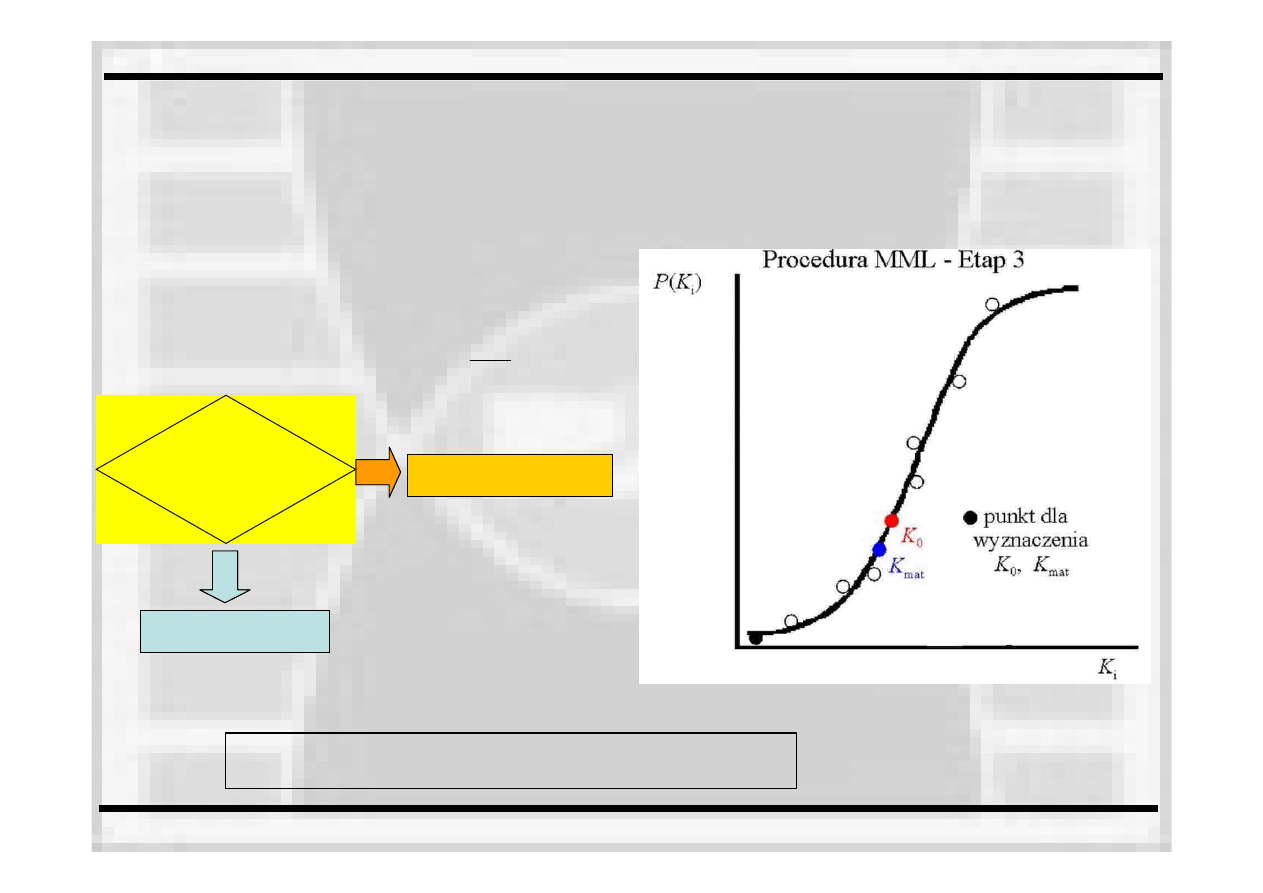
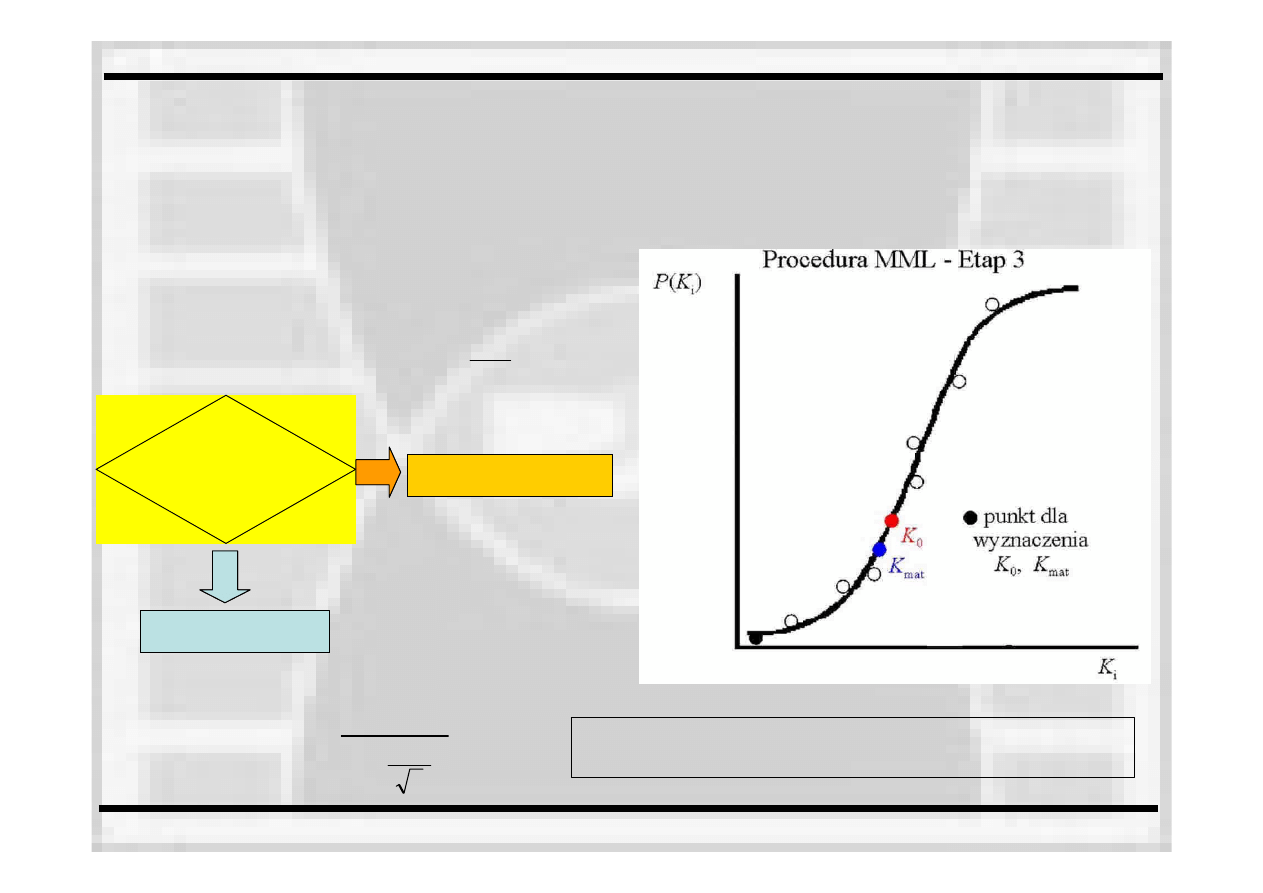
Etap 3. Oszacowanie K
mat
z minimalnej
wartości P(K
i
) dla liczby próbek n>9
(
)
25
.
0
min
(min)
min
(min)
0
2
ln
⎟
⎠
⎞
⎜
⎝
⎛
−
+
=
n
K
K
K
K
JC
K
0(min)
<0.9K
o(etap_2)
tak
nie
K
0(etap3)
=K
o(min)
K
0(etap3)
=K
o(etap2)
K
0(min)
<0.9K
o(etap_2)
tak
nie
K
0(etap3)
=K
o(min)
K
0(etap3)
=K
o(etap2)
Obliczenie odporności na pękanie ze
wzoru:
(
)
min
)
2
(
0
min
91
.
0
K
K
K
K
K
etap
mat
med
−
+
=
=
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w tej samej temperaturze
•
Etap 3. Oszacowanie K
mat
z minimalnej
wartości P(K
i
) dla liczby próbek n
≤9
(
)
25
.
0
min
(min)
min
(min)
0
2
ln
⎟
⎠
⎞
⎜
⎝
⎛
−
+
=
n
K
K
K
K
JC
K
0(min)
<0.9K
o(etap_2)
tak
nie
K
0(etap3)
=K
o(min)
K
0(etap3)
=K
o(etap2)
K
0(min)
<0.9K
o(etap_2)
tak
nie
K
0(etap3)
=K
o(min)
K
0(etap3)
=K
o(etap2)
Obliczenie odporności na pękanie ze
wzoru:
r
K
K
etap
25
.
0
1
20
20
(min)
0
)
3
(
0
+
−
+
=
(
)
min
)
3
(
0
min
91
.
0
K
K
K
K
K
etap
mat
med
−
+
=
=
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w tej samej temperaturze
•
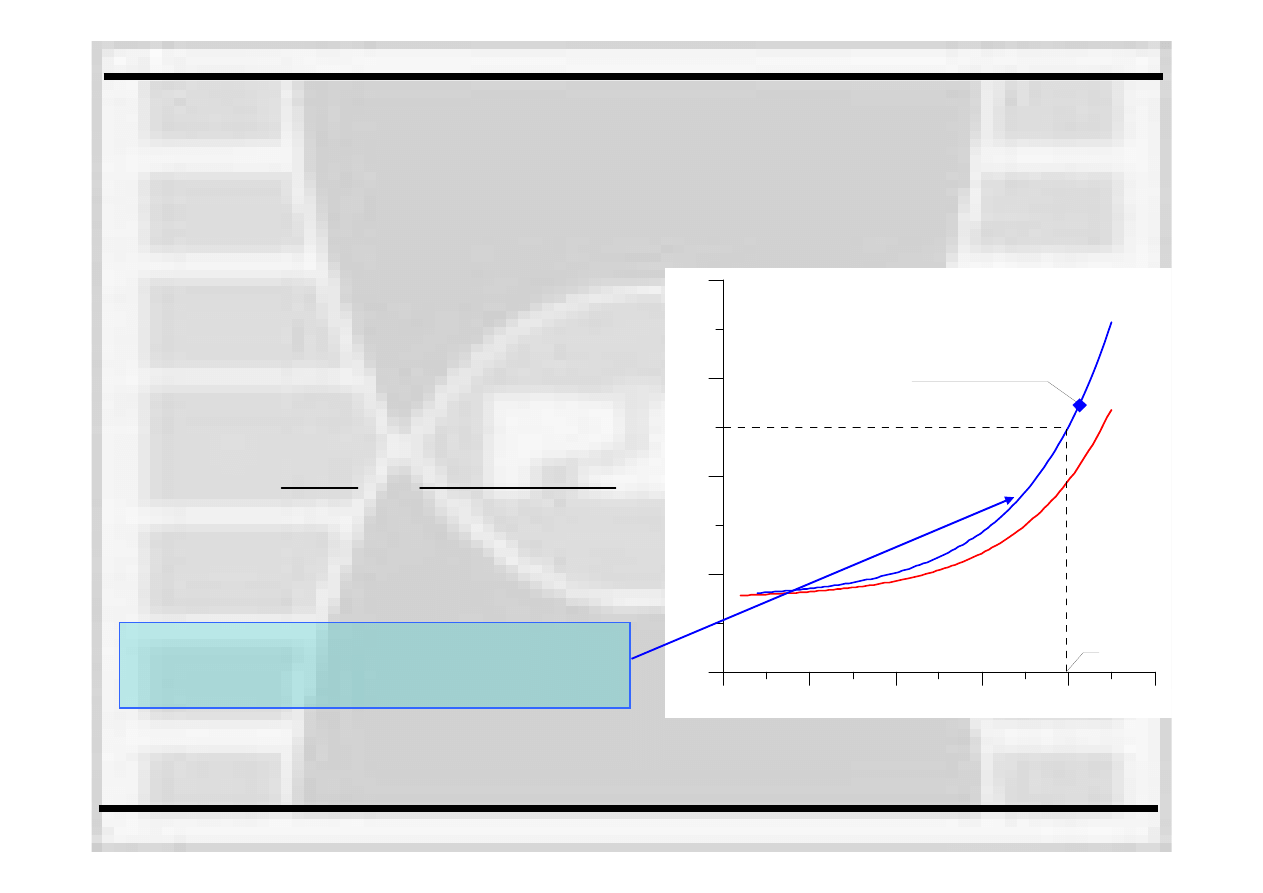
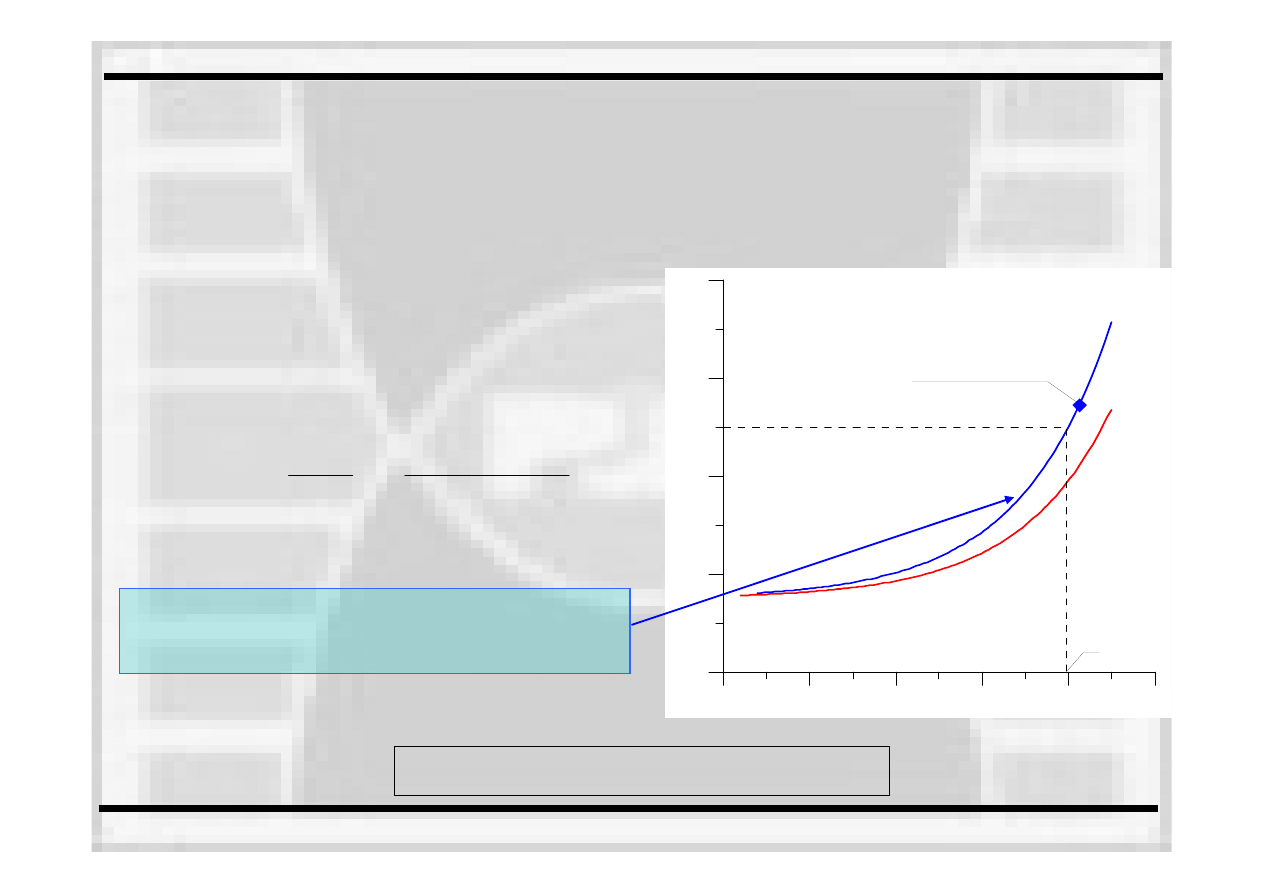
Wykreślenie krzywej wzorcowej –
zależności pomiędzy temperaturą
badania a odpornością
na pękanie –
jest
to krzywa „MASTER CURVE”
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
=
70
30
ln
019
.
0
1
)
_
(
0
i
etap
mat
bad
K
T
T
-200
-150
-100
-50
0
50
0
40
80
120
160
K
mat
K
mat
(T
bad.
, P
f
=0.5)
T,
O
C
T
0
K
mat
(P
f
=0.2)
100
(
)
[
]
0
019
.
0
exp
70
30
T
T
K
mat
−
⋅
+
=
Wyznaczenie temperatury T
0
odpowiadającej
odporności na pękanie równej 100MPa
⋅m
0.5
Wykreślenie krzywej MASTER CURVE,
korzystając z równania:
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w tej samej temperaturze
•
Wykreślenie krzywej wzorcowej –
zależności pomiędzy temperaturą
badania a odpornością
na pękanie –
jest
to krzywa „MASTER CURVE”
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
=
70
30
ln
019
.
0
1
)
_
(
0
i
etap
mat
bad
K
T
T
-200
-150
-100
-50
0
50
0
40
80
120
160
K
mat
K
mat
(T
bad.
, P
f
=0.5)
T,
O
C
T
0
K
mat
(P
f
=0.2)
100
(
)
[
]
0
019
.
0
exp
70
30
T
T
K
mat
−
⋅
+
=
Wyznaczenie temperatury T
0
odpowiadającej
odporności na pękanie równej 100MPa
⋅m
0.5
Wykreślenie krzywej MASTER CURVE,
korzystając z równania:
Można wyznaczyć
MASTER CURVE z różnym
prawdopodobieństwem zniszczenia P
f
stosując
równanie:
[
]
25
.
0
min
)
_
(
0
min
)
1
ln(
)
(
f
i
etap
mat
P
K
K
K
K
−
−
−
+
=
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w tej samej temperaturze
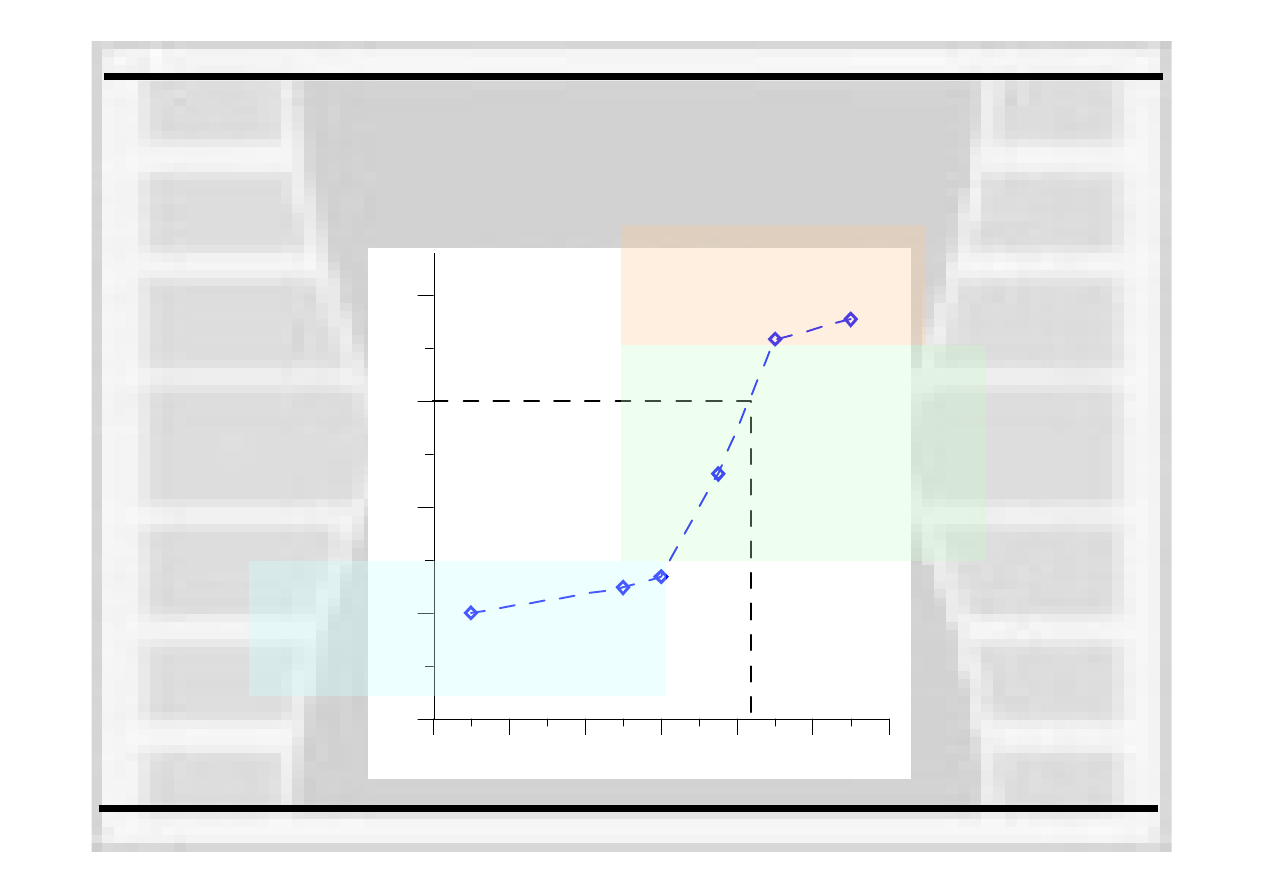
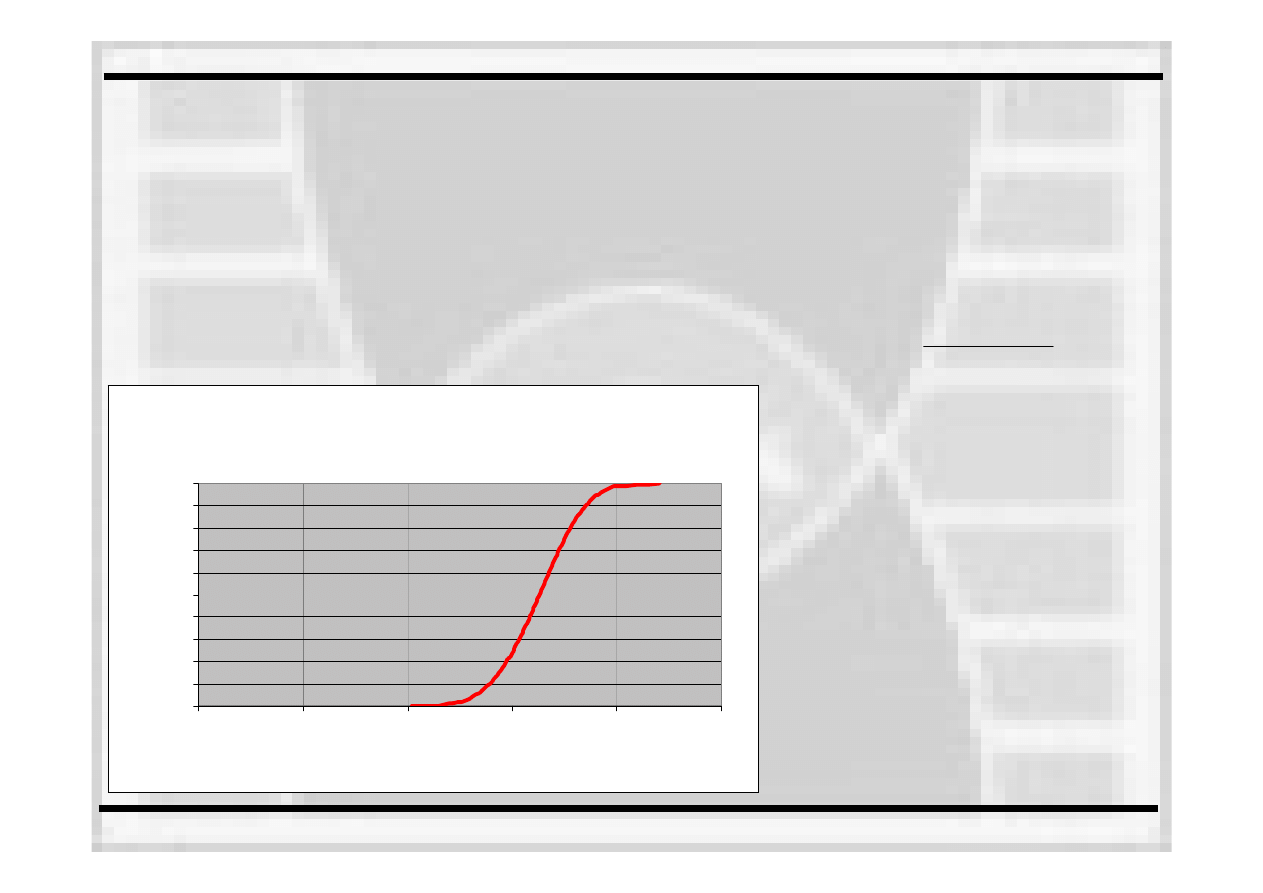
Zmiana odporności na pękanie Kmat wraz z założonym
prawdopodobieństwem zniszczenia Pf
0
10
20
30
40
50
60
70
80
90
100
0,00
10,00
20,00
30,00
40,00
50,00
Kmat [MPa*m^0,5]
Pf
[
%
]
•
Wykreślenie zmiany odporności na pękanie K
mat
w funkcji
prawdopodobieństwa zniszczenia P
f
4
0
20
20
exp
1
}
{
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
−
=
m
mat
mat
K
K
K
P
Można to wykonać
po każdym
etapie analizy, gdzie oznaczono
odporność
na pękanie K
mat
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w tej samej temperaturze
•
Wpływ temperatury badania i prawdopodobieństwa zniszczenia P
f
na krzywą
MASTER CURVE
-80
-40
0
40
20
40
60
80
100
120
T,
o
C
K
, M
P
a
(m
)
1/
2
dla T
0
(-20; -30; -41
o
C)
dla T
0
(-52; -70
o
C)
-40
0
40
0
40
80
120
160
T,
o
C
K
, M
P
a(
m)
1/
2
P
f
= 0.5
P
f
=0.9
P
f
=0.1
Wykresy krzywych wzorcowych dla P
f
=0.5
uzyskane z analizy MML dla różnych zbiorów
próbek
–
wpływ temp. na MASTER CURVE
Wykresy „Master Curve”
uzyskane dla próbek
badanych w temperaturze –30
O
C –
wpływ
prawdopodobieństwa zniszczenia na MASTER
CURVE
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w różnej temperaturze
•
cenzurowanie wyników badań,
•
wyznaczenie metodą
iteracyjną
temperatury
charakterystycznej T0, odpowiadającej odporności na
pękanie równej K
Jc
=100 MPa
⋅m
0.5
(I etap analizy MML);
•
sporządzenie wykresów „Master Curve”
dla
prawdopodobieństwa zniszczenia równego 63%
oraz dla prawdopodobieństwa zniszczenia na poziomie 50%
(II etap analizy MML)
[
]
[
]
(
)
[
]
[
]
{
}
0
)
(
019
,
0
exp
77
11
)
(
019
,
0
exp
20
)
(
019
,
0
exp
77
11
)
(
019
,
0
exp
1
5
0
0
4
1
0
0
=
−
+
−
−
−
−
+
−
∑
∑
=
=
n
i
i
i
i
JC
n
i
i
i
i
T
T
T
T
K
T
T
T
T
δ
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w tej samej temperaturze
•
Przedstawienie charakterystyk odporności na pękanie w jednostkach
WIN:
)
1
/(
2
ν
δ
−
=
E
mR
K
C
e
JC
•
Dopasowanie odporności na pękanie do próbki o grubości 25 mm:
(
)
ych
ferrytyczn
stali
dla
),
m
MPa
(
20
25
/
)
(
min
25
.
0
min
min
25
=
−
+
=
K
B
K
K
K
K
B
)
1
/(
2
ν
−
=
E
J
K
IC
JC
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w różnej temperaturze
•
Wyznaczenie temperatury T
0
odpowiadającej odporności na pękanie
równej 100 MPa
⋅m
0.5
[
]
)
(
019
,
0
exp
77
31
)
_
(
0
0
i
etap
m
T
T
K
−
+
=
)
(
91
.
0
min
0
min
K
K
K
K
m
mat
−
+
=
[
]
[
]
(
)
[
]
[
]
{
}
0
)
(
019
,
0
exp
77
11
)
(
019
,
0
exp
20
)
(
019
,
0
exp
77
11
)
(
019
,
0
exp
1
5
0
0
4
1
0
0
=
−
+
−
−
−
−
+
−
∑
∑
=
=
n
i
i
i
i
JC
n
i
i
i
i
T
T
T
T
K
T
T
T
T
δ
•
Wstępna analiza danych:
•
Wyznaczenie odporności na pękanie
jako mediany ze zbioru danych:
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w różnej temperaturze
•
Etap 1. Standardowa analiza uzyskanych
rezultatów. Oszacowanie medialnej
wartości temperatury T
0
Cenzurowanie danych
1
;
:
dla
)
(
=
<
i
JC
cen
JC
JC
i
i
K
K
K
δ
0
;
:
dla
)
(
)
(
=
=
≥
i
cen
JC
JC
cen
JC
JC
K
K
K
K
i
i
δ
(
)
5
.
0
)
(
30
/
e
o
cen
JC
R
Eb
K
=
Ponowne wyznaczenie temp. T
0
[
]
[
]
(
)
[
]
[
]
{
}
0
)
(
019
,
0
exp
77
11
)
(
019
,
0
exp
20
)
(
019
,
0
exp
77
11
)
(
019
,
0
exp
1
5
0
0
4
1
0
0
=
−
+
−
−
−
−
+
−
∑
∑
=
=
n
i
i
i
i
JC
n
i
i
i
i
T
T
T
T
K
T
T
T
T
δ
Wyznaczenie odporności na pękanie jako
mediany ze zbioru analizowanych danych
)
(
91
.
0
min
0
min
K
K
K
K
m
mat
−
+
=
[
]
)
(
019
,
0
exp
77
31
)
1
(
0
0
etap
m
T
T
K
−
+
=
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w różnej temperaturze
[
]
[
]
(
)
[
]
[
]
{
}
0
)
(
019
,
0
exp
77
11
)
(
019
,
0
exp
20
)
(
019
,
0
exp
77
11
)
(
019
,
0
exp
1
5
0
0
4
1
0
0
=
−
+
−
−
−
−
+
−
∑
∑
=
=
n
i
i
i
i
JC
n
i
i
i
i
T
T
T
T
K
T
T
T
T
δ
•
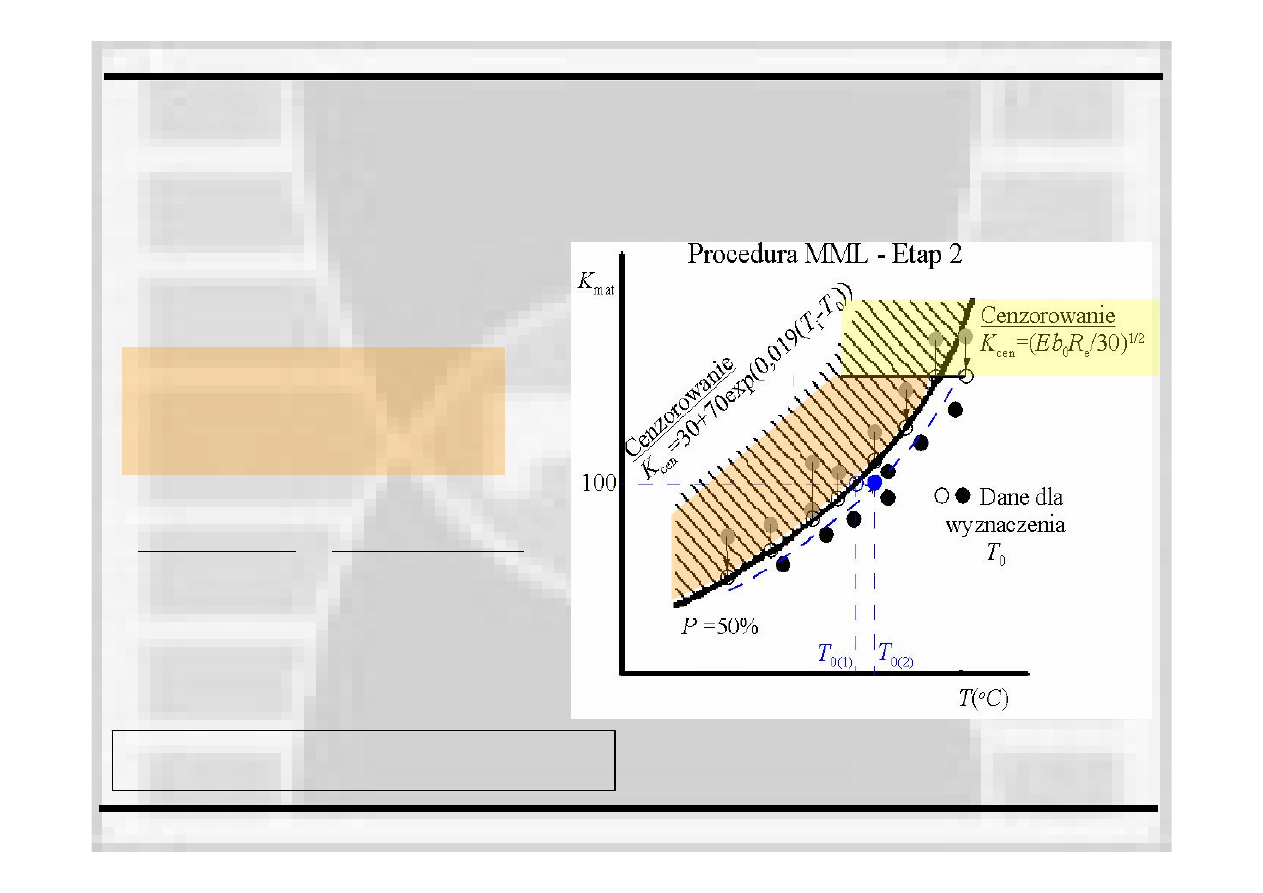
Etap 2. Oszacowanie temperatury T
0
z dolnego zakresu danych
Cenzurowanie danych
Ponowne wyznaczenie temp. T
0
Wyznaczenie odporności na pękanie jako
mediany ze zbioru analizowanych danych
[
]
0
);
(
)
(
:
)
(
)
(
dla
)
(
019
.
0
exp
70
30
)
(
0
0
=
=
>
−
+
=
i
i
CENZ
i
i
i
CENZ
i
i
i
CENZ
T
K
T
K
T
K
T
K
T
T
T
K
δ
[
]
)
(
019
,
0
exp
77
31
)
2
(
0
0
etap
m
T
T
K
−
+
=
)
(
91
.
0
min
0
min
K
K
K
K
m
mat
−
+
=
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w różnej temperaturze
(
)
019
.
0
77
11
2
ln
ln
max
4
/
1
min
)
3
(
0
(max)
0
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
−
=
=
n
K
K
T
T
T
i
i
etap
•
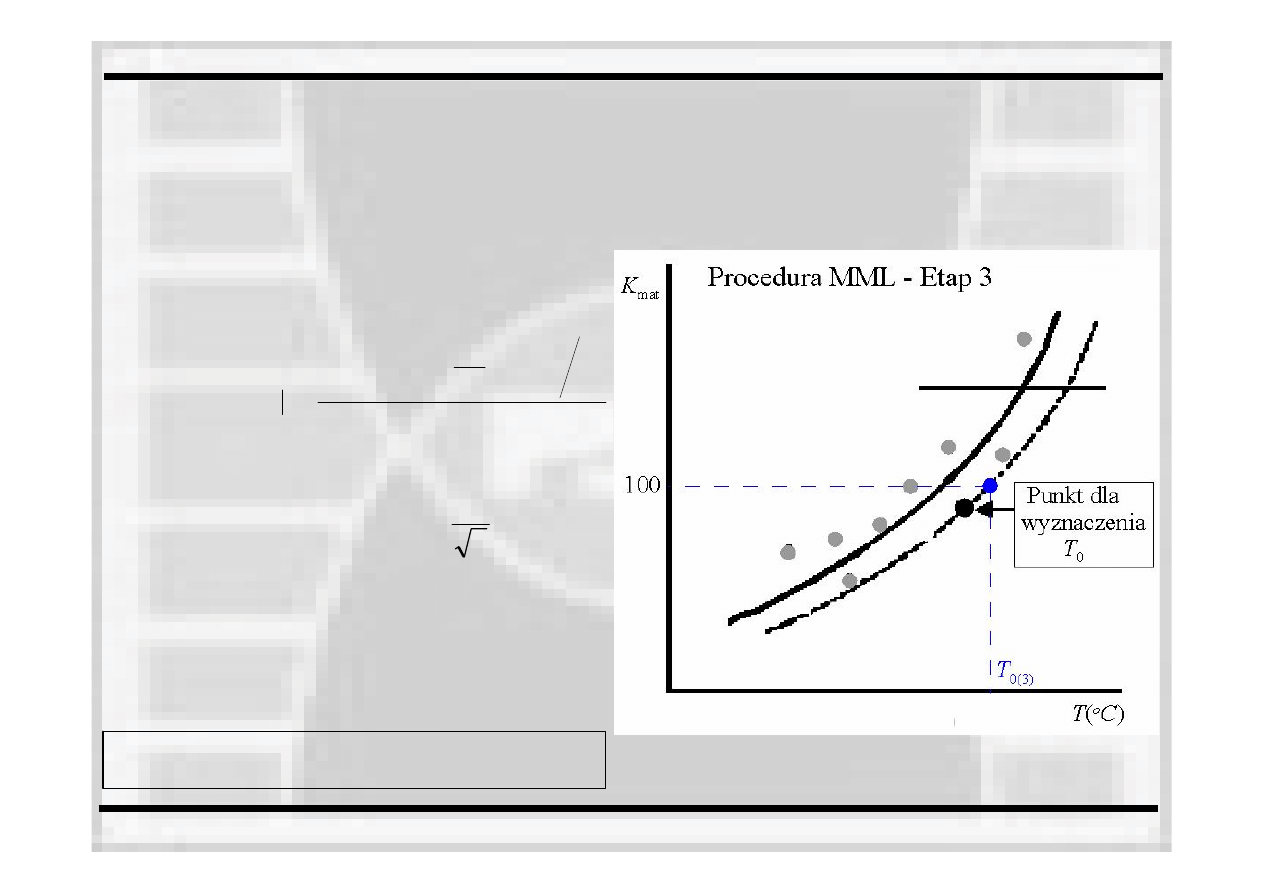
Etap 3. Analiza ostateczna zbioru danych
Wyznaczenie temp. T
0
dla zbioru danych
w liczbie n>9
Wyznaczenie temp. T0 dla zbioru danych w
liczbie n>9
Wyznaczenie odporności na pękanie jako
mediany ze zbioru analizowanych danych
r
T
T
etap
14
(max)
0
)
3
(
0
+
=
[
]
)
(
019
,
0
exp
77
31
)
3
(
0
0
etap
m
T
T
K
−
+
=
)
(
91
.
0
min
0
min
K
K
K
K
m
mat
−
+
=
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w tej samej temperaturze
Zmiana odporności na pękanie Kmat wraz z założonym
prawdopodobieństwem zniszczenia Pf
0
10
20
30
40
50
60
70
80
90
100
0,00
10,00
20,00
30,00
40,00
50,00
Kmat [MPa*m^0,5]
Pf
[
%
]
•
Wykreślenie zmiany odporności na pękanie K
mat
w funkcji
prawdopodobieństwa zniszczenia P
f
4
0
20
20
exp
1
}
{
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
−
=
m
mat
mat
K
K
K
P
Można to wykonać
po każdym
etapie analizy, gdzie oznaczono
odporność
na pękanie K
mat
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML dla zbioru próbek
badanych w różnej temperaturze
•
Wpływ temperatury i grubości na odporność
na pękanie
Wpływ grubości i temp. badania na
odporność
na pękanie. Im mniejsza
grubość
tym większa odporność
na
pękanie. Im niższa temp. Tym
niższa wartość
odporności na
pękanie.
Wpływ grubości i temp. badania na
odporność
na pękanie dla B=25mm.
Im mniejsza grubość
tym większa
odporność
na pękanie. Im niższa
temp. Tym niższa wartość
odporności na pękanie.
Wpływ grubości i temp. badania na
średnią
wartość
odporność
na
pękanie dla B=25mm. Im mniejsza
grubość
tym większa odporność
na
pękanie. Im niższa temp. Tym
niższa wartość
odporności na
pękanie.
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Metoda MML –
wpływ liczby
wyników na temperaturę
T
0
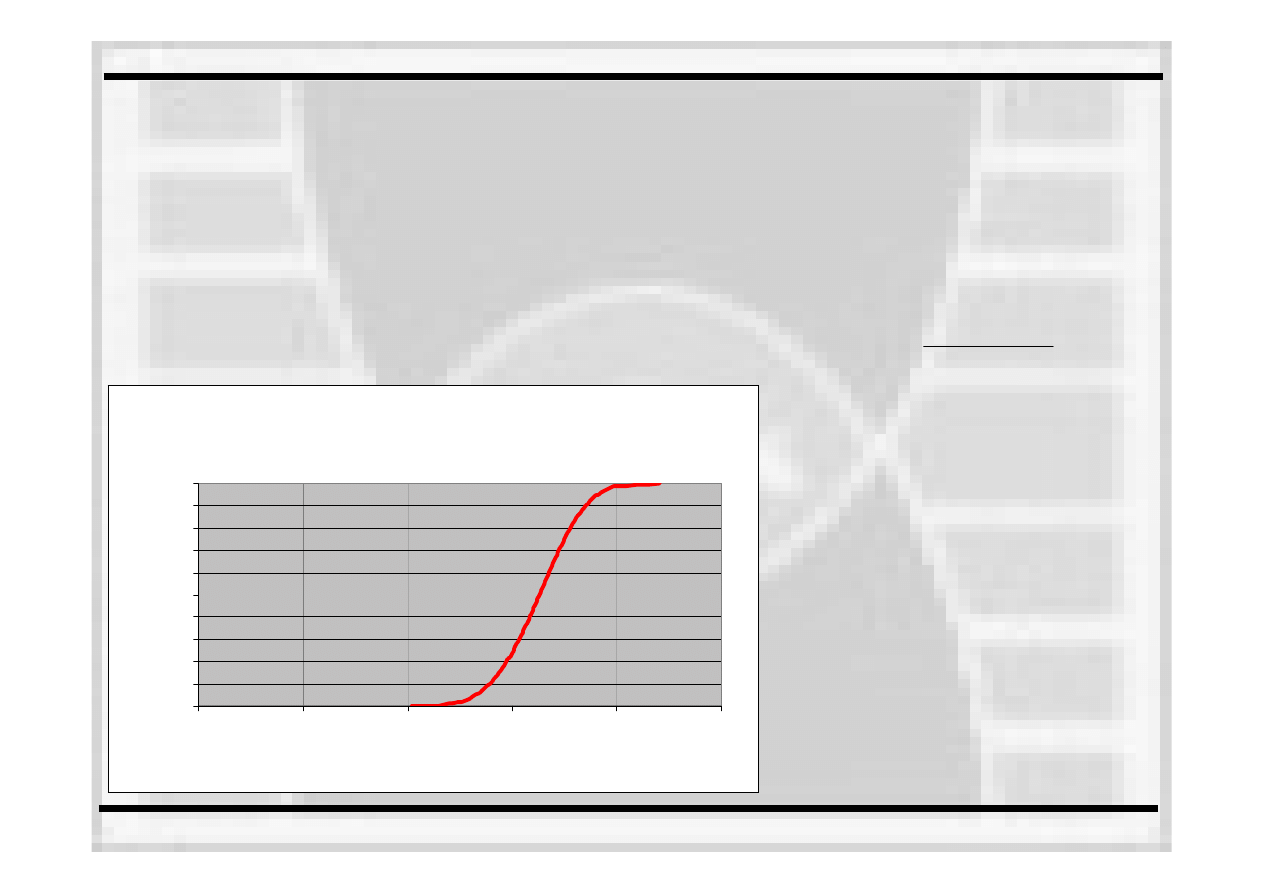
Porównanie wartości temperatur odniesienia T
0
,
wyznaczonych dla każdej z grup próbek
badanych w tej samej temperaturze z wartością
, wyznaczoną
dla prób wykonanych
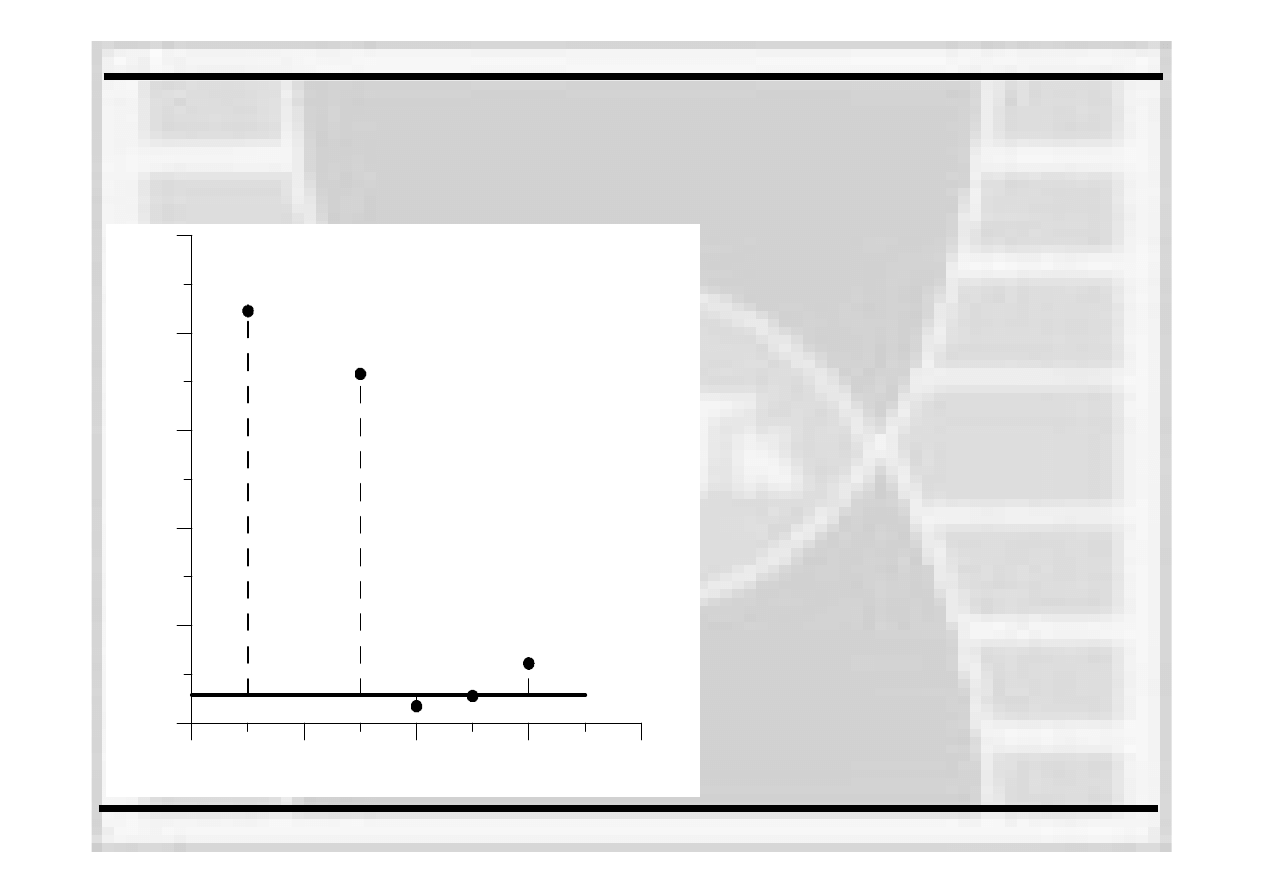
w różnych temperaturach.
Najdokładniejszy wynik uzyskuje się
dla zbioru
próbek badanych w różnych temperaturach.
Rozważa się
bowiem całe spectrum badań. Im
mniej próbek badanych w tej samej temp. (np.
temp. -70
°C oraz -50°C w obu przypadkach było
po odpowiednio 4 i 6 próbek) tym mniej
dokładny wynik wyznaczania T
0
zgodnie z
dla danych badanych w tej samej
temp., z wynikiem dla różnych temp. badania.
Większa liczba próbek poprawia wynik (temp. -
°C, -30°C, -20°C –
odpowiednio 12, 16 i 10
próbek). Im większa liczba próbek, przede
wszystkim większa od 9, tym wynik
wyznaczania temp T
0
ze zbioru próbek
badanych w tej samej temp. Jest bardziej
zbliżony do wyniku uzyskanego dla zbioru
próbek badanych w różnej temp.
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Wykonanie ćwiczenia -
sporządzenie
sprawozdania –
część
I
•
Analiza uzyskanego zbioru danych –
wykres zbiorczy
•
Oszacowanie wartości średniej, mediany, wartości
minimalnej i maksymalnej ze zbioru zadanych danych
doświadczlanych
•
Zastosowanie metody MML dla danych badanych w tej
samej temperaturze: przedstawienie wyników obliczeń
na każdym etapie obliczeń
–
wyznaczenie odporności
na pękanie K
mat
jako mediany ze zbioru, obliczenie
temperatury T
0
wraz z wykreśleniem krzywej MASTER
CURVE dla prawdopodobieństwa zniszczenia P
f
={0.2;
0.5; 0.7; 0.95}; wykreślenie po każdym etapie
krzywych prawdopodobieństwo zniszczenia w funkcji
odporności na pękanie;
www.tu.kielce.pl/~mgraba
Copyright
©2008 Marcin Graba –
Politechnika Świętokrzyska w Kielcach
WYZNACZANIE ODPORNOŚCI NA PĘKANIE MATERIAŁÓW KRUCHYCH –
METODA MML
Wykonanie ćwiczenia -
sporządzenie
sprawozdania -
część
II
•
Porównanie rezultatów uzyskanych na każdym etapie
procedury MML –
zestawienie wyników odporności na
pękanie K
mat
, temp. T
0
, oraz krzywych
prawdopodobieństwo zniszczenia w funkcji
odporności na pękanie, a także krzywych MASTER
CURVE;
wnioski;
•
Porównanie rezultatów analizy MML (podanych
powyżej) z wynikami analizy wstępnej, w której liczono
średnią, medianę, wartości minimalną
i maksymalną
ze zbioru danych;
wnioski;
•
Wnioski końcowe przeprowadzonej analizy danych;